Coordination of opposite-polarity microtubule motors

Abstract

Many cargoes move bidirectionally, frequently reversing course between plus- and minus-end microtubule travel. For such cargoes, the extent and importance of interactions between the opposite-polarity motors is unknown. In this paper we test whether opposite-polarity motors on lipid droplets in Drosophila embryos are coordinated and avoid interfering with each other's activity, or whether they engage in a tug of war. To this end we impaired the minus-end transport machinery using dynein and dynactin mutations, and then investigated whether plus-end motion was improved or disrupted. We observe a surprisingly severe impairment of plus-end motion due to these alterations of minus-end motor activity. These observations are consistent with a coordination hypothesis, but cannot be easily explained with a tug of war model. Our measurements indicate that dynactin plays a crucial role in the coordination of plus- and minus-end–directed motors. Specifically, we propose that dynactin enables dynein to participate efficiently in bidirectional transport, increasing its ability to stay “on” during minus-end motion and keeping it “off” during plus-end motion.

Introduction

Microtubule-based motors are essential for many intracellular transport processes, and there have been tremendous advances in clarifying how they produce force. However, this knowledge is not sufficient to understand how they perform their function in the cell; it is as important to elucidate how the activity of these motors is employed in a controlled manner. In principle, such regulation could operate at two levels: (a) controlling the properties of single motors, such as processivity or speed of travel; and (b) controlling how multiple motors, either of the same or different type, work together. There have been great advances in identifying receptors that link certain individual motors to specific cargoes (Tai et al., 1999; Kamal and Goldstein, 2000; Kamal et al., 2000; Schnorrer et al., 2000), and biochemical and genetic approaches have identified potential regulators of motor function (Shetty et al., 1998; Verhey et al., 1998; Bowman et al., 1999). Although the mechanisms that control individual motors are still mysterious, in vitro analysis suggests specific biochemical models (Niclas et al., 1996; Hackney and Stock, 2000) whose in vivo relevance is currently being investigated. In contrast, whether motor activity is at all regulated at the level of multiple motors is unknown, and proposed mechanisms regarding how coordination might occur have remained vague by necessity (Hancock and Howard, 1998; Welte et al., 1998).

That several motors act together on a single cargo is particularly evident in bidirectional cargo motion. For example, a subset of axonal vesicles reverses course frequently between plus- and minus-end motion (Gilbert and Sloboda, 1984; Leopold et al., 1990; Overly et al., 1996; Waterman-Storer et al., 1997). Many organelles display similar bidirectional motion along microtubules, such as mitochondria (Hollenbeck, 1996), melanosomes (Rogers et al., 1997; Wu et al., 1998), certain vesicles in the secretory and endocytic pathways (Hayden, 1988; Wacker et al., 1997; Lochner et al., 1998; Valetti et al., 1999; Murray et al., 2000), lipid droplets in Drosophila embryos (Welte et al., 1998), and in mammalian fibroblasts (Valetti et al., 1999), neurofilaments (Shah et al., 2000), RNP granules (Köhrmann et al., 1999), and viruses (Suomalainen et al., 1999; Smith et al., 2001; Suomalainen et al., 2001). Despite this constant back-and-forth motion, such cargoes can achieve polarized distributions in the cell by regulating the relative contributions of the plus- and minus-end motors (Hollenbeck, 1996; Welte et al., 1998).

Presumably, these cargoes simultaneously carry the minus-end motor cytoplasmic dynein and a kinesin-family member (Rogers et al., 1997). How do these opposite-polarity motors work together on the same cargo? There are two fundamentally different ways in which they might interact (Fig. 1): (a) they might engage in a tug of war; or (b) their activities might be coordinated. In the tug of war model, opposite-polarity motors are active at the same moment and compete with each other (Fig. 1 A). Motion results when one set of motors overwhelms the other. In the motor coordination model, minus-end motors are turned off when plus-end motors are active, and vice versa; competition is thus avoided (Fig. 1 B).

Figure 1.

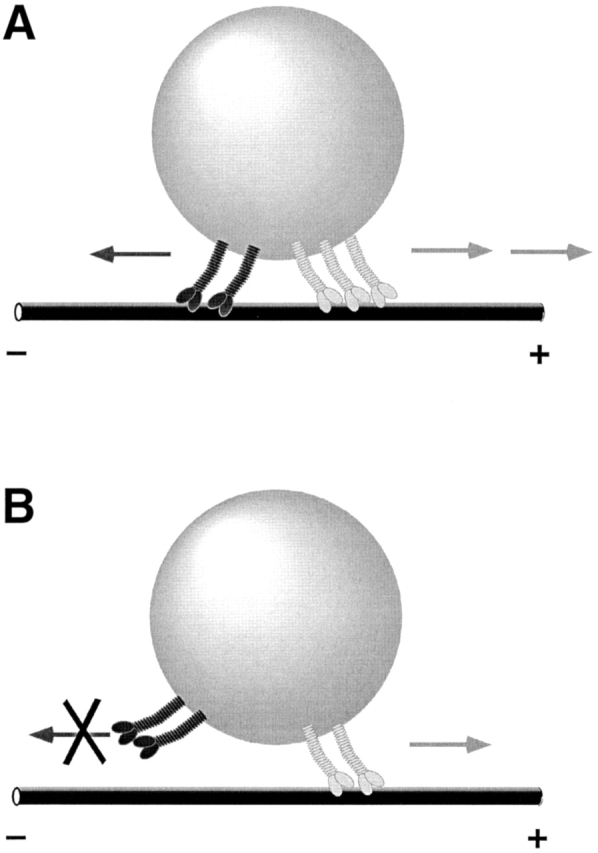
Models for how opposite-polarity motors on single cargoes might interact. (A) In the tug of war model, opposite-polarity motors are active simultaneously. Net motion results when one set of motors successfully competes against the opposing motors. (B) In the motor coordination model, competition is avoided because when plus-end motors are active, minus-end motors are turned off and vice versa. For clarity, only the cargo and the motors are depicted; hypothetical molecules that allow the motors to assemble into complexes and that mediate interactions between motors are not shown.

In principle, one can distinguish between these two scenarios by interfering with one motor and determining whether the motion in the opposite direction is affected. The two models predict different outcomes. If the motors engage in a tug of war, impairing one motor will put the opposing motor in a better competitive position and should result in improved motion in the opposite direction. Stronger impairments should result in even less ability to oppose the competing motor. In contrast, if motors are coordinated, the specific nature of motor impairment will determine the effect on the opposite motion. For example, if a mutation interferes with motor coordination, it might impair the opposing motion; mutations that do not alter coordination could alter one direction, whereas the other could remain unchanged. In the coordination model, there would be no necessary correlation between the two directions; how much motion driven by the minus-end motor is impaired need not determine whether or how strongly the opposing plus-end motion is affected.

Previous attempts to interfere with one type of motor have frequently resulted in impairment of the opposing motion. For example, in squid axoplasm, inhibition of minus-end motion via antibodies results in cessation of motion for both directions (Waterman-Storer et al., 1997), and complete inactivation of cytoplasmic dynein in mammalian fibroblasts abolishes bidirectional motion of lipid droplets (Valetti et al., 1999). Genetic analysis of axonal transport in Drosophila found impairment of long-distance transport for both directions whether plus- or minus-end motors were mutated (Martin et al., 1999). Although suggestive, these results do not prove that motors in these systems are coordinated because indirect effects on the opposing motors could not be excluded. Motors frozen in their tracks by antibodies might sterically hinder the progress of other motors (Waterman-Storer et al., 1997). Build-up of organelles in mutant axons might clog transport in both directions, preventing cargo from moving past organelle jams in the narrow confines of the axon (Martin et al., 1999).

To distinguish between the tug of war and motor coordination scenarios, we use the bidirectional transport of lipid droplets in Drosophila embryos (Welte et al., 1998; Gross et al., 2000). In this model system it is possible to genetically manipulate motors to partially inhibit their function, without causing generalized defects in cell structure or development. Further, the consequences of these manipulations can be assessed directly at the level of individual cargoes. Nanometer scale tracking allows quantitation of motion parameters, and the force powering transport can be measured using optical tweezers (Figs. 2 and 3). This stalling force varies developmentally in a quantized fashion (multiples of 1.1 pN), suggesting changes in the number of active motors, with up to five motors per individual droplet (Welte et al., 1998).

Figure 2.

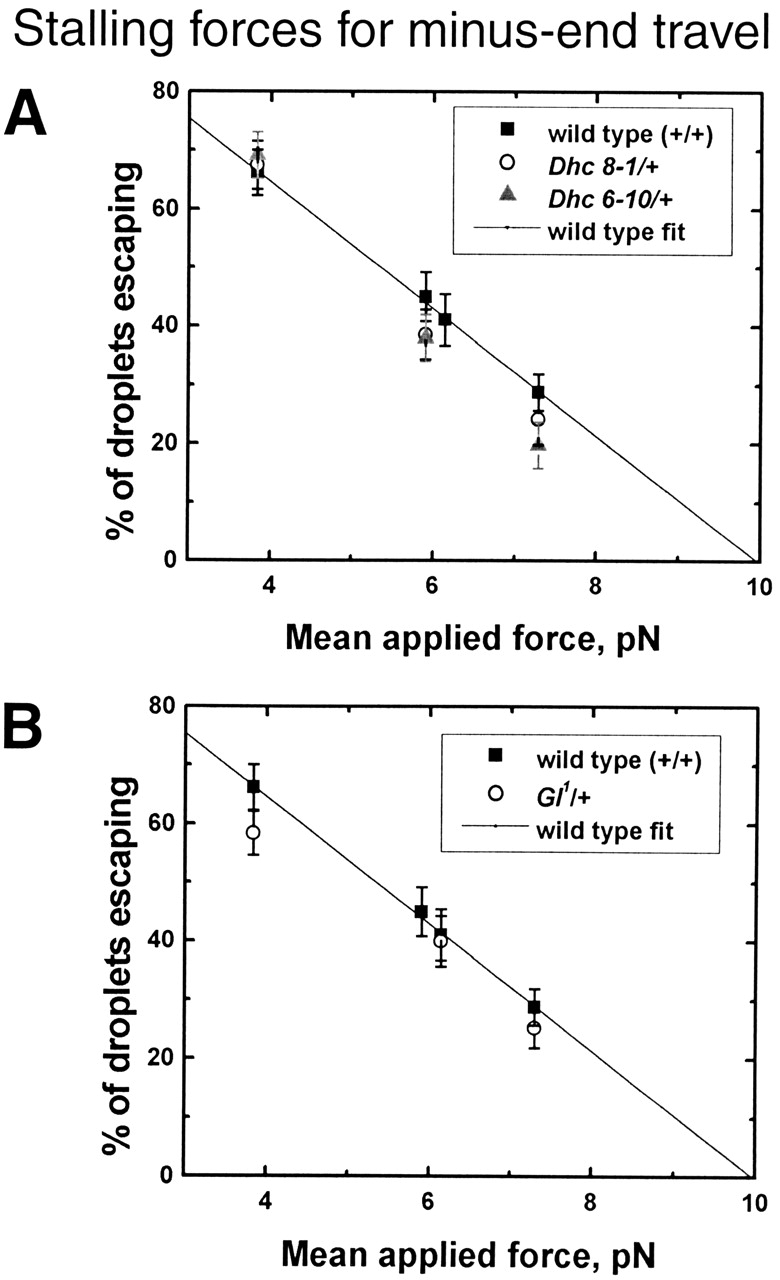
Droplet stalling forces for minus-end travel. The panels show the percentage of droplets stalled in different genetic backgrounds as a function of force applied by optical tweezers. (A) Wild- type versus Dhc64C ^6–10/+ and Dhc64C ^8–1/+; (B) Wild-type versus Gl¹/+. To avoid bias, force measurements were performed in a blind fashion, with the genotype of the embryo being measured unknown to the person performing the force measurement. Each data point is derived from measurements on six to seven embryos in phase II, with ∼30 minus-moving droplets tested per embryo. See Materials and methods for a discussion how applied force and stalling force are related.

Figure 3.

Droplet stalling forces for plus-end travel. As for Fig. 2, the panels show the percentage of droplets stalled as a function of applied force. (A) Wild-type versus Dhc64C ^6–10/Dhc64C^8–1; (B) wild-type versus Dhc64C ^6–10/+ and Dhc64C ^8–1/+; (C) wild-type versus Gl¹/+. Forces were determined as for Fig. 2, in the same embryos.

We have previously shown that cytoplasmic dynein powers minus-end–directed droplet travel (Gross et al., 2000). In this paper we investigate the interaction between opposite-polarity motors by impairing minus-end motion using either mutations in the dynein heavy chain (Dhc64C) or through a mutation (Gl ¹) that alters dynein's essential cofactor dynactin. We find that these alleles alter various aspects of plus-end motion. In particular, we show that the Gl ¹ allele of dynactin and the Dhc64C ^{8- 1} allele of dynein impair plus-end motion even more strongly than they affect minus-end motion, decreasing plus-end but not minus-end stalling forces. These results imply that the mutations impair the ability of dynein to be coordinated with the plus-end motors, artificially inducing a tug of war state that is avoided in the wild-type.

Results

Plus-end motion in embryos in which minus-end stall forces are reduced

Because complete interference with minus-end motor function might lead to severe disruption of cellular organization and secondary, nonspecific effects on plus-end motion, we sought to only partially disrupt cytoplasmic dynein. We had previously identified one genetic background that fulfills this requirement: female flies transheterozygous for two weak alleles of the gene encoding the heavy chain of cytoplasmic dynein (Dhc64C ^6–10 and Dhc64C ^8–1) lay eggs that undergo overall normal development, but in which minus-end transport of lipid droplets is disrupted (Gross et al., 2000). Relative to wild-type minus-end motion, lipid droplets move for shorter distances, with slower velocities and, most importantly, display significantly reduced minus-end stalling forces (Gross et al., 2000). Although the molecular lesions in these alleles have not yet been identified, they encode at least partially functional heavy chains because homozygous animals develop up to pupal stages, whereas strong loss-of-function alleles result in embryonic death more than 5 d earlier (Gepner et al., 1996).

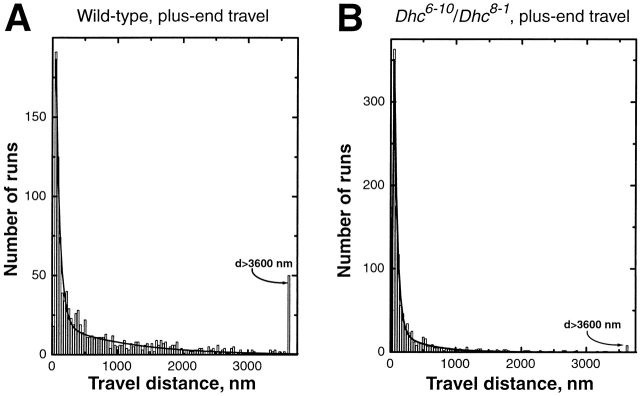
If plus- and minus-end–directed motors on the droplets typically engage in a tug of war, the impaired ability of dynein to produce force should put less resistance on motion in the plus-end direction and thus result in higher plus-end stalling forces. Depending on how such a reduction in force correlates with other motion parameters, this may also result in improvement of other aspects of plus-end motion, e.g., in longer travel distances and higher travel velocities. However, we found that these predictions of the tug of war model were not fulfilled. Most importantly, the force required to stop plus-end-moving droplets in this genetic background was decreased rather than increased (Fig. 3 A). In addition, droplet velocity was reduced relative to the wild-type (see below, and Fig. 4 B); the mean plus-end travel distance was reduced by a factor of 2.7 (Table I), and the frequency of pauses was increased (Table II, second column). These results strongly suggest that in this genetic background dynein is interfering with plus-end motion in a way that it does not in the wild-type.

Figure 4.

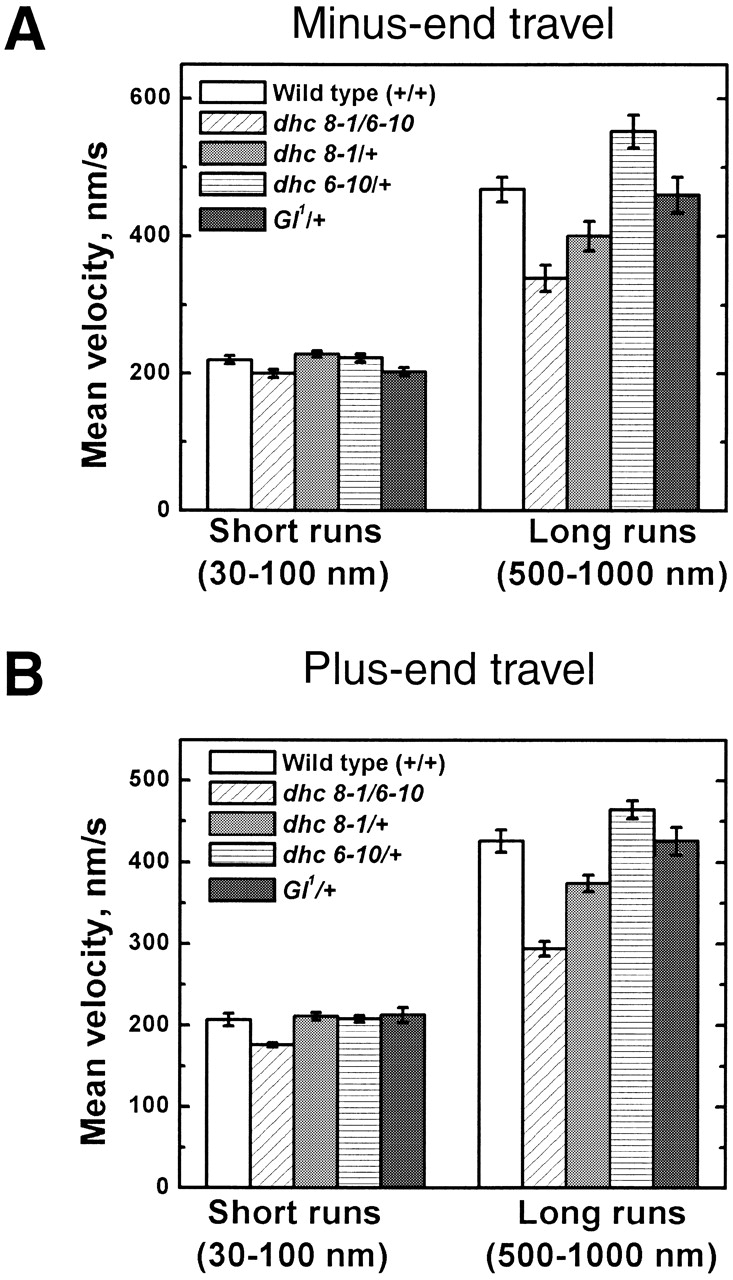
Mean travel speed as a function of run distance, for minus- (A) and plus-end (B) motion. The average speed of short (30–100 nm) or long (500–1000 nm) runs is shown, for droplets moving in wild-type, Dhc64C ^6–10/Dhc64C^8–1, Dhc64C ^8–1/+, Dhc64C ^6–10/+, and Gl ¹/+ genetic backgrounds. Data are from six to seven phase II embryos per genotype, with 120 to 170 runs per embryo analyzed. The error bars are the standard error of the average.

Table I. Physical parameters of droplet motion in various genetic backgrounds.

	Mean travel distance	Distance constant short–slow state D S	Distance constant long–fast state D L	χv 2, P(χv 2)	Number ratio R SL
	nm	nm	nm
Minus end
wild-type (*)	620 ± 31	98 ± 8	1068 ± 149	1.20, 0.19	2.15 ± 0.59
Dhc64C 6-10 /Dhc64C 8-1(*)	168 ± 8	44 ± 4	209 ± 15	0.41, 0.97	2.25 ± 0.58
Dhc64C 6-10 /+	494 ± 25	100 ± 6	903 ± 133	1.09, 0.37	1.50 ± 0.50
Dhc64C 8-1 /+	287 ± 19	91 ± 7	648 ± 167	0.86, 0.73	4.44 ± 2.09
Gl 1/+	370 ± 28	52 ± 7	379 ± 54	0.97, 0.59	2.42 ± 0.77
Plus end
wild-type (*)	842 ± 35	67 ± 6	1144 ± 140	0.98, 0.51	1.05 ± 0.22
Dhc64C 6-10 /Dhc64C 8-1	311 ± 18	52 ± 4	440 ± 41	0.92, 0.61	1.26 ± 0.41
Dhc64C 6-10 /+	557 ± 25	88 ± 7	783 ± 64	0.69, 0.85	2.42 ± 0.69
Dhc64C 8-1 /+	377 ± 21	74 ± 9	402 ± 40	0.72, 0.91	1.45 ± 0.41
Gl 1/+	403 ± 26	75 ± 8	583 ± 91	0.89, 0.70	2.44 ± 0.82

Droplet motion in phase II embryos was characterized by centroid tracking and statistical analysis of travel distances as described (Gross et al., 2000). To characterize the two travel states, histograms of travel distance, D, like the ones in Figs. 5 and 6, were fitted to the sum of two exponential functions: y(D) = A _S exp(−D/D _S) + A _L exp(−D/D _L). χ_ν ² values and corresponding probabilities indicate the goodness of this fit. D _S and D _L measure the average travel distance of runs in the short–slow and the long–fast travel state, respectively. The number ratio R _SL is the number of short runs divided by the number of long runs, and thus measures the relative frequency of the two travel states (see Gross et al., 2000 and Materials and methods for details regarding how these parameters are derived). The data in rows labeled (*) are from our previous analysis of droplet travel (Gross et al., 2000) and are included for comparison.

Table II. Characterization of pauses in droplet motion.

	Pause duration	Time between pauses	Percentage reversals associated with a pause
	s	s
Pauses after minus-end travel
wild-type (*)	0.62 ± 0.03	5.03 ± 0.31	13.8
Dhc64C6-10/Dhc64C 8-1 (*)	0.76 ± 0.03	4.24 ± 0.31	17.4
Dhc64C6-10/+	0.62 ± 0.03	3.99 ± 0.29	14.2
Dhc64C8-1/+	0.70 ± 0.03	2.98 ± 0.18	17.5
Gl 1/+	0.64 ± 0.04	4.24 ± 0.31	13.4
Pauses after plus-end travel
wild-type (*)	0.55 ± 0.20	7.63 ± 0.45	11.7
Dhc64C6-10/Dhc64C8-1	0.71 ± 0.03	3.98 ± 0.19	18.7
Dhc64C6-10/+	0.60 ± 0.03	5.90 ± 0.32	12.7
Dhc64C8-1/+	0.71 ± 0.04	3.94 ± 0.23	16.7
Gl 1/+	0.65 ± 0.04	4.90 ± 0.30	13.7

Droplet motion in phase II embryos was characterized by centroid tracking. Pauses after minus-end or plus-end travel were recognized automatically by custom software and quantitated as described previously (Gross et al., 2000; Materials and methods). (First column) Average pause duration. (Second column) Time between pauses, a measure for how frequently pauses occur. (Third column) Fraction of reversals associated with a pause. This parameter indicates whether droplets typically pause first before reversing travel direction. In all cases, a majority of reversals occurs without a detectable pause. The data in rows labeled (*) are from our previous analysis of droplet travel (Gross et al., 2000) and are included for comparison.

To determine how the drastic reduction in travel distance comes about, we examined in more detail the properties of plus-end “runs” (i.e., periods of travel not interrupted by pauses or reversals). In the wild-type, both plus-end and minus-end runs belong to one of two travel states: a short–slow state characterized by low velocities (∼200 nm/s) and short travel distances (D _S, ∼80 nm), and a long–fast state with higher velocities (∼450 nm/s) and longer travel distances (D _L, ∼1000 nm) (Gross et al., 2000; Table I). Because travel distances for each state are described by a decaying exponential function, the mechanisms that terminate runs in either state appear to be governed by a single rate-limiting step that acts with constant probability. During development, control of net droplet transport is achieved by regulating the average travel distances D _S and D _L as well as the relative frequency R _SL of the two travel states (Gross et al., 2000).

As in the wild-type (Fig. 5 A), plus-end run lengths in the mutant background were well described by the sum of two exponentials (Fig. 5 B). Short-moving droplets displayed significantly lower travel velocities than long-moving ones (Fig. 4 B). We conclude that both travel states are present in the mutant embryos and that the dynein mutations do not fundamentally alter the properties of plus-end motion, but rather change its quantitative parameters. The average travel distance for long–fast runs was severely reduced (D _L, Table I), and the mean velocity of both long and short plus-end runs was reduced relative to the wild-type (Fig. 4 B). Thus, although the tug of war model predicts improved plus-end motion when the minus-end motor is impaired, by all quantitative measures, plus-end motion was significantly impaired. This suggests that the tug of war model is insufficient to account for the observed droplet behavior; in the wild-type, opposing motors do not usually interfere with each other.

Figure 5.

Distribution of lengths of droplet travel in the plus-end direction (35-nm bins). The location of individual droplets as a function of time was determined with nanometer-level resolution using centroid analysis, and periods of uninterrupted motion (runs) were automatically detected with a custom program (Gross et al., 2000). Histograms shown are of plus-end run distances in (A) wild-type and (B) Dhc64C ^6–10/Dhc64C^8–1 embryos. The general shape of the histograms was the same, well fit by the sum of two decaying exponentials (solid line; see Table I for values for these fits). For comparison, Panel A shows data previously published (Gross et al., 2000). Histograms are based on ∼950 total runs per genotype, from six to seven phase II embryos.

Plus-end motion when minus-end stall forces are normal, yet dynein is mutant

The observed lowered minus-end stalling force might indicate that some of the mutant dynein is in an aberrant rigor state, bound to the microtubule and interfering with all motion regardless of the direction of travel. In such a case, the observed impairment of plus-end motion could be due to a “locked-up” state of dynein rather than to a breakdown of coordination. Therefore, we searched for conditions in which dynein was mutant but able to produce normal minus-end stall forces and thus was not in a rigor state.

To affect cytoplasmic dynein less severely, we combined Dhc64C ^6–10 and Dhc64C ^8–1 individually with a wild-type Dhc64C allele. Individuals of these genotypes (Dhc64C ^6–10/+ and Dhc64C ^8–1/+) are fully viable and fertile. Droplet motion in such embryos exhibited both travel states since run lengths were well fit by the sum of two exponentials (unpublished data; Table I, χ_ν ²), and short-moving droplets had significantly slower velocities than fast moving ones (Fig. 4 B). The mutants impaired dynein-driven minus-end motion only with respect to the relative frequency of the two travel states and the average travel distances achieved in these states (Table I). Stall forces were unaffected and indistinguishable from wild-type (Fig. 2 A).

We next quantitated plus-end droplet behavior. Although plus-end travel in both mutant backgrounds displayed the two travel states characteristic of wild-type, mean travel distances were significantly reduced (Table I) and pausing rates were increased (Table II, second column). The relative frequency of the short-slow state was greatly increased in Dhc64C ^6–10/+ embryos, yet unaltered in Dhc64C ^8–1/+ embryos (Table I, R _SL). In contrast, plus-end stall forces were normal in Dhc64C ^6–10/+ embryos, while they were reduced in Dhc64C ^8–1/+ embryos (Fig. 3 B). Thus, we observe distinct impairment of plus-end motion in the two mutants.

Such allele-specific effects are not consistent with the tug of war model because in these embryos the ability of dynein to produce force and to support cargo transport at normal velocities was not impaired. Therefore, in both genotypes, dynein should be able to oppose the plus-end motor just as in the wild-type. However, such allele-specific effects are not surprising if the impairment of plus-end motion is due to loss of motor coordination. Hence, the specifics of the mutation will determine which parameters of motion will be affected. The variation in phenotype between the two alleles suggests that effects on plus-end travel distance, on plus-end stall force, and on the relative frequency of travel states are separate, and partially depend on the details of the loss of motor coordination.

Plus-end motion in embryos expressing a mutation in the dynein regulator dynactin

Although the preceding analysis strongly argues against a simple tug of war model for droplet transport, it does not give insight into the mechanism that underlies motor coordination. The Dhc64C ^6–10 and Dhc64C ^8–1 alleles genetically interact with a mutation (Gl ¹) in a subunit of the essential dynein cofactor dynactin, enhancing or suppressing the Gl ¹ eye defect, respectively (McGrail et al., 1995; unpublished data). This observation prompted us to investigate the role of dynactin in plus-minus coordination.

Dynactin has been implicated both in the attachment of dynein to its cargo and in regulating dynein's processivity. Complete loss of dynactin, e.g., with Gl (Glued) null mutations, results in lethality (Harte and Kankel, 1982; Swaroop et al., 1986). We used the dominant allele Gl ¹ to impair, yet not completely abolish, dynactin function. Animals expressing both the mutant and wild-type Glued proteins show defects in intracellular transport, such as mislocalization of photoreceptor nuclei and aberrant accumulation of vesicles in axons (Fan and Ready, 1997; Martin et al., 1999). Dosage studies indicate that Gl ¹ acts as an antimorph, blocking the function of the wild-type gene product (Harte and Kankel, 1982; Fan and Ready, 1997).

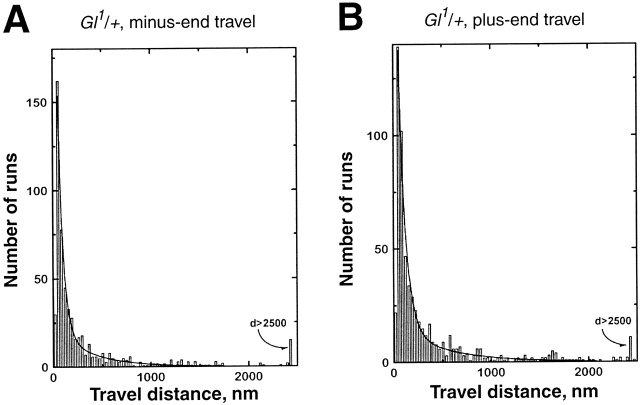
Whereas the mutant form of the protein is present in embryos laid by Gl ¹ heterozygous mothers (McGrail et al., 1995), we have observed no gross defects in embryonic development. The qualitative features of lipid droplet motion were also the same as in the wild-type. The distribution of run lengths for both plus- and minus-end motion was described by the sum of two decaying exponentials (Fig. 6 A, B; Table I, χ_ν ²) suggesting that droplets exhibit both the short–slow and long–fast travel states.

Figure 6.

Distribution of lengths of droplet travel in the Gl¹ background (35-nm bins), for (A) minus-end and (B) plus-end travel. Histograms and fits were done as for Fig. 5. The general shape of the histograms was again well fit by the sum of two decaying exponentials (solid lines, see Table I for values). The histograms are based on droplets tracked in six phase II embryos.

As expected from a mutation in a dynein cofactor, minus-end motion was impaired. Average travel distance was dramatically reduced, due to reduction in average travel for both the long-fast and the short-slow travel state (Table I, D _L and D _S). Other quantitative parameters like droplet velocities (Fig. 4 A), stall forces (Fig. 2 B), and the relative frequency of the long-fast and the short-slow state (Table I, R _SL) were the same as in the wild-type. There was only a slight increase in the number of pauses, and no increase in pause duration (Table II, first column).

We next examined whether this impairment of minus-end motility was accompanied by effects on plus-end travel. In contrast to the very specific minus-end effect, Gl ¹ altered many aspects of plus-end motility. We observed a doubling of the ratio of short runs to long runs (Table I, R _SL), a reduction of the average travel distance for long–fast travel (Table I, D _L), a steep increase in pause frequency (Table II, second column), and a slight increase in pause length (Table II, first column). In addition, Gl ¹ significantly reduced the forces required to stall plus-end moving droplets (Fig. 3 C). Because minus-end stall forces are unaltered, this decrease provides independent evidence for the inadequacy of a simple tug of war model for droplet motion. This observation also suggests that dynactin is necessary for motor coordination.

Discussion

In bidirectionally moving cargoes, the manner in which opposite-polarity microtubule motors are active has been difficult to determine, yet it provides an essential background for understanding how cargo motion is regulated. If opposite-polarity motors engage in a tug of war and cargo motion results when one class of motors overwhelms the other, then the cell could control the net direction of transport by biasing the outcome of the tug of war, e.g., by changing the number of active plus-end motors bound to the cargo. In contrast, motor activity might be coordinated, so that when plus-end motors are active, minus-end motors are turned off, and vice-versa. In this case, coordination allows control of the direction of net transport: to bias net transport toward the plus end, it is sufficient to keep the minus-end motors “off” and thus the plus-end motors “on” for longer times. In this paper, we have shown that for Drosophila lipid droplets, interference with the minus-end motor can impair plus-end motion, a result inconsistent with the tug of war model and supporting the coordination model.

Opposite-polarity motors on lipid droplets are coordinated

In vitro experiments have given equivocal results concerning the extent to which dynein can compete with a plus-end motor. In a microtubule-gliding assay with both kinesin and dynein present, microtubules traveled bidirectionally and displayed reduced velocities in both travel directions (Vale et al., 1992). This indicates that dynein can successfully compete against kinesin. In contrast, Muresan et al. observed only plus-end motion whenever cytoplasmic dynein and kinesin were both present (and presumably active) either on beads incubated with squid axoplasm or on vesicles isolated from axons (Muresan et al., 1996). They concluded that plus-end motors generally overwhelm cytoplasmic dynein, possibly because dynein is not able to produce force continuously like kinesin, or because dynein is not strongly bound to the cargoes. However, in vivo droplets driven by dynein are able to move against a constant force applied by an optical trap (Gross et al., 2000). This should also be true when a force is applied by an opposite-polarity motor.

If plus- and minus-end motors on lipid droplets simply compete with each other, mutations that decrease the stall force for minus-end travel should improve plus-end motion, whereas mutations that result in a wild-type minus-end stall force should not affect plus-end travel. In all four instances we examined, this was not the case: minus-end mutations resulted in impairment of plus-end motion in an allele-specific manner. These observations are not consistent with the tug-of-war model. We conclude that in the wild-type, plus- and minus-end motors are coordinated, and postulate that the Dhc64C or Gl ¹ mutations impair this coordination. Reduced plus-end stalling forces in the mutants would then result from a partial tug of war, where dynein is aberrantly active, opposing plus-end motion. Consistent with such a view, the magnitude of the reduction of the plus-end stalling force in the Gl ¹ background is approximately what would be expected due to a single inappropriately active dynein (Welte et al., 1998; Gross et al., 2000).

Previous studies had noticed that treatments intended to impair minus-end motion can affect plus-end transport (Waterman-Storer et al., 1995, 1997; Martin et al., 1999). However, it was impossible to exclude that these effects arose indirectly due to steric hindrance or a “traffic jam”: dynein impairment might cause minus-end moving organelles to accumulate and block the progress of other, plus-end moving vesicles (Martin et al., 1999). Rather than being affected directly, plus-end motion would be normal until a vesicle's motion was obstructed by other stalled vesicles.

Under the conditions we examined, there is no evidence for a general, nonspecific breakdown of motor-driven transport. All the genotypes analyzed support normal embryonic development, and we have observed no obvious droplet accumulations or organelle traffic jams. In particular, minus-end motion in Gl ¹, Dhc64C ^6–10/+, and Dhc64C ^8–1/+ embryos remains robust with most motion parameters close to wild-type; thus, these mutations do not induce a rigor state in dynein and a generalized arrest of motion. In addition, because our measurements are made only on lipid droplets that are sufficiently far from other droplets that they are not directly pushing on each other, we can exclude indirect effects due to track obstructions. We conclude that the impaired minus-end motors on a given droplet alter the function of the plus-end motors on the same droplet.

It appears unlikely that the effects we observe result from an altered dynamics, orientation, or density of the microtubules. Microtubule growth and shrinkage are too slow (typically <50 nm/s) in comparison to observed droplet velocities of 200–1000 nm/s to significantly contribute to the motion we observe. Overall microtubule organization appears unchanged in all mutant backgrounds because embryos develop grossly normally and net transport of lipid droplets and yolk vesicles in phase II has the same directionality as in the wild-type. For Gl ¹/+ embryos, we have directly demonstrated that microtubule directionality is indistinguishable from wild-type embryos, using markers for microtubule plus- and minus ends (unpublished data). Finally, microtubule density might affect properties of motion if individual cargos move simultaneously along more than one microtubule and the number of microtubules serving as tracks is altered in the various genotypes. Whereas it is formally possible that single cargoes contact several microtubules, we have no evidence that this occurs. And in genotypes for which minus-end stalling forces are wild-type, the number of minus-end motors in contact with the microtubules is apparently not altered, and thus, our line of reasoning applies regardless how many tracks are simultaneously used.

The mechanism of coordination

How is motor coordination achieved? Motors might not interfere with each other because they are never bound to the cargo at the same time. This notion is inconsistent with the data because alteration of dynein and dynactin function alters properties of plus-end motion, indicating that the minus-end motors are present on the droplets when the plus-end motors are active.

In embryos mutant for the klar gene, transport differs from wild-type travel in a manner consistent with plus- and minus-end motors being engaged simultaneously (Welte et al., 1998), both for plus- and for minus-end moving droplets. Therefore, the Klar protein may be part of a coordination complex that turns minus-end motors off when plus-end motors are active, and vice versa. However, the sequence of Klar has not provided mechanistic clues into how coordination occurs (Mosley-Bishop et al., 1999).

The analysis reported here suggests that motor coordination involves two separable mechanisms. When either cytoplasmic dynein or the dynactin complex are not fully functional, the process that keeps dynein inactive while the plus-end motor is active (plus-minus coordination) is altered, whereas the reciprocal process (minus-plus coordination) appears intact. We propose that dynactin usually turns dynein off during plus-end motion, and that certain Dhc64C alleles impair dynein's ability to respond to dynactin's regulatory activity. For dynactin to function as such a coordinator may require that it can respond to the state of the plus-end motor, possibly by directly contacting it. At least one member of the kinesin superfamily indeed interacts physically with dynactin (Blangy et al., 1997). Once the identity of the motor driving plus-end droplet motion is known, it will be possible to dissect how minus-plus coordination is achieved.

To elucidate the precise role of dynactin in coordination, it will be necessary to understand exactly how Gl ¹ dominantly interferes with dynactin function. The Gl ¹ allele encodes a truncated polypeptide that lacks the domain responsible for binding to the Arp1 filament of dynactin, but that retains the sites that mediate interactions with microtubules and dynein (McGrail et al., 1995; Waterman-Storer et al., 1995). McGrail et al. have proposed that Gl ¹ may titrate a crucial dynactin cofactor or that Gl ¹ protein may compete with wild-type dynactin for binding sites on dynein or on microtubules (McGrail et al., 1995). Cargoes with multiple dyneins, such as lipid droplets, would thus carry either a reduced amount of dynactin, with some dyneins being dynactin-free, or carry a mixture of wild-type and faulty dynactin. In the future, these possibilities can be distinguished by determining biochemically or immunologically whether Gl ¹ alters the amount or composition of dynactin on lipid droplets, in particular whether the truncated Gl¹ protein is physically associated with droplets.

Many cargoes move bidirectionally along microtubules just like Drosophila lipid droplets (Introduction). It is likely that most fast bidirectional transport employs cytoplasmic dynein for minus-end motion because it is the only known minus-end motor capable of moving at velocities above 300 nm/s. The identification of dynactin as regulating motor interactions is thus of general significance.

Dynactin as a regulator of minus-end travel distance

In the Gl ¹ heterozygous background, minus-end run lengths are severely decreased. Although dynactin has been proposed to link dynein to certain cargoes (Waterman-Storer et al., 1997; Muresan et al., 2001), several lines of evidence argue that droplet-dynein binding is not noticeably impaired: minus-end moving droplets show only a small increase in pauses during minus-end motion (Table II, second column), no increase in random diffusion (unpublished data), and no reduction in stalling force, suggesting that the number of active dyneins on the droplets is not reduced. These observations are consistent with in vitro findings (Lacey and Haimo, 1994; Tai et al., 1999) that cytoplasmic dynein can interact with phospholipid membranes and transmembrane proteins directly.

If the link of the motor to the cargo is intact, the reduced travel distance indicates that the attached motors move less far when dynactin is impaired. We have previously proposed that cargo travel distance in the wild-type is not limited by motor processivity, but instead is controlled by a mechanism (a switch) that terminates runs and immediately initiates travel in the opposite direction (Gross et al., 2000). Within this conceptual framework, Gl ¹ could decrease travel distance by reducing the processivity of dynein so that it falls off the microtubule even before the switch terminates runs or by altering the properties of the switch. Dynactin has indeed been proposed to increase dynein's processivity (Waterman-Storer et al., 1995); and in vitro beads moved by cytoplasmic dynein move farther in the presence of dynactin (King and Schroer, 2000). However, there is little evidence that in the Gl ¹ background motor processivity has become limiting: the droplets are still moved by multiple dyneins, yet travel distances are even shorter than for a single dynein unaided by dynactin in vitro (Wang et al., 1995; King and Schroer, 2000). In addition, we have no indication that dynein simply detaches from the tracks at the end of runs, because as in the wild-type, most minus-end runs end in immediate reversals (Table II, C). Therefore, we propose that travel distance control is still dominated by the switch mechanism and conclude that dynactin plays a role in the switch.

In this paper, we have suggested two distinct roles for dynactin in dynein regulation. On the one hand, we propose that dynactin is required for motor coordination, keeping dynein “off” during plus-end motion. On the other hand, we postulate a role in the minus-to-plus-end switch; in this role, dynactin keeps dynein “on” and thus delays the onset of plus-end motor activity. It is possible that dynactin's in vitro effects on motor processivity will provide insight into these seemingly opposed functions. For example, the switch mechanism may promote pulling dynein off the track and dynactin counteracts this by holding dynein close to the microtubule. During plus-end motion, dynactin may hold dynein away from the microtubule, in response to plus-end motor activity. Therefore, both functions may result from how dynactin presents dynein to the microtubule.

Materials and methods

Fly stocks

We employed Oregon-R as our wild-type strain and stocks carrying chromosomes with the dynein heavy chain alleles Dhc64C ^8–1 or Dhc64C ^8–1 (Gepner et al., 1996) or the p150/Glued allele Gl ¹ (Harte and Kankel, 1982) over balancer chromosomes. To measure the effects of individual alleles, these mutant stocks were first crossed to Oregon-R to remove the balancer chromosomes from the genetic background, and embryos laid by females heterozygous for the mutant chromosome were analyzed. To analyze droplet motion in the absence of any wild-type dynein, we created a stock transheterozygous for the two dynein heavy chain alleles (Gross et al., 2000).

Force measurements

Force measurements were performed as described (Welte et al., 1998). We used embryos during early cellularization stages (phase II) and measured the percentage of minus- or plus-traveling droplets escaping from the optical tweezers as a function of applied force (controlled by changing the laser power). These measurements allowed us to determine a “stalling force,” i.e., the mean force required to stop a moving droplet (Welte et al., 1998). To avoid bias, force measurements were performed in a blind fashion, with the genotype of the embryo being measured unknown to the person performing the force measurement.

Particle tracking and analysis

We measured all droplet motion parameters in embryos of early cellularization stages (phase II). As described (Welte et al., 1998), dechorionated embryos were flattened into halocarbon oil. Video-enhanced DIC recordings of moving droplets were made onto videotape with a 100× 1.3 NA plan-neofluor objective and a 10× eyepiece in front of the video camera (Welte et al., 1998; Gross et al., 2000). Appropriate sequences from the video recording (usually ∼1-min duration (with 30 frames per second) were then analyzed. The location of individual droplets as a function of time was determined with nanometer-level resolution using centroid analysis. A custom program (Gross et al., 2000) parsed data into pauses and periods of uninterrupted motion (runs). The duration of pauses and the lengths and velocities of plus- and minus-end–directed runs were statistically analyzed. Histograms of run lengths had the same overall shape for each travel direction and genotype examined. These histograms were fit to the sum of two decaying exponentials, starting at bin 2 and using all bins with six or more counts (Gross et al., 2000). In each case, the data were well described by this functional form (Table I, χ_ν ²). From these fits, we calculated distance constants D _S and D _L, and the number ratio R _SL (Gross et al., 2000). D _S and D _L are the average travel distances of the short–slow and long–fast travel states, respectively. R _SL is the relative frequency of the two states.

Pause parameters were calculated as in Gross et al. (2000). Briefly, the time between pauses was determined by dividing the total time droplets were moving in either the minus- or plus-end direction by the number of minus-pauses (pauses after minus-end motion) or plus-pauses (pauses after plus-end motion), respectively. The percentage reversals associated with pauses was calculated by dividing the number of minus-pauses that are followed by plus-end motion by the total number of minus-plus reversals (for minus-pauses) or by the total number of plus-minus reversals (for plus-pauses).