Sulfonylurea Receptors Type 1 and 2A Randomly Assemble to Form Heteromeric K_ATP Channels of Mixed Subunit Composition

Abstract

ATP-sensitive potassium (K_ATP) channels play important roles in regulating insulin secretion, controlling vascular tone, and protecting cells against metabolic stresses. K_ATP channels are heterooctamers of four pore-forming inwardly rectifying (Kir6.2) subunits and four sulfonylurea receptor (SUR) subunits. K_ATP channels containing SUR1 (e.g. pancreatic) and SUR2A (e.g. cardiac) display distinct metabolic sensitivities and pharmacological profiles. The reported expression of both SUR1 and SUR2 together with Kir6.2 in some cells raises the possibility that heteromeric channels containing both SUR subtypes might exist. To test whether SUR1 can coassemble with SUR2A to form functional K_ATP channels, we made tandem constructs by fusing SUR to either a wild-type (WT) or a mutant N160D Kir6.2 subunit. The latter mutation greatly increases the sensitivity of K_ATP channels to block by intracellular spermine. We expressed, individually and in combinations, tandem constructs SUR1-Kir6.2 (S1-WT), SUR1-Kir6.2[N160D] (S1-ND), and SUR2A-Kir6.2[N160D] (S2-ND) in Xenopus oocytes, and studied the voltage dependence of spermine block in inside-out macropatches over a range of spermine concentrations and RNA mixing ratios. Each tandem construct expressed alone supported macroscopic K⁺ currents with pharmacological properties indistinguishable from those of the respective native channel types. Spermine sensitivity was low for S1-WT but high for S1-ND and S2-ND. Coexpression of S1-WT and S1-ND generated current components with intermediate spermine sensitivities indicating the presence of channel populations containing both types of Kir subunits at all possible stoichiometries. The relative abundances of these populations, determined by global fitting over a range of conditions, followed binomial statistics, suggesting that WT and N160D Kir6.2 subunits coassemble indiscriminately. Coexpression of S1-WT with S2-ND also yielded current components with intermediate spermine sensitivities, suggesting that SUR1 and SUR2A randomly coassemble into functional K_ATP channels. Further pharmacological characterization confirmed coassembly of not only S1-WT and S2-ND, but also of coexpressed free SUR1, SUR2A, and Kir6.2 into functional heteromeric channels.

INTRODUCTION

ATP-sensitive potassium (K_ATP) channels link the metabolic status of a cell to its membrane excitability because their activities are uniquely modulated by intracellular adenine nucleotides (Ashcroft, 2005). K_ATP channels are expressed in the pancreas, brain, and muscles and are critical in regulating insulin secretion, controlling vascular tone, and protecting cells against metabolic insults (Aguilar-Bryan and Bryan, 1999; Yamada and Inagaki, 2005). Mutations in the pancreatic K_ATP channels can cause permanent neonatal diabetes mellitus (PNDM) and persistent hyperinsulinemic hypoglycemia of infancy (PHHI) (Ashcroft, 2005). Mutations in the cardiac K_ATP channels can cause dilated cardiomyopathy (Bienengraeber et al., 2004). Prinzmetal angina has been proposed to be linked to dysfunction of the smooth muscle K_ATP channels (Miki et al., 2002).

Each K_ATP channel comprises two types of subunits (Inagaki et al., 1995). Kir6, an ∼40-kD protein belonging to the inwardly rectifying potassium (Kir) channel family, is the pore-forming subunit. The cytosolic domains of the tetrameric Kir6 channel contain four inhibitory ATP-binding sites (Nichols, 2006). The sulfonylurea receptor (SUR), an ∼180-kD ATP-binding cassette (ABC) protein, is the regulatory subunit of the K_ATP channel. SUR associates with Kir6, predominantly through its unique N-terminal transmembrane domain, TMD0, and increases the intrinsic Po of the channel (Chan et al., 2003). SUR exerts two effects on the nucleotide sensitivities of the Kir6 channel. First, it sensitizes the channel to ATP inhibition by ∼10-fold (Tucker et al., 1997). Second, it activates the channel by interaction of two MgATP/ADP molecules with its two nucleotide-binding domains. Pharmacologically, SUR harbors the binding sites for the inhibitory sulfonylurea and the stimulatory potassium channel opener drugs, which are used to treat diabetes and hypertension, angina, PHHI, respectively (Touati et al., 1998; Darendeliler et al., 2002; Ashcroft, 2005; Jahangir and Terzic, 2005). Both classes of drugs bind mainly to the ABC core domain of SUR (the parts of SUR after TMD0; Gribble and Reimann, 2002; Moreau et al., 2005). The K_ATP channel complex, comprising four Kir6 and four SUR (Clement et al., 1997; Shyng and Nichols, 1997), is a unique example of complex regulation of a potassium channel by an ABC protein.

In mammals, there are two Kir6 and two SUR genes (Kir6.1 and Kir6.2; SUR1 and SUR2) (Aguilar-Bryan and Bryan, 1999; Shi et al., 2005). SUR2 has two major spliced variants, SUR2A and 2B, which differ only in their C- terminal 42 amino acids. It is believed that different Kir6 combine with different SUR to form the various native K_ATP channels. For example, the pancreatic, cardiac, and smooth muscle K_ATP channels are made up of SUR1+Kir6.2, SUR2A+Kir6.2, and SUR2B+Kir6.1/Kir6.2, respectively. Different SUR subtypes respond differently to intracellular nucleotides, sulfonylureas, and potassium channel openers, while Kir6.1 and Kir6.2 have similar ATP sensitivities. Therefore the metabolic sensitivities (Liss et al., 1999; Dabrowski et al., 2003; Masia et al., 2005) and the pharmacological properties (Gribble and Reimann, 2002; Moreau et al., 2005) of a K_ATP channel are largely determined by its constituent SUR.

A common theme in many families of ion channels is the association of different but similar protein members (Jan and Jan, 1990) to form heteromers with novel properties. Kir6.1 and Kir6.2, being 64% identical, display overlapping tissue expressions and form heteromeric complexes when coexpressed (Babenko et al., 2000; Cui et al., 2001; Pountney et al., 2001; van Bever et al., 2004). On the contrary, based on the study from Giblin et al., it is generally accepted that SUR1 cannot coassemble with SUR2 to form K_ATP channels (Giblin et al., 2002; Babenko, 2005; Neagoe and Schwappach, 2005; Tricarico et al., 2006), even though SUR1 and SUR2 share ∼65% identity and are coexpressed in many cell types (Baron et al., 1999; Liss et al., 1999; Shi et al., 2005; Tricarico et al., 2006). In this study, we examine whether SUR1 and SUR2 can coassemble to form functional K_ATP channels.

The main strategy we adopted here is based on the coexpression of two different Kir subunits with strikingly different rectification properties (i.e., voltage-dependent block of intracellularly applied polyamines, such as spermine): one weak and one strong inward rectifier. Three SUR-Kir6.2 tandems were used in our study: S1-WT, S1-ND, and S2-ND (S1 = SUR1, S2 = SUR2A, WT = Kir6.2, ND = Kir6.2[N160D]). The N160D mutation converts Kir6.2 from a weak to a strong rectifier (Shyng et al., 1997) and was used to tag the SUR covalently linked to it. By expressing each tandem construct in Xenopus oocytes, we first characterized the rectification properties of these three homomeric channels by studying the conductance–voltage (g/V) relationships of their macroscopic currents obtained from inside-out patches in the absence and in the presence of internal spermine. Next, we studied the assembly of SUR1 with SUR1 by coexpressing S1-WT and S1-ND. Then, we investigated whether SUR1 and SUR2A can coassemble by coexpressing S1-WT with S2-ND. From global fits to families of conductance curves obtained over a range of spermine concentrations (5–1,000 μM), a >300-mV voltage span (−140 to +180 mV), and an ∼10-fold range of RNA mixing ratios, we conclude that SUR1 and SUR2A subunits can coassemble randomly to form heteromeric channels. Finally, we coexpressed Kir6.2 with free SUR1, SUR2A, or equal molar amounts of SUR1 and SUR2A and measured both their ATP and tolbutamide dose responses. These results also confirm that SUR1 and SUR2A must be able to coassemble. The coassembly of different SUR subtypes to form functional channels provides a mechanism to increase the functional and pharmacological diversities of native K_ATP channels.

MATERIALS AND METHODS

Molecular Biology

To construct the SUR1-Kir6.2 tandem (S1-WT), we first replaced the start codon of Kir6.2 by a glycine linker containing a BamHI and a SalI site located at its 5′ end. The stop codon of FSUR1 (this construct contains a FLAG epitope–coding sequence before the second codon of SUR1) was replaced by a SalI site. A BamHI site was located before the FLAG sequence. S1-WT was made by inserting FSUR1 between the BamHI and SalI sites of the modified Kir6.2. SUR1-Kir6.2[N160D] was similarly constructed by using a plasmid containing Kir6.2[N160D]. To make SUR2A-Kir6.2[N160D] (S2-ND), the single XbaI site at codon 1383 of SUR2A was silently mutated and the stop codon of SUR2A was substituted by a new XbaI site. The coding sequence of Kir6.2[N160D] with a glycine linker located at its 5′ end was amplified by PCR and inserted into the single XbaI site of the modified SUR2A. All constructs were carried by the pGEMHE vector (Liman et al., 1992). Mutations were introduced by Quikchange mutagenesis (Stratagene) and confirmed by sequencing. The peptide sequences of the linkers in S1-WT/ND and S2-ND were VDGRG₈DI and SRGRG₈DI, respectively. RNAs were made by in vitro transcription and two to three different dilutions of each RNA were run on denaturing agarose gels containing ethidium bromide. RNA concentrations were estimated by comparing their fluorescence intensities to those of calibrated RNA markers when visualized under UV.

Isolation and Injection of Xenopus Oocytes

For two-electrode voltage clamp (TEVC) experiments, 0.5 ng of S1-WT, 1.5 ng of S2-ND, 0.5 ng of S1-WT+1.5 ng of S2-ND, 0.4 ng of SUR1+0.1 ng of Kir6.2, 0.4 ng of SUR1+0.1 ng of Kir6.2+1.5 ng of S2-ND or 0.1 ng of Kir6.2+1.5 ng of S2-ND were injected into Xenopus oocytes. For patch clamp experiments, 6 ng of S1-WT, S1-ND, or S2-ND was injected; for S1-WT+S1-ND or S1-WT+S2-ND coexpression experiments, 1.5+4.5 ng, 3+3 ng, and 4.5+1.5 ng of the two cRNAs were used, to achieve ∼1:3, 1:1, and 3:1 molar ratios, respectively, of the two cRNAs; 3 ng of SUR1 (or SUR2A)+0.5 ng of Kir6.2 or 1.5 ng of SUR1+1.5 ng of SUR2A+0.5 ng of Kir6.2 were injected for the ATP and tolbutamide dose response experiments. Xenopus oocytes were prepared as described before (Fang et al., 2006). In brief, female Xenopus laevis were anaesthetized with 0.15% MS222 (pH 7.5) for ∼15 min. Ovarian sacs were removed through a small incision on one side of the abdomen. The incision was sutured and the animal was allowed to recover. All animal procedures were in accord with the IACUC. Oocytes were treated with 1–2 mg/ml collagenase (Worthington) in OR2 solution (in mM: 82.5 NaCl, 2 KCl, 1 MgCl₂, 5 HEPES, pH 7.5) and selected for injection. Injected oocytes were cultured in OR2 supplemented with Ca²⁺ (1.8 mM), penicillin (50 U/ml), streptomycin (50 μg/ml), and gentamicin (100 μg/ml) (all antibiotics were purchased from Invitrogen).

Electrophysiology

TEVC was performed using an OC-725C amplifier (Warner Instruments). Bath solution contained (in mM) 96 KCl, 2 NaCl, 1 MgCl₂, 5 HEPES, 1.8 CaCl₂ (pH 7.5). 3 M sodium azide (in water; Sigma-Aldrich), 340 mM diazoxide (in DMSO; Sigma-Aldrich), 200 mM pinacidil (ethanol; Sigma-Aldrich), 20 mM glibenclamide (DMSO; Sigma-Aldrich), and 1 M BaCl₂ (water) were used as stocks. To monitor whole-cell conductance, oocyte membrane was held at 0 mV and a 1-s ramp from −100 to +100 mV was applied at a 1.5-s interval. Currents were filtered at 1 kHz and sampled at 2 kHz. Currents at −80 mV from the ramp were used to plot the time courses and for comparing current magnitudes. Patch clamping was performed using an Axopatch 200B amplifier (Axon Instruments). Patch pipettes were pulled from borosilicate glass (Warner G85150T-3) and fire polished to tip resistances of 0.8–1.5 MΩ. Pipette solution contained (in mM) 0.3 CaCl₂, 1 MgCl₂, 1.98 KH₂PO₄, 8.02 K₂HPO₄, and 78 KCl (pH 7.4) (Guo and Lu, 2003). Bath solution contained 5 K₂EDTA, 1.98 KH₂PO₄, 8.02 K₂HPO₄, and 68 KCl (pH 7.4). Seal resistances were typically 10–50 GΩ, and patches were excised into an inside-out configuration. A 10 mM spermine (Sigma-Aldrich) stock was freshly prepared by dissolving spermine in the bath solution and the pH was readjusted to pH 7.4. Patches were held at −100 mV while being superfused for at least 15 s by a bath solution with or without spermine. A ramp protocol was then used to obtain the current−voltage (I/V) relationships of the macroscopic currents. Currents were filtered at 1 kHz and sampled at 4 kHz. For patches expressing S1-ND or S2-ND, ramp voltages ranged from −140 to +140 mV. For patches expressing S1-WT, S1-WT+S1-ND, or S1-WT+S2-ND, the ramp was extended from −140 to +190 mV. We used a ramp speed of 0.14 mV/ms, which resulted in I/V curves identical to those obtained from a voltage step protocol with a 0.5-s pulse duration at 5, 20, and 100 μM SPM. Except for the S2-ND homomeric channels, 5 mM ATP could completely inhibit the currents and was applied at the end of the experiments to estimate the leak. Leak currents from patches containing only S2-ND could be safely ignored because only patches expressing large macroscopic S2-ND currents (>2 nA at −140 mV) were included into our analyses. 250 mM sodium ATP (Sigma-Aldrich) and 10 mM tolbutamide (ICN biomedicals) stocks were dissolved in the bath solution. Both ATP and tolbutamide were applied to the internal side of the patches. For some of the ATP and tolbutamide experiments (Figs. 9 and 10) the zero current level was obtained from the segment of the current recording just before patch excision (i.e., cell-attached) which typically contained no, or just a few, channel openings with low Po.

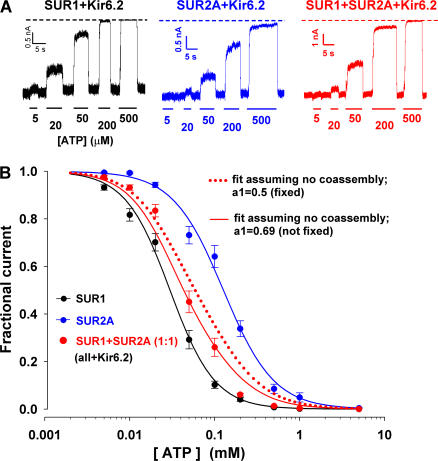
Figure 9.

Dose responses for ATP inhibition of channels obtained by coexpression of free SUR1, SUR2A, and Kir6.2 suggest the coassembly of free SUR1 with free SUR2A. (A) Representative current traces obtained in inside-out patches from oocytes expressing SUR1+Kir6.2 (black trace), SUR2A+Kir6.2 (blue trace), or SUR1+SUR2A+Kir6.2 (SUR1:SUR2A=1:1; red trace). The membrane was held at −100 mV and ATP at various concentrations was applied to the bath solution as indicated. (B) Fractional currents remaining in the presence of various concentrations of cytosolic ATP in patches excised from oocytes expressing SUR1+Kir6.2 (black symbols), SUR2A+Kir6.2 (blue symbols), or SUR1+SUR2A+ Kir6.2 (red symbols). Black and blue solid lines show fits to the Hill equation of the data for SUR1+Kir6.2 and SUR2A+Kir6.2, respectively. Fit parameters are listed Fig. 1 A. Red dotted and solid lines illustrate predicted curves for SUR1+SUR2A+Kir6.2 assuming that SUR1 does not coassemble with SUR2A. The red dotted line is the simple arithmetic average of the two Hill functions obtained for SUR1+Kir6.2 (black line) and SUR2A+Kir6.2 (blue line), expected if SUR1 and SUR2A protein was expressed at an equal molar ratio but did not coassemble. The red solid line is the best fit to the SUR1+SUR2A+Kir6.2 data by a mixture of the two parent Hill functions, with the fractional amplitude of channels formed from SUR1+Kir6.2, a ₁, left as a free parameter. This fit returned a ₁ = 0.69 ± 0.06, but still failed to describe the data.

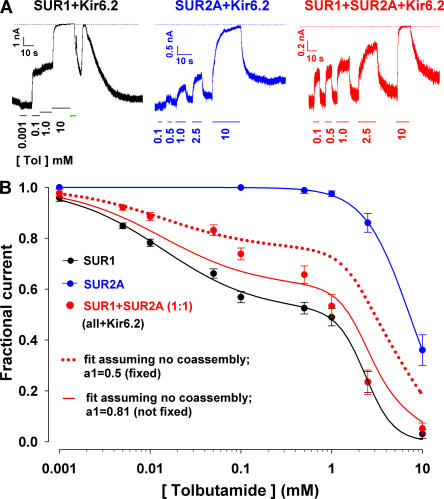
Figure 10.

Dose responses for tolbutamide inhibition of channels obtained by coexpression of free SUR1, SUR2A, and Kir6.2 suggest the coassembly of free SUR1 with free SUR2A. (A) Representative current traces obtained in inside-out patches from oocytes expressing SUR1+Kir6.2 (black trace), SUR2A+Kir6.2 (blue trace), or SUR1+SUR2A+Kir6.2 (SUR1:SUR2A=1:1; red trace). The membrane was held at −100 mV and tolbutamide at various concentrations was applied to the bath solution as indicated. The green line indicates the application of 2.5 mM ATP. The biphasic current increase during the washout of ATP is a perfusion artifact. (B) Fractional currents remaining in the presence of various concentrations of cytosolic tolbutamide in patches excised from oocytes expressing SUR1+Kir6.2 (black symbols), SUR2A+Kir6.2 (blue symbols), or SUR1+SUR2A+Kir6.2 (red symbols). The solid black line is a fit of Eq. 1 to the SUR1+Kir6.2 data, yielding fit parameters K _i1 = 14 ± 4 μM, h ₁ = 0.83 ± 0.15, K _i2 = 2.4 ± 0.2 mM, h ₂ = 2.8 ± 0.9, and L=0.51 ± 0.04. The blue solid line is a fit to the Hill equation of the data for SUR2A+Kir6.2, yielding fit parameters K _i = 7.19 ± 0.06 mM, n = 1.74 ± 0.02. Red dotted and solid lines illustrate predicted curves for SUR1+SUR2A+Kir6.2 assuming that SUR1 does not coassemble with SUR2A. The red dotted line is the simple arithmetic average of the two fit functions obtained for SUR1+Kir6.2 (black line) and SUR2A+Kir6.2 (blue line), expected if SUR1 and SUR2A protein was produced at an equal molar ratio but did not coassemble. The red solid line is the best fit to the SUR1+SUR2A+Kir6.2 data by a mixture of the two parent functions, with the fractional amplitude of channels formed from SUR1+Kir6.2, a ₁, left as a free parameter. This fit returned a ₁ = 0.81 ± 0.07, but still failed to describe the data.

Data Analysis

To construct averaged ramp I/V relationships ramp currents were averaged over blocks of ∼150 neighboring sample points, yielding a representative average ramp current value per ∼5 mV of membrane voltage. Averaged ramp I/V curves were leak-subtracted by subtracting the I/V curve obtained in the presence of 5 mM ATP in the same patch. To alleviate the problem of slow time-dependent rundown, each I/V curve was then normalized by dividing the current with the absolute value observed around −140 mV. Chord conductances ĝ were calculated by dividing the normalized current with membrane voltage (E _K = 0), the chord conductance at V _m = 0 was obtained by third order polynomial interpolation. Relative chord conductances (g _rel) for a given spermine concentration were obtained by dividing the chord conductance in the presence of spermine with that in its absence (g _rel = ĝ/ĝ(0 SPM)).

Global fitting was done by calculating the total sum of the squared errors between a fit function of the form described in the text (compare, Eq. 8) and each of the points of four g _rel/V curves obtained in the same patch at four different spermine concentrations. This error function was then minimized with respect to the free parameters using a downhill simplex algorithm. Monotonity constraints among free parameters were imposed by running the optimization algorithm on a suitably transformed parameter space. Global fitting of S1-WT, S1-ND, and S2-ND data involved 5, 3, and 3 free parameters. Global fitting of S1-WT+S1-ND at RNA mixing ratios of 1:1, 1:3, and 3:1 involved 10, 1, and 1 free parameters. Global fitting of S1-WT+S2-ND at RNA mixing ratios of 1:1, 1:3, and 3:1 involved 13, 4, and 4 free parameters.

ATP dose response curves were fitted to the Hill equation for S1-WT, S1-ND, S2-WT, S2-ND, SUR1+Kir6.2, and SUR2A+Kir6.2, and to a weighted average of the two parent curves for coexpression experiments using S1-WT+S2-ND or SUR1+SUR2A+Kir6.2. The tolbutamide dose response curve for SUR2A+Kir6.2 was also fitted by the Hill equation, while that for SUR1+Kir6.2 was fitted to the function defined in Gribble et al. (1998), i.e., to

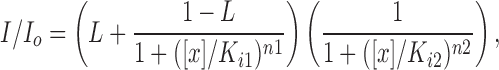(1)

where [x] is the concentration of tolbutamide. The tolbutamide dose response curve for SUR1+SUR2A+Kir6.2 was fitted to a weighted average of the two parent curves.

Statistics

Data are presented as mean ± SEM. Significances were assessed using Student's t test.

Online Supplemental Material

This paper contains one supplemental figure (Fig. S1, available at http://www.jgp.org/cgi/content/full/jgp.200709894/DC1), which shows that the covalent linkage in S1-WT is not required for S1-WT to suppress the basal currents and increase the glibenclamide-sensitive currents of oocytes expressing S2-ND. This provides evidence that the coassembly of SUR1 with SUR2 to form heteromeric K_ATP channels does not require the covalent linkage between SUR and Kir6.2.

RESULTS

K_ATP Channels Formed from SUR-Kir6.2 Tandems Display Identical ATP Sensitivity and Similar Pharmacology to Channels Formed from Nonconjugated SUR and Kir6.2 Subunits

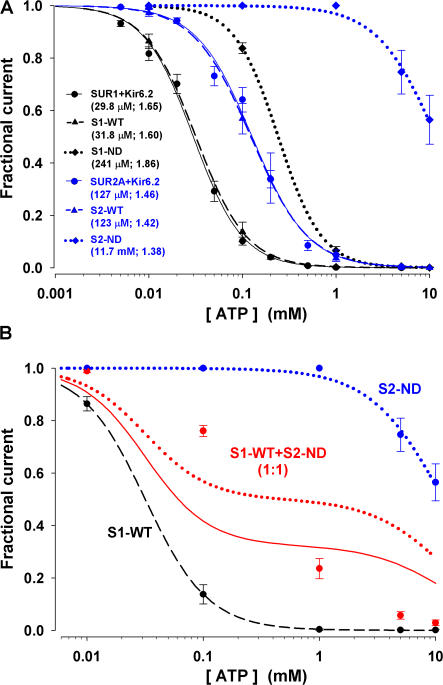
Since the main strategy of this study was to coexpress various SUR-Kir6.2 dimers, we first investigated whether the covalent linkage between SUR and Kir6.2 leaves basic channel properties intact. To this end, current responses to different internal ATP concentrations were measured in inside-out patches for oocytes expressing SUR1+Kir6.2, SUR2A+Kir6.2, S1-WT, S1-ND, S2-WT, or S2-ND; and the resulting ATP dose response curves were fitted by the Hill equation (Fig. 1 A). The ATP sensitivities of the channels formed from S1-WT and SUR1+Kir6.2, or from S2-WT and SUR2A+Kir6.2 were indistinguishable (Fig. 1 A). Our data also indicate that SUR1-based channels are approximately fourfold more sensitive to ATP inhibition than SUR2A-based channels (K_i = ∼30 and 120 μM, respectively). In contrast, the K_i for S1-ND and S2-ND were eightfold and 95-fold larger than those from S1-WT and S2-WT, respectively. Therefore, the N160D mutation greatly decreased the ATP sensitivities of the channels (also see Shyng and Nichols, 1997) but this effect is more pronounced when Kir6.2 is associated with SUR2A. We also screened further pharmacological properties of the tandem channels using TEVC. Just like channels formed from SUR1+Kir6.2, S1-WT channels also exhibited insignificant basal currents and were similarly activated by sodium azide, a metabolic inhibitor, and further stimulated by diazoxide, a potassium channel opener relatively specific to SUR1 (Fig. 2 A and Fig.S1 A, available at http://www.jgp.org/cgi/content/full/jgp.200709894/DC1; also see insets). Finally, >90% of the total activated current from S1-WT channels was inhibited by 10 μM of the sulfonylurea glibenclamide (Fig. 2, A and B). Similarly, S2-ND retained its sensitivity to pinacidil, a SUR2-specific potassium channel opener (Fig. S1). Therefore, the covalent linkage between SUR and Kir6.2 does not affect the basic properties of the K_ATP channels, suggesting that K_ATP channels assembled from four tandem constructs assemble into a native-like octameric structure.

Figure 1.

Dose response curves for ATP inhibition reveal no effect of tandem linkage on ATP sensitivity and suggest coassembly of S1-WT with S2-ND. (A) Fractional currents remaining in the presence of various concentrations of cytosolic ATP for channels formed by SUR1+Kir6.2, S1-WT, S1-ND (black circles, triangles, and diamonds), SUR2A+Kir6.2, S2-WT and S2-ND (blue circles, triangles, and diamonds). The lines are fits to the Hill equation of the data obtained for the different channel groups. The values of K _i and the Hill coefficient (n) are listed. The K_i and n of SUR1+Kir6.2 and S1-WT, or of SUR2A+Kir6.2 and S2-WT, are indistinguishable. (B) Fractional currents remaining in the presence of various concentrations of cytosolic ATP in patches excised from oocytes injected with an equal molar amount of S1-WT and S2-ND cRNA (red symbols). The data and fit lines for homomeric S1-WT (black) and S2-ND (blue) channels are replotted from A for comparison. The red solid line is the best fit to the S1-WT+S2-ND coexpression data assuming that S1-WT and S2-ND do not coassemble; i.e., a mixture of the two Hill functions obtained for homomeric S1-WT (black dashed line) and S2-ND (blue dotted line) was fitted by leaving the fractional amplitude (a ₁) of the S1-WT component as the sole free parameter. This fit returned a ₁ = 0.68 ± 0.14, but clearly failed to describe the data. The red dotted line is the fit to the same data with a ₁ fixed to 0.5.

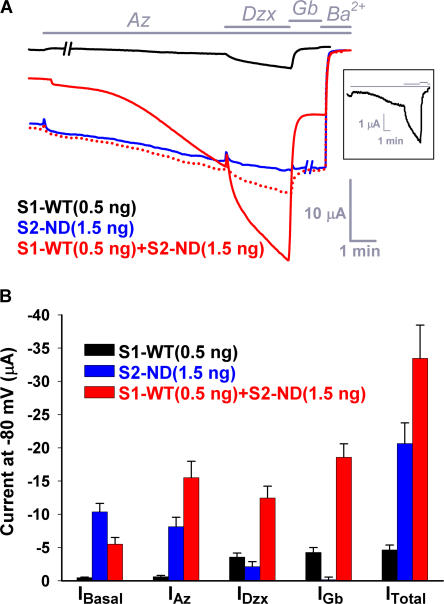
Figure 2.

Coassembly with S1-WT reduces the basal whole-oocyte current and increases the glibenclamide-sensitive current of S2-ND. (A) Time courses of representative whole-cell currents recorded from oocytes expressing S1-WT (0.5 ng; black trace), S2-ND (1.5 ng; blue trace), and S1-WT+S2-ND (0.5 ng and 1.5 ng, respectively; red trace). Currents were recorded at −80 mV by TEVC (see Materials and methods). 3 mM sodium azide (Az), 340 μM diazoxide (Dzx), 10 μM glibenclamide (Gb), and 3 mM BaCl₂ were applied to the bath solution as indicated by the labeled horizontal bars. Approximately 1-min stationary sections (−//−) were omitted from the S1-WT (black) and S2-ND (blue) traces to align the timing of all drug applications for all three traces. The red dotted line is the sum of the black and blue traces and illustrates the whole-cell current expected for an oocyte coexpressing S1-WT and S2-ND assuming that the two subunits do not coassemble. The inset shows the entire S1-WT current trace at an expanded current scale. (B) Bar chart summary of the mean basal (I_Basal), azide-activated (I_Az), diazoxide-activated (I_Dzx), and glibenclamide-sensitive (I_Gb) current components, as well as of the total currents (I_Total) in oocytes expressing S1-WT, S2-ND, and S1-WT+S2-ND.

ATP Sensitivities and Pharmacological Properties of the Whole-Cell Currents of Oocytes Coexpressing S1-WT and S2-ND Already Indicate Coassembly of SUR1 and SUR2A

If SUR1 and SUR2A cannot coassemble to form heteromeric K_ATP channels, then the currents recorded from oocytes injected with both S1-WT and S2-ND cRNAs are expected to equal the sum of the individual currents recorded under identical conditions from oocytes injected with either S1-WT or S2-ND cRNA. Fig. 1 B shows the ATP dose response curve of normalized currents obtained in patches from oocytes injected with an equal molar amount of S1-WT and S2-ND (red circles). Clearly, this curve is not well fitted assuming that S1-WT and S2-ND do not coassemble—whether the molar ratio of S1-WT to S2-ND protein is constrained to 1:1 (red dotted line) or left as a free parameter (red solid line). We also compared the whole-cell current characteristics of oocytes injected with S1-WT (0.5 ng), S2-ND (1.5 ng), or a mixture of S1-WT and S2-ND (0.5 ng + 1.5 ng) cRNA. In contrast to oocytes injected with S1-WT cRNA (Fig. 2 A, black line), those injected with S2-ND exhibited a large basal current, reflecting the low sensitivity of the S2-ND channels to ATP inhibition (blue trace in Fig.2 A; compare, Fig. 1 A). This current was further activated, albeit slowly, by 3 mM sodium azide, but was insensitive to diazoxide (the small current increase in Fig. 2 A is due to the continued activation by sodium azide), and also to glibenclamide, likely due to the high Po of the channel harboring the N160D mutation (Shyng et al., 1997). The total current, including the basal and the azide-activated components, was completely blocked by 3 mM Ba²⁺. A representative recording from an oocyte injected with 0.5 ng of S1-WT together with 1.5 ng of S2-ND is also shown in Fig. 2 A (red solid trace). This current trace is substantially different from the arithmetic sum of the currents obtained for S1-WT and S2-ND (red dotted trace). Noticeably, the basal current is only half while the glibenclamide-sensitive current is ∼4.5-fold of the respective sum obtained for these individual current components of S1-WT and S2-ND (Fig. 2 B). Similarly, the azide-activated and diazoxide-activated currents of oocytes coexpressing S1-WT+S2-ND were significantly larger than the respective sums of the individual currents. Hence, these preliminary “mixing” experiments already provide strong evidence against the conventional assumption that SUR1 and SUR2A cannot form heteromeric K_ATP channels.

A Quantitative Approach to Study the Coassembly of SUR1 and SUR2A: Spermine Block of K_ATP Channels Formed from the Coexpression of S1-WT and S2-ND

The strategy of coexpressing pore-forming subunits with largely different rectification properties has been successfully used to investigate the coassembly of different Kir subunits and the stoichiometry of SUR1 and Kir6.2 subunits within the assembled K_ATP channels (Glowatzki et al., 1995; Shyng and Nichols, 1997). If the g/V relationships in the presence of a cytosolic blocker (e.g., spermine) are sufficiently different for two types of pore-forming subunits, then heterooligomeric channels, which contain both types of subunits, will be betrayed by intermediate rectification behavior. By careful analysis, the relative abundances of the various classes of heterooligomeric channels can be estimated. To this end, g/V relationships are fitted with sums of Boltzmann functions, each representing one class of heterooligomers, and the fractional contribution of each such component is estimated from the fits.

An inherent limitation of this approach is that the fitting of the g/V relationships is overparameterized: a relatively small amount of data (i.e., a single g/V curve) is fitted with a large number of parameters. For example, in the case of a tetrameric pore assembly, a mixture of five Boltzmann functions is fitted. This involves altogether 10 free parameters (two for each intermediate Boltzmann component, plus four for the fractional amplitudes) for fitting a single g/V curve (Shyng and Nichols, 1997). A second problem is that the wild-type (WT) Kir6.2 subunit is so weakly rectifying. As a result, the g/V curves of WT channels obtained at the low spermine concentrations and over the restricted voltage range used in previous studies cannot be reliably fitted by a Boltzmann function.

To obtain more solid support for such fits we decided to study the g/V curves of our channel constructs (a) over a >300-mV voltage range (−140 to +180 mV), (b) over a 200-fold range of spermine concentrations (5 to 1,000 μM), and, for coexpression experiments, (c) over an ∼10-fold range of RNA mixing ratios (1:3 to 3:1). We then used global fitting of families of g/V curves using the same sets of free parameters. This approach greatly reduces the ratio of the number of fitted parameters versus the amount of supporting experimental data.

Spermine Block of S1-WT Channels Is Best Described by the Sum of a Boltzmann Function and a Voltage-independent Leak

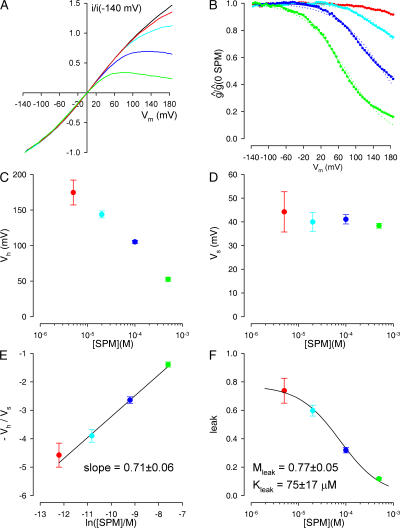
We first characterized spermine block of homotetrameric K_ATP channels assembled from four tandem S1-WT subunits by excising macropatches from oocytes expressing this construct. We obtained ramp current–voltage (I/V) relations in the presence of 5, 20, 100, and 500 (or 1,000) μM spermine in the same patch, and the series of test I/V ramps were bracketed by control I/V ramps in the absence of spermine. Background currents, estimated at the end of each experiment by obtaining an I/V curve in the presence of 5 mM ATP, were in each case negligible but were nevertheless subtracted from all data before analysis. Although in some patches we could observe a slow rundown over the time course of an experiment, we found that the shape of the initial and the final control I/V curves remained identical, indicating a slow voltage-independent loss of active channels over time. To compensate for this rundown effect, we normalized all our I/V relationships to the absolute value of the current observed at very negative voltages (−140 mV). Such a family of normalized I/V curves, obtained from a single patch containing S1-WT channels, is shown in Fig. 3 A. Relative conductance–voltage (g _rel/V) curves for a given spermine concentration (Fig. 3 B, colored symbols) were constructed by calculating for each voltage the ratio of the chord conductances in the presence and absence of spermine.

Figure 3.

Dissection of the voltage-dependent and voltage-independent components of spermine block for S1-WT channels. (A) Family of normalized, leak-subtracted ramp I/V curves obtained in a patch containing S1-WT channels in the absence of (black line), or in the presence of 5 (red line), 20 (cyan line), 100 (blue line), and 500 μM (green line) spermine. (B) Family of g _rel/V curves obtained from the I/V curves shown in A (solid symbols, color coding as in A). Dotted and solid lines represent fits to the individual g _rel/V curves of simple Boltzmann functions without (dotted lines) or with (solid lines) an added constant “leak.” (C–F) Plots of the fit parameters V _h (C), V _s (D), and leak (F), obtained by fitting individual g _rel/V curves with Eq. 2, and of the ratio −V _h/V _s (E), as a function of spermine concentration. Color coding is the same as in A. The black line in E was obtained by linear regression, that in F by a nonlinear least-squares fit to Eq. 7. Obtained parameters are presented in the panels.

To test whether the speed of our ramp protocol was slow enough to allow equilibration of spermine at each voltage, we compared the I/V curves obtained with our ramp protocol to those constructed from the steady current sections of a step voltage protocol executed in the same patch. We obtained identical I/V curves using both protocols (unpublished data); therefore, our g _rel/V curves describe steady-state block by spermine.

As a first approach, we attempted to fit each g _rel/V curve (obtained at a given spermine concentration) individually, using a simple Boltzmann function. To our surprise we found that even at high spermine concentrations and at extremely depolarized voltages the conductances did not converge toward zero. Thus, the g _rel/V curves were much better fitted by allowing for a constant, voltage-independent conductance (the “leak”) in addition to the voltage-dependent Boltzmann function (Fig. 3 B, blue and green solid vs. dotted lines), i.e., by a fit function of the form

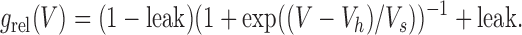(2)

We next examined how the parameters (V _h and V _s) of the fitted Boltzmann function depended on spermine concentration. Following the classical formalism of voltage-dependent block (Woodhull, 1973), the relative conductance reflects simple binding of the blocker, i.e.,

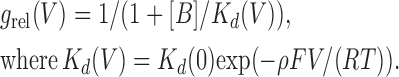(3)

K_d(0) is the dissociation constant of the blocker at 0 mV, ρ is the apparent charge of the blocker, F = 96,500 C/mol, R = 8.31 Jmol⁻¹K⁻¹, T is temperature in °K, and [B] is the concentration of the blocker in the bulk solution. Eq. 3 predicts a Boltzmann function with parameters

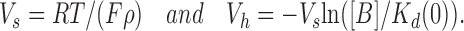(4)

At a first approximation our observed parameters were consistent with this simple formalism, i.e., we found that V _s remained independent of spermine concentration (Fig. 3 D), while V _h declined approximately linearly with the logarithm of the latter (Fig. 3 C). However, at a more detailed level we found significant deviation from the above simplified picture. In particular, when we plotted −V_h/V_s as a function of ln([B]) we obtained a straight line (Fig. 3 E) whose slope (0.71 ± 0.06) was significantly smaller than unity, as would have been predicted by Eq. 4. This suggested that the g _rel/V curves might be better described by a function of the form

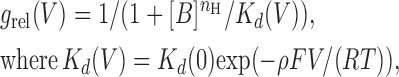(5)

and n _H < 1 for S1-WT. This equation predicts a Boltzmann function with parameters

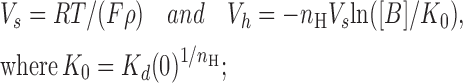(6)

the predictions of these equations are consistent with all our observations summarized in Fig. 3 (C–E).

Finally, we examined the dependence of the “leak” on spermine concentration (Fig. 3 F, colored symbols) and found that it could be reasonably described by a simple voltage-independent binding equation (Fig. 3 F, solid fit line) of the form

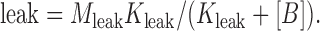(7)

The dissected voltage-dependent and -independent components described in Eqs. 5–7 were then reassembled to yield the function

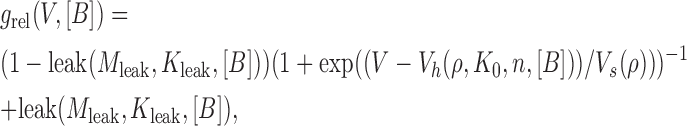(8)

where V_s(ρ), V_h(ρ, K ₀, n _H, [B]), and leak(M _leak, K _leak, [B]) are given by Eqs. 6 and 7. With the five parameters K ₀, ρ, n _H, M _leak, and K _leak left free, Eq. 8 could be used for global fitting of our data obtained under different conditions. Indeed, we could obtain a reasonable fit to the ensemble of all four g _rel/V curves obtained in the same patch at four different spermine concentrations (Fig. 4 B, black fit lines).

Figure 4.

Spermine block of homotetrameric S1-WT, S1-ND, and S2-ND channels characterized by global fitting. (A, C, and E) Families of normalized ramp I/V curves obtained in patches containing S1-WT (A), S1-ND (C), and S2-ND (E) channels; in the absence of (black lines), or in the presence of 5 (red lines), 20 (cyan lines), 100 (blue lines), and 500 μM (green lines) spermine. Except for S2-ND, the ramp I/V curves were leak subtracted. (B, D, and F) Families of g _rel/V curves obtained from the I/V curves shown in (A, C, and E) (solid symbols, color coding as in A, C, and E). Families of solid black lines represent global fits to the ensembles of four g _rel/V curves. Obtained fit parameters were K ₀ = 3.19 mM, ρ = 0.67, n _H = 0.86, M _leak = 0.67, K _leak = 121 μM for S1-WT (B); K ₀ = 2.31 μM, ρ = 3.34, n _H = 1.13 for S1-ND (D); and K ₀ = 4.69 μM, ρ = 3.05, n _H = 1.26 for S2-ND (F).

S1-ND and S2-ND Channels both Show Strongly Rectifying, yet Significantly Different, Patterns of Spermine Block

The S1-ND and S2-ND constructs, when expressed alone, also resulted in macroscopic K⁺ currents. However, as expected, the I/V relationships for these two constructs became strongly rectifying in the presence of intracellular spermine (Fig. 4, C and E; compare to Fig. 4 A). For these two constructs the individual g _rel/V curves were well described by simple Boltzmann functions without a constant leak. Therefore, we globally fitted the ensemble of all four g _rel/V curves obtained in the same patch at different spermine concentrations with Eq. 8, by fixing the leak term to zero, i.e., with only three free parameters (Fig. 4, D and F, solid black lines).

The conductance properties of the S1-ND and S2-ND constructs were qualitatively similar, with K ₀ values approximately three orders of magnitude smaller and ρ values approximately four times larger than for S1-WT, and with n _H values significantly larger than unity (Fig. 4 D, F, and Table I). However, the parameters obtained for S1-ND and S2-ND were slightly but significantly different from each other, suggesting that SUR1 and SUR2A can differentially influence the conformation of the pore.

TABLE I.

Average Parameters of Various Homomeric or Heteromeric Channels Obtained from Global Fitting

S1-WT+S1-ND
Component	0	1	2	3	4
K 0 (μM)	2.48 ± 0.17 (14)	6.97 ± 0.49 (14)	288 ± 9.9 (14)	2220 ± 313 (14)	3610 ± 458 (15)
ρ	3.08 ± 0.07 (14)	2.89 ± 0.07 (14)	2.63 ± 0.03 (14)	0.83 ± 0.03 (14)	0.66 ± 0.02 (15)
n H	1.13 ± 0.01 (14)	0.97 ± 0.03 (14)	0.82 ± 0.02 (14)	0.81 ± 0.02 (14)	0.77 ± 0.03 (15)
M leak	–	–	–	–	0.72 ± 0.04 (15)
K leak (μM)	–	–	–	–	99.1 ± 11 (15)
S1-WT+S2-ND
Component	0	1	2	3	4
K 0 (μM)	6.55 ± 0.34 (14)	219 ± 3.6 (14)	2570 ± 391 (14)	3230 ± 185 (14)	3610 ± 458 (15)
ρ	2.84 ± 0.05 (14)	2.74 ± 0.05 (14)	1.49 ± 0.13 (14)	0.75 ± 0.03 (14)	0.66 ± 0.02 (15)
n H	1.25 ± 0.01 (14)	0.93 ± 0.05 (14)	0.92 ± 0.04 (14)	0.91 ± 0.04 (14)	0.77 ± 0.03 (15)
M leak	–	–	–	–	0.72 ± 0.04 (15)
K leak (μM)	–	–	–	–	99.1 ± 11 (15)

Components 0–4 for S1-WT+S1-ND and S1-WT+S2-ND are defined in the text. The parameters listed for component 4 were obtained by fitting data from homomeric S1-WT channels. The parameters listed for components 0 for S1-WT+S1-ND and S1-WT+S2-ND were obtained by fitting data from homomeric S1-ND and S2-ND channels, respectively.

Coassembly of S1-WT and S1-ND subunits follows a pattern of free binomial mixing

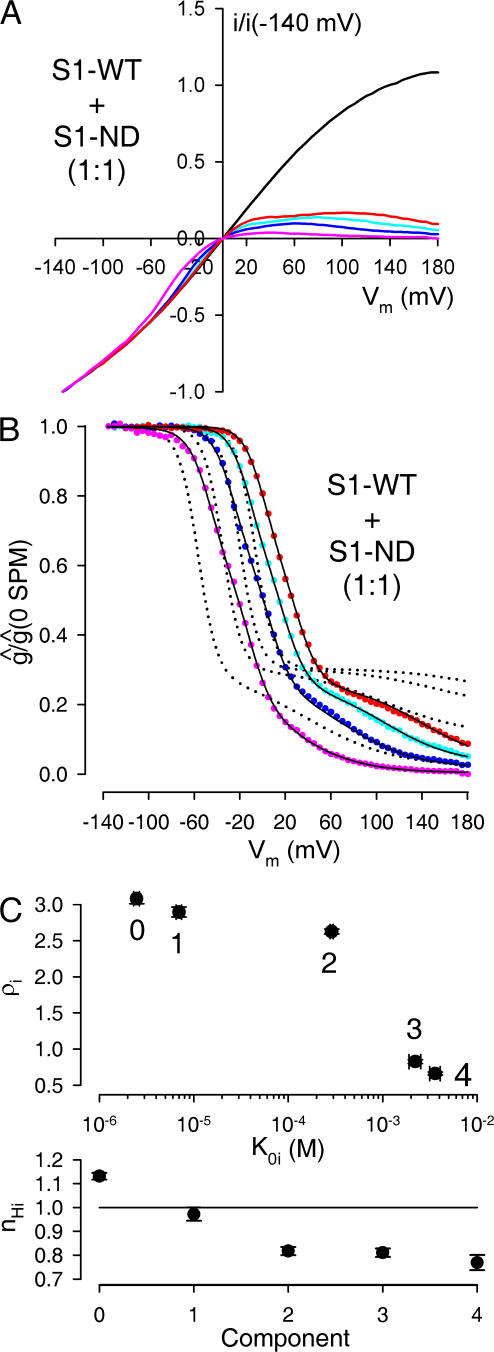
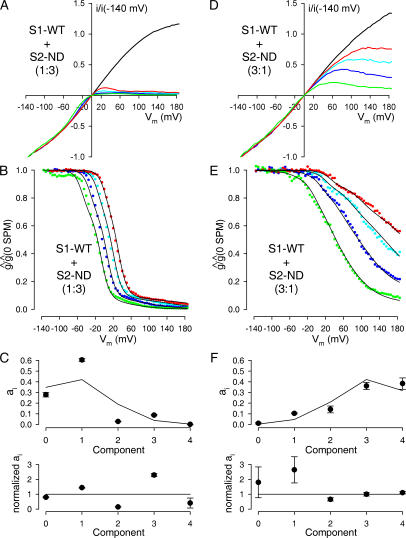
We next tested whether S1-WT and S1-ND could coassemble into functional channels by studying the effect of spermine in patches excised from oocytes that had been injected with equal amounts (3+3 ng) of cRNA encoding for these two tandem constructs (Fig. 5 A). If the two types of construct could not coassemble then in such patches all channels should be either S1-WT or S1-ND homotetramers, and the g _rel/V curves should be well described by a weighted average of those of the two parent constructs (compare, Fig. 4, B and D). Fig. 5 B demonstrates that this was not the case. The best global fit to the family of g _rel/V curves assuming a mixture of the two parent components clearly failed to describe the data (Fig. 5 B, dotted lines), indicating that heteromeric channels containing both S1-WT and S1-ND subunits were present in the patch.

Figure 5.

Spermine block of channels resulting from coexpression of a 1:1 molar ratio of S1-WT and S1-ND subunits reveals random coassembly. (A) Family of normalized, leak-subtracted ramp I/V curves, obtained in a patch from an oocyte injected with a 1:1 molar ratio of S1-WT+S1-ND cRNA; in the absence of (black line), or in the presence of 5 (red line), 20 (cyan line), 100 (blue line), and 1,000 μM (pink line) spermine. (B) Family of g _rel/V curves obtained from the I/V curves shown in A (solid symbols, color coding as in A). The family of solid black lines represents a 10-free parameter global fit to the ensemble of the four g _rel/V curves, assuming random coassembly. Obtained fit parameters were p = 0.46, K ₀₁ = 7.02 μM, ρ₁ = 2.83, n _H1 = 0.97, K ₀₂ = 247 μM, ρ₂ = 2.47, n _H2 = 0.77, K ₀₃ = 2.30 mM, ρ₃ = 0.87, n _H3 = 0.77. The parameters for components 0 and 4 were fixed to the values shown in Table I. The family of dotted black lines represents the best global fit assuming no coassembly between S1-WT and S1-ND subunits. (C) Visual display of average fit parameters for components i = 0…4. Numbers in the top panel identify components.

To obtain information on the relative abundance of the five putative channel populations containing 0, 1, 2, 3, and 4 S1-WT subunits we fitted the obtained families of g _rel/V curves with a mixture of five functions of the form given in Eq. 8, using the following constraints. First, the parameters of components 0 (4 S1-ND subunits) and 4 (4 S1-WT subunits) were fixed to the averages obtained for the corresponding homotetrameric channels (Table I). Second, we assumed a monotonous change of all parameters as a function of the number of S1-WT subunits (i.e., K _0,i ≤ K _0,i+1; ρ_i ≥ ρ_i+1; n _H,i ≥ n _H,i+1). Third, in initial trials in which we left the leak parameters of the intermediate components free, these fits invariably returned M_leak,i = 0 for all i = 0,..3, suggesting that the presence of one mutant Kir subunit is sufficient to suppress the leak component described in Eq. 8. We therefore only allowed three free parameters (K _0,i, ρ_i, and n _H,i) for each of components 1, 2, and 3.

If, as expected, the single point mutation N160D in the Kir6.2 subunit does not greatly alter subunit folding and assembly, then the relative abundances of the channel populations containing 0, 1, 2, 3, and 4 S1-WT subunits (a _i; i = 0, 1, 2, 3, 4) should follow a binomial distribution described by equation

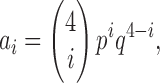(9)

where p is the fraction of all tandem constructs in the membrane that contain a WT pore subunit (Glowatzki et al., 1995), and q = 1 − p. Thus, all a _i values are functions of the single parameter p, leaving 10 free parameters in the global fitting process. As expected, the families of g _rel/V curves obtained for S1-WT+S1-ND coexpression experiments using a 1:1 mixing ratio of cRNAs could be perfectly fitted assuming free binomial mixing (Fig. 5 B, solid black lines), and these fits returned p values close to 0.5 (p = 0.46 ± 0.005; n = 14), i.e., p:q ratios close to the expected ratio of 1:1 (p:q = 1:1.19 ± 0.02). The averages of the parameters obtained for K _0,i, ρ_i, and n _H,i (i = 1, 2, 3) are plotted in the panels of Fig. 5 C, and summarized in Table I.

Fit Parameters Obtained for Heteromeric S1-WT/S1-ND Channel Populations, and Free Binomial Mixing, Adequately Describe Spermine Block over a Tenfold Range of RNA Mixing Ratios

If the three intermediate components that appeared in the g _rel/V curves in the S1-WT+S1-ND coexpression experiments are truly attributable to heteromeric channels containing 1, 2, and 3 S1-WT subunits, and if the parameters we obtained from these fits regarding these components (Fig. 5 C and Table I) are correct, then a mixture of the same five mathematical functions, albeit with altered fractional amplitudes, should adequately describe the families of g _rel/V curves even if S1-WT and S1-ND subunits are coexpressed at nonequal ratios. Moreover, if our conclusion of random mixing is correct, then the fractional amplitudes of these components should still follow a binomial distribution, albeit with an altered p value.

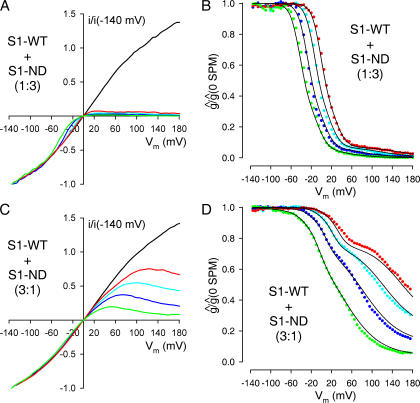
To test the reliability of our analytical procedure, we injected oocytes with S1-WT and S1-ND cRNAs premixed at molar ratios of 1:3 and 3:1, and then studied the voltage dependence of spermine block of the resulting channels (Fig. 6, A and C). We then performed a global fit to the resulting families of g _rel/V curves (Fig. 6, B and D, colored symbols) with only p left as a free parameter, while all other parameters were fixed to their average values obtained in the 1:1 coexpression experiments described in the previous section (Fig. 5 C and Table I). Despite the fact that in these experiments an ensemble of four curves was fitted using a single free parameter, these fits provided a reasonable description of the observed data under both situations (Fig. 6, B and D, solid black lines). Moreover, we obtained p values close to 0.25 (0.32 ± 0.01; n = 9) and 0.75 (0.75 ± 0.008; n = 5), respectively, for the 1:3 and 3:1 coexpression experiments, i.e., p:q ratios close to the expected values of 1:3 (1:2.12 ± 0.13) and 3:1 (3.00 ± 0.12: 1).

Figure 6.

Spermine block of channels resulting from coexpression of a 1:3 or 3:1 molar ratio of S1-WT and S1-ND subunits verifies the global fitting procedure. (A and C) Families of normalized, leak-subtracted ramp I/V curves obtained in patches from oocytes injected with a 1:3 (A) or 3:1 (C) molar ratio of S1-WT+S1-ND cRNA; in the absence of (black lines) or in the presence of 5 (red lines), 20 (cyan lines), 100 (blue lines), and 500 μM (green lines) spermine. (B and D) Families of g _rel/V curves obtained from the I/V curves shown in A and C (solid symbols, color coding as in A and C). Families of solid black lines represent global fits to the ensembles of four g _rel/V curves assuming random coassembly, but allowing for only a single free parameter (p). All other parameters were fixed to the values shown in Table I. Obtained fit parameters were p = 0.28 in B and p = 0.76 in D.

S1-WT and S2-ND Subunits Readily Coassemble in a Random Manner

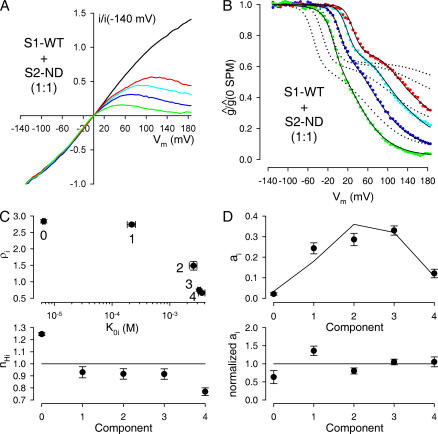
We next proceeded to address a possible coassembly of S1-WT and S2-ND subunits by first injecting oocytes with a 1:1 molar ratio of the two parental cRNAs. As before, we obtained I/V relationships in the presence of different concentrations of spermine (Fig. 7 A) and constructed families of g _rel/V curves (Fig. 7 B, colored symbols).

Figure 7.

Spermine block of channels resulting from coexpression of a 1:1 molar ratio of S1-WT and S2-ND subunits reveals near-random coassembly. (A) Family of normalized, leak-subtracted ramp I/V curves, obtained in a patch from an oocyte injected with a 1:1 molar ratio of S1-WT+S2-ND cRNA; in the absence of (black line), or in the presence of 5 (red line), 20 (cyan line), 100 (blue line), and 500 μM (green line) spermine. (B) Family of g _rel/V curves obtained from the I/V curves shown in (A) (solid symbols, color coding as in A). The family of solid black lines represents a 13-free parameter global fit to the ensemble of the four g _rel/V curves, allowing for nonrandom coassembly. Obtained fit parameters were a ₁ = 0.306, a ₂ = 0.261, a ₃ = 0.244, a ₄ = 0.188, K ₀₁ = 172 μM, ρ₁ = 2.84, n _H1 = 0.95, K ₀₂ = 2.49 mM, ρ₂ = 1.28, n _H2 = 0.95, K ₀₃ = 2.82 mM, ρ₃ = 0.78, n _H3 = 0.95. The parameters for components 0 and 4 were fixed to the values shown in Table I. The family of dotted black lines represents the best global fit assuming no coassembly between S1-WT and S2-ND subunits. (C) Visual display of average fit parameters for components i = 0…4. Numbers in the top panel indicate the identities of the components. (D) Average fractional amplitudes a _i (top) and normalized fractional amplitudes (bottom) obtained for components i = 0…4. For normalization, a p value was first calculated using Eq. 10; each a _i value was then divided by the fractional amplitude expected for a binomial distribution generated by that particular p (Eq. 9).

Following the reasoning discussed earlier for the S1-WT+S1-ND coexpression experiments, we first tried whether the families of g _rel/V curves could be described by a simple weighted average of those of the two parent constructs (Fig. 4, compare B and F).

However, these attempts again clearly failed to provide an adequate description of the data (Fig. 7 B, dotted lines). This is a clear indication that heteromeric channels containing both S1-WT and S2-ND subunits were present in the membrane, i.e., that SUR1 can coassemble with SUR2A.

But to what extent does such coassembly occur? To try to address this question we performed global fitting in a similar way as described above for the S1-WT+S1-ND coexpression experiments, except that we did not impose the constraint of simple binomial mixing; i.e., the fractional amplitudes a _i of the five components were left free. Although this resulted in altogether 13 free parameters for the fitting process, it must be appreciated that this procedure provided adequate fits to an ensemble of four curves obtained at four different spermine concentrations (Fig. 7 B, solid black lines). The averages of the parameters obtained for K _0,i, ρ_i, and n _H,i (i = 1, 2, 3) are plotted in the panels of Fig. 7 C and summarized in Table I.

If our interpretation of the intermediate components of these fits is correct, i.e., if these are attributable to heteromeric channels containing 1, 2, and 3 S1-WT subunits, then using our obtained estimates of fractional amplitudes a _i (Fig. 7 D, top, black symbols), we can estimate the total fractions of S1-WT (p) and S2-ND subunits (q) in the membrane as

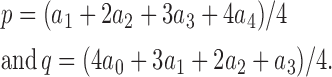(10)

As expected for a 1:1 RNA mixing ratio, we obtained p values of close to 0.5 (p = 0.57 ± 0.001 (n = 14)), i.e., p:q ratios close to the expected ratio of 1:1 (p:q = 1.35 ± 0.06:1).

Finally, using these p and q values and Eq. 9 we can also calculate what a _i values would be expected for random binomial mixing (Fig. 7 D, top, solid line). This comparison reveals that our observed fractional amplitudes are similar to those expected for random mixing of S1-WT and S2-ND subunits. For each of the five components, the observed a _i values are within twofold of those expected for random mixing, as revealed by a plot of normalized a _i values (Fig. 7 D, bottom) obtained by dividing each a _i with the respective value calculated using Eq. 9.

Fit Parameters Obtained for Heteromeric S1-WT/S2-ND Channel Populations Adequately Describe Spermine Block over a 10-Fold Range of RNA Mixing Ratios

To test the reliability of our approach we again asked whether a mixture of the same five mathematical functions are able to describe the families of g _rel/V curves even if S1-WT and S2-ND subunits are coexpressed at nonequal ratios. To this end, we injected oocytes with S1-WT and S2-ND cRNAs premixed at molar ratios of 1:3 and 3:1, and then studied the voltage dependence of spermine block of the resulting channels (Fig. 8, A and D). We then fitted the resulting families of g _rel/V curves (Fig. 8, B and E, colored symbols) while leaving only the fractional amplitudes a _i as free parameters; all other parameters were fixed to their average values obtained in the 1:1 coexpression experiments above (Fig. 7 C and Table I). These fits, although using only four free parameters, provided a reasonable description of the observed families of g _rel/V curves under both situations (Fig. 8, B and E, solid black lines). Moreover, when we then calculated p and q values using Eq. 10, we again obtained p values close to 0.25 (0.23 ± 0.008; n = 5) and 0.75 (0.75 ± 0.02; n = 5), respectively, for the 1:3 and 3:1 coexpression experiments, i.e., p:q ratios close to the expected values of 1:3 (1:3.34 ± 0.16) and 3:1 (3.11 ± 0.41:1). Finally, as far as the moderate quality of these fits allows us to draw quantitative conclusions about the fitted fractional amplitudes a _i, the latter seemed to loosely follow the respective binomial distribution in both cases (Fig. 8, C and F).

Figure 8.

Spermine block of channels resulting from coexpression of a 1:3 or 3:1 molar ratio of S1-WT and S2-ND subunits verifies the global fitting procedure. (A and D) Families of normalized, leak-subtracted ramp I/V curves obtained in patches from oocytes injected with a 1:3 (A) or 3:1 (D) molar ratio of S1-WT+S2-ND cRNA; in the absence of (black lines), or in the presence of 5 (red lines), 20 (cyan lines), 100 (blue lines), and 500 μM (green lines) spermine. (B and E) Families of g _rel/V curves obtained from the I/V curves shown in A and D (solid symbols, color coding as in A and C). Families of solid black lines represent global fits to the ensembles of four g _rel/V curves allowing for only four free parameters (a ₁…a ₄). All other parameters were fixed to the values shown in Table I. Obtained fit parameters were a ₁ = 0.590, a ₂ = 0.022, a ₃ = 0.065, a ₄ = 0.003 in B; and a ₁ = 0.091, a ₂ = 0.170, a ₃ = 0.359, a ₄ = 0.363 in E. The p values calculated from a _i using Eq. 10 were p = 0.21 in B, and p = 0.74 in E.

ATP and Tolbutamide Sensitivities of Channels Formed from the Coexpression of Free SUR1, SUR2A, and Kir6.2 also Reveal the Coassembly of SUR1 and SUR2A

Finally, we asked whether the coassembly of SUR1 and SUR2A to form heteromeric K_ATP channels requires the artificial covalent linkage between the SUR and Kir6.2 subunits in our tandem constructs. Since homomeric SUR1 and SUR2A channels show very different ATP and tolbutamide sensitivities (Fig. 1 A; Gribble et al., 1998), we took advantage of these two properties to probe for the coassembly of SUR1 and SUR2A when free SUR1, SUR2A and Kir6.2 are coexpressed. Fig. 9 A shows representative current traces in the presence of various internal ATP concentrations from inside-out macropatches excised from oocytes injected with SUR1+Kir6.2, SUR2A+Kir6.2, or SUR1+SUR2A (1:1 molar ratio)+Kir6.2 cRNAs. Fig. 9 B shows the extracted ATP dose response curve for SUR1+SUR2A+Kir6.2 (red symbols); the curves for SUR1+Kir6.2 (black) and SUR2A+Kir6.2 (blue) are replotted from Fig. 1 A for comparison. The dose response curve for SUR1+SUR2A+Kir6.2 was in between those of the homomeric channels but was clearly not well fitted assuming that SUR1 and SUR2A do not coassemble; i.e., a weighted average of the SUR1+Kir6.2 and SUR2A+Kir6.2 fit curves failed to describe the SUR1+SUR2A+Kir6.2 data, whether the two fractional amplitudes were fixed to 0.5 or left free (red dotted and red solid lines, respectively). Next, we tested the current responses to tolbutamide in patches obtained from oocytes expressing SUR1, SUR2A, or SUR1+SUR2A(1:1 molar ratio)+Kir6.2 (Fig. 10 A), and constructed averaged tolbutamide dose–response curves (Fig. 10 B). Consistent with prior reports, the curve for homomeric SUR1 channels suggested two binding sites with different affinities for tolbutamide (black symbols and line), while that for SUR2A channels revealed only one low affinity tolbutamide binding site (blue symbols and line; Fig.10 B) (Gribble et al., 1998). Again, the tolbutamide dose–response curve obtained from oocytes coexpressing SUR1 and SUR2A (red symbols) was in between those of the homomeric channels but could not be fitted assuming no coassembly between SUR1 and SUR2A (Fig.10 B, red lines).

DISCUSSION

Giblin et al. (2002) did not find evidence, biochemical or functional, that SUR1 and SUR2A could interact and concluded that SUR1 and SUR2 cannot form functional heteromeric K_ATP channels. Contradictory to this study, several reports suggested/indicated that SUR1 and SUR2 can coassemble into functional channels. First, single K_ATP channels obtained from rat atrial myocytes displayed both SUR1 and SUR2 properties (Baron et al., 1999). Second, three populations of dopaminergic neurons, expressing Kir6.2 with SUR1, SUR1+SUR2B, and SUR2B, displayed K_ATP currents with high, intermediate, and low sensitivities, respectively, to tolbutamide and metabolic inhibition (Liss et al., 1999). Importantly, the currents with intermediate tolbutamide sensitivity were best fitted with a single Hill equation, a result inconsistent with a mixed population of homomeric channels with no coassembly of SUR1 and SUR2B. Third, the attenuations of cardiac K_ATP currents by antisense oligodeoxynucleotides directed against SUR1, SUR2, or both suggested the presence of native SUR1-SUR2 hybrid channels (Yokoshiki et al., 1999). Amid such controversy, we have revisited this unsettled issue of whether, and to what extent, different SUR subtypes are compatible for coassembly.

We used two approaches to study this question. The more direct approach we used was to study the pharmacological properties, such as ATP and tolbutamide sensitivities, of the currents present in oocytes coexpressing free SUR1, SUR2A, and Kir6.2, and to compare these properties to those observed in oocytes expressing homomeric SUR1 or SUR2A channels. These data are inconsistent with a model in which SUR1 and SUR2A do not coassemble (Fig. 9 B and Fig. 10 B). Our lack of knowledge of the ATP or tolbutamide sensitivities of the various possible heteromeric channel populations introduces too many free parameters to allow us to construct a detailed model of coassembly for fitting the relatively small amount of data contained in a dose response curve. Nevertheless, these qualitative studies strongly suggest that SUR1 and SUR2A can form heteromeric K_ATP channels.

The second, more quantitative, approach, the focus of this study, was based on spermine block of channels formed by coexpressing two dimeric constructs, S1-WT and S2-ND (S1-WT+S1-ND served as a control for coassembly). Three potential concerns need to be addressed before this methodology can be given credit. The first, immediate question is whether, and to what extent, the channels formed from tandem dimers resemble native channels. Our experiments testing ATP sensitivity, as well as responsiveness to pharmacological agents like sulphonylureas and K⁺ channel openers, confirmed that dimeric channels retained the properties of the nonconjugated wild-type channels (Fig. 1 A, Fig. 2 A, and Fig. S1 A). A second concern is whether the artificial linkage created in the tandems could potentially force the coassembly of SUR1 and SUR2A. This is highly unlikely. First, our studies on ATP and tolbutamide responses of free SUR1+SUR2A+Kir6.2 (Figs. 9 and 10) already show that the covalent linkage is not necessary for the coassembly of SUR1 and SUR2A. Second, the large suppression of basal currents and the enhancement of glibenclamide-sensitive currents in oocytes expressing S1-WT+S2-ND, as compared with those expressing only S2-ND (Fig. 2 A), are strong indicators of coassembly of S1-WT and S2-ND. However, these same effects were also observed in oocytes expressing SUR1+Kir6.2 together with S2-ND (Fig. S1). Therefore, the covalent linkage in S1-WT is not required for its coassembly with S2-ND. Finally, one could argue that our experiments using spermine only report on the coassembly of the pore-forming Kir subunits. Thus, it remains a formal concern that when S1-WT and S2-ND are coexpressed, misshapen “monster” channels might form. For example, one could imagine that three S2-ND subunits might be completed by only the Kir portion of an S1-WT protein (yielding a pore with intermediate spermine sensitivity), while the missing fourth SUR subunit is recruited from only the SUR portion of a fourth S2-ND protein. However, besides steric considerations which render the existence of such channels highly unlikely, the following experimental evidences argue for a normal, native-like coassembly of the tandem channels. First, the pharmacological properties of the currents recorded from oocytes coexpressing S1-WT+S2-ND (Fig. 2) provided evidence for coassembly based on properties that solely depend on the SUR portion of the tandems, suggesting that in the heteromeric channels both types of SUR must be present. Second, we found that coexpression of only Kir6.2 with S2-ND exerts a dominant negative effect resulting in almost complete suppression of S2-ND currents (Fig. S1, green). This is a clear indication that any S2-ND–based channels into which a single free Kir6.2 became incorporated could not be completed into a functional channel by only the SUR portion of a fourth S2-ND protein. Thus, recruitment of a fourth S2-ND tandem into the channel complex is prevented by the presence of the small free Kir subunit, let alone then by the presence of an entire huge S1-WT protein, the Kir portion of which forms part of a functional pore. All these evidences validate our approach to use tandem dimers to study the coassembly of SUR1 and SUR2A in a quantitative manner.

Our study of spermine block of S1-WT channels over a large voltage range and a series of spermine concentrations revealed two interesting unexpected properties of steady-state block of the WT Kir6.2 pore by spermine. First, the smaller than expected shifts of the steady-state g _rel/V curve upon incremental changes in spermine concentration results in an apparent negative cooperativity (Fig. 3, B and E). This might be the result of a less-than-linear dependence on concentration of the apparent on-rate of the blocker (i.e., if the apparent on-rate is approximated by k _on∼[B]^n_H , where n _H < 1). Second, the voltage-independent “leak” component of the g _rel/V curves suggests that the voltage-dependent binding of spermine in a relatively shallow site in the pore does not, per se, completely occlude ion passage. The remaining conductance for K⁺ ions (the “leak”) might be modulated by binding of spermine to some other (superficial) site on the channel, outside the membrane electrical field. The exact biophysical mechanism of these phenomena was irrelevant to the questions tackled by this study, and was therefore not further considered. However, these observations provide an interesting starting point for future studies of spermine on- and off-rates that will help clarify the unusual interaction of spermine with the weakly rectifying Kir6.2 pore.

The mutant Kir6.2[N160D] pore revealed another interesting unexpected phenomenon: its pore character is slightly, but distinctly, different, depending on whether it is fused to SUR1 or SUR2A (Fig. 4, compare D and F; and Table I). Consistent with this finding, the shift in ATP sensitivity caused by the N160D pore mutation is much more pronounced in the S2-tandem than in the S1-tandem. Thus, SUR1 and SUR2A differentially modulate the conformation of the pore- forming Kir6.2 subunit.

Unfortunately, the latter finding impeded our original plan of using the fit parameters obtained for the intermediate components in S1-WT+S1-ND coexpression experiments to then fit the S1-WT+S2-ND coexpression data. This resulted in a much larger number of free parameters in the latter experiments and finally motivated us to turn to global fitting of larger sets of data. Nevertheless, the fact that in both S1-WT+S1-ND and S1-WT+S2-ND coexpression experiments the parameters obtained for a 1:1 RNA mixing ratio then proved adequate to fit the data obtained using either 1:3 or 3: 1 ratios increases our confidence that these parameters are really representative of heteromeric S1-WT/S1-ND and S1-WT/S2-ND channels assembled at various subunit stoichiometries.

Our data indicate that S1-WT and S1-ND, or S1-WT and S2-ND, can randomly coassemble to form functional K_ATP channels (Figs. 5–8 ). The fact that S1-WT and S1-ND coassemble indiscriminately indicates that the N160D point mutation per se does not influence coassembly of Kir6.2 subunits either in a positive or in a negative manner. Consequently, the observed coassembly of SUR1 and SUR2A subunits should happen identically in the presence of only WT Kir6.2 subunits.

In conclusion, we have demonstrated that, when coexpressed within the same cell, SUR1 and SUR2A will coassemble randomly. Our data indicate that in a cell that expresses approximately equal amounts of SUR1 and SUR2A ∼86% of all K_ATP channels will contain both types of subunits, while only ∼14% will remain homomeric (Fig. 7 D). Based on our results it seems very likely that heteromeric K_ATP channels are formed in native cells coexpressing SUR1 and SUR2; this may explain the displayed current phenotypes, such as intermediate metabolic sensitivities and pharmacological profiles observed in such cells (Baron et al., 1999; Liss et al., 1999; Poitry et al., 2003; Yunoki et al., 2003). The physiological role of these heteromeric channels during metabolic stresses, as well as their responses to drugs such as sulfonylureas and potassium channel openers, remain to be established.