Coordination of Growth Rate, Cell Cycle, Stress Response, and Metabolic Activity in Yeast

Abstract

We studied the relationship between growth rate and genome-wide gene expression, cell cycle progression, and glucose metabolism in 36 steady-state continuous cultures limited by one of six different nutrients (glucose, ammonium, sulfate, phosphate, uracil, or leucine). The expression of more than one quarter of all yeast genes is linearly correlated with growth rate, independent of the limiting nutrient. The subset of negatively growth-correlated genes is most enriched for peroxisomal functions, whereas positively correlated genes mainly encode ribosomal functions. Many (not all) genes associated with stress response are strongly correlated with growth rate, as are genes that are periodically expressed under conditions of metabolic cycling. We confirmed a linear relationship between growth rate and the fraction of the cell population in the G0/G1 cell cycle phase, independent of limiting nutrient. Cultures limited by auxotrophic requirements wasted excess glucose, whereas those limited on phosphate, sulfate, or ammonia did not; this phenomenon (reminiscent of the “Warburg effect” in cancer cells) was confirmed in batch cultures. Using an aggregate of gene expression values, we predict (in both continuous and batch cultures) an “instantaneous growth rate.” This concept is useful in interpreting the system-level connections among growth rate, metabolism, stress, and the cell cycle.

INTRODUCTION

The most fundamental system-level challenge for cell physiology, especially for microorganisms, is the achievement of balanced growth in the face of a fluctuating environment. A variety of cellular processes, carried out by proteins expressed from thousands of genes, have to be coordinated to allow cells to efficiently reproduce, grow and compete for resources. Among the processes that have to be coordinated are the extraction of energy and metabolites from the environment; biosynthesis of appropriate amounts of hundreds of molecules large and small; and the events of the cell division cycle, including replication of the DNA and assembly and segregation of subcellular organelles and structures. All of this coordination has to be done in such a way as to allow the cell to modify its activities, often on a very short time scale, when the environment changes.

The goal of understanding how cells achieve balanced growth (or growth homeostasis) has been pursued since the middle of the 20th century, and much progress has been made. In today's textbooks, one can find coherent (if not quite comprehensive) accounts of metabolic regulation of all kinds: regulation of macromolecular synthesis, control of the cell cycle, assembly and distribution of organelles, and response of these processes to all kinds of environmental perturbations and stresses. However, until recently, there have been no ways of following the expression of all genes at once. Of necessity, therefore, progress has been made by focusing on the roles of individual genes in each process, often through mutations in them. In the last decade, microarray technology has allowed genome-scale gene expression studies of the yeast cell cycle (Cho et al., 1998; Spellman et al., 1998; Pramila et al., 2006; Kudlicki et al., 2007); the response to various stresses (Gasch et al., 2000; Gasch et al., 2001), and a variety of metabolic circumstances, such as the diauxic shift from growth on glucose to growth on ethanol (DeRisi et al., 1997; Brauer et al., 2005) and growth at steady state in a variety of limiting nutrients (Boer et al., 2003; Saldanha et al., 2004; Regenberg et al., 2006; Castrillo et al., 2007). A couple of recent studies (Klevecz et al., 2004; Tu et al., 2005) examined gene expression during oscillatory behavior in chemostats, from which emerged a potential connection with cell cycle control (Futcher, 2006).

We sought to explore, systematically and quantitatively, the relationship between the growth rate and genome-wide patterns of gene expression in exponentially growing, nominally unstressed yeast cultures. We specifically sought to determine which (if any) yeast genes are expressed at a level (measured as mRNA concentration using DNA microarrays) simply correlated to a cell's growth rate, independent of the environmental factors that ultimately mandate the observed instantaneous growth rate. In addition to gene expression, we measured the fraction of unbudded cells (i.e., in the G0/G1 stages of the cell cycle) and the concentrations of glucose and ethanol in the media.

Like other recent studies (Regenberg et al., 2006; Castrillo et al., 2007), we exploited the chemostat continuous culture system (Monod, 1950; Novick and Szilard, 1950) to provide steady-state conditions at different constant growth rates in a variety of media where the growth rate-limiting nutrient is known. The chemostat allows one to control the growth rate of the organism by adjusting the flow rate of fresh medium into the growth chamber providing a defined environment amenable to genome-scale analyses (Hoskisson and Hobbs, 2005).

By analyzing mRNA abundance data we obtained from 36 chemostat cultures (six different limiting nutrients each at six different growth rates), we found that a surprisingly large fraction (∼27%) of all yeast genes are expressed (as measured by relative mRNA abundance) in a way that is closely correlated (either negatively or positively) with the growth rate of the culture. We verified quantitatively, and extended to the conditions of steady-state culture, the relationship between growth rate and the fraction of unbudded cells first suggested by Unger and Hartwell (1976). We also discovered a striking difference between growth limitation by ammonium, sulfate, or phosphate (“natural nutrients”; cf. Saldanha et al., 2004) as distinguished from the nutrients made essential by mutations conferring auxotrophic requirements. When the growth of cultures (either steady state or batch) is limited by phosphate, ammonia, or sulfate, unused glucose is spared, as one might expect, whereas when growth is limited by auxotrophic requirements, excess glucose is completely consumed.

We interpret these results as reflections of system-level regulatory mechanisms, as yet only partially understood, that must underlie the coordination of the growth rate with gene expression, entry into the cell division cycle, the stress response, and energy metabolism.

MATERIALS AND METHODS

Culture Conditions, Strains, and Media

Yeast cultures were grown in chemostats under 36 different continuous culture conditions, namely, six different limiting nutrients each at six different dilution rates. The dilution rates (and therefore the culture's average exponential growth rate, μ) ranged from ∼0.05 h⁻¹ (corresponding to a cell doubling time of about 14 h) to more than 0.3 h⁻¹ (doubling time of about 2 h), and they were verified directly by collecting effluent into graduated cylinders. Chemostat growth was limited by one of the following nutrients: glucose (G), ammonium (N), phosphate (P), sulfate (S), leucine (L), or uracil (U). Chemostats were established in 500-ml fermenter vessels (Sixfors; Infors AG, Bottmingen, Switzerland) containing 300 ml of culture volume, stirred at 400 rpm, and sparged with five standard liters per minute humidified and filtered air. Chemostat cultures were inoculated, monitored and grown to steady state as described previously (Brauer et al., 2005). All cultures were monitored for changes in cell density and dissolved oxygen and grown until these values remained steady for at least 24 h.

For nonauxotrophic limitations (G, N, P, and S), we used strain DBY10085 (relevant genotype Mata MAL2-8C), which is the prototrophic CEN.PK-derived strain described by van Dijken et al. (2000). For limitations with uracil (U) or leucine (L), we used nonreverting mutant versions of the same strain, i.e., DBY9492 (ura3-52) or DBY9497 (leu2-3leu2-11), respectively.

Chemostat cultures were grown in minimal defined (MD) media supplemented with glucose (G, N, P, and S limitations), L limitation, or U limitation. Concentrations of the limiting nutrient were adjusted downward in each MD medium formulation. Detailed base media compositions are given in Table 1. These solutions were autoclaved and supplemented with glucose, metals, and vitamins (and necessary uracil or leucine), added via sterile filtration as described previously (Saldanha et al., 2004).

Table 1.

Composition of chemostat media (values in grams per liter)

Compound	Limiting condition
	G	N	P	S	L	U
CaCl2·2H2O	0.1	0.1	0.1	0.1	0.1	0.1
NaCl	0.1	0.1	0.1	0.1	0.1	0.1
MgSO4·7H2O	0.5	0.5	0.5		0.5	0.5
MgCl·6H2O				0.412
KH2(PO4)2	1	1		1	1	1
KCl			1
(NH4)2SO4	5		5		5	5
NH4Cl				4.05
Glucose	0.8	5	5	5	5	5
Leucine					0.015
Uracil						0.005
Vitamins and metals	As detailed in Saldanha et al. (2004)

Batch culture media were identical to chemostat media except that they contained 1% glucose. Phosphate limiting medium contained a final concentration of 10 mg/ml potassium phosphate and was supplemented with either 200 mg/l final leucine or 40 mg/l final uracil where appropriate. Uracil limiting medium contained 4 mg/l uracil, and leucine limiting media contained 40 mg/l leucine.

The patterns of gene expression in the chemostat under nutrient limitation closely approximate the patterns found in batch cultures in the same medium at the point that the concentration of the limiting nutrient falls to the value found in the corresponding chemostat (Saldanha et al., 2004; Brauer et al., 2005). Thus, there is a well-defined point of correspondence between the physiology of the cells in chemostats and batch cultures in the same medium.

Measurement of Culture Growth Parameters

At each time point, 2 ml of culture was withdrawn and sonicated for 10 s, just enough to break up all clumps of cells, as confirmed in the light microscope. Sonicated cultures were examined under a light microscope at 200× magnification for identification of the proportion of cells with no buds, with small buds or with large buds. Culture density was measured both by absorbance at 600 nm and with a Coulter counter (model Z2; Beckman Coulter, Fullerton, CA), set to count cells with volumes between 8.0 and 250.0 fl; data describing the distribution of cell volumes also were recorded.

Residual glucose and ethanol concentrations were assayed as described by Brauer et al. (2005), and residual phosphate was measured as described by Saldanha et al. (2004).

RNA Isolation, Labeling, Microarray Hybridization, and Data Collection

Samples from chemostats (10 ml) were harvested for RNA by siphoning through a drop-tube followed by vacuum filtration onto nylon filters. Filters were immediately placed into tubes containing liquid nitrogen and stored at −80°C until extracted for RNA.

RNA for microarray analysis was extracted by the acid-phenol method and cleaned using RNeasy mini columns (QIAGEN, Valencia, CA). RNA was amplified and labeled using the Agilent low RNA input fluorescent linear amplification kit (P/N 5184-3523; Agilent Technologies, Palo Alto, CA). This method entails initial synthesis of cDNA by using a poly(T) primer attached to a T7 promoter. Labeled cRNA is subsequently synthesized using T7 RNA polymerase and either cyanine (Cy)3 or Cy5 UTP. Each Cy5-labeled experimental cRNA sample was mixed with the Cy3-labeled reference cRNA and hybridized were hybridized for 17 h at 60°C to an Agilent Yeast V2 oligo microarray. Microarrays were washed, scanned with an Agilent DNA microarray scanner (Agilent Technologies), and analyzed using Agilent Feature Extraction Software version 7.5. Resulting microarray intensity data were submitted to the PUMA Database (http://puma.princeton.edu) for archiving and analysis.

Features flagged as outliers due to low intensity or poor quality were excluded, and the results for each gene, and time point were expressed as the log₂ of the sample signal divided by the signal in the reference channel. The reference RNA for all samples was taken from the glucose-limited chemostat grown at a dilution rate of 0.25 h⁻¹.

Analysis of Gene Expression Data

Hierarchical Clustering.

Expression data were clustered by gene, using the UPGMA algorithm of Eisen et al. (1998). Clusters with an average expression that was either nutrient specific or correlated with growth rate were identified.

Functional Annotation.

Sets of genes were assigned process, function, and cellular components according to the annotations from the Gene Ontology (GO) (Ashburner et al., 2000). The significant representation of GO terms in the set was evaluated by GO Term Finder at the Saccharomyces Genome Database, and by the GO-TermFinder perl module (Boyle et al., 2004) using the Bonferroni-correct p value. Ontologies used were downloaded 7 August 2007 from http://www.geneontology.org, and the GO gene associations for the yeast genome were obtained from the Saccharomyces Genome Database (http://www.yeastgenome.org).

Singular Value Decomposition.

We applied singular value decomposition (SVD) (Alter et al., 2000) to the expression data matrix to identify the major sources of variation in the data. Missing data were imputed using the k-nearest neighbors algorithm (KNN imputation) (Troyanskaya et al., 2001), with k = 10.

Linear Regression Model for Gene Expression Data.

For each of the resulting 5537 genes, expression was individually modeled as a linear function of growth rate. For each gene, this yielded a slope, baseline, and goodness of fit (R²); this slope measures the magnitude of the change in gene expression due to growth rate. We computed p values to assess the significance of slopes and R² values by using the bootstrap technique (Efron, 1993), and we corrected for multiple hypotheses using the False Discovery Rate procedure (Benjamini and Hochberg, 1995). In each bootstrap replicate, a value was drawn at random, with replacement, from each of six sets of six columns (corresponding to chemostat cultures with the same flow rate, regardless of nutrient limitation). The linear model described above was then applied to each of 100,000 replicates, and the parameters describing slope and intercept were retained; see Supplemental Table S1 for complete results. The analysis was performed using R (R Development Core Team, 2007) and MATLAB (Mathworks, Natick, MA).

The distributions of regression slopes corresponding to lists of genes of interest were compared with the bootstrap-generated null distribution. For each such list, a pair of p values was computed to assess the statistical significance of the corresponding sensitivity to growth rate, using a Kolmogorov–Smirnov two-sample test and/or a Wilcoxon–Mann–Whitney two-sample test.

Tests for Correlation with Growth Rate.

Genes were ordered by their bootstrap p value for the slope coefficient relating expression to growth rate. Thus, genes with low ranks were those whose expression profiles correlated significantly with growth rate, either positively or negatively. Bootstrap p values were also computed for R² to assess the significance of a linear response to growth, as captured by the regression model, as opposed to nonlinear response to growth, which we could not exclude a priori (see Supplemental Table S1).

Using these p values, we sought to identify a smaller set of genes that was stringently defined as responding specifically to growth. To do so, we looked for genes whose response to growth was significant (either positive or negative), whose response profile across flow rates was linear beyond chance, and whose response did not change substantially across nutrient limitation regimes. Applying these filters generated a list of 72 genes (“calibration genes” in Supplemental Table S1).

Prediction of Relative Instantaneous Growth Rates.

Relative instantaneous growth rates for novel microarray data were estimated with a linear model calibrated using the regression results from our nutrient limitation data. Specifically, the expression of gene g in microarray condition c was represented as follows:

The expression y_g,c is thus a sum of a condition-specific baseline b_c, a gene-specific baseline b_g, a linear growth rate response with slope x_g to the condition's chemostat flow rate r_c, and an “error” term e_g,c that captures leftover gene-specific variation (both biological and noise).

For any new microarray, the relative growth rate r_c (along with the condition-specific baseline b_c) is unknown. We produce an estimate of the relative growth rate (and of the baseline) by leveraging the regression estimates (of slope and gene-specific baseline) that were obtained for the 72 calibration genes (with bootstrapped p values <10⁻⁵ for both linear fit and slope) in our nutrient limitation data. By assuming an initial estimated baseline b_c⁰ = 0, the relative growth rate and condition-specific baseline are estimated by iteratively updating their values according to the following equations:

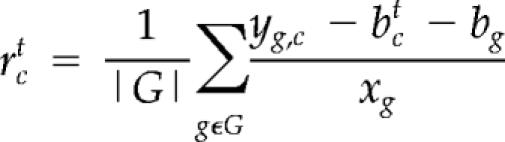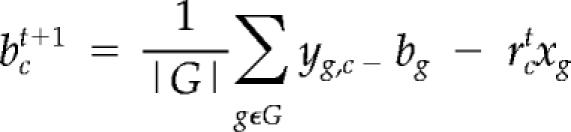For further details, see (Airoldi et al., 2007).

Complete data sets and supplemental materials are archived at http://growthrate.princeton.edu.

RESULTS

To study, systematically and quantitatively, the effect of growth rate on genome-wide gene expression, the cell cycle, and metabolism, we made measurements from 36 chemostat cultures, each of which was at steady state at one of six different growth rates ranging from from 0.05 h⁻¹ (corresponding to a doubling time of about 14 h) to more than 0.3 h⁻¹ (doubling time ∼2 h). All were derivatives of strain CEN.PK growing in the same basic medium, but with one of six different growth rate-limiting nutrients: G, N, S, P, U (in a nonreverting ura3 mutant), or L (in a nonreverting leu2 mutant).

The Fraction of Unbudded Cells Is Linear with Growth Rate for All Limiting Nutrients

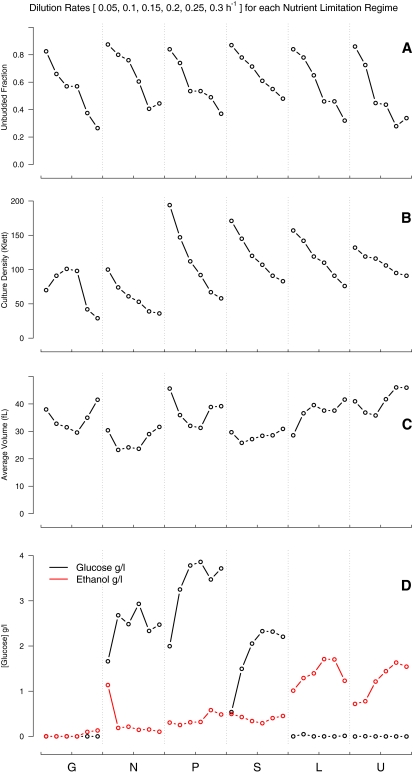
As estimated by phase-contrast microscopy (and verified by measurements of DNA content in a fluorescence-activated cell sorter; Supplemental Figure S1), the fraction of cells in an unbudded (G0 or G1) phase of the cell cycle was a linear function of the dilution rate D (u = 0.936–1.971D; R² = 0.836). The slope of the regression line does not vary significantly between growth conditions (Figure 1A); thus, the expectation of Unger and Hartwell (1976), that slower growing cells spend an increasing proportion of the cell division cycle in G0/G1, was satisfied to considerable precision in all cases. Some previous studies (Rivin and Fangman, 1980; Guo et al., 2004) have found this expectation is not satisfied in nitrogen limitation; we found no significant difference (Supplemental Figure S2). In our experiments, over a nearly sevenfold range of growth rates, yeast cells in balanced growth that grow more slowly spend quantitatively correspondingly larger fractions of the cell doubling time in the unbudded (G0/G1) phase of the cell cycle.

Figure 1.

Measured characteristics of cultures at steady state. Limiting nutrients at bottom of figure. Within each limitation, dilution rates are ordered from 0.05 to 0.3 h⁻¹ in 0.05 h⁻¹ increments. (A) Fraction of unbudded cells. (B) Steady-state culture density in Klett units. (C) Average cell volume. (D) Residual glucose and ethanol levels.

This result stands in contrast to the observation of (Saldanha et al., 2004), who found that in batch cultures starving for phosphate or sulfate, cells accumulate in the unbudded state (G0/G1) within a cell generation of the exhaustion of the limiting nutrient, whereas batch culture auxotrophs starving for leucine or uracil fail to show this orderly response. Here, where cells are growing slowly but not yet actually starving, we see that there is no difference in the fraction of cells in G0/G1 in the chemostats: the same linear relationship with growth rate was observed with all limiting nutrients.

The other cell parameters were consistent with theoretical expectation (Kubitschek, 1970) and previous experience. With the exception of the glucose-limited cultures, cell density is roughly a linear function of the dilution rate (Figure 1B). The case of glucose is more complex, reflecting relatively well understood changes in glucose metabolism at higher steady-state growth rates (Kasper von Meyenburg, 1969; Postma et al., 1989; Alexander and Jeffries, 1990). Average cell volume varies across dilution rate in a complex manner for all limiting nutrients (Figure 1C), with differences that range between 16% (for sulfur) and 31% of the maximum (for phosphate and uracil). However, again with the exception of the glucose-limited cultures, the calculated total cell volume (average cell volume times number of cells) is proportional to the total cell mass (Supplemental Figure S3; R² = 0.819).

Glucose Consumption and Ethanol Production in Nonglucose-Limited Chemostats Depends on the Nature of the Limiting Nutrient

We measured the residual glucose and ethanol in all 36 chemostats, as described in the Methods. The results (Figure 1D) for the glucose-limited chemostats were unremarkable: residual glucose was very low for all growth rates, and only a very small amount of ethanol was produced (and that only at higher growth rates). In contrast, where glucose was not limiting, there were striking differences. In the cases of limiting ammonia, phosphate or sulfate, high levels of glucose remained, and relatively modest amounts of ethanol were produced. In the leucine- and uracil-limited chemostats, the residual glucose was very low, and most of it seemed to have been fermented to ethanol.

This bifurcation of response between phosphate or sulfate limitation, on the one hand, and leucine or uracil limitation, on the other, corresponds to a difference observed previously in batch cultures (Saldanha et al., 2004) found prompt accumulation (within a single cell cycle) of cells in G0/G1 in the cases of limitation by phosphate or sulfate, but not by leucine or uracil. This result suggests that there are at least two mechanisms that relate growth rate and metabolism: one that continuously controls entry into the cell cycle at low growth rates, when cells are not yet starving, and another when cells actually exhaust their limiting nutrients. The failure to limit fermentation and spare the glucose in our leucine and uracil chemostats, and the failure to promptly stop the cell cycle in batch cultures starving for leucine or uracil, may reflect a common signaling failure in case of the auxotrophic limitations.

We studied batch cultures to determine whether this inability to limit glucose consumption is a general phenomenon and not limited to continuous culture conditions. To this end, we compared glucose consumption of auxotrophs and prototophs in batch cultures containing growth-limiting concentrations of phosphate, leucine, or uracil (see Materials and Methods for details). Growth was followed for 24 h, and the glucose consumed was measured during late exponential (t = 8 h) and stationary (t = 24 h) phases. The amount of glucose consumed (normalized to cell number) was approximately twofold higher in auxotrophs that were starved for their auxotrophic requirement compared with either a prototrophic control or to the same strains starved for phosphate and supplemented with ample leucine or uracil (Table 2). Excess consumption of glucose was observed in the late exponential and in the stationary phase of growth (Figure 1). In agreement with (Saldanha et al., 2004), we found that cells grown under these conditions do not mount an appropriate cell cycle arrest upon depletion of an unnatural limitation, but they do arrest in G1/G0 when supplemented with their auxotrophic requirement and starved for phosphate (a natural limitation; Supplemental Figure S2). Thus, glucose wasting in auxotrophs growth-limited for their requirement is not limited to continuous cultures, and this phenomenon, and the failure to arrest the cell cycle first noted in Saldanha et al. (2004), is a feature of which essential nutrient is exhausted first and not of the genotype of the strain.

Table 2.

Response to nutrient limitations in batch culture

Strain	Limiting nutrient	Supplement	Glucose 8 h	Consumed 24 h	% G0/G1 24 h
Prototroph	Phosphate	None	5.91	13.44	91
leu2	Phosphate	Excess leucine	5.04	10.15	93
ura3	Phosphate	Excess uracil	4.78	10.06	92
leu2	Leucine	None	10.22	18.70	60
ura3	Uracil	None	9.86	24.13	73

Batch cultures of isogenic CEN.PK derivatives were grown in chemostat minimal medium containing 1% glucose with limiting phosphate (10 mg/l), leucine (40 mg/l), or uracil (4 mg/l) supplements as described in Materials and Methods. Excess leucine and uracil, when provided, was 200 and 40 mg/l, respectively. The growth curves are shown in Supplemental Figure S3. Specific glucose consumption was calculated for time (t) as the normalized fraction of glucose consumed (grams per liter) using the equation ([glucose]_initial − [glucose]_t)/[glucose]_initial)/cells/ml.

Growth Rate Accounts for a Large Fraction of the Signal in the Gene Expression Pattern

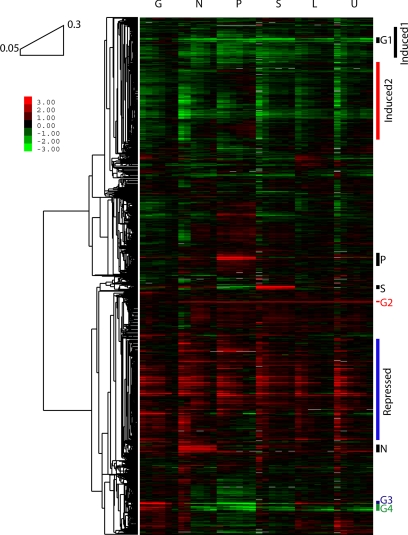
Hierarchical clustering (Eisen et al., 1998) of gene expression from the 36 chemostats is shown in Figure 2. Visual inspection of Figure 2 shows a pattern that is strikingly similar for the six different media, with large groups of genes that increase their expression with increasing growth rate, and comparably large groups decreasing their expression with increasing growth rate. In addition, there are much smaller clusters of genes that are expressed strongly in only one or two media; in general, these do not show as much relationship to growth rate. Fewer than 8% of the genes respond in a uniform, nutrient-specific manner (Figure 2). The largest nutrient-specific cluster, responding to phosphate limitation, comprises just 133 genes (2.4% of the total).

Figure 2.

Hierarchical clustering of expression values across dilution rates and limiting nutrients. Clustering by Pearson correlation reveals many up- and down-regulated clusters spanning all nutrient limitations (e.g., Induced1, Induced2, Repressed) and few smaller gene groups regulated in a nutrient-specific manner (e.g., G1–G4, P, S, and N). Reference for all samples is from a glucose-limited chemostat at 0.25 h⁻¹. Conditions are as described in Figure 1.

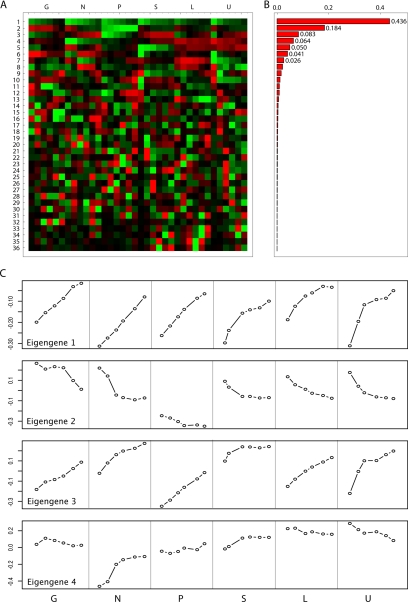
Singular value decomposition analysis (Alter et al., 2000) of these data are visualized in Figure 3A. The fractional information in each eigengene (Figure 3B) shows that the first eigengene accounts for 43.6% of the variation in gene expression present in the data set. The projection of this eigengene correlates very strongly with the culture specific growth rate (R² = 0.69; p < 10⁻⁹), indicating that a large fraction of the signal in gene expression is growth rate specific. Figure 3C shows the average expression as a function of growth rate for the first four eigengenes. From this, one can clearly see that expression of the first eigengene is largely independent of the nature of the limiting nutrient, whereas the second and third eigengenes show both strong growth rate correlation and nutrient specific effects, notably for phosphate (eigengene 2) and sulfate (eigengene 3) limitation. When we come to the fourth eigengene, very little relationship to growth rate remains. The sum of the information in the first three eigengenes amounts to nearly 70% of the total variation.

Figure 3.

SVD decomposition of expression data. Singular value decomposition of the growth rate/nutrient limitation microarray data shows that a large portion of the variation in gene expression (>70%) is related to changes in growth rate. Secondary eigengenes also capture nutrient-specific responses (e.g., phosphate and sulfate). (A) 36 eigengenes. (B) Eigengene weights (eigenvalues). (C) Expression levels of the four most significant eigengenes.

Expression of Many Genes Is Strongly Influenced by Growth Rate to a Degree Characteristic for Each Gene

For each of the 5537 genes in the imputed data, expression was individually modeled as a linear function of growth rate (independent of limiting nutrient). Of these, 3049 genes (55.1%) have expression patterns than fit (at a bootstrapped p < 0.05) this linear model; of these, approximately half (1470, or 26.5% of all genes) have expression patterns that respond significantly (bootstrapped p < 0.05) to growth rate.

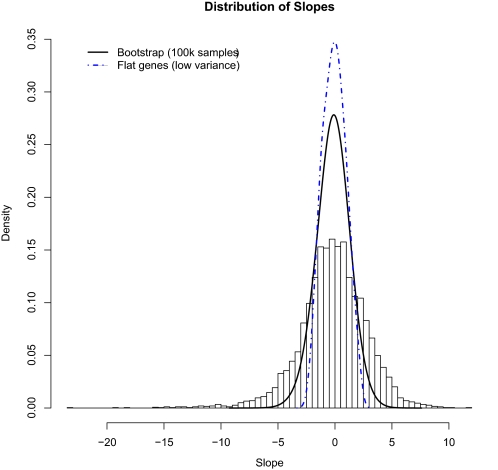
For those genes whose expression is correlated to growth rate, the magnitude of the effect of growth rate on gene expression is given by the slope of the regression of expression on growth rate. The distribution of these slopes (shown in Figure 4 as a histogram) is significantly broader than the null distribution generated by bootstrap sampling (SD 2.97 vs. 1.41). By plotting the positions of a set of genes on this histogram, one can see systematic relationships between the aggregate response to growth rate and any other characteristic a query set of genes might share. In Supplemental Table S1 (see also http://growthrate.princeton.edu), we provide data for all the genes, including the significance with which their expression correlates with growth rate. On the website, we also provide a simple utility that plots the distribution of growth rate slopes for any query set of genes relative to the overall distribution shown in Figure 4.

Figure 4.

Distribution of experimental growth rate responses versus bootstrapped background distribution. A histogram of the estimated regression slopes for 5537 genes is compared with a 100,000-point bootstrapped null distribution of slopes (density estimate; black, solid line) and to the distribution of slopes corresponding to genes that do not respond to growth rate (density estimate; dash-dotted, blue line). The expression responses of genes in our microarray data are significantly broader than expected by chance, whereas genes we determine to be largely unresponsive to changes in growth rate have slopes near zero.

Functional Roles of Genes Strongly Correlated with Growth Rate

To identify the most prominent of the potential functional reasons for the correlation between the expression of some genes and the growth rate, we chose 1608 genes whose expression was best linearly correlated with growth rate (Supplemental Table S2; see Materials and Methods for the details). One subset (337 genes) had negative slopes (more than 1.5 standard deviations less than the average), another subset (291 genes) had positive slopes (more than 1.5 standard deviations more than the average), and the third had low variability (bootstrapped p < 10⁻⁴) and low slope (within 0.5 SD of average), i.e., their expression was not detectably related to growth rate (see the dash-dotted blue line in Figure 4).

Each of these subsets was submitted to GO Term Finder (Boyle et al., 2004) querying all three ontologies (Process, Molecular Function, and Cellular Component). The nature of the GO hierarchy produces highly redundant results in this situation. To maintain only the biologically and statistically strongest relationships, we limited further analysis to GO terms with p < 10⁻³. These results were sorted by the fraction of genes hit within each GO term, and we focused on the terms in which this fraction was at least 10%. The final result (Table 3 and Supplemental Table S2) gives a very clear picture: the processes associated with the gene subset whose expression is negatively related to growth rate are focused on energy metabolism, especially oxidative metabolism; the only functional category that met our stringent criteria was oxidoreducase activity, and the only cellular component implicated at this level of statistical stringency was the peroxisome. Our negatively growth-correlated subset contained 25 and 67% (designated term fraction in Table 3) of the genes annotated to peroxisomes and the peroxisomal matrix, respectively.

Table 3.

GO annotation of genes according to growth rate response

Slope >1.5 SDs below average	337 genes
Process	p value	Gene hits	Term size	Term fraction (%)
Fatty acid β-oxidation	1.80E-04	6	8	75.0
Glutamine family amino acid catabolic process	4.20E-04	7	13	53.8
Energy reserve metabolic process	2.61E-05	12	36	33.3
Glucose metabolic process	8.10E-04	14	65	21.5
Monosaccharide metabolic process	1.10E-04	18	92	19.6
Hexose metabolic process	9.50E-04	16	85	18.8
Cellular carbohydrate metabolic process	7.75E-12	40	213	18.8
Monocarboxylic acid metabolic process	5.86E-06	23	124	18.5
Carbohydrate metabolic process	1.37E-12	43	233	18.5
Energy derivation by oxidation of organic compounds	4.59E-06	25	143	17.5
Generation of precursor metabolites and energy	5.02E-07	30	181	16.6
Coenzyme metabolic process	1.40E-04	22	135	16.3
Alcohol metabolic process	2.80E-04	24	163	14.7
Carboxylic acid metabolic process	6.52E-05	37	312	11.9
Organic acid metabolic process	6.52E-05	37	312	11.9
Function
Oxidoreductase activity	1.50E-07	38	270	14.1
Component
Peroxisomal matrix	1.45E-06	8	12	66.7
Microbody	3.53E-05	14	57	24.6
Peroxisome	3.53E-05	14	57	24.6
Slope >1.5 SDs above average	291 genes
Process
Protein import into mitochondrial matrix	1.00E-07	11	22	50.0
Maturation of SSU-rRNA	1.68E-10	17	44	38.6
Protein import into mitochondrion	4.67E-07	13	37	35.1
Protein targeting to mitochondrion	2.23E-05	13	49	26.5
Mitochondrial transport	6.11E-05	14	62	22.6
Ribosome biogenesis and assembly	4.73E-15	57	402	14.2
Ribonucleoprotein complex biogenesis and assembly	2.20E-12	58	473	12.3
Translation	8.47E-19	83	686	12.1
rRNA metabolic process	8.51E-05	29	247	11.7
rRNA processing	1.60E-04	28	240	11.7
Macromolecule biosynthetic process	1.16E-19	97	881	11.0
Function
snoRNA binding	5.52E-06	11	32	34.4
Structural constituent of ribosome	3.72E-43	71	230	30.9
Protein transporter activity	2.10E-04	12	53	22.6
Structural molecule activity	3.34E-30	72	357	20.2
Component
Mitochondrial outer membrane translocase complex	2.04E-05	6	8	75.0
Cytosolic large ribosomal subunit (sensu Eukaryota)	3.72E-25	37	97	38.1
Cytosolic small ribosomal subunit (sensu Eukaryota)	1.27E-15	24	64	37.5
Cytosolic ribosome (sensu Eukaryota)	1.02E-43	64	176	36.4
Cytosolic part	2.36E-41	65	197	33.0
Large ribosomal subunit	8.13E-26	44	142	31.0
Ribosomal subunit	4.18E-44	73	240	30.4
Small ribosomal subunit	7.37E-16	29	98	29.6
Ribosome	9.44E-38	80	357	22.4
Small nucleolar ribonucleoprotein complex	3.39E-07	23	132	17.4
Nucleolar part	4.92E-10	31	179	17.3
Ribonucleoprotein complex	1.10E-35	101	623	16.2
Nucleolus	1.44E-10	42	304	13.8
Nonmembrane-bound organelle	1.96E-27	118	1033	11.4
Intracellular non-membrane-bound organelle	1.96E-27	118	1033	11.4
Cytosol	2.69E-13	69	626	11.0
Unresponsive genes	980 genes
Process
80 biological processes	<1.00E-03			>10.0
Function
Exoribonuclease activity, producing 5′-phosphomonoesters	6.60E-04	13	23	56.5
Exoribonuclease activity	6.60E-04	13	23	56.5
Exonuclease activity, active with either ribo- or deoxyribonucleic acids and producing 5′-phosphomonoesters	8.10E-04	15	30	50.0
Guanyl-nucleotide exchange factor activity	7.40E-04	17	37	45.9
General RNA polymerase II transcription factor activity	6.19E-05	25	62	40.3
GTPase regulator activity	5.50E-04	27	77	35.1
RNA polymerase II transcription factor activity	4.90E-04	37	123	30.1
Transcription regulator activity	2.01E-09	90	327	27.5
Protein binding	1.40E-04	121	585	20.7
Hydrolase activity	1.61E-05	160	802	20.0
Component
∼40 cellular components	<1.00E-03			>10.0

An equally clear picture emerged from the GO term analysis of the subset of genes whose expression is positively correlated with growth rate. About half of all the yeast genes associated with mitochondrial protein import are found in this subset, and substantial fractions of all the genes associated with translation, ribosome biogenesis, and rRNA metabolism are represented. Consistently, ribosomal constituents (mitochondrial as well as cytosolic) are very strongly represented in both the Function and Component hierarchies.

In contrast, the 980 genes whose expression is robustly independent of growth rate are annotated (with similar statistical certainty and with similar Term Fraction values) to very many (∼80) diverse GO terms. The many processes that underlie basic cytoplasmic cell biology or nonnucleolar nuclear biology are well represented in this subset of genes, i.e., those whose expression is unrelated to the growth rate.

Genes Whose Expression Is Correlated with Growth Rate Are Highly Represented in the “Environmental Stress Response”

One of the questions that can be addressed using the tools developed above is the relationship between growth rate and the many genes whose expression changes regardless of the nature of the environmental stress imposed. In their data set of 156 such stress conditions, Gasch et al. (2000) found two clusters of genes that were either induced or repressed together in this way, which they called the environmental stress response (ESR) genes.

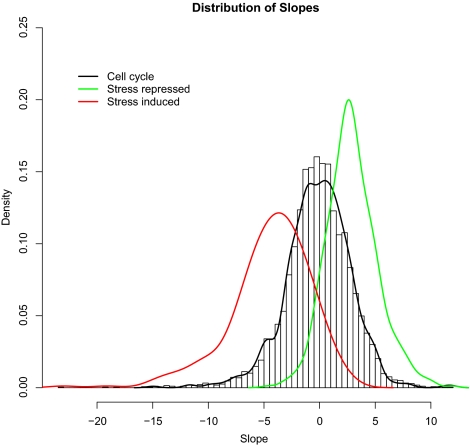
The distributions of the 283 genes in the ESR-induced cluster (red) and the 585 genes in the ESR-repressed cluster (green) are superimposed on the histogram of expression versus growth rate slopes in Figure 5. Both clusters had very high representations of growth rate-correlated genes and constitute sets of statistically significant outliers to the overall distribution of slopes.

Figure 5.

Transcriptional response of stress-related and cell cycle-related genes to changes in growth rate. Genes expressed periodically during the cell cycle (black line; Spellman et al., 1998) are distributed essentially as background, whereas genes induced (red line) or repressed (green line) by stress (Gasch et al., 2000) tend to be conversely repressed or induced as growth rate increases.

The 283-gene “ESR-induced cluster” has p values corresponding to Kolmogorov–Smirnov and Wilcoxon–Mann–Whitney two-sample tests practically equal to zero (see Materials and Methods), indicating that this cluster has a very significant representation of genes whose expression is negatively correlated with growth rate. In fact, nearly one quarter of the top 500 genes with negative growth rate regulation are in the ESR-induced cluster found by Gasch et al. (2000). The remaining 376 genes are enriched for GO process annotation terms relating to carbohydrate metabolism, particularly respiratory metabolism and oxidative phosphorylation. The component annotation terms indicate a significant enrichment in genes for proteins localized to the lytic vacuole and the peroxisome.

The “ESR-repressed” cluster (585 genes) also has Kolmogorov–Smirnov and Wilcoxon–Mann–Whitney two-sample test p values of approximately zero, indicating a highly significant positive correlation with growth rate. Again, the 500 genes with the most significant positive correlations between expression and growth rate include 227 of the ESR-repressed genes. The remaining growth rate correlated genes are significantly enriched for GO process terms that include membrane lipid biosynthesis and protein import into the mitochondrion.

The most significant components of the first (growth rate correlated) eigengene (Figure 3) are also enriched for genes in the ESR. When genes were ranked by their projection onto eigengene 1, a Wilcoxon-Mann-Whitney rank sum test shows that those genes identified by (Gasch et al., 2000) as being either induced or repressed in response to stress had a significantly lower than expected rank (t = 11.626, df = 5535, p < 10⁻¹⁵). This is further evidence that the ESR genes contribute strongly to the first eigengene and therefore to the growth rate pattern seen in the expression data.

Not all the ESR genes are expressed in such a way as to be signficantly correlated with growth rate in our data. We detected no enrichment, for example, in genes for chaperone proteins and for some other classes of classical stress response genes. The significant majority of stress-induced genes that are expressed at increasingly low growth rates are related to oxidative metabolism; of 131 genes, 16% are oxidoreductases.

These results raise the possibility that many of the ESR genes as defined previously may in fact not be responding directly to stress, but instead are responding to a reduction in growth rate secondary to the stress. A similar suggestion has recently been made in (Castrillo et al., 2007) based on a similar set of observations.

Growth Rate and Cell Cycle-regulated Genes

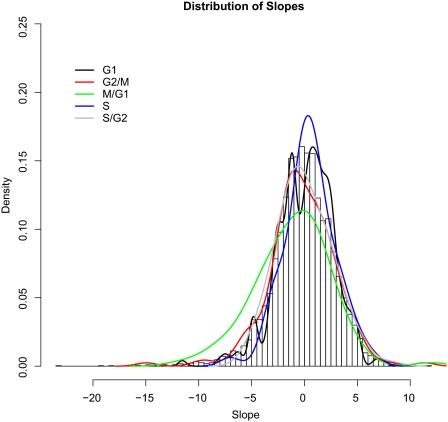
The distribution of regression slopes of the 800 genes identified by (Spellman et al., 1998) as having a strong cell cycle component in expression was nearly identical to the distribution of slopes for all genes (Figure 5, black line). A breakdown by cell cycle phase gives nearly identical results (Figure 6), the exception being in the M-G1 phase, which is slightly enriched for genes that have a negative correlation between expression and growth rate. Of the 89 M-G1 specific genes, 24 have a growth rate dependence that is >1 SD from the mean of all genes. These results are consistent with the idea that slower growing cells spend more time waiting for START, i.e., in the M-G1 interval of the cell cycle.

Figure 6.

Distribution of growth rate response slopes for genes specific to individual cell cycle phases. A breakdown of cell cycle specific gene response to growth rate by phase shows little variation from background. The 89 genes expressed in the M-G1 phase have a slight tendency to be down-regulated as growth rate increases.

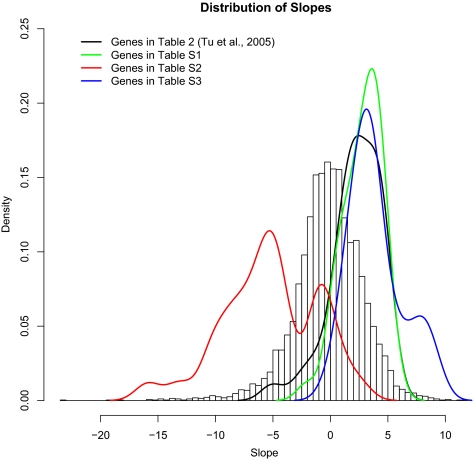
A different picture emerges under the special conditions of continuous culture that produce periodic cycles of metabolism (Tu et al., 2005; see also Kasper von Meyenburg, 1969; Klevecz et al., 2004). Under these circumstances, a high degree of periodicity in expression is seen for more than half of all yeast genes, vastly many more than the 800 or so detected in synchronized cells growing under more standard conditions (Spellman et al., 1998; Pramila et al., 2006; Kudlicki et al., 2007). It is of interest to see whether the several classes of genes distinguished by their relative expression during the metabolic cycling described and analyzed by Tu et al. (2005) are correlated with growth rate in our chemostat steady-state conditions. In Figure 7, we plotted four sets of genes identified by (Tu et al., 2005) relative to the histogram of regression slopes introduced in Figure 4: the “most periodic” (Tu et al., 2005, their table 2) and the mitochondrial ribosomal, peroxisomal, and cytoplasmic ribosomal clusters (Tu et al., 2005, their supplemental tables S1, S2, and S3, respectively). The results clearly show that the peroxisomal distribution (red line) is bimodal, with the majority class consisting of genes whose expression is negatively correlated to growth rate in ordinary conditions (i.e., these genes, in ordinary conditions, are more strongly expressed at lower steady-state growth rates in all media we tested). The minority peak includes some of the same ESR-induced genes that we identified above as not changing with growth rate. The other three groups, so clearly distinguished in the metabolic cycling conditions of (Tu et al., 2005), are all positively correlated with growth rate under normal conditions (with a small subset of the ribosomal group extremely strongly correlated with growth rate).

Figure 7.

Distribution of regression slopes for metabolic cycling conditions of Tu et al. (2005). In our expression data, Tu et al.'s “most periodic” genes during metabolic cycling (their table 2; black line) are induced as growth rate increases, as are their mitochondrial and cytoplasmic ribosomal clusters (their supplemental tables S1 and S3; green and blue lines). Peroxisomal genes (their supplemental table S2; red line) respond bimodally to growth rate, with the majority showing negative correlation and the minority not responding substantially to growth rate (including several stress response genes).

A Linear Model That Successfully Predicts Relative “Instantaneous Growth Rate” in Nonsteady-State Cultures

The results of our study identify a number of genes (on the order of one quarter of all genes in the genome) that are strongly correlated with growth rate at steady state, regardless of the limiting nutrient. Furthermore, there are many nonsteady-state conditions (notably the many stresses studied by Gasch et al. (2000) and the several kinds of synchronized cultures) in which there seems to be a systematic relationship to growth rate-related gene expression patterns. Indeed, these results encouraged the idea that much of the gene expression signature of “environmental stress” might actually reflect a changing growth rate secondary to stress. It, therefore, seemed possible that one might use the pattern of expression of a suitably chosen set of genes strongly correlated to growth rate as a way to estimate the instantaneous growth rates of nonsteady-state cultures, even cultures in which the growth rate is changing rather quickly in time.

To this end, we produced a simple linear model (described in Materials and Methods) calibrated using the 72 genes best correlated to growth rate in our 36 chemostats and least sensitive to nutrient-specific effects. We performed a number of cross-validation experiments on our chemostat data to estimate the model's expected error when inferring the relative growth rate for a novel microarray (Supplemental Figure S5).

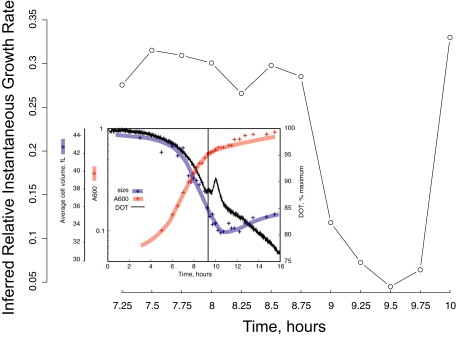
We tested the model using the data from Brauer et al. (2005), which followed genome-wide gene expression during the diauxic shift from glucose fermentation to respiratory growth on the evolved ethanol in batch culture. The experiments included measurements of residual glucose, ethanol, dissolved oxygen, and bud index. Brauer et al. (2005) found that the cells seem to stop growing, as judged from a discontinuity in both dissolved oxygen and bud index, just when the glucose is exhausted at about nine hours after the beginning of their experiment. Figure 8 shows the instantaneous growth rate inferred from our model on the same axis used by Brauer et al. (2005). It is clear that the inferred rate falls sharply at about this time and rises again as the cells, following the shift, resume growing on the ethanol. It is worth noting that Brauer et al. (2005) interpreted their gene expression patterns in terms of an environmental stress response caused by the starvation.

Figure 8.

Inferred instantaneous growth rates in batch culture undergoing the diauxic shift. The main figure shows the relative growth rates inferred by our linear model from microarray data in Brauer et al. (2005). The inset, from Brauer et al. (2005) demonstrates that their observed variations in cell volume and dissolved oxygen exactly match our predicted cessation of growth as the diauxic shift occurs (∼9.25–9.75 h).

DISCUSSION

We studied 36 yeast chemostat cultures growing at six different growth rates under six different nutrient limitations: glucose, sulfate, phosphate, ammonium, leucine (in a nonreverting leu2 mutant), and uracil (in a nonreverting ura3 mutant). By using a variety of different nutrients to limit growth rate, we could focus on quantitative relationships with growth rate per se, and not with the particular nutrient regime that limits the growth rate. Our data agree very well with the results of others who have done similar studies (Boer et al., 2003; Saldanha et al., 2004; Regenberg et al., 2006; Castrillo et al., 2007), both with respect to genes that are responsive to particular limitations and with respect to genes that respond mainly to growth rate.

Analysis of the small clusters of genes associated with particular limitations basically recapitulates results obtained previously by Saldanha et al. (2004). Most of the genes specifically associated with sulfate, phosphate, uracil, or leucine limitation are readily understood in terms of known metabolic pathways and transport systems. The data and the analysis of genes whose responses are specific to glucose and nitrogen limitations also agree well with previous work (Boer et al., 2003; Regenberg et al., 2006; Castrillo et al., 2007). We do not discuss any of these further here.

Expression of About One Quarter of All Yeast Genes Is Correlated with Growth Rate, but the Magnitudes of the Slope of the Relationship Are Characteristic for Each Gene

By a statistical analysis, we identified a large number of genes (∼27% of all yeast genes) each of whose expression is linearly correlated (either negatively or positively) with the growth rate, independent of the limiting nutrient. Some of these genes were much more strongly affected by growth rate than others, again independent of the identity of the limiting nutrient. Both hierarchical clustering and SVD analysis of the entire chemostat data set indicates that the correlation between the steady-state level of mRNA and the nominal growth rate applies to many genes.

Castrillo et al. (2007) recently published a set of data entirely consistent with the data set presented here for glucose, nitrogen, sulfur, and phosphate limitations. Although Castrillo et al. (2007) explored some very similar experimental conditions, they took a technology survey approach that included proteomic and metabolomic data in addition to gene expression levels. Their analysis is focused on the identification and behavior of individual genes (e.g., TOR1) that regulate pathways involved in growth regulation, whereas we attempted a system-level description of the relationship between growth rate and gene expression, control of the cell cycle, and metabolism. To this end, we combined traditional observation-based data analysis, including clustering and decomposition techniques, with a statistical, model-based study of our gene expression data. The fact that many genes are expressed in a way correlated with growth rate, independent of the identity of limiting nutrient, emerged as a strong conclusion from both studies.

To gain a deeper and less descriptive understanding of the biological roles of genes whose expression level correlates with growth rate per se, we introduced another level of analysis. We took advantage of the observation that expression of some genes changes more profoundly with differences in growth rate than others (i.e., the slope of the regression varies from very negative to very positive). We did extensive bootstrap analysis to determine the statistical significance of the slopes, because correlation itself will naturally be stronger when the slope is steeper: the bootstrap p values indicate how robust the determination of the slope is statistically.

The combination of each gene's growth rate slope (i.e., strength of transcriptional response) and the bootstrap p values of these slopes (i.e., their statistical significance), given in Supplemental Table S1 for all genes, allows the rigorous identification of genes responding strongly to growth rate in a nutrient-independent manner. A histogram of the slopes for all yeast genes allows one to visualize the growth rate sensitivity of a single gene or a list of genes relative to the overall distribution (Figures 5–7). These methods (also available at http://growthrate.princeton.edu) facilitate the use of the information from this data set to make inferences for our own analysis, and to analyze the results of others (see below).

To focus on the biology of gene expression as a function of growth rate, we defined (see Materials and Methods for statistical detail) a subset of 1,608 genes that correlate with a characteristic slope: 337 had a negative slope, 291 a positive slope, and 980 a slope near zero (i.e., their expression was roughly the same at all growth rates). The point to be emphasized here is that this stringent a selection of 337 + 291 = 628 (i.e., ∼10% of all yeast genes) necessarily underestimates the number of genes with nonzero slopes, because genes with smaller (positive or negative) slopes and/or noisy data are likely to fail the statistical tests. The SVD and clustering estimates (which suggest larger numbers of growth rate responsive genes) are surely closer to reality; we, therefore, suggest that expression of at least 27% of yeast genes is correlated with the nominal growth rate in chemostats, regardless of the nature of the limiting nutrient.

Functional Roles of Genes Whose Expression Is Most Strongly Related to Growth Rate

GO Term Finder analysis of the subsets of genes with well-defined slopes (Table 3 and Supplemental Table S2) presents a very clear picture. The positive-slope subset of 291 genes focuses on the translation machinery, both cytosolic and mitochondrial. This result has very strong precedents in the literature of both bacterial and yeast physiology, where the correlation between the number of ribosomes and the growth rate was noted very early (Maaloe and Kjeldgaard, 1966; for more recent reviews, see Nomura, 1999; Warner, 1999; Zhao et al., 2003). The biological logic for this relationship is virtually self-evident: to grow at a faster rate, more proteins must be made per unit time, which is facilitated by having more ribosomes per cell.

Many different regulatory mechanisms (most prominent among them the TOR1 signaling system) have been implicated in this connection (for review, see De Virgilio and Loewith, 2006a,b). Of particular relevance are the results of Jorgensen et al. (Jorgensen et al., 2004; Jorgensen and Tyers, 2004), who found a connection between ribosome biosynthesis and cell cycle entry at START (Hartwell, 1974; Hartwell et al., 1974) via the regulation of both processes by the products of SFP1 and SCH9.

The negative-slope subset of 337 genes relates to functions associated with oxidative energy metabolism, especially those carried out in peroxisomes. Peroxisomes have been associated with fatty acid metabolism, with oxygen metabolism (particularly reactive oxygen) and, more recently, with autophagy (for reviews, see Kim and Klionsky, 2000; van Roermund et al., 2003; Monastyrska and Klionsky, 2006; Rottensteiner and Theodoulou, 2006; Wanders and Waterham, 2006). The biological logic here is less obvious, although the benefits of engaging in autophagy and degradation of cellular materials during nutrient limitation are clear. Another possibility relates to the metabolism of reactive oxygen species, for which there might be more need when time between cell division cycles is longer. A purely metabolic logic (e.g., a need for more beta-oxidation of fatty acids at slow growth rates) is more difficult to rationalize. Although reasonable when carbon (in our case glucose) is limiting, it is not obvious how this might work for the other limitations, especially those that leave high concentrations of residual glucose in the medium at steady state.

The statistically derived growth rate-independent subset (980 genes) is, in this context, equally informative. It includes a large number of GO terms that cover much of the remaining yeast cell biology. These 84 GO process terms notably include such areas as transcription, DNA metabolism, chromatin remodeling, proteolysis, protein secretion and even the cell cycle, among many others (Supplemental Table S2 shows an even larger diversity at only slightly lower p values).

The Idea of an Instantaneous Growth Rate

In previous publications (Saldanha et al., 2004; Brauer et al., 2005), we showed that the overall pattern of gene expression in chemostats closely approximates that found in batch cultures that are running out of the same limiting nutrient. At about the time that the residual level of the limiting nutrient in the batch culture reaches the level found in the corresponding steady-state chemostat, the pattern of gene expression in batch approaches that of the chemostat culture. The simplest interpretation of these results is that somehow the cells have a way of sensing their instantaneous growth rate. This interpretation is fortified by our ability to predict, with a simple quantitative linear model, the instantaneous growth rate of a batch culture undergoing the diauxic shift (Figure 8). Our predictions correspond well to the variations in dissolved oxygen that were measured at the time by Brauer et al. (2005).

The mechanism(s) that underlie this coordination of gene expression must be largely independent of the nature of the growth limitation and also must require very little time to execute relative to the doubling time. The entire fall and resurgence of the growth rate in the diauxic shift experiment covers less than a doubling at the fastest rate on glucose. In this context, it is very interesting to note that the GO terms (mainly ribosomal functions) for our positively correlated gene set corresponds almost exactly to the set identified by Grigull et al. (2004) in their study of genes regulated post-transcriptionally by mRNA stability. It is entirely possible to imagine that when growth slows for any reason, even transiently, translation rates fall concomitantly, and the mRNAs jointly identified by Grigull et al. (2004) and by the data provided here become almost immediately unavailable. The concentration of one or more of these RNAs might, directly or indirectly, be the carrier of the information that signals the instantaneous growth rate to other cellular regulatory systems.

The ability to estimate instantaneous growth rates from patterns of gene expression could turn out to be a useful tool. Because it seems that one can estimate this parameter in diverse media and in batch cultures where the growth rate is changing (and in continuous cultures), it may be a useful tool for normalizing quantitative comparisons among experiments done under different conditions (which may otherwise give results that are systematically biased because of differences in growth rates).

Instantaneous Growth Rate and the Environmental Stress Response

Among the positively correlated genes, we found many (but not all) of the genes whose expression declined during the environmental stress response as defined by (Gasch et al., 2000); among the negatively correlated, we found many (but not all) of the genes whose expression increased in the Gasch experiments. Similar data were reported recently in Castrillo et al. (2007). A connection between growth rate and stress resistance has experimental precedent: Elliott and Futcher (1993) found that yeast grown in batch at slower growth rates by using relatively poor sources of carbon or nitrogen are more resistant to stress, which one might infer to mean induction of the stress-response genes. Much more recently, gene expression data consistent with such a connection have been reported by Slattery and Heideman (2007).

These results raise the possibility that much (but probably not all) of what has been defined as environmental stress response might equally well be thought of as a general response to changes in the instantaneous growth rate. Because it consists mainly of the most growth rate-sensitive genes, much of the response could be secondary to a much smaller number of specific responses to individual environmental stresses. It also is worth noting here that the steady state mRNA concentrations of the positively growth rate-correlated genes fall remarkably rapidly after applications of stresses (Gasch et al., 2000), consistent with the idea of regulation at the level of mRNA degradation (Grigull et al., 2004) and transcription.

It may well turn out that regulatory mechanisms and even actual regulators are shared and overlap between responses to specific stress and simple reductions in instantaneous growth rate.

At Least Two Mechanisms Must Exist Connecting Entry into the Cell Division Cycle with Metabolism

We found a simple linear relationship, again independent of the limiting nutrient, between steady-state growth rate and the fraction of unbudded (i.e., G0/G1) cells, consistent with the hypothesis (first proposed by Unger and Hartwell, 1976) that at reduced growth rates, yeast cells spend correspondingly increased amounts of time in the phase of the cell cycle just before “START” (i.e., the activation of the cyclin-dependent kinase Cdc28p; Pringle and Hartwell, 1981). This relationship holds for all nutrient limitations and accords generally with current views of cell cycle regulation (e.g., Laabs et al., 2003; Verges et al., 2007; for recent reviews, also see Futcher, 2002; Jorgensen and Tyers, 2004; Schneider et al., 2004; Bloom and Cross, 2007). Our observations support a mechanism that is independent of the nature of growth limitation. The classical model wherein START is passed when the cyclin/DNA ratio is above a threshold is such a model, and it is consistent with these data.

However, the results from batch cultures cannot be explained so simply. As found in Saldanha et al. (2004), we again observed that ura3 or leu2 auxotrophs depleted of limiting uracil or leucine do not properly arrest growth in an unbudded state, whereas the same strains will arrest properly when limited on phosphate with excess uracil or leucine (Table 2). This result is not easily reconciled with the classical models; indeed, it is in apparent conflict with the observation that these same auxotrophs limit entry into the cell cycle in just the same way as do prototrophs in limiting glucose, ammonia, phosphate or sulfate (which we call natural nutrients, after Saldanha et al., 2004).

This result is made more interesting by our additional remarkable observation, in both batch and continuous cultures, that excess glucose is spared when cultures limit on the natural nutrients, whereas it is fermented completely to ethanol when cultures are limited by auxotrophic requirements. The combination of a defective regulation of the cell division cycle with uncontrolled glucose fermentation is reminiscent of the “Warburg effect” in human cancer cells. (Warburg, 1956) reported a now general observation that most human cancer cells, even under aerobic conditions, will exhaust the glucose in their medium by fermentation to lactate, whereas normal cells and tissues will spare the glucose (for review, see Kim and Dang, 2006).

Together, these results point to the existence in Saccharomyces cerevisiae of at least two regulatory systems that function in coordinating growth rate, cell division, and metabolism. One of these, which seems to be independent of the type of nutrient limitation, seems to continuously limit entry into the cell cycle based on the growth rate without producing a full cell cycle arrest. This could be the mechanism envisioned in the classical models. The other, which we believe functions only when a natural nutrient is totally depleted, seems to cause a more complete cell cycle arrest in batch cultures and, we suggest, may also act to prevent unlimited fermentation of any remaining glucose.

We suggest that both of these mechanisms must somehow respond to the instantaneous growth rate: one acts in a graded manner limiting cell cycle entry, and the other acts only when starvation is imminent.

Is There a Connection between Growth Rate Control and the Metabolic Cycling Phenomenon?

One of the more surprising results we obtained is that of the ∼800 genes that seem to be periodically expressed during cells synchronized in all the standard ways (Spellman et al., 1998; Pramila et al., 2006), relatively few were strongly correlated to growth rate with steep slopes. Because there is such a large difference in the fraction of cells in G0/G1 at low growth rate compared with high, we anticipated that we might see more than the relatively modest enrichment we found in the genes whose mRNA abundance peaks in M/G1 (Figure 6). What was not observed by Spellman et al. (1998) or Pramila et al. (2006) when they synchronized cells with mating factors, drugs or cdc mutants, was periodicity of expression of the several major classes of genes we found strongly correlated, negatively or positively, with growth rate.

A similar analysis using the data of Tu et al. (2005), which derives from cultures synchronously undergoing metabolic cycling, produced a completely different picture (Figure 7), even though they used the same CEN.PK strain we used. Many (>800) genes are periodically expressed in the metabolic cycling regime. There seems to be a striking concordance between the sets of genes that Tu et al. (2005) see strongly expressed during the several phases of their metabolic cycle and the subsets of genes we defined as being most correlated with growth rate. It is important to note that in all the metabolic cycling experiments, the genes that are periodic under the standard synchronization conditions are generally also periodically expressed, with periods synchronized to the metabolic cycles (Klevecz et al., 2004; Tu et al., 2005; Kudlicki et al., 2007). The set of genes associated with the “oxidative phase” of the metabolic cycle is bimodal in Figure 7, but the majority of the genes are the same ones associated with the peroxisome and its metabolic functions. The sum of all the genes associated with the other phases roughly comprises our gene subset whose expression is positively correlated with growth rate and whose functions are strongly associated with the cytoplasmic and mitochondrial translational machinery.

What are we to make of this concordance? One simple hypothesis, which is quite testable, is that there is a metabolic cycle under all conditions, but only under the conditions used by Tu et al. (2005) and Klevecz et al. (2004) do entire cultures become synchronous, possibly because of changes in the medium (e.g., dissolved oxygen, pH, and residual glucose). The only immediate difficulty with this hypothesis is that synchronization of the cell division cycle under the classical conditions, in several laboratories, produced no sign of synchronization of expression of the characteristic subsets of genes found during metabolic cycling (Tu et al., 2005), stress response (Gasch et al., 2000), or by correlation with growth rate in continuous culture (Castrillo et al., 2007; this study).

Another way to look at the problem, which is more difficult to test, is to suppose that the conditions of metabolic cycling involve changes in the extracellular medium, as described above, that result in changes in the instantaneous growth rate. This would result in periodicity of the genes strongly correlated to the instantaneous growth rate. The suggestion by Futcher (2006); compare (Kuenzi and Fiechter, 1969; Kasper von Meyenburg, 1969), which posits that cells use accumulated stores of fermentable sugar to provide a “finishing kick” to metabolism that allows the cells to pass START, is a nice variant of this idea.

Both Tu et al. (2005) and others (Futcher, 2006; Chen et al., 2007) imagine that some or all of the evolutionary pressure that results in metabolic cycling might be driven by the need to minimize (or avoid entirely) the damage to DNA from the inevitable reactive oxygen by-products of respiratory metabolism. The prominence of genes associated with peroxisomal functions supports such a proposal. Lower growth rates require longer exposure to oxidative metabolism in order to produce enough energy, and this might be the reason that genes encoding the peroxisomal functions are preferentially expressed.

CONCLUSIONS

We have shown that a large fraction of all yeast genes are expressed to a degree that is linearly related to the growth rate, regardless of the nature of the limitation on growth. The slopes, indicating the relation of each gene's expression to growth rate, can be used to evaluate the likelihood that changes in gene expression might be related to changes (apparent or not) in growth status of yeast cells. On this basis, we have found that there may well be changes in what we define as instantaneous growth rate in cells undergoing a stress responses or metabolic cycling.

In the Supplement Material and on our website http://growthrate.princeton.edu, we provide, in addition to an extensive new expression data set, growth rate sensitivity information for every yeast gene. We also provide computational tools that allow these tables to be used to evaluate other data sets even when the growth rate is changing, uncertain, or unknown.

We also describe a new phenomenon in yeast, analogous to the glucose wasting Warburg effect in cancer cells. Auxotrophs starving for their growth requirements waste glucose and fail to arrest properly at G0/G1. Neither phenotype is seen when the same cells are starved for phosphate or sulfate. We interpret these results as indicating that there must be at least two mechanisms that connect metabolism and entry into the cell division cycle, both of which must somehow sense the instantaneous growth rate.