Aging and Intraindividual Variability in Performance: Analyses of Response Time Distributions

Abstract

It has been suggested that older adults are more variable in their performance because they are more prone to lapses of either attention or intention. In the present experiment, 9 young and 9 older adults each performed nearly 2,000 trials of a same–different judgment task. As expected, older adults were slower and more variable than young adults. When the age-related difference in speed was taken into account, however, the older adults were, if anything, less variable than the young adults. When younger and older adults' RT distributions were analyzed using quantile–quantile plots and by fitting ex-Gaussian and Weibull functions, there was no consistent evidence that older adults' distributions were more skewed than young adults', as would be predicted by age-related increases in lapses of attention or intention. Importantly, there was a positive, linear relation between RT and intraindividual variability, and the same relation was observed both within subjects (practice increased speed and reduced variability) as well as between subjects (regardless of age, slower individuals were more variable). Thus, the present results suggest that there may be a general law governing the relation between average RT and variability, and that the greater performance variability of older adults primarily reflects their greater average RTs.

Is the performance of an older person more variable than that of a younger person, and if so, what does this say about the effect of age on the reliability with which an individual can process information? For years, cognitive aging research largely ignored this question, focusing instead on age differences in average levels of performance. Recently, there has been increased interest in individual variability in several fields, including behavior analysis (e.g., Blough, 2000; Neuringer, 2002), behavioral and neuro-economics (e.g., Glimcher, 2005; Glimcher, Dorris, & Bayer, 2005), and cognitive aging (e.g., Ferraro & Moody, 1996; Hultsch, MacDonald, & Dixon, 2002; Luszcz, 2004; Rabbitt, Osman, Moore, & Stollery, 2001; Robertson, Myerson, & Hale, 2006) as researchers have come to appreciate the potential significance of this topic.

With respect to cognitive aging, for example, individual older adults' performance on response time (RT) tasks is more variable than that of young adults. One straightforward interpretation is that older adults are more variable simply because they are slower (e.g., Cerella & Hale, 1994; Myerson, Adams, Hale, & Jenkins, 2003; Myerson, Hale, Hirschman, Hansen, & Christiansen, 1989). After all, RT distributions have been extensively studied in a variety of species, including pigeons (e.g., Blough, 2000), rats (e.g., Stebbins, 1962), and monkeys (e.g., Stebbins & Miller, 1964), as well as humans (for a review, see Luce, 1986), and typically, variability has been found to increase with average RT.

In fact, it is possible that the relation between variability and average RT may rise to the level of a general law of behavior. Myerson and Hale (1993) reanalyzed RT data from younger and older adults tested on four different cognitive tasks (Cerella, DiCarra, Williams, & Bowles, 1986), ranging in difficulty from basic choice reaction time to word matching, and reported that a single linear function accurately described the relation between variability and average RT across all tasks. Importantly, the younger and older adults did not differ in this regard. Although the analysis was strongly suggestive, it was admittedly post-hoc, and to the best of our knowledge the generality of this finding has not been tested.

Another source of difficulty in interpreting the greater variability of older adults' performance derives from the fact that much of the data on aging and intraindividual variability is based on performance during a brief initial exposure to an experimental task when performance is improving rapidly (Hultsch et al., 2002). This is problematic because the speeded performance of older adults has been shown to improve more with practice than that of younger adults (Cerella, 1990). Even when greater exposure to the tasks is provided, typically all of the responses from the beginning to the end of an experimental condition are analyzed, rather than restricting the analysis to asymptotic performance (e.g., West, Murphy, Armilio, Craik, & Stuss, 2002). Thus, it is possible that the greater variability reported for older adults may simply reflect the fact that their RTs improve more with practice.

Alternatively, age differences in variability may reflect fundamental differences in cognitive ability and/or brain function. Stuss and his colleagues have reported that increased intraindividual variability in RTs may indicate the presence of frontal lobe lesions (Stuss, Murphy, Binns, & Alexander, 2003), a finding which is particularly relevant to the study of older adults given that the frontal lobes are more susceptible to the deleterious effects of aging than other areas of the brain (Moscovitch & Winocour, 1992; Raz, 2000). West, an advocate of the frontal lobe hypothesis of cognitive aging (West, 1996), proposed that age-related deficits in the functioning of the prefrontal cortex result in decreased stability of executive control, which leads to greater variability and increased skew in an individual's RT distribution (West et al., 2002).

According to West et al. (2002), decreased stability of executive control is associated with an increase in lapses of “intention.” These lapses, when they occur, result in very long RTs and increase the variability of an individual's performance. West et al. further proposed that because intentional lapses lead to RTs that are much longer than an individual's modal RT, they cause older adults' RT distributions to show much greater positive skew than those of younger adults. Similarly, Bunce, Warr, and Cochrane (1993) have suggested that aging is associated with an increase in “attentional blocks,” and these blocks or lapses in attention are also hypothesized to result in very long RTs. As with intentional lapses, attentional blocks predict both greater variability and greater positive skew in the RT distributions of older adults. The similarity between the predictions of intentional and attentional lapses could pose a problem for distinguishing the two hypotheses, but this would only be an issue if it were to turn out that older adults' distributions are actually more skewed.

The literature on the effects of age on the skew of RT distributions is no clearer than that on variability per se. It has long been known that older adults' RT distributions have longer tails (e.g., Fozard, Thomas, & Waugh, 1976; Smith, Poon, Hale, & Myerson, 1988), but there is currently no consensus regarding interpretation of this phenomenon. Early researchers simply noted that age differences clearly were much larger on individuals' slowest responses than on their fastest response. Later researchers compared corresponding quantiles of RT distributions and concluded that the RT distributions were simply magnified, but did not differ in shape (Salthouse, 1993; Smith et al., 1988).

More recently, a number of researchers have addressed this issue by fitting ex-Gaussian functions to RT distributions. The ex-Gaussian function, which typically provides a good fit to such distributions, is the convolution of a Gaussian function and an exponential function. It has three parameters: mu and sigma are, respectively, the mean and standard deviation of the Gaussian component, and tau is both the mean and the standard deviation of the exponential component.1 The RT distributions of older adults typically are associated with larger values of tau, which have been interpreted as indicating greater skew, leading in turn to speculations regarding age-related increases in attentional lapses, failures of inhibition, and fluctuations in the efficiency of executive processing (e.g., Balota, Cortese, Sergent-Marshall, Spieler, & Yap, 2004; McAuley, Yap, Christ, & White, 2006; Spieler, Balota, & Faust, 1996; West, 1999; West et al., 2002).

Unfortunately, tau is not an adequate measure of the skew of an ex-Gaussian distribution. Tau reflects the absolute length of the right-hand tail of a distribution, whereas in statistics, skew is a measure of the asymmetry of a distribution (i.e., the length of the right-hand tail relative to the length of the left-hand tail). One relevant, but potentially troublesome, consequence is that simple slowing, in which all RTs are multiplied by a constant, will produce an increase in tau but leave skew unchanged. If one wants to measure skew using the parameters of an ex-Gaussian distribution and avoid this problem, a more appropriate measure of skew is the ratio of tau to sigma (Heathcote, Brown, & Mewhort, 2002). The larger this ratio, the more skewed the distribution. To the best of our knowledge, however, previous studies have not compared the tau/sigma ratio in younger and older adults. The only study to actually measure skew as defined in mathematical statistics (i.e., as the normalized third central moment of a distribution or skewness, which, like the tau/sigma ratio, remains constant over changes in scale; Hays, 1994) did not examine asymptotic performance (Salthouse, 1993).

Weibull distributions (Luce, 1986; Rouder, Lu, Speckman, Sun, & Jiang, 2005) and quantile-quantile (Q–Q) plots (Chambers, Cleveland, Kleiner, & Tukey, 1983; Myerson et al., 2003) represent two other approaches to comparing the shapes of RT distributions. To the best of our knowledge, neither of these approaches has been applied to the current problem. Like the ex-Gaussian, the Weibull is of interest in part because its parameters may be used to characterize the shape of individual RT distributions. More specifically, the Weibull function has a shift parameter, a scale parameter, and a shape parameter. The shift parameter measures the location of the leading edge of the RT distribution and may reflect sensory/motor speed, whereas the scale parameter is a measure of the spread of the distribution and may reflect information-processing speed. Most importantly for the present purposes, the shape parameter provides a measure of the skew of the distribution. The exponential distribution is a special case of the Weibull with a shape parameter of 1.0. As the shape parameter approaches 3.4, the Weibull becomes approximately normal. Thus, lower values of the shape parameter for the older adults would indicate more skew.

Q–Q plots, which are constructed by plotting the quantiles of one distribution as a function of the corresponding quantiles of a reference distribution, represent another useful approach to comparing the shapes of distributions. (Quantiles are the values, such as quartiles or deciles, which divide a cumulative distribution function into a given number of equal, ordered parts.) One of the principal advantages of Q–Q plots is that they are atheoretical, requiring no assumptions about the shapes of either of the two distributions being compared (Myerson et al., 2003). Anything other than a strictly linear relationship between the two sets of quantiles would indicate a difference in the shapes of the two distributions being compared. More specifically, positive curvature (acceleration) would indicate that the distribution whose quantiles provide the y coordinates of the data points is more skewed than the distribution providing the x coordinates. In contrast, greater dispersion in the absence of a difference in skew would be indicated by a linear relation with a slope greater than 1.0.

The goal of the present study was to determine whether or not older adults are more variable than younger adults, once differences in learning rates and speed of responding are taken into consideration, and also whether their RT distributions are more skewed. Toward this end, we trained younger and older adults on a same–different judgment task and examined both their initial performance as well as their performance once asymptotic levels had been reached. Data were analyzed by comparing the semi-interquartile (SIQ) ranges of individual RT distributions, examining the shapes of these distributions using Q–Q plots, and by comparing the parameters of ex-Gaussian and Weibull distributions fit to the data from younger and older participants. In addition, we calculated the skewness statistic (i.e., the third moment of the individual RT distributions), because West et al.'s (2002) theory predicts that older adults' distributions, in addition to being more variable, will also be more skewed than would be expected based on their slower RTs. Finally, we sought to determine whether there is a general relation between variability and average RT that describes not only differences between individuals, but also differences within individuals, such as those due to practice.

Method

Participants

Nine young adults (7 women and 2 men) and 9 older adults (6 women and 3 men) participated in the study. The young adults (ages 19 to 22 years, M  =  20.9, SD  =  1.05) were Washington University undergraduate volunteers, and the older adults (ages 70 to 78 years, M  =  73.9, SD  =  3.10) were recruited from a pool of volunteers maintained by the Aging and Development Program of the Psychology Department at Washington University. There was no significant difference between the amount of education received by the young adults and that received by the older adults, t (17) < 1.0. Young adults received course credit for their participation; older adults were given $20 remuneration.

Prospective participants were screened for medical conditions known to affect performance and were disqualified if they reported having certain neurological problems (e.g., stroke, severe head injury, or Parkinson's disease), medical problems (e.g., congestive heart failure, diabetes, or thyroid disease), or depression. Visual acuity was tested using a standard wall-mounted eye chart, and prospective participants whose corrected acuity was less than that required to easily perceive the stimuli used in the experiment (20/50) were excluded.

Apparatus

The same–different judgment RT task was programmed using SuperLab Pro (Cedrus Corp., San Pedro, CA) software. Administration of the task was controlled by a desktop personal computer. Stimuli were presented on a 17-in. color monitor positioned at a comfortable viewing distance (approximately 60 cm) from each participant. Participants responded to stimuli using a six-button response box (Cedrus Corp., San Pedro, CA), which had the middle four buttons removed.

Task and Procedure

The same–different judgment RT task required participants to decide if two characters presented on the monitor were from the same category. There were two categories: letters (e.g., D, S, T) and nonletter symbols, including digits (e.g., 5, *, &). Participants were instructed to press the right button on the response box if both characters were from the same category. Participants were instructed to press the left button if the two characters were from different categories.

The beginning of each trial was indicated by a red plus sign presented in the center of the monitor for 750 ms. After a randomly chosen foreperiod duration of 500, 750, or 1000 ms, a pair of black characters of various fonts, each approximately 20 mm in height, were displayed side by side and centered within a 108 mm × 56 mm white rectangle. The centers of the characters were separated by approximately 27 millimeters. If a participant responded correctly to a trial, the box and characters disappeared and were replaced with the red plus sign, signaling the beginning of the next trial. On incorrect trials, feedback was provided via a brief tone occurring immediately before the red plus sign appeared. Feedback was not given on correct trials.

Participants were tested individually in a quiet room that was softly illuminated in order to minimize glare. After consent, health information, and demographic data were obtained, a visual acuity test was administered. Before beginning the same–different judgment RT task, participants were read aloud the task instructions, which also were displayed on the monitor, and asked if they understood the task or had questions. Once it was determined that participants understood the task, six practice trials were administered. Then, if they had no further questions, the experimental trials were administered. Otherwise, they were given the instructions again and allowed to repeat the practice trials before beginning the experimental trials. The experimenter did not remain in the room during the presentation of the experimental trials.

There were 1917 experimental trials consisting of 480 same trials in which both characters were letters, 480 same trials in which both characters were nonletter symbols, and 957 different trials in which one character was a letter and one was a nonletter symbol. (A total of 960 different trials was planned; however a programming error resulted in the omission of three trials.) Use of a variety of different fonts made it possible to present a unique combination of stimuli on each trial. In order to minimize fatigue, the experimental trials were presented in three sessions separated by 15-min breaks. In addition, each session was divided into blocks (six for the first session and seven for each of the last two sessions) of 96 trials each, and participants were given the opportunity to rest briefly between each block. Within each block, trials were not self-paced, but instead a serial choice reaction time procedure was used, such that each response triggered the presentation of the stimuli for the next response. Such procedures place much greater demands on a subject's attention, and thus provide a more rigorous test of a subject's tendency toward attentional lapses, than do self-paced procedures. All experimental trials were presented in the same random order to each participant. Participants were instructed to respond as rapidly and as accurately as possible.

Results

Outliers for each individual's RT distributions were trimmed by excluding response latencies longer than 10,000 ms or shorter than 150 ms from all analyses. These relatively lenient criteria were used in order to ensure that all meaningful data were included in the analyses, while at the same time minimizing the inclusion of data that were likely the result of events unrelated to the task (e.g., sneezes or inadvertent button presses). On average, each individual had less than one trial trimmed from each of the two conditions, and there were no age differences in the number of trials trimmed. As is typically done, RTs from incorrect trials also were discarded. There was very little difference in accuracy between the young and older adults: 93.8% correct for the young adults and 94.8% correct for the older adults.

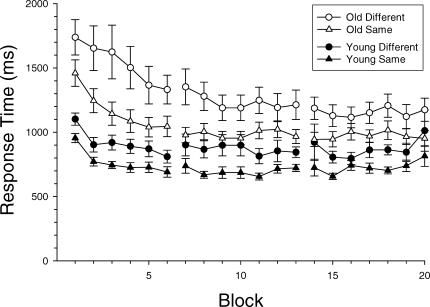
Figure 1 shows group mean RTs plotted as a function of block for both young and older adults. As may be seen in this figure, the older adult group was slower than the young adult group, and RTs decreased in the first session at a greater rate for older adults than for young adults. From the first block to the sixth and final block of the session, older adults' RTs decreased by 414.4 ms in the same condition, on average, and by 406.4 ms in the different condition. In contrast, young adults' RTs decreased by only 263.7 ms and 291.7 ms in the same and different conditions, respectively. Clear age differences in RTs were still present at the end of the first session, however, and as may be seen, these differences remained relatively stable across the 14 blocks of the second and third sessions.

Fig 1.

Mean response times (and standard errors) for both young and older adults in the same and different conditions plotted as a function of block and partitioned by session.

In the first session, the RTs of older adults tended to be more variable than those of young adults. The mean SIQ range for older adults in the same condition was 463.8 ms whereas the mean SIQ range for the young adults was 292.4 ms; in the different condition, the mean SIQ range was 595.5 ms for older adults and 334.4 ms for young adults. It should be noted, however, that the improvements in RTs observed in the first session would necessarily be incorporated into individual RT distributions from that session, confounding analysis of age differences in variability. Thus, it is possible that the larger SIQ ranges of older adults observed in the first session merely reflect the fact that the older adults showed more improvement.

Importantly, the improvement in speed of responding largely ceased by the second session for both age groups. Moreover, despite the fact that the accuracy of responses also improved with practice over that observed in the first session, there was very little difference in accuracy between the older adults (M  =  95.9% correct) and the young adults (M  =  94.6% correct) in the second and third sessions. Given both the stable levels of RTs and the nearly equivalent accuracy levels, the data from these sessions appear to provide a valid basis for assessing the source of age differences in intraindividual variability.

Semi-Interquartile Ranges and Medians

RT distributions are typically quite skewed (Luce, 1986), and the SIQ range provides a good descriptive measure of the spread of a skewed distribution because, in comparison to the standard deviation, it is less sensitive to the extreme values. Medians are to be preferred to means as measures of the central tendency of skewed distributions for the same reason (Hays, 1994).

Although the average size of the age difference in SIQ ranges decreased with practice, older adults' SIQ ranges were larger than those of the young adults even after performance stabilized (i.e., in the second and third sessions). In the same condition, the mean SIQ range for the older adults was 350.7 ms whereas the mean SIQ range for the young adults was 250.6 ms; in the different condition, the mean SIQ ranges were 411.8 ms for the older adults and 304.6 ms for the young adults. Thus, even after the confound of age differences in improvement with practice was eliminated by focusing on the stable data from the second and third sessions, an age difference in variability remained.

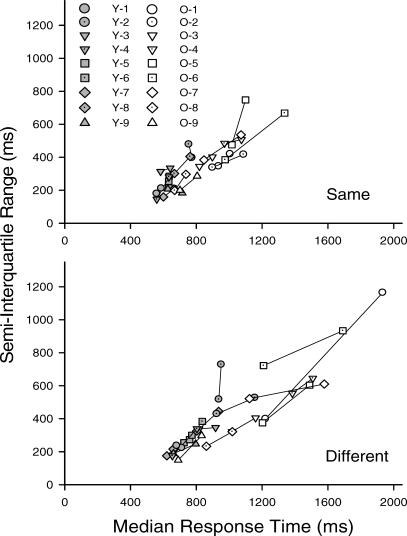
It should be noted, however, that the older adults were not just more variable—they were also slower. The means of the median RTs of the older adults were 870.1 ms and 1070.1 ms in the same and different conditions, respectively, whereas the corresponding values for the young adults were 623.9 ms and 746.7 ms. Because the dispersion of RT distributions tends to increase as the average RT increases (Luce, 1986), it is possible that the age differences in variability observed in the second and third sessions merely reflect the slower responding of the older adults. Consistent with this hypothesis, inspection of Figure 2 (which plots the SIQ range for each individual as a function of his or her median RT) reveals that there is a strong linear relation between RT and intraindividual variability that holds across individuals, across sessions, across conditions, and across age groups.

Fig 2.

Individual young and older adults' semi-interquartile ranges in the same (upper panel) and different (lower panel) conditions of their first session, as well as their second and third sessions, plotted as a function of median response time. Each line connects first session performance with the second and third session performance of the same individual.

All of the older adults' median RTs for sessions 2 and 3 from both same and different conditions were lower than their corresponding median RTs for session 1, and their SIQ ranges all decreased accordingly. In the young adult group, the decreases in median RT were smaller overall, and although all improved in the same condition, two individuals (Y2 and Y5) actually failed to improve in the different condition. Given the smaller and more uneven effects of practice in the young adults, it is perhaps not surprising that not all showed a decrease in SIQ range, although only one (Y2, who failed to improve in the different condition) showed an increase greater than 25 ms. Nevertheless, analyses of the data (to which each individual contributed two data points, one from the first session and one from the second and third sessions, thereby making possible examination of differences between individuals and practice effects within individuals) revealed that SIQ range was strongly correlated with the corresponding median RT for both groups in both conditions (all rs > .71). A single linear relation accounted for 66.7% of the variance in the data shown in both panels of Figure 2. Allowing for separate parameters for session 1 versus sessions 2 and 3 accounted for only an additional 0.1% of the variance, and allowing for separate parameters for young and older adults accounted for only 2.5% more variance than did a single line.

Once the strong linear relation between median RT and SIQ range is taken into account, it becomes apparent that the stable responding of the older adults was no more variable than would be expected based on their median RTs. This may be seen by focusing on the region of overlap in asymptotic median RT (from approximately 650 to 1000 ms) in Figure 2. Within this region, each older adult's SIQ range is actually less than the SIQ range for the young adult with the closest matching median RT. Thus, the present results provide no evidence that the greater variability of older adults' RTs is anything other than a by-product of age-related slowing.

Quantile–Quantile Plots

In order to compare the shapes of younger and older adults' RT distributions and determine whether older adults' RT distributions showed greater skew than those of young adults, we plotted the quantiles of the older adults' RT distributions as a function of the corresponding mean quantiles of the young adults. The technique of calculating the mean quantiles of distributions is known as Vincentizing (after Vincent, 1912), and it is often used to summarize a set of individual RT distributions because the mean, variance, and shape of a Vincentized distribution are approximately equal to the average of the means, variances, and the shapes of the individual distributions that make up the set (Ratcliff, 1979).

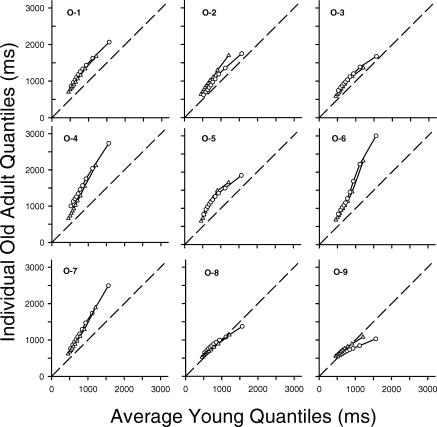
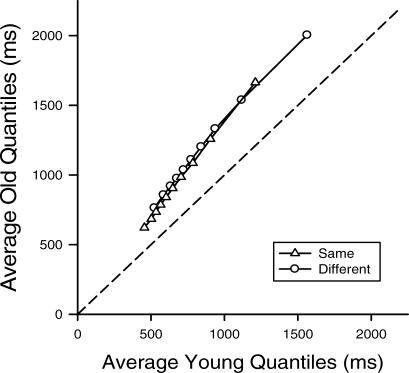
For the present analyses, we first calculated the quantiles of each individual's RT distribution in the same and different conditions based on the combined RTs from the second and third sessions. Then we determined the young adult Vincentized distribution for each condition by calculating the average of each quantile from the 5^th to the 95^th percentile, in increments of 5 percentiles, resulting in 19 quantiles in all. Next, we constructed Q–Q plots in which each individual older adult's quantiles were plotted as a function of the corresponding quantiles of the Vincentized distributions for the young adult group (see Figure 3). We then used the same process, this time calculating the average quantiles for the older adult group, in order to construct Q–Q plots that compared the Vincentized distributions of the two age groups (see Figure 4).

Fig 3.

Individual older adults' quantiles for the same (triangles) and different (circles) conditions plotted as a function of the average young adult quantiles. Data points represent the 5^th, 15^th, 25^th, … 95^th percentiles of the younger and older adults' response time distributions. The dashed line represents equal performance: If an older adult's response times did not differ from those of the average young adult, the data points would fall along this line.

Fig 4.

Average older adult quantiles for the same (triangles) and different (circles) conditions plotted as a function of the average young quantiles. Data points represent the average 5^th, 15^th, 25^th, … 95^th percentiles of the younger and older adults' response time distributions. The dashed line represents equal performance: If younger and older adults' average response times did not differ, the data points would fall along this line.

Consider the following alternative outcomes, some of which could occur in combination:

1. If there is no age difference in the RT distributions, then when the quantiles of older adults are plotted as a function of the quantiles of young adults, the resulting data points will fall along the diagonal line corresponding to y  =  x (i.e., the equality diagonal).

2. If the RTs at all quantiles are slower by the same amount, such as might result from an age-related increase in the time necessary for the sensorimotor component of the response, then all of the data points will simply be shifted up and lie along a line with a slope equal to 1.0 that is parallel to the equality diagonal but above it.

3. If there is a global magnification of the RT distribution without any change in shape, such as might result from general slowing, then not only will all the points be above the equality diagonal but in addition, they will all fall along a straight line with a slope greater than 1.0.

4. If there is a difference in the shape of the RT distributions, the data points will fall along a curve rather than along a straight line. More specifically, if there is an increase in skew, as has been hypothesized to be the effect of age on RT distributions, then the curve describing the relation between the corresponding quantiles of older and younger adults will be positively accelerated.

As may be seen in Figure 3, there was considerable diversity in the Q–Q plots of the older adults. Nevertheless, certain commonalities are apparent. Notably, the fastest responses of all of the older adults, as indicated by the leftmost data points in each Q–Q plot, are slower than those of the young adult average, as indicated by the fact that these points lie above the equality diagonal. Moreover, 7 of the older adults (all but O-8 and O-9) have all of their data points above the diagonal, indicating that for these individuals, all of their responses were slower than the corresponding responses of the average young adult.

With respect to the question of skew, examination of the degree and direction of the curvature in the individual Q–Q plots yielded little evidence of positive acceleration. Instead, the plots tend to show linear or even negatively accelerated relations between the quantiles of young and older adults, with older adults' quantiles from the different condition showing slightly more negative acceleration than the quantiles from the same condition. Curvature was quantified by fitting second-order polynomial functions to the data and examining the coefficient for the quadratic term (see the columns labeled B₂ in Table 1). In both conditions, the majority of the quadratic coefficients were negative, providing evidence against the hypothesis that older adults' distributions are more skewed than young adults' distributions.

Table 1.

Parameter values for second-order polynomial regressions of individual older adults' quantiles on the corresponding average young adult quantiles for the same and different conditions.

Subject	Same			Different
	B0	B1	B2	B0	B1	B2
O-1	−23.27	2.05	−1.84E-04	−18.35	1.91	−3.68E-04
O-2	−64.39	1.63	−1.45E-04	−297.20	1.95	−4.08E-04
O-3	−291.61	2.21	−6.97E-04	−34.96	1.69	−3.76E-04
O-4	−273.15	2.04	−5.10E-05	−23.27	2.05	−1.84E-04
O-5	−823.51	3.86	−1.46E-03	−87.59	2.11	−5.40E-04
O-6	453.08	−0.02	1.28E-03	−486.93	2.49	−1.49E-04
O-7	141.15	0.79	5.35E-04	−107.74	1.66	3.00E-06
O-8	172.06	0.79	3.00E-06	161.64	1.06	−1.88E-04
O-9	86.45	1.15	−2.70E-04	248.72	0.66	−1.04E-04

The Vincentized RT distributions for each age group provide a way of summarizing the results for the individual distributions. As may be seen in Figure 4, the shapes of the younger and older adult groups' Vincentized RT distributions were very similar, as indicated by the approximate linearity of the relation between corresponding quantiles in both conditions. This linearity, taken together with the fact that the slopes are both obviously greater than 1.0, implies that the older adult distributions, on average, tend to be simple magnifications of those of young adults. Consistent with the magnification hypothesis, simply multiplying the young adult quantiles by a slowing factor of 1.4 accounted for 98.5% of the variance in the older adult quantiles. If anything, the relations between the corresponding quantiles of the Vincentized distributions seen in the Q–Q plot appear to be slightly negatively curved. Polynomial equations were fit to the data in order to assess this curvature, and the values of the quadratic coefficients were negative (−0.252E-3 and −0.272E-3 for the same and different conditions, respectively), as was the case for the quadratic coefficients in the majority of the individual cases. These results suggest that the older adults' RT distributions are, if anything, slightly less skewed than those of the younger adults.

Skewness

The preceding Q–Q analyses provide information as to how the shapes of the RT distributions of the older adults compare to those of the young adults, but they do not provide a quantitative measure of exactly how skewed the distributions of either group actually are. The degree of asymmetry in a distribution may be measured in a variety of ways, but the standard measure in mathematical statistics is the normalized third central moment of the distribution, also known as the skewness (Hays, 1994). If a distribution is perfectly symmetrical, its skewness is equal to zero. Distributions skewed to the right have positive skewness values; distributions skewed to the left have negative skewness values.

Skewness measures for the individual young and older adults, calculated using the SKEW function in Microsoft Excel (Redmond, WA), are reported in Table 2. Although there is considerable diversity in the observed skewness values, they are consistent in indicating that the RT distributions for all individual participants were highly asymmetrical. The mean skewness values for the group of older adults were 3.27 and 3.28 for the same and different conditions, respectively, whereas the corresponding values for the younger adults were 3.94 and 4.56. Thus, the skewness measures provide no support for the notion that the RT distributions of older adults are more asymmetrical than those of younger adults.

Table 2.

Skewness measures for the RT distributions of individual young and older adults in the same and different conditions.

Young			Older
Subject	Same	Different	Subject	Same	Different
Y-1	10.27	6.25	O-1	3.92	7.13
Y-2	2.99	2.95	O-2	5.89	1.85
Y-3	7.64	5.51	O-3	1.74	1.82
Y-4	3.27	4.98	O-4	2.58	2.55
Y-5	4.21	1.97	O-5	1.76	2.42
Y-6	2.53	2.15	O-6	2.71	2.71
Y-7	5.12	8.27	O-7	5.90	3.88
Y-8	2.77	5.59	O-8	2.24	1.99
Y-9	2.71	3.36	O-9	2.73	5.18

Ex-gaussian Parameters

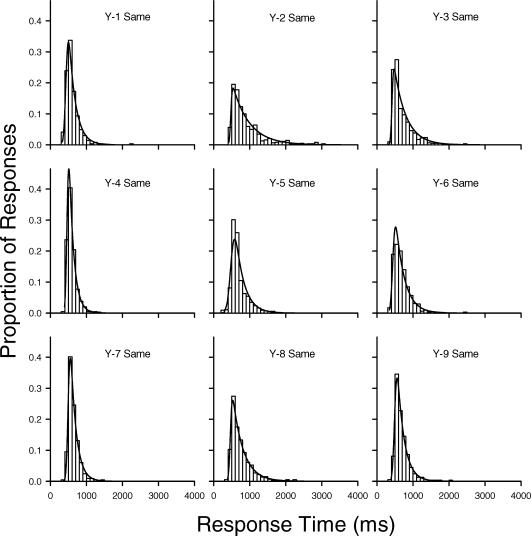
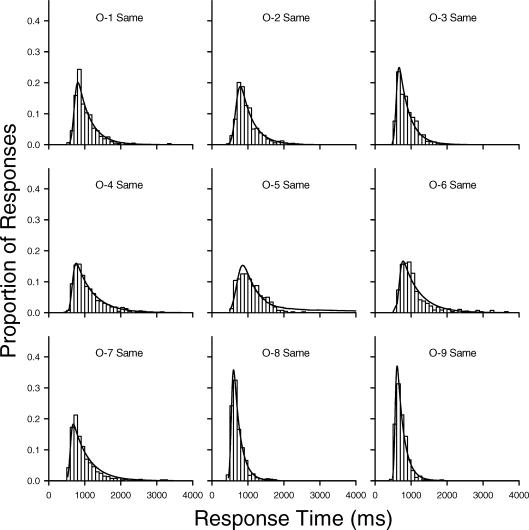
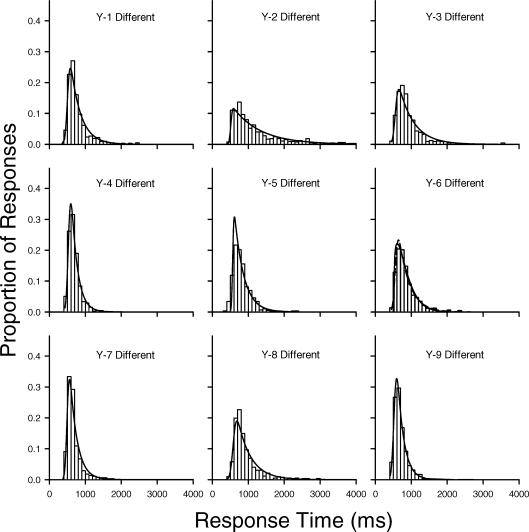
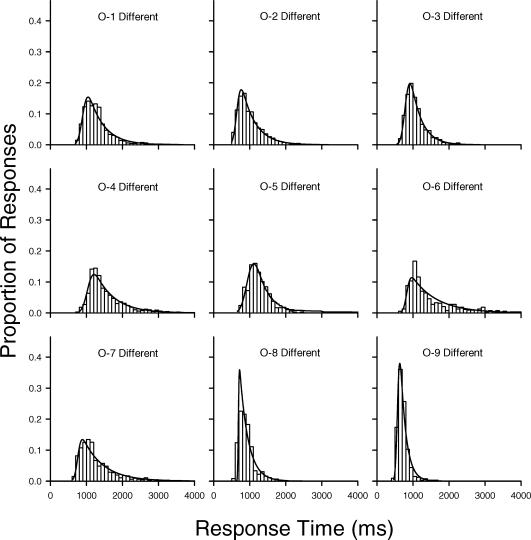
The results described so far appear to contradict previous conclusions regarding age differences in skew that were based on analyses of the parameters of ex-Gaussian functions fit to older and younger adults' RT distributions. Such ex-Gaussian analyses were also conducted on the present data using RTSYS (Heathcote, 1996). Figure 5 depicts normalized frequency histograms and the best-fitting ex-Gaussian probability density functions (solid curves) for the young adults in the same condition, and Figure 6 depicts the best-fitting ex-Gaussian functions for the older adults in this condition. Figures 7 and 8 depict the corresponding data for the young and older adults in the different condition. Visual inspection of the correspondence between the histograms and the ex-Gaussian functions reveals that the fits are quite good.

Fig 5.

Normalized frequency histograms for individual young adults with best-fitting ex-Gaussian density functions (solid curves) for response times in the same condition.

Fig 6.

Normalized frequency histograms for individual older adults with best-fitting ex-Gaussian density functions (solid curves) for response times in the same condition.

Fig 7.

Normalized frequency histograms for individual young adults with best-fitting ex-Gaussian density functions (solid curves) for response times in the different condition.

Fig 8.

Normalized frequency histograms for individual older adults with best-fitting ex-Gaussian density functions (solid curves) for response times in the different condition.

The means and standard deviations of the ex-Gaussian parameters are given in Table 3. (The parameter estimates for each individual in each condition are provided in Appendix A). Recall that the mu and sigma parameters represent the mean and standard deviation, respectively, of the Gaussian component of an ex-Gaussian distribution, whereas the tau parameter represents both the mean and standard deviation of the exponential component. Importantly, the exponential tail of an ex-Gaussian distribution grows as tau increases. Because of this, tau has sometimes been used as a measure of skew, although this is only appropriate when the other parameters remain constant (or nearly so). A better measure of the degree of asymmetry, particularly when comparing groups like older and younger adults who, as may be seen in Table 3, tend to differ in sigma and mu as well as tau, is the ratio of tau to sigma (Heathcote et al., 2002). The older adults in the present study had larger tau values, on average, than younger adults, but they had smaller mean tau/sigma ratios: 6.07 for the younger adults versus 5.38 for the older adults in the same condition; 6.90 versus 5.41, respectively, in the different condition.

Table 3.

Mean ex-Gaussian parameter values and mean Tau/Sigma ratios (with their standard deviations) as a function of age group and condition.

Condition	Mu		Sigma		Tau		Tau/Sigma
	M	SD	M	SD	M	SD	M	SD
Same
Young	464.26	26.90	46.17	15.47	247.39	103.21	6.07	3.73
Older	635.59	62.95	63.76	25.77	341.82	107.45	5.38	2.07
Different
Young	537.52	30.89	50.32	12.54	327.57	184.92	6.90	5.37
Older	800.74	151.42	84.98	37.88	396.46	170.58	5.41	3.59

Weibull Parameters

Weibull probability density functions, calculated using the Regression Wizard in SigmaPlot 9.0 (SPSS Inc., Chicago, IL), also provided good fits to the RT distributions of the younger and older adults. The means and standard deviations of the parameters of the best-fitting Weibull functions are given in Table 4, and the Weibull parameter estimates for each individual in each condition are provided in Appendix B</intraref>. Although the older adults in present study had larger shift and scale parameters, on average, than the younger adults, they also had larger shape parameters: 1.20 for the older adults versus 1.16 for the younger adults in the same condition; 1.37 versus 1.25, respectively, in the different condition.

Table 4.

Mean Weibull parameter values and standard deviations as a function of age group and condition.

Condition	Shift		Scale		Shape
	M	SD	M	SD	M	SD
Same
Young	449.62	35.16	247.59	72.35	1.160	0.139
Older	606.29	68.88	379.10	119.16	1.197	0.160
Different
Young	512.68	37.96	319.89	116.39	1.254	0.175
Older	729.38	151.35	466.22	137.40	1.371	0.299

To interpret these values, recall that the shift parameter of the Weibull function measures the displacement of the distribution along the abscissa, the scale parameter provides a measure of the spread of a distribution, whereas the shape parameter reflects the skew of a distribution. When the shape parameter equals 1.0, the distribution has the shape of a simple exponential distribution; as the shape parameter increases, the distribution becomes increasingly symmetrical, having a shape that is approximately normal when the shape parameter equals 3.4. In sum, the smaller the value of the shape parameter, the more skewed the distribution. Thus, rather than showing greater skew, the evidence provided by the younger and older adults' Weibull shape parameters is consistent with the evidence provided by the other measures used in this study. Taken together, the converging evidence indicates that, on average, the RT distributions of the older adults were not more skewed than those of the young adults; to the contrary, the older adults' distributions tended, if anything, to be slightly more symmetrical.

Discussion

The goal of the present study was to compare intraindividual variability in older and younger adults on a serial choice reaction time task. Consistent with previous research, the older adults in the present study showed greater intraindividual variability in their RTs than did young adults. Moreover, when ex-Gaussian functions were fit to individual participants' RT distributions, estimates of the ex-Gaussian's tau parameter were higher for the older adults, on average, than for the young adults, a result that in previous studies has been interpreted as indicating that the distributions of older adults are more skewed than those of younger adults (e.g., Balota et al., 2004; McAuley et al., 2006; Spieler et al., 1996; West, 1999; West et al., 2002). Also consistent with much previous research, the older adults' RTs were slower than those of the young adults, and the older adults showed greater decreases in their response latencies as a function of practice (Cerella, 1990).

Both of these latter results (i.e., slower responding and greater improvements with practice) can confound interpretation of differences in variability, and in our analyses we took a number of steps to avoid these confounds and, unlike most previous studies, used a variety of measures in order to try and obtain converging evidence as to whether older adults' RTs really are more variable and more skewed than those of younger adults. First and foremost, in order to avoid the interpretational problems caused by age differences in the effects of practice, our analyses focused on stable performance after extended practice, an approach that seems more direct than attempting to control statistically for practice effects (e.g., Hultsch et al., 2002). Second, we examined the relation between speed of responding (measured as median RT) and intraindividual variability (measured as the SIQ range) in order to compare older adults' intraindividual variability not just with that of younger adults, but also with what would be expected of the older adults based simply on their slower response times. Third and finally, we used a variety of techniques to examine skew, including Q–Q plots and normalized measures of distribution shape (i.e., the skewness statistic, the tau/sigma ratio in ex-Gaussian analyses, and the shape parameter in analyses involving fits of the Weibull function) that in various ways removed the potential confound of age differences in response speed.

When the confounds of differential practice effects and slower responding were removed or controlled, the present results revealed little in the way of age differences in either intraindividual variability or the shape of RT distributions. Older adults, on average, were no more variable than would be expected based on their slower RTs, as revealed by comparing SIQ ranges plotted as a function of median RTs. Moreover, when the difference in speed was eliminated as a potential confound, the RT distributions of older adults were revealed to be slightly less skewed than the younger adults' distributions.

Converging evidence for this finding came from the negative quadratic coefficients of second-order polynomial functions fit to the corresponding quantiles of older and younger adults' RT distributions, as well as the smaller skewness values for older adults and the lower tau/sigma ratios and higher shape parameter values obtained in ex-Gaussian and Weibull curve-fitting analyses. These differences in skew, although consistent, tended to be small. Indeed, nearly all of the variance (98.5%) in the average older adult quantiles could be accounted for by assuming that they were simply 1.4 times slower than the corresponding average young adult quantiles.

The present results, although not unprecedented (e.g., Salthouse, 1993, Smith et al., 1988), provide strong evidence against the notion that older adults are slower than young adults because they suffer from attentional or intentional lapses. Such lapses, which have been attributed to frontal lobe damage (e.g., West, 1999; West et al., 2002), are thought to be reflected in increased means, greater intraindividual variability, and more skewed RT distributions in older adults. The present results provide no evidence of such lapses. Instead, we attribute previous findings of greater skew in older adults' RT distributions to some combination of the potentially confounding methodological features that we deliberately avoided in the present study.

In addition to these methodological differences, the present study also differed from previous efforts in the number of subjects tested, how intensively they were studied, and the number of analytical approaches that were used to provide converging evidence. The use of a smaller than usual number of subjects, in particular, raises the question of sampling error. Smaller samples have a greater likelihood of being unrepresentative of the populations from which they were drawn. Nevertheless, the present samples exhibit the characteristics typical of larger younger and older adult samples (age differences in average RTs, in measures of variability, and in the absolute length of the tails of their RT distributions), indicating that the present samples were not unusual, at least with respect to the phenomena of interest in the present study (i.e., the source of the slower responding and the greater variability of older adults' RTs).

A failure to adequately avoid or control for potential confounds could partially explain the preponderance of studies reporting greater intraindividual variability in the RTs of older adults relative to young adults. Consistent with the present study, for example, Shammi, Bosman, and Stuss (1998) found that statistically controlling for mean levels of performance on a choice RT task effectively removed the effects of age on variability. Their participants performed the choice RT task in two separate sessions, each consisting of 180 trials. In contrast, Hultsch and his colleagues (Hultsch et al., 2002) have reported that the variability of older adults on the same type of task was greater than that of young adults, even when differences in mean RT were statistically controlled. We would note, however, that the participants in their studies received only 60 trials, one-third of the number used by Shammi et al. (and less than one-thirtieth of the number in the present study).

How many trials are enough when one wants to compare RT distributions? The answer depends partly on the task and the time necessary to achieve asymptotic performance. For example, West et al. (2002) compared older and young adults' performance on a speeded 1-back memory task that is more difficult than a simple choice RT task, and that, as a result, requires more practice. Both older and younger adults' RTs on the 1-back task decreased continuously over four sessions of practice in the West et al. study, and as in the present and previous studies, the older adults improved much more. Based on the estimates of tau and sigma provided for each group in each session, we calculated the ratios and found that in the first session, the ratio of tau to sigma was greater for the older adults. In the fourth and final session, however, the situation was reversed: Older adults' distributions (as measured by the tau/sigma ratio) were less skewed than those of the young adults.

Overall, West et al. (2002) found significant age differences in tau but not in sigma, and cited this as evidence of an age-related decrease in the stability of executive control. The mean estimate of sigma in the older adults was more than one third larger than the estimate in the younger adults, however, and the failure to obtain significance with a difference that large may say more about measurement reliability than about a specific deficit in executive processing. Thus, in order to obtain reliable estimates of the form of RT distributions, more difficult tasks may require both more trials before behavior becomes stable, and more trials after stability is reached.

We are not the first to reach the conclusion that the RT distributions of older and younger adults have the same shape. Salthouse (1993) reached conclusions similar to ours by comparing the skewness statistics for older and younger adults' individual RT distributions. He also reported that controlling for age differences in the fastest RTs (i.e., the fastest percentiles) nearly eliminated the effects of age on the slowest RTs (i.e. those in the tails of the distributions). Based on these results, Salthouse concluded that the distributions of older adults are simply shifted and magnified versions of the distributions of young adults, with no differences in the tails of the distributions of older adults of the kind that would be expected if older adults experienced greater lapses of attention. Our results strongly support these conclusions.

As noted previously, age-related increases in skew have been attributed to a decrease in the ability to maintain attention (Bunce et al., 1993; West, 1999) or intention (West et al., 2002), both of which have been hypothesized to be the result of an age-related decrease in frontally mediated executive control processes. The present study, like that of Bunce et al., used a serial choice reaction time procedure. Such a procedure provides a rigorous test of both attentional and intentional lapses even when the decisions to be made are relatively simple. Because trials are not self-paced, but instead are triggered by the response on the previous trial, participants are required to focus their attention uninterruptedly on the task. Despite this demand for sustained attention, the results of the analyses of the Q–Q plots, the ratio of the ex-Gaussian tau and sigma parameters, and the Weibull shape parameter, all converge in failing to support the notion that the performances of older individuals are plagued by more frequent lapses of attention or intention.

Although we found no evidence of more attentional or intentional lapses in older adults, our results do not challenge either the well-established finding that the frontal lobes are more susceptible to the deleterious effects of aging than other areas of the brain (Moscovitch & Winocour, 1992; Raz, 2000) or the increased intraindividual variability in performance that has been observed in neuropsychological patients with frontal damage (e.g., Stuss et al., 2003). What our results do challenge is the attempt to extrapolate from these two findings and to interpret age differences in intraindividual variability in healthy adults in terms of frontal deficits.

Our results also do not challenge published reports of correlations between intraindividual variability and higher-order cognitive functions in older adults (e.g., Rabbitt et al., 2001), nor do they challenge the results of studies suggesting that variability is more correlated with a variety of other measures in older adults than in young adults (e.g., Ferraro & Moody, 1996). What we would suggest, however, is that examination and interpretation of such correlations must proceed with the same kind of careful attention to the potential confounds presented by the correlation between average response speed and variability, and by the contribution of changes in performance with practice to measures of variability, that was exercised in the present study. In fact, the present results suggest that the observed greater variability of older adults' performance was primarily a reflection of the general principle that variability is greater when RTs are longer.

This principle appears to apply when slower older adults are compared with faster younger adults, when slower individuals are compared with faster peers from the same age group, and when an individual's initially slower performance is compared with faster performance after extended practice. In the present study, an increasing linear relation between RT and variability was observed within as well as between subjects, and when this relation was taken into account, the older adults were, if anything, less variable than the young adults. That is, the observed linear relation accounted for the effects of practice on intraindividual variability, as well as both age differences in variability and differences in variability among individuals of similar age. Importantly, the variability of other behavioral measures, such as memory span, is not systematically related to the average level of performance in either young or older adults, even when the RT variability of those same individuals is related to their average RT (Robertson et al., 2006). This finding raises the possibility that the lawful relation between the variability and average level of an individual's RTs involves mechanisms specific to RTs. Moreover, examination of RT data from experiments involving pigeons, rats, and monkeys (e.g., Blough, 2000; Stebbins, 1962; Stebbins & Miller, 1964) reveals the generality of this relation.

Finally, our results suggest that older adults, although slower at processing information than younger adults, nevertheless can do so as reliably as younger adults. That is, older adults appear no more likely than younger adults to miss cues or fail to make timely decisions due to temporary lapses, at least on simple information-processing tasks like those used in the present study. Although the number of participants in our study was small, they were typical of their age groups with respect to those aspects of their performance deemed most relevant to the issue at hand. Nevertheless, systematic replication with larger samples would be desirable. Furthermore, researchers should consider using procedures and measures similar to those of the present study to explore a wider range of tasks in order to establish the generality of the present findings. In particular, examination of tasks that vary widely in complexity and in the role played by putative executive processes would be useful. If true age differences in the shape of RT distributions are to be found, this might be the way to find them—or alternatively, to establish that such differences do not exist.

Appendix A

Ex-Gaussian parameters for each individual as a function of age group and condition.

Age	Same				Different
	Mu	Sigma	Tau	Tau/Sigma	Mu	Sigma	Tau	Tau/Sigma
Young
Y-1	434.86	49.73	188.82	3.80	504.95	52.58	283.53	5.39
Y-2	477.17	31.91	465.53	14.59	513.20	36.26	767.73	21.17
Y-3	419.02	32.57	329.13	10.11	560.76	59.73	419.83	7.03
Y-4	463.58	37.40	130.45	3.49	531.26	50.46	171.34	3.40
Y-5	484.17	82.86	234.66	2.83	566.63	26.55	259.55	9.78
Y-6	444.21	50.85	242.90	4.78	559.37	56.86	296.47	5.21
Y-7	496.61	42.91	154.78	3.61	494.17	46.58	201.62	4.33
Y-8	465.02	38.88	290.01	7.46	582.62	68.03	368.28	5.41
Y-9	493.68	48.39	190.25	3.93	524.69	55.85	179.79	3.22
Older
O-1	712.33	66.03	344.87	5.22	904.90	102.14	416.46	4.08
O-2	670.92	88.84	331.41	3.73	648.65	82.69	372.43	4.50
O-3	591.03	50.58	282.96	5.59	796.36	96.06	293.38	3.05
O-4	657.96	64.27	473.09	7.36	1042.09	122.18	526.09	4.31
O-5	706.94	118.03	388.33	3.29	958.17	144.05	313.37	2.18
O-6	676.35	61.59	453.00	7.36	831.60	77.72	689.57	8.87
O-7	600.88	47.28	431.83	9.13	763.58	75.87	564.62	7.44
O-8	543.83	41.74	183.50	4.40	686.27	17.16	234.82	13.68
O-9	560.06	35.50	187.37	5.28	575.03	46.94	157.39	3.35

Appendix B

Weibull parameters for each individual as a function of age group and condition.

	Same			Different
	Shift	Scale	Shape	Shift	Scale	Shape
Young
Y-1	419.12	193.08	1.21	487.60	271.86	1.19
Y-2	501.14	383.54	1.00	536.06	587.54	1.00
Y-3	412.62	279.22	1.00	544.61	372.17	1.21
Y-4	436.04	162.93	1.33	480.29	224.93	1.52
Y-5	479.33	222.43	1.05	505.63	332.12	1.40
Y-6	396.89	304.38	1.34	523.54	336.62	1.23
Y-7	472.47	175.85	1.28	481.07	191.97	1.23
Y-8	456.53	293.32	1.05	585.42	318.55	1.05
Y-9	472.45	213.61	1.18	469.92	243.23	1.46
Older
O-1	693.72	348.61	1.11	796.70	529.65	1.51
O-2	630.28	374.67	1.19	594.95	450.37	1.22
O-3	544.64	358.36	1.27	717.86	393.46	1.35
O-4	641.70	480.96	1.04	1038.00	517.05	1.00
O-5	553.50	595.65	1.52	748.89	561.43	1.84
O-6	666.11	419.59	1.11	807.29	655.72	1.00
O-7	677.10	400.00	1.00	736.36	553.28	1.16
O-8	523.11	204.02	1.19	600.11	328.18	1.65
O-9	526.43	230.05	1.33	524.27	206.86	1.61