Dynein-Mediated Cargo Transport in Vivo

Abstract

Cytoplasmic dynein is a microtubule-based motor with diverse cellular roles. Here, we use mutations in the dynein heavy chain gene to impair the motor's function, and employ biophysical measurements to demonstrate that cytoplasmic dynein is responsible for the minus end motion of bidirectionally moving lipid droplets in early Drosophila embryos. This analysis yields an estimate for the force that a single cytoplasmic dynein exerts in vivo (1.1 pN). It also allows us to quantitate dynein-mediated cargo motion in vivo, providing a framework for investigating how dynein's activity is controlled. We identify three distinct travel states whose general features also characterize plus end motion. These states are preserved in different developmental stages. We had previously provided evidence that for each travel direction, single droplets are moved by multiple motors of the same type (Welte et al. 1998). Droplet travel distances (runs) are much shorter than expected for multiple motors based on in vitro estimates of cytoplasmic dynein processivity. Therefore, we propose the existence of a process that ends runs before the motors fall off the microtubules. We find that this process acts with a constant probability per unit distance, and is typically coupled to a switch in travel direction. A process with similar properties governs plus end motion, and its regulation controls the net direction of transport.

Introduction

Cytoplasmic dynein is a minus end–directed microtubule-based motor that participates in a wide range of cellular transport processes, from mitosis, and retrograde axonal transport, to the accumulation of pigment granules in melanophores (Holzbaur and Vallee 1994; Schroer 1994; Vallee and Sheetz 1996). During animal development, this motor plays roles in oogenesis, axonal guidance, and nuclear migration. It has even been co-opted by neurotropic viruses, allowing them to spread through neurons (Sodeik et al. 1997; Suomalainen et al. 1999). Loss of cytoplasmic dynein function leads to severe growth inhibition in fungi (Xiang et al. 1995) and to cell death in flies (Gepner et al. 1996).

Because cytoplasmic dynein has to perform multiple and diverse tasks, it seems likely that its activity is highly controlled. Consequently, there is great interest in identifying regulators of dynein, and traditional approaches from genetics, biochemistry, and molecular biology have yielded promising candidates (for reviews see Gill et al. 1991; Bowman et al. 1999; Nurminsky et al. 1998). However, at the moment, we still lack a framework for interpreting the function of such regulatory molecules because little is known about how dynein moves cargoes along microtubule tracks in vivo. Different scenarios could be envisioned. For example, dynein's processivity (the average number of steps the motor can take before falling off the microtubule) might be limiting. Indeed, in vitro, single microtubule motors travel only for limited distances because at each step they have a constant probability of falling off the microtubule track. If motors similarly fall off in vivo, cargoes might pause or even diffuse randomly afterwards until another motor engages. Under this scenario, a regulator of dynein might alter motor processivity directly or, if multiple motors work together, change how many motors are engaged on the cargo. Additional motors would be expected to allow the cargo to move for longer distances since when any one fell off the microtubule, the others could continue to transport the cargo; this would also keep the cargo close to the microtubule, giving the detached motor an opportunity to reengage. In another scenario, dynein's processivity might be sufficiently high that the cargo does not fall off the microtubule. Thus, some other process is required to end motion. Such a process could function in a variety of ways, e.g., turning off dynein after a predetermined number of steps. In this case, dynein-mediated transport could be regulated by altering the process that terminates motion. To distinguish between these and other models, biochemical or genetic characterization of the regulatory molecules involved is not sufficient. Rather, it is essential to monitor dynein-driven cargo motion in real time.

Crucial insight into the mechanism that controls motor activity can be gained from the statistics of the distance traveled in a single run (i.e., a segment of uninterrupted motion): different processes ending runs are expected to lead to different types of distributions. For example, if motion ends (because at each step the motor falls off with a constant probability), then a histogram of travel distances would be described by a simple decaying exponential curve, which is the distribution observed in vitro for a bead moved by a single kinesin or axonemal or cytoplasmic dynein (Block et al. 1990; Wang et al. 1995; Sakakibara et al. 1999). If a run ends based on how far the motor has traveled, then the travel distances would be expected to cluster around a specific value, and the exact distribution could provide insight into how the number of steps is measured.

Such quantitative characterization is complicated because in many situations dynein-driven travel constantly alternates with excursions in the opposite direction (Rogers et al. 1997; Suomalainen et al. 1999). Despite such back and forth motion, the cargo can still achieve net transport on longer time scales if the average travel distance for minus end motion is larger than that for plus end motion, or vice versa (Welte et al. 1998). In cases of such bidirectional motion, it is crucial to sample images of cargo motion rapidly. This has proven to be challenging: in vivo, many different classes of cargo move simultaneously, often with different characteristics but not readily distinguishable by their appearance. While it is possible to focus on a single type of cargo by using fluorescent tags, following their motion with confocal microscopy typically allows sampling, at most, a few frames a second, severely limiting the temporal resolution. Purified in vitro systems with a defined class of cargo might overcome this problem because under these circumstances it would be possible to follow cargo with video-enhanced differential interference microscopy, at standard video frame rates (30 frames/s). However, because dynein is complex and requires a number of accessory proteins for correct function, reconstituting bidirectional motion in vitro has proven to be extremely difficult. Given dynein's sensitivity to biochemical manipulations, any bidirectional motion established in vitro would have to be calibrated against well-characterized in vivo transport.

We have previously described a new in vivo model system to study bidirectional transport: lipid droplets in early Drosophila embryos (Welte et al. 1998). Because the droplets are large and distinct, they can be accurately followed by standard video-enhanced differential interference contrast microscopy, allowing good temporal and spatial measurements of cargo motion. In addition, this model system shows developmentally controlled switches in the direction of net transport and allows the analysis of mutants; thus, the properties of droplet motion can be examined under different conditions.

In this paper, we show that mutations in the dynein heavy chain gene alter the minus end motion of individual lipid droplets. Because dynein localizes to the lipid droplets, we conclude that dynein is responsible for the minus end transport of the droplets. Droplet motion is composed of pauses and runs of varying lengths, but droplets rarely diffuse out of the plane of focus. Using newly developed tools to automatically track and characterize droplet motion, we quantify dynein-driven cargo transport and find that under several different conditions both pauses and runs are characterized by simple exponential distributions. These observations exclude a large class of models describing how dynein activity is controlled. Most runs do not end in pauses, but result in immediate switching of travel direction. Because runs are shorter than expected if droplets are moved simultaneously by multiple motors, we propose that they are not limited by the processivity of the motors, but are instead cut short by a different mechanism.

Materials and Methods

Immunolocalization

Embryos were disrupted on polylysine-treated glass slides (10-well slides with Teflon coating; Polysciences, Inc.) in 3 μl of buffer (35 mM Pipes, 5 mM MgSO₄, 5 mM EGTA, 0.5 mM EDTA, plus a cocktail of protease inhibitors; Schroer et al. 1989). Lipid droplets were briefly allowed to adsorb to the glass, preparations were fixed for 8 min with an equal volume of 37% formaldehyde, washed extensively (PBS 0.1% Triton X-100), and blocked overnight in PBS with 10% BSA and 0.1% Triton X-100. We probed for dynein by indirect immunofluorescence (using a tertiary antibody conjugated to Alexa488), using mouse monoclonal 74.1, which by Western analysis specifically recognizes dynein intermediate chain (Dic) in a number of vertebrate species (Dillman and Pfister 1994) and cross-reacts with a major band of ∼80 kD in Drosophila embryo lysates (data not shown). Preparations were counterstained with Nile red (0.8 mg/ml in PBS with 1% BSA) to label lipid droplets (Greenspan et al. 1985) and inspected on a Zeiss confocal microscope. The staining intensity, density of droplets, and Dic signal varied across preparations. In areas with low density of signal, we compared droplets that appeared to be associated with punctate Dic staining (defined as the center of the Dic staining less than a droplet diameter from the center of the droplet) to the rest of the microscopic field. Examining nine such fields, we found that, on average, the fraction of dynein signal associated with droplets was ∼100-fold higher than expected for association by chance based on the observed density of Dic in the field overall. In wholemount preparations of unsquashed embryos, punctate Dic signal also appeared to be associated with lipid droplets (data not shown). However, in this case, we could not rule out that apparent colocalization was simply because of the high density of Dic signal throughout the cytoplasm.

To judge how large the signal from a single dynein molecule would appear in these preparations, we estimated that the bridge provided by primary, secondary, and tertiary antibodies would position any one fluorophore up to 50 nm from the antigen (fully extended antibody molecules are ∼25 nm long; Silverton et al. 1977). Since there are three copies of Dic per cytoplasmic dynein and the antibody bridges can be multiply branched, the fluorophores are expected to be spread out over an area at least 100 nm in diameter. For a 63× 1.4 NA objective, the full width half maximum of the confocal point-spread function is ∼0.23 μm (Shaw 1995). The deconvolution of this point-spread function with an object of 0.1-μm spatial extent would yield an object of 0.33-μm apparent size, which is similar to the sizes we observe for the Dic signal. This appearance of the Dic signal does not allow us to determine if there are more than one dynein present per staining entity. The lipid droplet distribution in whole embryos was determined as described (Welte et al. 1998). Fluorescent images were assembled in Adobe Photoshop.

Force Measurements

Force measurements were performed as described in Welte et al. 1998, by measuring the percentage of minus- or plus-traveling droplets escaping from the optical tweezers at different laser powers.

Particle Tracking and Analysis

As described in Welte et al. 1998, embryos of the appropriate developmental stage were flattened into halocarbon oil, and video-enhanced differential interference contrast recordings of moving droplets were made onto videotape with a 100× 1.3 NA plan-neofluor objective, and a 10× eyepiece in front of the video camera (see Welte et al. 1998). Appropriate sequences from the recording (usually ∼1-min duration [with 30 frames per second]) were transferred onto the hard disk of a Silicon Graphics O2, using the proprietary SGI frame grabbing software, with JPEG compression.

The motion of individual droplets was determined by tracking them using the Isee image-processing software package (Inovision Corp.). Two types of calibrations of the accuracy of position detection were performed. First, the inherent noise of this process was determined to be ∼±8 nm p-p, found by recording and tracking images of a droplet fixed to the coverslip. Second, the subpixel resolution of the tracking software was confirmed by tracking images of a bead affixed to a translational stage moved with nanometer resolution in a triangle wave. No deviations from linear displacement were observed, and the residual (i.e., the difference between the data points and a straight line fit to the data) was zero mean and again showed roughly 8-nm p-p noise.

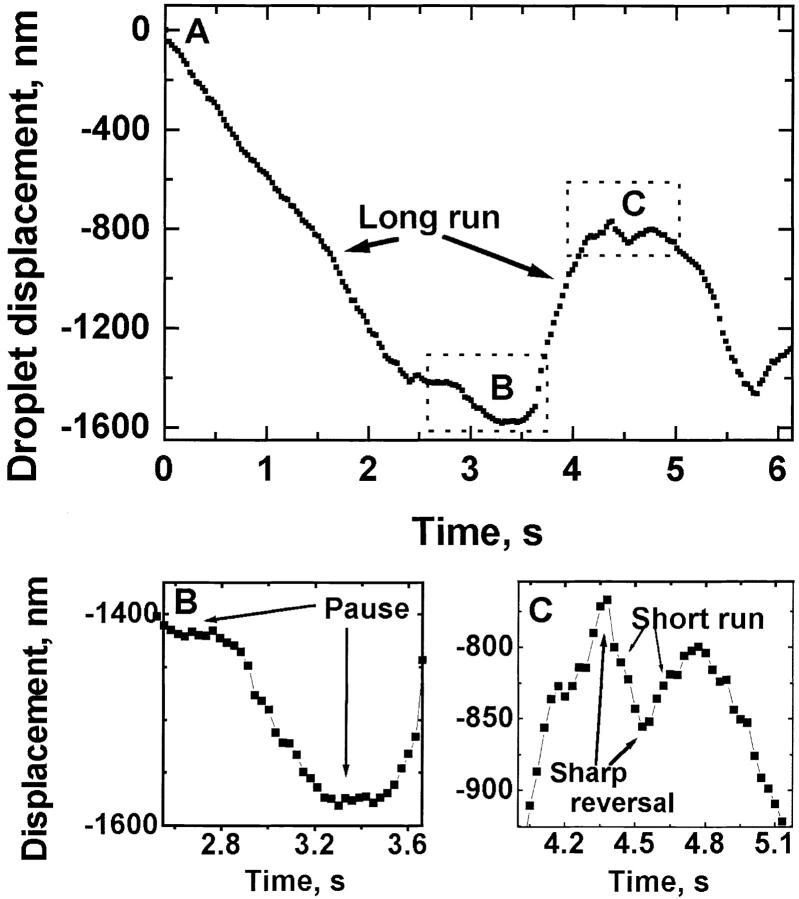
Once the x-y location of individual droplets was known as a function of time, motion along a particular microtubule was determined by projecting the motion onto the best fit line to the droplet's trajectory (Welte et al. 1998). This record of displacement versus time (see Fig. 4 for a portion of a typical record) was analyzed with custom software (the parsing program) that determined reversal points and pauses, breaking down the record into portions of plus end travel, minus end travel, and pauses. Minus end runs could be preceded either by a pause or a plus end run, and could be ended either by the occurrence of a pause or a reversal resulting in plus end run.

Figure 4.

(A) Track of the motion of a representative lipid droplet, with both plus and minus end runs of greatly varying lengths. Decreasing ordinate values correspond to minus end motion. One example each of a long minus end and plus end run is labeled. Dotted boxes labeled B and C indicate the regions that are magnified in B and C. (B) Portion of A showing two pauses. (C) Portion of A showing typical sharp reversals (no obvious pause involved). One example each of a short minus end and plus end run is labeled.

To avoid the effects of noise, for a displacement to be scored as a run it needed to be at least 30-nm long, and last at least 0.16 s. Pauses were operationally defined as periods when there was <30 nm displacement for a duration of at least 0.23 s, with the additional condition that the mean velocity had to be <50 nm/s.

Because a combination of algorithms was used to determine when a droplet was moving or paused, the parsing program was tested in two ways. First, the program was tested on a data set previously analyzed by hand, and the two methods yielded the same results. Next, the program was run on simulated data with noise (8 nm, peak-to-peak, experimentally derived from tracking a fixed droplet), where the plus and minus end runs were drawn from double exponential distributions with known distance constants, and the pauses were drawn from a single exponential distribution with known time constant. The distance and time constants were chosen to be approximately the same as those found experimentally. The simulated data were treated as experimental data and analyzed in the same manner. This produced histograms similar to the histogram in Fig. 6, and the correct distance constants were recovered (to within experimental error) when the histograms were fit to a double exponential. The chi-squared values of the fits to the simulated data were in the same range as the fits to the experimental data.

Figure 6.

Distribution of lengths of droplet travel in the minus end direction (35-nm bins). The location of individual droplets as a function of time was determined with nanometer-level resolution using centroid analysis (Welte et al. 1998). Histograms shown are of run distances of droplets moving in the minus end direction during phase II for wild-type (A) and Dhc64C mutant (B) embryos, and during phase III in wild-type embryos (C). Very short runs were difficult to detect, so many such runs (first bin) were presumably missed. In both cases, the general shape of the histograms was the same and well fit by the sum of two decaying exponentials (solid lines, see also Table ). The exponential fit started with bin 2, and used all bins with five or more counts.

To check for the possibility of artifacts in data analysis, the analysis was also run on simulated data with noise (8 nm, peak-to-peak, experimentally derived from tracking a fixed droplet), where the plus and minus end runs were drawn from single exponential distributions with known distance constants, and the pauses were drawn from a single exponential distribution with known time constant. In this case, the resultant histograms were well described by a single decaying exponential as judged by chi-squared values, and the correct distance constants were recovered to within experimental error.

Results

Cytoplasmic Dynein Transports Lipid Droplets

Based on the relatively high speed of droplet transport, we had previously proposed that minus end motion employed cytoplasmic dynein (Welte et al. 1998). In this case, dynein should be present on the droplets. To test this possibility, we stained fixed embryos with Nile red to specifically label lipid droplets (Greenspan et al. 1985), and with an antibody against the intermediate chain of cytoplasmic dynein (Dic; Dillman and Pfister 1994). In many cases, lipid droplets were associated with a single spot of Dic staining (not shown). However, punctate Dic staining was abundant throughout the cytoplasm, so we could not rule out that this colocalization was spurious. Therefore, we attempted to dilute lipid droplets away from other embryonic material by disrupting individual embryos in a drop of buffer on a polylysine-treated microscope slide. After a brief period to allow organelles to adhere to the slide, these preparations were fixed and stained for lipid droplets and dynein intermediate chain as for whole embryos. Staining intensity, the density of droplets, and the Dic signal varied across preparations; in favorable regions of the slide, up to 25% of the lipid droplets were next to single spots of dynein staining (Fig. 1); no such association was observed when the primary antibody was omitted from the staining reaction (not shown). To determine whether this association was significant, we compared droplets that appeared to be associated with punctate Dic staining (defined as the center of the Dic staining less than a droplet diameter from the center of the droplet) to the rest of the microscopic field. The probability of the observed association was ∼100-fold higher than expected for association by chance based on the observed density of Dic in the field overall.

Figure 1.

Physical association between cytoplasmic dynein and lipid droplets. Lipid droplets were diluted away from other organelles and unattached motors by squashing single embryos in buffer. Preparations were fixed and treated with the droplet-specific dye Nile red (red) and an antibody against the intermediate chain of dynein (Dic, green; Dillman and Pfister 1994). In many instances, lipid droplets had a punctate Dic signal associated with them, with little Dic staining in the general background. This association was ∼100-fold more frequent than expected by chance alone. Otherwise identically treated preparations for which incubation with the primary antibody was omitted showed no punctate staining on lipid droplets (not shown). Although our previous force measurements suggest that single droplets carry multiple dyneins in multimotor complexes (Welte et al. 1998), the apparent size of the Dic signal does not provide insight into the structure of these complexes because under the experimental conditions used even a single dynein molecule would be expected to yield a signal spread over a region ∼0.3 μm in diameter (see Materials and Methods). Bars, 1 μm.

To test whether this localization was functionally important, we investigated whether lipid droplet motion was altered when dynein function was impaired genetically. Ideally, one would inspect droplet behavior in embryos in which dynein function is completely eliminated. However, this was not possible because cytoplasmic dynein is provided to the early embryo by the mother and is necessary for the earlier processes of oogenesis (Gepner et al. 1996) and proper establishment of the syncytial blastoderm (Robinson et al. 1999). Instead, we inspected the progeny of mothers carrying hypomorphic mutations in Dhc64C, the single gene for the heavy chain of cytoplasmic dynein (Gepner et al. 1996). Although all known mutations in Dhc64C are homozygous lethal, a combination of two weak alleles, Dhc64C^8-1 and Dhc64C^6-10, supports development to fertile adults. Embryos laid by these mothers developed seemingly normally through cellularization and early gastrulation.

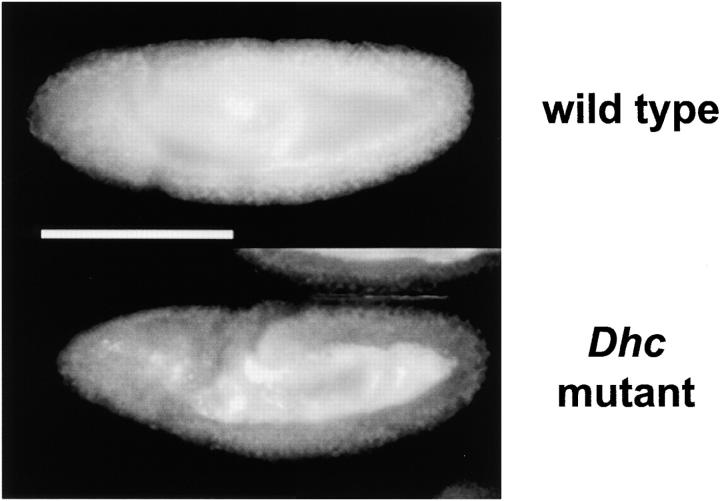
However, global transport of lipid droplets was disrupted in the Dhc64C mutant embryos (Fig. 2). In the wild type, there are three phases of net droplet transport (Welte et al. 1998). At the syncytial blastoderm stage (phase I), droplets move bidirectionally, but show no net displacement. During early cycle 14 (phase II), lipid droplets display net plus end transport, whereas at the onset of gastrulation (phase III) they undergo net minus end transport (Welte et al. 1998). In Dhc64C mutant embryos during phase II, droplets accumulated in the center, towards the plus end of microtubules, similar to wild type (data not shown). However, they failed to redistribute towards the minus ends (the periphery) during gastrulation (Fig. 2). This depletion of lipid droplets in the periphery results in embryos that are abnormally transparent from gastrulation onward (not shown), reminiscent of the failure of net minus end droplet transport due to mutations in the klar gene (Welte et al. 1998).

Figure 2.

We compared lipid droplet distribution in embryos laid by wild-type flies (Oregon-R) or by flies transheterozygous for two weak alleles of Dhc64C, the gene for the heavy chain of cytoplasmic dynein (Gepner et al. 1996). Fixed embryos were stained for lipid droplets as described in Welte et al. 1998. In both genotypes, droplets accumulate in the center, towards the plus end of microtubules, in early cycle 14 (not shown); in Dhc64C mutants, they fail to redistribute towards the minus ends (the periphery) during gastrulation. Bar, 200 μm.

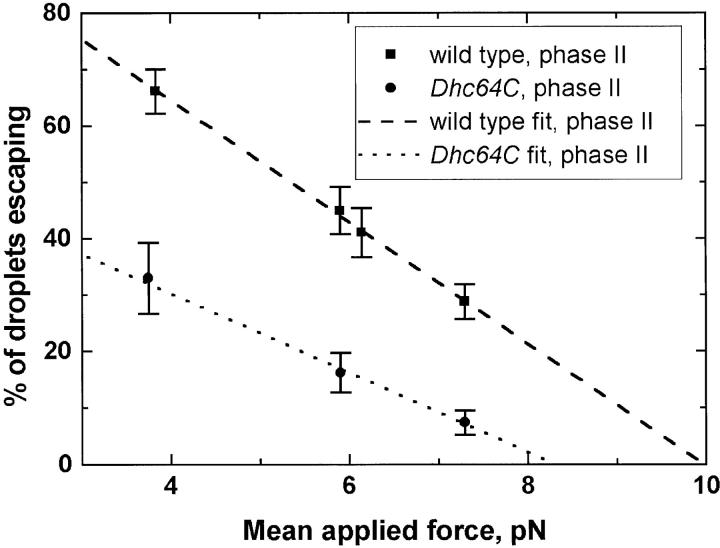
Characterization of the motion of individual lipid droplets demonstrated that in the Dhc64C mutants, transport was already altered during phase II. Using optical tweezers and the previously described squash-mount preparations of embryos (Welte et al. 1998), we determined the force necessary to stop droplets moving in the minus end direction. This force was reduced in the mutant (Fig. 3). In addition, all other parameters of motion we can measure were impaired (see below). Because genetic alteration of cytoplasmic dynein alters transport of individual droplets as well as their global distribution, we conclude that the localization of dynein to lipid droplets is functionally important.

Figure 3.

Droplet stalling force measurements, showing the percentage of droplets stalled as a function of applied force, for droplets moving towards microtubule minus ends, in wild-type or Dhc64C mutant backgrounds. Because droplets need to be clearly moving to attempt to stop them, these measurements represent the behavior of droplets moving long distances (see text). To avoid bias, force measurements were made in a blind fashion, with the genotype of the embryo being measured unknown to the person making the force measurement. Each data point is derived from measurements on six to seven embryos, with ∼30 minus-moving droplets tested per embryo.

We have previously argued that lipid droplets carry multiple motors of the same kind, each capable of exerting a stalling force of 1.1 pN (Welte et al. 1998). The identification of cytoplasmic dynein as mediating minus end motion, thus, implies that this is the force a single cytoplasmic dynein produces in vivo. This value is very similar to the recently determined stall force of 1.2 pN for axonemal dynein in vitro (Sakakibara et al. 1999).

Quantifying Dynein-driven Droplet Motion

The identification of cytoplasmic dynein as the relevant minus end motor allowed us to use this experimental system to examine the properties of wild-type dynein-driven cargo transport in vivo. Since it is the balance between minus and plus end motion that determines the direction of net transport (Welte et al. 1998), we were especially interested in characterizing how far droplets travel before reversing course. In vitro, glass beads moved by cytoplasmic dynein travel for greatly varying distances before falling off the track and exhibiting Brownian motion (Wang et al. 1995). To compare this behavior to minus end motion in vivo, we tracked droplets in squash-mount embryo preparations at 30 Hz with nanometer level resolution, focusing on genetically wild-type embryos in phase II. Minus end droplet motion persisted for greatly varying distances, but droplets rarely appeared to diffuse away, either sidewise or out of the plane of focus. Rather, continuous motion in the minus end direction (a run) was typically followed by immediate travel in the plus end direction or by short periods of pausing (a pause), after which droplets either continued moving towards the minus end or reversed their direction of travel (Fig. 4). To characterize minus end motion in greater detail, we developed procedures to quantitate these pauses and runs. We used custom software to divide records of droplet motion versus time into periods when the droplet was moving towards the microtubule plus or minus end or was paused. This automated analysis allowed us to process enough data for statistical analysis of run lengths, reversals, and pauses.

Pause Durations Are Characterized by a Decaying Exponential Distribution

To our knowledge, there has been no previous quantitation of pausing for any microtubule-based transport, either in vitro or in vivo. Thus, it is unclear whether pauses play an important role in determining the properties of transport. Pauses might constitute irrelevant interruptions, unrelated to the processes that control travel distance, or they might be crucial points of transition. For example, when RNA polymerase advances along its DNA substrate during transcription, pauses are associated with the action of regulatory mechanisms and can result in transcription termination (Yarnell and Roberts 1992; Rasmussen and Lis 1993).

For lipid droplets, we defined pauses operationally as periods when the droplet remained motionless (average velocity of <50 nm/s) for at least 0.23 s (corresponding to seven successive video frames). Such pauses appeared to constitute a well-defined state: there was no net displacement, with roughly Gaussian zero-mean histograms of this random displacement (data not shown). Additionally, paused droplets showed no significant velocity: they moved at average speeds of <14 nm/s, well separated from the typical speed of 150 nm/s of even the slowest moving droplets (see below).

Because pauses after minus end motion (“minus-pauses”) are potentially different from pauses after plus end motion (“plus-pauses”), minus- and plus-pauses were analyzed separately. To characterize minus end travel, we focus here on minus-pauses. On average, minus-pauses occurred approximately every 5 s of uninterrupted travel and lasted for an average of ∼0.6 s. Droplets spent ∼9% of the time in pauses (Table ). Pause duration was well described by a single decaying exponential y(t) = A exp(−t/t ₀) (Fig. 5 A). This functional form suggests that the probability of exiting from a pause is constant over time. For a decaying exponential, the time constant t₀ is equal to the average duration of the pause.

Table 1.

Characterization of Pauses in Droplet Motion, from Tracking Analysis

	A Time between pauses	B Pause duration	C Percent pauses ending in reversals	D Percent reversals involving a pause	E Total percent time paused
	s	s
Pauses after minus end travel
Wild type, phase II	5.03 ± 0.31	0.62 ± 0.03	34.6	13.8	9.05
Dhc64C, phase II	2.68 ± 0.12	0.76 ± 0.03	30.9	18.3	22.2
Wild type, phase III	6.25 ± 0.47	0.60 ± 0.04	43.2	13.9	11.06
Pauses after plus end travel
Wild type, phase II	7.63 ± 0.45	0.55 ± 0.2	27.0	11.7	9.05

The time between pauses (A) was determined by dividing the total time that droplets were moving in either the minus or plus end direction by the number of minus-pauses or plus-pauses, respectively. The percent pauses ending in reversals (C) was calculated by dividing the number of minus-pauses that are followed by plus end motion by the total number of minus pauses, or vice versa for the plus end motion. The percent pauses associated with reversals (D) was calculated by dividing the number of minus-pauses that are followed by plus end motion by the total number of minus-plus reversals (for minus-pauses) or by the total number of plus-minus reversals for plus-pauses. The percent time paused (E) is a global measure of pausing, and does not differentiate between plus and minus pauses (hence the same number for wild-type phase II motion, regardless of travel direction). E was calculated by dividing the total time the droplets were paused by the total time they were tracked.

Figure 5.

Distribution of pause lengths in phase II: (A) minus-pauses (i.e., pauses following minus end motion). (B) plus-pauses (i.e., pauses following plus end motion). The solid line is the best fit single decaying exponential, y(t) = A exp(−t/t ₀). In A, the fit parameters are A = 292 ± 40, t₀ = 0.24 ± 0.01, with a reduced chi-squared value of 0.51, and corresponding probability P = 88%. In B, the fit parameters are A = 152 ± 40, t₀ = 0.29 ± 0.05, with a reduced chi-squared value of 0.85, and corresponding probability P = 63%. Minus-pauses in the Dhc64 mutant were also well fit by a decaying exponential (not shown).

We next asked if there was a link between pauses and the other discontinuity in droplet motion, reversal of direction. To quantitate, we calculated the percentage of pauses resulting in reversals (i.e., a minus-pause followed by plus end motion); and the fraction of total reversals associated with a pause. Reversals and pauses can occur in the absence of one another, and most pauses do not lead to reversals. While pauses might in principle be important in altering net transport by cutting plus or minus end travel short and inducing reversals, in fact their impact seems to be limited. Only ∼13% of the reversals are associated with pauses (Table ), and the percentage of plus-to-minus reversals associated with the pauses (11.7%) is roughly the same as the percentage of minus-to-plus reversals associated with pauses (Table , 13.8%).

Since our detection threshold for pauses is 0.23 s, there may be additional reversals that are associated with very short periods of cessation in motion that are below our detection threshold. To estimate the frequency of such reversals, we fit an exponential to the 100 pauses that do result in a minus-plus reversal (A = 46 ± 9, t₀= 0.4 ± 0.04, χ² = 0.59). By extrapolation, we would predict an additional 110 reversals that were associated with pauses too short to be detected. However, there were roughly 800 minus-plus reversals observed in the data set. This leaves the majority of reversals (∼590) unassociated with pauses, suggesting that reversals occur primarily independent of pauses, and that pauses are not crucial for understanding how far droplets move towards the minus end before reversing course.

Distribution of Run Lengths

Since reversals occur independent of pauses, we investigated whether they could be related to the lengths of runs by examining the periods when droplets are moving uninterrupted in the minus end direction. Such runs varied greatly in length, from 30 (at the limit of resolution for our method to unambiguously determine a moving droplet) to >4,000 nm, with mean velocities during the entire run from 150 to 2,000 nm/s. Because pauses were relatively rare, most of these runs were directly followed by a run in the plus end direction. The distribution of run lengths provides insight into how travel distance is controlled: a process that acts with constant probability (such as motors falling off) would result in a distribution described by a simple decaying exponential, whereas mechanisms that turn off the motor after a certain distance has been traveled would result in clustering of travel distances around that value. Further scenarios are possible.

The histogram of phase II run lengths (Fig. 6 A) approximated a simple, monotonically decaying curve, reminiscent of the decaying exponential distributions observed for various individual motors in vitro (Block et al. 1990; Wang et al. 1995; Sakakibara et al. 1999). However, when we attempted to fit such a functional form to the data, no choice of parameters gave a good fit: the reduced χ² values were at best 3, corresponding to a probability of <0.01% that the observed distribution was described by a single decaying exponential. This failure to find a good fit might simply be an artifact, if there were systematic errors in the underlying data. However, the observed random noise of the position versus time data was small (8 nm, peak-to-peak, see Materials and Methods), so that the error associated with a particular bin is relatively independent of the mean values of the runs in that bin. Indeed, when we use the analysis algorithm on simulated position versus time data with added noise (with individual plus and minus end runs drawn from single decaying exponential distributions), our analysis yielded histograms that were well fit by this functional form, with the correct distance constants (see Materials and Methods). Thus, a single decaying exponential could have been detected if it were present, but does not account for the distribution of travel lengths we observe in vivo.

This analysis suggested that the underlying distribution was more complicated. The histogram was indeed described (χ² = 1.20; P = 19%) by the sum of two decaying exponentials y(D) = A _S exp(−D/D _S) + A _L exp(−D/D _L), with distance constants D_S = 98 nm and D_L = 1,068 nm (Fig. 6 A, Table ). Using simulated data with added experimentally derived noise, we confirmed that our analysis did in fact recover the correct distance constants and amplitudes for data described by the sum of two decaying exponentials (see Materials and Methods). Additionally, trying to fit this simulated data with a single decaying exponential did not yield a good chi-squared value.

Table 2.

Physical Parameters of Droplet Motion

	Mean travel distance	Short amplitude AS	Short distance constant DS	Long amplitude A L (set to 1)	Long distance constant D L	χ2, P(χ2)	Number ratio RSL
	nm		nm		nm
Minus end
Wild type phase II	620 ± 31	23.4 ± 2.2	98 ± 8	1 ± 0.2	1,068 ± 149	1.20, 0.19	2.15 ± 0.59
Dhc mutant phase II	168 ± 8	10.7 ± 1.2	44 ± 4	1 ± 0.2	209 ± 15	0.41, 0.97	2.25 ± 0.58
Wild type phase III	602 ± 37	27.2 ± 3.1	83 ± 8	1 ± 0.2	1,048 ± 175	0.93, 0.68	2.15 ± 0.65
Plus end
Wild type phase II	842 ± 35	18 ± 2	67 ± 6	1 ± 0.1	1,144 ± 140	0.98, 0.51	1.05 ± 0.22
Wild type phase III	415 ± 24	18 ± 2	96 ± 8	1 ± 0.2	780 ± 108	0.95, 0.56	2.22 ± 0.62

Droplet motion was characterized by tracking analysis. The amplitudes and distance constants result from fitting histograms of travel distance, D, like the ones in Fig. 6 and Fig. 8, to the sum of two exponential functions: y(D) = A _S exp(−D/D _S) + A _L exp(−D/D _L). χ² values and corresponding probabilities are indicated. Because the absolute values of the amplitudes are a function of the number of runs analyzed, which was not exactly the same in each case, we normalized the amplitudes to facilitate comparison (see ). The number ratio R _SL is the integrated number of short runs divided by the integrated number of long runs and, thus, shows the relative frequency of one relative to the other.

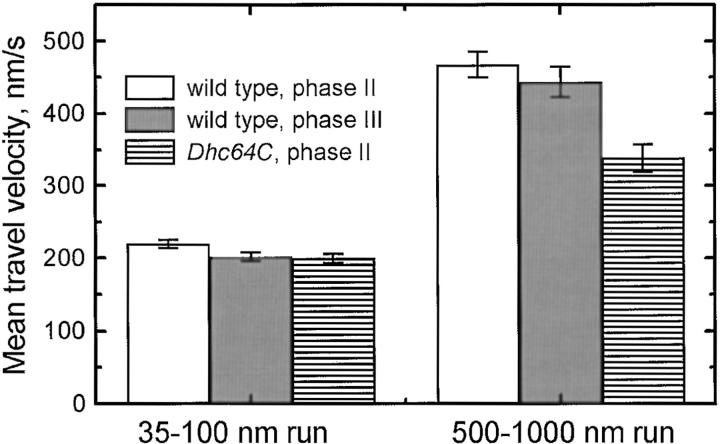
One possible explanation for the need to use the sum of two decaying exponentials to describe the histograms is that there are two distinct states of droplet travel: short runs (average travel distance 98 nm) and long runs (average travel distance 1,068 nm). Consistent with this view, droplets traveling for short distances have lower speeds than those traveling long distances (Fig. 7). To determine the relative frequency of these states, we derived the ratio R_SL of the number of short runs and long runs from the exponential fits (see ). There were roughly twice as many short runs as long runs (R_SL= 2.15, Table ).

Figure 7.

Mean travel speed as a function of run distance for minus end motion. The average speed of short (35–100 nm) or long (500–1,000 nm) runs is shown, for droplets in wild-type embryos from phase II and phase III and in Dhc64C mutant embryos from phase II. The error bars are the standard error of the average.

Run Lengths Are Described by the Same Functional Form under Different Conditions

It is possible that the biologically relevant description of the distribution of travel distances is another functional form (function A), and that the sum of two decaying exponentials simply happened to be a reasonable approximation of function A in the particular case we examined. Under different conditions, function A might vary and would no longer be well approximated by the sum of two exponentials. To address this issue, we examined motion in the Dhc64C mutant and at different developmental stages.

In the Dhc64C mutant, our analysis of stall forces (Fig. 3) had revealed that dynein-mediated droplet transport is already impaired during phase II. However, qualitatively, the motion of droplets was nevertheless very similar to the motion in the wild type, with runs of varying lengths, reversals, and pauses. Pauses were again not obligatorily linked to reversals in direction (Table ), but they were longer and their frequency was increased (Table ). Runs in the minus end direction were greatly affected, with average distance traveled reduced by more than a factor of three (Table ). Despite this, the shape of the distribution of run lengths resembled the one observed in the wild type (Fig. 6 B). It was again not possible to fit this histogram to a single decaying exponential (not shown), but the sum of two exponentials provided an excellent fit (Table , χ² = 0.41, P = 97%). The relative frequency of short versus long runs was indistinguishable from the wild type (R_SL, Table ). However, both distance constants were markedly reduced, suggesting that both short and long runs employ cytoplasmic dynein.

As a second test of how generally the two exponential functional form describes the distribution of droplet travel, we analyzed droplet motion in wild-type embryos during phase III. Relative to phase II, the direction of net transport in phase III is reversed and towards the minus end, and stall forces are reduced (Welte et al. 1998). Droplet motion displayed runs, pauses, and reversals, with pauses and reversals not obligatorily linked (Table ). Again, the histogram of run lengths for minus end motion was a simple monotonically decaying curve (Fig. 6 C), but was not described by a single exponential. However, it was well fit by the sum of two exponentials (Table , χ² = 0.93, P = 68%). Interestingly, this distribution was also quantitatively the same as the phase II distribution (Fig. 6 A): the magnitude of both distance constants and the relative frequency of short to long runs were indistinguishable in the two phases (Table ).

Thus, in all three cases examined, the distribution of travel distances is well described by the sum of two exponentials. This suggests that this functional form reflects general attributes of dynein behavior in vivo. We propose the existence of two distinct states of dynein-driven droplet travel, responsible for short and long runs, respectively. Because in all cases short runs had lower velocities than the corresponding long runs (Fig. 7), we will refer in the following to short-slow and long-fast travel states.

Control of Net Transport

Previously, we had shown that the net transport of lipid droplets results from the balance between plus and minus end transport, and that the developmental shift in net transport is due to a change in the average length of plus end motion, whereas the average length of minus end motion remains constant (Welte et al. 1998). The conceptual framework we developed for the description of cytoplasmic dynein might also be useful for understanding how this developmental regulation occurs. Therefore, we extended our analysis to plus end motion in wild-type embryos during phase II and phase III.

Qualitatively, plus end motion was similar to minus end motion. Pauses and reversals could also occur independently of each other, and pause lengths fit a single decaying exponential (Fig. 5 B). Unlike minus end travel, the average distance traveled between phase II and phase III varied by roughly a factor of two (Table ). Nevertheless, the distribution of run lengths in both phases was well described by the sum of two exponentials (Fig. 8a and Fig. b, Table ), and short and long runs differed in their velocities (data not shown). Thus, motion driven by the as-yet-unidentified motors powering motion in the plus end direction can also be broken down into pauses: short-slow travel and long-fast travel.

Figure 8.

Distribution of lengths of droplet travel in the plus end direction during phase II (A) and phase III (B). In both cases, the general shape of the histograms was the same, and was well fit by the sum of two decaying exponentials (solid lines, see also Table ). Note the reduction of long-travel events in B relative to A. Histograms and fits were done as in Fig. 6.

Plus end motion was qualitatively similar in both phase II and phase III, suggesting that the same processes regulate motion in the two phases. This framework enabled us to ask which quantitative changes are responsible for the decrease in average distance traveled between phases II and III (Table ). There were two: droplets in the long-fast state traveled for significantly shorter distances (Table , D_L), and fewer droplets were in this state (Table , R_SL). Surprisingly, the distance constant for the short-slow travel state (D_SL) even increased somewhat (Table ), which would tend to increase overall travel distance, but this was not enough to compensate for the other changes. Thus, the developmentally controlled reversal in net transport is brought about by changes in two parameters of plus end motion: the relative frequency of the two travel states and the distance constant for long-fast travel.

Discussion

Many cytoplasmic organelles show bidirectional movement along microtubules (Gilbert and Sloboda 1984; Hayden 1988; Leopold et al. 1990; Hollenbeck 1996; Overly et al. 1996; Rogers et al. 1997; Waterman-Storer et al. 1997; Suomalainen et al. 1999), which is similar to what we have described for the lipid droplets in our preparations. In spite of this constant bidirectional motion, such organelles ultimately achieve discrete polarized concentrations in the cell. The final distributions must depend on the frequency and duration of runs particles make in each direction. Previously, these properties have been studied for single motors and artificial cargoes in vitro (Block et al. 1990; Wang et al. 1995; Sakakibara et al. 1999). The Drosophila lipid droplet system provides a unique opportunity to study these parameters in a situation approaching in vivo conditions.

In vitro, motors have a finite probability of falling off the microtubule at each attempted step. If the distances cargoes travel in vivo reflect this processivity, characterization of the motor itself might be sufficient to understand how travel lengths are determined in a cell. However, if motor processivity is not limiting, other mechanisms must terminate runs, and their properties have to be unraveled to understand what controls travel distance. For lipid droplet motion, we propose the following model: run lengths are determined not by inherent motor processivity but by an additional mechanism. This mechanism acts as a switch, both ending runs and immediately reversing travel direction.

Long-Fast Travel: The Relationship between Motor Processivity and Run Length

To evaluate our model, we can take advantage of the stall force measurements that allow us to estimate the number of active motors on the droplets. The stall forces vary developmentally in a quantized fashion, suggesting that lipid droplets simultaneously engage multiple motors of the same type (Welte et al. 1998). Because stall forces can only be determined for droplets traveling long distances, this argument applies to the long-fast travel state.

If droplet travel distances are solely determined by the processivity of multiple independently acting motors, travel distance should increase with motor number because when one motor detaches from the microtubule, the others remain bound, giving the detached motor a chance to reengage. This increased travel distance is indeed observed in vitro, where beads with multiple kinesin motors move distances much longer (>4 μm, ended by encountering the end of the microtubule) than the 1,400-nm average distance traveled by beads with single motors on them (Block et al. 1990). If another mechanism ends runs before processivity becomes limiting, there need not be a correlation between motor number and travel distance. For lipid droplets, stall forces change between phases II and III, which is consistent with a change in motor number from 5 to 4 motors (Welte et al. 1998), but the average minus end travel distance is constant (Table ). Thus, for long-fast minus end travel, a mechanism other than processivity must end runs.

A clear prediction of this model is that travel distances should be shorter than expected from the inherent processivity of the motors. In vitro, a single cytoplasmic dynein can move glass beads processively for an average distance of 800 nm (Wang et al. 1995) and for roughly double that distance if assisted by the cofactor dynactin (King and Schroer 2000). Dynactin is ubiquitously expressed and present in Drosophila embryos (McGrail et al. 1995). Thus, for embryonic lipid droplets engaging five independently acting motors, one would expect travel distances of many micrometers, just like for beads with multiple kinesins. Even for a worst-case scenario that dynein is not assisted by dynactin and that motors cannot reengage because they fall off the cargo once they detach from the microtubule, a simple simulation assuming five active dyneins (data not shown) yields an average travel distance of 1,800 nm, which is considerably longer than the 1,070-nm observed for droplets in phase II. Thus, in vivo, runs are cut short before motor processivity becomes limiting.

This conclusion is also supported by the rarity of pauses. If runs ended because of limited motor processivity, they should typically be followed by pauses because the motors would no longer be attached to the microtubule. However, in vivo, runs are usually followed by immediate reversals (see also below).

Properties of the Mechanism that Terminates Long-Fast Runs

What type of process might end runs before the inherent motor processivity becomes limiting? A study of the in vitro behavior of motors (Vale et al. 1992) suggests one model: namely, that reversals in direction, and thus end of runs, result from competition between opposite polarity motors. In these experiments, simultaneous activity of dynein and kinesin in a microtubule gliding assay resulted in back and forth motion of microtubules, with sharp reversals of direction. The underlying mechanism was unclear, but apparently involved simultaneous activity of both types of motors; relative to gliding driven by any one class of motors, velocity decreased by a factor of two if both motors were present. This situation likely does not apply to reversals following long-fast travel of lipid droplets, where plus and minus end motors do not appear to be active simultaneously (Welte et al. 1998; our unpublished observations).

Thus, a novel mechanism must be responsible for determining travel distance on lipid droplets. Our analysis allows us to characterize some of its properties. The fact that the long-fast travel distances are described by a single exponential distribution suggests that the probability of ending a run remains constant during travel. This observation is not consistent with a mechanism that measures travel distances, e.g., one for which the likelihood of a run ending increases when the droplet has traveled a certain distance. Rather, it suggests that the mechanism that terminates a run is governed by a single rate-limiting step.

When runs end, are motors simply detached from their track? In that case, runs should typically be followed by the droplet diffusing away or pausing. However, such diffusion is almost never seen and pauses are rare. Instead, when droplets reverse direction of travel, they move in the opposite direction without delay, as if the motor for the opposite direction of travel becomes active as soon as the activity of the other motor ends. This observation suggests that the activity of the opposing motors is closely linked. Therefore, we propose that the process responsible for ending runs is a switch, which both coordinates plus and minus end motors, and determines when runs end.

The motor for plus end travel has not yet been identified. Thus, we cannot determine if long-fast plus end runs are also shorter than predicted from motor processivity in vitro. However, because this travel state is described by a single exponential distribution and is followed by immediate reversals, it seems likely that it is also governed by a switch. Since the probability for long-fast plus end travel to terminate changes during development, and its change controls the direction of net droplet transport, the cell can apparently regulate the properties of these switches.

The Short-Slow Travel State

Short-slow travel shares many qualitative properties with long-fast travel. Run lengths are characterized by a single exponential distribution, and the end of runs are followed by immediate reversals in travel direction. However, quantitatively short-slow travel displays much shorter distance constants and reduced travel velocities. These differences might suggest that droplets in these two states are powered by distinct motors. However, for minus end travel, both states are altered in the Dhc64C mutant (Table ), implying that they are due to cytoplasmic dynein functioning in two different modes.

One possibility is that the short-slow state is due to interference between the multiple motors on the lipid droplet. For example, a single dynein might occasionally lock-up, possibly because communication between its two head domains fails (Hancock and Howard 1998; Iyadurai et al. 1999). On vesicles driven by a single motor, this would lead to a pause. On droplets driven by multiple dyneins, one locked-up motor would oppose the progress of the droplet, slowing it down and possibly reducing overall processivity. Such interference might also arise from plus end motors inappropriately active during minus end motion: in the in vitro competition assay mentioned above (Vale et al. 1992), kinesin slowed dynein-driven microtubule gliding by a factor of two (and vice versa). Interestingly, velocities of the short-slow travel state are similarly only half of those in the long-fast state. This similarity raises the possibility that short-slow runs are ended by motor competition as in the in vitro competition assay and not like long-fast runs by the action of a switch. This issue will be resolvable in the future once switches have become molecularly and genetically characterized.

Our quantitation of dynein-driven cargo movement in early Drosophila embryos provides a conceptual framework for investigating the molecular basis of transport regulation in vivo. We are proposing the existence of switches that end runs and coordinate opposite polarity motors. The challenge for the future will be to identify the molecular components of these switches and to determine which of their biochemical properties control the probability for terminating a run. Given dynein's diverse roles in many cellular transport processes, similar switches will likely be crucial for determining net transport of other organelles wherever bidirectional transport is observed.

R_SL was calculated according to the formula

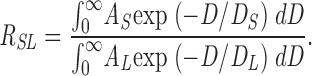The long amplitude, A_L, was set to one by dividing it by the original long amplitude, A_LRaw, and the associated error was calculated by dividing the raw standard error (from the fit) by A_LRaw. The corresponding short amplitude A_S was calculated by dividing the raw short amplitude A_SRaw by A_LRaw, and its associated error was also divided by A_LRaw.