Abstract
To probe the dynamics and size of lipid rafts in the membrane of living cells, the local diffusion of single membrane proteins was measured. A laser trap was used to confine the motion of a bead bound to a raft protein to a small area (diam ≤ 100 nm) and to measure its local diffusion by high resolution single particle tracking. Using protein constructs with identical ectodomains and different membrane regions and vice versa, we demonstrate that this method provides the viscous damping of the membrane domain in the lipid bilayer. When glycosylphosphatidylinositol (GPI) -anchored and transmembrane proteins are raft-associated, their diffusion becomes independent of the type of membrane anchor and is significantly reduced compared with that of nonraft transmembrane proteins. Cholesterol depletion accelerates the diffusion of raft-associated proteins for transmembrane raft proteins to the level of transmembrane nonraft proteins and for GPI-anchored proteins even further. Raft-associated GPI-anchored proteins were never observed to dissociate from the raft within the measurement intervals of up to 10 min. The measurements agree with lipid rafts being cholesterol-stabilized complexes of 26 ± 13 nm in size diffusing as one entity for minutes.
Keywords: laser trap, lipid raft, protein diffusion, single particle tracking, thermal position fluctuation analysis
Introduction
Membrane microdomains enriched in glycosphingolipids and cholesterol and containing glycosylphosphatidylinositol (GPI) -anchored proteins have been proposed as lateral structural components of the plasma membrane (Simons and Ikonen 1997). These microdomains have been implicated in the polarized sorting of proteins (Keller and Simons 1998) and cellular signaling (Stauffer and Meyer 1997; for reviews see Brown and London 1997, Brown and London 1998). Imagining these microdomains as floating complexes in the membrane, Simons and Ikonen 1997 referred to them as lipid rafts. To understand the role of rafts in cells, a characterization of their dynamics is needed. Therefore, we have studied the local diffusion of single rafts in the plasma membrane of living cells.
Rafts are thought to form by self-association of sphingolipids because of their long and mostly saturated hydrocarbon chains. The interaction between glycosphingolipids can be enhanced by hydrogen bonds between their headgroups. The voids between the hydrocarbon chains caused by the rather bulky headgroups would be filled by cholesterol, which might also participate in the hydrogen bonding to the sphingolipids. Although cholesterol has been shown to be essential for raft formation, the precise nature of its interaction with sphingolipids remains unclear. A complementary view of sphingolipid–cholesterol rafts is that they form separate liquid-ordered phases in the bilayer, which are dispersed in the liquid-disordered matrix formed by unsaturated glycerophospholipids (Brown and London 1997; Ge et al. 1999). The liquid-ordered phase in a lipid bilayer, as characterized by highly ordered carbon chains coupled with a high degree of rotational freedom, was first described by Ipsen et al. 1987.
Biochemically, the components of lipid rafts are characterized by their insolubility in the detergent Triton X-100 at 4°C, forming so-called detergent insoluble glycolipid-enriched complexes (DIGs) that are enriched in cholesterol, glycosphingolipids, sphingomyelin, and saturated glycerophospholipids (Brown and Rose 1992; Parton and Simons 1995). Because of their high lipid content DIGs are found in the low density fraction after gradient centrifugation (Brown and Rose 1992; Fiedler et al. 1993). Proteins that are DIG-associated after the detergent extraction are assumed to have been raft-associated in the membrane. Depletion of cholesterol from cells renders raft-associated proteins detergent soluble (Kilsdonk et al. 1995; Scheiffele et al. 1997; Keller and Simons 1998).
The existence of lipid rafts in the plasma membrane of living cells has been demonstrated recently, but controversy persists and the exact structure of rafts remains unclear. Varma and Mayor 1998 used fluorescent resonance energy transfer between GPI-anchored proteins in living CHO cells to show that these proteins were clustered in lipid domains that were likely to be smaller than 70 nm in diameter explaining why rafts never have been observed in light microscopy. While another fluorescent resonance energy transfer study failed to detect any significant clustering of GPI-anchored proteins in the apical membrane of fixed MDCK cells (Kenworthy and Edidin 1998), Friedrichson and Kurzchalia 1998 have shown that GPI-anchored proteins in MDCK cells existed in clusters by using short chemical cross-linkers. Harder et al. 1998 used antibodies against raft-associated proteins to cocluster the small rafts into large super rafts, which were detectable by light microscopy. To understand the role of rafts in cell signaling and protein sorting, a characterization of the stability and mobility of solitary rafts in the plasma membrane of living cells is needed. Studying the local diffusion of single raft proteins over minutes with high resolution should provide information about the dynamic properties of rafts, because the protein diffusion in a simple lipid bilayer depends on the size of the protein and the viscosity of the surrounding lipid bilayer as described by the Saffman-Delbrück relation (1975). Diffusion measurements in cell membranes using FRAP or video-based single particle tracking (SPT) have so far deviated from this simple relation. This discrepancy is thought to be caused by collisions of the diffusing protein with immobile obstacles and fences in the cell membrane (Saxton 1982, Saxton 1989; Kusumi and Sako 1996). Locally, on a length scale smaller than the average distance between obstacles, the cell membrane can be approximated as a lipid bilayer. Therefore, we have measured the local viscous drag of single raft proteins using a novel microscopic method (Florin et al. 1998; Pralle et al. 1998). A microsphere, attached to the protein studied, is confined by a laser trap and the sphere's thermal position fluctuations inside the trapping potential are tracked with subnanometer and microsecond resolution. The damping of these fluctuations yields directly the viscous drag γ on the sphere and the attached protein. The viscous drag determined with a temporal resolution of 0.3 s relates to the diffusion coefficient D of a freely diffusing protein via the Einstein relation: D = k B T/γ (k B T being the thermal energy). The local diffusion coefficients obtained with this method for protein diffusion in the plasma membrane are the first to agree with the results from artificial lipid bilayers.
This novel microscopic technique allowed us to compare the diffusion of proteins with different membrane anchors in intact rafts to that of proteins in rafts disintegrated by cholesterol depletion and to the diffusion of a nonraft protein. The viscous drag of three raft-associated proteins, two with a GPI anchor and one transmembrane protein, is independent of the type of membrane anchor, and significantly larger than the one of nonraft proteins. After cholesterol depletion, the viscous drag of raft-associated proteins decreases to the level of the nonraft protein, whereas the diffusion of the nonraft protein remains unchanged. The mean radius of the raft assemblies obtained from these measurements is 26 ± 13 nm.
Materials and Methods
Instrumentation
Our instrument combines a laser trap implemented in an inverted microscope (Axiovert 35; Carl Zeiss) with fast three-dimensional position detection (see Fig. 2). The trapping laser, a Nd:YVO4 laser (λ = 1064 nm, model T20-B10-106Q; Spectra Physics), is directed by a scanning mirror mounted on a triple-axis piezo (PiezoSystems Jena) into the microscope and focused in the object plane by an oil immersion objective lens (Plan Neofluor 100×, NA 1.3; Carl Zeiss). The condenser back focal plane (BFP) is projected onto a quadrant photodiode (QPD) (model S5981; Hamamatsu) via a dichroic mirror. To reduce the mechanical noise, the microscope's stage is replaced by a custom made stage to which the objective lens and the condenser with the detection system are rigidly connected. The two-photon fluorescence (TPF) intensity is measured by a photomultiplier (model R2949; Hamamatsu). All signals recorded are amplified and low pass–filtered (50 kHz) by amplifiers developed at EMBL. A transputer data acquisition board (model ADWin F5; Jäger Electronics) is used for recording and to provide the axial feedback controlling the interaction force between the sphere and the membrane. To move the trapping focus along the optical axis, the objective lens is mounted on a piezo drive (model PiFoc P-721; Physik Instrumente). In addition, the temperature-controlled sample chamber is placed on a piezo scan stage with capacitive position sensors and digital feedback (model NPS-XY-100A; Queensgate).
Figure 2.
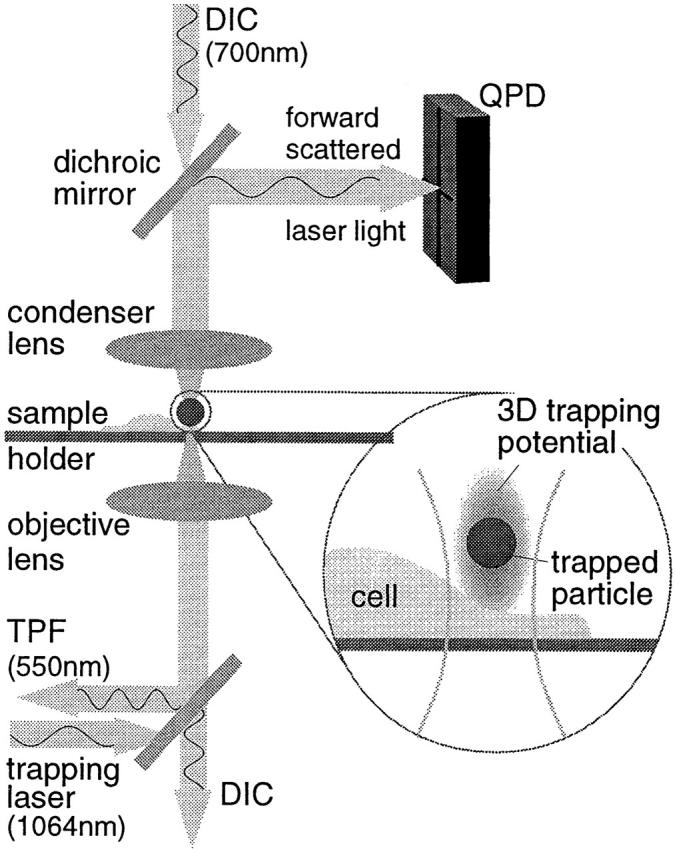
Optical paths in our instrument, built around an inverted microscope with DIC equipment whose wavelength of 700 nm is chosen to reduce photon damage on the cells. The IR-laser trapping beam is focused on the sample by an oil immersion objective lens mounted on a piezo. The forward-scattered laser light is collected by the condenser lens and projected by a dichroic mirror onto the quadrant photodiode (QPD) for the particle tracking. The two-photon fluorescence (TPF) is detected confocally by a photomultiplier.
To determine the average axial position of the sphere in the trap, the fluorescence intensity emitted by the fluorophores inside the spheres excited by the trapping laser is measured (Florin et al. 1996). This signal is used as input for the feedback minimizing the force exerted by the sphere on the membrane. For the high resolution particle tracking, we detect the interference of the forward scattered laser light with the reference beam with a QPD in the BFP. The lateral position is the difference of two halves of the QPD (Gittes and Schmidt 1998), whereas the axial position is determined from the intensity of the scattered laser light reaching the QPD (Pralle et al. 1999). For a sphere with 0.2-μm diam, the lateral and axial resolution at 50 kHz bandwidth are better than 1 and 5 nm, respectively.
Because the response of the QPD depends on the properties of sphere and the laser focus, it is necessary to calibrate the signal with the sphere used for an experiment at a location near the actual measurement. The local detector sensitivity β is determined from the thermal position fluctuations using the Stokes drag γ of the sphere. Analogous to the local viscosity measurements (see below), the autocorrelation time of the position movements τ and the spring constant of the trap are calculated, being now an uncalibrated spring constant κ̆(in units Nm/Volt2 instead of N/m). Because γ = κτ and κ = κ̆β2, the sensitivity β is determined from β2 = 6τηr/κ̆τ, which is valid for a sphere in a harmonic potential as long as the position fluctuations remain within the linear response range of the detector, and the calibration is performed in the solution. We calibrated the detector to be at least ten times the diameter of the sphere away from any surface, so the influence of the surface is smaller than 2% (Happel and Brenner 1965; Pralle et al. 1998).
Local Viscosity Measurement
The motion of a Brownian particle in a harmonic potential is characterized by an exponentially decaying position autocorrelation function ≪r o·r t≫=r 2exp−tτwith the mean square amplitude r 2=k B T κανδ τηε ψορρελατιον τιμε τ = γ/κ. Thus, the local viscous drag γ and the diffusion coefficient D = k B T/γ of a sphere in a harmonic potential are calculated from the measured correlation time τ of the motion and the stiffness κ of the potential (Pralle et al. 1998).
The stiffness of a potential can be determined by measuring the position distribution of a trapped particle (Florin et al. 1998) using the Boltzmann probability P(r)dr to find a thermally excited particle in a potential V(r) at position r in the interval [r,r + dr] is P(r) = c · exp[−V(r)/kBT], with c chosen to normalize ∫P(r)dr = 1. Conversely, the trapping potential is given by the probability distribution as V(r) = −kBT · lnP(r) + kBT · ln(c), where c is an offset. This method allows to profile the trapping potential even below the thermal energy with a temporal and spatial resolution given by the strength of the potential and the bead size, while requiring only minimal knowledge about the system, i.e., the temperature. In our experiments, the lateral spring constant of the laser trap was adjusted to about k ∼1 μN/m for a sphere of 0.2-μm diam. The sample chamber was maintained at 36 ± 1°C, which leads to lateral position fluctuations of ±60 nm RMS displacement.
To achieve diffusion coefficient measurements with errors <10%, the observation interval has to be ∼1,000-fold longer than the correlation time τ (estimated using methods developed by Bartlett 1946). Hence, the temporal resolution of the viscosity measurement is limited by the sphere's motion and not by the bandwidth of the detection. The sphere's position was recorded every 18.75 μs; for some long-time observations the recording interval was increased to 50 μs. The three-dimensional position distribution of the bead was used to visualize the cellular surface in the area of the measurement. Only experiments in which the surface was normal to the optical axis of the microscope were selected for further analysis. The position fluctuations along each detector axis were evaluated independently. To determine τ, overlapping intervals of 0.3 s were used. The autocorrelation function in each interval was calculated and fitted by an exponential decay from 0.15 to 25 ms. The potential κ and the viscous drag γ = κτ were computed for each interval and plotted against time.
Over the time course of an experiment, the viscous drag of the free bead, of the same bead near the membrane, and bound are determined (see Fig. 3). Each value was measured for 2–10 s, so that mean (x) and SD (σ) for each individual molecule is determined. These distributions were taken to compute the probability densities for all molecules measured: f(x) = n −1Σni = 1 G(x,σ) as shown in Fig. 4 and Fig. 5.
Figure 3.
The lateral viscous drag γ (A), the lateral spring constant κx (B) and autocorrelation time τx (C) of a 0.2-μm sphere binding to a PLAP molecule plotted against time. The time trace shows three regions corresponding to the reference measurement away from the surface (I), the approach of the bead to the membrane, the diffusion near the plasma membrane (II), and after binding to the membrane protein (III). The κx (B) remains unchanged during the experiment, whereas τx (C) changes as γ (A).
Figure 4.
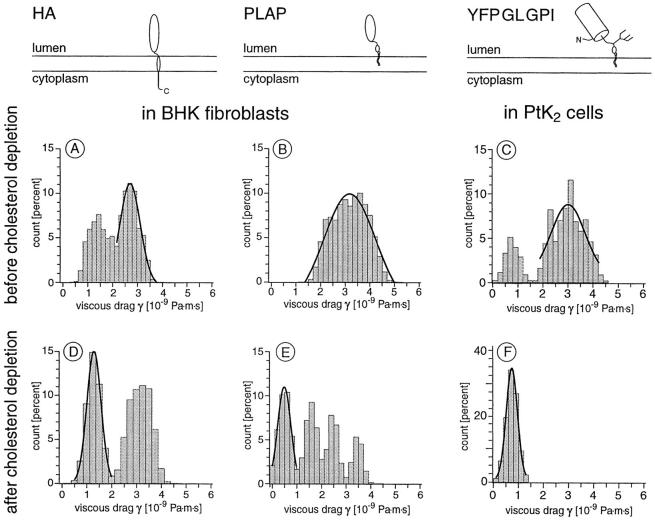
Overview of the raft-associated constructs used and distributions of the viscous drags measured for single proteins before (A–C) and after cholesterol depletion (D–F). The peaks containing the majority of molecules were fitted by a Gaussian. 67% of HA molecules in BHK cells had a higher viscous drag than the remaining 33% (A, n = 12, P < 0.01). PLAP expressed in BHK had only one peak (B, n = 20), whereas 76% of YFPGLGPI expressed in PtK2 cells had a viscous drag larger than the remaining 24% (C, n = 29, P < 0.001). After cholesterol depletion the distributions were shifted toward lower viscous drags (D–F). HA in BHK was shifted slightly to equal amounts of molecules in both peaks (D, n = 10). The effect on GPI-anchored proteins was more pronounced: 40% of PLAP in BHK cells had a greatly reduced viscous drag (E, n = 15, P < 0.1), 60% yielded only slightly reduced values (the multiple peaks are not statistically significant, P > 0.1). The effect of cholesterol depletion was most pronounced for YFPGLGPI. In PtK2 all YFPGLGPI had extremely reduced viscous drags (F, n = 9, P < 0.001).
Figure 5.

The viscous drag measured for the nonraft transmembrane protein LYFPGT46 in PtK2 before (A) and after (B) cholesterol depletion. All LYFPGT46 molecules in PtK2 had the same viscous drag (A, n = 13), which remained unchanged after cholesterol depletion (B, n = 8).
Saffman-Delbrück Model of Protein Diffusion
The diffusion of a transmembrane protein moving in an obstacle-free lipid bilayer has been described by Saffman and Delbrück 1975 using a hydrodynamic model treating the bilayer as a continuum. The viscous drag on a cylindrical particle with radius r in a homogenous lipid bilayer of thickness h is γ = 4πηm h/(ln(ηm h/ηwr) − ε), where ηw denotes the viscosity of the surrounding fluid, ηm the viscosity of the lipid bilayer, and ε denotes Euler's constant (0.5772; Saffman and Delbrück 1975). This approximation is valid for proteins with radius r large compared with the lipid molecules and for ηm ≫ ηw, which is fulfilled for cellular membranes (Peters and Cherry 1982). Peters and Cherry 1982 have shown that the Saffman-Delbrück relation correctly predicts the lateral and rotational diffusion for bacteriorhodopsin in DMPC vesicles. The mathematical solution of Saffman and Delbrück required θ = (ηw+ ηcr/ηmh) to be ≪1, with ηc being the viscosity of the cytoplasm. Because ηc ∼1.5 · ηw (Swaminathan et al. 1997) and thus θraft ∼ 0.08, the difference between the Saffman-Delbrück solution and the more elaborate solution of Hughes et al. 1981, Hughes et al. 1982, which is valid up to θ ≲ 1, is negligible.
Cell Culture and Transfection
BHK-21 cells were grown in supplemented Glasgow (G) -MEM (including 5% FCS, 10% phosphate tryptose broth, 10 mM Hepes, pH 7.3, 2 mM glutamine, 100 units/ml penicillin, and 10 mg/ml streptomycin), and passaged every 3 d. For the studies, BHK cells were plated at low density on coverslips. PtK2 cells were grown in supplemented MEM (containing 10% FCS, 2 mM glutamine, 100 units/ml penicillin, and 10 mg/ml streptomycin). They were used at ∼50% confluency. The experiments were carried out in cell culture medium supplemented with 5 mg/ml fish skin gelatin (FSG) to reduce the nonspecific adsorption and were filtered (0.1 μm SuporeAcrodisc; Gelman Sciences).
To express influenza virus hemagglutinin (HA) or placental alkaline phosphatase (PLAP), BHK cells were transiently transfected using Lipofectamine (GIBCO BRL) according to the instructions of the manufacturer. The cells were cotransfected with a soluble YFP (encoded for by plasmid pEYFP-N1; CLONTECH Laboratories) to facilitate the selection of expressing cells. Experiments were performed 16–36 h after transfection.
The transiently transfected cells had normal morphology and were viable for several days. LYFPGT46 and YFPGLGPI were expressed in PtK2 cells by infection for 1 h at 37°C with recombinant adenoviruses encoding for the constructs, and experiments were performed 12–36 h after transfection. For cholesterol depletion, the cells grown on coverslips were washed in serum-free culture medium and incubated with 10 mM methyl-β-cyclodextrin for 30 min at 37°C. This procedure was reported to extract ∼60% of total cellular cholesterol from BHK cells (Keller and Simons 1998). After a wash in normal culture medium, the coverslips were transferred to the microscope. The measurements were performed within 1 h of the cholesterol depletion.
Protein Constructs and Generation of Recombinant Adenoviruses
The transient expression of PLAP in BHK and the BHK clone stably expressing PLAP have been described previously (Harder et al. 1998). YFPGLGPI, containing YFP as the ectodomain connected to a GPI anchor, was produced and characterized by Keller (Keller, P., D. Toomre, J. White, and K. Simons, manuscript in preparation). The expression of HA in BHK cells has been characterized previously (Scheiffele et al. 1997).
LFPGT46 is an artificial secretory protein containing the signal sequence of rabbit lactase-phlorizin hydrolase (Mantei et al. 1988), the fluorescent protein, a consensus N-glycosylation site, the transmembrane domain of the human LDL receptor (Yamamoto et al. 1984), and the cytoplasmic tail of CD46 (Maisner et al. 1997; Teuchert et al. 1999) containing the sequence stretch FTSL that allows basolateral transport. A DNA fragment encoding the signal sequence was generated by PCR with an NheI site and a consensus Kozak sequence at the 5′ end, and a PstI site at the 3′ end. Primers used were as follows: 5′-TAGCTAGCCACCATGGAGCTCTTTTGG-3′ (forward primer) and 5′-ATCCTGCAGAGATTCCCAGTCTGA-3′ (reverse primer). This PCR fragment was ligated into NheI-PstI–digested pEYFP-N1, yielding the secreted protein LYFP. Next, we have inserted the CD46 cytoplasmic tail into LYFP. This was accomplished with two codon–optimized complementary oligonucleotides creating a BsrGI site at the 5′ end and a NotI site at the 3′ end. The forward oligonucleotide was 5′-GTACAAGTCCACCTACCTCACCGACGAACCCACCGAGAAGTCAAATTTACCTCCCTCTGAAGC-3′ (TCC replacing the TAA stop codon of YFP is underlined). The reverse oligonucleotide was 5′-GGCCGCTTCAGAGGGAGGTAAATTTGACTTCTCGGTGGGTTTCGTCGGTGAGGTAGGTGGACTT-3′. The annealed oligonucleotides were ligated into BsrGI-NotI–digested LYFP, yielding LYFP46. Finally, a DNA fragment encoding a consensus N-glycosylation site and the human LDL receptor transmembrane domain was generated by PCR. Primers used were as follows: 5′-CTGTACAAGCTTAACGGATCCAAGCTTCAGCGGCCGCACCAAGCTCTGG-GCGA-3′ (forward primer, N-glycosylation site NGS in bold, LDL receptor sequence underlined) and 5′-CTTGTACAGGTTCTTAAGCCGCCAGTTCTT-3′ (reverse primer). This PCR fragment was directionally ligated into BsrGI-digested LYFP46, yielding LYFPGT46. Recombinant adenoviruses were generated with the system described by He et al. 1998. In brief, LYFPGT46 was released as a NheI-XbaI fragment that was directionally ligated into XbaI-digested pShuttle-CMV. After homologous recombination with pAdEasy-1, recombinant adenoviruses were generated in 293 cells as described (He et al. 1998). It was sorted to the basolateral membrane when expressed in MDCK cells and did not associate with rafts (Keller, P., unpublished results).
The cDNA for the EGFP used for the blocking of the antibodies was subcloned by PCR from pEGFP-N1 (CLONTECH Laboratories) into a derivative of pET9 (Stratagene, modified by Gunter Stier, EMBL). 6xHis-tagged EGFP was purified from Escherichia coli Bl21(DE3) using nickel affinity chromatography.
Bead Coating and Antibodies
Orange fluorescent (530 nm ex./560 nm em.) carboxyl-modified latex beads from Molecular Probes with a nominal diameter of 0.2 μm (radius = 108 ± 4 nm) were used. The beads were coated with the antibodies by adsorption, based on modified procedures of Sako and Kusumi 1995. Before coating, the spheres were washed three times in 0.2 M boric acid buffer (adjusted to pH 9 using 1 M NaOH), and then they were incubated with 1 mg/ml antibody in a 50-mM MES buffer, pH 6, for 30 min at room temperature. After coupling, the spheres were incubated for 30 min with 10 mg/ml FSG and washed twice in 10 mg/ml FSG in PBS; another wash was added immediately before the experiment. To optimize the spheres for single membrane protein binding, they were incubated with free ligand, i.e., EGFP (White, EMBL) or PLAP (Sigma Chemical Co). In the case of EGFP, 15 nl of the EGFP solution (1 mg/ml) was added to 10 μl of a 1% aqueous suspension of antibody-coated spheres. Adding 50 nl of GFP inhibited binding to cells completely. Because of the lack of soluble forms of HA, the antibody concentration on the surface of the sphere was diluted by coadsorption of an unspecific antibody at a ratio of 1:4.
mAbs against human PLAP were obtained from DAKO. Rabbit polyclonal antibodies were raised against human PLAP (Sigma Chemical Co.). mAbs HA were prepared as described (Matlin et al. 1981; Scheiffele et al. 1997). Polyclonal antibodies against XFP were raised in mice (LeBot, EMBL).
Results
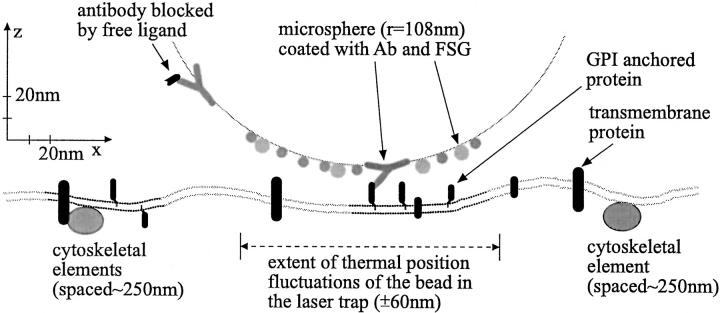
The viscous drag of an individual membrane protein in the plasma membrane of living cells, maintained in a closed microscope chamber heated to 36 ± 1°C, was measured by observing the thermal position fluctuations of an attached microsphere (radius = 108 nm; Fig. 1). The damping of the motion is expected to be dominated by the viscous drag on the membrane domain of the protein because of the 1,000-fold higher viscosity of the lipid bilayer compared with the aqueous medium. We used a laser trap to capture the sphere and place it onto the cell membrane while controlling the interaction force. The motion of the sphere was first recorded in the bulk solution, then near the membrane, and finally after binding to the membrane protein. The comparison of these three measurements allowed us to separate the influence of the sphere diffusing unbound near the membrane from the binding of the bead to the membrane protein. The continuous observation with high temporal resolution enabled us to directly observe the binding event. To demonstrate that the measurements were not influenced by the sphere size, some experiments were performed with smaller spheres (radius = 55 nm), yielding similar results (data not shown).
Figure 1.
Scaled model of the experimental situation: a sphere (r = 108 nm) bound via an adsorbed antibody to a GPI-anchored protein that is part of a raft domain. The lipid bilayer is symbolized by the double row of gray dots with black sections symbolizing raft domains. The extent of the thermal position fluctuations observed in the experiments (± 60 nm) is marked. It is much smaller than the smallest estimates of the spacing of immobile cytoskeleton-anchored obstacles to free diffusion of 300–500 nm (Sako and Kusumi 1995). The cytoskeletal elements drawn here are 250 nm apart.
High Resolution Particle Tracking in a Trapping Potential
We implemented an optical trap in an inverted microscope using a near infrared laser that simultaneously excites the fluorophores inside the trapped microsphere via a two-photon process (Fig. 2). The dependence of the TPF intensity on the sphere's position relative to the focus of the trapping laser provides an axial displacement sensor used to control the force exerted by the sphere on the membrane below 0.1 pN. To record the thermal position fluctuations, we developed a fast three-dimensional position sensor based on the interference of the transmitted laser light with the light scattered by the trapped particle (Gittes and Schmidt 1998; Pralle et al. 1999). The interference pattern was detected with a quadrant photodiode in the backfocal plane of the condenser lens (Fig. 2).
Local Viscous Drag of Single Membrane Proteins
The particle tracking in a trapping potential allowed us to calculate the viscous drag and the trapping potential at a temporal resolution of 0.3 s and for an area of 100 nm in diameter. The viscous drag γ of the particle was computed as the product of the autocorrelation time τ of the position fluctuations and the spring constant κ of the trapping potential (see Materials and Methods).
Fig. 3 depicts a typical measurement of the lateral viscous drag γ, spring constant κ of the trapping potential, and autocorrelation time τ of the movement plotted against time. The measured viscous drag γ is the sum of the Stokes drag of the sphere γs = 6πηw r and the viscous drag of the protein in the lipid bilayer γp. The Stokes drag of the sphere was measured in the bulk solution, ∼2 μm above the plasma membrane (Fig. 3 A, I). Near a surface, like the membrane, diffusion is reduced because of the spatial confinement (Happel and Brenner 1965). Therefore, the viscous drag of the sphere was measured again after positioning it near the membrane (Fig. 3 A, II), resulting in an increase by a factor b = 2.2 ± 0.2 compared with the Stokes drag of the sphere in solution. This increase would correspond to a separation of 15 ± 7 nm between the sphere and a clean, smooth surface. After binding to the membrane protein (Fig. 3 A, III), the total viscous drag γ = b · γs + γp was measured and used to calculate the viscous drag of the protein γp. We only included measurements in our analysis in which the strength of the lateral potential was not increased by binding to the membrane protein to ensure that the proteins measured were freely diffusing and not tethered to the cytoskeleton (Fig. 3 B).
To determine the stability and size of the rafts, viscous drag measurements were performed on a series of proteins that are known to be components of rafts, as defined by association with DIGs and floatation to low density in a density gradient (Brown and Rose 1992; Fiedler et al. 1993). We have compared two proteins with the same membrane anchor (GPI anchor), but different ectodomains, as well as protein constructs with the same ectodomain, but different membrane anchors, to exclude possible influences of the protein ectodomains on diffusion. To distinguish between diffusion inside the rafts and diffusion of the entire raft, we compared raft proteins with different membrane anchors, a GPI anchor, and one with a transmembrane domain, before and after cholesterol depletion (Fig. 4). The GPI-anchored proteins were PLAP and a GPI-anchored yellow color variant of the green fluorescent protein (YFPGLGPI) (Harder et al. 1998; Keller, P., D. Toomre, J. White, and K. Simons, submittedmanuscript for publication). The transmembrane raft protein was HA (Scheiffele et al. 1997). To determine the viscosity of the plasma membrane outside of rafts, we used a transmembrane construct containing a YFP ectodomain fused to the transmembrane domain of the LDL receptor (LYFPGT46).
To facilitate the comparison to previous work in BHK fibroblasts (Scheiffele et al. 1997; Harder et al. 1998), PLAP and HA were transfected into BHK cells using Lipofectamine. The YFP fusion proteins were expressed in PtK2 cells whose large, extremely flat surface provides very good experimental conditions for diffusion measurements. For the expression in PtK2, recombinant adenoviruses were used to avoid the possible influence of Lipofectamine on membrane viscosity. The general results agreed for the two cell types, expression methods, different expression levels, as well as for stable and transient transfections of PLAP. However, we observed differences in the intensity of the effect of cholesterol depletion between the two cell types.
To ensure binding of the bead to a single membrane protein, we have reduced the number of proteins present in the cells by selecting for weakly expressing ones using the YFP fluorescence. The number of active antibody sites per bead was minimized in the case of anti-PLAP and anti-GFP beads by adding free ligand, a high concentration of which would block binding completely and, for HA, by replacing the major part of the antibodies on the bead with an unrelated antibody. The concentration of the free ligand was chosen to reduce the active binding sites per bead to below 10. The probability for single binding to surface proteins is very high due to the geometric constrictions. To verify this assumption, the fraction of beads bound and the time passed in contact with the membrane before binding were analyzed using Poisson statistics. Under the blocking conditions used, only a fraction of these beads was bound after being in contact with the membrane for 50 s (25% for PLAP, 30% for YFPGLGPI and HA, and 20% for LYFPGT46), whereas 95% of the unblocked beads bound within a few seconds. A Poisson statistic for single binding fitting this behavior provides an estimate of <25 possible binding sites to ensure single binding during the observation interval, and predicts that under the conditions used, >80% of the beads would bind to a single surface protein.
Viscous Drag of Raft-associated Proteins
Fig. 4 displays the distribution of viscous drag measurements for the raft-associated proteins PLAP, YFPGLGPI, and HA. Except for PLAP in untreated cells and YFPGLGPI in cholesterol extracted cells, the distributions of single molecule viscous drag measurements have two peaks. For the transmembranous HA expressed in BHK cells, we measured γ = (2.9 ± 0.7) × 10−9 Pa·s·m (67%) and γ = (1.4 ± 0.4) × 10−9 Pa·s·m (33%) (n = 12, P < 0.01, Fig. 4 A). The GPI-anchored protein PLAP had γ = (3.2 ± 0.8) × 10−9 Pa·s·m (n = 20, 100% raft-associated, Fig. 4 B), which is the summary of measurements performed on a stably expressing BHK cell line and on transiently transfected BHK cells. 76% of YFPGLGPI expressed in PtK2 cells had γ = (3.0 ± 0.9) · 10−9 Pa·s·m, whereas 24% of YFPGLGPI had γ = (0.7 ± 0.3) × 10−9 Pa·s·m (n = 29, P < 0.001, Fig. 4 C). Thus, for all three proteins, the majority of molecules had a viscous drag ∼3 × 10−9 Pa·s·m. This value was independent of the type of membrane anchor of the protein and remained unchanged for ∼1 min, which was the maximal time period continuously accessible in these experiments. For YFPGLGPI and HA, a fraction of the proteins was found to have a lower viscous drag, which was dependent on the type of membrane anchor (P < 0.1).
Effect of Cholesterol Extraction
To investigate the effect of cholesterol depletion on rafts, cholesterol was extracted from the cells by incubation with methyl-β-cyclodextrin. Extraction of cholesterol from cells results in the dissociation of proteins from rafts and the disappearance of the proteins from the floating fraction in density gradient centrifugation (Cerneus et al. 1993; Scheiffele et al. 1997; Ledesma et al. 1998). PtK2 and BHK cells were treated according to the same protocol that had been shown to extract ∼60% of the total cellular cholesterol in BHK cells (Keller and Simons 1998).
The distribution of viscous drag measurements of the transmembrane raft protein HA in BHK cells was shifted slightly after cholesterol depletion: 50% of HA molecules had γ = (1.2 ± 0.6) × 10−9 Pa·s·m, whereas 50% of HA remained unchanged at γ = (3.1 ± 0.6) × 10−9 Pa·s·m (n = 10, Fig. 4 D). The effect on the GPI-anchored proteins was clearer: 40% of PLAP in BHK cells had a greatly reduced γ = (0.6 ± 0.4) × 10−9 Pa·s·m (n = 15, P < 0.01, Fig. 4 E). 60% of the measurements yielded values up to the result obtained for PLAP molecules before cholesterol extraction (Fig. 4 B, the multiple peaks are not statistically significant [P > 0.1]). The change in the PtK2 cells was even more pronounced. The viscous drag of the raft-associated protein YFPGLGPI was (0.7 ± 0.6) × 10−9 Pa·s·m for all molecules measured (100%, n = 9, Fig. 4 F). This is more than a fourfold reduction from the value obtained for 75% of YFPGLGPI before cholesterol extraction and agrees with the value obtained for the remaining 25% before extraction (Fig. 4 C).
Viscous Drag of Nonraft Transmembrane Proteins
To determine the viscosity of the plasma membrane outside of rafts, the local viscous drag of the nonraft transmembrane protein LYFPGT46 was measured. This construct comprised YFP as ectodomain, the transmembrane domain of the LDL receptor and the cytoplasmic tail of CD46 containing a basolateral targeting signal, which, however, does not function as an endocytosis signal (Maisner et al. 1997). In PtK2 cells γ = (1.1 ± 0.5) × 10−9 Pa·s·m was determined for LYFPGT46 (n = 13, Fig. 5 A). Using a construct of the human transferrin receptor, we measured comparable viscous drags in BHK cells (data not shown).
Effect of Cholesterol Extraction
To study whether cholesterol extraction has an effect on the diffusive behavior of nonraft proteins, we measured the viscous drag of LYFPGT46 after depletion of cholesterol from the cells. Their viscous drag did not change, remaining at γ = (1.1 ± 0.4) × 10−9 Pa·s·m for 100% of the molecules (n = 8, Fig. 5 B).
Stability of Raft Association
The viscous drag was measured continuously over a period of ∼1 min. Depending on the time that the antibody-coated bead bound to the membrane protein, this provides an observation interval for the protein diffusion of 10–50 s. During this interval, we have never observed that a raft-associated protein has dissociated from the raft (n = 50).
To address the question whether raft proteins would stay associated with these domains on longer time scales and would diffuse over the cell surface together with the rafts, spheres bound to GPI-anchored raft proteins were released from the laser trap after the measurement (Fig. 6 A, II). The spheres were allowed to diffuse for 2, 5, or 10 min over several micrometers of cell surface (5–10 μm), and they were captured again. The new measurement yielded comparable values (n = 6, Fig. 6 A, III).
Figure 6.
(A) The lateral viscous drag γ of a 0.2-μm sphere bound to PLAP plotted against time. After a first measurement (II), the sphere was released diffusing freely for 10 min, typically for a distance of ∼10 μm over the cell surface. The laser trap was repositioned to trap the sphere again, and new local viscous drag measurements were performed (III). (B) The lateral viscous drag γ of a 0.2-μm sphere bound to YFPGLGPI plotted against time. During the experiment (t = 43–48 s), the laser trap was used to move the sphere 1 μm laterally on the cell surface.
To probe the raft association on intermediate length scales (∼1 μm) the raft-associated proteins were translocated on the cell. After binding to the raft protein, the laser trap was used to move the sphere at a speed of ∼250 nm/s for ∼1 μm while continuously monitoring the position fluctuations. Fig. 6 depicts a trace of the viscous drag of a YFPGLGPI molecule during such motion: after binding to the membrane protein, the trap and sphere were moved laterally (Fig. 6 B). The viscous drag remained unchanged, indicating that the raft was dragged along as the bead was moved (n = 4).
Discussion
To understand the role of rafts in cell signaling and protein sorting, knowledge about raft dynamics will be needed. Therefore, we have characterized the stability and size of rafts in cell membranes on a time scale from seconds to minutes by measuring the local viscous drag of single membrane proteins. The size dependence of the viscous drag of a protein diffusing in a lipid bilayer was described by Saffman and Delbrück 1975. In dimyristoylphosphatidylcholine (DMPC) bilayers, their theory has been validated by Peters and Cherry 1982 who used FRAP to measure the diffusion coefficient of bacteriorhodopsin to be between 0.15 × 10−8 cm2/s and 3.4 × 10−8 cm2/s, depending on the protein/lipid ratio. In contrast, analysis of protein movement in the plasma membrane has produced various results. While assays using FRAP follow an ensemble of protein molecules, the application of SPT to plasma membrane components permits observation of movements of individual protein molecules. From many different measurements, it has become clear that the long range protein diffusion observable by video-based SPT is hindered in cell membranes by obstacles and fences, and the diffusion coefficients obtained are much slower than predicted by the Saffman-Delbrück model (Saxton 1982, Saxton 1989; Sako and Kusumi 1994; Kusumi and Sako 1996). Tomishige et al. 1998 found an 8-fold increase in the diffusion of the Band3 protein in erythrocyte ghosts for the microdiffusion, when they increased the temporal resolution from 33 to 0.22 ms. In the present study, we have not only improved the temporal and spatial resolution more than 10-fold, to 18.75 μs and 5Å, but moreover, have used the laser trap to confine the motion of bead and attached protein to a small region (diam ≤ 100 nm). The latter approach provided extended observation periods of obstacle-free diffusion of single membrane proteins as verified by profiling the confining potential from the thermal position fluctuations. The obtained local diffusion coefficients of proteins in the plasma membrane in intact cells agree for the first time well with the Saffman-Delbrück model, e.g., for LYFGT46 the viscous drag measurement translates into a diffusion coefficient D = 3.9 × 10−8 cm2/s at 36°C. The precision afforded by the excellent spatial and temporal resolution of this new method allowed us to go one step further and compare the behavior of proteins associated with lipid rafts with the one of nonraft proteins.
The distributions of the raft-associated proteins show a minority of molecules with low viscous drag, but most of the molecules have a large viscous drag. This higher value is the same for all three constructs independent of their type of membrane anchor or ectodomain. Therefore, we think that this value is correlated to the diffusion of the raft itself. However, the smaller viscous drag value measured for a few molecules depends on the type of membrane anchor of the protein. These molecules are assumed to be currently in a nonraft environment. The degree of raft association determined by our measurements (PLAP 100%, YFPGLGPI 76%) agrees with the raft association observed by the detergent extraction method: PLAP 90% (Brown and Rose 1992), YFPGLGPI 70% (Keller, P., D. Toomre, J. White, and K. Simons, manuscript in preparation). After cholesterol depletion, the viscous drag values of raft proteins are reduced, with a significantly larger reduction for GPI-anchored proteins than for transmembrane proteins. The majority of molecules for each protein has viscous drag values comparable to the minority population before extraction, agreeing with the interpretation that these are molecules without raft environment. The effect of cholesterol depletion is more pronounced in PtK2 cells than in BHK cells. Possibly, PtK2 cells are more susceptible to cholesterol extraction because of their large plasma membrane area per cell. Cholesterol depletion had no effect on the diffusion of nonraft proteins. The distribution of viscous drags measured for LYFPGT46 shows only one peak that does not shift upon cholesterol depletion.
Fig. 7 summarizes the means of the majority of molecules for each raft and nonraft protein studied. Important to note is that two GPI-anchored proteins with different ectodomains (PLAP and YFP) yield similar results, whereas GPI-anchored YFP diffuses differently from transmembrane-anchored YFP, showing that the local viscous drag is determined by the membrane domain of the protein. Why do our data indicate that rafts diffuse as a small unit? First, some of the raft proteins (PLAP and YFPGLGPI) are attached to the membrane by a lipid anchor that just penetrates the outer leaflet of the bilayer, whereas HA is a transmembrane protein traversing both leaflets. Nevertheless, all three proteins diffuse as if connected to a stable membrane domain of similar size with a viscous drag significantly larger than that of the nonraft transmembrane protein LYFPGT46 (P < 0.01). Second, after depleting cholesterol from the cell membrane, the viscous drag of raft proteins is greatly reduced: the transmembrane protein HA shows a viscous drag similar to the nonraft transmembrane protein LYFPGT46, which is equivalent to a threefold reduction. However, the viscous drag of the GPI-anchored proteins is reduced about fivefold and is lower than that exhibited by the nonraft transmembrane proteins (P < 0.1). After cholesterol depletion, GPI-anchored raft-proteins diffuse faster than transmembrane raft proteins, even though in untreated cells they behave the same. The cholesterol depletion has negligible effect on the nonraft transmembrane proteins, indicating that the viscosity of the cell membrane outside of the raft domains remains unchanged. We interpret this difference in behavior as dissociation of the raft assembly or as segregation of the proteins from the lipid raft. After cholesterol depletion, the raft proteins diffuse like nonraft proteins, with the diffusion coefficient becoming dependent on the type of the membrane anchor. An alternative explanation for this reduction of the viscous drag would be that the diffusion observed was actually within a large raft, and that the viscosity of the raft domain was changed by cholesterol extraction. However, protein diffusion in a lipid bilayer depends approximately linearly on the membrane viscosity. Therefore, the latter interpretation is not compatible with the observation that cholesterol depletion reduces the viscous drags for GPI-anchored proteins fivefold, whereas the one of transmembrane raft proteins only threefold. The larger viscous drag of raft compared with nonraft proteins indicates that they are anchored to a membrane patch with a larger diameter than the transmembrane domain of the LDL receptor. Third, the absence of any change after translocating spheres bound to a raft protein laterally over the cell shows that the lipid rafts are moved together with the protein. The other explanation for these data would be that rafts are larger than 1 μm, which would contradict the observations published previously using fluorescence methods (Harder et al. 1998; Varma and Mayor 1998). The local viscous drag on all raft-associated proteins remained unchanged during the entire observation interval of 50 s. Thus, raft proteins stay raft-associated for at least 1 min. Experiments observing the raft protein diffusion intermittently over extended time intervals indicate that raft proteins can diffuse over the cell surface while being raft-associated for up to 10 min. Taken together, these points let us conclude that the raft association of proteins is quite stable on the time scale of at least 1 min, and that rafts diffuse as one entity, which means that the diffusion coefficient measured is dominated by the motion of the entire raft.
Figure 7.
Summary of the local viscous drags measured for the GPI-anchored raft-markers PLAP and YFPGLGPI and the transmembrane raft protein HA, as well as the values obtained for the nonraft transmembrane protein LYFPGT46 (solid bars, measurements under normal conditions; hatched bars, after cholesterol depletion).
Consequences for the Raft Model
Our data agree with the model suggested by Simons and Ikonen 1997 of cholesterol-stabilized rafts associating with proteins in the native state of the cell membrane. Other models have suggested that proteins associate with rafts only after clustering, which might induce the separation of lipids and cause raft formation. Alternatively, the affinity of proteins associating with rafts would be so low that only clustering would stabilize the association. These latter models do not fit our observations, that proteins associate with rafts without clustering and that raft proteins are not moved out of the rafts when translocated with the laser trap. Based on our results, we can add the following details to the raft model. The cholesterol-stabilized rafts diffuse at least on a time scale of ∼1 min as one entity over the cell surface. The GPI-anchored proteins neither leave the rafts on this time scale nor can they be moved out of the rafts laterally. However, the measurements give no direct estimate for the mobility of the proteins within the raft. From the autocorrelation function of the position fluctuations, it is possible to estimate an upper limit for the protein diffusion within the raft. The proteins cannot diffuse as fast as or faster than the raft itself because the protein motion would dominate the measurement. Also, a 5-fold slower motion inside the raft would be visible in the autocorrelation function as a second exponential decay, only a 20-fold slower diffusion would probably be lost in the signal noise. Hence, the proteins could diffuse inside the rafts with maximally D ≤ 0.05 × 10−8 cm2/s. Even at this reduced mobility raft proteins would reach the edges of their raft at least once every millisecond. Although we have not observed proteins to leave the rafts, little is known yet about the exchange of lipid components between rafts and the surrounding membrane. Our observation that the GPI-anchored raft proteins and the transmembrane raft protein diffuse alike indicates that the linkage between the outer and inner leaflet of the lipid bilayer is in both cases similar. Thus, we assume a strong coupling between the two halves of the bilayer. Nevertheless, we cannot exclude that this coupling is being strengthened by transmembrane raft proteins.
Estimation of the Raft Size
If the raft diffuses as a stable structure as our results suggest, then the size of the raft can be estimated from the local viscous drag measurements. The Saffman-Delbrück model provides the simplest description of the viscous drag of a protein with radius r diffusing in a lipid bilayer with the membrane viscosity ηm and thickness h (Saffman and Delbrück 1975; see Materials and Methods). It was shown to be a valid model for protein diffusion in lipid bilayers (Peters and Cherry 1982; Vaz et al. 1984), and bilayers containing other mobile proteins can be described by an increased effective viscosity (Cherry and Godfrey 1981; Saxton 1987).
Therefore, the Saffman-Delbrück model was applied to estimate the size of rafts. To obtain the membrane viscosity, we used the result of the nonraft protein LYFPGT46, which has a single transmembrane domain. Recently, Eskandari et al. 1998 have measured the transmembrane area of several membrane proteins and estimated that a single transmembrane helix occupies 1.4 nm2. Membrane thickness h and viscosity ηm are coupled as h · ηm in the Saffman-Delbrück relation. Our data for the nonraft transmembrane protein are best fit by h · ηm = (6.3 ± 1.2) × 10−10 Pa·s·m. Therefore, the viscosity of a membrane with h = 5 nm would be ηm = 0.13 ± 0.03 Pa·s. This value agrees well with the viscosity of a DMPC bilayer (ηm = 0.11 Pa·s; Peters and Cherry 1982). To address possible influences from an extracellular coating, we performed some measurements with a construct of the human transferrin receptor with a modified cytoplasmic tail (data not shown). The derived membrane viscosity agrees well with the value for h · ηm obtained here. Also, the fact that HA in cholesterol-depleted cells diffused just like LYFPGT46 dismisses any effect from an extracellular coating. In addition, an extracellular coating would not influence the diffusion in a protein-radius–dependent manner. Under these conditions, the estimated radius of the rafts is r = 26 ± 13 nm. This estimate is also obtained with the formula for protein diffusion of Hughes et al. 1981, Hughes et al. 1982, which includes coupling to the surrounding medium, because the viscosity of water and the cytoplasm are low compared with the membrane viscosity (Swaminathan et al. 1997). The broad distribution of viscous drag values observed for the rafts studied indicates that even one raft type in one cell might have a distribution of sizes, and that the size of a single raft might be dynamic. Nevertheless, transferring these values to other cell types and non-GPI–anchored proteins might not always be possible since raft size and stability are most likely dependent on the lipid and protein constituents. Indeed, recent data suggest that rafts in the apical membrane of MDCK behave differently from rafts in fibroblasts (Verkade et al. 2000).
According to our study, rafts in the plasma membrane of fibroblast-like cells diffuse as a rather stable platform with an average area of 2,100 nm2. The size estimate allows an assessment of the maximal contents of one raft. If these were composed purely of lipid molecules, having a radius comparable to phosphoethanolamine (r = 0.44 nm), one raft would contain almost 3,500 lipid molecules. How many proteins a raft contains depends on how densely packed the proteins would be. If they were as densely packed as rhodopsin molecules are in frog rods (Blasie and Worthington 1969), or as the spikes in the envelope of Semliki Forest virus (Cheng et al. 1995), a raft would contain 55–65 proteins, respectively. Clearly, the packing density in a lipid raft in a mammalian plasma membrane would be lower. Indeed, recent results using fluorescent folate to measure the fluorescent resonance energy transfer between folates bound to folate receptors indicate that few of the receptors are clustered and many more are monomers. Further, these clusters consist of multiple GPI-anchored proteins if they exist in the same cell and are disrupted if cholesterol levels are depleted (Varma, R., and S. Mayor, personal communication).
Implications for Raft Function
The consequences of a small raft size and stable association is that proteins within rafts would be restricted in their interactions with other proteins. To use rafts as platforms in membrane trafficking (e.g., in apical transport from the Golgi complex) would imply that these rafts have to be clustered together by an apical sorting machinery to form a container comprising several rafts. Also, the formation of caveolae at the plasma membrane would involve the invagination of several rafts to form one caveola. Often caveolae are found like grapes in large clusters, thus comprising a reservoir of rafts with associated proteins at the cell surface.
A growing body of evidence implicates lipid rafts in signal transduction. Well-studied examples include IgE receptor signaling and T and B cell activation. If rafts normally contain only a limited set of proteins, then clustering of rafts would be necessary to achieve the concentration of interacting molecules required to elicit a signal above the activating threshold. There is ample indication that clustering is an essential feature of signal transduction processes involving rafts.
Acknowledgments
We thank T. Harder, A. Rietfeld, P. Scheiffele and D. Toomre for many insightful discussions. We acknowledge T. Harder, N. LeBot, P. Scheiffele and J. White for protein constructs and antibodies.
The project was partially supported by the German Science Foundation.
Footnotes
Abbreviations used in this paper: DIG, detergent insoluble glycolipid-enriched complex; GFP, green fluorescent protein; GPI, glycosylphosphatidylinositol; HA, influenza virus hemagglutinin; LFPGT46, artificial transmembrane YFP; PLAP, placental alkaline phosphatase; SPT, single particle tracking; TfR, transferrin receptor; TPF, two-photon fluorescence; YFP, yellow color variant of green fluorescent protein; YFPGLGPI, artificial GPI-anchored YFP.
References
- Bartlett M.S. On the theoretical specification of sampling properties of autocorrelated time series. J. R. Stat. Soc. 1946;8:B27–B34. [Google Scholar]
- Blasie J.K., Worthington C.R. Molecular localization of frog retinal receptor photopigment by electron microscopy and low-angle X-ray diffraction. J. Mol. Biol. 1969;39:407–416. doi: 10.1016/0022-2836(69)90135-1. [DOI] [PubMed] [Google Scholar]
- Brown D.A., Rose J.K. Sorting of GPI-anchored proteins to glycolipid-enriched membrane subdomains during transport to the apical cell surface. Cell. 1992;68:533–544. doi: 10.1016/0092-8674(92)90189-j. [DOI] [PubMed] [Google Scholar]
- Brown D.A., London E. Structure of detergent-resistant membrane domainsdoes phase separation occur in biological membranes? Biochem. Biophys. Res. Comm. 1997;240:1–7. doi: 10.1006/bbrc.1997.7575. [DOI] [PubMed] [Google Scholar]
- Brown D.A., London E. Functions of lipid rafts in biological membranes. Annu. Rev. Cell Dev. Biol. 1998;14:111–136. doi: 10.1146/annurev.cellbio.14.1.111. [DOI] [PubMed] [Google Scholar]
- Cerneus D., Ueffing P.E., Posthuma G., Strous G.J., van der Ende A. Detergent insolubility of alkaline phosphatase during biosynthetic transport and endocytosisrole of cholesterol. J. Biol. Chem. 1993;268:3150–3155. [PubMed] [Google Scholar]
- Cheng R.H., Kuhn R.J., Olson N.H., Rossman M.G., Choi H.-K., Baker T.S. Nucleocapsid and glycoprotein organization in an enveloped virus. Cell. 1995;80:621–630. doi: 10.1016/0092-8674(95)90516-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cherry R.J., Godfrey R.E. Anisotropic rotation of bacteriorhodopsin in lipid membranes. Comparison of theory with experiment. Biophys. J. 1981;36:257–276. doi: 10.1016/S0006-3495(81)84727-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eskandari S., Wright E.M., Kreman M., Starace D.M., Zampighi G.A. Structural analysis of cloned plasma membrane proteins by freeze-fracture electron microscopy. Proc. Natl. Acad. Sci. USA. 1998;95:11235–11240. doi: 10.1073/pnas.95.19.11235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiedler K., Kobayashi T., Kurzchalia T.V., Simons K. Glycosphingolipid-enriched, detergent-insoluble complexes in protein sorting in epithelial cells. Biochemistry. 1993;32:6365–6373. doi: 10.1021/bi00076a009. [DOI] [PubMed] [Google Scholar]
- Florin E.-L., Hörber J.H.K., Stelzer E.H.K. High resolution axial and lateral position sensing using two-photon excitation of fluorophores by a cwNd:YAG laser. Appl. Phys. Lett. 1996;69:446–448. [Google Scholar]
- Florin E.-L., Pralle A., Stelzer E.H.K., Hörber J.H.K. Photonic force microscope calibration by thermal noise analysis. Appl. Phys. 1998;A 66:S75–S78. [Google Scholar]
- Friedrichson T., Kurzchalia T.V. Microdomains of GPI-anchored proteins in living cells revealed by crosslinking. Nature. 1998;6695:802–805. doi: 10.1038/29570. [DOI] [PubMed] [Google Scholar]
- Gittes F., Schmidt C.F. Interference model for back focal plane displacement detection in optical tweezers. Opt. Lett. 1998;23:7–9. doi: 10.1364/ol.23.000007. [DOI] [PubMed] [Google Scholar]
- Ge M., Field K.A., Aneja R., Holowka D., Baird B., Freed J.H. Electron spin resonance characterization of liquid ordered phase of detergent-resistant membrane from RBL-2H3 cells. Biophys. J. 1999;77:925–933. doi: 10.1016/S0006-3495(99)76943-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Happel J., Brenner H. Low Reynolds number hydrodynamics. Prentice Hall; New Jersey: 1965. [Google Scholar]
- Harder T., Scheiffele P., Verkade P., Simons K. Lipid-domain structure of the plasma membrane revealed by patching of membrane components. J. Cell Biol. 1998;141:929–942. doi: 10.1083/jcb.141.4.929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He T.C., Zhou S., DaCosta L.T., Yu J., Kinzler K.W., Vogelstein B. A simplified system for generating recombinant adenoviruses. Proc. Natl. Acad. Sci. USA. 1998;95:2509–2514. doi: 10.1073/pnas.95.5.2509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes B.D., Pailthorpe B.A., White L.R. The translational and rotational drag on a cylinder moving through a membrane. J. Fluid Mech. 1981;110:349–356. [Google Scholar]
- Hughes B.D., Pailthorpe B.A., Sawyer W.H., White L.R. Extraction of membrane microviscosity from translational and rotational diffusion coefficients. Biophys. J. 1982;37:673–676. [PMC free article] [PubMed] [Google Scholar]
- Ipsen J.H., Karlström G., Mouritsen O.G., Wennerström H., Zuckerman M.J. Phase equilibria in the phosphatidylcholine-cholesterol system. Biochim. Biophys. Acta. 1987;905:162–172. doi: 10.1016/0005-2736(87)90020-4. [DOI] [PubMed] [Google Scholar]
- Keller P., Simons K. Cholesterol is required for surface transport of influenza virus hemagglutinin. J. Cell Biol. 1998;140:1357–1367. doi: 10.1083/jcb.140.6.1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilsdonk E.P.C., Yancey P.G., Stoudt G.W., Bangerter F.W., Johnson W.J., Phillips M.C., Rothblat G.H. Cellular cholesterol efflux mediated by cyclodextrins. J. Biol. Chem. 1995;270:17250–17256. doi: 10.1074/jbc.270.29.17250. [DOI] [PubMed] [Google Scholar]
- Kenworthy A., Edidin M. Distribution of a glycosylphosphatidylinositol-anchored protein at the apical surface of MDCK cells examined at a resolution of <100Å using imaging fluorescence resonance energy transfer. J. Cell Biol. 1998;14:68–84. doi: 10.1083/jcb.142.1.69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kusumi A., Sako Y. Cell surface organization by the membrane skeleton. Curr. Opin. Cell Biol. 1996;8:566–574. doi: 10.1016/s0955-0674(96)80036-6. [DOI] [PubMed] [Google Scholar]
- Ledesma M.D., Simons K., Dotti C.G. Neuronal polarityessential role of protein-lipid complexes in axonal sorting. Proc. Natl. Acad. Sci. USA. 1998;95:3966–3971. doi: 10.1073/pnas.95.7.3966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maisner A., Zimmer G., Liszewski M.K., Lublin D.M., Atkinson J.P., Herrler G. Membrane cofactor protein CD46 is a basolateral protein that is not endocytosedimportance of the tetrapeptide FTSL at the carboxyl terminus. J. Biol. Chem. 1997;272:20793–20799. doi: 10.1074/jbc.272.33.20793. [DOI] [PubMed] [Google Scholar]
- Mantei N., Villa M., Enzler T., Wacker H., Boll W., James P., Hunziker W., Semenza G. Complete primary structure of human and rabbit lactase-phlorizin hydrolaseimplications for biosynthesis, membrane anchoring and evolution of the enzyme. EMBO (Eur. Mol. Biol. Organ.) J. 1988;7:2705–2713. doi: 10.1002/j.1460-2075.1988.tb03124.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matlin K.S., Reggio H., Helenius A., Simons K. Infectious entry pathway of influenza virus in canine kidney cell line. J. Cell Biol. 1981;91:601–613. doi: 10.1083/jcb.91.3.601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parton R.G., Simons K. Digging into caveolae. Science. 1995;269:1398–1399. doi: 10.1126/science.7660120. [DOI] [PubMed] [Google Scholar]
- Peters R., Cherry R.J. Lateral and rotational diffusion of bacteriorhodopsin in lipid bilayersexperimental test of the Saffman-Delbrück equations. Proc. Natl. Acad. Sci. USA. 1982;79:4317–4321. doi: 10.1073/pnas.79.14.4317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pralle A., Florin E.-L., Stelzer E.H.K., Hörber J.H.K. Local viscosity probed by photonic force microscopy. Appl. Phys. 1998;A 66:S71–S73. [Google Scholar]
- Pralle A., Prummer M., Florin E.-L., Stelzer E.H.K., Hörber J.H.K. Three-dimensional high-resolution particle tracking for optical tweezers by forward scattered light. Micr. Res. Tech. 1999;44:378–386. doi: 10.1002/(SICI)1097-0029(19990301)44:5<378::AID-JEMT10>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- Saffman P.G., Delbrück M. Brownian motion in biological membranes. Proc. Natl. Acad. Sci. USA. 1975;72:3111–3113. doi: 10.1073/pnas.72.8.3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sako Y., Kusumi A. Compartmentalized structure of the plasma membrane for receptor movements as revealed by a nanometer-level motion analysis. J. Cell Biol. 1994;125:1251–1264. doi: 10.1083/jcb.125.6.1251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sako Y., Kusumi A. Barriers for lateral diffusion of transferrin receptors in the plasma membrane as characterized by receptor dragging by laser tweezersfence versus tether. J. Cell Biol. 1995;129:1559–1574. doi: 10.1083/jcb.129.6.1559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton M.J. Lateral diffusion in an archipelagoeffects of impermeable patches on diffusion in a cell membrane. Biophys. J. 1982;39:165–173. doi: 10.1016/S0006-3495(82)84504-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton M.J. Lateral diffusion in an archipelago. The effect of mobile obstacles. Biophys. J. 1987;52:989–997. doi: 10.1016/S0006-3495(87)83291-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton M.J. Lateral diffusion in an archipelago. Distance dependence of the diffusion coefficient. Biophys. J. 1989;56:615–622. doi: 10.1016/S0006-3495(89)82708-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheiffele P., Roth M.G., Simons K. Interaction of influenza virus hemagglutinin with sphingolipid-cholesterol membrane domains via its transmembrane domain. EMBO (Eur. Mol. Biol. Organ.) J. 1997;16:5501–5508. doi: 10.1093/emboj/16.18.5501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons K., Ikonen E. Functional rafts in cell membranes. Nature. 1997;387:569–572. doi: 10.1038/42408. [DOI] [PubMed] [Google Scholar]
- Swaminathan R., Hoang C.P., Verkman A.S. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cellscytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys. J. 1997;72:1900–1907. doi: 10.1016/S0006-3495(97)78835-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stauffer T.P., Meyer T. Compartmentalized IgE receptor-mediated signal transduction in living cells. J. Cell Biol. 1997;139:1447–1454. doi: 10.1083/jcb.139.6.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teuchert M., Maisner A., Herrler G. Importance of the carboxyl-terminal FTSL motif of membrane cofactor protein for basolateral sorting and endocytosis. Positive and negative modulation by signals inside and outside the cytoplasmic tail. J. Biol. Chem. 1999;274:19979–19984. doi: 10.1074/jbc.274.28.19979. [DOI] [PubMed] [Google Scholar]
- Tomishige M., Sako Y., Kusumi A. Regulation mechanism of the lateral diffusion of band 3 in erythrocyte membranes by the membrane skeleton. J. Cell Biol. 1998;1424:989–1000. doi: 10.1083/jcb.142.4.989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varma R., Mayor S. GPI-anchored proteins are organized in submicron domains at the cell surface. Nature. 1998;6695:798–801. doi: 10.1038/29563. [DOI] [PubMed] [Google Scholar]
- Vaz W.L.C., Goodsaid-Zalduondo F., Jacobson K. Lateral diffusion of lipids and proteins in bilayer membranes. FEBS (Fed. Eur. Biochem. Soc.) Lett. 1984;174:199–207. [Google Scholar]
- Verkade P., Harder T., Lafont F., Simons K. Induction of caveolae in the apical plasma membrane of MDCK cells. J. Cell Biol. 2000;148:727–739. doi: 10.1083/jcb.148.4.727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto T., Davis C.G., Brown M.S., Schneider W.J., Casey M.L., Goldstein J.L., Russell D.W. The human LDL receptora cysteine-rich protein with multiple Alu sequences in its mRNA. Cell. 1984;39:27–38. doi: 10.1016/0092-8674(84)90188-0. [DOI] [PubMed] [Google Scholar]