Capturing cell-fate decisions from the molecular signatures of a receptor-dependent signaling response

Abstract

We examined responses of the B-cell antigen receptor-dependent intracellular signaling network to targeted perturbations induced through siRNA-mediated depletion of select signaling intermediates. The constituent nodes displayed graded sensitivities, which resulted from the differential effects of perturbations on the kinetic and quantitative aspects of phosphorylation at each node. By taking the rate of initial phosphorylation, rate of subsequent dephosphorylation, and the total intensity of phosphorylation at each node as separate signaling parameters, we generated data-driven models that accurately predicted the cellular responses of apoptosis, proliferation, and cytokine secretion. Importantly, the effects of perturbation on the primary target alone did not yield successful models. Rather, it also required incorporation of secondary effects on many other nodes. A significant feature of these models was that the three signaling parameters derived from each node functioned largely as independent entities, making distinctive contributions to the cellular response. Thus, the kinetic and quantitative features of phosphorylation at a node appear to play discrete roles during signal processing.

Introduction

The response of a cell to external cues is mediated through a cascade of coupled biochemical reactions that eventually regulate components responsible for cellular phenotypic functions. The initial conceptualization of the signaling machinery was as a composite of discrete, linear pathways. More recent detailing of the extent and diversity of intra-pathway cross-talk has, however, ceded to the current view of the system as a complex network (Weng et al, 1999; Barabasi and Oltvai, 2004; Bar-Yam and Epstein, 2004; Sachs et al, 2005). The signaling network is now considered to represent the central functional module of a cell that, in turn, is connected to several other modules that are responsible for phenotypic function (Hartwell et al, 1999). These latter include those that govern the transcriptional, translational, motility, and secretory activity of the cell. A notable aspect of signaling is that transmission is also coupled with processing of information, where the interactions between individual components provide the interfaces for computation of information through intra-cascade feedback regulation and cross-talk with other pathways. It is this information-processing capability of the signaling network that is responsible for the context specificity of the cellular response.

Networks are generally abstracted as a series of nodes that are interconnected through linkages, with each link representing the interaction between two components (Strogatz, 2001; Papin et al, 2005). Implicit in the ‘network' view of the signaling system is the recognition that a study of signaling cannot be approached by ‘reductionist' examinations of individual molecules or pathways. This arises from the fact that, in a network, the components become involved in a collective dynamic behavior that none of the individual molecules can exhibit in isolation (Kholodenko, 2006). Consequently, a proper understanding of cellular responses to external stimuli calls for a more global analysis that examines the topology and emergent features of the signaling network.

Although significant progress has been made toward understanding its structural aspects (Schlessinger, 2000; Irish et al, 2004; Natarajan et al, 2006), the inherent complexity of the signaling network has rendered it difficult to examine the properties that govern its dynamic behavior. Complexity of the signaling network stems from the intricate connectedness of its large number of interacting constituents (Oda et al, 2005; Oda and Kitano, 2006). Further, this connectedness is dynamic in nature and involves a complicated circuitry consisting of varying combinations of feedback, feed-forward, cross-talk, and scaffolding interactions (Xia et al, 2004). It is this complexity that has also obscured answers to some of the most fundamental questions relating to the mechanisms underlying signal transmission and processing. Thus, a key unanswered issue is that of whether the emergent properties of the network derive from the reactions between only a few core components or whether it represents an integrated output involving all of its parts. This question is especially relevant to understanding how signal processing is achieved. Thus, for example, factors controlling signal flow could be evenly distributed across the entire network. Alternatively, as is the more conventional view, signal flow could be modulated through differential usage of various individual signaling pathways. Resolution between these and other possibilities is clearly critical for an eventual understanding of how context specificity is achieved, in a stimulus-dependent cellular response. From a more practical perspective, such resolution is also crucial for the interpretation of the effects resulting from targeted perturbations of signaling components as achieved by siRNA-mediated depletion or with specific pharmacological inhibitors.

In the present work, we studied the adaptability of the B-cell antigen receptor (BCR)-dependent signaling network (Dal Porto et al, 2004; Jumaa et al, 2005) through systematic perturbations at several of its nodes. A coarse-grained analysis of the resulting effects provided a glimpse into how cellular response is determined by the network activity. The individual nodes displayed variable sensitivities to each of the targeted perturbations performed, yielding a unique pattern of signaling features in each case and—thereby—a particular cellular phenotypic response. By using these perturbation-induced alterations in network properties as the input data, we were able to successfully generate mathematical models that accurately predicted cellular responses in terms of proliferation, apoptosis, and cytokine secretion. Importantly, in addition to the effects of perturbation on the target protein, successful model generation also required incorporation of the secondary effects on the other nodes of the signaling network. In other words, cellular responses were defined by the manner in which a given perturbation propagates through the components of the signaling network. Also interesting was the fact that, at least based on our models, the description of a cellular response did not involve any specific grouping of nodes acting in a discrete manner. Rather it appears that specific kinetic and/or quantitative parameters were selectively extracted from multiple nodes to define a particular cellular response.

Results

Dynamics and sensitivity of BCR-dependent signaling

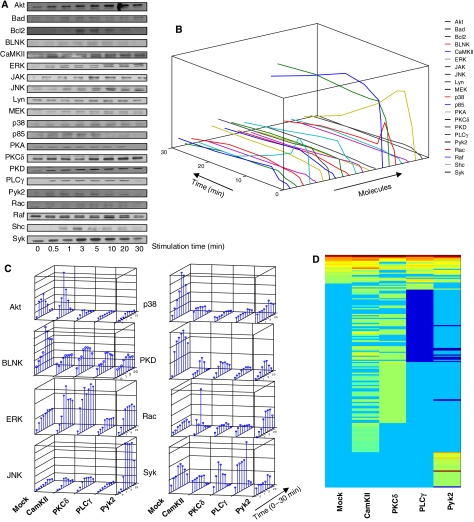
Murine B lymphoma, A20, cells were stimulated with the F(ab)₂ fragment of anti-mouse IgG (anti-IgG) antibodies and the time-dependent phosphorylation of a panel of 21 signaling intermediates was subsequently followed. This panel was collectively representative of the known BCR-dependent signaling pathways. Figure 1A shows that all of these molecules were indeed phosphorylated in response to cell stimulation, although there were individual variations in the kinetics, magnitude, and stability of phosphorylation. Densitometric scans of these blots were subjected to a normalization exercise using internal controls as normalizers and a specifically coded algorithm that corrects for both intra- and inter-gel variations in band intensities by fitting the cubic spline curve from normalized with that of the unnormalized data (Supplementary Figure S1). This enabled us to obtain profiles for each signaling intermediate (Figure 1B), where the deviation from the phosphorylation curves from multiple experiments was within 20%.

Figure 1.

Signaling from the B-cell receptor and the effects of individual perturbations. (A) Phosphorylation profiles obtained for the selected signaling molecules from one of four separate experiments. The phosphorylation site-specific antibodies used are listed in Supplementary Table S6, along with the relevant references. The western blots obtained were then normalized using our MATLAB Toolbox as described in Supplementary Figure S1. The resulting plots for all the signaling molecules are shown in (B) (Z-axis value ranges from 100 to 3000). (C) Effects of siRNA-mediated depletion of either CaMKII, PKCδ, PLCγ, or Pyk2 on the time-dependent phosphorylation profiles of a representative panel of signaling intermediates. For comparative purposes, the corresponding profiles obtained in mock-siRNA-treated cells (see Materials and methods) are also shown. Each bar represents the extent of phosphorylation obtained at the indicated time point, and the values were obtained after applying the normalization procedure on three separate experiments as described in Supplementary Figure S1. (D) Summarized results, in the form of a heat map, of a microarray analysis of gene expression under various perturbation conditions indicated. (List of genes in the order of their up- or downregulation is given in Supplementary Table S7.)

Therefore, to dissect factors contributing to context-dependent signal processing, we employed siRNA to specifically deplete cells of a given signaling intermediate. The aim here was to monitor the consequences of this depletion on BCR-dependent signal transduction. As an initial test of the potential of such an approach, we selected a subset of four proteins—PKCδ, CaMKII, PLCγ, and Pyk2—for these studies. Cells were independently depleted of each of these intermediates (Supplementary Figure S2), and the time-dependent phosphorylation profiles of the remaining molecules were determined (Supplementary Figure S3–S5 and Supplementary Table S6).

As the representative results in Figure 1C show, the depletion of any given component from the signaling network resulted in significant alterations in phosphorylation profiles of the other intermediates. Importantly, this effect was not localized, but extended over to intermediates that were not within the canonical ‘signaling pathways' to which each of the depleted molecules belonged. A good example of this is the marked effect of Pyk2 depletion on the phosphorylation profiles of Akt, JNK, p38, and PKD (Figure 1C). Similarly, phosphorylation of BLNK—an early intermediate in BCR signaling—was significantly affected by inhibition of expression of downstream intermediates, such as CaMKII or PKCδ. These long-range effects are consistent with our current acceptance of extensive cross-talk between signaling pathways, leading to the functioning of the signaling machinery as a complex and integrated network.

Altered network behavior correlates with alterations in signal processing

To ascertain whether the modulations seen in Figure 1C also reflect alterations in signal processing, we performed a microarray analysis of the very early genes induced under these individual conditions. Stimulation of mock siRNA-treated cells with anti-IgG for 30 min led to the reproducible induction of 20 genes at the end of a period of an additional 30 min (Figure 1D). This profile, however, was markedly altered in cells that had been individually depleted of each of the intermediates prior to stimulation. Thus, several additional genes were either strongly induced (CaMKII, Pyk2, and PKCδ) or downregulated (PLCγ) (Figure 1D and Supplementary Table S7). Interestingly, the most notable effect of siRNA-mediated suppression of a signaling molecule was the significant spread in the number of genes influenced by BCR activation. Thus, the total number of BCR-sensitive genes, under these experimental conditions, increased to 27, 90, 59, and 40 in cells depleted of CaMKII, PKCδ, PLCγ, and Pyk2, respectively.

We next explored the likelihood that the altered gene expression profiles in Figure 1D may exert differential effects at the level of the cellular response. This was achieved by classifying these genes using the Ingenuity Pathway Analysis (IPA) program (Calvano et al, 2005). Ten separate gene regulatory networks that included one or more of this set could be extracted from the IPA knowledge base. The most significant of these was a Myc-centric network with a proposed function in cell cycle regulation. All the molecular components of this network were present among the gene list described in Figure 1D. Stimulation of mock siRNA-treated cells resulted in the upregulation of only a few genes within this module, with Egr1 being the most significant. Depletion of any of the signaling intermediates, however, resulted in a marked alteration with several additional genes being either strongly induced or inhibited (Supplementary Figures S8 and S9). In addition to alterations in the number of genes expressed within this module, quantitative changes in the level of expression of several genes were also observed. Thus, the effects of siRNA-mediated perturbations on the signaling network, seen in Figure 1C, do in fact translate into significant alterations at the level of at least some of the gene regulatory modules. The latter can then be expected to also impact on the cellular response.

Sampling of the network behavior through targeted perturbations

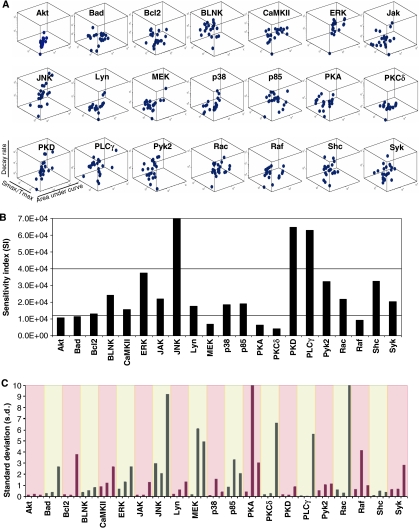
The indication from Figure 1 that siRNA-induced perturbations provided a promising strategy to study the relationship between the behavior of the signaling network and the cellular phenotypic response prompted us to extend our studies by individually depleting cells of all the remaining molecules being monitored. The consequent effects on BCR-dependent signaling were then examined. Thus, combining with the data in Figure 1C, these experiments collectively yielded phosphorylation profiles of 21 signaling molecules, measured over 8 time points, and under 21 independent conditions of perturbation (Supplementary Figures S3–S5). Each of these profiles was then taken for the derivation of three separate parameters that are henceforth termed as signaling parameters. These were (i) S_max/t_max, where S_max represents the amplitude of the peak and t_max the time (in minutes) taken to reach this value and corresponds to a measure of activation rate; (ii) the total area under the phosphorylation curve (A); and (iii) the rate of dephosphorylation from the peak value. The distribution of these values, in three-dimensional (3D) space, for each molecule under the various conditions employed is shown in Figure 2A.

Figure 2.

Signaling nodes display graded sensitivities to diverse network perturbations. As described in the text, we first obtained the phosphorylation profiles for each of the 21 signaling molecules, under the 21 independent conditions of perturbation. Results obtained from three such experiments were then taken to generate a normalized profile (as described for Figure 1B) for each signaling molecule and each perturbation condition. Individual profiles were then taken for deriving the values of S_max/t_max, decay rate, and the total area under the curve. (A) Spread of the values obtained, for each of these signaling intermediates, under the 21 separate conditions of perturbation. This distribution is shown in the form of a three-dimensional (3D) box for each intermediate, and each data point corresponds to the values of the three signaling parameters obtained, for a given perturbation condition. The extent of spread in the distribution provides a relative measure of the sensitivity of a given node to the various perturbations. (B) Quantitative differences in nodal sensitivity, represented here as sensitivity index (SI), which was calculated by measuring distance in the 3D parametric space traveled by the node in response to the various perturbations. (C) Standard deviation for all the three parameters of each node under all the perturbation conditions (sequence of parameters for any given node in the graph is area, decay rate, and S_max/t_max). Each colored segment of this graph specifies a given node (indicated on the X-axis) with the three corresponding bars describing (from left to right) the deviations in area, S_max/t_max, and decay rate, respectively.

A cursory examination of this figure reveals that the individual molecular signals differ widely in terms of their response to the different perturbations performed. Thus, there were cases such as Akt where the close clustering of data points was indicative of its relative resistance to alterations in network composition by siRNA (Figure 2A). In contrast, the large spread of the data cluster for molecules such as JNK and PLCγ revealed the presence of nodes with a high degree of sensitivity to the perturbations. Notably, several of the target molecules also fell in an intermediate category of being sensitive to some of perturbations, but displaying resistance to others. Thus, at least within the limitations of this study, the constituent nodes of the signaling network appear to represent a multivariate group with highly divergent properties.

To obtain a more quantitative estimate of the degree of susceptibility of individual nodes, we adopted the solution to the standard ‘Traveling Salesman Problem' to the data in Figure 2A. This involved an estimation of the minimum path that would thread through the data points resulting from the perturbation of each given signaling molecules, as depicted in Figure 2A. The path lengths thus obtained provided a measure of the extent of fluctuation in properties of the individual nodes in response to the various perturbations performed. Consequently, these values were taken to represent an index of sensitivity (sensitivity index; SI). The results shown in Figure 2B further reinforce that the individual components of the signaling network display graded sensitivities to the siRNA-mediated perturbations. The overall variation in sensitivities observed spanned a near 20-fold range of SI values, with PKCδ representing the most resistant end of the spectrum and JNK the most vulnerable (Figure 2B). These observations lend further support to the emerging notion that modulations in signal processing may be mediated through non-identical participation of the individual nodes of the signaling network (Janes et al, 2005).

An intriguing aspect of the SI values described in Figure 2B was that they were defined by asymmetric contributions from the individual signaling parameters, with the pattern of these contributions varying from one node to another. This is exemplified by the analysis presented in Figure 2C, which gives the standard deviation (s.d.) from the mean of the fold change in a given signaling parameter from the corresponding value obtained for that parameter in mock siRNA-treated cells. Thus, a low value for the standard deviation for a given node-derived signaling parameter would be indicative of the fact that it displays similar levels of susceptibility to the various perturbations performed. As opposed to this, a high standard deviation would identify instances where the extent of susceptibility was highly dependent upon the nature of the perturbation. It is evident from the results in Figure 2C that, for any given node, the s.d. values for variability differed significantly for the individual signaling parameters and that the pattern was not uniform across the nodes. Thus, while Bad, Bcl2, PKCδ, PLCγ, Rac, and Syk were all defined by a selectively high s.d. values for the decay rate, it was the high s.d. value for S_max/t_max that described PKA and Raf (Figure 2C). These corresponding values were uniformly low for all three signaling parameters for Akt and PKD, whereas the contributions were relatively more graded for the remaining molecules. Importantly, a comparable SI value for any two nodes did not necessarily imply similar sensitivities along the three signaling parameter coordinates. This aspect is highlighted by the examples of PKD and PLCγ, both of which share similar values for SI (Figure 2B). Nonetheless, the sensitivity of PLCγ was typified by a wide range of fluctuations in decay rate depending upon the perturbation performed. As opposed to this, such a distinction was less evident for PKD where all three signaling parameters displayed a more uniform range of variations to all the induced perturbations (Figure 2C). Thus, the collective results in Figure 2 reveal that the sensitivity of any node to perturbations is an emergent feature that in turn is defined by the relative susceptibility of each of the signaling parameters to a given perturbation. Importantly, the pattern of perturbation-induced sensitivities of the signaling parameters appears to vary across the nodes of the signaling network. This feature could have important implications during context-specific processing of signal. Further, these results also suggest that nodal participation during signal processing may likely be more accurately defined by taking into consideration the relative weights of contributions from these signaling parameters.

Network perturbations translate into altered cellular responses

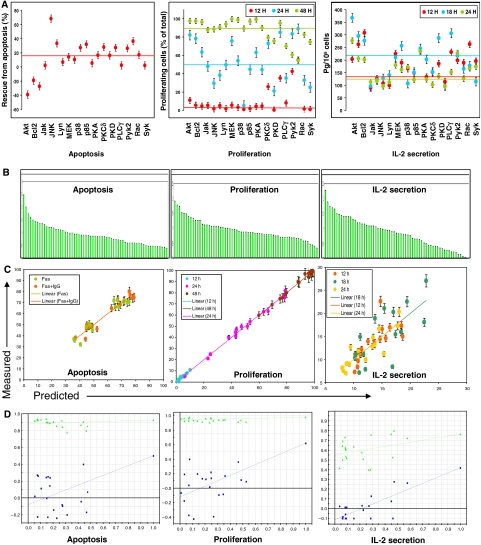
The phenotypic response of a cell is usually context dependent, being determined by the nature of the extracellular stimulus. Such a choice of response output from a variety of possibilities derives from the stimulus-specific signaling patterns that propagate through the network. Our initial findings in Figure 1 that siRNA-mediated perturbations of the BCR signaling network significantly affected the subsequent gene expression profile led us to next examine the consequences on the cellular response. For this exercise, we studied three separate anti-IgG-induced responses of the cell. These were proliferation, secretion of IL-2 (Kakiuchi et al, 1991), and protection against Fas-mediated apoptosis (Wang et al, 2000). For our initial set of experiments, we randomly selected 15 of the perturbation conditions described in Figure 2A and the resulting anti-IgG-dependent cellular responses for each of these conditions, in the three separate response modes, were determined. These results are shown in Figure 3A. At first sight, it is evident that the induced perturbations had a significant impact on all the three cellular response modes. Importantly, the effects varied widely with the nature of the target.

Figure 3.

Perturbation-induced alteration in cellular responses and their analysis by data-driven modeling. (A) Anti-IgG-dependent cell responses obtained for the various siRNA-treated cells, when measured either as protection against Fas-induced apoptosis, proliferation, or IL-2 secretion. The 15 molecules separately depleted for these experiments are indicated on the X-axis. The color of the closed circle indicates the time point at which that particular measurement was made, and the colored lines in each box indicates the corresponding value obtained in mock siRNA-treated cells, at the indicated time point. Proliferation was measured as the percent of total cells in cycle, whereas apoptosis is described as the percent of Fas-stimulated cells that were rescued from apoptosis when cells were also simultaneously stimulated with anti-IgG. In this latter case, negative values indicate enhancement of apoptosis when the relevant signaling intermediate was depleted. Values are from one of three (cytokine), or two (proliferation and apoptosis) separate determinations. (B) Ranking of the individual VIPs in the descending order of their significance for the three different responses as indicated. (Parameters along with their respective VIP values for all the three responses are listed in decreasing order in Supplementary Table S10.) (C) Distribution of the observed versus predicted values along the regression line, for the three independent responses. The color code used for the various time points is indicated. (D) Results of the validation of our model based on 20 different iterations of the data set corresponding to each of the cellular responses. The green line represents R2 values, whereas the blue line represents the Q2 values.

To extract a possible causal relationship between perturbation-induced alterations in the behavior of the signaling network and the cellular response, we took these two data sets into a partial least square (PLS) model where the signaling parameters served as the independent variables (X), while the dependent variables (Y) were defined by the cell response profiles. Here, our decision to treat the three signaling parameters, derived from each node, as independent entities was based on the desire to test our interpretation from Figure 2 that these features may be more relevant for defining the cellular output. Thus, 945 such parameters obtained (derived from the phosphorylation profiles of 21 signaling molecules obtained from 15 perturbation conditions) were taken as the X variables, and incorporated into a PLS model along with about 100 response data columns as the Y variables.

A PLS analysis reduces the multiple dimensions of the data set to a principal component space and regresses the independent and dependent principal components. This reduction in dimensionality requires fewer unknown coefficients, which in turn are constrained better by the observations (Janes et al, 2005; Jaqaman and Danuser, 2006). Our initial efforts, however, were not very successful. Although a model could be generated, its predictive ability, however, was poor. A likely explanation for this could be the indiscriminate inclusion of all the signaling metric dimensions for generating the model. It is possible that at least some of these could be either redundant or irrelevant in the context of the specific cellular response being examined.

In spite of the poor prediction ability of our initial model, a subsequent analysis—nonetheless—yielded some interesting insights. This involved a determination of the variable importance in projections (VIPs), an analysis that defines the degree of covariance between the independent and dependent variables. As evident from the VIP plots shown in Figure 3B (and Supplementary Table S10), each cellular response was characterized by a gradation in VIP values for the individual signaling parameters. Expectedly, the gradation obtained for each of the cellular response was distinct from that of the others. Intriguingly, however, the three signaling parameters representing a given node did not cluster together in the VIP gradient for any of the responses. Rather, they behaved in a more autonomous fashion displaying significant differences at the level of the VIP values, within a given phenotypic response (Figure 3B). These observations lend further support to the possibility that individual signaling parameters, derived from a node, play distinctive roles during signal processing.

As the next step, we attempted to improve our PLS model by filtering out the potential ‘noise' from our data set. For this exercise, only those VIPs with a projection value of >0.6 were selected as the ‘response-specific' VIPs. The PLS models obtained with these selected VIPs are depicted in Figure 3C. As shown, significantly improved models were obtained with a prediction accuracy of >90% for all the three cellular responses. At one level, the accuracy of these models indicates that the data set of independent variables employed was sufficient to capture signatures correlating with the three measured cellular responses. Further, it was also interesting that the spectra of VIPs that defined the individual cellular responses were overlapping, but not identical. This further confirms that, for each node, the three signaling parameters (activation rate, area, and decay rate) contribute to various extents to the response-specific signature. In other words, rather than being dependent upon participation of discrete nodes, signal processing may in fact involve combinations of molecular signals that represent separate characteristic features of the phosphorylation profile of each node.

Having obtained satisfactory models for the training data set, we next sought to establish their validity by verifying whether the combination employed was the best possible one for predicting the relevant response. Twenty different iterations with varying combinations of each data set were performed and the models thus generated were compared for the ‘goodness of fit.' A model is considered to be valid if no other member of the iterated set has a higher value for either R2, the fraction of the variations of the X and Y variables explained by each extracted component, or Q2, the fraction of the total variations that can be predicted by the model. Figure 3D shows that this was indeed the case, thus confirming that our model was the best possible one for the given data set. In addition to this exercise, we also verified that the calculated root mean square error was well within the significant range for each case, and that the DmodX—which determines the distance of individual variables from the model—was also within the critical limit as set by the model (not shown). Further, to exclude any possibility of biasness in the model, we randomly picked perturbation conditions and varied the number of conditions used to train the data set. The majority of these cases yielded an equally good model with minimum variation in the VIP values and their ranking. Finally, we also attempted to determine the minimum number of conditions required to create a predictive model. As one would expect for any multivariate analysis, sufficient variance in the data set is a pre-requisite for constructing a good model. We could go as low as six perturbation conditions, in multiple combinations, without significantly affecting the predictive ability of the model. Below this number, however, we failed to extract any principal component and were unable to build a model.

Model-based prediction of cellular responses

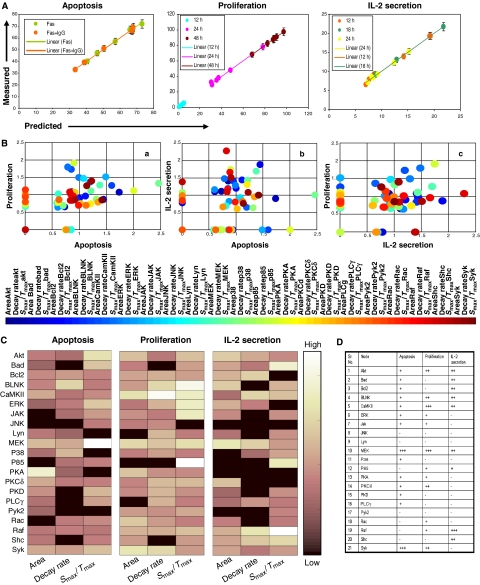
To further validate the VIPs identified in our PLS model, we tested the ability of the model to predict responses for an untrained data set. For this exercise, we felt that the most stringent test would be to predict responses for data obtained from the siRNA-mediated perturbations of additional signaling molecules. As already indicated, the PLS models described in Figure 3C were derived from the results obtained from a set of 15 perturbations. Therefore, we next took the data from the remaining six perturbations (Figure 2) for incorporation into the PLS model. Although this collectively represented a total of 378 signaling parameters, only the significant response-specific parameters—as decided by the VIP significance cutoff in our base model (Figure 3B)—were included in the validation models. In parallel, we also measured cell proliferation, IL-2 secretion and Fas-mediated apoptosis, as described above, under each of these perturbation conditions. As shown in Figure 4A, our model was able to predict all the three responses, for all the independent conditions, with a very high degree of accuracy. The correlation between the predicted and the experimentally observed values for all the three responses was >95%. The accuracy of these predictions for the untrained data set confirms that the molecular features or VIPs captured by our PLS model represent an accurate description of cell-fate decisions, in the three separate response modes studied.

Figure 4.

Validating the PLS model and defining response-specific VIP fingerprints. Cellular responses were generated for the six additional perturbation conditions (siRNA for Bad, BLNK, CaMKII, ERK, Raf, and Shc), and the resulting values were incorporated into the PLS model as described in the text. A comparison of the predicted versus the experimentally determined (mean of three experiments±s.d.) values for each of the responses is shown in (A). (B) Distribution of signaling parameters—as VIPs—in the three combinatorially possible two-dimensional spaces (see text for details). The color of each closed circle represents a numerical calibration of the respective VIPs, along all the three response axes and their identity is described by the colored bar shown below. (C) VIP distribution as a fingerprint for the three separate responses. Included in this fingerprint is a color-coded indication of the relative importance of a given VIP, the scale of which is described by the pseudo-color bar. (D) Minimal necessary nodal features required to generate a valid model for each of the three responses are tabulated (see text for details).

VIP fingerprints define the molecular signature of the cellular response

A significant aspect of our PLS model was that it provided additional confirmation for the fact that each of the signaling parameters makes distinct contributions to the cellular response. To characterize this further, we examined the distribution of the response-specific VIPs in terms of their relative contribution to the different cellular responses. This characterization is shown in Figure 4B, where the distribution of these molecular signals in the 3D response space has been projected onto separate two-dimensional (2D) planes, each representing a combination of two of the three responses studied. Thus, for example, panel ‘a' of Figure 4B shows the distribution of the molecular signals between the apoptosis and proliferation axes. At one level, although the majority of implicated VIPs overlap between both responses they, nonetheless, vary in terms of the significance of their relative contribution along either axis. In addition, a unique subset of VIPs that were specific to either the proliferative or apoptotic response is also evident. The remaining two projections shown in Figure 4B also show similar features, leading to the suggestion that signal processing involves a combinatorial process that integrates over both specific and weighted contributions of the VIPs.

This aspect is particularly highlighted by the illustration in Figure 4C, which emphasizes that each cellular response is characterized by a unique VIP signature. At one level, only about 15% of the VIPs were found to be truly ‘response unique,' with the remainder showing overlapping contributions to either two or all three of the responses. Importantly, however, the VIPs from the latter group also displayed some degree of selectivity. Thus their contributions to the multiple responses were not uniform but, rather, were differentially weighted along the independent axes. For example, while the activation rate of MEK-1/2 (i.e. S_max/t_max) contributed significantly to apoptosis, it was the corresponding area and decay rate parameters that were more relevant for IL-2 production, whereas all the three parameters contributed to comparable levels in the case of proliferation. A similar distinction was also seen in the case of Akt where its activation rate was biased toward apoptosis, whereas both the area and activation rate components were weighted in favor of proliferation; with IL-2 secretion receiving prominent contributions from area and decay rate (Figure 4C). CaMKII further exemplified the unequal contribution of signaling parameters, derived for each node, to the different cellular responses. Here, the selectivity exhibited by activation rate can be described as proliferation/IL-2 secretion>apoptosis; whereas that for area as proliferation>apoptosis>IL-2 secretion; and that for the decay rate as proliferation>IL-2 secretion>apoptosis (Figure 4C).

Another significant aspect highlighted by Figure 4C is the fact that the node-specific signaling parameters can make independent contributions even within a given cellular response. Thus, in the case of apoptosis for example, the activation rate of PLCγ was more significant than area, with no contribution from decay rate. Similarly, for proliferation, the decay rate of Lyn was more significant relative to activation rate, whereas area was relatively unimportant. Such trends were also evident for the IL-2 secretion response as typified by the example of ERK-1/2. Here, the observed hierarchy of significance in terms of parameter contribution was area>decay rate>activation rate (Figure 4C).

The results in Figure 4B and C, therefore, collectively identify that each cellular response is characterized by a small subset of ‘response-unique' VIPs, in addition to a larger number of overlapping VIPs that make weighted contributions to the different responses. In a separate exercise, we verified that the response-unique VIPs were alone insufficient to generate a satisfactory model. Conversely, removal of these response-unique VIPs from the models described in Figure 3C severely compromised their prediction ability (not shown). Thus, it is the spectrum of VIPs involved, along with the distribution of the weights of their individual contributions, which cumulatively defines the signature of the cellular response along any given axis.

The implication that stems from our above interpretation is that a stimulus-dependent cellular response cannot be adequately described by considering discrete contributions from subsets of nodes within the signaling network. Rather, it argues that specific features (i.e. activation rate, area, or decay rate), selectively extracted from the various nodes, function as the more relevant entities in defining a particular cellular response. To explore this further, we re-examined the PLS models described in Figure 3C in terms of the minimum number of top-scoring VIPs required to derive a successful model in each case. Our objective here was to first define the core, node-specific, variables that encode information relevant to the independent cellular response, and then examine their distribution. For this exercise, our criteria for retention of validity of the model was based on the comparison of R2 and Q2 values obtained over 20 iterations.

The top-ranking 18 VIPs were sufficient to produce valid models for both the apoptosis and cytokine secretion responses, whereas the proliferation response required inclusion of the top 20 VIPs. Figure 4D shows the node-specified distribution of the core VIPs obtained for each response. Here, the number of positive signs against each node indicates the number of VIPs, derived from that node, that constitute this core group for each response. It is evident from this figure that nodal signals were grossly under-represented in each of the three cases. Thus—in the entire data set—only MEK-1/2 (for apoptosis and proliferation), Syk (for apoptosis), and Raf-1 (for IL-2 secretion) were represented by all the three extracted parameters (i.e. VIPs). The remaining nodes were only represented by either one or, in fewer cases, two VIPs. Statistically, the nodal signals constituted less than 20% of the core group of VIPs across all the three responses, whereas 85% (18 of 21) of the nodes examined were represented in this list by at least one VIP (Figure 4D).

We also undertook an additional exercise wherein we assumed perfect specificity in the model. In other words, we trained our model to conditions wherein only perturbation of the target protein was considered, while phosphorylation at all the other molecules was considered to be unchanged from that obtained in mock siRNA-treated cells. Such an analysis, however, did not yield a valid model for any of the cellular responses studied. In all cases, the values of Q2 obtained ranged from 0.1 to 0.35 (Supplementary Figure S11), which was indicative of poor predictive ability. These results are consistent with earlier observations (Kemp et al, 2007) and support that signal processing requires information to be derived from multiple nodes distributed across diverse signaling pathways.

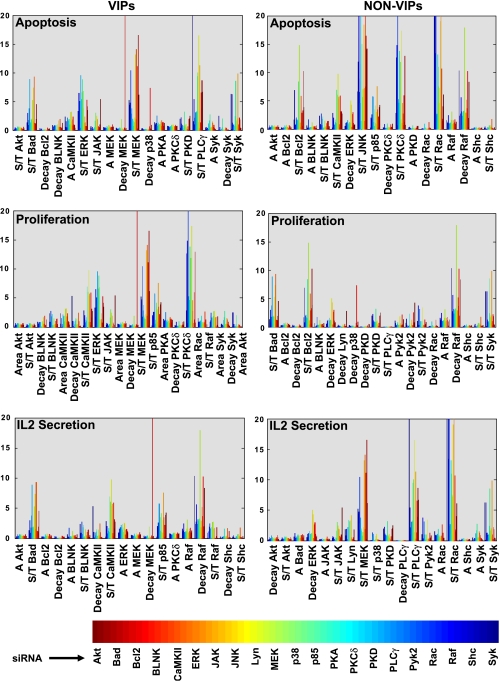
Finally, we also recognized the need to verify that our PLS models were indeed response specific, and that the multiple regression analysis involved did not select VIPs simply on the basis of their inherent instability. For this exercise, we compared the relative stability of both VIPs and non-VIPs for each of the three cellular responses. Relative stability was calculated as the fold-change in the parameter value from that obtained in mock siRNA-transfected cells, under each perturbation condition, and the results are shown in Figure 5. It is obvious here that VIPs could not be distinguished from non-VIPs simply on the basis of their sensitivity to perturbations. This was equally true for all the cell responses studied (Figure 5), thereby highlighting the specificity of the PLS models described here.

Figure 5.

Specificity versus sensitivity of signaling parameters toward cellular response. The siRNA-induced variations in values of the individual signaling parameters are depicted here. Values are shown in terms of their fold variation over that obtained for the corresponding parameter in cells treated with mock siRNA. These results are depicted in the form of a comparison between specific top-scoring VIPs from the minimal model (left panel) and non-VIPs (right panel). In these graphs, the signaling parameters are indicated on the X-axis, and the 21-perturbation conditions are described by the reference color bar.

The collective results in Figures 4 and 5 further confirm that stimulus-dependent cellular responses are not specified by the combination of nodes participating in a discrete fashion. Rather, they are more likely dictated through the combinations of VIPs that are expressed across the signaling network.

Prediction of cellular apoptotic responses to pharmacological inhibitors

To further substantiate both the PLS model and the interpretations that were derived from it, we employed an alternate approach for perturbing the signaling network. Thus, A20 cells were treated with a range of pharmacological inhibitors, at concentrations of five-fold above their IC₅₀ values, prior to stimulation with anti-IgG. The inhibitors used were wortmannin (inhibitor of PI-3-kinase), PD98059 (inhibitor of MEK-1/2), SB203580 (inhibitor of p38), KN62 (inhibitor of CaMKII/IV), rottlerin (inhibitor of PKCδ), H89 (inhibitor of PKA), and U73122 (inhibitor of PLCγ). The phosphorylation profiles for the various signaling intermediates and the subsequent values for the three signaling parameters were then determined for each instance as described in Figure 1B (Supplementary Table S12). In parallel, the effect of these inhibitors on the anti-IgG-mediated protection from Fas-induced apoptosis of the cells was also determined. The corresponding data sets were then taken for incorporation into a PLS model. For this exercise, however, the X variables were restricted to only those apoptosis-specific VIPs that were listed in the minimal model described in Figure 4D. As is evident from the results in Figure 6A, an excellent correlation could be obtained between the experimentally observed and the predicted responses. Thus, at one level, these latter results provide additional experimental support for our earlier inference that individual, node-derived signaling parameters play distinct roles during signal processing. Importantly, the accuracy of the model in Figure 6A also points to the potential utility of the approach described. Thus, at least in the case of a lymphoma cell line, it appears possible to predict the outcome of treatment with a range of pharmacological agents.

Figure 6.

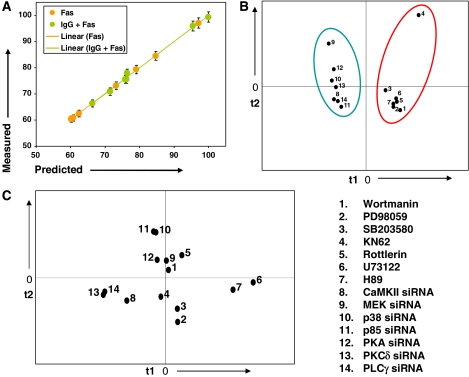
Pharmacological inhibitors as treatment conditions for measuring signaling parameters. (A) Observed versus predicted scatter plot for anti-IgG-dependent apoptosis response following treatment with the various pharmacological inhibitors described in the text. Values for only those VIPs extracted by the minimal model described in Figure 4D were taken to predict cellular responses here. (B) Projection of the various inhibitors, and the corresponding siRNAs, treatment conditions as separate perturbation conditions on a plane consisting of the top two principle components t1 and t2. The latter were obtained in a separate principle component analysis. The scores plot (treatment conditions) on the t1 versus t2 axes shows distinct clustering of inhibitor- and siRNA-treatment conditions, respectively. (C) Projection of the corresponding apoptotic responses following treatment with either siRNA or pharmacological inhibitors (as described for B) on a similar plot. The numbers used are identical to that described in (B).

The experiments performed in Figure 6A also gave us an opportunity to compare how distinct modes of perturbation impact on the behavior of the signaling network. Whereas the strategy employed here involved inhibition of activation of select target proteins, the approach described in Figures 1, 2, 3, 4 and 5 exploited the technique of siRNA to selectively deplete the target protein from the signaling network. The question of how genetic versus pharmacological modulation of the target protein compares in terms of influencing the cellular response is a long-standing one with several important implications (Knight and Shokat, 2007). We, therefore, performed a principal component analysis on the network measurements obtained either with the seven inhibitors employed in Figure 6A or from experiments where the protein targets of these inhibitors were selectively depleted by siRNA (Figure 1B). The objective here was to examine how fundamentally different perturbations, of the same set of target molecules, are projected in the principal component space.

Figure 6B shows the results of such an analysis in the form of a scatter plot between the top two principal component dimensions (t1 and t2). This plot shows how individual perturbations are situated or clustered with respect to each other in the data. The distinction between siRNA-mediated versus pharmacological inhibition of the target proteins is clearly evident here. Thus, each of these perturbation modalities yielded distinct clusters, indicating that the mode of inhibition of activity at a node leads to distinctive effects on the overall behavior of the signaling network. Consistent with this interpretation, the cellular responses to these two distinct modes of perturbation also did not co-cluster in a scatter plot between the two principal component axes (PC1 versus PC2; Figure 6C).

Defining an apoptosis response axis based on the signaling parameters

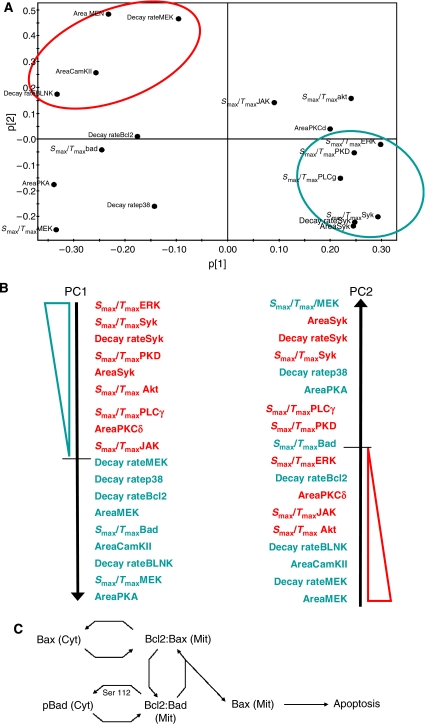
Having achieved a minimal VIP-based model that could capture the molecular signatures characterizing distinct cell-fate decisions (Figure 4D), we next focused on determining whether the signaling parameters could be grouped to define a response-specific axis. Here again we restricted our examination, as a representative example, to the apoptosis response. Thus, the distribution of the apoptosis-specific signaling parameters between the first two principle components (PC1 and PC2) was analyzed (Figure 7A). This led to the identification of two separate clusters, present diagonally in the PC1 versus PC2 plot, which represented high-value parameters in either of these components (shown in circles in Figure 7A). Although additional clusters were also present, they overlapped significantly between both components and, therefore, were not considered suitable for classification. The principal component-biased clusters were then arranged in the descending order of their projections onto the respective components as shown in Figure 7B. A subsequent analysis of the correlation of each of these parameters with the apoptosis response revealed an intriguing distinction between these two principle component axes. On PC1, the signaling parameters clustered into two distinct groups depending on whether they displayed a positive (shown in red) or negative (shown in blue) correlation with the apoptosis response (Figure 7B). No such distinction was evident for the alignment on PC2. Thus, a response axis for apoptosis could be defined on the basis of the projections of the signaling parameters, extracted from the minimal PLS model, onto PC1. Importantly, the ability of this model to identify such a response-specific axis, from the multidimensional space of variables, testifies to the robustness of our model.

Figure 7.

A response axis based on the signaling parameters for apoptosis. (A) Distribution of signaling parameters onto principle components 1 and 2 for the apoptotic response. The shaded areas show the two clusters of signaling parameters identified. (B) Arrangement of signaling parameters, in a descending order, on the two principle components, respectively. Parameters shown in red were positively correlated with apoptosis, while those in blue were negatively correlated with apoptosis. (C) Schematic representation of a cellular apoptotic response module consisting of three nodes, Bad, Bcl2 and Bax. Bax, a known pro-apoptotic protein is mainly cytoplasmic (Cyt) before being recruited to mitochondria (Mit), a process dependent on Ser70 phosphorylation of Bcl2. In mitochondria, Bad can displace Bax from the Bcl2-Bax complex, thereby promoting apoptosis through the oligomerization of Bax. Phosphorylation of Bad at either Ser112 or Ser136, however, leads to inhibition of this activity. As a result, Bad translocates to the cytoplasm where it is then sequestered by the chaperone 14-3-3, leading to inhibition/reduction of apoptosis.

The principal component-based response axis shown in Figure 7B revealed some interesting departures from the canonical view of the apoptosis response. An example of this was the co-segregation of both Bad and Bcl2 in the cluster that displayed a negative correlation. While this is in keeping with the known anti-apoptotic role of Bcl2 it is, however, inconsistent with the fact that Bad is generally considered to be pro-apoptotic. In our experiments, we had monitored for the phosphorylation of Bad at Ser112, a modification known to inhibit formation of complexes between Bcl2 and Bad (Zha et al, 1996). In the case of Bcl2, it was phosphorylation at Ser70 that was examined. This event has been shown to induce the translocation of Bax from cytosol to mitochondria, thereby promoting apoptosis (Ishikawa et al, 2003). As shown in Figure 7C, these three molecules, together with the related members, constitute the terminal modules for regulating apoptosis.

Notably, the signaling parameters that co-segregated along PC1 were the decay rate of Bcl2 phosphorylation at Ser70, and the activation rate of Bad phosphorylation at Ser112. An increase in the dephosphorylation rate of Bcl2 would thus serve to minimize the levels of mitochondria-localized Bax, resulting in a negative effect on the extent of apoptosis. In this connection, phosphorylation of Bcl2 at Ser residues has been shown to inactivate its anti-apoptotic properties in lymphoid cells (Haldar et al, 1995). In parallel with this observation, an increase in the rate of phosphorylation of Bad at Ser112 would relate to the rapidity with which it loses its ability to neutralize the death-repressor activity of Bcl2 (Figure 7C). Thus, one can readily visualize a regulatory loop wherein the activation rate of Bad phosphorylation at Ser112 and the decay rate of Bcl2 phosphorylation at Ser70 act in a cooperative manner to modulate the apoptotic response. We recognize, however, that this proposed scheme represents a gross over-simplification and ignores the effects of many other important players and regulatory features in this process. Nonetheless, it serves to provide a glimpse into how signaling parameters can potentially function as relatively distinct entities, and thereby influence signal processing.

Discussion

In this work, we studied BCR-dependent signaling by examining the temporal modulation in phosphorylation profiles of a select subset of signaling intermediates. While it is generally accepted that cell-fate decisions are imprinted in the form of regulatory motifs within the molecular constituents of the signaling network (Kashtan and Alon, 2005; Ma'ayan et al, 2005; Prill et al, 2005), our goal was to probe the related issue of how these features are variably interpreted to yield distinct cellular phenotypic responses. For this exercise, we adopted an approach wherein we selectively perturbed the BCR signaling network, and then examined for the consequences on both network behavior and the cellular output. We reasoned that correlations between these two outcomes could provide us with insights into how signal processing is achieved, as well as the basis for its inherent plasticity.

An initial examination of the results revealed that the siRNA-mediated depletion of the cellular concentrations of any given node led to a substantial alteration in the BCR-dependent phosphorylation profiles of at least several of the other nodes of the signaling network. Importantly, the nature of these effects were varied, with parameters such as the rate and amplitude of phosphorylation, and the stability of the phosphorylated state being differentially influenced at each of the susceptible nodes. To therefore capture these effects more precisely, we condensed each of the resulting phosphorylation profiles into three signaling parameters that collectively defined both its quantitative and kinetic features. This characterization provided a unique description of phosphorylation at each node, under each of the various conditions tested. An empirical examination of how these parameters were influenced by the diverse, siRNA-mediated, perturbations supported that the individual nodes could be characterized as being either resistant, sensitive, or flexible (i.e. resistant to some perturbations but sensitive to others) to such effects. We propose that this graded sensitivity displayed by the various nodes represents an important feature that contributes to the robustness of the signaling network. A network wherein all of its constituent nodes display a similar susceptibility quotient can be expected to be brittle, lacking the ability to adapt in response to environmental perturbations.

Significantly, we also found that the sensitivity of each node to perturbations represented a multivariate property, being defined by the relative extent of contributions from the three constituent signaling parameters. Thus, at one level individual nodes were distinguished from each other by the differing contributions from each of the signaling parameters to the overall sensitivity. This aspect was further accentuated by the fact that individual signaling parameters also displayed a wide range of sensitivity profiles that varied from one node to another. As a result of these twin features, the response of the signaling network to each of the various perturbations was expressed through combinatorial variations in the pattern of the signaling parameters, at each of the component nodes. In other words, the emergent features of the signaling network appear to be defined by modulation in the values of the signaling parameters that are contributed by each node.

That the combinatorial manipulation of node-derived signaling parameters may be relevant for shaping stimulus-induced cell response decision was suggested by our subsequently derived mathematical models probing the relationship between the signaling response and defined cellular outputs. Data-driven modeling represents an important approach for deriving mechanistic insights, with quantitative PLS modeling providing a viable strategy for evaluating hypothesis on causal relationships (Janes and Yaffe, 2006). The strength of a PLS analysis lies in its ability to best describe how the independent and dependent variable groups covary, thus identifying and quantitatively supporting the proposed relationships used to construct the model.

We were able to generate minimum redundancy models successfully for all the three cellular responses, and these models survived stringent validation by accurately predicting the dependent variables from an untrained data set. An important aspect of these models, however, was that they could be generated only by treating the individual signaling parameters as functionally independent entities, and not by grouping them in a node-specific manner. As a result, the signaling features specifying the three cell responses could be described in terms of largely overlapping sets of VIPs, where the distinctions with regard to cell fate were best captured by distinctions in the relative weights of contributions from these VIPs. This aspect could be further highlighted by our subsequent extraction, as an example, of a response-specific axis for cellular apoptosis. Thus, our PLS models provide additional support to the earlier inference that the emergent properties of the signaling network derive from modulations in the values of the signaling parameters that are contributed by each node. Further, they also reveal that response-specific signal processing involves the quantitative combination of these signaling parameters derived from the participating nodes.

It is important to emphasize that the signaling parameters described here are, in reality, multivariate properties that represent the end result of several biochemical reactions and/or interactions. Thus, variations in the kinase–phosphatase equilibrium (Hunter, 2000; Ostman and Bohmer, 2001), the kinetics of assembly and disassembly of multimolecular complexes nucleated on scaffolding molecules (Pawson and Scott, 1997; Bauman and Scott, 2002; Morrison and Davis, 2003), and the various feedback loops that exist in the signaling network (Bhalla and Iyengar, 1999; Bhalla et al, 2002; Angeli et al, 2004), all exert distinct effects on the individual signaling parameters at a given node. In other words, each of the signaling parameters measured, in fact, encapsulate distinct features of the overall network dynamics. Given this intricate level of the circuitry, then it becomes difficult to envisage a selective and discrete function for individual nodes in defining cell-fate decisions. Rather, as suggested here, an information-processing mechanism that involves specific nodal features seems more likely.

Our experiments employing pharmacological inhibitors yielded additional support for the validity of our PLS models, and the resulting inference that it is the properties of the VIPs rather than that of discrete nodes that best capture decisions related to the cellular response. The technique of siRNA depletes the concentration of the target protein, thereby bringing about a quantitative alteration in the composition of the signaling network. Pharmacological inhibitors, on the other hand, suppress the activity of the target enzyme without influencing either its concentration or the constitutive inter-molecular interactions that it engages in. Although both approaches may potentially be associated with some degree of nonspecificity these, however, are expected to be non-overlapping. Whereas siRNA may sometimes lead to off-target silencing effects, pharmacological inhibitors—many of which are competitive inhibitors—can also inhibit other enzymes with structurally homologous catalytic sites. Nonetheless, in spite of their intrinsic differences, both approaches yielded network-level perturbations. That is, in addition to the primary target, phosphorylation at several other nodes was also significantly affected.

The similar findings with both approaches also allowed us further probe the central question of what is the extent of information that has to be taken into account when predicting a phenotypic outcome of a target-specific perturbation. The relatively wide coverage of the constituent nodes of the signaling network that was obtained here permitted us to unambiguously resolve this issue. In either instance, we were unable to obtain satisfactory models by only incorporating the specific, on-target effects. Rather, models with high predictive accuracy could only be obtained after the secondary effects experienced by the other nodes of the network were taken into account. While it is possible that our data would also incorporate nonspecific effects, these are expected to make only minor contributions and, more importantly, are unlikely to show any overlap between the two distinct perturbation modalities employed. Consequently, both of these approaches yielded to the common insight that the prediction of a cellular response cannot be made solely on the basis of how a given perturbation influences the target protein alone. Rather, measurements of how this perturbation propagates to the other nodes of the network also need to be taken into consideration.

Thus, in summary, our present study provides an intriguing perspective on the functioning of the signaling network. Specification of distinct cell-fate decisions is generally thought to involve variations in the relative participation of individual signaling pathways. Our present results, however, reveal that it is the signaling parameters, derived from each node, that in fact constitute the functional entities involved in signal processing. The independent functioning of these parameters ensures that the signal output can be modulated in a combinatorial manner in response to different perturbations. Earlier studies have identified response-specific signaling axes to be defined by a molecular basis set (Janes et al, 2005). It was subsequently proposed that such signaling axes represent unique points of convergence in the network architecture, where common effectors are employed to generate diverse outcomes (Miller-Jensen et al, 2007). It will be interesting to determine whether the signaling parameters described by us can also be implicated in the generation of diversified outputs from such effectors.

Lymphocytes are continually faced with the need to make decisions regarding cell fate depending on the environmental milieu and their maturational state (Santana and Esquivel-Guadarrama, 2006; McHeyzer-Williams and McHeyzer-Williams, 2007). Importantly, a significant proportion of these outcomes, which range from apoptosis to cell proliferation and differentiation, are mediated through engagement of the cell surface receptor for antigen. Thus, for example, whereas antigen binding to the BCR on an immature B cell induces apoptosis, binding of the same antigen to the BCR on a mature B cell leads to activation of the cell (Thomas et al, 2006). Further, we have previously shown that parameters such as affinity and association rate constants of antigen binding exert a significant impact on the subsequent fate of the cell (Manivel et al, 2000; Chaturvedi et al, 2002). A confounding question, therefore, has been one of how such a diverse range of cell-fate decisions are mediated by the BCR. Here, our present finding that the nodes of the signaling network can collectively exhibit diverse, context-unique patterns of VIP signatures may provide an insight into how this is achieved.

Materials and methods

Stimulation of cells and detection of phosphoproteins

A20 cells (1 × 10⁷/ml) were stimulated with the F(ab)₂ fragment of goat anti-mouse IgG at a final concentration of 25 μg/ml in RPMI for a period of up to 30 min (Singh et al, 2005). At appropriate times, aliquots of cells were collected, centrifuged, and the cell pellets stored in liquid nitrogen. Just prior to electrophoresis, cells were lysed in lysis buffer (20 mM HEPES, 10 mM NaCl, 1.5 nM MgCl₂, 0.2 mM EDTA, 0.5% Triton X-100, 0.5 mM DTT, 1 mM sodium orthovanadate, 1 mM NaF, and a cocktail of protease inhibitors) followed by removal of the nuclear material and other debris through centrifugation. The detergent-soluble proteins were then resolved by SDS–PAGE. Specific proteins and phosphoproteins (all phospho-specific antibodies, as described in Supplementary Table S6, were from Cell Signaling Technologies) were detected by western blot using appropriate antibodies. Autoradiographs thus obtained were digitized on a molecular dynamics-computing densitometer using the ImageQuant software (GE Healthcare) at a stringent resolution of 50 pixels and 12 bits. Minimum intensity surrounding the bands on the film was taken as its background and subtracted to give the true intensity. These values were then imported for normalization into our algorithm designed on a MATLAB platform (described in detail in Supplementary Figure S1) and the results are presented in Supplementary Table S13.

siRNA-mediated depletion of signaling intermediates

All the specific siRNAs were procured from Santa Cruz Biotechnology Inc. HiPerfect (Qiagen) was used for transfection of cells with the siRNAs (at a final concentration of 100 nM) strictly following the protocol supplied by the manufacturer. In initial standardization experiments, the silencing obtained was between 70 and 95% at 48 h after transfection, as detected by western blotting (see Supplementary Figure S2). The list of catalog numbers and source of siRNAs and antibodies used to detect the knockdown efficiency is provided in Supplementary Table S14. For all of the experiments described here, a parallel control set was always included wherein cells were treated with siRNA specific for GFP (mock siRNA-treatment).

Illumina bead array analyses

Cells were stimulated with anti-IgG for 30 min after which they were washed and cultured in the absence of IgG for an additional period of 30 min. Total cellular RNA (200 ng), isolated from each group, was used as the starting material and samples were prepared in accordance with the instructions provided by the manufacturer (Illumina, San Diego, CA). The samples were hybridized by the Finnish DNA Microarray Centre to Illumina Sentrix Mouse-6 Expression BeadChip arrays containing over 47 000 probes covering approximately 30 000 mouse genes. The data were quantile normalized (Bolstad et al, 2003) and log-transformed using R package limma (Wettenhall and Smyth, 2004), a part of the Bioconductor project (http://www.bioconductor.org). Microsoft Access and Excel for Windows softwares were used for further data processing. Expression of a gene was considered to be upregulated if the signal log ratio between the reference and the target samples was higher than one (>2-fold increase) and the detection P-value of the target sample was >0.95. Similarly, a gene was defined as downregulated if the signal log ratio was less than minus one (>2-fold decrease) and the detection P-value of the reference sample was >0.95. Genes that presented a consistent change in all of the three separate biological repeats were considered as differentially expressed (Supplementary Table S15). Gene annotations were obtained from Illumina. The microarray data were also analyzed through the use of Ingenuity Pathways Analysis (Ingenuity^® Systems; www.ingenuity.com) (Supplementary Figures S8 and S9). Results of the microarray experiments are available in the ArrayExpress database (accession no. E-TABM-360).

Measurement of IL-2 secretion

A20 cells (0.2 × 10⁶) were plated in a 96-well plate and stimulated with anti-IgG (25 μg/ml). IL-2 secreted into the culture supernatant was then measured at 12, 18, and 24 h later by ELISA (eBioscience) (data are presented in Supplementary Table S16).

Cell proliferation

Cells were labeled with carboxy fluoroscein succinimidyl ester (CFSE) for 10 min at a final concentration of 5 μM, washed twice with RPMI and plated in the wells of a 96-well plate and stimulated with anti-IgG (25 μg/ml). At time points of 12, 24, and 48 h later, the cells were harvested, analyzed by flow cytometry, and relative proliferative response was measured as a function of decrease in CFSE fluorescence (Supplementary Table S16).

Anti-IgG-mediated reversal of Fas-induced apoptosis

A20 cells were treated with either anti-Fas antibodies (100 ng/ml) alone, anti-IgG (25 μg/ml) alone, or a combination of both for a period of 6 h. At the end of this period, PI staining, followed by flow cytometry determined the proportion of apoptotic cells (Supplementary Table S16).

PLS analysis

The PLS model was constructed by including all the signaling variables X and the dependant variables Y (responses) using the software suite from UMETRICS, SIMCA-P 11.5. PLS finds the linear (or polynomial) relationship between Y and X (predictor variables) expressed as

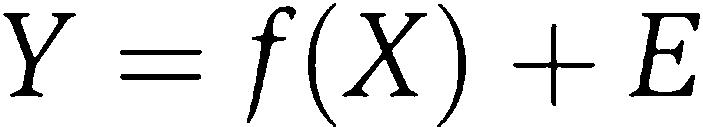PLS is easily understood geometrically, where the matrices X and Y are seen as N points in two different spaces, the X space with K axes and the Y space with M axes, K and M being the number of columns in X and Y. PLS modeling consists of simultaneous projections of both the X and Y spaces on low-dimensional hyper planes. PLS components are computed by iterative regression to capture the successive signal–response dimensions from the data set. VIP, also known as variable importance in the projection, is the influence of predictor variable X on the response Y and was calculated using the same software.

Supplementary Material

Supplementary Figures and Tables

Supplementary Table S12

Supplementary Table S13

Competing Interests Statement The authors declare that they have no competing financial interests.