Network Inference, Analysis, and Modeling in Systems Biology

Cells use signaling and regulatory pathways connecting numerous constituents, such as DNA, RNA, proteins, and small molecules, to coordinate multiple functions, allowing them to adapt to changing environments. High-throughput experimental methods enable the measurement of expression levels for thousands of genes and the determination of thousands of protein–protein or protein–DNA interactions. It is increasingly recognized that theoretical methods, such as statistical inference, graph analysis, and dynamic modeling, are needed to make sense of this abundance of information. This perspective argues that theoretical methods and models are most useful if they lead to novel biological predictions and reviews biological predictions arising from three systems biology topics: graph inference (i.e., reconstructing the network of interactions among a set of biological entities), graph analysis (i.e., mining the information content of the network), and dynamic network modeling (i.e., connecting the interaction network to the dynamic behavior of the system). The methods and principles discussed in this perspective are generally applicable, and the examples were selected from plant biology wherever possible.

INTRODUCTION

To understand the function of a cell or of higher units of biological organization, often it is beneficial to conceptualize them as systems of interacting elements. For such a systems-level description (which represents the main goal of systems biology), one needs to know (1) the identity of the components that constitute the biological system; (2) the dynamic behavior of these components (i.e., how their abundance or activity changes over time in various conditions); and (3) the interactions among these components (Kitano, 2002). Ultimately, this information can be combined into a model that is not only consistent with current knowledge but provides new insights and predictions, such as the behavior of the system in conditions that were previously unexplored.

The origins of systems biology can be traced back to systems theory, a line of inquiry based on the assumptions that all phenomena can be viewed as a web of relationships among elements, and all systems can be handled by a common set of methods (von Bertalanffy, 1968; Weinberg, 1975; Bogdanov, 1980; Heinrich and Schuster, 1996; Francois, 1999; Voit, 2000). Early attempts at systems-level understanding of biology suffered from inadequate data on which to base the theories and models; however, the recent advent of high-throughput technologies brought an abundance of data on system elements and interactions, leading to a revival of systems biology.

In some cases, the organization of the network of interactions underlying a biological system is straightforward (e.g., a linear chain of interactions), while in other cases a more formal representation, offered by mathematical graph theory (Bollobás, 1979), is required. The simplest possible graph representation reduces the system's elements to graph nodes (also called vertices) and reduces their pairwise relationships to edges (also called links) connecting pairs of nodes (Figure 1). The nodes of (sub)cellular systems may be genes or mRNA, protein, or other molecules. Directed edges (also called arcs) have a specified source (starting) node and target (end) node and are most suited to represent chemical transformations and regulatory relationships. Nondirected edges are most appropriate for mutual interactions, such as protein–protein binding or for relationships whose source and target are not yet distinguishable. Depending on the availability of information, edges are characterized by signs (positive for activation and negative for inhibition) or weights quantifying confidence levels, strengths, or reaction speeds. As the abundance of cellular constituents spans a large range and varies in time, nodes also need to be characterized by quantitative information describing the concentration of the corresponding molecules or the copy number of the corresponding mRNAs; this information is usually denoted as node state (or status).

Figure 1.

Hypothetical Network Illustrating Network Analysis and Dynamic Modeling Terminology.

(A) The interaction graph formed by nodes A to F consists of directed edges signifying positive regulation (denoted by terminal arrows), such as AB and ED, directed edges signifying negative regulation (denoted by terminal filled circles), such as FE and autoinhibitory (decay) edges (denoted by terminal filled circles) at nodes B to F. The graph contains one feed-forward loop (ABC; both A and B feed into C) and one negative feedback loop, EDF, which also forms the graph's strongly connected subgraph. The in-cluster of this subgraph contains the nodes A and B, while its out-cluster is the node C.

(B) The node in-degrees (k_in) that quantify the number of edges that end in a given node range between 0 (for node A) and 4 (for node C). The node out-degrees (k_out), quantifying the number of edges that start at a given node, range between 1 (for C) and 3 (for B and E). The graph distance (d) between two nodes is defined as the number of edges in the shortest path between them. For example, the distance between nodes E and D is one, the distance between nodes D and E is two (along the DFE path), and the distance between nodes C and A is infinite because no path starting from C and ending in A exists. The betweenness centrality (b) of a node quantifies the number of shortest paths in which the node is an intermediary (not beginning or end) node. For example, the betweenness centrality of node A is zero because it is not contained in any shortest paths that do not start or end in A, and the betweenness centrality of node B is three because it is an intermediary in the ABD, ABDF, and ABDFE shortest paths. The in-(out-)degree distribution, [P(k_in) and P(k_out)] quantifies the fraction of nodes with in-degree k_in (out-degree k_out). For example, one node (C) has an out-degree of one; two nodes (E and F) have an out-degree of two and three nodes (A, B, and D) have an out-degree of three; the corresponding fractions are obtained by dividing by the total number of nodes (six). The distance distribution P(d) denotes the fraction of node pairs having the distance d. The betweenness centrality distribution P(b) quantifies the fraction of nodes with betweenness centrality b.

(C) Hypothetical time courses for the state of each node in the network (denoted by S_A to S_E). The node states in this example can take any real value and vary continuously in time. The initial state (at t = 0) has state 1 for node A and 0 for every other node. Each node state approaches a steady state (a state that does not change in time), indicated in the last column (at t = ∞) of the time course. Network inference methods presented in section 2 use expression knowledge (such as the logarithm of relative expression with respect to a control state) such as this state time course to infer regulatory connections between nodes (i.e., the interaction network shown in [A]). State time courses like this also arise as outputs of continuous models.

(D) The transfer functions of a hypothetical continuous deterministic model based on the interaction network (A) that leads to the time course under (C). Each transfer function indicates the time derivative (change in time) of the state of a node (denoted by a superscript ′ on the node state) as a function of the states of the nodes that are sources of edges that end in the node, including the node itself if it has an autoregulatory edge. The transfer functions in this hypothetical example are linear combinations of node states, with a positive sign for activating edges and negative sign for inhibitory edges, and all coefficients (parameters) are equal to unity. In general, transfer functions are nonlinear and have parameters spanning a wide range.

(E) Hypothetical discrete time courses for each node in the network, where the node states can only take one of two values: 0 (off) and 1 (on). Discrete states such as this are obtained using a suitable threshold and classifying expression values as below threshold (0) and above threshold (1). The initial state (at t = 0) has state 1 for node A and state 0 for all other nodes. As in (C), each node reaches a steady state, indicated in the last column (at t = ∞) of the time course. Binary time courses such as this form the basis of Boolean network inference methods presented in section 2. State time courses like this also arise as outputs of Boolean models.

(F) The transfer functions of a hypothetical Boolean model based on the interaction network (A) that leads to the time course in (E). Each transfer function indicates the state of the node at the next time instance (t + 1), denoted by a superscript asterisk on the node state, as a logical (Boolean) combination of the current (time t) states of the nodes that are sources of edges that end in the node. In this case, the autoinhibitory edges are not incorporated explicitly, assuming that positive regulation, when active, can overcome autoinhibition. Decay (switching off) after the positive regulators turn off is taken into account implicitly by not including the current state of the regulated node in its transfer function. It is assumed that the state of the node A does not change in time. The inhibitory edge FE is taken into account as a “not S_F” clause in the transfer function of node E. More than one activating edge incident on the same node in general can be combined by either an “or” or “and” relationship, depending on whether they are closer to being independent (in case of “or”) or conditionally dependent or synergistic (in case of “and”). In this example, the edges AC and BC are assumed to be synergistic and independent of EC, and the edges BD and ED are assumed to be independent of each other.

This essay focuses on the biological predictions arising from three related topics of importance in systems biology: graph inference, graph analysis, and dynamic network modeling. Graph inference refers to the problem in which the information on the identity and the state of a system's elements is used to infer interactions or functional relationships among these elements and to construct the interaction graph underlying the system. Graph analysis means the use of graph theory to analyze a known (complete or incomplete) interaction graph and to extract new biological insights and predictions from the results. Dynamic network modeling aims to describe how known interactions among defined elements determine the time course of the state of the elements, and of the whole system, under different conditions. A dynamic model that correctly captures experimentally observed normal behavior allows researchers to track the changes in the system's behavior due to perturbations. These three lines of inquiry are often combined in the literature since they provide three facets of the same objective: to understand, predict, and if possible control (tune toward a desired feature) the dynamic behavior of biological interacting systems. The possible predictions obtained from these methods range from prediction of new interactions (from graph inference and analysis), identification of key components and pathways (from graph analysis and dynamic network modeling), determination of key parameters (from dynamic modeling), and distillation of key features, such as interaction or functional motifs (from all three methods combined).

INFERENCE OF INTERACTION NETWORKS FROM EXPRESSION INFORMATION

The most prevalent use of graph inference is using gene/protein expression information to predict network structure (i.e., to predict which gene/protein influences which other genes/proteins through transcriptional, posttranscriptional, translational, or posttranslational regulation). A predicted regulatory relationship among two genes can be verified by experimental testing of the interactions and regulatory relationships among the two genes/proteins.

Genes with statistically similar (highly correlated) expression profiles in time or across several experimental conditions can be grouped using clustering algorithms (Wen et al., 1998; Tavazoie et al., 1999). Clustering tools such as the Arabidopsis coexpression tool, based on microarray data from the Nottingham Arabidopsis Stock Centre (Craigon et al., 2004), allow users to quantify gene coexpression across selected experiments or the complete data set (Jen et al., 2006). These methods give insight into groups of genes that respond in a similar manner to varying conditions and that might therefore be coregulated (Qian et al., 2001); however, that two nodes belong to the same group does not imply a causal relationship among them. The ability to extract meaning from clustering depends on the user's prior biological understanding of the objects that are organized. Most applications derive biological insight through “guilt by association;” that is, they predict the function of unknown gene products by their association with recognized clusters (Schuldiner et al., 2005; Bjorklund et al., 2006).

Data analysis methods, such as principal component analysis and the partial least-squares method, aim to highlight the global patterns in the expression of a large number of genes/proteins by condensing the multivariate data into just two or three composite variables that capture the maximal covariation between all the individual patterns. The partial least-squares method is also able to test a proposed causal relationship by splitting variables into independent variables and dependent variables, simultaneously identifying the principal components of the dependent and independent block and relating them by a linear relationship (Janes and Yaffe, 2006). This method was used to link the level of 19 proteins involved in apoptotic signaling in human colon adenocarcinoma cells to four quantitative measures of apoptosis, leading to the prediction of cell death responses to molecular perturbations and of the roles of key signaling intermediaries (Janes et al., 2005). A study combining principal component analysis with a number of machine learning algorithms applied to a comprehensive Arabidopsis thaliana gene expression data set identified 50 previously unannotated genes that are potentially involved in plant response to abiotic stress (Lan et al., 2007). Preliminary experimental validation of the predicted function of one of these genes was presented by Lan et al. (2007).

Bayesian methods aim to find a directed, acyclic (i.e., feedback loopless) graph describing the causal dependency relationships among components of a system and a set of local joint probability distributions that statistically convey these relationships (Friedman et al., 2000). The starting edges are established heuristically based on an initial assessment of the experimental data and are refined by an iterative search-and-score algorithm until the causal network and posterior probability distribution best describing the observed state of each node are found (Yu et al., 2004). Bayesian inference was recently used to infer the signaling network responsible for embryonic stem cell fate responses to external cues based on measurements of 28 signaling protein phosphorylation states across 16 different factorial combinations of stimuli. The inferred network predicted novel influences between ERK phosphorylation and differentiation as well as between RAF phosphorylation and differentiated cell proliferation (Woolf et al., 2005).

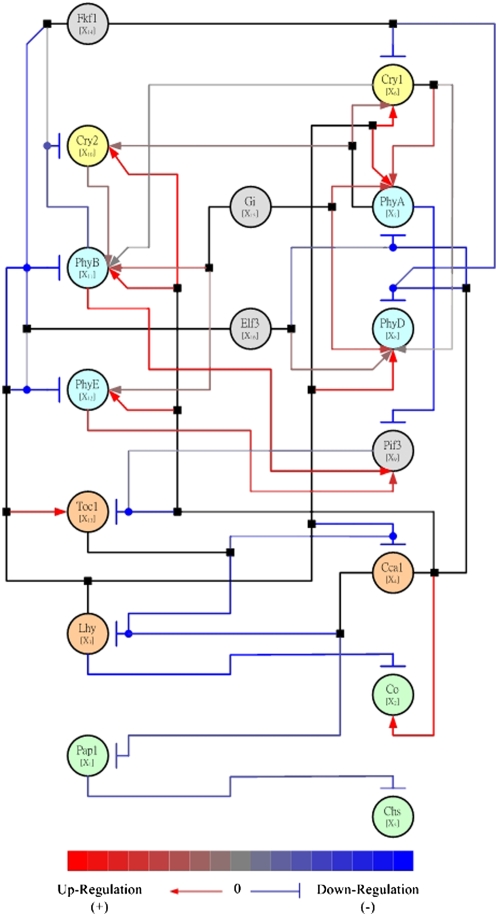
Model-based methods of regulatory network inference from time-course expression data seek to relate the rate of change in the expression level of a given gene with the levels of other genes. Continuous methods postulate a system of differential equations (Chen et al., 1999), while discrete methods assume a logical (Boolean) relationship (Shmulevich et al., 2002). Experimental data on gene expression levels is substituted into the relational equations, and the ensuing system of equations is then solved for the regulatory relationships between two or more components (Figure 1). Because often there are far more biochemical components in the network than there are experimental time points, multiple networks will be possible solutions; these are filtered by making plausible assumptions on the objectives of the underlying system, such as economy of regulation (reflected by having the fewest edges that satisfy the conditions) or maximal biomass production flux (Gupta et al., 2005). A recent plant biology application of this method used microarray data to infer circadian regulatory pathways in Arabidopsis. The resulting network (Figure 2) was supported by agreement with known regulatory relationships between biological clock components and photoperiodic genes and was used to predict novel putative relationships between cryptochrome and phytochrome genes (Chang et al., 2005).

Figure 2.

Illustration of Network Inference: The Predicted Pathway of the Circadian Regulatory System of Arabidopsis According to Chang et al. (2005).

The network nodes (ovals) represent genes and are differentiated by color into cryptochrome (yellow), phytochrome (light blue), clock genes (orange), light-dependent downstream genes (light green), and other relevant genes (gray). The edges (lines) represent inferred causal relationships in a spectrum between activation (red) and repression (blue). Edges corresponding to activation are additionally marked by terminating arrows, and inhibitory edges are marked by terminating blunt segments. Combinatorial regulation is indicated by edge junctions shown as filled squares or circles. A filled square attached to a line indicates where an edge starting from a regulatory node bifurcates to affect several downstream nodes. A filled circle attached to a line indicates the case when several upstream nodes regulate the same target node. Figure reproduced from Chang et al. (2005).

Metabolic pathway reconstruction from known reaction stoichiometric information is usually performed by constraint-based deterministic methods, such as flux balance analysis (Reed and Palsson, 2003) or S-systems, power-law approximations of enzyme-catalyzed reactions (Irvine and Savageau, 1990). For example, a constraint-based optimization method allowed identification of changes in an Escherichia coli genome-scale metabolic model that were needed to minimize the discrepancy between model predictions of optimal flux distributions and experimentally measured flux data (Herrgard et al., 2006).

Several types of experimental results are best interpreted as indirect causal evidence that indicates the involvement of a protein or molecule in a certain process or pathway. Differential responses to a stimulus in wild-type organisms versus an organism where the respective protein's expression or activity is disrupted is an example of such indirect causal evidence connecting the stimulus, protein, and response. These observations can be represented by two intersecting paths (successions of adjacent edges; see below) in the underlying interaction network: one connecting stimulus to response and the other connecting the protein to response. Graph-based inference algorithms integrate indirect causal relationships and direct interactions to find the most parsimonious network consistent with all available experimental observations (Li et al., 2006; Albert et al., 2007b). This method was used to reconstruct the signal transduction network corresponding to stomatal closure in plants in response to the stress hormone abscisic acid (ABA; Li et al., 2006) and is implemented in the software NET-SYNTHESIS (Albert et al., 2007a).

NETWORK ANALYSIS

Depending on the types of interaction or regulatory relationships incorporated as edges of the biological interaction graph, several distinct network types have been defined. In protein interaction graphs, the nodes are proteins, and two proteins are connected by a nondirected edge if there is strong evidence of their association. The full representation of transcriptional regulatory maps associates two separate node classes with transcription factors and mRNAs, respectively, and has two types of directed edge, which correspond to transcriptional regulation (which can be positive or negative) and translation (Lee et al., 2002). Metabolic networks have been represented in various degrees of detail, two of the simplest being the substrate graph, whose nodes are reactants and whose edges mean co-occurrence in the same chemical reaction, and the reaction graph, whose nodes are reactions and whose edges mean sharing at least one metabolite (Wagner and Fell, 2001). Signal transduction networks involve both protein interactions and biochemical reactions, and their edges are mostly directed, indicating the direction of signal propagation. Finally, composite networks superimpose protein–protein and protein–DNA interactions (Yeger-Lotem et al., 2004), protein–protein interactions, genetic interaction, transcriptional regulation, sequence homology, and expression correlation (Zhang et al., 2005) or metabolic reactions and transcriptional regulation of metabolic genes (Herrgard et al., 2006).

The development of high-throughput interaction assays (e.g., yeast two-hybrid, split ubiquitin, and chromatin immunoprecipitation assays) and of curated databases has led to the generation of large-scale interaction networks for a considerable number of organisms. In plant biology, the first large-scale Arabidopsis interactome (protein interaction network) was recently predicted from the knowledge of interacting Arabidopsis protein orthologs in Saccharomyces cerevisiae, Caenorhabditis elegans, Drosophila melanogaster, and Homo sapiens (Geisler-Lee et al., 2007). As illustrated in this section, graph analysis of the currently available (sub)cellular networks reveals a significant degree of consensus among their organizational features, as well as a few notable differences. Note, however, that there is a considerable level of variation in the number of networks available for each interaction type, in the coverage of these networks, and in the confidence of the interactions included in the network; thus, the predictions arising from network analysis may need updating as more information becomes available.

The organizational features of interaction graphs can be quantified by network measures whose information content ranges from local (e.g., properties of single nodes or edges) to network-wide (e.g., whether all nodes are connected). These two seemingly disparate scales are intimately linked in networks, as global connectivity is realized by a succession of adjacent edges. Thus, as we will see later, sometimes a surprisingly small number of linked events can lead to wide consequences. The most often-used network measures describe the connectivity (reachability) among nodes, the importance (centrality) of individual nodes, and the homogeneity or heterogeneity of the network in terms of a given node property (Figure 1).

A path (sequence of adjacent edges) (Bollobás, 1979) signifies a transformation route from a nutrient to an end product in a metabolic network or a chain of ligand-induced reactions in a signal transduction network. The distance (path length) between any two nodes in a network is defined to be the number of edges in the shortest path connecting those nodes. If the edges of a network are weighted (e.g., with rate constants), then the distance between two nodes will be the sum of edge weights along the path for which this sum is a minimum (Dijkstra, 1959). The average path length of several large cellular networks, including metabolic networks (Jeong et al., 2000; Wagner and Fell, 2001), transcriptional networks (Lee et al., 2002), protein interaction networks (Giot et al., 2003; Yook et al., 2004), and signal transduction networks (Ma'ayan et al., 2005) is less than four. This result predicts that these networks are capable of rapid response to inputs or perturbations. Cellular networks also tend to exhibit path redundancy and the availability of multiple paths between a pair of nodes (Papin and Palsson, 2004; Li et al., 2006). This network feature reflects cellular networks' capacity to employ multiple channels between the same input and output and predicts that these networks will be able to efficiently compensate for perturbations in the preferred pathway.

In many networks, only a fraction of the nodes in the network will be accessible (connected) to any given node. The subset of nodes connected by paths in both forward and reverse directions form the so-called strongly connected cluster. One can also define the in-cluster (nodes that can reach the strongly connected cluster but that cannot be reached from it) and out-cluster (the converse). Nodes of each of these subsets tend to have a shared task; for example, in signal transduction networks, the nodes of the in-cluster tend to be involved in ligand-receptor binding; the nodes of the strongly connected cluster form a central signaling subnetwork; and the nodes of the out-cluster are responsible for the transcription of target genes and for phenotypic changes (Ma'ayan et al., 2005).

All protein interaction networks mapped so far, including the predicted Arabidopsis interactome, have a strongly connected cluster connecting the vast majority of the proteins (Giot et al., 2003; Yook et al., 2004; Geisler-Lee et al., 2007). This finding predicts a capacity for pleiotropy, since perturbations of a single gene or protein can propagate through the network and can have seemingly unrelated or broad effects. By contrast, the currently available maps of transcriptional networks do not have significant strongly connected components, suggesting a unidirectional regulation mode with relatively little transcriptional crosstalk (Balázsi et al., 2005). The currently available metabolic and signal transduction networks are more connected, with 50 to 60% of the nodes forming the largest strongly connected component (Ma and Zeng, 2003; Ma'ayan et al., 2005). This intriguing range of interconnectivity from relatively unidirectional transcriptional regulatory maps to strongly connected protein interaction maps is affected by several factors. First, the fact that protein interactions are represented by nondirected edges is due to the constraints of current experimental assays; as new information on the source and target of protein interactions leads to assigning directions to some of the edges, the size of the strongly connected component may decrease. Second, some transcriptional regulatory networks are less well mapped than protein interaction networks, and new additions to these networks may increase their connectivity. Third, as transcription factors are often regulated posttranslationally, an integrated transcriptional/(post)translational regulatory network would be a more appropriate representation and may have more connectivity and feedback than a map focused on transcriptional regulation alone. It will be interesting to follow whether new experimental evidence and novel network representations decrease the range of connectivity among molecular interaction networks.

In addition to the clusters characterizing the global (whole network level) connectivity of cellular networks, one also can identify recurring interaction motifs, which are small subgraphs (i.e., subsets of the full graph) that have well-defined topologies. Interaction motifs, such as autoregulation (usually a negative feedback; Figure 1) (Shen-Orr et al., 2002; Balázsi et al., 2005), feed-forward loops (Figure 1; Shen-Orr et al., 2002; Balázsi et al., 2005), or triangles of protein interactions (Giot et al., 2003; Wuchty et al., 2003; Ma'ayan et al., 2005), have a higher frequency than expected based on the subgraph statistics of comparable model networks (also referred to as null models). Moreover, exhaustive analysis of the dynamic behaviors supported by three- and four-node motifs revealed that dynamic stability to small perturbations in node states is highly correlated with the relative frequency of these motifs (Prill et al., 2005). These observations led to the prediction that interaction motifs form functionally separable building blocks of cellular networks (Mangan and Alon, 2003), described in detail by Alon (2006). For example, the abundance of negative feedback loops in the early steps of signal transduction networks and of positive feedback loops at later steps suggest mechanisms to filter weak or short-lived signals and to amplify strong and persistent signals (Ma'ayan et al., 2005).

The number, directionality, and strength of connections associated with a given node can be synthesized into measures of that node's centrality (importance). The simplest such measure is the node degree, or the number of edges adjacent to that node. If the directionality of interaction is important, a node's total degree can be broken into an in-degree and out-degree, quantifying the number of incoming and outgoing edges adjacent to the node (Figure 1). The importance of any particular node in mediating propagation or flow within the network is quantified by its betweenness centrality, which is defined as the fraction of shortest paths between pairs of other nodes passing through that node (Freeman, 1977) (Figure 1).

While the node degree or betweenness centrality of a specific node is a local topological measure, this local information can be synthesized into a global description of the network by reporting the degree distribution P(k), which gives the fraction of nodes in the network having degree k. A significant number of cellular interaction networks, including protein interaction networks (Jeong et al., 2001; Giot et al., 2003; Yook et al., 2004; Geisler-Lee et al., 2007), metabolic networks (Jeong et al., 2000; Wagner and Fell, 2001; Arita, 2004; Tanaka, 2005), signal transduction networks (Ma'ayan et al., 2005), and transcriptional regulatory networks (Guelzim et al., 2002; Lee et al., 2002), exhibit a high heterogeneity (diversity) for node centralities that precludes the existence of a typical node that could be used to characterize the rest of the nodes in the network. Networks with this high heterogeneity are often referred to as scale free (reviewed in Albert and Barabási, 2002; Barabási and Oltvai, 2004). The degree distribution of scale-free networks is generally close to a power law P(k) = Ak^−γ, where A is a normalization constant and the degree exponent γ is between 2 and 3. Exceptions from the heterogeneity associated with power-law distributions are also notable: the in-degree distribution of transcriptional networks and the degree distribution of enzymes have a small range, reflecting that combinatorial regulation by several transcription factors is less frequent than regulation of several targets by the same transcription factor and that enzymes catalyzing several different reactions are rare.

In scale-free networks, small-degree nodes are most common; however, the highest-degree nodes have degrees that are orders of magnitude higher than the average degree. Such highest-degree (or in general highest-centrality) nodes are commonly referred to as hubs. This heterogeneous structure leads to the prediction that in scale-free networks random node disruptions do not cause a major loss of connectivity, whereas the loss of the hubs causes the breakdown of the network into isolated clusters (Albert and Barabási, 2002). This point has been experimentally corroborated in S. cerevisiae, where the severity of a gene knockout has been shown to correlate with the number of interactions in which the gene's products participate (Jeong et al., 2001; Said et al., 2004). High degree is a practical but nevertheless insufficient predictor of functional importance, as there are several examples of low-degree nodes that are critical for certain outcomes (Holme et al., 2003; Almaas et al., 2005; Mahadevan and Palsson, 2005; Li et al., 2006). Ultimately, a high-precision prediction of functionally important nodes will need to take into account the biological identity of the nodes and the synergistic and dynamic aspects of the interactions and will therefore require significantly more input information than what it currently available for most interaction networks. Given the state of the knowledge on these networks, a suitable combination of node degree with betweenness centrality, and possibly other centrality measures, will offer the optimal trade-off between predictive power and practicality.

The graph measures described above, alone or combined with additional information regarding the network nodes (such as the functional annotation of the corresponding genes/proteins), provide testable biological predictions on several scales, from single interactions to functional modules. The functions of unannotated proteins can be inferred on the basis of the annotation of their interacting partners, as it was done for S. cerevisiae and Arabidopsis proteins using interaction, coexpression, and localization data (Vazquez et al., 2003; Lee et al., 2004; Geisler-Lee et al., 2007). New protein interactions can be predicted using machine learning algorithms based on the presence of abundant interaction motifs within the network (Albert and Albert, 2004). New protein functions and interactions can be inferred through global alignment between protein interaction networks in different species (Kelley et al., 2004). Conversely, protein interaction networks of two species can be used to augment sequence-based homology searches as a basis for orthology prediction; in a recent analysis of D. melanogaster and S. cerevisiae, in 61 out of 121 cases with ambiguous homology assignment, the network supported a different orthologous protein pair than that favored by sequence comparisons (Bandyopadhyay et al., 2006). The connected subgraphs of a probabilistic S. cerevisiae gene–gene linkage network have been used to identify highly connected gene clusters (modules). The demonstrably coherent functional annotation of genes within each cluster allowed the annotation of unknown proteins that are part of the cluster (Lee et al., 2004). Finally, construction of an integrated transcriptional and metabolic network allowed global predictions of growth phenotypes and qualitative gene expression changes in E. coli (Covert et al., 2004) and yeast (Herrgard et al., 2006).

DYNAMIC MODELING

The nodes of cellular interaction networks represent populations of proteins or other molecules. The abundances of these populations can range from a few copies of an mRNA, protein, or metabolite to hundreds or thousands of molecules per cell, and they vary in time and in response to external or internal stimuli. To capture these changes, the interaction network needs to be augmented by quantitative variables indicating the state (i.e., expression, concentration, or activity) of each node and by a set of equations indicating how the state of each node changes in response to changes in the state of its regulators. In other words, the interaction network needs to be developed into a dynamic network model.

Dynamic network models have as input the interaction network, the transfer functions describing how the state of each node depends on the state of its regulators, and the initial state of each node in the system. Examples of transfer functions include mass action kinetics for chemical reactions or Hill functions for regulatory relationships and include several kinetic parameters whose values need to be known or estimated. If the model refers to spatio-temporal phenomena, such as those based on cell-to-cell communication, the node states and transfer functions will depend on spatial coordinates (Mjolsness et al., 1991; Palsson and Othmer, 2000). Given the interaction network, transfer functions, and initial states, the model will output the time evolution of the state of the system. The most basic qualitative feature of a dynamic system is the number and type of different behaviors, often called attractors, that are found in the infinite time limit. All initial conditions that evolve to a given attractor constitute its basin of attraction. The attractors of gene regulatory networks are thought to correspond to distinct cellular states (Kauffman, 1993) or cycles (e.g., circadian rhythms; Goldbeter, 2002), while the attractors of a signal transduction network correspond to steady state (time-independent) or sustained oscillatory response(s) to the presence of a given signal (Tyson et al., 2003).

A validated dynamic model that correctly captures experimentally observed normal behavior allows researchers to track the changes in the system's behavior due to perturbations, to discover possible covariation between coupled variables, and to identify conditions in which the dynamics of variables are qualitatively similar. It is easier to use a model to search for perturbations that have a significant or beneficial effect on system behavior than it is to perform comparable experiments on the living system; for example, models can predict multiple small perturbations that produce large effects when combined.

While the benefits of using verified models are obvious, the information and data requirements necessary to construct a verifiable dynamic model are daunting for all but the smallest systems. Additionally, modelers need to balance a set of features that are nonexclusive but nevertheless cannot be maximized simultaneously. Ideally, a good model should have a low level of uncertainty in the interactions, equations, and parameters used; it should be relatively easy to run or construct; it should provide a high level of understanding or insight; it should be simple and elegant; its predictions should be highly accurate; it should be general (be applicable to a large number of systems); and it should be robust (insensitive to small changes in parameters or assumptions) (Haefner, 2005).

Dynamic modeling frameworks are usually classified along two axes: continuous versus discrete and deterministic versus stochastic. The first classification refers to the level of detail in the representation of the node state, while the second indicates whether the transfer functions incorporate any uncertainty or variability. Since variability and noise are pervasive in biological systems, a continuous stochastic model has the highest potential to accurately describe the system; however, it also has the highest requirement for input information. A continuous deterministic model, the most frequently used middle ground, represents the limit of the corresponding continuous stochastic model as the number of molecules becomes large or the noise decreases to zero. Only continuous deterministic models readily allow theoretical methods such as bifurcation analysis (Goldbeter, 2002; Tyson et al., 2003), that is, the analysis of where the system's dynamics changes as a function of various parameters. The conclusions of these analyses can then contribute to the selection of the best-suited high-level stochastic models. Discrete deterministic models exhibit a high level of abstraction in that they classify node states into just a few categories of expression or activity. On the plus side, this means that they require relatively little detailed input and can be constructed in cases where the large number of unknowns makes continuous models impractical or even impossible. On the minus side, the predictions of these models are more coarse grained and less quantitative than the predictions of continuous models.

Continuous deterministic models characterize node states by concentrations and describe the rate of production or decay of all components by differential equations based on mass action–like kinetics (Figure 1; Irvine and Savageau, 1990). When built on a solid starting knowledge of the elementary biochemical reactions and the associated reaction rates, these models can efficiently explore alternative hypotheses and predict the effect of perturbations. For example, a differential equation-based model of an 11-node signaling network responsible for programmed cell death after infection of Arabidopsis with Pseudomonas syringae led to significant refinement of the signaling circuitry (by discounting two previously proposed negative feedback loops) and of the kinetic parameters (Agrawal et al., 2004). When the number of constituents is small, optimization methods can be used to estimate parameters that best account for measured dynamic behaviors. For example, continuous deterministic modeling of the three-node circadian clock of Arabidopsis, combined with optimization-based parameter estimation and sensitivity analysis, led to the prediction of two new network nodes and of a novel architecture of three coupled feedback loops (Locke et al., 2005, 2006; Zeilinger et al., 2006). Experiments on clock component deletion mutants confirmed the predicted architecture and identified the gene GIGANTEA as a major component of one of the predicted novel network nodes (Locke et al., 2006).

Continuous deterministic models of simple regulatory or signaling networks can also be coupled with descriptions of cell growth and mechanics to explain spatio-temporal pattern formation in cell colonies or tissues. For example, a recent model of plant organ positioning driven by auxin patterning predicts that the underlying mechanism is a feedback loop between relative auxin concentrations in adjacent cells and auxin efflux direction. It is proposed that this feedback is realized through the putative auxin efflux mediator PIN1 whose cycling between internal and membrane compartments is auxin regulated in such a way that a higher auxin concentration in a neighboring cell leads to an increased PIN1 localization at the membrane toward that cell, resulting in a higher auxin transport into that cell (Jönsson et al., 2006).

The stochasticity (nondeterminism) of biological processes is usually taken into account by appending stochastic (noise) terms to differential equations. Discrete events (such as the initiation of transcription) and low abundances for certain molecules can be incorporated by characterizing the node states by the copy number of each molecule and describing the time evolution of the probabilities of each of a system's possible states (Rao et al., 2002; Andrews and Arkin, 2006). A recent model of the ethylene signaling pathway and its gene response in Arabidopsis combines chemical kinetics for signaling proteins with a probabilistic description of the target genes' states (Diaz and Alvarez-Buylla, 2006). This model reproduces the experimentally observed differential responses to different ethylene concentrations and predicts that the pathway filters rapid stochastic fluctuations in ethylene availability.

Discrete deterministic models usually characterize network nodes by two binary states corresponding to, for example, an expressed or not expressed gene, an open or closed ion channel, or above-threshold or below-threshold concentration of a molecule. The change in state of each regulated node is generally described by a logical function using the Boolean operators “and,” “or,” and “not” (Figure 1). Boolean models can predict dynamic trends in the absence of detailed kinetic parameters. For example, a Boolean gene regulatory network model of Arabidopsis floral organ development (Mendoza and Alvarez-Buylla, 1998; Espinosa-Soto et al., 2004) offered a mechanistic and dynamic explanation for the conceptual ABC model (Coen and Meyerowitz, 1991), successfully reproduced experimental gene expression patterns in wild-type and mutant plants, and predicted that cell fate determination is determined by the network architecture rather than precise interaction parameters or initial conditions. The model also proposed four novel interactions and predicts the effects of evolutionary differences in the network architecture between Arabidopsis and Petunia hybrida. A Boolean model of the signal transduction network mediating abscisic acid–induced stomatal closure (Li et al., 2006) reproduced experimental results at both the pathway and whole-cell physiological level, predicted that the network's response is robust against a significant fraction of possible perturbations and provided a ranking of network nodes in terms of their essentiality (Figure 3).

Figure 3.

Illustration of Predictions from a Discrete Dynamic Model: The Percentage of Simulated Stomata That Attain ABA-Induced Closure as a Function of Time Steps in Li et al. (2006).

This Boolean model circumvents the lack of information in the timing of each process, in the internal states of signaling proteins, and in the concentrations of small molecules by performing a large number of simulations that sample equally over relative durations and node initial states. The results are reported as the percentage of simulations that attain the on state for the node closure. In all panels, black triangles with dashed lines signify the model's representation of normal (wild-type) response to ABA stimulus. Open triangles with dashed lines show that in the wild type, the percentage of closed simulated stomata decays in the absence of ABA.

(A) The model predicts that disruption of depolarization (open diamonds) or anion efflux at the plasma membrane (open squares) cause total loss of ABA-induced closure.

(B) The model predicts that perturbations in sphingosine-1-phosphate (dashed squares), phosphatidic acid (dashed circles), or pH_c (dashed diamonds) lead to reduced closure probability.

(C) The model predicts that abi1 recessive mutants (black squares) show faster than wild-type ABA-induced closure (ABA hypersensitivity). Blocking Ca_c²⁺ increase (black diamonds) causes slower than wild-type ABA-induced closure (ABA hyposensitivity) in the model. Figure reproduced from Li et al. (2006).

Hybrid dynamic models meld a Boolean description of combinatorial regulation with continuous synthesis and decay by describing each node with both a continuous variable (akin to a concentration) and a Boolean variable (akin to activity) (Glass and Kauffman, 1973; Chaves et al., 2006). For example, a hybrid model of the transcriptional regulation of the Endo16 sea urchin gene revealed that its spatial control during embryonic development is mediated by a cis-regulatory switch (Yuh et al., 2001), and a hybrid model of D. melanogaster embryonic segmentation predicts that transient disregulation of posttranslational modifications can have effects as severe as gene knockouts (Chaves et al., 2006).

While the details of different dynamic models can be significantly different, and the predictions offered by them are specific to the systems they refer to, there is a considerable level of common insight arising from these models. For example, there is increasing evidence that molecular networks are constructed from simpler modules with generic input-output properties not unlike those of electric circuits (Alon, 2006). Some of these modules exhibit perfect adaptation to a signal (i.e., they exhibit a transient response to changes in signal strength, but their steady state response is independent of the signal strength), switch abruptly and irreversibly from low to high response at a critical (bifurcation) value of the signal, or show sustained oscillations in the response variable (Tyson et al., 2003). Frequently, these dynamic behaviors do not depend on the details of the transfer functions or on the kinetic parameters and are determined by the underlying network; for example, positive feedback loops (either mutual activation or antagonism) may create a discontinuous switch, negative feedback often leads to homeostasis, and sustained oscillations require a negative feedback loop with a time delay. The pursuit of general insight from integrating the lessons learned from specific models is an emergent and rapidly developing topic in systems biology.

CONCLUSIONS

Systems biology develops through an ongoing dialog and feedback among experimental, computational, and theoretical approaches. High-throughput experiments reveal, or allow the inference of, the edges of global interaction networks. Graph-theoretical analysis of these networks enables insight into the organization of cellular regulation, feeds back to network inference (Albert and Albert, 2004; Gupta et al., 2006; Horvath et al., 2006; Christensen et al., 2007), and allows specific biological predictions. Dynamic modeling of systems with specified inputs and outputs allows the identification of key regulatory components or parameters. Experimental testing of model predictions enables the validation or refinement of the model, which in turn paves the way to more predictions and ultimately the generation of new biological knowledge.

Network analysis and dynamic network modeling represent complementary approaches most appropriate for different network scales. Network analysis can be readily performed on networks with tens of thousands of nodes and edges; however, it cannot explicitly incorporate the temporal and quantitative aspects of the processes corresponding to the edges of the network. Detailed deterministic or stochastic models allow for high-fidelity dynamic analysis of small networks but increase dramatically in complexity even for small increments in the number of nodes and edges and thus can hardly be used meaningfully on large-scale networks. A potential middle ground is emerging through the development of qualitative modeling techniques that map the propagation of context-dependent signals through a network (Ma'ayan et al., 2005; Prill et al., 2005; Li et al., 2006).

This perspective essay has shown a small sample of network-based modeling in systems biology; the interested reader is referred to excellent review articles and books written from different perspectives (Goldbeter, 2002; Tyson et al., 2003; Barabási and Oltvai, 2004; Ma'ayan et al., 2004; Haefner, 2005; Alon, 2006; Palsson, 2006). To date, much of systems biology research has focused on single-celled organisms, which de facto precludes assessment of endogenous cell–cell signaling. As the scope of inquiry expands from cells to organs and organisms as systems, plants provide unique opportunities to study organism-level responses to environmental challenges. Indeed, while animals tend to rely on behavioral adjustments to evade environmental stress, plants are more likely to emphasize stress resistance and recovery mechanisms. Moreover, the modular structure of plants causes relatively weak coupling between different parts of the same plant as well as significant differences in these parts' microenvironments. Given also that plant signal transduction mechanisms are at least as developed as those of animals and use many conserved components (e.g., heterotrimeric G-proteins and cytosolic Ca²⁺), plants can eminently serve as model systems and will undoubtedly gain in importance as the field of systems biology matures. Most of the literature on systems biology shares the view that in order for the research community to develop the sophisticated interplay of theory, computation, and experiment that will be needed to understand and manipulate cellular regulatory systems, we will first need to learn to communicate effectively. I hope the examples shown in this perspective will facilitate new and fruitful dialogs.