Imaging Ventricular Fibrillation

Abstract

Ventricular fibrillation (VF) had been traditionally considered as a highly disorganized process of random electrical activity emanating from multiple, short-lived, reentrant electrical waves. It is the incessant breakup of wave fronts and the creation of new daughter waves (wavebreaks) that perpetuate VF. Other studies described VF as a process with a substantial degree of structure embedded in seemingly random events where VF is spatially organized as a small number of relatively large domains, each with a single dominant frequency. VF is then driven by the domain with the highest activation frequency representing a ‘mother rotor’ which drives the surrounding myocardium except at boundaries with more refractory tissues.

Voltage-sensitive dyes and optical mapping provide a powerful technique that has been extensively applied to study the structure and organization of VF and has revealed how cellular properties, fiber orientation and metabolism influence VF. This brief review will discuss signal processing methods used to investigate mechanisms underlying VF, namely: a) Fast Fourier Transform (FFT), b) Time-Frequency Domain analysis (TFD), c) Time-lag correlation, d) Mutual Information (MI) analysis and e) Phase Reconstruction techniques to identify phase singularities and wavebreak locations. In addition, several cellular properties that have been shown to influence the structure of VF such as a) the dispersion of repolarization, b) low tonicity/osmolarity, and c) the amplitude of K⁺ currents will be discussed as determinants of VF. Finally, recent image analysis routines were used to identify wavebreak sites and revealed that wavebreaks are caused by abrupt spatial dispersion of voltage (V_m) oscillations.

Introduction

Ventricular fibrillation (VF) has been characterized as disordered contractions of the heart with complex ECG patterns. The mechanisms underlying VF have been linked to the development of vortex-like reentry or spiral waves. In this context, non-stationary (meandering or drifting) spiral waves and/or their turbulence via wave breakups could account for the complex morphology of electrocardiograms (ECG) in VF. The dynamics of wavelets; that is, their life span, dimensions and trajectory may in principle vary spatially due to spatial heterogeneities of cellular properties such as refractoriness, restitution kinetics of action potential durations, and fiber anisotropy. The spatial organization and the parameters that influence wave instabilities in VF are important to understand the mechanisms responsible for the maintenance of VF and to develop more effective approaches to interrupt arrhythmias.

VF has been traditionally investigated by analyzing activation maps to search for the possible clues of where and how wave front instabilities are created. However, due to the complexity of wave propagation and their sudden changes in directions, it was very difficult to quantitatively analyze the structure and dynamics of VF. Therefore, VF has been investigated with indirect methods by grouping regions with common properties or similar electrical activity. Several algorithms have been applied to test for similarities of V_m properties within groups of sites or contiguous regions of myocardium including common dominant frequencies,^{1, 2} wave front dynamics^{3, 4} and regions with a high level of cross correlation.^{5, 6}

Fluorescence imaging technique with voltage-sensitive dyes provided high spatial and temporal maps of activation in VF allowing for more detailed analyses. This is because 1) fluorescence changes from voltage-sensitive dyes are similar to transmembrane potential recorded with an intracellular microelectrode, 2) recording from multiple locations can be easily obtained with high speed imaging devices such as photodiode arrays, CCD or CMOS cameras with greater spatial resolution, 3) anatomical landmarks can be easily identified from the raw image of heart, 4) propagation pathways can be determined with greater accuracy because electrical activity is recorded from contiguous regions of tissue without dead space between recording sites, and 5) other parameters can be simultaneously recorded such as intracellular Ca²⁺ concentration. In this report, we summarize some of the imaging data from our lab that pertain to the investigation of spatial and temporal organization of VF and their relationship to static (coronary vessels) and dynamic (due to abrupt dispersion of repolarization) functional blocks and/or fiber orientations.¹⁸

Results and Discussion

Ventricular fibrillation (VF) has been linked to the development of vortex-like reentry or spiral waves which have been studied in computer simulations,^{19, 20} tissue slices and perfused hearts.^{21, 22} In this context, non-stationary (meandering or drifting) spiral waves and/or their turbulence could account for the complex morphology of electrocardiograms (ECG) in VF. VF has been traditionally investigated by analyzing activation maps but the complex waveforms recorded in VF and the algorithms used to derive activation maps have made it difficult to interpret the underlying mechanisms. Another approach is to analyze voltage oscillations in the frequency domain using Fast Fourier Transforms (FFT) and to represent reentrant circuits as sources of periodic wave formation.^{1, 2, 8}

FFT analysis was used to investigate the influence of action potential durations (APDs) and refractory periods (RP) on VF dynamics in perfused guinea pig hearts by comparing APD gradients during sinus rhythm to VF elicited by burst pacing. In VF, the average inter-activation interval (AI) were shorter at the apex (57.5 ± 8.1 ms) than the base (76.1 ± 1.5 ms, n = 6, p<0.05) and had gradients similar to APD gradients (correlation coefficient = 0.71 ± 0.04). Local velocity vectors appeared randomly oriented and FFT power spectra were broad (10–24 Hz) with multiple peaks (n=6). Increasing APDs by blocking the delayed K⁺ rectifying current I_Kr (E-4031 = 0.5 μM, n=3) shifted FFT spectra from complex to a single low dominant frequency (10 Hz) and altered repolarization yet the correlation between maps of mean AI and RPs were retained.⁸ Thus, FFT spectral analysis demonstrated that VF was driven by a multiple wave-make and wave-break mechanism and the local RP influences VF dynamics by limiting the range of VF frequencies and AIs at each site.

Time-Frequency Domain Analysis-Lifespan of VF Frequencies

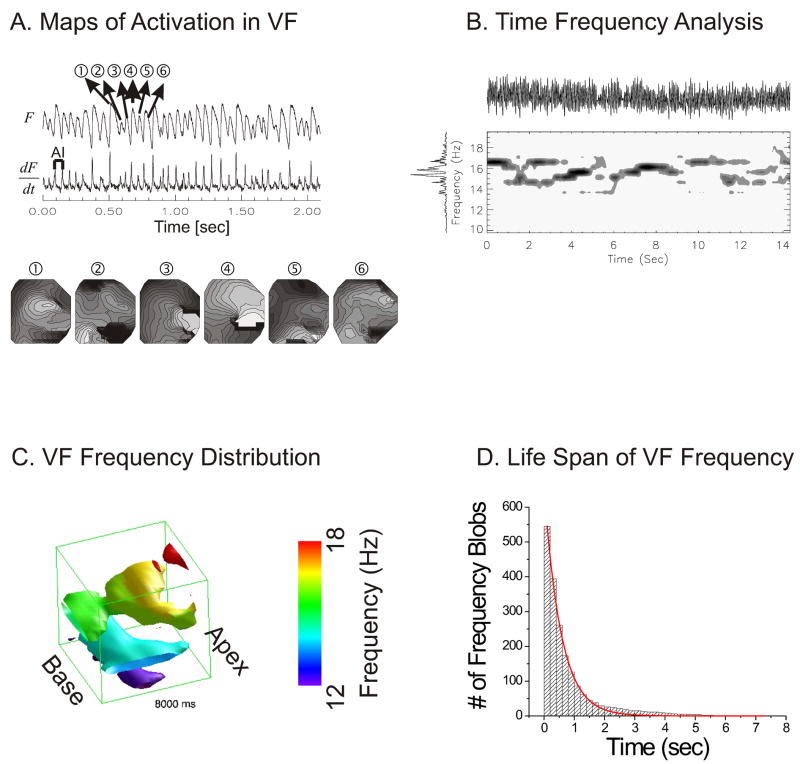
Figure 1A illustrates an optical trace of membrane potential (F) recorded by a single element of a 16×16 photodiode array from a rabbit pig heart in VF. The first derivative (dF/dt) made it possible to identify the time point when most of the cells viewed by that diode depolarize and these activation time-points are used to generate maps of activation for 6 consecutive beats of VF (panels 1–6 associated with V_m oscillations 1–6).

Figure 1. Time frequency analysis of VF traces.

(A) A typical example of fluorescence trace recorded from one pixel (top trace) and their first derivatives (bottom trace). Activation maps of 6 consecutive VF beats (lower panel) show a marked lack of reproducibility and periodicity of the depolarization sequence. Isochrones are 1 ms apart; bright to dark represents the sequence of depolarization. (B) Time frequency distribution (TFD) from one pixel. TFD was calculated by cone shaped kernel (1.5 s window) over normalized optical traces. Top: optical trace, Left: overall FFT spectra. Contour map: spectrogram with isolines drawn every 12.5 % of maximum. Spectrograms plot frequency (ordinate) vs. time (abscissa) and is shown for 14 s of VF; the darker the color, the higher the energy density at that frequency. (C) Spatial distribution of VF frequencies. Time-frequency analysis was extended to all photodiodes and the spatial distribution of VF frequencies at time t was reconstructed as iso-surface plots. (D) Life span of VF frequencies. The majority of VF frequencies lasted less than 1 s (half life = 0.39 ± 0.13 s).

To overcome the limitations of FFT spectral analysis, time-frequency analysis was applied to determine the time-course and life span (creation and annihilation) of frequency sources during VF.⁸ To determine the time when individual FFT peaks occurred, voltage oscillations were represented in time and frequency domains by generating a standard spectrogram.⁹ As shown in Figure 1B, the FFT spectrum (left vertical trace) of membrane potential oscillations from a single pixel (top trace) displays all the frequencies recorded in a 14 s interval of VF. To analyze Vm signals during VF in time and frequency domains, a spectrogram (short-time Fourier Transform) was generated for each pixel by calculating the FFT spectrum for a brief Gaussian window of 1.5 s, then shifting the window stepwise in time (Δt = 1 ms) and remeasuring the FFT spectrum at successive t intervals (Fig. 1B middle panel). The spectrogram plots frequency (ordinate), versus time (abscissa) and energy density where the darker the color, the higher the energy density at that frequency. The spectral peaks in the time-frequency representation were enhanced using a cone shaped smoothing kernel and showed that in VF multiple frequencies co-existed at the same site, and frequency peaks appeared and disappeared abruptly.⁹ The time frequency analysis shown in Figure 1B was extended to all 252 diodes on the array and the distribution of VF frequencies P(x,y,f) at time t is visualized as an isosurface plot in space (x,y) and frequency (z) axis (Figure 1C). The isosurface plot shows that frequency peaks are not uniformly distributed but that certain frequencies appear in small contiguous regions of ill defined shape. A contiguous object in space and frequency domain is defined as a VF frequency blob because a common method to identify such objects uses a blob-coloring algorithm. VF frequency blobs are formed by pixels that are contiguous in space and frequency and are assigned the same color. Frequency blobs in different regions of the heart can be tracked as a function of time until they either split in two or more blobs or disappear. Thus, V_m oscillations are transferred to time and frequency domains to visualize the creation and annihilation of each frequency component in VF in time and space. The lifespan of VF frequency blobs was calculated for 4 rabbit hearts (2-min intervals) such that >500 VF frequency blobs were tracked in time to calculate their lifespan. As shown in figure 1D, a histogram of lifespan was generated and was fitted to a first order exponential decay curve. The data showed that lifespan of frequency blobs from birth to either annihilation or breakup to another frequency had a half life of 0.39 ±0.13 seconds (n=4).⁹

Time frequency analysis was used to test the effects of low tonicity/osmolarity or the activation of the volume regulated (or swelling-activated) chloride current, (I_Cl,vol) on action potential and VF dynamics and in the process attempt to reconcile differences in FFT spectra reported in various studies.^23–25 Hypo-osmotic solution (± 45 mM Mannitol) in guinea pig hearts shortened APDs by ~ 20% and increased APD gradients between right and left ventricles (21 ± 7 → 41 ± 10 ms, n = 4). In VF, hypo-osmotic solution increased VF frequencies (15.3 ± 1.2 to 28.9 ± 3.6 Hz, n = 11) in about 20 min, transforming complex fast Fourier transformation spectra to a single dominant high frequency, on the left but not the right ventricle.²³ Blockade of I(Cl,vol) reversed the organized VF back to a complex VF with lower (13.5 ± 3.7 Hz in left ventricle) frequencies (n = 8), indicating that I(Cl,vol) underlies the changes in VF dynamics.²³ Consistent with this interpretation, the levels of ClC-3 channel protein were 27% greater on left than right ventricles (n = 10), and computer simulations showed that insertion of I(Cl,vol) transformed complex VF to a stable spiral. The differential expression of ClC-3 channels and the activation of I(Cl,vol) by decreasing osmolarity (45 mOsm) has a major impact on VF dynamics by transforming random multiple wavelets to a highly organized VF with a single dominant frequency.²³ Besides ClC-3, the outward component of the background rectifier current I_K1 may also be a determinant of VF dynamics; where the higher levels of current in the right ventricle provide a mechanism for wavefront fragmentation and low levels of current in the left ventricle stabilize high frequency (25–32 Hz) rotors.¹⁷

Correlation and Mutual Information (MI) analysis

Several groups have applied correlation length analysis, the distance over which V_m oscillations in one region are correlated to V_m in another region of the heart.^{5, 6, 11, 12} Bayly et al., mapped V_m using an equidistant grid of surface electrodes on a pig heart, the cross correlation of electrogram signals was found to decay exponentially with increasing distance.¹¹ The decay rate of the cross correlation was used to calculate a correlation length which was in the range of 4~10 mm or considerably smaller than the size of the heart. The short correlation lengths suggested the co-existence of multiple independent reentrant circuits in VF. By analogy with correlation length analysis, spectral coherence applied to V_m during atrial and ventricular fibrillation exhibited a similar rate of decay as a function of distance.^{26, 27}

Cross correlation and Mutual Information of optical Vm signals using a 16×16 element photodiode array was used to investigate the spatial organization of VF in perfused rabbit hearts.¹³

Cross correlation (CC) calculates the correlation coefficient between two signals after shifting time lag.¹¹ The cross correlation of two optical traces, at pixels X and Y and time lag (L) was defined as

$$R_{XY}(L)=\{\begin{array}{l}\frac{\sum _{k=0}^{N-L-1}(X_{k+L}-\overline{X})(Y_k-\overline{Y})}{\sqrt{\sum _{k=0}^{N-1}{(X_K-\overline{X})}^2\sqrt{\sum _{k=0}^{N-1}{(Y_K-\overline{Y})}^2}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{ForL}<0\hfill \\ \frac{\sum _{k=0}^{N-L-1}(X_k-\overline{X})(Y_{k+L}-\overline{Y})}{\sqrt{\sum _{k=0}^{N-1}{(X_K-\overline{X})}^2\sqrt{\sum _{k=0}^{N-1}{(Y_K-\overline{Y})}^2}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{ForL}\ge 0\hfill \end{array}$$

Where X̄ and Ȳ are means of corresponding series and N is the number of points in the series. Cross correlation (CC) analysis was done as follows. (a) The correlation coefficient between a V_m signal at a reference pixel and a V_m signal at another site was calculated as a function of time lag,11 (b) the calculation was extended between the reference pixel and all other pixels on the map and (c) the time-lag that produced the maximum correlation coefficients were determined. Cross correlation maps were generated by selecting a reference pixel, calculating the maximum cross correlation (CC_max) with all other pixels and displaying isochrones of maximum correlation coefficients. Contour maps were shown in gray scales, the darker region the higher correlation and isolines were drawn every 10 % of maximum correlation coefficient.

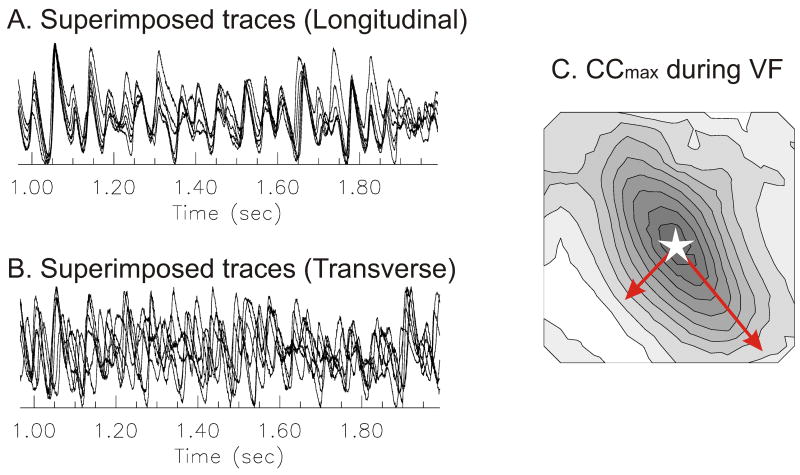
In perfused rabbit hearts, the decay of CC_max with distance exhibited a wide variance or a broad range of CC_max values between pixels separated by the same distance.¹³ To better understand the cause of this wide variation, the distribution of CC_max during VF was compared to the activation pattern obtained when pacing at the center of the left ventricle. In this case, CC_max was mapped by choosing a reference pixel at the center of the field-of-view and calculating CC_max between the reference and all other pixels. The activation map while pacing the center of the left ventricle was anisotropic with an elliptical pattern with its major and minor axis aligned with the longitudinal and transverse orientation of epicardial myocytes (not shown). VF was then induced in the same heart by a burst of electrical stimuli and V_m oscillations exhibited a CC_max gradient, being high near the reference point (open star) and decreasing systematically at farther sites (Figure 2C). Interestingly, CC_max maps were also elliptical in shape, with a major axis at 127.9° (or −52.1°) that was aligned with the major axis of the activation pattern, the orientation of the longitudinal conduction velocity and the long axis of fibers on the left ventricle. The principal angle of the CC_max map (127.7 ± 7.8 °) was compared to the angle of longitudinal action potential propagation (132.5 ± 12.0) using paired t-test which failed to detect statistically significant differences between the two angles (n=6, paired t-test p = 0.345 > 0.05). CC_max maps were also generated from the same heart and VF data by re-calculating CC_max for different reference pixels. Similar elliptical CC_max maps were obtained regardless of the chosen reference point; suggesting that the anisotropies of cell-cell coupling influence the spatial correlation of V_m oscillations during VF. These findings were highly reproducible in all rabbit hearts regardless of the location of the reference points. The correlation length (distance at which the correlation is 0.5) was also calculated from first order exponential curve fitting (y = e^−d/τ).¹³ The correlation length was 3.6 ± 0.3 mm along the longitudinal axis and 2.2 ± 0.2 mm along the transverse axis, with a ratio of 1.63 ± 0.20 (n= 6/6, analysis of 2–8 s of VF).¹³ The results indicated that cell-cell coupling and tissue anisotropy influence the synchronization and wave propagation of V_m, even in VF.

Figure 2. Tissue anisotropy and maximum cross correlation (CC_max) map in VF.

(A&B) Superimposed traces along longitudinal and transverse direction (see arrows in panel C). Note that activations across the longitudinal direction are well synchronized compared to the transverse direction. (C) Map of CC_max. The map of CC_max during VF was generated as described in Methods. The pixel at the center of the array was chosen as the reference site (open star). The map revealed an anisotropic distribution of CC_max, with elliptical patterns of CC_max similar to the elliptical pattern of propagation obtained by pacing the heart at the center of the field-of-view (panel D). Isochronal lines are drawn every 10% of maximum CC_max. (D) Activation map during stimulation. The heart was stimulated near the center of field-of-view (open star) and the activation map was displayed as a contour map. Activation was faster along the longitudinal axis of fiber on the left epicardium, resulting in an elliptical spread of propagation. Isochronal lines are drawn every 1 ms.

When 2 signals are independent, CC_max is most likely zero; however, if CC_max is zero, the 2 signals may still be interdependent and may be linked by a nonlinear function. Therefore CC_max may fail to detect spatial organization of VF if a nonlinear association exists between two locations. To confirm findings with CC_max, MI of V_m from different sites was analyzed because it remains sensitive to nonlinear association. Maps of MI coincided with CC_max maps and revealed the influence of tissue anisotropy on VF.¹³

Spatially discordant Vm Oscillations cause Wave Breaks

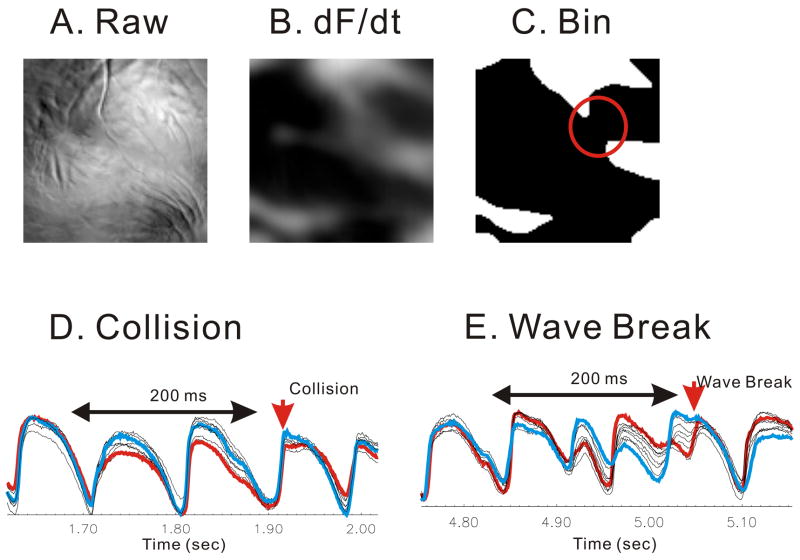
Wave fractionations was identified by tracking V_m oscillations optically at unprecedented spatial (100×100 pixels) and temporal (2000 frames/s) resolution using a CMOS camera viewing the anterior surface (1×1 cm²) of perfused guinea pig hearts (n=6).¹⁸ Figure 3A displays a raw fluorescence image from the anterior surface of a guinea pig heart stained with di4-ANEPPS and recorded with the CMOS camera. VF was induced by burst stimulation and wave front dynamics were highlighted first by taking the first derivative (dF/dt) of V_m (Fig. 3B) then converting the image into binary images to enhance the contrast between each wave front and the adjacent background (Fig. 3C). A region based image analysis was used to automatically detect wave fractionation which fell into 3 categories: decremental conduction (49±7%), wave collisions (32±8%), and wavebreaks where waves split into daughter wavelets (17±2%). Wave fractionations occurred at a frequency of 34±4 splits/s·cm² and their locations were analyzed with respect to anatomical obstacles, fiber orientation and V_m oscillations at neighboring sites. Once a wave fractionation site was identified to a given pixel representing 100×100 μm² of tissue, V_m oscillations at the 8 nearest neighbors were examined just before, during and after the wave break occurred. The collision and annihilation of wave fronts was associated with homogeneous V_m oscillations (Fig. 3D) In contrast, wavebreaks coincided with discordant alternans where V_m amplitudes and durations shifted from high-low to low-high on opposite sides of wavebreak sites (Fig. 3E). Thus, V_m discordant alternans cause wavebreaks because of abrupt dispersion of refractoriness.

Figure 3. Discordant alternans before wavebreaks.

Wavebreaks were detected by tracking split of wave fronts into multiples. Traces around neighboring 8 pixels showed spatially discordant alternans before wave breaks occurred. (A) snapshot of fluorescence image. (B) first derivative image to isolate wave fronts. (C) automated wavebreak detection (red circle). The degree of local synchronization was calculated using cross correlation among neighboring pixels. (D) Case of collision. V_m traces were synchronized before the wave split. Cross correlations from 200 ms traces (see figure) were calculated from all possible pairs of 8 neighboring pixels. The minimum correlation was 0.59 ± 0.05 (n=5). Traces in blue and red represent the pair of minimum correlation. (E) Case of wave break. V_m traces were highly asynchronous with out-of-phase alternantion. The minimum correlation was 0.47 ± 0.05, significantly lower than collision case (n=5, p=0.012).

Discussion

Optical mapping techniques used to image cardiac arrhythmias have made important contributions to our understanding of the nature and structure of VF. With further improvements in the quality of the data with respect to signal to noise ratio, spatial and temporal resolution and with the abatement of motion artifacts, we expect that these techniques will be successfully applied to hearts under various disease states such as ischemia and other metabolic deficiencies where the amplitude and kinetics of optical APs are typically reduced. The latest CMOS cameras provide unparallel data quality which makes it possible to record action potentials with high signal to noise ration, to identify activation times through the maximum of the first derivative of the action potential upstroke and delineate activation wave fronts with great accuracy. In turn, these technical advances make it possible to apply digital image analysis algorithms to visualize activation wave fronts, and wavebreaks during VF. Wavebreak locations identified by image analysis routines are considerably less prone to false positives due to baseline instabilities and low S/N ratio of voltage signals compared to phase singularities identified by phase reconstruction techniques. Thus, wavebreak sites detected by image analysis routines did not occur preferentially at anatomical obstacles (i.e. large coronary vessels) or sites with a particular fiber orientation but occurred at sites surrounded by discordant voltage alternations. Technical advances in optical mapping are poised to make even greater contributions to cardiac electrophysiology through the development of probes to track changes in membrane potential; ionic concentrations (inside and outside myocytes); metabolic and oxidation-reduction state of the heart, in combination with signal processing techniques (Time frequency domain analysis, cross correlation, mutual information and image analysis routines).