Probing the structural hierarchy and energy landscape of an RNA T-loop hairpin

Abstract

The T-loop motif is an important recurrent RNA structural building block consisting of a U-turn sub-motif and a UA trans Watson–Crick/Hoogsteen base pair. In the presence of a hairpin stem, the UA non-canonical base pair becomes part of the UA-handle motif. To probe the hierarchical organization and energy landscape of the T-loop, we performed replica exchange molecular dynamics (REMD) simulations of the T-loop in isolation and as part of a hairpin. Our simulations reveal that the isolated T-loop adopts coil conformers stabilized by base stacking. The T-loop hairpin shows a highly rugged energy landscape featuring multiple local minima with a transition state for folding consisting of partially zipped states. The U-turn displays a high conformational flexibility both when the T-loop is in isolation and as part of a hairpin. On the other hand, the stability of the UA non-canonical base pair is enhanced in the presence of the UA-handle. This motif is apparently a key component for stabilizing the T-loop, while the U-turn is mostly involved in long-range interaction. Our results suggest that the stability and folding of small RNA motifs are highly dependent on local context.

INTRODUCTION

The folding of RNA is considered to be hierarchically organized (1–10). Four distinct stages can be distinguished: secondary structure formation, collapse mediated by metal ion condensation (11–14), partial helix assembly based on limited number of native tertiary interactions and conformational search leading to the final native structure. The last step (conformational search) is highly sequence dependent and requires the formation of recurrent structural motifs, small sets of nucleotides that code for specific folds. A powerful approach to solving the RNA folding problem lies in studying these recurrent structural motifs, to establish (i) how these motifs fold as independent units and (ii) how these units further assemble and guide the folding of the larger RNA molecule.

The RNA hairpin motif is one of the most common recurrent secondary structure elements found in naturally occurring RNA. Hairpin motifs generally contain a loop 4–7 nt long (15), with the UNCG or GNRA tetraloops (N = any nucleotide; R = purine) and the T-loop occurring most frequently (15–20). These loops share a number of similarities including a non-Watson–Crick closing base pair (bp) and the reversal of the direction of the RNA backbone. For tetraloop and T-loop motifs, this is accomplished by the U-turn sub-motif of specific sequence signature 5′-(g/u)NR-3′ (17,21). Many hairpins in RNA are thermostable (22,23) and are involved in tertiary structure formation (15,24). GNRA and UNCG hairpins have been extensively studied and are known to fold autonomously in the absence of long-range tertiary interaction. It has been suggested that these hairpins contribute as nucleation sites for the folding of larger RNA sequences (25). NMR and X-ray studies of tetraloop hairpins in isolation (18,26–28) or within the context of larger RNA molecules (29–34) have shown well-defined conformers with unique hydrogen bond networks in solution as well as within crystal packing. However, more recent experimental studies (18,25) on RNA tetraloop hairpins in isolation suggest the existence of alternate loop conformations not previously observed by NMR or X-ray crystallography, intimating that local environment can modulate the conformations of these and other motifs. Additional recent studies using ultrafast femtosecond spectroscopy has probed similar alternate base stacking patterns in the GNRA tetraloop, further supporting the notion of dynamic, rather than static, RNA motifs (35).

This work focuses on the folding of the T-loop, both in isolation and as part of a hairpin. Most experimental and theoretical studies focus on the more common GNRA and UNCG tetraloops (25,36–41), hence, our motivation to investigate alternate hairpin systems in an attempt to address the effects of sequence and structural parameters on hairpin folding (42). The T-loop motif was first observed in tRNAs and later found in viral RNAs, tmRNAs and ribosomal RNA (16). It is an important structural building block involved in formation of long-range tertiary interactions (16). The original definition of the T-loop included as key components: a U-turn motif, a UA trans Watson–Crick/Hoogsteen (W/H) bp stacked on a Watson–Crick bp and several bulging residues 3′ to the conserved adenosine (16). It was later discovered that the T-loop motif could also exist in single strand non-ordered regions without requiring the U:A trans W/H bp to be stacked on a WC bp (20). The definition of the T-loop motif, as a 5-nt loop formed of a U-turn and a UA trans W/H closing bp (20), was thus adopted in this article. Precisely how each key component of the T-loop contributes to the stability, folding and function of this motif remains poorly understood.

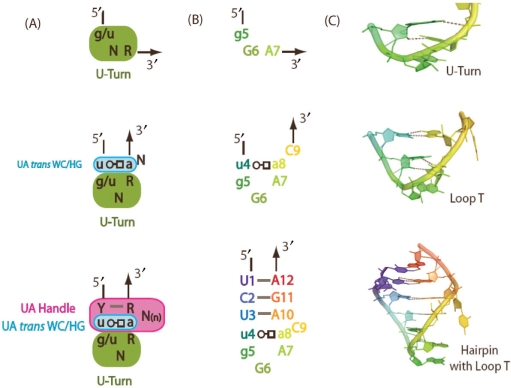
In this study, we present all-atom explicit solvent simulations of the T-loop using an enhanced sampling technique known as replica exchange molecular dynamics simulations (REMD) (43–45). The T-loop studied here consists of the U-turn sub-motif often found in the GNRA tetraloop, the U-A trans W/H closing bp, and a single nucleotide bulge at the 3′ end of the conserved adenine (Figure 1). The hairpin includes the T-loop and a 3-bp long stem. When the U:A trans W/H bp is stacked on a WC bp in the presence of a hairpin stem, a new motif called the UA-handle is created (Verzemnieks and Jaeger, manuscript in preparation). Consequently, our model system can be decomposed into many different subunits/components and it represents a minimal RNA structure with realistic hierarchical organization that is amenable to computational studies (Figure 1).

Figure 1.

T-loop RNA hairpin with its components: (A) sequence signature of the U-turn sub-motif, the U:A trans W/H bp, the UA-handle and the T-loop. The UA-handle motif comprises at least 5 nt that form a U:A trans W/H bp, a WC pb and a bulge. N stands for any nucleotides (G, A, U or C); R stands for purine (G or A); Y stands for pyrimidine (U or C). (B) Sequence of the motifs simulated in this study, which includes the U-turn motif, the closing U:A trans W/H bp, the single nucleotide C in bulge, the UA-handle and the hairpin stem. (C) 3D structures of the corresponding model systems in their crystal conformation. The trans W/H base pair is indicated according to the nomenclature of base pairs defined by Leontis and Westhof (60).

Our interests here are to (i) compare the behavior a sub-motif (T-loop) with and without a local context (the stem), (ii) address how and when the sequence information in the T-loop is used to guide RNA folding, (iii) compare the mechanism by which the T-loop hairpin folds with that of the tetraloop hairpins (that share the U-turn submotif and the non-Watson–Crick closing base pair with the T-loop hairpins) and (iv) probe the energy landscape for folding of the RNA hairpin.

METHODS AND MODELS

Models and sequences

Simulations were performed on two molecules: a T-loop in isolation and a hairpin containing the T-loop (see Figure 1). The T-loop in isolation has sequence 5′-UGGAAC-3′. The hairpin containing the T-loop has sequence 5′-UCU-[UGGAAC]-AGA-3′. Starting structures for both molecules were dissected from the crystal structure of Haloarcula marismortui large ribosomal subunit (Residues 310–321, PDB:1JJ2) (33,46).

Replica exchange molecular dynamics (REMD) simulation of T-loop in isolation and as part of a hairpin

Replica exchange molecular dynamics (REMD) simulations were performed on the isolated T-loop and on the hairpin systems described above using the Sander module from the Amber 8 package (47) and the Amber parm99 force field (48). The systems were neutralized by sodium counter-ions and solvated in explicit TIP3P water (49) using the LeaP module. A truncated octahedron water box was used such that the RNA starting structure is no less than 10 Å from the edge of the water box. Hydrogen-containing bonds were constrained by the SHAKE algorithm (50). Long-range electrostatic interactions were treated using the Particle Mesh Ewald method (PME) (51), and non-bonded cutoffs of 10 Å were used in the simulation. The system was minimized using the steepest-descent (500 steps) followed by the conjugate gradient (500 steps) method. Equilibration was performed under constant temperature and pressure of 1 atm. Production runs were carried out under constant temperature and volume. Constant temperature or constant pressure is achieved using the weak-coupling algorithm (52). The integration time-step is 2 fs.

The simulation of the T-loop in isolation involved 28 replicas at 28 different temperatures ranging from 298 to 400 K. Each replica of the T-loop in isolation was simulated for 20 ns, with a cumulative simulation time of 560 ns. The hairpin simulation involved 30 replicas at 30 different temperatures ranging from 298 to 400 K. Each replica of the hairpin was simulated for 80 ns, with a cumulative simulation time of 2.4 μs. Temperatures were exponentially spaced. The acceptance ratio for replica exchange is within the range of 10–20%. The starting structure for the T-loop in isolation is a coil-like structure obtained from a standard MD simulation at 300 K. The hairpin simulations were initiated from two different starting structures: a random collapsed conformer generated from a standard MD simulation at 300 K and the crystal conformer from the ribosome.

Convergence of the data is confirmed by calculating the PMFs with increasing simulation time. For example, PMFs were calculated for 20–40 ns, 20–60 ns and 20–80 ns for the hairpin (see Figure S1, Supplementary Data).

Data analysis

Standard parameters such as radius of gyration (Rg), root mean square deviation (RMSD) and number of hydrogen bonds are calculated using Carnal and Ptraj from Amber8 package (47). A hydrogen bond is formed when the hydrogen bond donor (the heavy-atom to whom the hydrogen is attached to) and acceptor (heavy-atom) are separated by <3.3 Å from each other. Additionally, the hydrogen bond donor (heavy-atom), the hydrogen atom, and the hydrogen bond acceptor (heavy-atom) are required to be aligned in a <20° angle. Native hydrogen bonds (NH) are defined as the ones present in the crystal conformer dissected from the ribosome. The number of non-native hydrogen bonds (NN) is calculated by subtracting the number of native hydrogen bond from the number of total hydrogen bond calculated based on the criteria mentioned above. Structures are visualized using Pymol (53) and UCSF Chimera (54).

The free-energy landscape for folding was characterized by determining potential of mean force (PMF) as a function of one or more order parameters at a given temperature. PMF has the units of energy and it gives information about the probability of being in a particular state or conformer such that lower energy corresponds to higher probability. Weighted Histogram Analysis Methods (WHAM) (55–57) is used to calculate PMFs. Data from all temperatures were taken into account during the PMF calculation. Data from the first 10 ns of each simulation were excluded from PMF calculations. For visual convenience, the energy of the lowest basin in each PMF has been shifted to zero. For the T-loop in isolation, the histogram grid size is 0.1 Å (RMSD) and 0.1 Å (Rg). For the hairpin, the histogram grid size is 0.2 Å (RMSD), 0.1 Å (Rg), 1 (NH) or 1 (NN).

RESULTS

T-loop in isolation and as part of a Hairpin

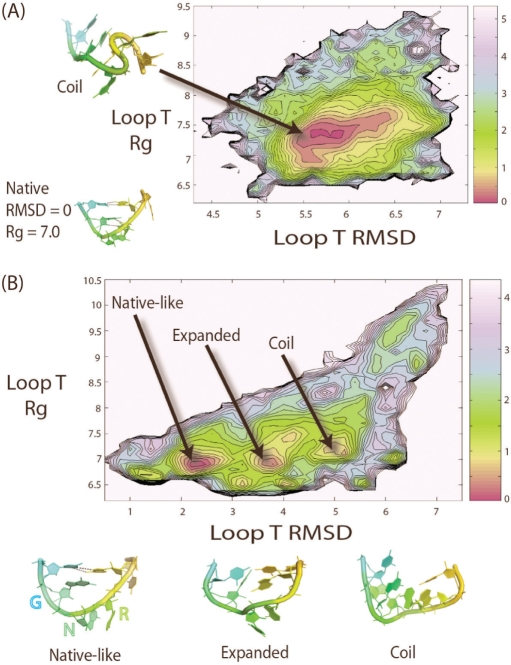
In order to compare the folding of the T-loop sub-motif in the presence and absence of a local context (the stem), we determined potentials of mean force (PMF) of both the T-loop in isolation and as part of a hairpin as a function of the all-atom RMSD of the T-loop (with respect to the crystal conformer) and Radius of gyration (Rg). The T-loop in isolation shows a PMF at 300 K with one major basin centered around Rg values of 7.4 Å and all-atom RMSD ranking between 5.5 and 6 Å (Figure 2A). Visual analysis of the structures within the cluster reveals that the T-loop in isolation tends to be in a coil conformation such that base stacking interactions are optimized. The presence of U-turn sub-motif does not seem to have any effects on the conformation of the T-loop in isolation. Kinks found in the backbone of T-loop are often necessary to fulfill optimal base stacking interactions. Overall, the coil structures deviate significantly from the T-loop crystal conformation and contain none of the signature hydrogen bonds belonging to this particular motif. These results indicate that the T-loop in isolation has no tendency to fold into its well-recognized crystal conformers (18). Neither of its structural components (U-turn or U:A trans W/H bp) is capable of directing the folding of the T-loop motif in this context. A suitable local environment appears critical for the formation of a U-shaped loop.

Figure 2.

(A) The PMF of T-loop in isolation plotted as a function of T-loop Rg versus RMSD at 300 K. T-loop in isolation shows a single minimum in the PMF. A representative structure is shown at the top left of the plot. The native state is not populated and it is not shown as a minimum on the plot. The PMF is plotted such that the energy of the global minimum is at 0 kcal/mol. (B) The PMF of the T-loop in the context of a hairpin at 300 K is plotted as a function of the T-loop RMSD versus Rg. For clarity, stems are not shown in the images. The PMF shows multiple distinct minima. All sample structures shown in the plot exhibit characteristic features (discussed in text) shared by the ensemble of structures found in the clusters. The energy of the global minimum (native) is 0 kcal/mol. The energy of the second minimum (expanded) is 0.4 kcal/mol. The energy of the third minimum (coil) is 0.6 kcal/mol. Each contour line represents an increase of 0.2 kcal/mol or a reduction in probability by ∼28%. A local minimum is considered to be significant when it contains more than 2% of the population and is separated by a barrier of at least 1.5 kcal/mol. All RMSD and Rg values are in units of Angstroms (Å). The PMF is plotted in units of kcal/mol, where 1 kcal roughly equals to 0.6 KT at 300 K.

In the presence of a stem, the PMF as a function of the T-loop RMSD (with respect to the crystal conformer) and the T-loop Rg is significantly different from that of the T-loop in isolation. Multiple distinct minima are observed (Figure 2B). The first minimum [observed at RMSD = 2.2 Å, Rg = 6.9 Å] corresponds to a relatively intact hairpin with native-like T-loops. In these conformers, we notice that the U4-A8 trans W/H closing bp is retained as part of the UA-handle (Figure 1), while the U-turn sub-motif (G5-G6-A7) loses its characteristic hydrogen bond contacts between the 2′ OH position of G5 and the N7 of A7. Both positions G6 and A7 of the U-turn tend to flip outside the loop and become fully solvated (Figure 2B). In some cases, they remain stacked outside the loop. We found the U-turn in the context of the T-loop to be much more flexible than within the context of a GNRA tetraloop, which is more restricted by internal base stacking contacts and may only allow its second nucleotide position (N) to flip out (25,38). This is expected because the third position of the loop (R) is stacked between the second position (N) and fourth position (A) in the context of a GNRA tetraloop. On the other hand, within the T loop context, A7 is at 7 Å from the U4-A8 trans W/H closing bp and only stacks with G6. Thus, the flexibility of the U-turn is highly context dependent. In the T-loop within natural structural contexts (i.e. in the presence of tertiary interactions), a nucleotide is often intercalated between the last position (R) of the U-turn and the UA-handle.

The second minimum [observed at RMSD = 3.8 Å Rg = 7 Å] corresponds to a more expanded T-loop in which the UA-handle in addition to the U-turn is lost. In the third minimum [observed at RMSD = 5.2 Å Rg = 7.1 Å], the T-loop starts to resemble a random coil. Our results suggest that the hairpin alone does not ensure the conformational stability of the U-turn sub-motif. Tertiary interactions are probably required to stabilize the U-turn. On the other hand, the UA-handle motif significantly stabilizes the U:A trans W/H bp through additional stacking and H-bond contacts with the apical WC bp of the stem (Verzemnieks and Jaeger, manuscript in preparation). In summary, we found that the conformation of the T-loop is highly dependent on the overall conformation of the hairpin and it is significantly different from the stacking dominated coil conformer adopted by T-loop in isolation.

The UA-handle motif requires at least one bulging nucleotide (C9) at the 3′ end of the conserved A8 to bridge the U:A trans W/H bp to its WC bp (Figure 1A). In UA-handle motifs from the ribosome, these bulging nucleotides are typically flipped outward to participate in additional tertiary interactions with their surrounding context (Verzemnieks and Jaeger, manuscript in preparation). We were not able to observe any flipping motion in the bulge nucleotide C9 during the 164 ns standard molecular dynamics simulation at 300 K (data not shown here). However, we did isolate structures whose bulge nucleotide C9 has flipped inward during the replica exchange simulation, hence the importance of using enhanced sampling techniques to probe RNA folding. Our data are consistent with the observation that additional stabilizing contacts are necessary for stabilizing the bulge nucleotide and preventing it from flipping inward in the context of the ribosome.

Free energy surface of the hairpin at 300 K and folding transition state

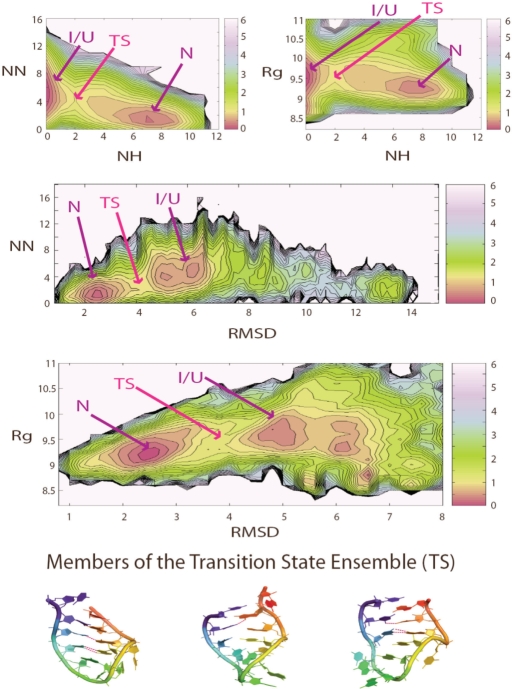
To gain insight into the energy landscape and folding mechanism of the T-loop hairpin, we determined the PMF using a larger range of structural parameters. At 300 K, at least two major basins are found when plotting the PMF as a function of the following parameters: Rg, RMSD of hairpin (compared to crystal conformer), number of native hydrogen bond (NH) and number of non-native hydrogen bonds (NN) (Figure 3). The basin with low RMSD (low NN or high NH), corresponds to the native basin, while the non-native basin is characterized by high RMSD (high NN or low NH). It is worth mentioning that when the PMF is plotted over a limited set of parameters, each local minimum shown on the PMF may correspond to an ensemble of structures that are quite different from each other, highlighting the difficulty in representing the entire spectrum of structural heterogeneity using a limited set of structural parameters. Nevertheless, we found the use of Rg versus RMSD as a good coordinate sets to distinguish native from non-native structures. When the PMF is plotted as a function of the RMSD versus Rg at 300 K (Figure 3), we found in addition to the deep native state minimum (N), a non-native basin containing several sub-basins corresponds to different trapped states. The relative energies of both the native and non-native basin are similar, which indicates that both minima are populated at this temperature and that additional interactions with the environment might be necessary to further stabilize one conformer over another.

Figure 3.

The PMFs of the RNA hairpin at 300 K are shown as a function of a number of order parameters. NH is the number of native hydrogen bonds and NN the number of non-native hydrogen bonds. Rg is the radius of gyration of the hairpin and RMSD is the root mean square deviation from the hairpin crystal conformation in the ribosome. The crystal structure has 12 native hydrogen bonds: 3 belong to the U-turn sub-motif, 2 belong to the U-A trans WC/H bp and 7 belong to the helical stem. Local minima are indicated in red. The transition state is defined as the barrier region between the native and non-native basins. The energy of the native and non-native basin is similar, and the energy of the transition state is at least 1.5 kcal/mol higher than the two basins. Sample transition state structures, which contain 1–3 native hydrogen bonds in the helical stem, are shown here. All RMSD and Rg values are in Angstroms units (Å). PMF is plotted in units of kcal/mol, where 1 kcal roughly equals to 0.6 KT at 300 K.

The native basin [at RMSD = 2–3 Å, Rg = 9–9.5 Å, NN = 1–2, NH = 7–9] includes the crystal-like states (N). The crystal structure has 12 native hydrogen bonds: 3 belong to the U-turn sub-motif, 2 belong to the U:A trans W/H bp and 7 belong to the helical stem. Visual analysis shows that state N has mostly complete stem formation (seven native hydrogen bonds). Most often, state N also has well-formed U:A trans W/H bp (two additional native hydrogen bonds). On the other hand, State N has a flexible U-turn and does not contain any of the three native hydrogen bonds associated with this sub-motif found in the crystal structure. State N is relatively compact due to its fully formed helical stem. We distinguish the non-native basin [at RMSD = 5–7 Å, Rg = 8.5–10 Å, NN = 2–10, NH = 0–1] into two classes of structures: intermediates (I), coil/unfolded (U). State I is dominated by structures that fold in a symmetrical fashion such that the base pairs in the stem are approximately aligned with each other. State I can be considered as the pre-zipping state. State I is almost always slightly more expanded than state N because the helical strands are not close enough to form hydrogen bonds. State U, on the other hand, often folds into a shape that does not resemble that of the native hairpin. State U is likely to require more extensive structural arrangement in order to fold correctly to state N. State U can either be more expanded or compact than state N depending on the nature of the coil structures. Structures within the non-native basin at 300 K are often stabilized by a number of non-native hydrogen bond instead of being completely random coils. Among all non-native hydrogen bonds present in the structures belonging to the non-native basin, ∼60% were contributed by hydrogen bond donors and acceptors present in the nucleotide base while the rest were contributed by backbone phosphate and 2′OH group in the sugar (data not shown here). State I is probably the product of specific collapse events while state U is likely to be a result of the non-specific collapse events proposed by Pande and coworkers in their study of the tetraloop hairpin (40).

A possible transition state is proposed here based on structures located in the barrier region between the two local minima referred to as the native and non-native basin (Figure 3). We define the transition state (Figure 3) as having the following parameters: Rg = 9–9.5 Å, RMSD = 3.5–4.5 Å, NH = 1–3, and NN = 2–5. We found the transition state to be very much hairpin like and containing 1–3 native hydrogen bond as well as helical twist. Zipping usually initiates within the stem region or, to a lesser extent, at the U:A trans W/H base pair. The barrier height between the native and non-native basins is ∼1.5 kcal/mol.

Temperature dependence of the RNA hairpin energy landscape

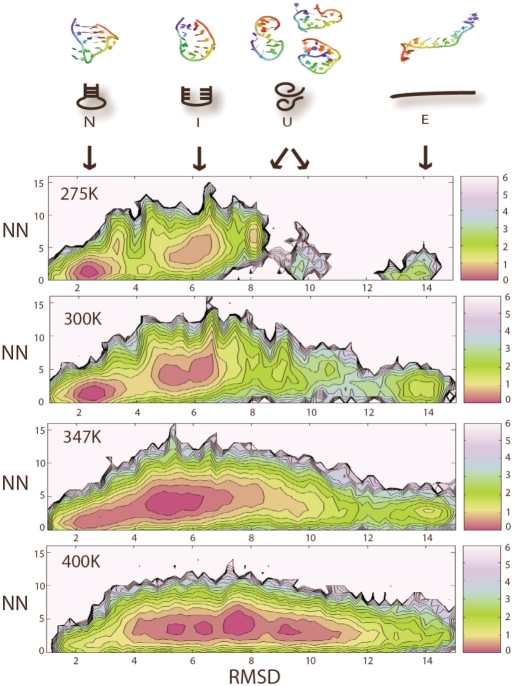
To assess the ruggedness of the energy landscape, we also investigate the temperature dependence of the RNA hairpin PMF. Here, we consider a minimum to be significant when it is separated by a barrier larger than 1.5 kcal/mol and contains at least 2% of the total population. At both low temperature (275 K) and room temperature (300 K), we observed local minima corresponding to state N, I and U, as defined above (Figure 4). Interestingly, we found that the U state from 275 K corresponds to a specific coil-like structure, while the U state at 300 K corresponds to a more heterogeneous population of coil structures. We speculate that the particular coil conformer observed at 275 K is only marginally stable at extremely low temperatures. When the temperature is raised slightly to 300 K, this particular coil conformer quickly overcomes energy barriers and inter-convert with other coil conformers or converts to more stable N and I state. As temperature is raised further to 347 K (Figure 4), N and I are no longer viewed as separate minima. At the same time, a newly emerged extended conformer E becomes more populated (where <0.7% of the structures belongs to E at 275 K, while 8% of the structures belongs to E at 347 K). At 400 K (Figure 4), state N is no longer significantly populated, signaling the final loss of native population. E is populated, but it ceases to be a separated minimum due to low barrier height at 400 K. The most populated structures at 400 K are coil-like unfolded structures (U), which are entropically favored due to their great structural heterogeneity. These structures seem to be flexible and rapidly inter-convert with each other due to the low barrier heights.

Figure 4.

Temperature dependence of the hairpin energy landscape. The PMF of the hairpin is plotted as a function of hairpin RMSD (compared of crystal conformer) versus the number of non-native hydrogen bonds (NN) at 275, 300, 347 and 400 K. Local minima are considered to be significant when they contains more than 2% of the population and are separated by a barrier of at least 1.5 kcal/mol. All RMSD values are in Angstroms units (Å). PMF is plotted in units of kcal/mol, where 1 kcal roughly equals to 0.6 KT at 300 K.

Fully extended state E only becomes significantly accessible when temperature is raised above 300 K, which implies that it might be isolated by a relatively high barrier that cannot be easily overcome at low temperatures. E is considered as a separate minimum, which differs from unfolded coil states U for several reasons. Visual analysis shows that E is a straight extended conformer stabilized by base stacking, which is more entropically unfavorable than the coil unfolded states. In addition, E appears to be a distinct minimum separated by a 1.5 kcal/mol barrier from the coil-like unfolded states at 347 K.

DISCUSSION

Due to the ruggedness of the energy landscape typically associated with RNA (58,59), RNA is prone to be trapped in meta-stable local minima. Recent kinetics data suggested that even the folding of a small 8-mer RNA hairpin consisting of a tetraloop and 2-bp long stem has a rugged energy landscape and requires a 4-state model to accurately describe its folding (36). In addition, several computational studies on RNA tetraloop hairpin have yield alternate 3-state folding models and competing folding mechanism referred to as expansion, unzipping and a combination of both (38,40). Here, we employed replica exchange algorithm in addition to standard molecular dynamics techniques during our simulations in order to enhance sampling.

Characterization of the T-loop motif and its structural components (U-turn and U:A trans W/H bp) in different structural contexts reveals that the T-loop itself, and especially the U-turn sub-motif, is an intrinsically flexible motif. Its sequence does not have a tendency to fold into conformations commonly associated with this motif in the ribosome and other naturally occurring RNAs. This is supported by the observation that the T-loop is usually found to participate in tertiary structure formation through long-range interactions (Verzemnieks and Jaeger, manuscript in preparation). While the U-turn sub-motif exhibits high conformational flexibility regardless of the helical stem, the U:A trans W/H bp, on the other hand, is more stable in the presence of a hairpin stem. It seems that although the T-loop can be considered as a 5-nte motif composed only of the U-turn and the U:A trans W/H bp, the stability of the T-loop is indeed enhanced by the stacking of an additional WC bp on the U:A trans W/H bp as found in the UA-handle (Verzemnieks and Jaeger, manuscript in preparation). In the scenario where this additional WC base pair is missing, the stability of the T-loop motif is probably more dependent on the structural context of the RNA and the availability of tertiary interactions. For example, the T-loop has been found to fold in the presence of another T-loop by providing intercalating bases to each other as seen in the S-domain of Rnase P and domain 1 of the 23S ribosomal RNA (34).

We speculate that the sequence information embedded in the U-turn sub-motif and T-loop are likely to be important during the later conformational search stage that eventually leads to native helix packing. Our results imply that the U-turn probably does not play an active role during the secondary structure formation despite its frequent occurrence. We speculate that while these ‘special’ terminal loops might stabilize the hairpin once it has formed, they do not necessarily contribute to the folding of the hairpin. This result reinforces the observation by Pleij and coworkers that hairpin folding kinetics are the same when a GNRA tetraloop is substituted by a non-GNRA tetraloop or when the loop size is increased from 4 to 6 nt (42). Comparable studies of the T-loop with a more stable UA-handle (Verzemnieks and Jaeger, manuscript in preparation) might be interesting for future investigation. The partially zipped hairpin-like transition state found in this study leads us to believe that zipping is extremely rapid and partially zipped structures are only short-lived transient species for a small hairpin. The transition state described above may be a feature of small hairpins whose stems length does not exceed a few nucleotides. As the stem lengthens, complete zipping might not be as rapid, however.

It is interesting to note that Gruebele and coworkers (36) observed unusual folding kinetics for a small UNCG tetraloop hairpin that were suggestive of an underlying rugged energy landscape. Our observation of multiple minima at different temperatures in the PMFs of the T-loop hairpin seems to corroborate their data (36). Although the actual structure and the nature of the minima may differ from case to case depending on the RNA system being studied (e.g. UNCG tetraloop hairpin versus the T-loop hairpin), we believe such phenomenon reflects the intrinsic ruggedness of the RNA energy landscape and it is a generic feature shared by many RNA molecules.

CONCLUSION

In this study, we investigate the structural hierarchy and energy landscape of an RNA T-loop hairpin. We found that the U-turn component of the T-loop motif is flexible both when the T-loop is in isolation and as part of a hairpin. The other component of the loop, the U:A trans W/H bp, can be stabilized in the context of the UA-handle motif when a stem is present. We speculate that the UA-handle plays an important role in stabilizing small RNA motifs such as the T-loop motif. Future experimental research in our laboratory will aim at further probing this idea. Our simulations indicate that the energy landscape for the folding of the T-loop hairpin is rugged. This roughness is likely a common feature of small RNA motifs and implies that additional help from the environment (via, for instance, interaction with neighboring residues or through long range interactions) is needed to stabilize a particular conformer over another and ensure correct folding.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.