Gaussian Induced Dipole Polarization Model

Abstract

A new induced dipole polarization model based on interacting Gaussian charge densities is presented. In contrast to the original induced point dipole model, the Gaussian polarization model is capable of finite interactions at short distances. Aspects of convergence related to the Gaussian model will be explored. The Gaussian polarization model is compared with the damped Thole-induced dipole model and the point dipole model. It will be shown that the Gaussian polarization model performs slightly better than the Thole model in terms of fitting to molecular polarizability tensors. An advantage of the model based on Gaussian charge distribution is that it can be easily generalized to other multipole moments and provide effective damping for both permanent electrostatic and polarization models. Finally, a method of parameterizing polarizabilities is presented. This method is based on probing a molecule with point charges and fitting polarizabilities to electrostatic potential. In contrast to the generic atom type polarizabilities fit to molecular polarizability tensors, probed polarizabilities are significantly more accurate in terms of reproducing molecular polarizability tensors and electrostatic potential, while retaining conformational transferability.

Introduction

In recent years, including polarization in Molecular Dynamics Simulations has been the center of a considerable amount of effort.^1,2 It is known that molecular dipole moments change significantly when transferred from gas to liquid phase; nonpolarizable classical force fields based solely on additive models are not able to capture this effect. Rather, permanent molecular dipole interactions are often enhanced to compensate.³

Including an explicit polarization term in the force field is a method to model these multibody effects in condensed phase, while still being able to correctly calculate gas phase properties, such as dimer geometries and interaction energies. Polarization is likely to be particularly important in accurate descriptions of biomolecular interactions. A further important advantage of using a polarizable force field relates to parameter development. If polarization is included, a force field may be parameterized to reproduce accurate gas-phase quantum data and then still be expected to do well in the liquid phase.

Several polarization models such as the Drude oscillator,^4,5 fluctuating charges,⁶ and induced dipoles^7–9 have been suggested for use in water models. However, the induced dipole model^1,2,10 and the fluctuating charge model^2,10 seems to have received the most attention in terms of force field development. The simplest induced dipole model places isotropic inducible point dipoles on each atom. If hyperpolarization effects, as might arise from strong electric fields, are absent, then the induced dipole responds linearly with respect to electric field. In this case, the induced dipole $\stackrel{\rightharpoonup }{\mu }$ on an atom is the product of the total electric field $\stackrel{\rightharpoonup }{E}$ and a scalar atomic polarizability α.

$$\stackrel{\rightharpoonup }{\mu }=\alpha \stackrel{\rightharpoonup }{E}$$ (1)

The total electric field is composed of the external electric field from permanent charge sources ${\stackrel{\rightharpoonup }{E}}^0$ and the contribution from other induced dipoles. To reproduce molecular polarizability tensors using isotropic atomic polarizabilities, induced dipoles within the same molecule should interact with one another.¹¹ Applequist et al. found parameters for this model by fitting atomic polarizabilities to experimental molecular polarizability tensors.¹²

The development of the interacting induced point dipole model was an important step in modeling polarization because it led to accurate calculations of molecular polarizability tensors. The most serious drawback to using the original point dipole model is known as the polarization catastrophe. This phenomenon happens when two mutually interacting inducible dipoles with atomic polarizabilities α₁ and α₂ diverge at a finite distance, given by:

$$R={\left(4{\alpha }_1{\alpha }_2\right)}^{1∕6}$$ (2)

During a molecular dynamics simulation, this situation leads to nonphysical forces and velocities causing the simulation to fail. Thole^13,14 remedied this problem by applying a damping function to dipole–dipole interactions. As an added feature, the damped model resulted in an improved fit to the molecular polarizability tensor data relative to the Applequist point dipole model.

An alternative to the damped interaction model by Thole, which has recently been suggested, is to employ interacting Gaussian densities rather than point dipoles.^15,16 An advantage of using a charge distribution model over the Thole model is that it may be readily generalized to other multipole moments. For example, a point charge could be replaced by a Gaussian ‘s’ orbital and a dipole could be replaced by a ‘p’ orbital.¹⁷ It has been shown that point multipoles are the large exponent limit of Hermite Gaussian functions.¹⁸ Indeed, multipoles in current force fields¹ could be replaced by Hermite Gaussian functions,¹⁹ which effectively damp short range electrostatic interactions and provide a more realistic description of penetration effects, and which can be significant in dimer geometries.^20,21

A peculiar aspect of the Gaussian model that relates to the polarization catastrophe should be pointed out. If the inducible point dipoles are replaced by inducible Gaussian dipoles, it might be expected that the interaction remains finite, since the interaction of two permanent Gaussian dipoles is finite at all distances. However for large exponents, the Gaussian dipoles start to behave like point dipoles, which interact strongly. If the exponents are too large, the interaction is too strong and a polarization catastrophe occurs. A relationship between the minimum diffuseness of the Gaussian exponent β and atomic polarizability α, namely:

$$\beta <\frac{1}{{\left(\alpha \frac{4}{3\sqrt{8\pi }}\right)}^{\frac{1}{3}}}$$ (3)

will be derived in the Appendix that will prevent a polarization catastrophe.

A similar analysis was performed on the Thole model,¹³ {ρ(u) = 3a/4π exp((au³)}, and the maximum value of the damping parameter a was found to be 1.0.

Here, the Gaussian induced dipole model is compared with the damped Thole and the Applequist point dipole models. In the same spirit as Thole and Applequist, transferable atom type polarizabilities will be derived for all three models by fitting to molecular polarizability tensors calculated at the B3LYP/cc-pVTZ level.

Polarizabilities generated by fitting to molecular polarizability tensor data are convenient in that they are transferable among related molecular classes, however they are limited in accuracy because they rely on the assumption of atom types. For example, all oxygen atoms are grouped into one class and assigned the same polarizability, regardless of the neighboring environment. In this paper, an independent procedure for generating atomic polarizabilities will be presented. It is based on probing a molecule with point charges^2,22 or external electric fields¹⁰ and calculating the response electrostatic potential, which is the potential generated by the molecule in the external field of the point charge probes minus the potential of the molecule in vacuum. Atomic polarizabilities are then fit to this response potential on a grid of points encompassing the molecule. Just as atomic charges fit to the electrostatic potential are found to reproduce molecular dipole moments,^3,23,24 probed polarizabilities fit to the electrostatic response potential are found to reproduce molecular polarizability tensors. In contrast to atom type polarizabilities, probed polarizabilities are optimized for specific molecules improving accuracy.

While nontransferable, Gaussian probed polarizabilities are readily computed. Like fitted atomic partial charges, probed polarizabilities are not transferable between molecules. However, probed polarizabilities are conformationally invariant, which is important for electrostatics of flexible molecules. The Gaussian polarization model is being incorporated into the AMBER²⁵ molecular dynamics simulation package. Probed polarizabilities will be generated for the AMBER^26,27 and GLYCAM²⁸ force fields, and the fitting program will be made available.

Method

Gaussian Model

In this section, aspects of implementing a Gaussian charge density model will be presented. In particular, the dipole–dipole interaction matrix and relationships for electric potential and fields will be needed for the Gaussian polarization model. Interaction energies can be expressed in terms of ‘effective’ electric fields between Gaussian particles. The ‘effective’ electric field rather than the ordinary electric field are used to induce polarization. It will be shown in a future paper that the use of ‘effective’ electric fields is necessary for the energy, work, and force for the Gaussian induced dipole model to have the same form as the induced point dipole model.²⁹ These results are stated below and a discussion of electric potential and fields is provided in Appendix A.

A Gaussian ‘s’ orbital charge density with nuclear center at $\overrightarrow{R}$, charge q, and exponent β is given by:

$${\rho }_s(\overrightarrow{r};\overrightarrow{R})=q{\left(\frac{{\beta }^2}{\pi }\right)}^{\frac{3}{2}}{e}^{-{\beta }^2{\mid \overrightarrow{r}-\overrightarrow{R}\mid }^2}$$ (4a)

Similarly, a Gaussian ‘p’ orbital density with dipole moment $\overrightarrow{\mu }$ is given by:

$${\rho }_p(\overrightarrow{r};\overrightarrow{R})=\overrightarrow{\mu }\cdot {\nabla }_R{\left(\frac{{\beta }^2}{\pi }\right)}^{\frac{3}{2}}{e}^{-{\beta }^2{\mid \overrightarrow{r}-\overrightarrow{R}\mid }^2}$$ (4b)

The interaction energies between two Gaussian ‘s’ and ‘p’ orbital densities at ${\overrightarrow{R}}_1$ and ${\overrightarrow{R}}_2$ with exponents β₁ and β₂ are given by^30,31

$$U_{\mathrm{ss}}=q_1{q}_2{\beta }_{12}{B}_0\left(x\right)$$ (5a)

$$U_{\mathrm{sp}}=q_1{\overrightarrow{\mu }}_2\cdot {\overrightarrow{R}}_{12}{\beta }_{12}^3{B}_1\left(x\right)$$ (5b)

$$U_{\mathrm{pp}}=\left({\overrightarrow{\mu }}_1{\overrightarrow{\mu }}_2\right){\beta }_{12}^3{B}_1\left(x\right)-{\beta }_{12}^6\left({\overrightarrow{\mu }}_1{\overrightarrow{R}}_{12}\right)\left({\overrightarrow{\mu }}_2{\overrightarrow{R}}_{12}\right)B_2\left(x\right)$$ (5c)

where^32,33

$${\beta }_{12}\equiv \frac{{\beta }_1{\beta }_2}{\sqrt{{\beta }_1^2{\beta }_2^2}}$$ (6)

$$\begin{array}{cc}\hfill {\overrightarrow{R}}_{12}& \equiv {\overrightarrow{R}}_1-{\overrightarrow{R}}_2\hfill \\ \hfill x& \equiv {\beta }_{12}{R}_{12}\hfill \end{array}$$ (7)

$$\begin{array}{cc}\hfill B_0\left(x\right)& \equiv \frac{erf\left(x\right)}{x}\hfill \\ \hfill B_1\left(x\right)& \equiv \frac{-1}{x}\frac{d}{dx}{B}_0\left(x\right)=\frac{1}{x^2}\left(\frac{erf\left(x\right)}{x}-\frac{2}{\sqrt{\pi }}{e}^{-x^2}\right)\hfill \\ \hfill B_2\left(x\right)& \equiv \frac{-1}{x}\frac{d}{dx}{B}_1\left(x\right)=\frac{1}{x^4}\left(3\frac{erf\left(x\right)}{x}-\frac{2}{\sqrt{\pi }}(3+2x^2)e^{-x^2}\right)\hfill \end{array}$$ (8)

and erf(x) is the error function defined by:

$$erf\left(x\right)\equiv \frac{2}{\sqrt{\pi }}{\int }_0^x\exp (-u^2)du$$ (9)

It should be noted that for large x, erf(x) → 1 and the point charge - point dipole behavior is recovered.

Equation (5c) can be rewritten as:

$$U_{\mathrm{pp}}={\overrightarrow{\mu }}_1\cdot {\overrightarrow{\overrightarrow{T}}}^{12}\cdot {\overrightarrow{\mu }}_2,$$ (10)

in which ${\overrightarrow{\overrightarrow{T}}}^{12}$ is the symmetric dipole–dipole interaction matrix given by:

$${\overrightarrow{\overrightarrow{T}}}^{12}={\beta }_{12}^3\left\{B_1\left(x\right)\overrightarrow{\overrightarrow{I}}-{\beta }_{12}^2{\overrightarrow{R}}_{12}{\overrightarrow{R}}_{12}{B}_2\left(x\right)\right\}$$ (11)

The potential V_s at ${\overrightarrow{R}}_1$ of a Gaussian ‘s’ orbital at ${\overrightarrow{R}}_2$ with charge q₂ and exponent β₂ is given by:

$$V_{\mathrm{s}}\left({\overrightarrow{R}}_1\right)=q_2{\beta }_2{B}_0\left({\beta }_2{R}_{12}\right)$$ (12)

Similiarly, the potential V_p at ${\overrightarrow{R}}_1$ of a Gaussian ‘p’ orbital at ${\overrightarrow{R}}_2$ with dipole q₂ and exponent β₂ is given by:

$$V_{\mathrm{p}}\left({\overrightarrow{R}}_1\right)={\overrightarrow{\mu }}_2{\overrightarrow{R}}_{12}{\beta }_2^3{B}_1\left({\beta }_2{R}_{12}\right)$$ (13)

The ordinary electric field at a single point from a Gaussian ‘p’ orbital can found by taking the negative gradient of eq. (13).

However, it proves much more convenient to define an ‘effective’ electric field ${\stackrel{\sim }{\overrightarrow{E}}}_{\mathrm{p}}^{2\to 1}$ arising from a Gaussian ‘p’ orbital with dipole ${\overrightarrow{\mu }}_2$ onto another Gaussian ‘p’ orbital with dipole ${\overrightarrow{\mu }}_1$ by:

$$U_{\mathrm{pp}}=-{\overrightarrow{\mu }}_1\cdot {\stackrel{\sim }{\overrightarrow{E}}}_{\mathrm{p}}^{2\to 1}$$ (14)

Using eq. (10), ${\stackrel{\sim }{\overrightarrow{E}}}_{\mathrm{p}}^{2\to 1}$ can be written as:

$${\stackrel{\sim }{\overrightarrow{E}}}_{\mathrm{p}}^{2\to 1}=-{\overrightarrow{\overrightarrow{T}}}^{12}\cdot {\overrightarrow{\mu }}_2$$ (15)

The ordinary potential and electric field arises from a single charge distribution, while the ‘effective’ electric field from one Gaussian particle to another takes into account both charge distributions. In Appendix A, ‘effective’ potentials and electric fields can be derived by considering the variation in energy when an infinitesimal Gaussian test particle is added to the system. Finally, the ‘effective’ electric field arising from a point charge source onto a Gaussian particle is given by:

$${\stackrel{\sim }{\overrightarrow{E}}}_q^{2\to 1}=q_2{\beta }_{12}^3{\overrightarrow{R}}_{12}{B}_1\left({\beta }_{12}{R}_{12}\right)$$ (16)

Polarization Model

The Gaussian induced dipole model is essentially that of Applequist and Thole, except that the dipole–dipole interaction matrix ${\overrightarrow{\overrightarrow{T}}}^{12}$ is given by eq. (11) and the electric fields used are ‘effective’ [eqs. (15) and (16)] between Gaussian particles. Each of the N particles has an isotropic polarizability α_i assigned to it. The induced dipole on particle i is the product of the atomic polarizability α_i and the sum of the external electric field due to permanent charges ${\overrightarrow{E}}^{0,i}$ and the electric field due to other induced dipoles, $-{\sum }_{j\ne i}{\overrightarrow{\overrightarrow{T}}}^{ij}{\overrightarrow{\mu }}^j$.

$${\overrightarrow{\mu }}^i={\alpha }_i\left({\overrightarrow{E}}^{0,i}-\sum _{j\ne i}{\overrightarrow{\overrightarrow{T}}}^{ij}\cdot {\overrightarrow{\mu }}^j\right)$$ (17)

This is a linear equation in ${\overrightarrow{\mu }}^i$, which can be solved and the molecular polarizability tensor can be calculated as in ref. 12 To summarize, the symmetric molecular polarizability tensor, ${\alpha }_{pq}^{\mathrm{mol}}$, is defined by:

$$\left(\begin{array}{c}\hfill {\mu }_x^{\mathrm{mol}}\hfill \\ \hfill {\mu }_y^{\mathrm{mol}}\hfill \\ \hfill {\mu }_z^{\mathrm{mol}}\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill {\alpha }_{xx}^{\mathrm{mol}}\hfill & \hfill {\alpha }_{xy}^{\mathrm{mol}}\hfill & \hfill {\alpha }_{xz}^{\mathrm{mol}}\hfill \\ \hfill {\alpha }_{yx}^{\mathrm{mol}}\hfill & \hfill {\alpha }_{yy}^{\mathrm{mol}}\hfill & \hfill {\alpha }_{yz}^{\mathrm{mol}}\hfill \\ \hfill {\alpha }_{zx}^{\mathrm{mol}}\hfill & \hfill {\alpha }_{zy}^{\mathrm{mol}}\hfill & \hfill {\alpha }_{zz}^{\mathrm{mol}}\hfill \end{array}\right)\left(\begin{array}{c}\hfill E_x^{0,\mathrm{mol}}\hfill \\ \hfill E_y^{0,\mathrm{mol}}\hfill \\ \hfill E_z^{0,\mathrm{mol}}\hfill \end{array}\right)$$ (18)

where ${\overrightarrow{\mu }}^{\mathrm{mol}}$ is the molecular induced dipole and ${\overrightarrow{E}}^{0,\mathrm{mol}}$ is an external electric field applied to the molecule. To solve for ${\alpha }_{pq}^{\mathrm{mol}}$, eq. (17) can be rewritten as

$$\stackrel{‒}{A}\stackrel{‒}{\mu }={\stackrel{‒}{E}}^0$$ (19)

where $\stackrel{‒}{\mu }$ and ${\stackrel{‒}{E}}^0$ are 3N column vectors, and $\stackrel{‒}{A}$ is a 3N × 3N matrix given by:

$$\stackrel{‒}{A}=\left[\begin{array}{cccc}\hfill {\alpha }_1^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\alpha }_2^{-1}\hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \dots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_{\mathrm{N}}^{-1}\hfill \end{array}\right]+\left[\begin{array}{cccc}\hfill 0\hfill & \hfill T^{12}\hfill & \hfill \dots \hfill & \hfill T_{1\mathrm{N}}\hfill \\ \hfill T^{21}\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \dots \hfill \\ \hfill T^{\mathrm{N}1}\hfill & \hfill T^{\mathrm{N}2}\hfill & \hfill \dots \hfill & \hfill 0\hfill \end{array}\right]$$ (20a)

or in tensor notation,

$${\stackrel{‒}{A}}_{pq}^{ij}=\frac{1}{{\alpha }_i}{\delta }_{ij}{\delta }_{pq}+T_{pq}^{ij}$$ (21b)

Solving for $\stackrel{‒}{\mu }$ in eq. (19),

$$\stackrel{‒}{\mu }=\stackrel{‒}{B}\stackrel{‒}{E}$$ (22)

where $\stackrel{‒}{B}\equiv {\stackrel{‒}{A}}^{-1}$. Since the total induced molecular dipole is found by summing the induced atomic dipoles, the calculated molecular polarizability tensor ${\alpha }_{pq}^{\mathrm{mol}}$ is the direct sum of $\stackrel{‒}{B}$ over particle number.

$${\alpha }_{pq}^{\mathrm{mol}}=\sum _{i=1}^N\sum _{j=1}^N{\stackrel{‒}{B}}_{pq}^{ij}$$ (23)

In the simple case of diatomic molecules, the polarizability tensor has two independent components: one parallel to the bond axis α_∥ and another perpendicular to the bond axis α_⊥. By considering two particles interacting in one dimension, these components can be derived for the Gaussian model by solving for ${\mu }_x^1$ and ${\mu }_x^2$ in eq. (17) using eq. (11):

$${\alpha }_{\parallel }=\frac{{\alpha }_1+{\alpha }_2+2{\alpha }_1{\alpha }_2{\beta }_{12}^{3}F\left(x\right)}{1-{\alpha }_1{\alpha }_2{\beta }_{12}^{6}F\left(x\right)F\left(x\right)}$$ (24a)

$${\alpha }_{\perp }=\frac{{\alpha }_1+{\alpha }_2-2{\alpha }_1{\alpha }_2{\beta }_{12}^3{B}_1\left(x\right)}{1-{\alpha }_1{\alpha }_2{\beta }_{12}^6{B}_1^2\left(x\right)}$$ (24b)

$$F\left(x\right)\equiv x^2{B}_2\left(x\right)-B_1\left(x\right)$$ (25)

where α_i are the polarizabilities, R is the separation, and β, B₁, B₂, and x are given by eqs. (6), (7), and (8).

Atom Type Polarizability Parameterization

To compare the Gaussian model with other induced dipole models, a set of atom type (AT) specific atomic polarizabilities has been derived by fitting to molecular polarizability tensors as in Thole¹³ and Applequist et al.¹² The geometries were optimized and molecular polarizability tensors were calculated at the B3LYP/cc-pVTZ level for a training set of 127 organic molecules. In this work all ab initio calculations were performed at the B3LYP/cc-pVTZ level using Gaussian 98.³⁴ Atomic polarizabilities were fit to this data using the Gaussian Model, the damped Thole model, and the Applequist point dipole model. For the Gaussian Model, the exponents β were fit with a single adjustable parameter a.

$$\beta =\frac{a}{{\left(\alpha \frac{4}{3\sqrt{8\pi }}\right)}^{\frac{1}{3}}}$$ (26)

The Thole model studied in this work is the same as that implemented in the AMOEBA force field.¹

$$\rho \left(u\right)=\frac{3a}{4\pi }\exp (-a{u}^3)$$ (27)

As in the Gaussian model, the parameter a in the Thole model was also allowed to vary. For both the Gaussian and Thole model, the polarization condition (see APPENDIX B) requires

$$a\le 1$$ (28)

The atomic polarizabilities were fit to the six independent components of the molecular polarizability tensor $({\alpha }_{xx}^{\mathrm{mol}},{\alpha }_{yx}^{\mathrm{mol}},{\alpha }_{yy}^{\mathrm{mol}},{\alpha }_{zx}^{\mathrm{mol}},{\alpha }_{zy}^{\mathrm{mol}},{\alpha }_{zz}^{\mathrm{mol}})$ over the molecular training set.

The root mean squared deviation (RMSD) in the tensor elements for a given molecule, α_rmsd, is defined by:

$${\alpha }_{\mathrm{rmsd}}\equiv \sqrt{\frac{1}{6}\sum _{p,q}^6{\left({\alpha }_{pq}^{\mathrm{mol}}-{\alpha }_{pq}^{0,\mathrm{mol}}\right)}^2}$$ (29)

where ${\alpha }_{pq}^{\mathrm{mol}}$ is the tensor calculated by the model and ${\alpha }_{pq}^{0,\mathrm{mol}}$ is the ab initio reference tensor. The fitting function χ² is defined as the sum of the squares of individual molecular tensor RMSDs:

$${\chi }^2\equiv \frac{1}{N}\sum _{i=1}^N{\alpha }_{\mathrm{rmsd},i}^2$$ (30)

where N is the number of molecules. The total RMSD over the data training set is then χ χ² was optimized using the nonlinear least squares Levenberg-Marquardt algorithm.³⁵ Tensor errors Δα are defined for each molecule as the tensor RMSD divided by the average eigenvalue of the molecular polarizability tensor α_eigen.

$$\Delta \alpha \equiv \frac{{\alpha }_{\mathrm{rmsd}}}{{\alpha }_{\text{eigen}}}$$ (31)

Probed Polarizability Parameterization Algorithm

Molecules were probed with point charges positioned around the molecule. For each probe charge, the electrostatic potential is computed on a grid of points encompassing the molecule. The atomic polarizabilities along with the exponent parameter a were fit to the response electrostatic potential comprised of the probed electrostatic potentials minus the vacuum electrostatic potential.

The ChelpG²⁴ electrostatic grid was employed with a grid spacing of 0.3 Å and an outer grid radius of 2.8 Å for each atom. The inner grid radii used were 1.45 Å for H, 1.5 Å for C, 1.7 Å for N, O, F, and 2.3 Å for second and third row elements. Point charges were placed along bond axes outside the vdW surface of the molecule defined by probe radii on each atom. The probe radii were chosen to be large enough to be outside the vdW radii of each atom, but close enough to adequately sample the polarization response. The probe radii were set to 2.0 Å for H, 2.5 Å for first row atoms (C, N, O, F), 3.0 Å for second row atoms (P, S, Cl), and 3.5 Å for third row atoms (Br). For each bond, both atoms comprising the bond were probed separately. A single probe charge was set along the bond axis. Initially, the probe was placed on the bond axis at the probe radii distance. However, if the probe charge happened to be inside any other atom's probe radius, the distance along the axis was increased in increments of 0.3 Å up to a maximum of 5.0 Å. If at 5.0 Å the probe charge was still inside another atom's probe radii, the probe charge was discarded. For sp² hybridized atoms or atoms containing lone pairs, an additional point charge was placed above and below the plane at the same distance from the nuclei as the bond axis probes (Fig. 1).

Figure 1.

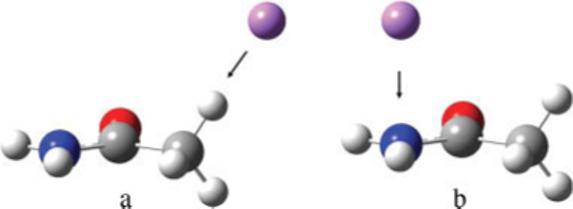
(a) H—C bond axis probe on acetamide and (b) out of plane probe on amido N. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

While the molecular polarizability tensor error depends weakly on the magnitude of the probe charge, it depends strongly on the sign of the charge. Thus, it was found that both positive and negative charges at each probe position are necessary. The probe charge magnitudes needed to be large enough to cause a measurable response in the electric potential, but not so large that hyperpolarization effects occur. In Figure 2, the error in molecular polarizability tensor Δα is plotted against probe charge magnitude for some sp³ and sp² first row molecules. Optimal probe charges of ±0.8e for first row sp³ atoms (C, H, O, N, F), ±0.5e for sp² first row atoms (C, O, N), and ±1.1e for second and third row atoms (P, S, Cl, Br) were inferred from the tensor errors.

Figure 2.

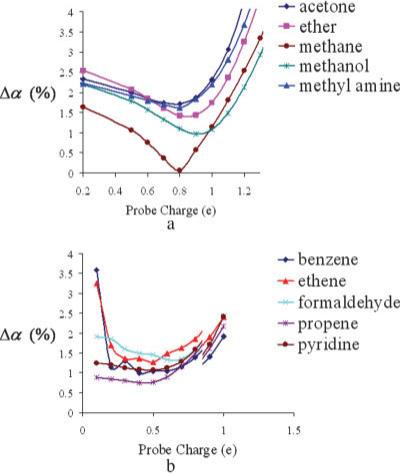
(a) Tensor error dependence Δα on probe charge magnitudes for sp³ C,N,O,H and (b) tensor error dependence Δα on probe charge magnitudes for sp² C,N,O. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

As an example, consider the probe positioning procedure for water in Figure 3. For each OH bond, a separate positive probe is placed next to both atoms making up the bond. This gives four bond axis probes. Since, water has an atom with lone pairs, positive probes are also placed above and below the plane containing the lone pair atom, giving two out of plane probes and six positive probes altogether. Negative charge probes are also placed at the same positions as the positive probes, giving 12 probe charges total. Another example is methane with four bonds and no lone pair or sp² atoms. The number of probe charges for methane is therefore 16.

Figure 3.

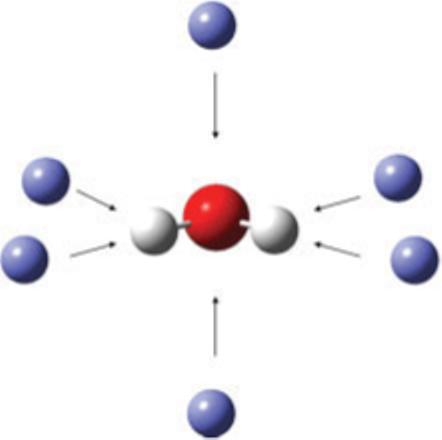
Positions of probe charges for water. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Probed polarizabilities for the Gaussian model were simultaneously fit to each grid of response electrostatic potentials generated by the point charge probes. The response electrostatic potential is the probed potential minus the vacuum potential. This response potential is directly compared with the potential arising from the Gaussian dipoles [eq. (12)]. The induced dipoles were allowed to interact through ‘effective’ electric fields with one another [eq. (15)] and the external probe charges [eq. (16)]. The induced dipoles were determined iteratively using eq. (17).

For each molecule, the optimizable parameters were the atomic polarizabilities and a single Gaussian exponent parameter a [eq. (26)]. If M is the number of grid of points from the ChelpG scheme and P is the number of charge probes, the fitting function χ² is defined by:

$${\chi }^2=\frac{1}{M\cdot P}\sum _{i=1}^M\sum _{j=1}^P{(V_{ij}^{\text{Gauss}}-V_{ij}^{\mathrm{QM}})}^2$$ (32)

$V_{ij}^{\mathrm{Gauss}}$ [eq. (13)] and $\Delta V_{ij}^{\mathrm{QM}}$ are the model Gaussian potential and ab initio response potential at the ith grid point of the jth probe charge, respectively. The response potential $\Delta V_{ij}^{\mathrm{QM}}$ is given by:

$$\Delta V_{ij}^{\mathrm{QM}}\equiv V_{ij}^{\mathrm{QM}}-V_i^{\mathrm{QM}}\left(\text{vacuum}\right)$$ (33)

where $V_{ij}^{\mathrm{QM}}$ is the ab initio potential at the ith grid point with the jth probe charge and $V_i^{\mathrm{QM}}$ (vacuum) is the ab initio vacuum potential at the ith grid point. χ² was optimized using the nonlinear least squares Levenberg-Marquardt algorithm.³⁵ The RMSD in response potential V_rmsd is given by the square root of χ² in eq. (32).

$$V_{\mathrm{rmsd}}=\sqrt{{\chi }^2}$$ (34)

Since the induced dipoles are linearly related to external electric field [eq. (19)], the contribution from intramolecular polarization is constant and only the response potential need be considered. By subtracting the vacuum potential from the total potential, the only contribution to the response potential is from induced dipoles arising from the external point charge source. The Gaussian inducible dipoles are allowed to interact with one another and the probe charge. In this way, the computed polarizabilities are unaffected by either the intramolecular polarization or the choice of the permanent electrostatic model (e.g., point charges,^3,23,24 point multipoles,^1,36 Hermite Gaussian functions,¹⁹ etc.). Thus, the permanent electrostatic model may be selected and optimized subsequent to the derivation of the polarizabilities.³⁷

Results

Tensor Fit Atom Type Polarizabilities

The Gaussian, Thole, and Point Dipole models were fit to ab initio molecular polarizability tensors for selected atom types (see Table1). For both the Gaussian and Thole models, the optimized parameters included the atomic polarizabilities and a single adjustable variable a, which represents the diffuseness or strength of the interactions. Generally, the larger the value of a, the stronger the induced dipole–induced dipole interactions. The optimized value of a for the Gaussian model (0.957), and for the Thole model (0.662) were both below 1.0, satisfying the catastrophe condition (see Appendix). The point dipole model has no damping correction, which is equivalent to allowing a → ∞ in either the Thole or Gaussian models.

Table 1.

Atom Type (AT) Polarizabilities (ų).

Atom type	Gaussian a = 0.957	Thole a = 0.662 (0.572)a	Applequist a → ∞
H	0.381	0.416 (0.427)a	0.181 (0.135)b
HP (ammonium H+)	0.141	0.119	0.051
C	1.090	1.010 (1.334)a	0.727 (0.878)b
C (aromatic, alkene)	1.362	1.407	0.620
N	0.801	0.709 (1.073)a	0.456 (0.530)b
NP (ammonium N+)	0.408	0.387	0.470
O	0.612	0.605 (0.837)a	0.303 (0.465)b
O2 (acid O−)	1.025	1.207	0.413
F	0.315	0.283	0.311 (0.320)b
Cl	1.921	1.844	1.778 (1.91)b
Br	2.934	2.791	2.734 (2.88)b
S	2.742	2.461	2.152
P	1.545	1.282	1.787
αrmsd (Å3)	0.260	0.280	0.615
Δα (%)	3.67	3.81	7.78

^aValues in parenthesis taken from ref. 12.

^bValues in parenthesis taken from ref. 11.

As in the original Thole¹³ paper, the atom types were generally the elements. An extra atom type was also set aside for an aromatic/alkene carbon atom. To study ionic parameters relevant to amino acids, ammonium N and H and carboxylate O atom types were also added. The optimized parameters, the RMSD values for the fits, and the errors for all three models are given in Table 1. For the 127 molecules studied, the Gaussian model (3.67% average error) performed slightly better than the Thole model (3.81% error) and much better than the point dipole model (7.78% error).

The original polarizabilities found by Thole¹³ and Applquist et al.¹² (Table 1) were derived by fitting to experimental gas phase molecular polarizability tensors. In general, these polarizabilities should be larger in magnitude than those fit from the B3LYP/cc-pVTZ data. Diffuse functions were not included in the cc-pVTZ basis set, in order to underestimate the gas phase polarizability to better approximate what is believed to be the liquid state polarizability.^38–40

The point dipole polarizabilities are smaller than the damped Thole or Gaussian polarizabilities. Point dipoles interact more strongly, because there is no damping and the parameters are smaller to compensate. A similar trend also exists between the Thole and Gaussian model; for most atom types, the polarizabilities in Thole are slightly smaller than in the Gaussian model. The reason for this is probably due to the fact that the Thole model density ρ ∼ exp(−βr³) decays faster than the Gaussian density ρ ∼ exp(−βr²). This would imply that the damping in the Thole model decays quicker than in the Gaussian model. Therefore, the Thole model is slightly more similar to the point dipole model than is the Gaussian model. To compensate for this behavior, the Thole polarizabilities and the damping parameter a are smaller than in the Gaussian model (a was defined in both models so that the polarization catastrophe occurs at a = 1.0).

The molecular polarizability tensor calculated from ab initio (QM) and the three models (Gauss, Thole, Point Dipole) are given, along with percent errors, for the illustrative case of benzene (Table 2). The results for the Gaussian model are almost identical to the Thole model, both with a tensor error Δα of 2.7%. For the point dipole model, Δα is significantly larger at 11.0%. Benzene was chosen as an example because aromatic compounds are a well-known case in which the point dipole model does not adequately reproduce the molecular polarizability tensor. Specifically, the component of the tensor perpendicular (z) to the molecular plane (xy) is underestimated. This is due to weak point dipole parameters interacting strongly with each other in the plane but not perpendicular to the plane.

Table 2.

Molecular Polarizability Tensor (ų) Using Atom Type (AT) Polarizabilities for Benzene.

	XX	YX	YY	ZX	ZY	ZZ	Δα (%)
Gauss	11.86	0.00	11.86	0.00	0.00	4.78	2.7
Thole	11.85	0.00	11.85	0.00	0.00	4.74	2.7
Applquist	10.67	0.00	10.67	0.00	0.00	2.75	11.0
QM	11.45	0.00	11.45	0.00	0.00	5.01

Though the Gaussian model gave a better fit than did the Thole model, the performance difference between the two models is small. This is in agreement with Thole's original work, in which seven different damping functions all gave similar RMSD fits to the data. As stated earlier, the main advantage of the Gaussian model over the Thole model is that point multipoles can be readily generalized to Hermite Gaussian charge densities.

Probed Polarizabilities

Comparison With Atom Type Polarizabilities

The probed method was applied to several test organic molecules. For each molecule, the error in the molecular polarizability tensor Δα [eq. (31)] and the RMSD in the response field V_rmsd [eq. (34)] are calculated using the probed polarizabilities and presented in Table 3. To compare with the generic atom type (AT) parameters, Δα and V_rmsd are also calculated using the set of AT polarizabilities. In virtually all cases, Δα and V_rmsd are significantly smaller for the molecule specific probed polarizabilities than the transferable AT polarizabilities.

Table 3.

Comparison of Probed and Atom Type Polarizabilities.

	a	Δα (%) Probed	Δα (%) Atom type	Vrmsd (10−3 e/Å) Probed	Vrmsd (10−3 e/Å) Atom type
Acetamide	0.906	1.30	2.33	1.61	2.06
Acetate anion	0.942	1.99	4.72	3.30	4.18
Acetic acid	0.920	1.55	7.04	1.61	2.30
Acetone	0.919	1.70	2.62	1.84	1.95
Ammonia	0.851	2.22	8.47	1.67	2.72
Ammonium cation	0.901	0.10	16.83	0.63	2.50
Benzene	0.966	0.85	2.33	2.24	2.58
Butadiene	0.984	2.45	7.13	2.45	2.85
Dimethyl ether	0.955	1.44	2.32	2.19	2.25
Dimethyl sulfide	0.948	1.79	2.99	2.50	2.91
Ethane	0.939	1.10	1.28	1.89	1.94
Ethene	0.961	2.65	6.39	2.19	2.65
Formaldehyde	0.974	2.13	2.83	2.22	2.33
Formamide	0.937	1.45	2.89	1.54	2.03
Hydrogen sulfide	0.893	1.78	13.20	3.68	5.55
Methane	0.901	0.05	2.21	1.89	2.03
Methanethiol	0.943	2.14	5.61	2.42	3.19
Methanol	0.948	1.10	5.30	1.79	2.36
Methyl amine	0.931	1.68	3.20	2.13	2.46
N-methyl formamide	0.935	1.33	2.72	1.90	2.21
Phosphate	0.799	1.02	0.72	2.79	3.51
Phosphoric acid	0.891	0.12	8.63	1.65	3.43
Propene	0.952	0.88	4.31	2.11	2.37
Pyridine	0.955	0.95	1.90	2.14	2.55
Pyrole	0.868	1.60	6.26	2.08	2.96
Sulfate	0.955	0.88	20.77	1.58	7.43
Sulfuric acid	0.958	1.15	21.76	1.38	6.84
Water	0.877	2.09	15.04	1.02	3.02
Average	0.926	1.37	6.42	2.01	3.04

Since the probed polarizabilities are fit to the response field, it is not surprising that these parameters perform significantly better than the AT parameters. For example, the V_rmsd (in 10⁻³ e/Å) for water is 1.02 using the probe polarizabilities and 3.02 using the AT polarizabilities. Another example is ammonia, in which V_rmsd is 1.67 using the probe polarizabilities and 2.72 using the AT parameters. The average of V_rmsd over all 28 molecules was found to be 2.01 for the probed polarizabilities and 3.04 for the AT polarizabilities. In other words, the RMSD in the response potential was on average 50% larger using the AT polarizabilities over the probed polarizabilities.

As seen in Table 3, the probed polarizabilities also resulted in much better tensor fits Δα than did the AT polarizabilities. The probed parameters had an average tensor error of 1.37% with a maximum error of 2.65%. This can be compared with the transferable AT parameters, which had an average error of 6.42% and a maximum error of 21.76%. This is remarkable since the AT parameters were fit to the tensor, while the probed polarizabilities used no tensor information in the fit.

The AT parameters do reasonable well if the molecule of interest was included in the atom type training set. As an example from Table 3, the probed polarizabilities gave a tensor error Δα of 1.44% for dimethyl ether and 1.79% for dimethyl sulfide. The AT parameters gave acceptable results for both molecules (2.32% and 2.99% errors, respectively). However, both of these molecules were used in the atom type (AT) training sets. On the other hand, sulfate and sulfuric acid were not included in the AT training set. For sulfate, Δα = 20.77% and for sulfuric acid, Δα = 21.76% using the AT parameters. This can be compared with the results using the probe polarizabilities: Δα = 0.88% for sulfate and Δα = 1.15% for sulfuric acid. The large errors in the AT parameters can be understood by examining the sulfur (S) polarizability. The probed parameters predicted α = 1.2 ų for S in sulfate, while the AT parameters used a generic sulfur value of α = 2.7 ų. The AT polarizability for S of 2.7 ų might be appropriate for thiols, however sulfate S is oxidized which should shift much of the electron density to the oxygens thereby lowering the polarizability of S. Of course, a new atom type could be added for sulfate S, and the parameters refit. An advantage of the probed molecule approach is that it eliminates the need to arbitrarily assign atom types or refit parameters.

The AT parameters were fit over a large collection of data to get the overall optimal molecular polarizability tensors. It is possible that the fitting procedure for the AT parameterization incorrectly assigned the atomic polarizabilities, but is still able to reproduce the tensor. As an example, the probed and AT atomic polarizabilities are given for acetamide in Figure 4. In Table4, the molecular polarizability tensor is given for both models and compared with the reference ab initio (QM) value. Since Δα = 1.30% for the probed and Δα = 2.33% for the AT parameters, both sets are able to reproduce the tensor. However, the AT polarizabilities are 20% smaller than probed polarizabilities for the amido C, N, and O atoms, while the AT polarizabilities on the polar H atoms are 30% larger to compensate. The probed polarizabilities suggest that the amido C (α_C = 1.20 ų) is more polarizable than the methyl C (α_C = 1.08 ų). In general, the probe polarizabilities find that sp² C is more polarizable than sp³ C (e.g., α_C = 1.05 ų for ethane and α_C = 1.40 ų for ethene).

Figure 4.

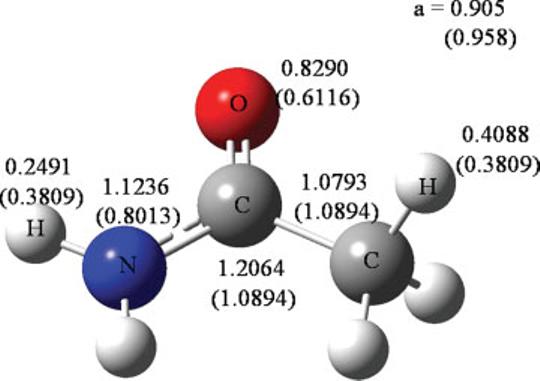
Probed and atom type (in parenthesis) polarizabilities in ų for acetamide. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Table 4.

Molecular Polarizability Tensor (ų) for Acetamide Calculated by B3LYP/cc-pVTZ (QM) and Probed Polarizabilities (Probe) and Atom Type Polarizabilities (AT) for the Gaussian Model.

	XX	YX	YY	ZX	ZY	ZZ	Δα (%)
QM	6.08	0.11	5.77	0.00	0.00	3.79
Probe	6.07	−0.03	5.80	0.00	0.00	3.88	1.3
AT	6.12	−0.15	5.87	0.00	0.00	3.68	2.3

A final example of the performance of the probed polarizabilities is given by the important case of water. The atomic polarizabilities are given in Figure 5 and the molecular polarizability tensors are given in Table5. The tensor error Δα is 2.09% using the probed polarizabilities and 15.04% for AT parameters. As noted earlier, the RMSD in response potential V_rmsd (10⁻³e/Å) is three times smaller using the probed polarizabilities (1.02) than the AT parameters (3.02). The poor results for water using the AT parameters are somewhat surprising since water was included in the AT training set. Furthermore, when two new AT polarizabilities were added specifically for water, α_O and α_H, and these polarizabilities were fit only to the tensor for water, then Δα was found to be 2.02% (the exponent parameter a was constrained to 0.879 to avoid overfitting). This would imply that the probed polarizabilities with Δα = 2.09% is near the limit, which would best reproduce the molecular polarizability tensor in the context of the isotropic induced Gaussian dipole model.

Figure 5.

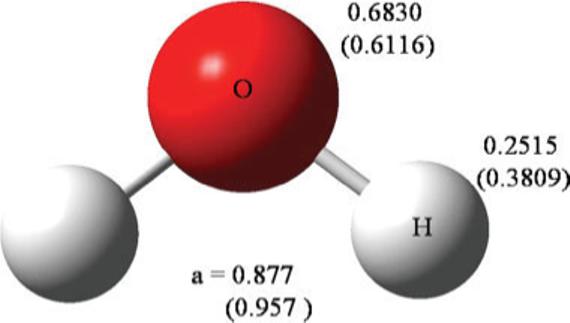
Probed and atom type (in parenthesis) polarizabilities in ų for water. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Table 5.

Molecular Polarizability Tensor (ų) for Water Calculated by B3LYP/cc-pVTZ (QM) and Probed Polarizabilities (Probe) and Atom Type Polarizabilities (AT) for the Gaussian Model.

	XX	YX	YY	ZX	ZY	ZZ	Δα (%)
QM	1.14	−0.09	1.20	0.00	0.00	0.82
Probe	1.11	−0.12	1.19	0.00	0.00	0.84	2.1
AT	1.32	−0.25	1.50	0.00	0.00	0.88	15.0

Limitations With the Isotropic Model

The probed polarizability scheme works well for ordinary organic containing C, O, N, H, S, and P. The optimized exponent parameter a has an average value of 0.926, which is below the polarization catastrophe upper bound of 1.0. In general, sp³ hybridized molecules performed slightly better than sp² molecules, (e.g., Δα = 1.10% for ethane, Δα = 2.65% for ethene). A possible reason for this is that the isotropic atomic polarizability model studied in this paper assumes spherically symmetric induced dipoles on each atom. The electron density around a sp³ hybridized molecule should be more spherically isotropic than a molecule which is sp² hybridized. Further evidence suggest that highly symmetric molecules give better results than molecules of lower symmetry, (e.g., Δα = 0.10% for ammonium cation and Δα = 2.22% for ammonia).

To further test the limits of the isotropic atomic polarizability Gaussian model, polarizabilities were computed for diatomic halides (Table6). During the optimization, the exponent parameter a diverged to infinity implying point dipole behavior and large errors occurred in the molecular polarizability tensors. These discrepancies can be rationalized by looking at the two independent tensor components: α_∥ which is the tensor component parallel to the bond axis and α_⊥ which is perpendicular to the bond axis [eqs. (24a) and (24b)]. In the diatomic halides, α_∥ is too small and α_⊥ is too large. For example in F₂, the ab initio values are α_∥ = 1.567 and α_⊥ = 0.431, and the optimized model values are α_∥ = 1.197 and α_⊥ = 0.722. In a purely additive polarization model, in which the isotropic induced dipoles do not interact with each other, the molecular polarizability tensor is isotropic, e.g. α_∥ = α_⊥ in the diatomic case. It is the interaction between the isotropic induced dipoles that causes anisotropy in the tensor, and α_∥ > α_⊥ in the diatomic molecule case. The larger the interaction, the greater the difference between α_∥ and α_⊥. The largest possible interaction is that of no field damping or induced point dipoles. For the diatomic halides, even point dipoles did not provide a sufficiently strong interaction to accurately reproduce α_∥ and α_⊥. The worst case is F₂, with Δα = 27.9%. These large differences between ab initio and derived values for α_∥ and α_⊥ implies that isotropic atomic polarizabilities on atoms alone are not a good approximation for diatomic halides or any other highly anisotropic molecule. If anisotropic atomic polarizabilities were employed,¹⁰ then the atomic polarizability tensor could have different components parallel and perpendicular to the bond axis. This would allow for the possibility of correctly calculating α_∥ and α_⊥ for the molecule even in the absence of induced dipole–induced dipole interactions. Anisotropic induced dipoles would be necessary to reproduce the tensor correctly for highly anisotropic molecules such as F₂. Anisotropic induced dipoles can be represented by generalizing the scalar atomic polarizability α to an atomic polarizability tensor α_pq.

Table 6.

α_∥ and α_⊥ in ų for Diatomic Halides Using Probed Polarizabilities.

	α∥		α⊥
Diatomic	QM	Probe	QM	Probe	Δα (%)
F2	1.567	1.197	0.431	0.722	27.9
Cl2	5.519	5.140	2.370	2.663	6.7
Br2	8.350	7.938	3.777	4.050	4.3

In all cases, a → ∞, indicating point dipole behavior.

The poor performance of the isotropic Gaussian model for the diatomic halides is due to a limitation in assuming isotropic atomic polarizabilities and not to the Gaussian model or the probed polarizabilities. To illustrate this, polarizabilities were fit solely to the tensor of F₂ for the point dipole, Gaussian, and Thole models (Table7). For the Gaussian and Thole models, the exponent parameter a was constrained to the maximum value of 1.0. The tensor errors Δα were 26.8% for the point dipole model, 27.2% for the Thole model, and 30.3% for the Gaussian model. The Thole model agreed more with the point dipole model than did the Gaussian model. This is a further evidence that the Thole model behaves slightly more like point dipoles than the Gaussian model. As mentioned earlier, a solution to this problem would be to employ anisotropic atomic polarizabilities.

Table 7.

α_∥ and α_⊥ in ų for F₂ Using Polarizabilities Fit to the Tensor for the Point Dipole, Thole, and Gaussian Models.

	α∥	α⊥	Δα (%)
QM	1.566	0.430
Point dipole	1.340	0.771	26.8
Thole (a = 1.0)	1.325	0.772	27.2
Gauss (a = 1.0)	1.232	0.784	30.3

However, the results for the diatomic halides mentioned above do not pose a serious limitation to the isotropic induced Gaussian model. Reasonable results were obtained when the probed method was applied to acid halides and halogenated organic molecules (Table8). The exponent parameter a for the nonhalide atoms was allowed to optimize (except for HF) while the halide exponent parameter was constrained to the maximum value of 1.0. The tensor errors Δα are much smaller for these halogen containing compounds cases (0.6−4.4%). Other anisotropic molecules not presented in Table 3 were also studied, many of which gave reasonable results for Δα: 2.0% for N₂, 5.1% for CN⁻ , 3.2% for CO, 2.4% for ethyne, 2.3% for CO₂, and 2.0% for CS₂.

Table 8.

Tensor Error Δα and Exponent Parameter a for Halogenated Molecules.

	aH,C	Δα (%)
CH3F	0.954	0.6
CH3Cl	0.933	3.3
CH3Br	0.922	3.6
HF	1.000	4.4
HCl	0.834	1.5
HBr	0.779	1.0

a = 1.0 for F, Cl, Br and a was allowed to optimize for C and H (except for HF).

Effects of Molecular Conformation

It would be highly desirable if the probed atomic polarizabilities could be fit to a single molecular conformation. To examine the extent to which polarizabilities were sensitive to conformation, probed polarizabilities derived for a single geometry were tested on other conformations generated by rotating internal torsion angles. It was found that probed polarizabilities generated from a single geometry could reproduce both the molecular polarizability tensor and also the response potential.

The effects of multiple torsion conformations on molecular polarizability tensor using a single set of atomic polarizabilities were tested on glycine dipeptide (Fig. 6). The torsion angles φ ≡ C1-N1-C2-C3 and ψ ≡ N1-C2-C3-N2 along the main axis were considered. The geometry was fully optimized at the B3LYP/cc-pVTZ level (φ, ψ = 180°, 180°), and atomic polarizabilities were generated for this single geometry using the probed method. The torsion angles φ and ψ were then rotated from 45° to 315° in increments of 30°. The two angles were constrained to the rotated values, while the rest of the geometry was allowed to relax. The molecular polarizability tensors for these constrained geometries were then calculated using the probed atomic polarizabilities generated from the single optimized geometry (φ,ψ = 180°, 180°) and then compared with the reference ab initio values at those rotated geometries. The error in the tensor Δα is presented for φ and ψ in Figure 7. Over the conformational space, the variation in the tensor between the optimized and the rotated geometries reached as high as 17.2% and averaged to 12.8%. Despite the large variation in the tensor, the error in the tensor Δα never increased above 1.5%, and the average of Δα over all conformations was found to be 0.87%. Similar results were found by rotating a single torsion angle along the X-C-C-Y axis for ethylene glycol, fluoropropane, and ${\mathrm{NH}}_2{\mathrm{CH}}_2{\mathrm{CH}}_2{\mathrm{CO}}_2^{-}$

Figure 6.

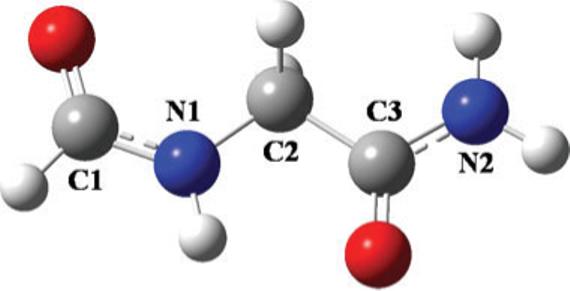
Glycine Dipeptide. φ ≡ C1-N1-C2-C3 and φ ≡ N1-C2-C3-N2.

Figure 7.

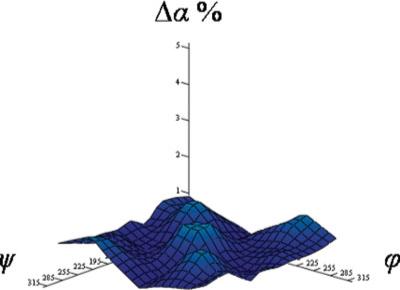
Tensor error Δα (%), dependence on φ and φ for glycine dipeptide.

The RMSD in the response potential V_rmsd was also found to be essentially invariant across multiple torsion conformations. The geometry of ${\mathrm{NH}}_2{\mathrm{CH}}_2{\mathrm{CH}}_2{\mathrm{CO}}_2^{-}$ was optimized and a set of probed polarizabilities were generated for this geometry, α⁰. At the fully optimized geometry, the torsion angle along the main axis of ${\mathrm{NH}}_2{\mathrm{CH}}_2{\mathrm{CH}}_2{\mathrm{CO}}_2^{-}$, ω_NCCC, was found to be 65.9°. ω_NCCC was then rotated and constrained to 0°, 60°, 120°, and 180° while the rest of the geometry was allowed to relax. Four new sets of probed polarizabilities were generated at each new torsion configurations, αⁱ (i = 1.4). In Figure 8, the response field RMSD V_rmsd was plotted for each of the rotated geometries using the optimized geometry set of polarizabilities, α⁰, and also the set of polarizabilities generated specifically for that geometry, αⁱ. It was found the relative error for V_rmsd between the two sets of polarizabilities was less than 1.0% for all four torsion geometries (see Fig. 8). This can be compared with an average relative error for V_rmsd between the probed and the AT polarizabilities of ∼50% (Table 3). Similar results were also found for ethylene glycol and fluoropropane.

Figure 8.

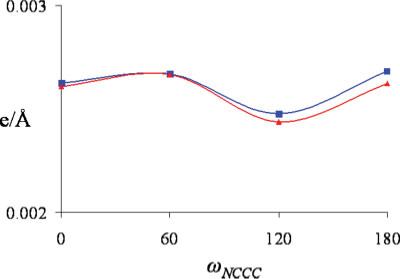
V_rmsd dependence on torsion angle for ${\mathrm{NH}}_2{\mathrm{CH}}_2{\mathrm{CH}}_2{\mathrm{CO}}_2^{-}$. Probed polarizabilities generated at the fully optimized geometry are in (blue, ■) and polarizabilities generated specifically for each torsion geometry is in (red, ▲).

Conclusions

The Gaussian polarization model has been examined as an alternative to the Thole model. Originally, the Thole model was designed to fix the polarization catastrophe problem associated with the point dipole model. In the Thole model, a damping function is applied to keep short-range induced dipole–induced dipole interactions finite. A more recent model based on replacing point dipoles with ‘p’ orbital Gaussian charge densities has also been suggested.^13,14 In the Appendix, it is shown that the Gaussian model is also capable of finite induced dipole–induced dipole interactions at short range. However, in order to prevent a polarization catastrophe at all distances, the Gaussian exponent should be sufficiently ‘diffuse’. A relationship on the maximum size of the Gaussian exponent and the polarizability was derived. A similar condition was also derived for the Thole model. In both the Gaussian and Thole models, the catastrophe condition is satisfied if the exponent parameter a is less than 1.0 [eqs. (26) and (27)].

The performance of the point dipole, Thole, and Gaussian isotropic induced dipole models have been compared by optimizing atom type atomic polarizabilities to molecular polarizability tensors calculated at the B3LYP/cc-pVTZ level on a data set of 127 organic molecules. The Gaussian model (3.67% avg. tensor error) performed slightly better the Thole model (3.81%) and much better than point dipole model (7.78%). The limits of using isotropic atomic polarizabilities can be seen by analyzing highly anisotropic molecules, such as diatomic halides. For these examples, the parameters tended towards strongly interacting point dipoles. To better represent these less common cases, anisotropic atomic polarizabilities are needed.

When atom type polarizabilities are derived by fitting to a data set of molecular polarizability tensors, a question arises: how transferable are these atom type parameters. Here, it was found that atom type polarizabilities are transferable only to the extent that the atom types are appropriately identified. An alternative method of optimizing polarizabilities, which is molecule specific, was also presented. It is based on probing a molecule with point charges and fitting the polarizabilities to the response field. The approach is similar to the derivation of atomic partial charges by electrostatic potential fitting, and many of the ideas were borrowed from the well-known ChelpG method. The probed polarizabilities were tested against atom type polarizabilities over 28 molcules. In all cases, the probed polarizabilities showed a significant improvement over the transferable atom type parameters. The probed method gave an average tensor error Δα of 1.41% and a maximum tensor error of 2.7%. This can be compared with the transferable atom type polarizabilities that yielded an average tensor error of 6.5% and a maximum error of 21.8%. The probed polarizabilities also predicted the response potential significantly better than the transferable atom type parameters. The average of response potential RMSD V_rmsd (in 10⁻³ e/Å) over the 28 molecules was 2.01 for the probed polarizabilities and 3.04 for the AT polarizabilities.

The probe charge method is capable of generating polarizabilities that are specific to the molecule and are therefore sensitive to each atoms chemical environment. For example, it was found that the polarizability on the carbon atom for methane, methanol, and fluoromethane was found to be 1.05, 0.85, and 0.75 ų, respectively. These values agree with chemical intuition in that electron withdrawing groups should lower the electron density and therefore the polarizability on the carbon atom. In general, it would be difficult to arrive at this level of sensitivity by fitting to tensor data alone because the molecular polarizability tensor has at most six independent components. In most cases, polarizabilities for a single molecule containing many atom types cannot be fit to the tensor alone because there is simply not enough data. Notably, it may be possible to use the probe method to derive transferable atom type polarizabilities. The probed charge method could be carried out separately on a large collection of molecules. The resulting parameters could be compared and generalizations relating atom types could then be made. However, if atom specific partial charges are used, it would seem natural to also assume atom specific polarizabilities.

It was also found that atomic polarizabilities are not sensitive to geometric rotations about torsion angles, as shown in the glycine dipeptide and ${\mathrm{NH}}_2{\mathrm{CH}}_2{\mathrm{CH}}_2{\mathrm{CO}}_2^{-}$. Both the molecular polarizability tensor and the response potential could be accurately reproduced over multiple conformations using a single set of probed polarizabilities. This very fortunate result is important in the construction or application of force fields for molecular simulation.

All of the atomic polarizabilities presented in this work are independent of the permanent electrostatic model used. The atom type polarizabilities were fit to molecular polarizability tensors and the probed polarizabilities were fit to the response electrostatic potential. Intramolecular polarization effects can be accounted for later when the permanent electrostatic model is fit. In this way, the atomic polarizabilities generated could be used in any electrostatic model; for example, point charges, point multipoles, or Hermite Gaussian functions.

Both the Thole and Gaussian isotropic polarizability models perform well for most organic molecules. Although the Gaussian model did slightly better than the Thole model over the 127 molecule atom type training set, the difference between the two in terms of performance is small. Although it was not tested, the probed procedure could be applied to the Thole model and still be expected to generate accurate results. The Thole model is somewhat arbitrary, since in the original Thole paper, seven different damping functions performed equally well in terms of fitting to tensor data. The main advantage of the Gaussian model over the Thole model is the possible generalization of other point multipoles to Gaussian charge densities.

Appendix A

In this section, results pertaining to potential and electric fields for Gaussian particles will be discussed. In particular an ‘effective’ electric field between Gaussian particles was introduced in eq. (14). The use of ‘effective’ electric potentials and fields is convenient because it explicitly takes into account the charge distributions from both particles. The ‘effective’ potential form a Gaussian particle can be derived by considering the variation in interaction energy of an infinitesimal Gaussian test charge with the Gaussian particle.

As noted earlier, the point charge limit can be found by taking the limit of large exponent β. For example, the interaction energies of a point charge q₁ with a Gaussian ‘s’ or ‘p’ charge density with exponent β₂, U_qs and U_qp, can be found by letting β₁ → ∞ and β₁₂ → β₂ in eqs. (5a) and (5b).

$$U_{qs}=q_1{q}_2{\beta }_2{B}_0\left({\beta }_2{R}_{12}\right)$$ (A1a)

$$U_{qp}=q_1{\overrightarrow{\mu }}_2{\overrightarrow{R}}_{12}{\beta }_2^3{B}_1\left({\beta }_2{R}_{12}\right)$$ (A1b)

The ordinary electrostatic potential of a charge distribution can be defined as the variation in interaction energy $\frac{\delta U}{\delta q_1}$ ⁴¹ when an infinitesimal point charge is added to the system. Therefore, the electrostatic potential (13a and 13b) of a Gaussian ‘s’ and ‘p’ orbital distribution can be obtained by differentiating eqs. (A1a) and (A2a) with respect to q₁.

Now consider a system composed only of Gaussian particles. It proves very convenient to define an analogous ‘effective’ potential Ṽ as the variation in interaction energy $\frac{\delta U}{\delta q_1}$ when an infinitesimal Gaussian charge q₁ with exponent β₁ is added to the system. The ‘effective’ potential on a Gaussian charge with exponent β₁ at ${\overrightarrow{R}}_1$ from a Gaussian ‘s’ and ‘p’ orbital at ${\overrightarrow{R}}_2$ with exponent β₂ can be found by differentiating eqs. (5a) and (5b) with respect to q₁:

$${\stackrel{\sim }{V}}_s\left({\overrightarrow{R}}_1\right)=q_2{\beta }_{12}{B}_0\left({\beta }_{12}{R}_{12}\right)$$ (A2a)

$${\stackrel{\sim }{V}}_p\left({\overrightarrow{R}}_1\right)={\overrightarrow{\mu }}_2\cdot {\overrightarrow{R}}_{12}{\beta }_{12}^3{B}_1\left({\beta }_{12}{R}_{12}\right)$$ (A2b)

The analogous ‘effective’ electric fields $\stackrel{\sim }{\overrightarrow{E}}$ between Gaussian particles can be found by taking the negative gradient of eqs. (A2a) and (A2b):

$${\stackrel{\sim }{\overrightarrow{E}}}_s^{2\to 1}=q_2{\beta }_{12}^3{\overrightarrow{R}}_{12}{B}_1\left({\beta }_{12}{R}_{12}\right)$$ (A3a)

$${\stackrel{\sim }{\overrightarrow{E}}}_p^{2\to 1}={\overrightarrow{\mu }}_2{\beta }_{12}^3{B}_1\left({\beta }_{12}{R}_{12}\right)-{\beta }_{12}^6\left({\overrightarrow{\mu }}_2{\overrightarrow{R}}_{12}\right){\overrightarrow{R}}_{12}{B}_2\left({\beta }_{12}{R}_{12}\right)$$ (A3b)

Using eq. (11), eq. (A3b) can be rewritten in terms of the dipole–dipole interaction matrix ${\overrightarrow{\overrightarrow{T}}}^{12}$ as

$${\stackrel{\sim }{\overrightarrow{E}}}_p^{2\to 1}=-{\overrightarrow{\overrightarrow{T}}}^{12}{\overrightarrow{\mu }}_2$$ (A4)

The interaction energy a Gaussian ‘p’ orbital with another Gaussian ‘s’ or ‘p’ orbital [eqs. (5b) and (5c)] can be conveniently be rewritten in terms of ‘effective’ electric fields.

$$U_{\mathrm{sp}}=-{\overrightarrow{\mu }}_1{\stackrel{\sim }{\overrightarrow{E}}}_s^{2\to 1}$$ (A5)

$$U_{\mathrm{pp}}=-{\overrightarrow{\mu }}_1{\stackrel{\sim }{\overrightarrow{E}}}_p^{2\to 1}$$ (A6)

Finally, the ‘effective’ electric field arising from a point charge source onto a Gaussian particle is found from eq. (A3a), with β₂ → ∞ and β₁₂ → β₁

$${\stackrel{\sim }{\overrightarrow{E}}}_s^{2\to 1}=q_2{\beta }_1^3{\overrightarrow{R}}_{12}{B}_1\left({\beta }_1{R}_{12}\right)$$ (A7)

Appendix B

In both the Gaussian and Thole models, it was stated previously that the exponent parameter a [eqs. (28) and (29)] should be less than 1.0 in order to prevent a polarization catastrophe. For the Gaussian model, this implies the induced charge density should be sufficiently diffuse. This condition will now be derived.

Consider two interacting inducible dipoles with polarizabilities α₁ and α₂ separated by a distance R along the x-axis. Since induced dipoles parallel to the separation axis interact more strongly than dipoles that are perpendicular to their separation axis, it suffices to consider dipoles interacting parallel to their separation axis. In order for the interaction between two dipoles to be finite, the denominator in eq. (26a) should be positive.

$$1>{\alpha }_1{\alpha }_2{\beta }_{12}^{6}F\left(x\right)F\left(x\right)$$ (B1)

where

$$F\left(x\right)\equiv x^2{B}_2\left(x\right)-B_1\left(x\right)$$ (B2)

and β₁₂ and x are defined by eqs. (6) and (7). F(x) is plotted in Figure 9.

Figure 9.

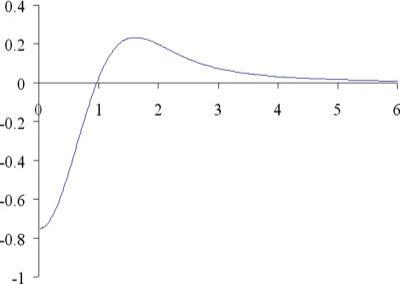
F(x) ≡ x²B₂(x) − B₁(x). Note the maximum value of |F(x)| occurs at x = 0. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Let

$$F_0\equiv \max \left\{\mid F\left(x\right)\mid \right\}=\frac{4}{3\sqrt{\pi }}\approx 0.752252778$$ (B3)

which occurs at x = 0.

If β₁ and β₂ are chosen such that

$${\beta }_i<\frac{1.0}{{\left({\alpha }_i\frac{4}{3\sqrt{8\pi }}\right)}^{\frac{1}{3}}}i=1,2$$ (B4)

then eq. (A1a) is valid for all x. [Note this equivalent to a < 1.0 in eq. (28)].

Proof:

$$\frac{1}{{\beta }_{12}^2}=\frac{1}{{\beta }_1^2}+\frac{1}{{\beta }_2^2}={\left(\frac{1}{{\beta }_1}-\frac{1}{{\beta }_2}\right)}^2+\frac{2}{{\beta }_1{\beta }_2}\ge \frac{2}{{\beta }_1{\beta }_2}$$ (B5)

or

$${\beta }_{12}^2\le \frac{{\beta }_1{\beta }_2}{2}$$ (B6)

Using eqs. (B3) and (B6), eq. (B1) becomes

$${\alpha }_1{\alpha }_2{\beta }_{12}^{6}F\left(x\right)F\left(x\right)\le {\alpha }_1{\alpha }_2{\beta }_{12}^6{F}_0^2\le {\alpha }_1{\alpha }_2{\left(\frac{{\beta }_1{\beta }_2}{2}\right)}^3{F}_0^2$$ (B7)

If β_i [eq. (B4)] and F₀ [eq. (B3)] is substituted into eq. (B7), eq. (B1) is satisfied.

A similar analysis can be applied to the Thole model. The dipole–dipole interaction is:⁸

$${\overrightarrow{\overrightarrow{T}}}^{\text{Thole}}=\frac{1}{R^5}\left\{R^2(1-e^{-a{u}^3})\overrightarrow{\overrightarrow{I}}-3\overrightarrow{R}\overrightarrow{R}(1-(1+a{u}^3)e^{-a{u}^3})\right\}$$ (B8)

where

$$u\equiv \frac{R}{{\left({\alpha }_1{\alpha }_2\right)}^{\frac{1}{6}}}$$ (B9)

The sign convention is that used in Applequist et al.¹² and Thole.¹³ In one dimension, the tensor can be solved for explicitly:

$${\alpha }_{\parallel }=\frac{{\alpha }_1+{\alpha }_2+2\sqrt{{\alpha }_1{\alpha }_2}\stackrel{\sim }{F}\left(u\right)}{1-\stackrel{\sim }{F}{\left(u\right)}^2}$$ (B10a)

$${\alpha }_{\perp }=\frac{{\alpha }_1+{\alpha }_2-2\sqrt{{\alpha }_1{\alpha }_2}\stackrel{\sim }{G}\left(u\right)}{1-\stackrel{\sim }{G}{\left(u\right)}^2}$$ (B10b)

where F̃(u) and G̃(u) are defined by:

$$\begin{array}{cc}\hfill \stackrel{\sim }{F}\left(u\right)& \equiv \frac{1}{u^3}(2-(2+3a{u}^3)e^{-au3})\hfill \\ \hfill \stackrel{\sim }{G}\left(u\right)& \equiv \frac{1}{u^3}(1-e^{-au3})\hfill \end{array}$$ (B11)

A catastrophe doesn't occur as long as the denominator of eq. (B10a) is positive.

$$1-\stackrel{\sim }{F}{\left(u\right)}^2>0$$ (B12)

Let

$${\stackrel{\sim }{F}}_0\equiv \max \left\{\mid \stackrel{\sim }{F}\left(u\right)\mid \right\}=a$$ (B13)

which occurs at u = 0. The catastrophe condition then becomes:

$$\stackrel{\sim }{F}{\left(u\right)}^2\le {\stackrel{\sim }{F}}_0^2<1$$ (B14)

i.e., a < 1.0.