Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2007 Mar 6;274(1615):1293–1299. doi: 10.1098/rspb.2007.0038

The ‘big spenders’ of the steppe: sex-specific maternal allocation and twinning in the saiga antelope

Aline Kühl 1,*, Atle Mysterud 2, Gennadiy I Erdnenov 3, Anna A Lushchekina 4, Iuri A Grachev 5, Amankul B Bekenov 5, EJ Milner-Gulland 1
PMCID: PMC2176182  PMID: 17341456

Abstract

In polygynous mammals, males generally benefit more from extra allocation of maternal resources than females. However, limitations to sex-specific allocation are usually ignored. We propose the ‘allocation constraint’ hypothesis, whereby maternal resource allocation is more likely to follow life-history predictions in single sex litters than in mixed sex litters, due to limitations in prenatal resource targeting. Consequently, for polygynous species, males in mixed litters are likely to receive suboptimal maternal investment, which may have a negative effect on lifetime reproductive success. We test this hypothesis for the saiga antelope (Saiga tatarica), a highly polygynous species with the highest level of maternal allocation reported among ungulates. At such high reproductive output levels, the limitations on additional investment in males are likely to be particularly acute. However, we demonstrate high levels of sexual dimorphism in both late-stage foetuses and newborn calves, including within the same litter. Male twins with a brother tended to be heavier than those with a sister. This may be due to allocation constraints or differences in maternal quality. We conclude that an explicit focus on potential constraints can enhance the progress in the field of sex-specific maternal allocation in polytocous species.

Keywords: Trivers and Willard model, ungulates, Saiga tatarica, Williams hypothesis, litter size, reproductive effort

1. Introduction

In polygynous mammals, the factors determining reproductive success differ strongly between the sexes, resulting in different evolutionary trajectories for males and females (Darwin 1871; Trivers 1972; Clutton-Brock et al. 1982). Females are primarily selected for their ability to raise offspring, with the largest allocation of resources during late gestation and lactation (Clutton-Brock et al. 1989). In males, however, body size appears to be a more important determinant of reproductive success due to strong male–male competition during short mating seasons. Since only the largest males are successful in reproduction, reproductive success is more variable in males than in females (Clutton-Brock et al. 1988). Hence, fitness is more strongly correlated with body mass at birth in males than in females (Kruuk et al. 1999). Life-history theory predicts that in polygynous mammals, male offspring benefit more from extra allocation of maternal resources than females (Trivers & Willard 1973; Charnov 1982). However, the extent to which this is a favourable reproductive tactic typically varies with maternal condition (Hewison & Gaillard 1999; West et al. 2000; Sheldon & West 2004), timing of breeding in seasonal environments (Holand et al. 2006) and litter size (Frank 1990).

Interspecifically, the level of resources females invest in their offspring varies greatly; typically smaller species invest relatively more compared to their body mass (Robbins & Robbins 1979). Within ungulates, the maternal investment spectrum ranges from mountain goats (Oreamnos americanus) with very small prenatal investment (Byers & Moodie 1990) to pronghorn (Antilocapra americana) with strong prenatal investment, where twinning is common and litter weight accounts for 15.5% of adult female body mass on average (Robbins & Robbins 1979). It has been suggested that in species with high investment in offspring, mothers are not able to invest additionally in sons and hence no sex-biased maternal investment would be expected (Byers & Moodie 1990); we shall refer to this as the ‘big spender constraint’ hypothesis (previously referred to as the ‘Byers and Moodie’ hypothesis in Byers & Hogg 1995).

The theory is more complicated for species with more than one offspring per reproductive attempt. This is because parents may obtain higher reproductive success by aiming for a larger litter size rather than adjusting the ratio of investment among sons and daughters (Williams 1979; McGinley 1984; Gosling 1986; Frank 1990). As the number of offspring sharing limited parental resources increases, the fitness return for both the sexes is predicted to eventually equalize because the extra fitness return from an increase in litter size outweighs the fitness return difference between the sexes (Frank 1987, 1990). For multi-offspring litters, Williams (1979) suggests that as maternal reproductive investment increases, litters should switch from being small and female biased to become large and male biased in the following sequence: F<M<FF<FM<MM<FFF, and so on. Only few studies with relatively small sample sizes have addressed this issue (Cassinello & Gomendio 1996; Nygren & Kojola 1997; Fernandez-Llario et al. 1999; Säde 2004). However, Williams (1979) made no predictions for within-litter investment nor have the empirical studies to date addressed this matter.

When resources are shared among several individuals within a litter, their condition not only depends on factors affecting the litter as a whole, but also on within-litter interactions, such as sibling rivalry or hormonal interactions (Fernandez-Llario et al. 1999; Carranza 2004; Uller 2006). Similarly, when siblings vary in sex, maternal investment should be sibling-specific. But there are likely to be limitations in the ability of a mother to differentially provision individual foetuses within the uterine environment. Such limitations are likely to be particularly acute when siblings are not of the same sex and are thus expected to have a different optimal weight. Non-optimal investment levels in mixed litters are likely to put the sibling with the higher optimal weight, generally the male, at a disadvantage. Even a relatively small decrease in male birth weight is likely to have an amplified negative effect on reproductive fitness in polygynous mammals (Clutton-Brock et al. 1988). Based on these limitations, we predict that for multi-offspring litters, allocation in single sex litters (e.g. FF, MM) is more likely to follow life-history predictions than in mixed sex litters e.g. FM (referred to as the ‘allocation constraint’ hypothesis). As a result, siblings with higher optimal weight are likely to receive suboptimal levels of maternal investment in mixed litters. In polygynous mammals, we would hence expect a male from a mixed litter to be at a disadvantage compared with a male from a single sex litter. Generally, offspring from mixed litters are predicted to fit less well with current theory on investment levels due to allocation constraints.

The saiga antelope (Saiga tatarica) is a migratory ungulate of the semi-arid steppe and desert regions of Eurasia with high levels of sexual dimorphism (adult male/female body mass: 1.44; females: 28.1 kg, males: 40.6 kg; Fadeev & Sludskii 1982) and frequent twinning (twinning rates from 25 to 65%; this study, Fadeev & Sludskii 1982). They are ‘big spenders’; litter mass at birth accounts for, on average, 16.9% of maternal body mass (up to 38% when triplets are included). This exceeds the level reported for pronghorn and is among the highest levels of reproductive output reported for ungulates (Robbins & Robbins 1979; Fadeev & Sludskii 1982). The saiga's life-history characteristics are unique and ideally suited for investigating sex allocation. In this study, we present the first test of the allocation constraint hypothesis and test the big spender constraint hypothesis on saigas. Furthermore, we examine whether the observed allocation pattern follows the sequence predicted by the Williams (1979) hypothesis.

2. Material and methods

Saiga antelope calves were weighed and measured in the approximately 750 km2 Chernye Zemli State Biosphere Reserve, Republic of Kalmykia, Russian Federation (46°05′ N and 46°20′ E) during 2003–2005. Adult saiga females were autopsied in the Betpak-dala region, Kazakhstan (45°–50° N and 62°–72° E), as part of the saiga population monitoring programme of the Academy of Sciences, USSR during March–May 1966–1978. These two datasets come from ecologically distinct populations and time periods, in which saigas were under very different anthropogenic pressures. During 2003–2005 in Kalmykia, the population was at historically very low numbers and births were concentrated in one aggregation within the reserve; the species as a whole is currently listed as critically endangered on the IUCN red list due to a more than 90% decline in numbers over the last 10 years or three generations (IUCN 2006). During 1966–1978, the Kazakhstan saiga population was abundant, stable and commercially hunted (Bekenov et al. 1998). Hence, a comparison between these datasets may reveal fundamental life-history characteristics, which constrain saiga reproductive allocation in a range of circumstances.

(a) Calf data

Data on saiga antelope calf body mass (Salter Little Samson scale, 6 kg×100 g), sex, age (hours), litter size as well as date and GPS position (Garmin eTrex) were collected during calving (2003–2005). A total of 1141 calves were captured, of which 625 (335 males and 290 females) contained no missing values for the analysis presented (table S1 in electronic supplementary material). For the first few days after birth, saiga calves remain bedded down on the ground and can be captured during this period (mean capture age (in hours) 24.41±0.63 (s.e.), range 1–72, n=832).

After initial observations by car of both the location and spread of the birth aggregation, a straight-line transect route was selected with the aim of crossing the area of highest concentration of calves. GPS-guided transect route location varied daily in position and direction to account for aggregation movement. Transects were walked by three people, each 25 m apart, covering a width of approximately 75 m and length of 8–10 km. Distance judgement was repeatedly trained within the reserve prior to fieldwork. Transects started outside the calving area, crossed the assumed centre and terminated if no calf was caught over at least 2 km. Disturbance was minimized through the involvement of local scientists and rangers expert in handling calves. Adult females return to feed their calves only in the early morning and late afternoon while the calves are hiding, thus transects were conducted between 11.00 and 15.00 to minimize disturbance. Previous studies suggest that these techniques have negligible effects on calf survival (Grachev & Bekenov 1993).

Saiga calf siblings remain closely together for the first few weeks after birth, and calf densities were generally sufficiently low to distinguish singletons, twins and triplets. The only exceptions to this were calves in particularly dense areas of the aggregation for which litter size could not be unambiguously determined (2004, n=16; 2005, n=209); these were subsequently excluded from analyses involving litter size. Calves were aged using a combination of behavioural and physiological indicators designed and tested during past saiga fieldwork (Lundervold 2001; Lundervold et al. 2003). Owing to the non-invasive sampling methods, employed because of the conservation status of the species, no data on individual adult females were obtained.

(b) Foetus data

Herds of saiga antelopes were driven into corrals by motorbikes and cars during culls in mid-April to early May 1966–1978 aimed specifically at scientific investigation, but using the standard methods employed in the commercial harvest (Bekenov et al. 1998). The timing of the cull meant that females were heavily pregnant. The date and number of foetuses per female were recorded for all females. For the majority of culled females, age was determined and for a subset, the gutted weight was determined using a hanging balance. To estimate a female's age, jaws were collected and taken back to the laboratory for detailed age estimation using tooth eruption and tooth wear analysis (Bannikow 1963; Lundervold et al. 2003). Sex was recorded for almost all foetuses and weight for the majority; however, foetus length, height at front leg and height at back leg were determined only for a relatively small sample. A hanging balance was used and foetus weight determined accurately to 100 g.

(c) Statistical analyses

We analysed variation in (ln) body mass of offspring and (ln) total litter mass using linear mixed effect (LME) models (Pinheiro & Bates 2000) after the graphical exploration of possible nonlinearity of covariates using additive models (Hastie & Tibshirani 1990). Our main quantity of interest is litter composition in terms of sex and litter size, which we fitted as a six-level factor (litter composition: M, F, M(M), F(F), M(F), F(M); M, male; F, female; sibling sex given in brackets for twins). After the establishment of significant differences between factor levels of the main effect of interest (litter composition), orthogonal contrasts were designed (tables S3 and S4 in electronic supplementary material) to enable the comparison of individual combinations of litter composition within both the calf and foetus models (Crawley 1993). In addition, we included other factors that may affect mass, such as year (categorical), Julian date, age of calf (in hours) and maternal age (in years; available only for the foetus data). The significance of each factor and their interactions was assessed by stepwise backwards regression from the full model (Crawley 1993). Year levels were collapsed if they were not significantly different from one another and if model deviance did not significantly increase (Crawley 2002). We nested individual offspring weights within sibling pairs by adding litter identity as a random factor within the LME models to control for dependency of offspring from the same litter (Pinheiro & Bates 2000).

When testing for differences in the extent of sexual dimorphism, we ran a linear model fitted with (ln) offspring weight as a response variable, but with litter size and sex (not litter composition) as explanatory variables. When error structure followed a gamma instead of a normal distribution, generalized linear models with gamma error distribution were fitted (Crawley 1993). We tested model fit with standard diagnostic tools for normality (resulted in p<0.05 in all the cases), heteroskedasticity and influential values (Cook's D). All probability values are two-tailed. Means are reported with their standard errors in the form means±s.e. All analyses were conducted in R v. 2.2.1 (R Development Core Team 2005).

3. Results

(a) Calves

The average body mass (s.e.) of newborn saiga antelopes was 3.49 kg (0.016), varying from 2.1 to 4.8 kg (table S1 in electronic supplementary material). Of these, 74.7% of litters were singletons, 25.0% were twins and 0.3% were triplets (n=696 litters; total sample with known litter size). Average total litter mass for twins was 6.71 kg (5.1–8.7 kg, n=116 litters), while the mass of the only triplet litter was 10.6 kg. Triplets were excluded from further analyses. Differences in weight between litter compositions (F, M, F(F), F(M), M(F) and M(M)) were found to be highly significant overall (ANOVA: F5,619=25.5, p<0.001). The observed number of mixed litters did not significantly vary from the expected numbers (χ2=1.675, n.s., N=131).

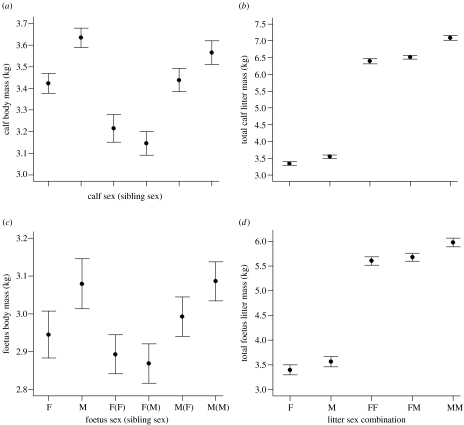
The model explained 24.6% (adjusted R2) of the variation in offspring body mass (for test statistics, see table S3 of electronic supplementary material). Singletons were consistently heavier than individual twins (figure 1, contrast 1 in table S3 of electronic supplementary material). Male offspring were consistently heavier than female offspring (figure 1, contrasts 2 and 3 in table S3 of electronic supplementary material). Sexual dimorphism was more pronounced in twins (mean difference 0.315 kg) than in singletons (mean difference 0.222 kg; GLM: litter size and sex interaction: F1,621=2.048, p=0.041), but differed depending on sex composition of the litter. If calves were ranked by weight within mixed litters, male calves had higher or equal rank in 78.5% of cases (χ2=21.06, p<0.001, N=65). Male–male twins tended to be heavier than males with a female sibling (figure 1, contrast 5 in table S3 of electronic supplementary material). By contrast, female offspring were of similar mass, irrespective of sibling sex (figure 1, contrast 4 in table S3 of electronic supplementary material). Body mass of offspring varied between years, being smaller in 2005 compared with 2003 and 2004. Age was included in the model to control for possible bias; older calves were heavier than younger ones. The later a calf was sampled in May, the heavier it was.

Figure 1.

Figure 1

Open in a new tab

The mass of saiga antelope (a,b) calves and (c,d) foetuses of different litter compositions. Individual weights are displayed in (a) and (c); total litter weights are displayed in (b) and (d). (a) Calf body mass (kg) of saiga antelope singletons and twins of different sex (predicted mean±s.e.; n=641) and (b) total litter mass (kg) of saiga antelope calves of different litter combinations (predicted mean±s.e.; n=639). (c) Foetus body mass (kg) of saiga antelope singletons and twins of different sex (predicted mean±s.e.; n=719) and (d) total litter mass of saiga antelope foetuses of different litter combinations in utero (predicted mean±s.e.; n=719).

(b) Foetuses

The average body mass of foetuses (sampled one to four weeks prior to birth) was 2.29 kg±0.024 (s.e.), varying from 0.6 to 4.8 kg (table S2 of electronic supplementary material). Of these, 34.5% of litters were singletons, 64.4% were twins and 1.1% were triplets (n=632 litters). Triplets were excluded from further analyses. Differences in weight between litter compositions (F, M, F(F), F(M), M(F) and M(M)) were found to be highly significant overall (ANOVA: F5,713=2.9, p=0.013). The observed number of mixed litters did not significantly vary from the expected numbers (χ2=0.058, n.s., N=274).

The model for saiga foetuses explained 59.1% (adjusted R2) of the variation in foetus body mass; a large part of which can be attributed to year effects (for test statistics, see table S4 of electronic supplementary material). Males were heavier than females in both singletons and twins (figure 1, contrasts 2 and 3 in table S4 of electronic supplementary material). Neither the extent of sexual dimorphism nor any of the other contrasts were found to be significant; however, the overall allocation pattern was qualitatively consistent with the one for calves (figure 1). Maternal age did not explain a significant amount of the variance in foetal weight and could be removed from the final model. The sample size for adult female weight was too small to test for the effects on foetus weight of different litter compositions. Foetuses were significantly heavier in 1968, 1969, 1972 and 1978 than in other years (table S4 in electronic supplementary material).

4. Discussion

In polygynous mammals, life-history theory predicts that male offspring benefit more from extra allocation of maternal resources than females (Trivers 1972); however, little is known about potential limitations to sex-specific allocation. Saiga litter mass accounted for 17% of adult female body mass on average, which is the highest reproductive output reported among ungulates (Robbins & Robbins 1979; Byers & Moodie 1990). Saiga antelopes are big spenders, nevertheless they consistently allocated more resources to male than female offspring, and we can thus reject the big spender constraint hypothesis, which was developed from studies of pronghorns (Byers & Moodie 1990). The lack of sex-specific investment in pronghorn must therefore be related to factors other than their high overall reproductive investment. One of those factors may be the intrauterine allocation mechanism of pronghorn whereby twins are invariably produced; this clearly warrants further study.

We are the first to report that the mass difference between male and female calves was larger for twins than for singletons. In addition, males were consistently larger than females, even within the same litter, suggesting that females are indeed able to target resources preferentially to males, even in utero. Furthermore, male offspring from female–male twin pairs tended to be smaller than those from a pure male–male pair (figure 1). This could suggest a penalty of having a sister and provide support for the allocation constraint hypothesis, whereby mothers have greater difficulty in optimally allocating resources to mixed sex pairs than single sex pairs. This would result in a suboptimal weight of the male foetus in female–male twin pairs. However, another potential explanation is that mothers with male–male offspring are of higher quality (Cassinello & Gomendio 1996). A foetus-driven process of hormonal or sibling interaction may also have led to the observed pattern, such as cumulative testosterone secretion by male foetuses leading to increased levels of maternal investment (Uller 2006). However, ultimately, resource allocation in utero is under maternal control, with the possibility of selective abortion under conditions of resource shortage (Alexander 1974). In contrast to males, resource allocation to female offspring was unrelated to sibling sex. Differences in offspring weight between years are likely to be due to environmental differences (Bekenov et al. 1998; Coulson et al. 2000).

The observed pattern is qualitatively the same for late-stage foetuses and newborn calves. The relatively high level of variability in the foetus weight data (see s.e. in figure 1) is likely to be due to the less accurate scales used for weighing foetuses, combined with the overall lower weight of foetuses and thus smaller differences in weight between individuals. This is likely to have contributed to the lack of significant differences between litter composition contrasts. The range of dates on which animals were sampled is also likely to have reduced the potential to discern effects.

Despite the Kalmykian and Betpak-dala populations being separated over a thousand kilometres and despite there being a 30–40-year gap between the sampling, the allocation pattern observed does not vary between the two sites. The Kalmykian saiga population has historically had a lower twinning rate than the Betpak-dala population (Sokolov & Zhirnov 1998). However, the extremely low twinning rates of approximately 25% described here for the Kalmykian population are lower than ever reported. This is likely to be the result of poaching pressure. First-year saiga females tend to give birth to singletons, whereas older females tend to give birth to twins (Fadeev & Sludskii 1982). A relative reduction in twins is thus likely to reflect a younger adult female population, the expected outcome of overharvesting. But even the extreme decline in population size, which has affected saigas throughout their range within the last decade (Milner-Gulland et al. 2001, 2003), does not appear to have had an impact on the fundamental reproductive pattern of maternal allocation presented.

Increases in sexual dimorphism among species are accompanied by decreases in the number of offspring per litter (Carranza 1996). In birds, parents are predicted to adjust their maternal resource allocation and even sex ratio according to rank within the brood (Carranza 2004). However, in mammals, there is very little empirical evidence and no specific theory regarding patterns of within-litter prenatal investment. Part of the reason for the general lack of theory and evidence is that only a limited number of highly dimorphic mammal species bearing multiple offspring per reproductive attempt exist to test hypotheses about maternal allocation. Maternal effort in individuals with varying litter size has been explored in a weakly sexually dimorphic species, the moose (Alces alces), but sample sizes were small and no clear pattern was observed (Nygren & Kojola 1997; Säde 2004). The well-known Williams (1979) hypothesis, referring to investment in total litters, predicts a sequence of litter type of F<M<FF<FM<MM and so forth as maternal condition increases. Maternal allocation within saigas followed this sequence qualitatively; however, FM litters were closer in mass to FF than to MM (figure 1). The same trend was observed in another highly dimorphic species, the Saharan arrui (Ammotragus lervia sahariensis), where FM litters did not differ from FF pairs in mass and were far smaller than MM litters overall (Cassinello & Gomendio 1996). Similarly, wild boar (Sus scrofa), the only species with large litters tested to date, appears to fit Williams' sequence (Fernandez-Llario et al. 1999). However, individual mass within litters was not reported in either study.

Our results show that in mixed twins, both the female and the male are lighter than their single sex twin counterparts, but much more so for males. Given that condition at birth is likely to be correlated with condition in adulthood in polygynous ungulates (Clutton-Brock et al. 1982), mixed litter individuals are expected to have a lower reproductive success. Compared with their female sibling, mixed litter males are likely to suffer markedly from a lower level of reproductive success due to the importance of body mass in securing mating opportunities for polygynous males. Future research should investigate how reproductive success varies between litter compositions and whether there is a correlation between maternal condition and production of single sex litters. One might suspect that it would be disadvantageous for any female, of whatever condition, to give birth to a mixed litter, especially if mixed litter males have a lower reproductive success than an average twin female. Despite this, we see no evidence for selective abortion in saiga antelopes; the number of mixed litters does not vary significantly from the predicted number in either calves or foetuses (table S1 and S2 in electronic supplementary material).

Evolutionary theories of optimal sex ratio adjustment have often been confronted with possible constraints regarding the proximate mechanism by which offspring sex can be determined (West & Sheldon 2002). However, little attention has been paid to potential constraints on sex-specific investment in offspring. After birth, it is easy to see that access to milk can be used as a mechanism by the female to bias her resource investment towards a certain sex, even in mixed litters; however, the mechanism involved in utero is less obvious. Williams (1979) ignored constraints on both post-natal and prenatal investment patterns when predicting total litter resource allocation (e.g. FF, FM or MM). Our study highlights the ability of big spenders to adaptively adjust maternal investment depending on the sex of offspring and that even mothers with twins have the ability to target extra resources to the male offspring prenatally. An explicit focus on potential constraints such as in our paper will improve our understanding of how both evolutionary and proximate mechanisms can jointly affect sex-specific investment patterns.

Acknowledgments

The work presented here adheres to the laws and scientific good practice of the countries concerned; we abide by the statement on ethical research published by the American Society on Animal Behavior http://asab.nothingham.ac.uk/downloads/guidelines2006.pdf

We thank the Russian Committee for the UNESCO MAB Programme (Moscow), the Centre for Wild Animals of Kalmykia, the staff of the Chernye Zemli State Biosphere reserve (Kalmykia) and the staff of the Institute of Zoology (Almaty, Kazakhstan) for their help and support. We thank Mick Crawley and Luca Borger for their statistical advice and Nils Bunnefeld, Denis Gorayev and Peter Kabat for their involvement in calf data collection. We are grateful for the comments made by Tim Coulson, Jean-Michel Gaillard and two anonymous referees. Financial support was provided by INTAS (Project 03-51-3579), the Darwin Initiative, the Wildlife Conservation Society and the Research Council of Norway (YFF project) and the Centre for Population Biology (Silwood) to A.M.

Supplementary Material

Electronic supplementary materials

Tables S1–S4

rspb20070038s18.doc (108.5KB, doc)

References

  1. Alexander R.D. The evolution of social behavior. Annu. Rev. Ecol. Syst. 1974;5:325–383. doi:10.1146/annurev.es.05.110174.001545 [Google Scholar]
  2. Bannikow A.G. A. Ziemsen Verlag; Wittenberg Lutherstadt, Germany: 1963. Die Saiga-Antilope. [The Saiga antelope] [Google Scholar]
  3. Bekenov A.B, Grachev I.A, Milner-Gulland E.J. The ecology and management of the saiga antelope in Kazakhstan. Mamm. Rev. 1998;28:1–52. doi:10.1046/j.1365-2907.1998.281024.x [Google Scholar]
  4. Byers J.A, Hogg J.T. Environmental effects on prenatal growth rate in pronghorn and bighorn: further evidence for energy constraint on sex-biased maternal expenditure. Behav. Ecol. 1995;6:451–457. doi:10.1093/beheco/6.4.451 [Google Scholar]
  5. Byers J.A, Moodie J.D. Sex-specific maternal investment in pronghorn, and the question of a limit on differential provisioning in ungulates. Behav. Ecol. Sociobiol. 1990;26:157–164. doi:10.1007/BF00172082 [Google Scholar]
  6. Carranza J. Sexual selection for male body mass and the evolution of litter size in mammals. Am. Nat. 1996;148:81–100. doi:10.1086/285912 [Google Scholar]
  7. Carranza J. Sex allocation within broods: the intrabrood sharing-out hypothesis. Behav. Ecol. 2004;15:223–232. doi:10.1093/beheco/arh004 [Google Scholar]
  8. Cassinello J, Gomendio M. Adaptive variation in litter size and sex ratio at birth in a sexually dimorphic ungulate. Proc. R. Soc. B. 1996;263:1461–1466. doi:10.1098/rspb.1996.0213 [Google Scholar]
  9. Charnov E.L. Princeton University Press; New York, NY: 1982. The theory of sex allocation. [Google Scholar]
  10. Clutton-Brock T.H, Guinness F.E, Albon S.D. Edinburgh University Press; Edinburgh, UK: 1982. Red deer. Behaviour and ecology of two sexes. [Google Scholar]
  11. Clutton-Brock T.H, Albon S.D, Guinness F.E. Reproductive success in male and female red deer. In: Clutton-Brock T.H, editor. Reproductive success. The University of Chicago Press; Chicago, IL: 1988. pp. 325–343. [Google Scholar]
  12. Clutton-Brock T.H, Albon S.D, Guinness F.E. Fitness costs of gestation and lactation in wild mammals. Nature. 1989;337:260–262. doi: 10.1038/337260a0. doi:10.1038/337260a0 [DOI] [PubMed] [Google Scholar]
  13. Coulson T.N, Milner-Gulland E.J, Clutton-Brock T. A comparison of the relative roles of density and climatic variation on fecundity rates in three contrasting ungulate species. Proc. R. Soc. B. 2000;267:1771–1779. doi: 10.1098/rspb.2000.1209. doi:10.1098/rspb.2000.1209 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Crawley M.J. Blackwell Scientific Publications; Oxford, UK: 1993. GLIM for ecologists. [Google Scholar]
  15. Crawley M.J. Wiley; Chichester, UK: 2002. Statistical computing. An introduction to data analysis using S-Plus. [Google Scholar]
  16. Darwin C. Appleton; New York, NY: 1871. The descent of man, and selection in relation to sex. [Google Scholar]
  17. Fadeev V.A, Sludskii A.A. Academy of Sciences, USSR; Alma-Ata, Kazakhstan: 1982. Saigak v Kazakhstane. [The Saiga in Kazakhstan] [Google Scholar]
  18. Fernandez-Llario P, Carranza J, Mateos-Quesada P. Sex allocation in a polygynous mammal with-large litters: the wild boar. Anim. Behav. 1999;58:1079–1084. doi: 10.1006/anbe.1999.1234. doi:10.1006/anbe.1999.1234 [DOI] [PubMed] [Google Scholar]
  19. Frank S.A. Individual and population sex allocation patterns. Theor. Popul. Biol. 1987;31:47–74. doi: 10.1016/0040-5809(87)90022-0. doi:10.1016/0040-5809(87)90022-0 [DOI] [PubMed] [Google Scholar]
  20. Frank S.A. Sex allocation theory for birds and mammals. Annu. Rev. Ecol. Syst. 1990;21:13–55. doi:10.1146/annurev.es.21.110190.000305 [Google Scholar]
  21. Gosling L.M. Biased sex-ratios in stressed animals. Am. Nat. 1986;127:893–896. doi:10.1086/284532 [Google Scholar]
  22. Grachev I.A, Bekenov A.B. The present state of saiga populations in Kazakhstan. Almaty. 1993;2:165–189. Zoologicheskoe issledovaniya v Kazakhstane [Zoological Research in Kazakhstan] [Google Scholar]
  23. Hastie T, Tibshirani R.Generalized additive Models1990Chapman and Hall; London, UK: [DOI] [PubMed] [Google Scholar]
  24. Hewison A.J.M, Gaillard J.M. Successful sons or advantaged daughters? The Trivers–Willard model and sex-biased maternal investment in ungulates. Trends Ecol. Evol. 1999;14:229–234. doi: 10.1016/s0169-5347(99)01592-x. doi:10.1016/S0169-5347(99)01592-X [DOI] [PubMed] [Google Scholar]
  25. Holand O, Mysterud A, Roed K.H, Coulson T, Gjostein H, Weladji R.B, Nieminen M. Adaptive adjustment of offspring sex ratio and maternal reproductive effort in an iteroparous mammal. Proc. R. Soc. B. 2006;273:293–299. doi: 10.1098/rspb.2005.3330. doi:10.1098/rspb.2005.3330 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. IUCN 2006 The IUCN red data book of threatened species. [See http://www.iucnredlist.org]
  27. Kruuk L.E.B, Clutton-Brock T.H, Rose K.E, Guinness F.E. Early determinants of lifetime reproductive success differ between the sexes in red deer. Proc. R. Soc. B. 1999;266:1655–1661. doi: 10.1098/rspb.1999.0828. doi:10.1098/rspb.1999.0828 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lundervold, M. 2001 Infectious diseases of saiga antelopes and domestic livestock in Kazakhstan. Ph.D. thesis, University of Warwick, UK.
  29. Lundervold M, Langvatn R, Milner-Gulland E.J. A comparison of age estimation methods for the saiga antelope Saiga tatarica. Wildl. Biol. 2003;9:219–227. [Google Scholar]
  30. McGinley M.A. The adaptive value of male-biased sex-ratios among stressed animals. Am. Nat. 1984;124:597–599. doi:10.1086/284299 [Google Scholar]
  31. Milner-Gulland E.J, Kholodova M.V, Bekenov A, Bukreeva O.M, Grachev I.A, Amgalan L, Lushchekina A.A. Dramatic declines in saiga antelope populations. Oryx. 2001;35:340–345. doi:10.1046/j.1365-3008.2001.00202.x [Google Scholar]
  32. Milner-Gulland E.J, Bukreeva O.M, Coulson T, Lushchekina A.A, Kholodova M.V, Bekenov A.B, Grachev I.A. Reproductive collapse of saiga antelope harems. Nature. 2003;422:135. doi: 10.1038/422135a. doi:10.1038/422135a [DOI] [PubMed] [Google Scholar]
  33. Nygren T, Kojola I. Twinning and fetal sex ratio in moose: effects of maternal age and mass. Can. J. Zool. Revue Canadienne De Zoologie. 1997;75:1945–1948. [Google Scholar]
  34. Pinheiro J.C, Bates D.M. Springer; New York, NY: 2000. Mixed-effects models in S and S-Plus. [Google Scholar]
  35. R Development Core Team. R Foundation for Statistical Computing; Vienna, Austria: 2005. R: a language and environment for statistical computing. [Google Scholar]
  36. Robbins C.T, Robbins B.L. Fetal and neonatal growth-patterns and maternal reproductive effort in ungulates and sub-ungulates. Am. Nat. 1979;114:101–116. doi:10.1086/283456 [Google Scholar]
  37. Säde S. Twinning rate and foetal sex ratio in moose Alces alces in Estonia during low-density and increasing population phases in relation to maternal age. Wildl. Biol. 2004;10:295–300. [Google Scholar]
  38. Sheldon B.C, West S.A. Maternal dominance, maternal condition, and offspring sex ratio in ungulate mammals. Am. Nat. 2004;163:40–54. doi: 10.1086/381003. doi:10.1086/381003 [DOI] [PubMed] [Google Scholar]
  39. Sokolov V.E, Zhirnov L.V, editors. The saiga: phylogeny, systematics, ecology, conservation and use. Russian Academy of Sciences; Moscow, Russia: 1998. [Google Scholar]
  40. Trivers R.L. Parental investment and sexual selection. In: Campbell B, editor. Sexual selection and the descent of man. Aldine Press; Chicago, IL: 1972. pp. 136–179. [Google Scholar]
  41. Trivers R.L, Willard D.E. Natural selection of parental ability to vary the sex ratio of offspring. Science. 1973;179:90–92. doi: 10.1126/science.179.4068.90. doi:10.1126/science.179.4068.90 [DOI] [PubMed] [Google Scholar]
  42. Uller T. Sex-specific sibling interactions and offspring fitness in vertebrates: patterns and implications for maternal sex ratios. Biol. Rev. 2006;81:207–217. doi: 10.1017/S1464793105006962. doi:10.1017/S1464793105006962 [DOI] [PubMed] [Google Scholar]
  43. West S.A, Sheldon B.C. Constraints in the evolution of sex ratio adjustment. Science. 2002;295:1685–1688. doi: 10.1126/science.1069043. doi:10.1126/science.1069043 [DOI] [PubMed] [Google Scholar]
  44. West S.A, Herre E.A, Sheldon B.C. The benefits of allocating sex. Science. 2000;290:288–290. doi: 10.1126/science.290.5490.288. doi:10.1126/science.290.5490.288 [DOI] [PubMed] [Google Scholar]
  45. Williams G.C. The question of adaptive sex ratio in outcrossed vertebrates. Proc. R. Soc. B. 1979;205:567–580. doi: 10.1098/rspb.1979.0085. doi:10.1098/rspb.1979.0085 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Electronic supplementary materials

Tables S1–S4

rspb20070038s18.doc (108.5KB, doc)

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES