Polarization transfer by cross-correlated relaxation in solution NMR with very large molecules

Abstract

In common multidimensional NMR experiments for studies of biological macromolecules in solution, magnetization transfers via spin–spin couplings [insensitive nuclei enhanced by polarization transfer (INEPT)] are key elements of the pulse schemes. For molecular weights beyond 100,000, transverse relaxation during the transfer time may become a limiting factor. This paper presents a transfer technique for work with big molecules, cross relaxation-enhanced polarization transfer (CRINEPT), which largely reduces the size limitation of INEPT transfers with the use of cross-correlated relaxation-induced polarization transfer. The rate of polarization transfer by cross-correlated relaxation is proportional to the rotational correlation time, so that it becomes a highly efficient transfer mechanism for solution NMR with very high molecular weights. As a first implementation, [¹⁵N,¹H]-correlation experiments were designed that make use of cross-correlation between dipole–dipole coupling and chemical shift anisotropy of the ¹⁵N—¹H-moieties for both CRINEPT and transverse relaxation-optimized spectroscopy (TROSY). When compared with INEPT-based [¹⁵N,¹H]-TROSY, these experiments yielded up to 3-fold signal enhancement for amide groups of a 110,000-Da protein in aqueous solution at 4°C. CRINEPT opens avenues for solution NMR with supramolecular structures such as membrane proteins solubilized in micelles or lipid vesicles, proteins attached to nucleic acid fragments, or oligomeric proteins.

Structure determination of proteins by NMR in solution (1) has so far been limited to the molecular weight range up to ≈30 kDa (2), and experiments yielding backbone assignments for ²H-labeled proteins up to ≈60 kDa have been reported (3). In larger molecular species, the standard experimental techniques (4, 5) lead to severe sensitivity loss because of transverse relaxation even when optimal isotope-labeling is used (6). The situation has recently been improved with the introduction of the transverse relaxation-optimized spectroscopy (TROSY) technique, which reduces transverse relaxation during evolution and observation periods in heteronuclear NMR experiments (7, 8). For example, for ¹⁵N—¹H-moieties in proteins, significant reduction of transverse relaxation during the ¹⁵N evolution and amide proton acquisition periods can be achieved at the highest presently available ¹H frequencies, and nearly complete cancellation is expected at ¹H frequencies near 1 GHz (7, 9). TROSY already has been applied for detailed NMR studies of a protein with molecular weight >100 kDa (8). Theoretical considerations indicate that TROSY will reach its limits at somewhat larger sizes because of rapid transverse relaxation during the insensitive nuclei enhanced by polarization transfer (INEPT)-type (10) magnetization transfers via scalar couplings between the different nuclei. This paper presents a transfer technique for work with very large molecules, cross relaxation-enhanced polarization transfer (CRINEPT), which is based on combining cross-correlated relaxation-induced polarization transfer (11–14) and polarization transfer via scalar couplings (10). To provide a foundation for practical applications of CRINEPT, the performance of the previously little-used cross relaxation-induced polarization transfer (CRIPT) is investigated for ¹⁵N—¹H-moieties of very large particles in solution, where one has cross-correlation between relaxation by dipole–dipole coupling and by chemical shift anisotropy (CSA). We then describe initial implementations of CRINEPT in [¹⁵N,¹H]-correlation experiments. Data sets are recorded for a ¹⁵N,²H-labeled protein for which the effective rotational correlation time was estimated to be ≳70 ns.

METHODS

Theoretical Considerations.

Transfer of in-phase ¹H coherence to antiphase ¹⁵N coherence in ¹⁵N—¹H-moieties by cross-correlation between dipole–dipole coupling and CSA relaxation (7, 11, 12, 14) is considered. By using the product operator formalism (15), the spin operator I corresponds to ¹H, S corresponds to ¹⁵N, and the two spins have a scalar coupling constant J_IS and resonance frequencies ω_I and ω_S. For large molecular sizes at high magnetic fields, only terms proportional to the spectral density function at zero frequency, J(0), need to be considered (7). For isotropic rotational tumbling, J(0) is equal to 2τ_c/5, where τ_c is the isotropic rotational correlation time of the molecule. The evolution of inphase coherence is coupled to the antiphase coherence via the cross-correlation relaxation rate R_C.

Starting with inphase magnetization on spin I at the start of the magnetization transfer period T, <I_x>(0), the buildup of antiphase coherence by CRIPT during T can be described by ref. 14:

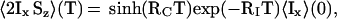1

with

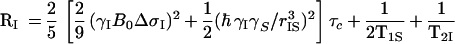2

and

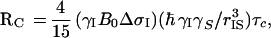3

where r_IS is the distance between the two nuclei involved, Δσ_I is the CSA of nucleus I, B₀ is the static magnetic field, and γ_I and γ_S are the gyromagnetic ratios of I and S. T_2I and T_1S account for the transverse relaxation of spin I and the longitudinal relaxation of spin S (7, 11, 16).

The relative efficiencies of polarization transfer with CRIPT (Eqs. 1-3) or with INEPT (10) at variable rotational correlation times τ_c are compared in Fig. 1a. The buildup of antiphase magnetization in INEPT is described by

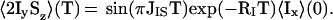4

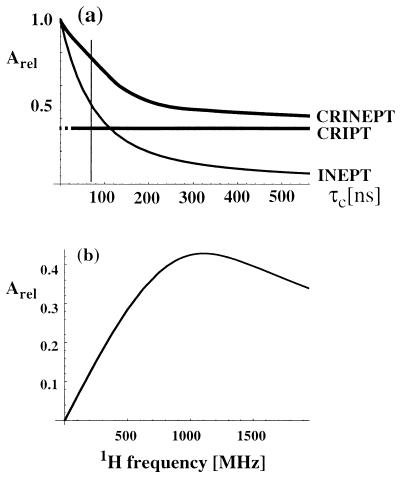
Because, in Eq. 1, the transfer time T appears always in a product with τ_c, the optimal transfer period for CRIPT is inversely proportional to τ_c. Therefore, with proper adjustment of T, the maximal amount of magnetization that can be transferred by CRIPT is independent of the molecular size (Fig. 1a), where one has to consider, however, that the optimal T for τ_c values shorter than ≈20 ns would be unreasonably long. In contrast, the efficiency of INEPT falls off rapidly with increasing size (Eq. 4; Fig. 1a). The magnetic field dependence of CRIPT for a ¹⁵N—¹H-moiety located in a β-sheet of a fully ¹⁵N,²H-labeled protein (Fig. 1b) shows that the maximum theoretical magnetization transfer with CRIPT is about half of the maximum transfer by INEPT and that maximal CRIPT transfer for a ¹⁵N—¹H moiety is obtained at ≈1 GHz (7–9). Fig. 1 further shows that CRIPT becomes more efficient than INEPT for molecules with τ_c ≳ 100 ns, but that INEPT contributes significantly to the polarization transfer up to τ_c ≈ 300 ns.

Figure 1.

(a) Plot of the relative magnetization transfer efficiencies using optimal transfer delays T (see Eqs. 1– 7) for CRIPT, INEPT, and CRINEPT at 750-MHz proton frequency versus molecular size represented by the isotropic rotational correlation time τ_c. The CRIPT graph is shown with a broken line for small τ_c values, to indicate that the optimal transfer time T would be unreasonably long. (b) Plot of the maximal polarization transfer obtainable with CRIPT versus the static magnetic field B_o represented by the corresponding ¹H frequency. The curves were calculated by using Eqs. 1-7 for a ¹⁵N—¹H-moiety located in a β-sheet of a fully ¹⁵N,²H-labeled protein. The following parameters were used (8): r_HN = 1.04 Å, Δσ_H = 15 ppm, and Θ_H = 10°. Remote protons considered are ¹H^N(i − 1), ¹H^N(i + 1), and ¹H^N(j) at distances of 4.3, 4.3, and 3.3 Å, respectively. These are typical values for a β-sheet in a ¹⁵N,²H-labeled protein, where i is the observed residue, (i − 1) and (i + 1) are the sequential neighbors, and j indicates a long-range contact across the β-sheet (1).

Based on the observations on CRIPT and INEPT in Fig. 1, and considering that systems with τ_c values in the range 50–300 ns will be of special practical interest, we combined the two polarization transfer mechanisms in CRINEPT, where proton antiphase coherence is generated during a delay T devoid of radio-frequency pulses, which results in the terms in Eqs. 5 and 6 for the CRINEPT transfer (obtained from the differential Eq. 32 in ref. 11):

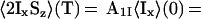5

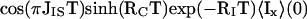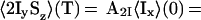6

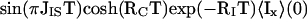Eqs. 5 and 6 are the x and y components of the resulting antiphase magnetization, respectively. The relative orientation of the resulting total magnetization therefore depends on τ_c and the mixing time T, and the transfer efficiency of CRINEPT represented by the signal amplitude A_I (Fig. 1) is proportional to the absolute value of the total antiphase magnetization:

7

With Eq. 7, the relative contributions of INEPT and CRIPT to the total polarization transfer can readily be evaluated whereas Eqs. 5 and 6 contain a mix of polarization transfer via scalar coupling (trigonometric functions) and CRIPT (hyperbolic functions) in both terms. For short τ_c, the rate R_C is negligibly small and only INEPT contributes to CRINEPT whereas, for long τ_c, R_C becomes large and CRIPT is the dominant polarization transfer mechanism (Eq. 3; Fig. 1a). In principle, CRINEPT is always superior to INEPT or CRIPT (Fig. 1a). However, free proton chemical shift evolution during CRINEPT transfers (Figs. 2c and 3) has to be handled by additional pulse sequence elements, which may reduce the overall sensitivity (see below).

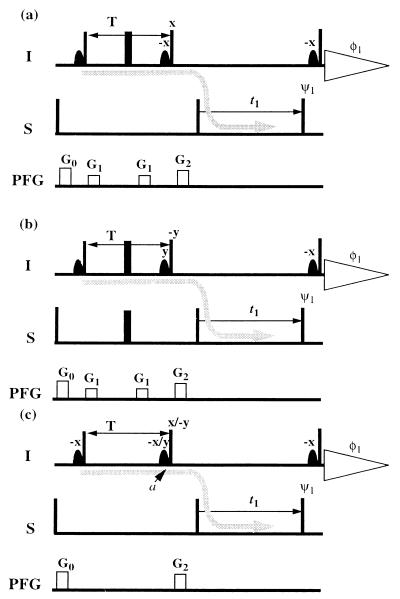
Figure 2.

Pulse sequences used for direct comparison of polarization transfer by CRIPT (a), INEPT (b), and CRINEPT (c). In each scheme, the coherence flow is indicated by a gray curved arrow. The narrow and wide bars indicate nonselective 90 and 180° pulses, which are applied with phase x unless indicated otherwise above the pulses; ψ₁ = (x, −x), φ₁ = (x, −x). Sine-bell shapes represent selective 90° pulses on the water resonance, which keep the water magnetization along +z during the whole sequence (17). On the line marked PFG, rectangles indicate pulsed magnetic field gradients applied along the z axis. The steady state magnetization of the S spins was suppressed by a 90° pulse on S followed by a pulsed field gradient before the first proton pulse. In c, two experiments are recorded, one with phase x and the second one with phase −y on the second proton pulse, as indicated. The phase of the associated water flip back pulse also is changed.

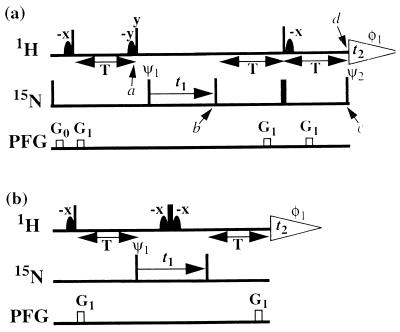
Figure 3.

[¹⁵N,¹H] correlation experiments using CRINEPT-based polarization transfer. (a) Fully relaxation-optimized [¹⁵N,¹H]-CRINEPT-TROSY. (b) [¹⁵N,¹H]-CRINEPT-HMQC-[¹H]-TROSY. Narrow and wide black bars indicate nonselective 90 and 180° pulses applied at the proton (¹H) or nitrogen (¹⁵N) frequency. Sine-bell shapes on the line marked ¹H indicate selective 90° pulses on the water resonance to keep the water magnetization along +z during the whole sequence (17, 30). The optimal length of the period T, as set according to Eq. 7, is typically between 3 and 5.4 ms. On the line marked PFG, rectangles indicate duration and strength of pulsed magnetic field gradients applied along the z axis. (a) G₀: 400 μs, 15 G/cm; G₁: 400 μs, 15 G/cm. (b) G₁: 1,000 μs, 30 G/cm. The phase cycles for both experiments are φ₁ = {x, −x}, ψ₁ = {x, −x}. All other radio-frequency pulses are applied with phase x, unless labeled differently. In a, two free induction decays are recorded for each t₁ increment, with ψ₂ = {x, x} and ψ₂ = {−x, −x}, respectively, and are added with a 90° phase correction in both dimensions. Quadrature detection in the ¹⁵N(t₁) dimension is achieved by the States-TPPI method (31) applied to the phase ψ₁. The water-selective pulses have a Gaussian shape and a length of 1.3 ms.

Pulse Schemes for Comparative Studies of Magnetization Transfer by CRIPT, INEPT, and CRINEPT.

The three experimental schemes in Fig. 2 were used for measurements of the efficiency of a single transfer from in-phase magnetization on ¹H^N to antiphase magnetization on ¹⁵N (arrows in Fig. 2) by the three transfer types considered in the preceding section. In each of the experiments, the ¹⁵N antiphase coherence is frequency labeled during t₁ and is transferred identically to ¹H^N antiphase magnetization with the two 90° pulses on I and S. In all experiments, the water magnetization is kept along +z during the whole sequence by using water-selective pulses (17).

In the scheme used for CRIPT (Fig. 2a), the inphase ¹H^N magnetization generated by the first 90° pulse is transferred to antiphase magnetization by cross-correlated relaxation, according to Eq. 1. The proton chemical shift evolution is refocused by a 180° pulse, which also decouples the protons from ¹⁵N. At the end of the period T, 90° pulses on I and S generate the antiphase coherence 2I_zS_y. The magnetization flow can be described in short notation as I_y → 2I_yS_z → 2I_zS_y (Fig. 2a). In the INEPT scheme (Fig. 2b), the flow of coherence is I_y → 2I_xS_z → 2I_zS_y.

In the CRINEPT transfer measurement (Fig. 2c), the absence of 180° radio frequency pulses during T results in magnetization transfer by cross-correlated relaxation as well as by scalar coupling. In addition, ¹H chemical shift evolution occurs during T. The resulting antiphase coherence at time a can be represented by the density matrix

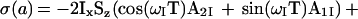8

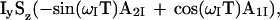where A_1I and A_2I are given by Eqs. 5 and 6. The CRINEPT transfer efficiency can be measured with two experiments that use, respectively, x and y phases for the second 90° proton pulse (Fig. 2c).

[¹⁵N,¹H]-Correlation Experiments Using CRINEPT and TROSY.

For practical applications of CRINEPT, we introduced a gradient during the period T (Fig. 3a), which changes Eq. 8 to

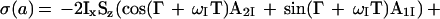9

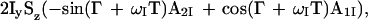The dephasing along the z axis because of the gradient is indicated by Γ = G₁γ_H τ z, where τ is the length of the pulsed field gradient, G₁ is its strength, and z describes the position of the observed spins along the z axis. Direct use of the CRINEPT transfer element as shown in Fig. 2c would result in reduced sensitivity because only half of the components of Eq. 9 can be recovered. In addition, a refocusing element has to be introduced in the pulse sequence to get a phase-sensitive [¹⁵N,¹H]-correlation experiment, as is demonstrated in the [¹⁵N,¹H]-CRINEPT-TROSY experiment of Fig. 3a. Alternatively, when omitting the second 90° proton pulse (Fig. 2c), zero- and double-quantum coherences are generated, and all of the terms of Eq. 9 can be transferred and refocused as demonstrated in the [¹⁵N,¹H]-CRINEPT–heteronuclear multiple-quantum correlation (HMQC) experiment of Fig. 3b.

The scheme of Fig. 3a represents a fully relaxation-compensated CRINEPT-correlation experiment. The following description retains only the magnetization components that lead to a detectable signal during the acquisition period. At time point a of the pulse scheme, after the first time period T, the magnetization is described by Eq. 9. Because of the subsequent pulses, only the first term of Eq. 9 is transferred to transverse magnetization on ¹⁵N, which is subsequently frequency-labeled during the time t_1, yielding the following terms at time b:

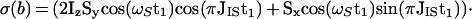10

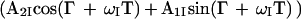The CRINEPT-based sequence elements between time points b and d refocus the precession of the proton chemical shift during the first CRINEPT element as well as the effect of the first gradient and immediately before the last 90° pulse on ¹⁵N the inphase term of Eq. 10 has evolved into the following coherences:

11

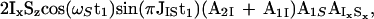where A_IxSx accounts for the relaxation of I_xS_x. A_2S and A_1S are calculated with Eqs. 5 and 6 after exchange of the indices I and S by using the relaxation rates R_I and R_C (Eqs. 2 and 3).

Finally, applying the last 90° pulse on ¹⁵N with the phase Ψ₂ = x + arctan(A_2S/A_1S) the following proton antiphase coherence is generated (A_S is calculated with Eq. 7 by replacement of the indices I with S):

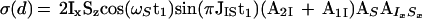12

The antiphase term of Eq. 10 is transformed to inphase:

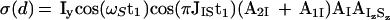13

where A_IzSz accounts for the reduction of the signal amplitude by relaxation of the I_zS_z state during the first period T within the refocusing element of Fig. 3a. The inphase and antiphase components in Eqs. 12 and 13 are separated by recording two free induction decays with inverted phase Ψ₂ (Fig. 3a).

A modified [¹⁵N,¹H]-HMQC experiment (18), [¹⁵N,¹H]-CRINEPT-HMQC-[¹H]-TROSY (Fig. 3b), is included here as an example of a scheme in which the complete CRINEPT-transferred polarization can contribute to the observed signal. Both transfer elements in this scheme are based on CRINEPT, and the different phases and chemical shift modulations obtained with the transfer according to Eq. 9 are optimally refocused by the 180° pulse on protons and the second CRINEPT element. The experiment does not include TROSY compensation during the ¹⁵N evolution period and therefore yields broader lines along the ¹⁵N frequency axis than the scheme of Fig. 3a.

Experimental.

The NMR experiments were recorded with 7,8-dihydroneopterin aldolase from Staphylococcus aureus. This protein is a homooctamer with subunits of 121 amino acid residues. For the experiments in this paper, it was isotope-labeled uniformly with ¹⁵N and in the extent of 75% with ²H, and it was studied at 4°C in 95% H₂O/5% ²H₂O by using a protein concentration of 0.4 mM. Based on measurements of the ¹⁵N T₁ and T₂ relaxation times (19) at 20°C, a preliminary estimate for a lower limit on the rotational correlation time τ_c under the conditions of the present experiments was established at 70 ns. All NMR spectra were measured on a Bruker (Billerica, MA) DRX-750 spectrometer equipped with four radio-frequency channels and a shielded pulsed-field gradient along the z direction.

RESULTS

Magnetization Transfer by CRIPT, INEPT, and CRINEPT.

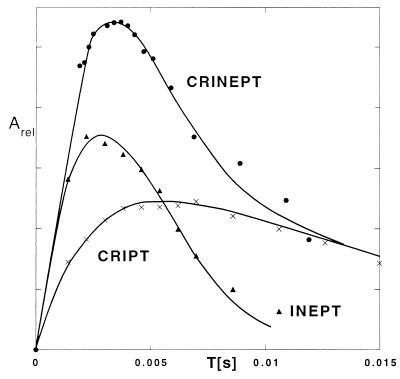
To provide a foundation for the use of CRINEPT, we evaluated the optimal transfer times T for each of the three transfer mechanisms of Fig. 2 in a macromolecular system with an effective rotational correlation time of ≈70 ns by using the ¹⁵N,²H-labeled S. aureus aldolase in H₂O solution at 4°C. The transfer efficiencies were measured from serial experiments by using the pulse sequences in Fig. 2 with variable transfer times T. The buildup curve for CRIPT from 0 to 15 ms shows a fast increase followed by a plateau and an exponential decay, which corresponds to Eq. 1 as demonstrated by the close fit obtained with the simulation (Fig. 4). The optimal transfer delay is ≈6 ms, with an observed range of 4–13 ms for different ¹⁵N—¹H groups in the aldolase.

Figure 4.

Buildup curves of magnetization transfer for CRIPT, INEPT, and CRINEPT for the well resolved ¹⁵N—¹H cross peak of [u-¹⁵N, 75%²H]-labeled S. aureus aldolase (32) at [ω₁(¹⁵N) = 121.0 ppm, ω₂(¹H) = 11.1 ppm] measured at 750 MHz (protein concentration 0.4 mM, solvent 95% H₂O/5%²H₂O, T = 4°C). The buildup curves were obtained from serial measurements with variable T values by using the pulse sequences of Fig. 2. For CRINEPT, two free induction decays with phases x and −y for the second ¹H radio-frequency pulse, respectively, were measured for each value of T (Fig. 2c), which doubled the measuring time when compared with a or b. The two subspectra thus obtained are cosine- or sine-modulated with regard to the proton chemical shift during the time period T and were used to calculate the absolute value intensity of the individual cross peaks, which represents the total CRINEPT-transferred polarization (Eq. 7). CRIPT, INEPT, and CRINEPT buildup curves were fitted by using Eqs. 1, 4, and 7, respectively, which resulted in R_I = 236 ± 10 s⁻¹ and R_C = 172 ± 13 s⁻¹ for CRIPT, R_I = 254 ± 18 s⁻¹ for INEPT, and R_I = 238 ± 13 s⁻¹ and R_C = 153 ± 13 s⁻¹ for CRINEPT.

For INEPT transfer with the same ¹⁵N—¹H-moiety as shown for CRIPT, the optimal delay is ≈3 ms (Fig. 4), and only ≈50% of the maximal transfer that would be obtainable without relaxation is achieved (Figs. 1a and 4). Nonetheless, for the presently studied system with τ_c = 70 ns, the observed INEPT transfer maximum exceeds the maximal CRIPT transfer by ≈1.5-fold (Fig. 4).

The experiments with CRINEPT (Fig. 4) and the fitting of Eq. 7 to the measured signal buildup confirm the theoretical prediction (Fig. 1a) that CRINEPT is in principle superior to INEPT and CRIPT for all correlation times. Depending on the experiment used, however, some coherence terms of Eq. 9 may not contribute to the detectable signal. In the system of Fig. 4, the optimal transfer delay for CRINEPT is ≈4 ms and thus lies between the optimal T values for the two basic experiments. The relative maximal transfers for CRINEPT, INEPT, and CRIPT are ≈7.6:5:3.4 (Fig. 4), which coincides well with the theoretical predictions for a protein with τ_c = 70 ns (Fig. 1a).

[¹⁵N,¹H]-Correlation Experiments with CRINEPT Transfers.

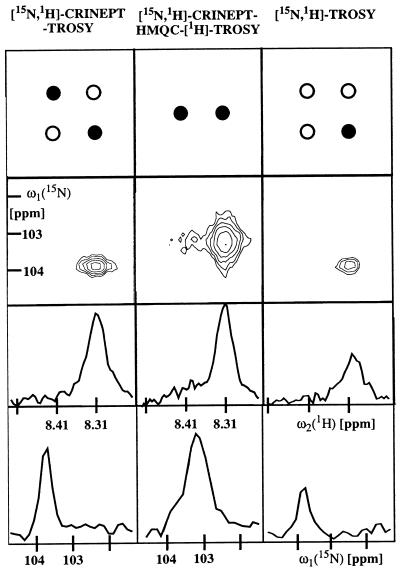
The [¹⁵N,¹H]-CRINEPT-TROSY experiment (Fig. 3a) includes transverse relaxation-optimization during the transfer delays as well as the evolution periods. For the peak shown in Fig. 5, comparison with [¹⁵N,¹H]-TROSY demonstrates that the new scheme preserves the narrow line shape and yields a 2-fold signal increase. For other fast relaxing aldolase signals, sensitivity gains between 1.5 and 3 were obtained. The experimental scheme of Fig. 3a has been designed to select the two multiplet components of the ¹⁵N—¹H signal indicated by the filled circles in the top row of Fig. 5 (Eqs. 12 and 13). In the spectra obtained with the aldolase, the more rapidly relaxing one of these two components is in most signals broadened beyond detection (Fig. 5, contour plot on the left). Both components could be observed only for one highly flexible backbone ¹⁵N—¹H group and for some of the arginine side chains.

Figure 5.

Comparison of signal intensity and lines shape for [¹⁵N,²H]-CRINEPT-TROSY (Fig. 3a), [¹⁵N,¹H]-CRINEPT-HMQC-[¹H]-TROSY (Fig. 3b), and [¹⁵N,¹H]-TROSY (33). The data were recorded with [u-¹⁵N, 75% ²H]-labeled S. aureus aldolase (32) in 95% H₂O/5% ²H₂O, T = 4°C at 750-MHz ¹H frequency. The backbone amide moiety of Gly 43 is shown. Before Fourier transformation, the three data sets were multiplied with a cosine window function in all dimensions and were transformed to a size of 256 × 2,048 complex points by using the program prosa (34). The total measuring time was 4 h per experiment, with t_{1 max} = 50 ms, t_{2 max} = 98 ms, T = 5.4 ms, and an interscan delay of 0.7 s. The panels at the top indicate the peak selections by the three experiments. As indicated by the black circles, only the most slowly relaxing component of the four-component signal is detected in TROSY (7), [¹⁵N,¹H]-CRINEPT-TROSY selects the slowest and fastest relaxing components, and [¹⁵N,¹H]-CRINEPT-HMQC-[¹H]-TROSY yields a doublet in the proton dimension. The contour plots contain the signal of the backbone ¹⁵N—¹H group of Gly-43. The two rows of panels in the lower half of the figure show cross sections along ω₂(¹H) and along ω₁(¹⁵N), respectively, through the peaks shown in the contour plots.

With the presently used system with τ_c ≈ 70 ns, the [¹⁵N,¹H]-CRINEPT-HMQC-[¹H]-TROSY experiment (Fig. 3b) yields high signal intensity because there is no loss of magnetization attributable to proton chemical shift evolution during the CRINEPT element. Because of the absence of TROSY-compensation in the indirect dimension, there is an ≈2-fold increase of the ¹⁵N-linewidth when compared with the other two experiments in Fig. 5 (bottom row). The overall result is that the peak amplitude over the noise is comparable to [¹⁵N,¹H]-CRINEPT-TROSY. Two multiplet peaks per ¹⁵N—¹H-moiety are expected because no decoupling is applied during acquisition (Fig. 3b). However, because of the fast relaxation of the lower-field component during the transfer elements and the t₁-evolution, only the more slowly relaxing component was detectable for most ¹⁵N—¹H groups in the aldolase (Fig. 5, contour plot in the center). This [¹⁵N,¹H]-correlation peak is in a different position from those of any of the components of the usual four-line correlation signal; that is, it is shifted ≈45 Hz upfield along ω₁(¹⁵N) when referenced to the TROSY component (Fig. 5, top row).

DISCUSSION

Currently, nearly all heteronuclear multidimensional NMR experiments use INEPT to transfer magnetization between different spin species (5), but the efficiency of INEPT deteriorates with increasing rotational correlation time τ_c (Fig. 1a). In contrast, transfer of polarization by CRIPT is independent of τ_c. Further, in amide groups, the efficiency of CRIPT increases with the strength of the external magnetic field up to ≈1 GHz proton frequency whereas the sensitivity of the INEPT transfer deteriorates further because of increased CSA relaxation. The present experiments with the 110-kDa S. aureus aldolase validate the theoretical considerations of Fig. 1, which predict that, for molecules with rotational correlation times from ≈50 to 300 ns, both INEPT and CRIPT promote substantial polarization transfer between ¹H and ¹⁵N in amide groups. This observation is exploited in CRINEPT.

The [¹⁵N,¹H]-HMQC experiment (18) contains inherently two CRINEPT-type transfers. Based on the present treatment of polarization transfer, the delays T in the HMQC transfer (Fig. 3b) can now be optimized for work with large molecules. However, because TROSY compensation of transverse relaxation can only be applied for ¹H (Fig. 3b) and the rate of transverse ¹⁵N relaxation will therefore increase with increasing molecular size, the performance of this scheme, when compared with [¹⁵N,¹H]-CRINEPT-TROSY, is predicted to deteriorate for systems with significantly longer τ_c values than 70 ns (Fig. 5).

For systems with τ_c ≳ 300 ns, CRIPT is predicted to be nearly as sensitive as CRINEPT (Fig. 1a). CRIPT then also could be used as a “filter” to eliminate resonances originating from smaller molecules because the optimal transfer time T is inversely proportional to τ_c (Eq. 1). CRINEPT-based [¹⁵N,¹H]-correlation experiments may be used as building blocks for more complex NMR experiments with large molecules, which may include simple two-dimensional experiments (1, 20, 21), triple-resonance experiments for sequential and intraresidual backbone assignments (4, 22, 23), experiments for side-chain assignments (24–26), and experiments for studies of molecular dynamics (19, 27–29). Although this paper is focused on optimizing magnetization transfer by cross-correlated relaxation between dipole–dipole coupling and CSA, more general use may cover other types of cross-correlated relaxation. Overall, CRINEPT combined with TROSY opens avenues for solution NMR studies with particle sizes of several hundred kilodaltons, such as membrane proteins solubilized in micelles or lipid vesicles, proteins attached to large nucleic acid fragments, or oligomeric proteins.

ABBREVIATIONS

CSA

chemical shift anisotropy

CRIPT

cross relaxation-induced polarization transfer

CRINEPT

cross relaxation-enhanced polarization transfer

HMQC

heteronuclear multiple-quantum correlation

INEPT

insensitive nuclei enhanced by polarization transfer

TROSY

transverse relaxation-optimized spectroscopy