A PHYSIOLOGIST’S PERSPECTIVE ON ROBOTIC EXOSKELETONS FOR HUMAN LOCOMOTION

Abstract

Technological advances in robotic hardware and software have enabled powered exoskeletons to move from science fiction to the real world. The objective of this article is to emphasize two main points for future research. First, the design of future devices could be improved by exploiting biomechanical principles of animal locomotion. Two goals in exoskeleton research could particularly benefit from additional physiological perspective: 1) reduction in the metabolic energy expenditure of the user while wearing the device, and 2) minimization of the power requirements for actuating the exoskeleton. Second, a reciprocal potential exists for robotic exoskeletons to advance our understanding of human locomotor physiology. Experimental data from humans walking and running with robotic exoskeletons could provide important insight into the metabolic cost of locomotion that is impossible to gain with other methods. Given the mutual benefits of collaboration, it is imperative that engineers and physiologists work together in future studies on robotic exoskeletons for human locomotion.

1. Introduction

Advances in robotic exoskeletons are moving forward at an unprecedented rate. In the last 5 years, there has been more progress in the field than in the preceding 40 years ^1–6. Currently, there are several groups around the world building powered lower limb exoskeletons or orthoses for assisting human movement ^7–16. The sensors, actuators, and computer processors used in the most advanced exoskeletons are much smaller and more powerful than those in predecessors. The market potential for robotic technology will further accelerate progress in the coming years ¹⁷. We are likely to see commercially available robotic exoskeletons within a few years ¹⁸.

Despite rapid progress in robotic exoskeleton design and technology, limited data is available on the human physiological response to exoskeleton use. Few published studies exist on the motor learning process or the metabolic energy requirements of locomotion with exoskeletons. While this is partially associated with the relative youth of the prototypes in development, another major cause is the background of researchers in the field. Development of exoskeleton technology requires sophisticated engineering training in mechatronics, controls, dynamics, and computer science. As a result, the most innovative and technologically advanced exoskeletons come from mechanical and electrical engineering departments at major research universities ¹⁸. The expertise of these researchers does not often include extensive knowledge human of movement physiology. This naturally leads the exoskeleton researchers to think in terms of control algorithms, feedback loops, actuator bandwidth, and power density rather than aspects of human locomotor physiology such as central pattern generators, internal models, proprioception, muscle mechanics, and oxygen consumption. Commercialization is another key factor in the scarcity of published data on the physiological response to exoskeleton use. The goal of developing a commercial product drives most of the leading research in robotic lower limb exoskeletons. Trade secrets and patent rights force the researchers to delay and/or censor publication of research results if not prevent publication altogether.

It is unfortunate that differences in training and research goals of engineers and physiologists often limit collaboration and communication between the two fields. A rich literature exists on human locomotion physiology that has dual implications for the design of robotic lower limb exoskeletons. Scientific written work on movement physiology goes back 170 years to the Weber brothers ¹⁹, and more broadly, over 2000 years to Aristotle’s De Motu Animalium ²⁰. Although the research questions typically asked by a physiologist differ substantially from those of an engineer, these questions are increasingly relevant to the design and control of robotic exoskeletons. Physiologists use experimental and analytical approaches to address questions about human locomotor agility and stability, motor learning processes, and metabolic energy costs. Physiologists regularly analyze the locomotor mechanics and energetics of people with normal gait and those with physical or neurological disabilities. The same approaches could answer key questions about the human response to exoskeleton use, such as: 1) How long does it take for a user to learn how to walk with an exoskeleton, and what neural mechanisms are involved?, 2) How does the user’s metabolic energy cost change when using an exoskeleton? and 3) How agile and stable is movement with an exoskeleton?

Published work from leading groups indicates that they have considered physiological and biomechanical principles to some extent during device development ^{8, 21–25}. However, exoskeleton research could further employ key principles and analytical tools from locomotor physiology to improve the design and testing of prototypes. Two goals in current exoskeleton research could particularly benefit from additional physiological expertise: 1) reduction in the metabolic energy expenditure of the user while wearing the device, and 2) minimization of the power requirements for actuating the exoskeleton.

Regardless of the functional goal of a particular lower limb exoskeleton, minimizing the user’s metabolic energy cost of movement while wearing the device is crucial. Some robotic exoskeletons are explicitly designed to reduce the cost of external load carriage, enabling users to travel long distances with heavy loads ^{7, 15}. Even in exoskeletons for rehabilitation or mobility assistance ^{8, 9}, minimization of metabolic energy expenditure will improve device usability. Thus, a shared design goal for most robotic lower limb exoskeletons is to reduce the metabolic cost of locomotion for the user.

A serious technological hurdle in robotic exoskeleton design is the development of power sources. The portability and field utility of current exoskeleton designs is limited by their relatively high power consumption and the limited specific power of current portable power units ^{22, 26}. Reduction of the power demands of robotic exoskeletons will allow smaller, lighter designs that are easier to use and more versatile. Exploiting biomimetic strategies for minimizing the energy requirements of exoskeletons will likely play a key role in the advancement of future designs.

In the following sections we discuss principles from locomotor physiology that have significant potential to improve these two key areas of exoskeleton design. A significant admission, however, is that many key issues in locomotor physiology are either not well understood or hotly debated among physiologists. Thus, we also consider the key role that lower limb exoskeletons can play in advancing our understanding of human physiology. The take home message here is that collaboration between engineers and physiologists could benefit both those interested in creating better devices and those interested in solving scientific puzzles.

2. Physiological Knowledge can Inform Exoskeleton Design

Knowledge from physiological research can reveal strategies for economical biomimetic designs and point to trouble-shooting techniques for testing exoskeleton prototypes. Below, we highlight the most relevant advances in physiological research, focusing on 1) the physiological basis of the relationship between mechanics and energetics and 2) the role of passive dynamics in improving the economy and control of locomotion.

2.1. The complex relationship between mechanics and energetics

The complex relationship between mechanical and metabolic energy use in human locomotion poses a serious challenge for optimizing exoskeleton design to reduce the user’s energy expenditure. A vast body of physiological research has focused on elucidating the relationship between locomotor mechanics and metabolic cost ^27–34. Nonetheless, the task remains a challenge because it is impossible to directly measure muscle mechanics and energetics simultaneously in humans. Ultrasonography allows muscle strain measurement of superficial muscles ³⁵, but not deeper muscle tissue. Computer simulations can often predict the relationship between muscle mechanics and energetics ^36–40. Without empirical data to verify the simulated results, however, it is difficult to validate their accuracy. For these reasons, direct measurements animal models have been critical in establishing the links between muscle mechanical performance and metabolic energy expenditure. Physiologists use a number of experimental approaches, from in vitro and in situ preparations of isolated muscle, to direct in vivo measures of muscle performance during natural locomotor behaviors. Insights from this field suggest a number of strategies for improved design and testing of exoskeleton prototypes.

2.1.1. Relating muscle mechanical performance to metabolic energy use

Muscle tissue requires metabolic energy (i.e. fuel) to develop force. The total energy consumption depends on both the force and work performed during the contraction. Early studies showed that isolated muscle requires some energy during active lengthening contractions (negative work), a little more energy during isometric contractions (force but no mechanical work) and the most energy during active shortening contractions (positive work) ^41–43. The metabolic energy demand for all of these actions increases with increasing muscle force.

The difficulty lies in linking mechanical and metabolic energy expenditure for whole body movements, which involve a combination of positive muscle work, negative muscle work and isometric muscle force production. A muscular efficiency, the ratio of mechanical energy output to metabolic energy input, can be calculated for shortening or lengthening muscle contractions. Isolated muscle experiments reveal muscular efficiencies of approximately 25% for positive work and −120% for negative work ^{42, 44, 45}. Muscular efficiency can predict the energetic cost of whole body movements that require predominantly positive or negative mechanical power output ^{41, 46, 47}; however, locomotion is typically rhythmic with muscles performing a mixture of negative and positive work.

Work-loop paradigms put isolated muscle under stretch-shortening cycles to reflect in vivo muscle actions more accurately than purely shortening or purely lengthening experiments ^{48, 49}. Measures of muscular efficiency during stretch-shortening cycles yield efficiencies that range from 15% to 52%, depending on a number of factors including the shape and frequency of the strain cycle and the muscle fiber type composition of the muscle studied ^{44, 50}.

Further, some of the cyclic negative and positive work in a rhythmic locomotor movement occurs as energy storage and recovery in the series elastic element of a muscle-tendon complex ^51–53. In vivo measures of muscle-tendon performance reveal that a muscle can contract with little length change while the in series tendon stores and releases elastic energy ^{54–58, 59}. This helps reduce the energetic cost of locomotion by reducing muscle work and allowing economic force development ⁵⁵. Nonetheless, many muscles have relatively little series elasticity, and must perform substantial positive and negative work ^{60, 61}.

Ultimately, the relative amounts of positive muscle work, negative muscle work, and isometric activation summed over all of the muscles determines metabolic energy expenditure for a given task. As result, whole body efficiency during human locomotion can range between 10 to 80% depending on the task ^{34, 62}.

2.1.2. Joint work does not relate directly to muscle work

Exoskeletons often actively assist the lower limbs using actuators in parallel with the joints (i.e. hip, knee, and/or ankle). The goal is to reduce the mechanical demand on the muscles by allowing external power sources to share the workload. However, the success of this exoskeleton design in reducing metabolic cost depends on an important implicit assumption: the work observed at a joint relates directly to the work performed by the muscles acting about that joint. If joint work relates directly to muscle work, an exoskeleton can reduce the net metabolic power by approximately four times the amount of positive mechanical power it generates (assuming a muscular efficiency of 25%; see above).

This assumption is tenuous for two reasons: 1) biarticular muscles can transfer energy between joints and 2) elastic structures perform much of the cyclic work at a joint. Biarticular muscles, which act across two joints, can transfer power between joints. Consequently, work observed at a given joint through inverse dynamics analysis ^{63, 64}, may not be performed exclusively by muscles at that joint ^65–67. Furthermore, as discussed above, compliant tendons in series with muscle tissue can perform much of the cyclic positive and negative work during locomotion ^51–53. For example, although the ankle joint performs substantial negative and positive work during the stance phase of locomotion ^{63, 64}, the active muscles at the ankle joint (soleus and gastrocnemius) perform little mechanical work ^57–59. Most of the work at the ankle is performed through energy storage and recoil from the Achilles tendon. Thus, knowledge of joint torques and angular changes during locomotion is insufficient to determine the underlying muscle dynamics.

These two factors, biarticular energy transfer and elastic energy cycling in tendons, lead to a poor correlation between joint work and muscle work during locomotion. Consequently, direct replacement of joint work by a powered exoskeleton will likely yield more modest reduction in metabolic power consumption than might be expected from an inverse dynamics analysis of gait.

2.1.3. Relating whole body mechanical energy to metabolic energy use

Based on the factors discussed above, it is clear that body mechanics do not relate directly with metabolic energy use. Despite these difficulties, physiologists have been able to partition the energetic cost of human walking and running into factors such as leg swing, body-weight support, forward propulsion, and center of mass movement ^{28, 30, 68–70}. A number of experimental paradigms have been useful in this partitioning of energetic cost. Simulated reduced gravity ^71–73, horizontal forces ^{69, 74–76}, inclines ^77–79, and added loads ^{70, 80, 81} can all perturb locomotor mechanics at the whole-body level to provide insight into the relative cost of different factors. The results suggest that total metabolic energy expenditure during locomotion is composed of 10–33% for leg-swing and 67–90% for body weight support and forward propulsion. However, this approach is unable to isolate the contributions of specific muscles to the metabolic cost of locomotion.

Recent animal experiments have partitioned metabolic energy delivery among individual muscles of the limb based on blood flow distribution. Under most locomotor conditions, rate of blood flow accurately indicates energy delivery to the tissues ⁸². These experiments provide another estimate of total energy requirements for tasks such as leg-swing, body weight support, load carriage, and mechanical work to move up an incline. Blood flow measurements suggest that 15–30% of the total energy use during locomotion is associated with co-contraction of antagonist muscles for joint stiffness ⁸³, and 26% is associated with leg-swing ⁸⁴. Additionally, these experiments reveal that specific limb muscles are preferentially recruited for tasks such as load carriage and moving up an incline ^{85, 86}. Exoskeletons could more effectively minimize metabolic energy expenditure if they target specific muscles associated with the desired locomotor task.

2.1.4. Using this knowledge to improve exoskeleton performance

How might engineers take better advantage of elastic energy storage and biarticular muscles in exoskeleton designs? In one interesting proposal, van den Bogert suggested that passive elastic exotendons could reduce the metabolic cost of walking ⁸⁷. This requires incorporation of appropriate multijoint connections with optimal moment arms and stiffness properties. In a recent study from our laboratory, we confirmed that elastic ankle braces can reduce muscle recruitment with little change in movement dynamics during hopping in place ⁸⁸. The passive elasticity provided by the brace likely reduces the muscle activation required to generate joint stiffness. We are now extending these studies to elastic knee braces with the goal of reducing the metabolic cost of human running ⁸⁹. At MIT, Herr and colleagues are developing orthoses and prostheses with multiarticular connections for transferring energy and actuators in series with compliant springs for storing and returning energy ^90–92. These approaches take inspiration from human musculoskeletal design and function to improve designs for lower limb exoskeletons.

Standard gait analysis techniques serve as important diagnostic tools to inform better exoskeleton design. Researchers have used inverse dynamics analysis to design exoskeletons that approximate normal human joint kinematic and kinetic patterns ^{21, 22}. Inverse dynamics analysis could be further employed to identify compensatory coordination strategies that increase the cost of locomotion with the exoskeleton. Potential changes in the distribution of joint torques and powers across the ankle, knee and hip due to exoskeleton loading can assessed by comparing joint dynamics during locomotion with and without actuation of the exoskeleton.

Another promising analytical tool will be the use of electromyography (EMG) to assess changes in muscle activation timing and amplitude during lower limb exoskeleton use. Given the complex relationship between metabolic and mechanical energy use, changes in muscle activity might better predict changes in metabolic cost than joint dynamics alone. If joint dynamics of locomotion with the exoskeleton remain similar to normal locomotion, changes in electromyography are likely to correspond to changes in metabolic energy demand. More specifically, electromyography could be used to 1) target and minimize muscle activity associated with the most metabolically demanding components of locomotion (e.g., push-off, swing, co-contraction for stiffness) and 2) diagnose and eliminate compensatory muscle coordination strategies by uncovering increases in activity of muscles that are normally quiet and not directly involved in the current task. These analytical tools will facilitate the design of exoskeletons that successfully reduce the metabolic cost of locomotion.

2.2 Passive dynamics can reduce locomotor energetics

The pioneering works of McMahon ^93–95 and McGeer ^96–99 form the cornerstone of the burgeoning theory of passive dynamics. This field is founded on the principle that stable locomotion can be accomplished with little energy input by harnessing the natural dynamics of the limbs. Consequently, the limbs need not be driven by actuators (muscles or motors) all of the time. Instead, natural movement and stable control can be achieved by inputting minimal actuator energy with strategic timing. In short, exploiting passive dynamics could lead to both simplified locomotor control and improved locomotor economy.

2.2.1. Passive dynamic walkers

Walking machines based on simple mathematical models have demonstrated the principles of passive dynamics. In the early 1990’s McGeer built an anthropomorphic machine without motors or controllers that could walk down a shallow slope by itself ⁹⁷. To move forward, the passive walker relied only on gravity and the natural pendular motion of the limbs. This demonstrates that stable walking requires little energy input. The initial prototype was based on a simple planar model composed of two rigid links (a stance limb and a swing limb) with a pin joint at the hip^97–100. Recently, researchers from Cornell University built a passive dynamic walking machine with arms, knees and powered ankles. This robot can walk on level ground with a mass specific cost of transport that is nearly identical to that observed for humans (~0.20) ¹⁰¹. The development of passive dynamic walking machines with economic and stable gait has revealed important principles of human locomotor mechanics and energetics.

2.2.2. Pendular motion of swing limb

Walking and running humans take advantage of the pendular motion of the swing limb. First proposed over 150 years ago by the Weber brothers ¹⁹, this has only recently become better understood. At preferred walking speeds, the swing leg behaves as a physical pendulum driven close to its natural frequency ^{93, 94, 102}. The total energetic cost of leg swing depends largely on frequency ⁶⁸, but also on swing amplitude and limb mass distribution ¹⁰³. At frequencies away from the limb’s natural frequency (slow or fast walking speeds), energy must be cyclically generated and dissipated by muscle-tendon complexes. Consequently, metabolic cost increases. Energetic cost can be minimized by operating the muscles as struts, contracting isometrically, while the in series tendons cycle energy and provide the required musculo-tendon displacement. This reduces the cost because muscle force production costs less metabolic energy than muscle work ⁴². A recent study provides evidence that humans use this strategy. With increasing movement frequency, the metabolic cost of leg swing increases in proportion to muscle force, not muscle work ⁶⁸. Utilizing the natural pendular dynamics of the swing leg minimizes muscle work and allows movement control through a more economic alternative: muscle force. Even so, the metabolic cost of leg swing could account for up to one third of the total metabolic cost of walking ⁶⁸.

2.2.3. Inverted pendulum in stance

Another pendular mechanism characteristic of walking occurs during the single support portion of stance. The stance limb guides the center of mass along a trajectory similar to an inverted pendulum, allowing cyclic exchange of gravitational potential energy and kinetic energy ^104–106. An inverted pendulum is energy conservative and theoretically requires zero mechanical work during single support. Although humans do not behave as pure inverted pendulums during single support ¹⁰⁷, they do save substantial energy through pendular exchange of energies ^{62, 108, 109}. Despite the savings from inverted pendular exchange, substantial energy is lost when the leading leg collides inelastically with the ground. To maintain steady walking, the energy lost in the collision must be replaced by muscle work. Most of the energy lost in step transitions is replaced during the period of double support ¹¹⁰. The metabolic cost of step transitions (collisions) might account for as much as 70% of the total metabolic cost of walking ¹¹⁰.

2.2.4. Timing and source of mechanical work (reducing collision costs)

One approach to minimizing energy expenditure during locomotion is to reduce collisional energy loss ¹¹¹. This is especially true for steady, level locomotion where net mechanical energy change over a step must be zero. That is, any energy lost in a step transition must be replaced by a power source.

Simple models and accompanying experiments on walking humans reveal that increasing both step length ^{110, 112} and step width ¹¹³ lead to higher collisional energy loss and higher metabolic energy expenditure. In addition, the timing and source of mechanical energy input are critical in determining the total collision cost. Simple walking models indicate a number of strategies for replacing the energy lost in collisions ^{111, 114}. One possible source is an impulse directed along the trailing limb. A pre-emptive push-off by the trailing limb directs the center of mass velocity upward and forward before the leading limb collides with the ground. This strategy minimizes energy loss and requires minimal power input ^{108, 111}. Experiments have confirmed that humans use this strategy ¹¹⁰ An alternative power input strategy, active hip actuation throughout stance, requires four times more mechanical energy than pre-emptive push-off ¹¹⁴. Hip power may become more important for tasks that require steady energy outputs (e.g. accelerating or uphill walking).

2.2.5. Using this knowledge to improve exoskeleton performance

Adhering to the principles of passive dynamics can help achieve both of the goals highlighted in the introduction: 1) reduction in the metabolic energy expenditure of the user while wearing the device and 2) minimization of the power requirements for actuating the exoskeleton.

First, it is critical for exoskeleton designers to realize that any disruption of the natural pendular mechanisms of gait (swing leg motion and the single support phase of walking) could result in increased muscle activation and metabolic cost. Therefore, exoskeleton designs should be versatile enough to toggle between active and passive modes. For example, active mode could provide power to the trailing limb in double support only and passive mode could allow unhindered motion during single support and swing. Additionally, passive modes require zero energy output from the exoskeleton actuators, reducing its overall power consumption.

The appropriate timing and source of energy input can minimize collisional energy loss. Humans and the most efficient bipedal robots power walking through a trailing limb push-off at the ankle, achieving very low mass specific cost of transport (~0.20) ¹⁰¹. Ankle power at push-off effectively reduces collision costs, placing less demand on the exoskeleton actuators while reducing the energy cost of the human user.

Exoskeleton hardware geometry and mass distribution are also key aspects of passive dynamics. Increased step length and step width both lead to increased collision costs. Therefore hardware designs should not restrict limb motion in ways that would cause wider or longer steps than would be freely chosen by the user. Designers should also limit the distal mass of the exoskeleton. Added distal mass increases leg swing costs due to added inertia and collision costs due to foot-ground impact. Furthermore, recent evidence suggests that the shape of the foot effects metabolic cost in walking ¹¹⁵. Careful design of limb geometry, mass distribution and foot shape will reduce energetic costs of locomotion.

Failure to incorporate the principles of passive dynamics into exoskeleton design could incur substantial energetic penalties. For example, bipedal robots that disrupt the ballistic phases of gait by constantly driving joint motion consume much more energy than their passive dynamic counterparts. The mass specific cost of transport for Honda’s ASIMO is a factor of 16 larger than the Cornell Efficient Biped ¹⁰¹. Another robot that exploits natural swing dynamics but drives the hip throughout stance (rather than impulsive ankle push-off) had a mass specific cost of transport that was 45% higher than the Cornell robot ^{101, 106}. In short, exoskeletons that take advantage of passive dynamics reduce energy consumption for both the human user and the exoskeleton actuators.

One way that passive dynamics might be facilitated in an exoskeleton is to allow the wearer’s nervous system to have direct control over actuation timing with electromyography. Humans are very good at incorporating passive dynamics into their movement pattern to save metabolic energy. If the wearer’s nervous system has the ability to control exoskeleton actuation, the wearer would likely adapt their motor pattern to maximize the use of passive dynamics (given the constraints of the hardware). Sankai and colleagues have built electromyography signals into the control algorithms of their Hybrid Assistive Limb (HAL) ¹¹⁶. No data have been published on the metabolic cost of walking with HAL, but it would be very interesting to perform a biomechanical analysis of walking with HAL to see if the wearer does indeed use principles of passive dynamics.

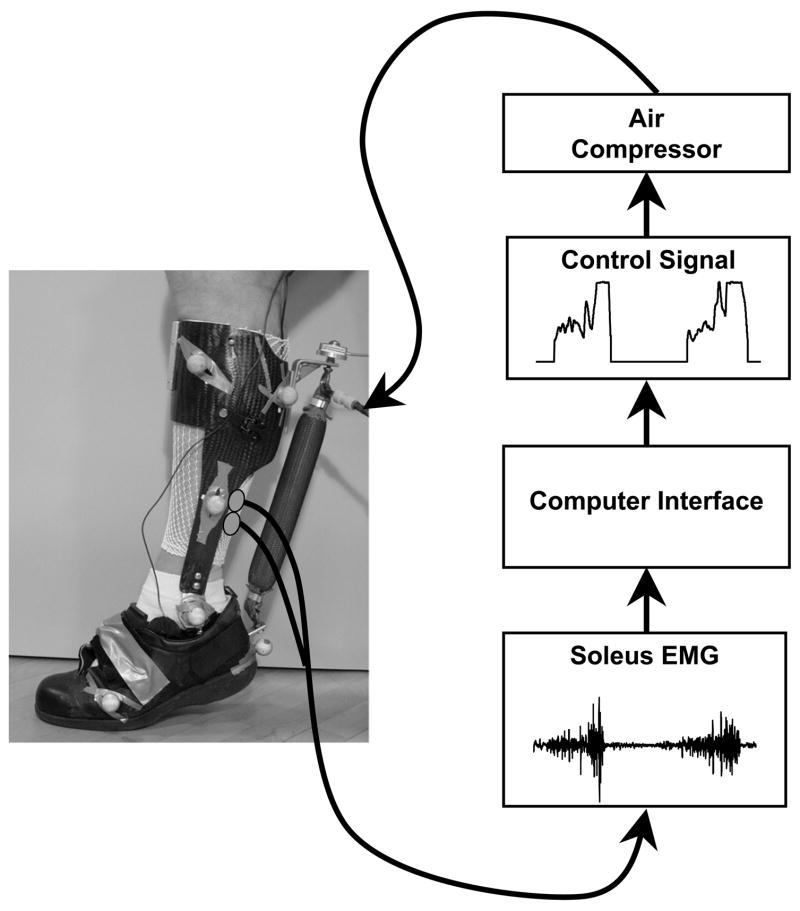
We have adopted a simpler electromyography control scheme for our research on powered lower limb orthoses: proportional myoelectric control ¹¹⁷. In our method, surface electromyography generates a feedforward command that scales with muscular recruitment to activate the exoskeleton. For example, to control ankle extension, EMG signals from biological ankle extensors (soleus, gastrocnemius) can be used to generate the command to an ankle torque actuator^{12, 13, 118} (Figure 1). It is our belief that the wearer will naturally adapt their muscle activation signal with practice to optimize the timing of the robotic assistance if they use an electromyography based control scheme.

Figure 1.

A pneumatically powered ankle-foot orthosis using proportional myoelectric control. Surface electrodes record the electromyography signal from the muscle of interest (soleus in this case) and send it to a computer for processing. The computer applies filters, a threshold, and a gain to generate a proportional control signal regulating air pressure in the artificial pneumatic muscle. Details are available in previous publications ¹², ¹³, ¹¹⁸.

3. Exoskeleton Research Can Reveal Principles of Human Locomotor Physiology

Many key issues in locomotor physiology are either not well understood or under heated debate. To this point in the paper, we have focused on the benefits of using knowledge from human physiology and biomechanics to improve exoskeleton design. Exoskeletons also have enormous potential to resolve fundamental questions in physiology and biomechanics.

Standard measurements of locomotor mechanics and energetics during walking with powered robotic devices could address key questions about the human response to exoskeleton use, such as: 1) How long does it take for a user to learn how to walk with the exoskeleton, and what neural mechanisms are involved? 2) How does the user’s metabolic energy cost change when using the exoskeleton?

We are currently using pneumatically-powered lower limb orthoses ^{12, 13, 118, 119} to examine the neural adaptation, mechanics and energetics of walking under powered walking conditions. The orthosis shell consists of lightweight carbon fiber and polypropylene with metal hinge joints (Figure 1). Artificial pneumatic muscles actuate the device, providing high power output while adding minimal weight ¹²⁰. We have tested proportional myoelectric, kinematic, and other control schemes ^{121, 122}.

3.1. Influence of controller type on locomotor adaptation to powered assistance

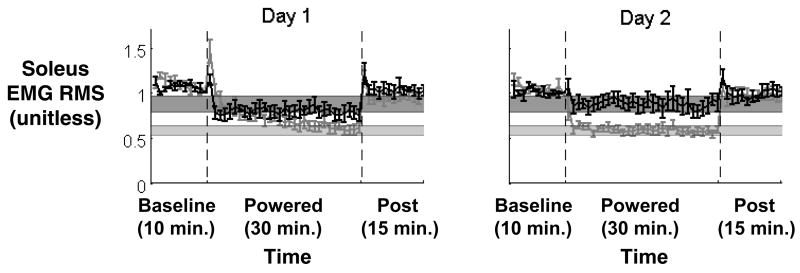
Work from our laboratory indicates that proportional myoelectric control allows the user to quickly adapt to exoskeleton use. This control system closely mimics the human sensorimotor loop and facilitates learning. It allows subjects to tune the amplitude and timing of exoskeleton assistance by adapting their own muscle activation patterns. In fact, subjects learn to turn down muscle activation to appropriately control the exoskeleton after only two thirty-minute training sessions (Figure 2)¹¹⁸. The orthosis essentially replaces some of the biological power production at the ankle joint with power from the artificial muscle.

Figure 2.

Ten subjects practiced walking with a single powered ankle-foot orthosis under soleus proportional myoelectric control. Subjects walked on a treadmill at 1.25 m/s for 55 minutes: 10 minutes with the orthosis unpowered (baseline), 30 minutes with the orthosis powered (powered), and 15 minutes with the orthosis unpowered again (post). Subjects completed two training sessions, three days apart (Day 1 and Day 2). A) Soleus root mean square electromyography (RMS EMG) during stance was normalized for each subject, averaged for each minute, and the mean value for each minute was calculated across all subjects (mean ± standard deviation, black circles and grey shading). Horizontal bars indicate steady state ranges. B) Ankle kinematic profiles and soleus electromyography profiles are displayed across training. Average data are shown for ankle joint kinematic profiles, soleus electromyography profiles. Within thirty minutes on Day 1, subjects returned to normal gait kinematics by reducing soleus muscle activation. On Day 2, subjects demonstrated a clear motor memory of orthosis dynamics. Curves are means across all subjects and the vertical bars indicate timing of the stance-swing transition. Data are from Gordon and Ferris ¹¹⁸

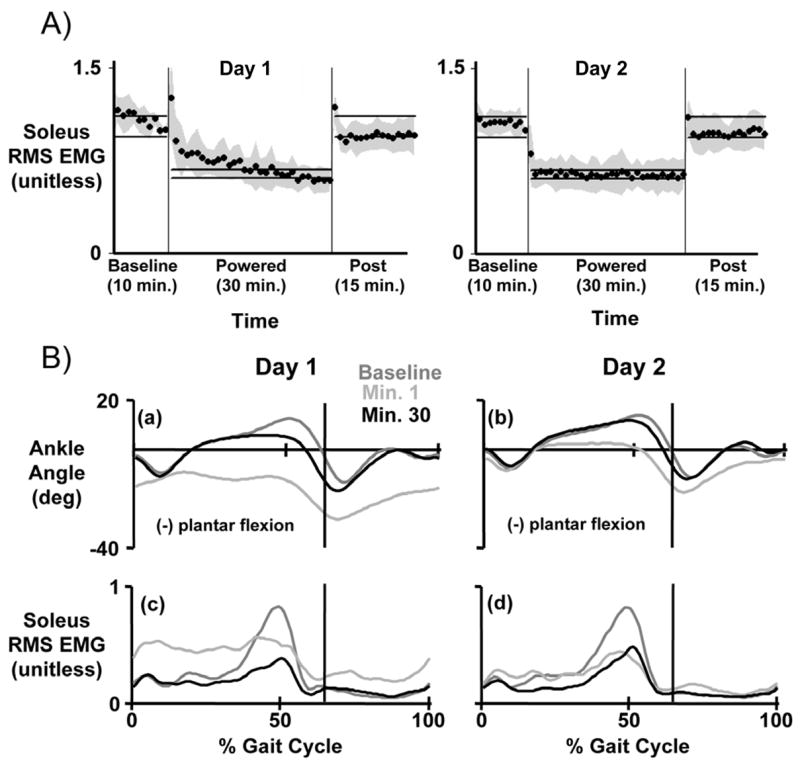
A recent investigation of two types of exoskeleton control further highlights the effect of control architecture on motor performance ¹²¹. Two groups of subjects used the same powered ankle-foot orthosis, but relied on different control schemes. One group used proportional myoelectric control (from soleus EMG) and the other group used kinematic control (a footswitch activated the artificial pneumatic muscle in a bang-bang mode when the forefoot was on the ground). Even with identical hardware and similar actuator timing, the two groups of subjects demonstrated markedly different walking patterns ¹²¹. An important aspect was that the wearer was able to alter the magnitude of orthosis torque in the proportional myoelectric control scheme by reducing soleus muscle activation. This was not possible in the footswitch control scheme. Results demonstrated higher muscle activation levels for the footswitch control subjects compared to the proportional myoelectric controller (Figure 3). Consequently, footswitch control acted more as a disturbance to walking dynamics than as a useful external power source. Although it is only one study, the potential implications of these findings are that exoskeletons under myoelectric control may be able to achieve lower metabolic cost than those under kinematic control.

Figure 3.

A comparison of locomotor adaptation to unilateral powered ankle-foot orthoses using two different controllers. Soleus electromyography root mean square (EMG RMS) activity is shown for each minute as mean ± 2 standard deviations across all subjects for each controller. Soleus proportional myoelectric control is shown in grey, and foot switch control is shown in black. Horizontal bars indicate steady state values for each controller (dark grey for footswitch, light grey for myoelectric control). When the orthosis is turned on by placement of the forefoot on the ground (footswitch control), subjects exhibit a smaller decrease in soleus muscle recruitment compared to proportional myoelectric control. Data are from Cain et al ¹²¹.

3.2. The metabolic cost of joint mechanical work

A common goal of lower limb powered exoskeletons is to reduce metabolic energy expenditure during locomotion. Nonetheless, we are aware of only one study that has reported oxygen consumption for powered walking (~13% decrease for powered vs. unpowered walking) ¹²³. Clearly more work needs to be devoted to assessing metabolic costs of exoskeleton use and importantly, relating those costs back to the walking dynamics.

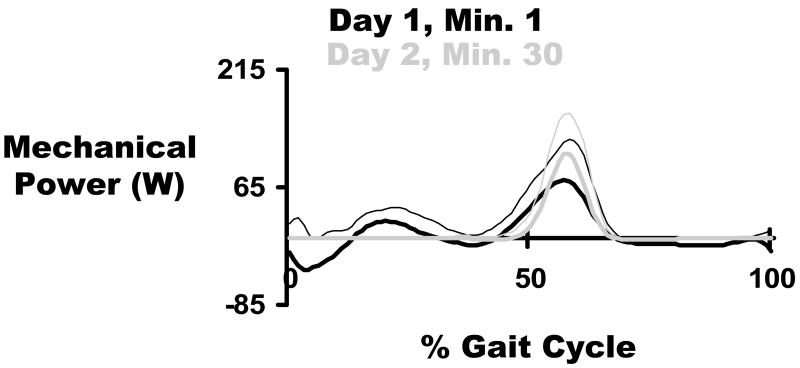
With our simple ankle-foot orthosis, we have found strong endorsement for trailing limb push-off as a preferred powering strategy in humans ¹¹⁸. With practice wearing the powered orthosis under proportional myoelectric control, subjects learned to produce a large burst of positive mechanical power timed immediately before toe-off (Figure 4) ¹¹⁸. This suggests that the human nervous system can selectively alter muscle activation to produce mechanically efficient dynamics. This study examined the ankle joint mechanics but not oxygen consumption. Based on the results, our current studies are looking more closely at the correlation between exoskeleton dynamics and metabolic cost during walking.

Figure 4.

Orthosis mechanical power walking under soleus proportional myoelectric control. Grey curves are the mean ± standard deviation for all subjects during the first minute of testing on Day 1. Black curves are the mean ± standard deviation for all subjects during minute 30 on Day 2. By the end of Day 2, the orthosis produced almost exclusively positive mechanical power, which was focused at the end of stance. The vertical black line represents the stance-swing transition timing in the gait cycle. Data are from Gordon and Ferris ¹¹⁸.

In one ongoing study, we trained subjects to walk with bilateral powered ankle-foot orthoses over three thirty-minute sessions. Preliminary data indicate that the metabolic cost of powered walking is ~10% lower than unpowered walking. We quantified the performance of the exoskeleton by dividing the mechanical power input of the orthoses by the metabolic power savings of the human user. This ratio is an indirect measure of the apparent joint efficiency. Our preliminary data indicate an apparent ankle joint efficiency of 40–60%. Given that vertebrate skeletal muscle has a maximum efficiency of ~25% for positive work, these results suggest that elastic energy storage and return in the Achilles tendon plays a substantial role in power production at the ankle. This conclusion agrees with recent studies using ultrasound to measure muscle and tendon displacements during human walking in vivo ^{57–59, 124, 125}. Another important implication of our results is that metabolic energy savings are likely to be much more modest than expected when using an exoskeleton to supplant joint work, especially at joints with considerable elastic compliance. Powering joints with less dependence on tendon stretch and recoil may lead to larger reductions in metabolic cost. Unfortunately, the ability to measure human muscle-tendon dynamics in vivo is limited so that it is not clear to what extent lower limb joints depend on elastic energy.

4. Conclusions and Future Directions

Increased collaboration between robotics engineers and physiologists will accelerate advancement in both fields. Engineers could achieve significant advances in exoskeleton design by employing key physiological principles and analytical tools. Two design goals could particularly benefit from physiological expertise: 1) reduction in the metabolic energy expenditure of the user while wearing the device, and 2) minimization of the power requirements for actuating the exoskeleton. These goals could be simultaneously realized through a number of biomimetic strategies for economic locomotion. Future design prototypes should strive to:

• use elastic mechanisms to perform matched negative and positive work

• transfer energy between joints using biarticular linkages

• test prototypes using electromyography (EMG), inverse dynamics analysis, and metabolic energy expenditure

• avoid disrupting passive pendular dynamics during swing and stance

• reduce collision costs by actively powering push-off at the ankle

Robotic lower limb exoskeletons also offer an innovative, untapped tool for studying movement physiology. We have highlighted recent research into the physiological response of the human user while walking with powered assistance. These initial studies provide important ground work, but much remains unknown. Future experiments should address the following questions:

• What neural mechanisms are involved in motor adaptation to powered assistance?

• What is the relative effect of actuating each of the limb joints (hip, knee, and ankle) on the total metabolic cost of walking?

• Are muscle strength characteristics limiting factors in agility or mobility?

Given the recent acceleration of exoskeleton research and development around the world, we look forward to the coming years and the contributions in both engineering and physiology that will result.

Biographies

Daniel Ferris received his B.S. in Mathematics Education from University of Central Florida in 1992, his M.S. in Exercise Physiology from University of Miami in 1994, and his Ph.D. in Human Biodynamics from University of California, Berkeley in 1998. He worked as a postdoctoral researcher in the UCLA Department of Neurology until 2000, and in the University of Washington Department of Electrical Engineering until 2001. He is currently an Associate Professor at the University of Michigan, Ann Arbor, in the Division of Kinesiology, Department of Biomedical Engineering, and Department of Physical Medicine and Rehabilitation. He studies the neuromechanical control of human locomotion in health and neurological disability. One focus of those studies is to build powered lower limb orthoses for assisting gait rehabilitation.

Gregory Sawicki received his BS in Mechanical Engineering from Cornell University 1999 and his MS in Mechanical Engineering from the University of California at Davis in 2001. He is a PhD student in the Division of Kinesiology and the Department of Mechanical Engineering at the University of Michigan, Ann Arbor. His current research uses robotic ankle exoskeletons to explore the relationship between ankle joint power and the metabolic cost of walking.

Monica Daley received her BS in Biology from the University of Utah in 1999, and her MA and PhD degrees in Biology from Harvard University in 2003 and 2006, respectively. She is currently a National Science Foundation Bioinformatics Postdoctoral Research Fellow in the Division of Kinesiology at the University of Michigan, Ann Arbor. Her research investigates the biomechanics and neuromuscular control of stable locomotion in complex environments. She uses in vivo muscle measurements and biomechanical analyses to investigate the relationship between muscle-tendon dynamics, joint mechanics and locomotor performance.