Restriction of Secretory Granule Motion near the Plasma Membrane of Chromaffin Cells

Abstract

We used total internal reflection fluorescence microscopy to study quantitatively the motion and distribution of secretory granules near the plasma membrane (PM) of living bovine chromaffin cells. Within the ∼300-nm region measurably illuminated by the evanescent field resulting from total internal reflection, granules are preferentially concentrated close to the PM. Granule motion normal to the substrate (the z direction) is much slower than would be expected from free Brownian motion, is strongly restricted over tens of nanometer distances, and tends to reverse directions within 0.5 s. The z-direction diffusion coefficients of granules decrease continuously by two orders of magnitude within less than a granule diameter of the PM as granules approach the PM. These analyses suggest that a system of tethers or a heterogeneous matrix severely limits granule motion in the immediate vicinity of the PM. Transient expression of the light chains of tetanus toxin and botulinum toxin A did not disrupt the restricted motion of granules near the PM, indicating that SNARE proteins SNAP-25 and VAMP are not necessary for the decreased mobility. However, the lack of functional SNAREs on the plasma or granule membranes in such cells reduces the time that some granules spend immediately adjacent to the PM.

Introduction

Exocytotic release of hormones and neurotransmitters is crucial for intercellular communication and synaptic transmission. After emerging from the trans-Golgi network, protein-containing secretory granules mature over many hours, during which time proteins are concentrated and processed, and low molecular weight factors and neurotransmitters are accumulated. The subsequent steps that allow the mature granules to undergo exocytosis are poorly understood. The steps must include movement to and association with the plasma membrane. The vast majority of studies concerning secretion measure only the final the events of fusion and release of granule contents. Although a great deal has been learned about the final steps, these studies have allowed only inferences to be made about the preceding steps, including the freedom or restriction of granule motion near the membrane before secretion.

Previous studies on chromaffin cells by two groups (Steyer et al. 1997; Oheim et al. 1998, Oheim et al. 1999; Steyer and Almers 1999; Oheim and Stuhmer 2000) employed an optical technique, total internal reflection fluorescence microscopy (TIRFM) (Axelrod 1981, Axelrod 2001; Stout and Axelrod 1989), to provide for the first time quantitative details about granule motion near the plasma membrane preceding and during exocytosis. The technique has also been used to study synaptic vesicles in the nerve terminal (Zenisek et al. 2000). TIRFM selectively illuminates subcellular features close (within ∼300 nm) to the plasma membrane at cell-substrate contact regions, without interference from optical signals from deeper within the cell. The previous studies with chromaffin cells used fluorescent weak bases that accumulate in acidic compartments within the cell, including chromaffin granules. A major finding in one of the studies was that upon stimulation with a secretagogue, the surface density of punctate fluorescent spots decreased. In addition, the movements of several spots were tracked over several minutes with decreased motion observed before a granule's disappearance, presumably release (Steyer et al. 1997; Oheim et al. 1999; Steyer and Almers 1999). The previous studies quantified some aspects of the basal state granule motion, predominately in the lateral (the “x-y” plane parallel to the membrane) direction.

Weak bases label all acidic compartments in the cell including those that are not chromaffin granules. In the present study, we have taken a different approach to label chromaffin granules. We have expressed by transient transfection in chromaffin cells a green fluorescent protein (GFP)–tagged protein that is sorted to secretory granules. The protein, pro-atrial natriuretic peptide (ANP)–GFP previously has been shown to be selectively stored in secretory granules in PC12 cells and to be secreted into the medium by secretagogues (Burke et al. 1997). The construct was successfully used to monitor secretory granule motion using epifluorescence and confocal microscopy.

The transiently expressed ANP-GFP is stored in chromaffin granules that become strongly fluorescent, rendering the granules excellent structures for analysis by TIRFM. We have performed a novel TIRFM analysis of the basal state motions of hundreds of granules in the direction normal to the membrane (the “z” direction) and find that the z motion of granules is much slower than would be expected from free Brownian motion, and is strongly restricted over tens of nanometer distances. Most surprisingly, the short term diffusion coefficients of granules decrease by two orders of magnitude in a continuous fashion within less than a granule diameter of the plasma membrane. Granule motions exhibit nondiffusive characteristics at both short (0.5 s) and long (tens of seconds) times.

The transient transfection technique also allowed us to determine the role of the v-SNARE VAMP (on the granule membrane) and the t-SNARE SNAP-25 (on the plasma membrane) in controlling granule motion. The light chains of two clostridia neurotoxins, tetanus toxin (TeNT) and botulinum neurotoxin type (BoNT/A), which cleave VAMP and SNAP-25, respectively (Niemann et al. 1994; Montecucco and Schiavo 1995; Hanson et al. 1997), were coexpressed with ANP-GFP. VAMP and SNAP-25 associate tightly together with plasma membrane syntaxin1A as a prelude to the final Ca²⁺-dependent fusion step (Ferro-Novick and Jahn 1994; Pfeffer 1994; Rothman 1994; Bajjalieh and Scheller 1995; Sutton et al. 1998). The toxins did not disrupt the restricted motion of granules that are approaching but not contacting the plasma membrane, indicating that SNARE proteins SNAP-25 and VAMP are not necessary for the decreased mobility. However, there is a decrease in the fraction of time that individual granules spend very close to the plasma membrane, consistent with a role for the SNARE complex in tethering the granule to the plasma membrane.

Materials and Methods

Chromaffin Cell Culture and Transfections

Chromaffin cell preparation, transient transfection, and human growth hormone secretion experiments were performed as described previously (Wick et al. 1993; Holz et al. 1994). Ca²⁺ phosphate precipitation was used for transfections according to Wilson et al. 1996. Cells were cultured in plastic culture wells (Costar) at a density of 1.2 × 10⁶ cells/cm². Chromaffin cells were transfected with a plasmid encoding pro-ANP-Emerald GFP (Han et al. 1999) to label chromaffin granules for TIRFM and confocal microscopy. For expression of clostridial neurotoxins, plasmids encoding the light chains of TeNT and BoNT/A were transfected into chromaffin cells in combination with ANP-GFP or human growth hormone (GH). For TIRFM experiments, cells were removed from these dishes using trypsin versine, and replated on collagen-coated glass coverslips (No. 2 thickness; Fisher Scientific). Experiments were performed 4–8 d after preparation of cultures in a physiological salt solution (PSS) containing (mM) 145 NaCl, 5.6 KCl, 2.2 CaCl₂, 0.5 MgCl₂, 5.6 glucose, 15 Hepes, pH 7.4, and 5 mg/ml bovine serum albumin, unless otherwise indicated.

Growth Hormone Release Assay

Secretion experiments were performed 4–5 d after chromaffin cells were transiently transfected with plasmids encoding the light chains of either TeNT or BoNT/A and human GH. Chromaffin cells were washed before the experiment with PSS containing (mM): 145 NaCl, 5.6 KCl, 2.2 CaCl₂, 0.5 MgCl₂, 15 Hepes, pH 7.4, 5.6 glucose, and 0.5 ascorbate. Cells were stimulated to secrete during a 2-min incubation in PSS with 20 μM 1,1-dimethyl-4-phenylpiperazinium (DMPP, a nicotinic agonist). GH released into the medium and retained in the cells was measured using a chemiluminescence assay (Nichols Institute). Endogenous catecholamine released into the medium and retained in the cells was measured with a fluorescence assay (Holz et al. 1982).

Immunocytochemistry

Cells were cultured and transfected in either eight-well chamber slides (Nalge-Nunc) or in wells in a 12-well plate (Falcon) that had the bottom of the wells drilled out and glass coverslips (No. 1 thickness; Fisher Scientific) glued on. The coverslips were collagen-coated before plating of cells.

Detection and Quantitation of Surface DBH

Cells were incubated with PSS (control) for 2 min, 20 μM DMPP for 2 min, or 2.2 mM barium (a PSS solution identical to that defined above except CaCl₂ is replaced with barium and no MgCl₂) for 15 min, and then immediately cooled to 1–2°C by placing the culture wells on a metal slab immersed in iced saline. All steps following this point were performed in the cold. Cells were fixed with 4% paraformaldehyde in 0.1 M cacodylic acid, and then quenched in 50 mM NH₄Cl. Cells were blocked with 0.1% gelatin in Tris-buffered saline for 20 min, then with Tris-buffered saline supplemented with 4% normal donkey serum for 30 min. Cells were then incubated for 1 h with rabbit antiserum directed against bovine dopamine-β-hydroxylase (1:1,000) supplemented with 4% normal donkey serum. After primary labeling, cells were washed four times, and then incubated for 70 min with purified donkey anti–rabbit IgG conjugated to lissamine-rhodamine (1:50) in PBS with 0.1% gelatin. Samples were visualized with TIRFM using rhodamine optics. Analysis of these images was performed using NIH Image. Images were first converted to eight-bit TIFF files, with the maximum intensity in a series of images set to a gray value of 255. Images were inverted and areas of cells in the brightfield images were outlined and from the corresponding TIRFM images the pixels, mean gray value, and standard deviation were calculated. A background level was obtained by selecting an area where there were no cells, and its mean gray value was subtracted from that where there were cells.

Detection of Surface ANP-GFP

Cells were stimulated for 2 min with 20 μM DMPP or CaPSS, and then immediately placed on ice. Some cells were incubated with primary antibody before fixation, while others were fixed before incubation with primary antibody, monoclonal anti–GFP primary antibody (1:500; Molecular Biology Laboratory). Cells were then fixed with 4% paraformaldehyde and 0.1 M cacodylic acid and quenched with 50 mM NH₄Cl. The plasma membrane was not rendered permeable with detergents or other lipid-disrupting agents. The secondary antibody was labeled with Alexa-568 (1:1,000; Molecular Probes, Inc.). GFP was visualized using FITC optics and anti–GFP using rhodamine optics on a confocal microscope. Alexa-568 fluorescence observed on the cell surface indicated the presence of ANP-GFP that had been secreted by exocytosis, but remained associated with the exterior surface of the plasma membrane.

Detection and Quantitation of f-Actin

Cells were incubated for 10 min with latrunculin B, fixed with 4% paraformaldehyde and 0.1 M cacodylic acid in PBS, and then quenched in 50 mM NH₄Cl. They were permeabilized with acetone for 5 min and blocked with 1% BSA in PBS for 30 min. Actin was labeled with Alexa-568-phalloidin for 1 h (1 U/ml; Molecular Probes, Inc.). Samples were visualized using confocal microscopy with rhodamine optics. Analysis of images of cells probed with Alexa-phalloidin was performed using Adobe Photoshop. The periphery of cells was outlined and the mean gray value was calculated, and the same was done with an area in the cytoplasm. A background was subtracted from the mean gray value, and the ratio of peripheral to cytoplasmic mean gray values was calculated.

Photometry of Total Cell Fluorescence

Chromaffin cells were transiently transfected with the ANP-GFP construct and replated onto glass coverslips. Fluorescence of GFP in living single cells was then visualized using a mercury arc lamp in a standard epi-illumination fluorescence microscope and quantitated using a photometer. The cells were continuously perfused for 5 min with PSS, and then for 20 min to Ca-free PSS containing 2.2 mM barium.

Total Internal Reflection Fluorescence Microscopy

In TIRFM, the excitation beam (typically from a laser) is incident upon a glass coverslip (on which the cells adhere) at a high enough angle for the beam to totally internally reflect. This generates an electromagnetic field (the “evanescent” field) in the aqueous phase that propagates along the surface but exponentially decays into the aqueous environment. At regions on the substrate where the cell adheres, the evanescent field will extend a short distance into the cytoplasm.

The characteristic depth d of the exponential decay depends upon the index of refraction of the glass substrate (1.52 here), the angle of the incident beam, and the index of refraction of the cytoplasm (see Axelrod 1981, Axelrod 2001). The prism-based TIRFM system used here was built around an upright microscope (Leitz Ortholux II with a 40× water immersion achromat objective; Carl Zeiss, Inc.; Fig. 1 shows schematic of optics). The incidence angle at the coverglass/water interface was 74.1°. Since the critical angle in this substrate needed to achieve TIRFM in a cell with a cytoplasmic refractive index of 1.38 is 65.2°, we were well within the range for producing an evanescent field. The characteristic 1/e depth d of the evanescent intensity under these experimental conditions is calculated to be 80 nm.

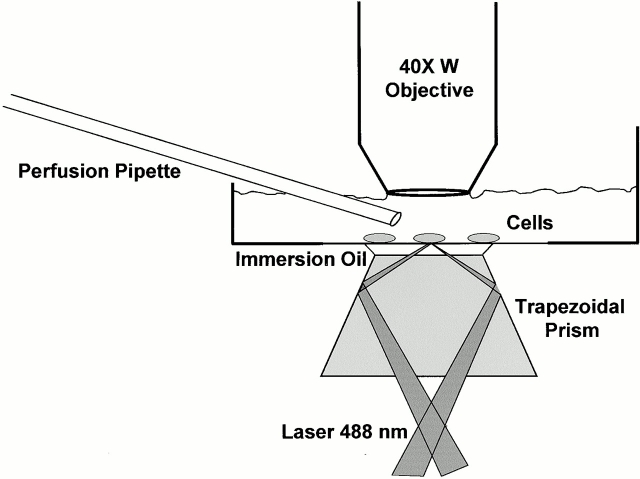
Figure 1.

TIRFM Optics. Cells are cultured on plastic culture dishes in which the bottom has been drilled out and a glass coverslip has been glued. The excitation light is provided by the 488-nm line of the laser focused by a long focal lengths just before the beam enters the microscope base. The beam then reflects up from the microscope's base optics, and TIRFM is created by a trapezoidal glass prism (flint glass, 1.648 refractive index, cut from a triangular prism commercially available from Rolyn Optics) mounted on the condenser mount. A thin layer of immersion oil separates the prism from the glass coverslip. The cells are visualized through a 0.75 NA 40× achromat water immersion objective (160-mm tube length) mounted on a Leitz Ortholux upright microscope. Local perfusion of individual cells can be performed by positioning a quartz pipette within a few hundred microns of the cell of interest.

The excitation light was provided by a 3-W argon ion CW laser (No. 95; Lexel). The total power at the sample plane, spread over a region of ∼180 × 360 μm on the sample, was ∼80 mW. Since the evanescent field intensity (on the water side of the interface) is approximately (but not exactly) the same as the incident light intensity (in the glass) (Axelrod 2001), the average light intensity as “seen” by the sample in the evanescent field is ∼1 μW/μm². Most digital images were collected by a cooled CCD camera (Pentamax; Princeton Instruments, with a 1400 sensor; Eastman Kodak Co., and operated with Winview software; Princeton Instruments), with region-of-interest cropping generally set to produce images of 200 × 300 pixels. Later experiments employed a cooled CCD camera (SensiCam; Cooke Corp., with an ICX061 progressive scan interline sensor; Sony, and software; Cooke Corp.). Except as noted, the interframe time was 0.5 s and the exposure time was 0.2 s. In the final images, each pixel corresponded to a square of 0.104 × 0.104 μm.

Software Identification of Granules

For the off-line analysis of each experiment, granules were located, identified, and tracked through a time-sequence stack of images entirely by computer using software written by the authors in the Interactive Data Language (IDL; Research Systems, Inc.). Each image in the stack was high-pass filtered to remove low spatial frequencies. The image was then smoothed by a traveling two-dimensional 3 × 3 pixel boxcar average (i.e., each pixel value was replaced by the average of the pixel values in the nine-pixel square box centered around that pixel). This smoothing procedure reduces shot noise but causes negligible blurring since it is performed on a distance scale comparable with the optical resolution. Off-cell locations were defined as those pixels with intensities that fall below a programmable threshold level in the unfiltered image; those pixel values were set equal to zero in the filtered image.

For each filtered image, the program identified granule locations one-by-one (starting with the location of the brightest pixel) if (a) the pixel intensity was greater than a user-defined threshold, (b) the intensity was a local maximum (i.e., brighter than the eight immediately surrounding pixels), and (c) the location was at least 0.6 μm away from every previously identified granule. The x-y position of the granule center was refined by calculating the “center of mass” of intensity for the selected pixel and its eight nearest neighbors. The average intensity in a circular region centered around the granule position (0.6-μm radius) region was calculated, and then the local average intensity as recorded just outside that circular region was subtracted. The relative z position of each granule from the substrate was then computed from the background-subtracted average intensity F assuming an exponential evanescent field decay according to:

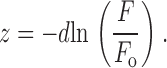1

Here, F _o is defined as the absolute brightest F found in the entire stack of images. The brightest granule at its brightest appearance thereby was assigned z = 0, and all others were assigned an increasingly positive z with decreasing brightness. Calculation of absolute z distances based on intensity assumes that all granules have the same intrinsic brightness. As discussed in detail later, the error incurred by this assumption can be corrected where necessary by using an experimentally measured spread of granule brightness.

Note that distance z is measured from the substrate, not from the plasma membrane. If the plasma membrane is not flat when apposed to the glass interface, then granules with different measured fluorescence but with the same amount of ANP-GFP may be at the same distance from the plasma membrane. For many purposes, however, the absolute z position is not as important as the motion Δz between a pair of frames, a quantity insensitive to the location of z = 0. The measured photobleaching (<0.5% per image) does not significantly affect measurements of Δz. is valid, not just for point sources of fluorescence, but for extended fluorescent objects including granules of any shape. When a granule moves a distance Δz as a whole, all the points within it suffer the same factor change in illumination intensity as a consequence of the exponential decay of the evanescent field. It is possible that a small portion of the illumination power is not directly evanescent, but instead might arise from scattering of evanescent light. This nonevanescent scattering will likely have a slower (and nonexponential) decay with respect to z than true evanescent light. In general then, use of , which ignores any scattering, will result in a small underestimate of the actual Δz.

The IDL program identified each granule in frame i of the time-sequence stack with a granule “parent” in frame i-1, from which it was the least lateral (x–y plane) distance. In cases where two or more granules identified the same parent, the more distant ones were declared to be “new” granules. Likewise, parent granules that were not selected as being closest to granules in subsequent frames were declared as “disappeared.” By this method, granules that might have disappeared for at least one frame were always identified as new upon their reappearance. The result of the granule identification procedure was a data stack of coordinates (x, y, z, t) for each granule, which also included encoded information about its first appearance and disappearance time.

Calculation of Motion Parameters

Calculations of diffusion coefficients, autocorrelation functions, histograms, and displacement versus time graphs, as well as the z dependences of granule number, diffusion coefficient, and residence time fraction, were all performed by the same system of IDL programs that identified and tracked granules.

Diffusion Coefficients.

The diffusion coefficient is derived from the average z motion for a particular granule from one frame to the immediately next one. It is defined as:

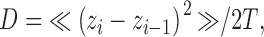2

where z_i is the z position in frame i, T is the interframe time, and the average < > is taken over all immediately sequential pairs of frames in which the same granule is identified. Different granules may have very different D values, from which histograms and averages can be derived. Note that the diffusion coefficient as defined here describes the average motion over the shortest time interval available and does not refer to any restriction of motion apparent only over longer times scales.

Autocorrelation of z Motion.

The step size Δz _i (≡ z_i − z_i−₁) recorded in an interframe interval T is an effective “velocity.” Negative values represent movements toward the plasma membrane, while positive movements are movements away from the plasma membrane. The time-autocorrelation function G(τ) of these Δz values is essentially a velocity autocorrelation that reports to what degree a velocity persists over time τ. (For pure diffusion, the velocity autocorrelation would show zero velocity persistence.) G(τ) for a particular granule is calculated for τ = jT as follows:

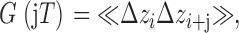3

where the average is taken by summing over all possible products with time separation τ = jT, and then dividing by the total number of products for each τ. For any particular granule, G(τ) is both noisy and variable, so we display averages of G(τ) over all granules. A positive G(τ) at nonzero τ indicates a bias toward a velocity persisting in the same direction; a negative G(τ) indicates that a velocity is biased toward a reversal in time τ.

Corrected Dependence upon z of Granule Population, Diffusion Coefficient, and Residence Time Fraction.

Several features of granule distribution and motion were determined as a function of z position. Although z position is inferred from fluorescence intensity (), individual granules have different intrinsic fluorescent intensities even at the same z. Therefore, the z position dependencies must be corrected for the intrinsic intensity distribution. The maximal intensity of individual granules in fixed cells was determined by measuring granule intensity in several consecutive confocal microscope slices spaced 0.5-μm apart. The maximal intensity for each granule was determined by fitting intensities in consecutive optical sections to a Gaussian distribution (Fig. 2). The range of peak intensities form a histogram when binned according to intensity. Since the resulting range of actual intrinsic intensities would be interpreted as a range of z positions under evanescent field illumination according to , the measured confocal peak intensity histogram can be rebinned according to an “equivalent” relative shift in z. In this rebinning, the brightest granules are grouped into a z _shift = 0 bin; progressively dimmer granules are grouped into a set of progressively larger z _shift bins. Note that z _shift does not refer to an actual z position, but only to the amount that the z positions of intrinsically dimmer granules would (falsely) appear to be shifted to larger z values relative to the brightest granules to account for their reduced intensity. The histogram of the number of granules h(z _shift) that appear to be located at relative position z _shift is normalized to the total number of granules analyzed so it is scaled as a fraction as shown in Fig. 2. This histogram is assumed to describe the intensity spread regardless of actual z position.

Figure 2.

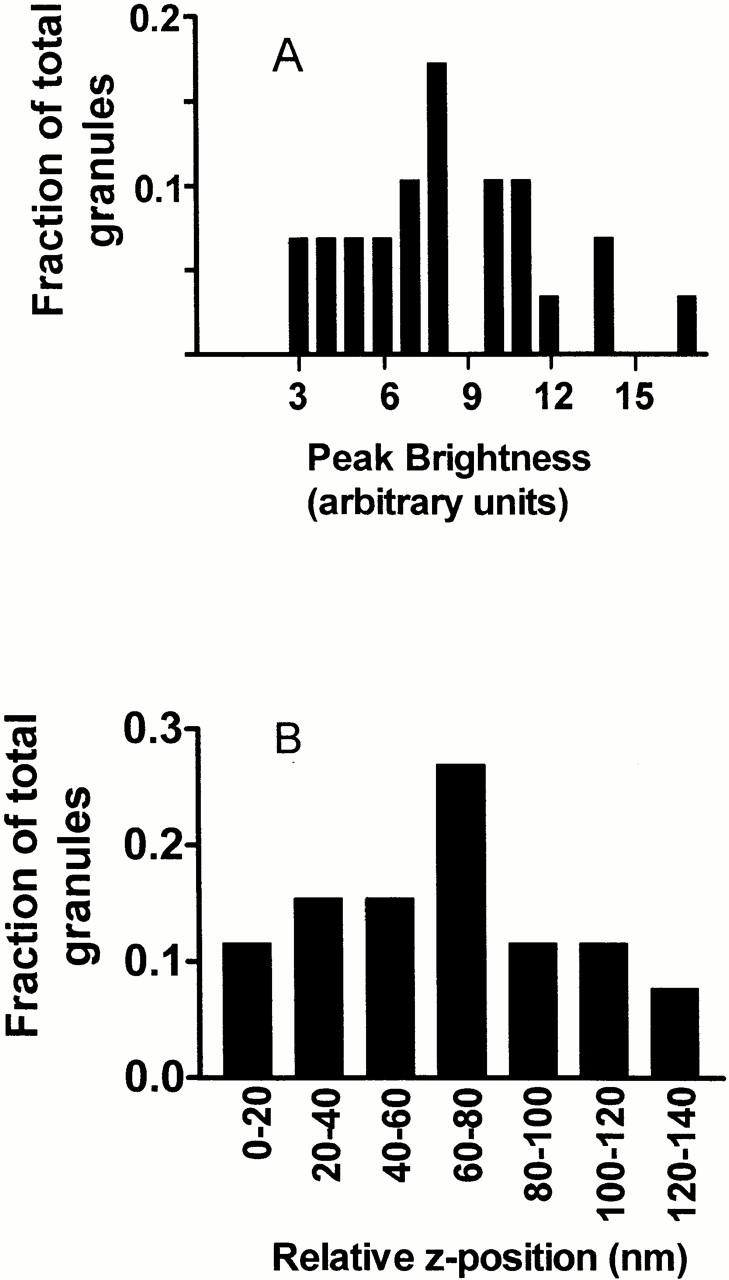
Histogram of Granule Brightness. (A) Peak intensities of granules obtained from consecutive confocal images expressed as fraction of total granules analyzed (n = 29 granules from two cells). (B) The peak intensities of granules from A, converted here to “relative z positions,” placed into bins of 20-nm width, and expressed as fraction of total granules analyzed (n = 29 granules). The conversion assumes that the intrinsically brightest granules in the histogram would be reported at a (presumably correct) z distance z ₀ by the IDL granule identification program, while intrinsically dimmer granules would be (incorrectly) reported to reside at a larger z distance z ₁. The difference (z ₁ − z ₀) is the relative z position plotted as the abscissa here.

The number of granules n′ (z′) interpreted to be in the vicinity of apparent position z′ (by direct application of ) is a convolution of the actual number of granules n(z) in the vicinity of actual position z with the histogram h(z _shift) where z _shift can be written as the difference between the apparent position z′ and the actual position z:

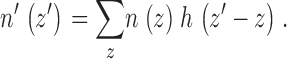4

For a countable set of discrete z bins, describes a system of linear equations that, in principle, could be solved for n(z) from the set of measured quantities n′(z′) and h(z′ − z) by Cramer's rule. In practice, experimental errors in n′(z′) and h(z′ − z) require a best-fit curve fitting procedure in which the set of numbers n(z) is regarded as a set of free fitting parameters (except restricted to nonnegative values), with the goal of creating a trial n′(z′) set that deviates from the actual n′(z′) by a minimized chi-square. To obtain smoother results, we first fit a smooth Gaussian + polynomial shape to the experimental h(z′ − z) before using it in , and we also performed a sliding three adjacent bin smoothing procedure to the fitting results for n(z) based on . The uncertainties in the estimates of n(z) for each z value bin were derived from the spread of n(z) values returned by repeated curve fitting to experimental n′(z′) data to which Gaussian-distributed random noise (with zero mean and a standard deviation equal to the experimental standard error) had been added.

Two physiologically interesting variables in addition to n(z) require correction for the range of intrinsic granule intensities: the diffusion coefficient D(z) and the fraction of time typically spent by a granule in the vicinity of a particular z position, denoted here by α(z). We describe here the correction procedure explicitly for D(z), but it is exactly analogous for α(z). The fraction of granules at an actual position z that appear to be at a particular z′ > z (because of their lower intrinsic brightness) is h(z′ − z), so the number of granules at an actual position z that appear to be at that particular z′ > z is then n(z)h(z′ − z). The diffusion coefficient of each of the granules at z is assumed to be D(z), so the apparent D′(z′) is a average over all the contributing D(z) values, weighted according to their number n(z)h(z′ − z):

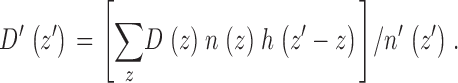5

Only the set of numbers D(z) (one number for each bin of z values) is unknown in and can be derived by a curve-fitting procedure analogous to that used to obtain n(z) from .

As mentioned previously, all the z position calculations refer to distance from the substrate and not from the plasma membrane, which may be spatially undulating. This uncorrected ambiguity is likely to result in an underestimate of any effects that occur as a function of distance from the membrane.

Results

Specificity of ANP-GFP for Marking Chromaffin Granules

To investigate whether the ANP-GFP was localized to chromaffin granules, the localization of the intrinsic fluorescence of GFP was compared with that of dopamine-β-hydroxylase, a marker for chromaffin granules in fixed cells. Cells expressing ANP-GFP could be readily distinguished from nontransfected cells, as the granules were strongly fluorescent and bright green in color. Dopamine-β-hydroxylase was detected by immunocytochemistry (Fig. 3). The intense punctate GFP fluorescence colocalized well with the generally weaker dopamine-β-hydroxylase (compare Fig. 3, left and middle). There was occasional, weak punctate GFP fluorescence that did not colocalize with dopamine-β-hydroxylase. In these cases, it is likely that ANP-GFP but not dopamine-β-hydroxylase from granules distant from the center of the optical section was detected.

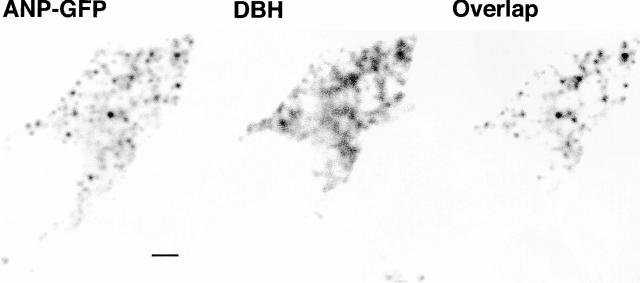
Figure 3.

ANP-GFP colocalizes with dopamine-β-hydroxylase (DBH). Immunocytochemistry was performed on chromaffin cells transfected with the ANP-GFP construct. Cells were fixed, and then permeabilized with absolute MeOH (−20°C). Cells were then processed for DBH (see Materials and Methods). (Left) GFP signal, (middle) anti–DBH signal, and (right) overlap of the GFP and anti–DBH signals. There was significant overlap of the GFP and DBH signals. Scale bar: 2 μm.

If the ANP-GFP is in chromaffin granules, then upon secretion the cellular GFP fluorescence should decrease. Indeed, whole cell fluorescence of transfected cells measured by photometry decreased upon stimulation for 20 min with 2.2 mM barium from 92.0 ± 2.0 (arbitrary units) for control cells (n = 3) to 54.4 ± 8.5 for barium stimulated cells (n = 3, P < 0.02), suggesting that the protein was released during secretion. The 41% decline is similar to the extent of catecholamine secretion induced by barium over a similar time period (Hampton and Holz 1983). These experiments indicate that ANP-GFP expressed by transient expression is sorted to chromaffin granules that are competent to undergo exocytosis.

Granules adjacent to the glass coverslip are among those competent to undergo exocytosis since TIRFM is readily able to detect the exposure of the intragranular antigenic sites of membrane-bound dopamine-β-hydroxylase on the extracellular surface of the plasma membrane after stimulation of the cells by nicotinic agonist or barium (data not shown, see Wick et al. 1997). Although whole-cell fluorescence decreased during stimulation of secretion, sudden disappearances of granules that could reflect exocytosis upon stimulation occurred only infrequently in TIRFM. Furthermore, at least some of these occurrences could have reflected granules moving into the cell away from the membrane rather than granules undergoing exocytosis. Conversely, partial release of granule contents or immediate appearance of another granule at the release site could lead to an underestimate of release rates. Finally, we found that ANP-GFP was incompletely released at the cell surface (as judged by confocal microscopy and immunocytochemistry using an antibody that recognized GFP: see Materials and Methods). The ANP-GFP that remained associated with the exterior of the cell was punctate and of similar dimensions as chromaffin granules (data not shown). The possibility cannot be excluded that rates of release or dispersal of ANP-GFP at the TIRFM surface are different than elsewhere. Thus, while ANP-GFP is an excellent marker for intracellular chromaffin granules, numerous ambiguities remain about its behavior during the exocytotic event. We have, therefore, focused on the quantitative analysis of chromaffin granule motion very near the membrane within unstimulated cells instead of on the release event itself.

Overview of Granule Motion in Three Dimensions

For most granules seen in time sequences of TIRFM images, movement is evident but restricted in all three dimensions. In the x–y plane, the motion is measured by changes in the “center of mass” position of the granule image over successive TIRFM frames. The great majority of such granules moved very little (less than their diameter, which happens to be approximately equal to the Raleigh resolution limit). However, <1% of the granules did move several granule diameters in the x–y plane over a period of several seconds. These infrequent large motions appeared to be directed. Out of a total of 1,018 granules analyzed on 18 different cells, only 8 granules moved >1 μm in the x-y plane during a 4 min period.

The emphasis in this study (in contrast to the earlier studies of Oheim et al. 1999; Steyer and Almers 1999; Oheim and Stuhmer 2000) is on the quantitative analysis of z motion (towards and away from the plasma membrane), which is evident as a seemingly random flickering fluorescence intensity in the exponentially decaying evanescent field. Motion in the z direction is of great importance for exocytosis since it brings the secretory granule into contact with the plasma membrane with which it fuses. Because the decay of the evanescent field with distance from the substrate is very steep (e-fold in 80 nm) and the granules are quite bright, measurements of granule motion in the z direction are extremely sensitive, with granule movements of 4 nm readily detectable (over the effects of shot noise and instrumental noise) for granules within the first 100 nm or so. Measurements of granule motion in the z axis are approximately one order of magnitude more precise than those in the x–y plane. Fig. 4 A shows TIRFM images taken every 0.5 s. The distances moved by three granules (Fig. 4 A, boxes) towards and away from the membrane were calculated and plotted in B. The largest movement of the granules in 0.5 s was ∼86.5 nm, much less than the diameter of the chromaffin granule (300 nm). Mean granule movement of a large number of granules was 26.6 ± 0.3 nm in 0.5 s (n = 21,530 individual granule motions).

Figure 4.

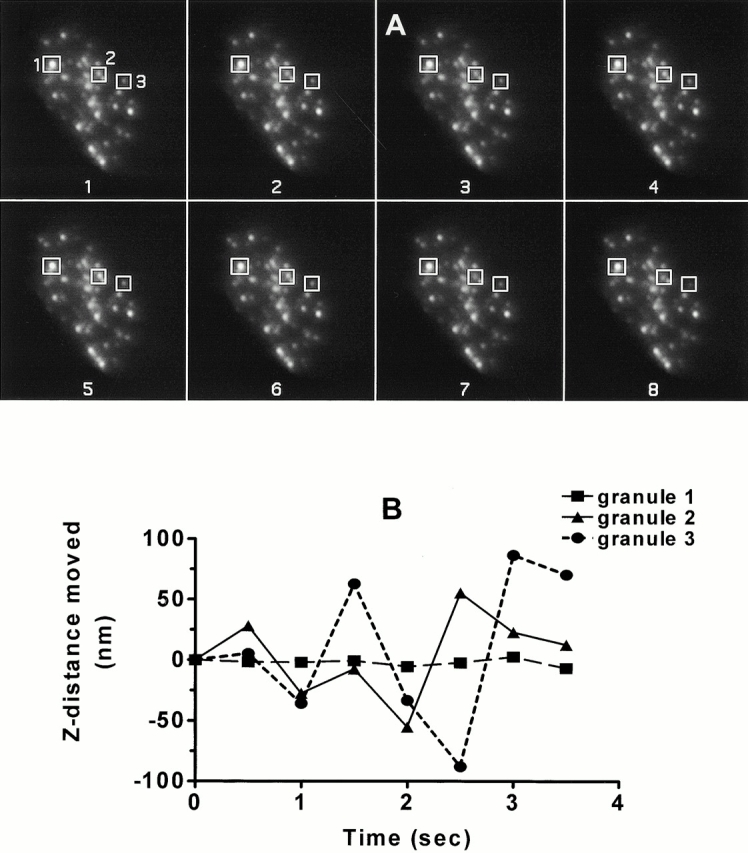
Granule motion in z plane can be quantitated from changes in fluorescence intensity. (A) Images were taken every 0.5 s for 2 min under basal conditions. Three granules were selected and their movement was monitored over time. The intensities of each granule changed over time, indicating movement back and forth in the z direction. (B) Changes in fluorescence intensity have been converted into the absolute value of changes in distance in nanometers the granule moves every 0.5 s.

Population Density and Residence Time of Granules Near the Plasma Membrane

The population of granules increases strongly at positions closer to the membrane (i.e., smaller z). Fig. 5 A shows this effect, which becomes apparent after the data is deconvoluted by taking into account the distribution of the intrinsic brightness of granules (see Materials and Methods). Because the precise distance of the plasma membrane from the glass interface may vary in an image, even the corrected distance of a granule from the plasma membrane has some uncertainty (see Materials and Methods). However, such undulations in the plasma membrane would only lead to an underestimate, not an overestimate, of the actual magnitude of the membrane-proximal population density peak (as corrected for intrinsic brightness) as plotted versus distance z from the substrate.

Figure 5.

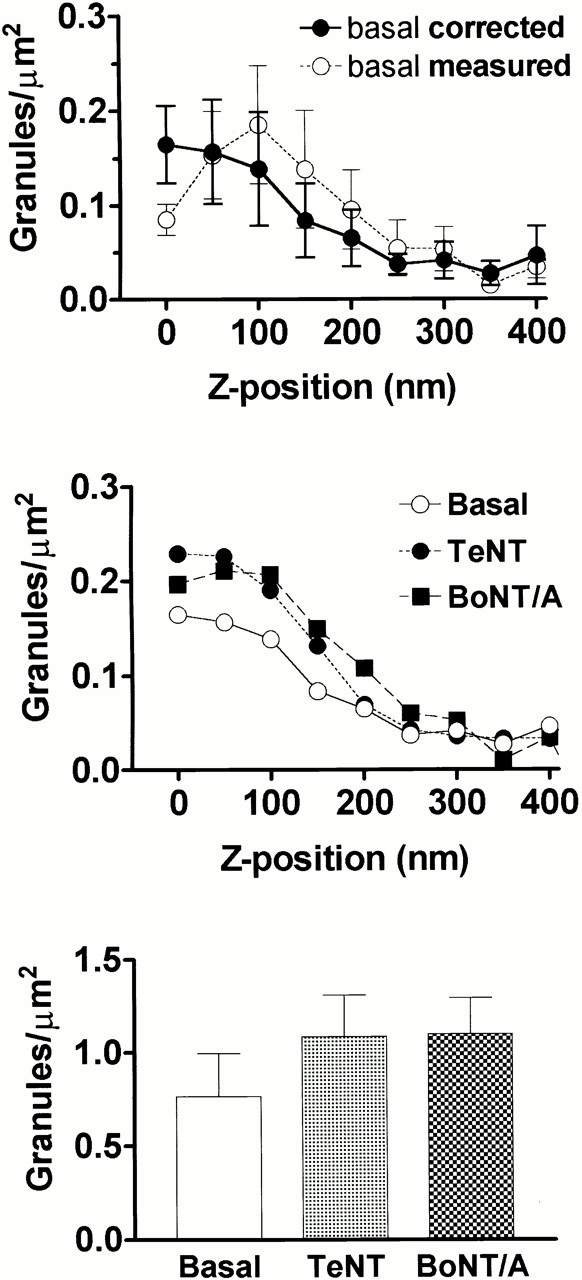
Concentration of granules versus z. The number of granules residing within a particular z position window inferred from their fluorescence intensities. (A) Basal cells. (•) The dependence after correction for intrinsic brightness variations, as described in Materials and Methods; (○) the uncorrected data for which the abscissa is based directly on . Values for uncorrected data are mean ± SEM, n = 9 cells; uncertainties for corrected data are derived as described in Materials and Methods. (B) Cells cotransfected with ANP-GFP and either TeNT or BoNT/A, compared with those transfected with ANP-GFP alone (the same as basal from A) (n = 8, 10, and 10 for TeNT, BoNT/A, and basal, respectively). These are all corrected for intrinsic brightness variations. (C) The number of granules in TIR was counted and the area of the cells in TIR was calculated. Granule density (granules/μm²) was 0.76 ± 0.23 for control cells (n = 10 cells), 1.08 ± 0.22 for cells expressing TeNT (n = 8 cells), and 1.10 ± 0.2 for cells expressing BoNT/A (n = 10 cells) (mean ± SEM).

Since most of the granules exhibit a random motion in the z direction, it is of interest to determine what fraction of the time is spent by a granule at the z positions visited. This data was obtained by tracking individual granules that are identified in at least 40 successive frames. We then averaged these fractions over all the tracked granules (Fig. 6 A) and corrected the results for distribution of intrinsic granule brightness (B, see Materials and Methods). The data indicate that granules in basal cells (•) tend to spend more of their time near rather than far from the plasma membrane, even if they visit a wide range of locations.

Figure 6.

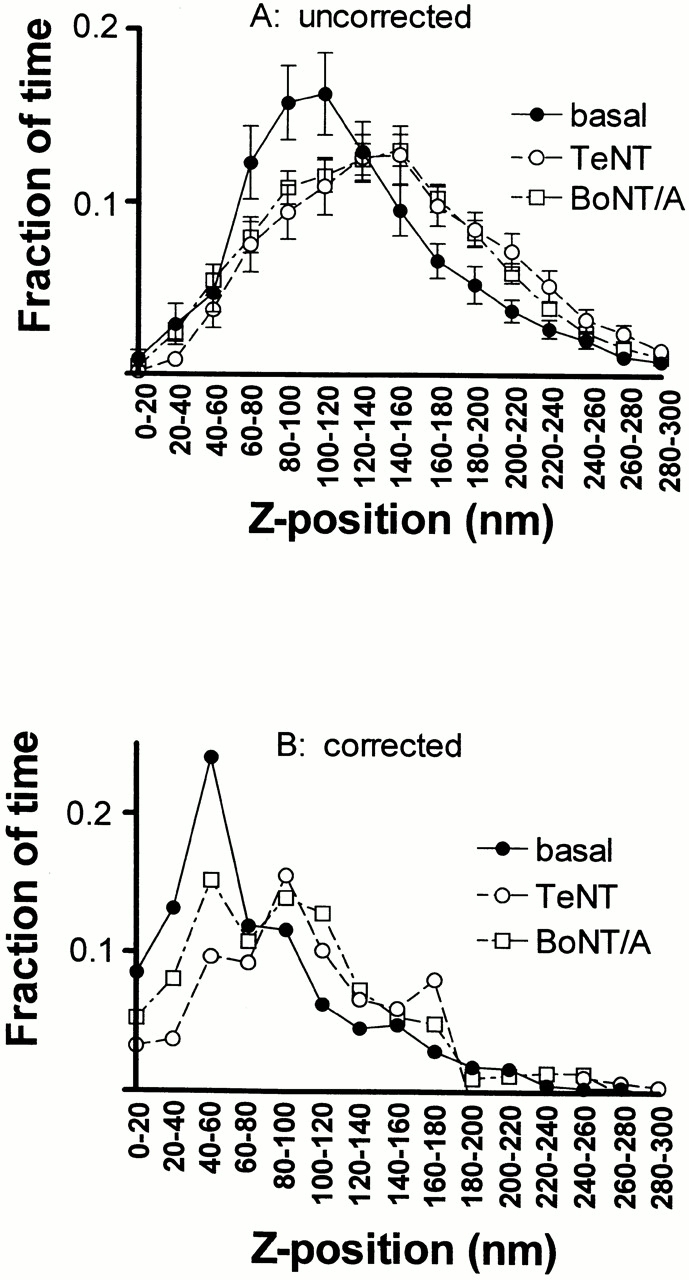
Fraction of visiting time versus z. For granules that can be continually tracked over at least 40 frames and that covered a total distance of at least 100 nm during this time, the fraction of the number of frames that the granule resides within a particular z-position window is plotted versus z position (divided into 20-nm-wide bins). Values are the mean ± SEM for basal cells (57 granules from 12 cells), TeNT expressing cells (54 granules from six cells), and BoNT/A-expressing cells (149 granules from eight cells). (A) These plots are uncorrected for variations in intrinsic brightness; the abscissa is based directly on . (B) These plots are corrected for variations in intrinsic brightness as described in Materials and Methods.

Granule Motion Is Restricted Over Long Times

To determine the characteristics of granule motion near the plasma membrane, motion in the z direction was plotted as (Δz)² versus time separately for each granule. Individual granules displayed variability in mobility; while some granules appeared to be confined, other granules did not. Fig. 7 A shows (Δz)² versus time plots that are averaged over all granules. The slope of the averaged data decreases with time. If the motion could be described as unidirectional linear flow, the (Δz)² versus time plot would be concave up; if it were unrestricted diffusion (or a random walk with a small step size), the (Δz)² versus time plot would be a straight line. The observed downward concavity indicates that the displacement over long times is not as great as would be expected from diffusion at the same rate deduced from the displacement over short times. This indicates that granule motion is somehow restricted or impeded over distance scales of ∼50 nm or more and time scales of a few seconds or more.

Figure 7.

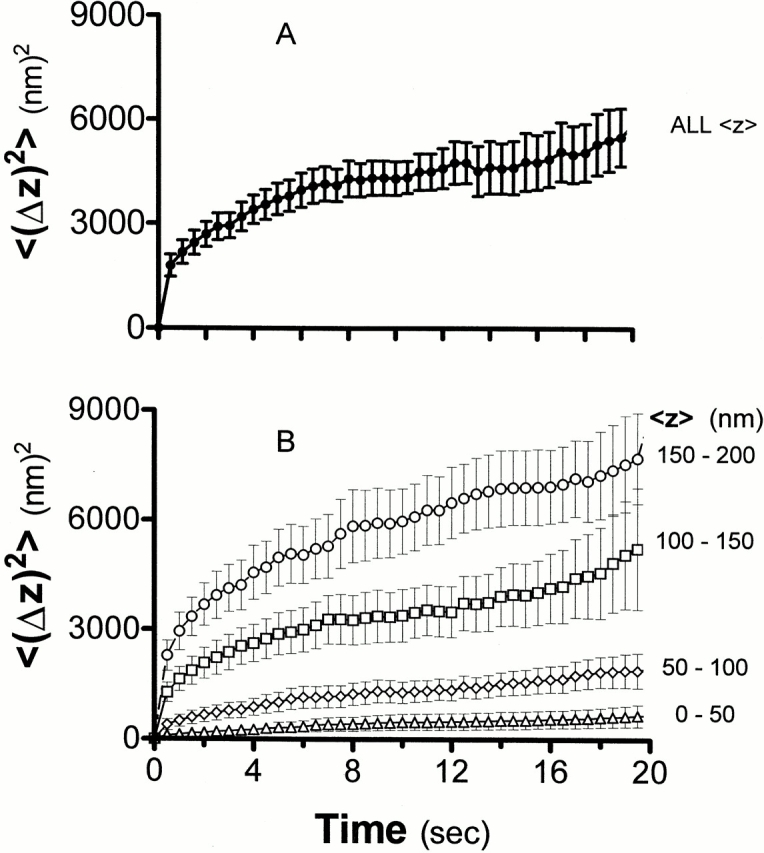
Long-term granule motion: <(Δz)²> versus t. The squared z distance (mean ± SEM) that individually tracked granules in basal cells moved from their initial position is plotted for each cumulative elapsed time point (0.5-s intervals) over the course of 2 min. Only granules that could be followed for at least 40 consecutive frames (20 s) were selected for analysis (128 granules total from 12 cells). (A) All such granules, regardless of z position. (B) Granules divided into pools based on their (uncorrected) z positions (averaged over all the frames in which each was tracked), as estimated from their intensities based on . The pools shown are the following: 0–50, 50–100, 100–150, and 150–200 nm (shown in thin lines). The plots are generally concave down rather than straight, showing that the motion at all z positions is confined, relative to free Brownian diffusion.

To determine whether granules closer to the plasma membrane were restricted to a greater degree than granules further within the cell, granules under basal conditions were divided into bins based on their relative z positions (averaged over the entire course of their appearance) with ranges of 0–50, 50–100, 100–150, and 150–200 nm. Granules further from the membrane moved larger distances than those closer to the plasma membrane (Fig. 7 B) in the same time interval.

Diffusion Coefficients versus Distance from Membrane

Because the motion of a typical granule over periods of several seconds is restricted and cannot be described by a single unambiguous diffusion coefficient over any time scale explored here, we calculated “short-term” diffusion coefficients (see Materials and Methods) that describes granule mobility between one frame and the next (0.5 s). The averaging called for by was performed by two different methods, as follows.

Diffusion coefficients for ∼40 individual granules were calculated based on averages within z position bins (as above) to determine whether the motion of individual granules decreased upon approach to the plasma membrane. Indeed, >80% of the granules had smaller diffusion coefficients when they visited z positions closer to the plasma membrane. Fig. 8 A shows the results for three granules that had been followed for 120 s.

Figure 8.

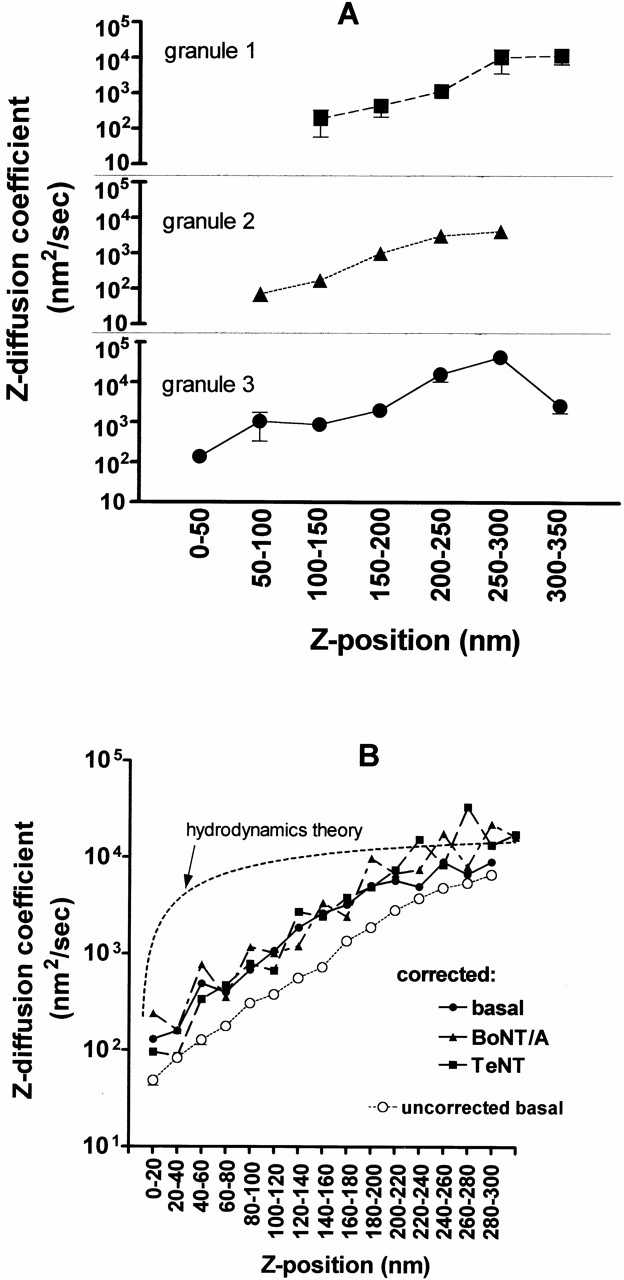
Rates of granule motion versus z position. (A) Three typical individual granules are tracked by imaging at 0.5-s intervals for 120 s. As each granule visits the indicated z range (as judged by intensity data and ), it displays particular z steps Δz. For each z range visited, the (Δz)² values are averaged separately for each granule, and a local “diffusion coefficient” is calculated according to . Values for each bin are the mean ± SEM. These three plots show a clear tendency of individual granules to greatly slow their motions (note the log scale of the ordinate) as they approach the membrane (smaller z). (B) All granules appearing in at least two consecutive frames as identified by the IDL program are tracked here. The (Δz)² values from all the steps of all the granules are pooled together according to the indicated z ranges, and the values within each pool are then averaged. The result is converted to a local diffusion coefficient Δz according to . Values are the mean ± SEM. Several plots are shown here. First, Δz for basal cells (○) is plotted against z values that are not corrected for expected variations in intrinsic granule brightness. In a second group, Δz is plotted against z values that are corrected for intrinsic granule brightness variations, according to the procedure described in Materials and Methods. This second group shows separate plots for: basal cells (•, 12 cells, and 21,090 individual motions, where each point the average of 383–2,934 motions), cells expressing TeNT (▪, six cells, and 9,665 individual motions, where each point is the average of 36–2,060 motions), and cells expressing BoNT/A (▴, eight cells, and 17,938 individual motions, where each point is the average of 64–2,761 motions). These plots all show that Δz smoothly increases with z, with no evidence of discrete steps. The dashed line with no data points is a plot of Δz versus z based on the hydrodynamic theory of Brenner 1961. This is the expected behavior of a 300-nm diameter sphere near a planar surface in an otherwise homogeneous viscous medium. The absolute scale of the theoretical Δz is adjusted to match the approximate experimental Δz values at z = 300 nm. The shape of the theoretical curve is clearly very different from the experimental curves.

The diffusion coefficient calculated by averaging over all the granules whose mean position (between two successive frames) fell in a particular z-position range shows the effect of motion retardation near the membrane dramatically. Over a distance equivalent to only one granule diameter, the average diffusion coefficient decreases by two orders of magnitude for granules nearer the membrane (Fig. 8 B). The strong dependence of D upon z is not qualitatively affected even after the deconvolution correction for varying intrinsic granule brightness.

The very low diffusion coefficients in close proximity to the plasma membrane suggest that granules are tethered or enmeshed in a network. If this is correct, further entrapment by chemical fixation should only have modest effects on granule motion. Indeed, fixation of cells with either 4% paraformaldehyde alone or 4% paraformaldehyde in combination with 0.1% glutaraldehyde decreased the overall average diffusion coefficient of granule motion by 42.6 or 62.6% (P < 0.0001), respectively, but did not abolish granule motion, and importantly did not alter the slope of the line (data not shown).

Histograms of z Motion

To determine whether there exist distinct pools of granules defined by distinct groups of diffusion coefficients, we calculated the average diffusion coefficients for granules that could be tracked for at least five consecutive frames, and made a histogram of these values (Fig. 9 A). If there are distinct pools of granules, that should be apparent in the histogram by the presence of more than one peak. However, when the average diffusion coefficients of 997 granules are plotted as a histogram, there is only one broad peak present. We conclude that while there is a wide distribution in granule diffusion coefficients, there is no distinct separation of states of motion of the granules. A histogram of all the (Δz)² values gathered from all the granules that appear in consecutive frames (Fig. 9 B) is also a broad continuum and shows no evidence of distinct states of motion.

Figure 9.

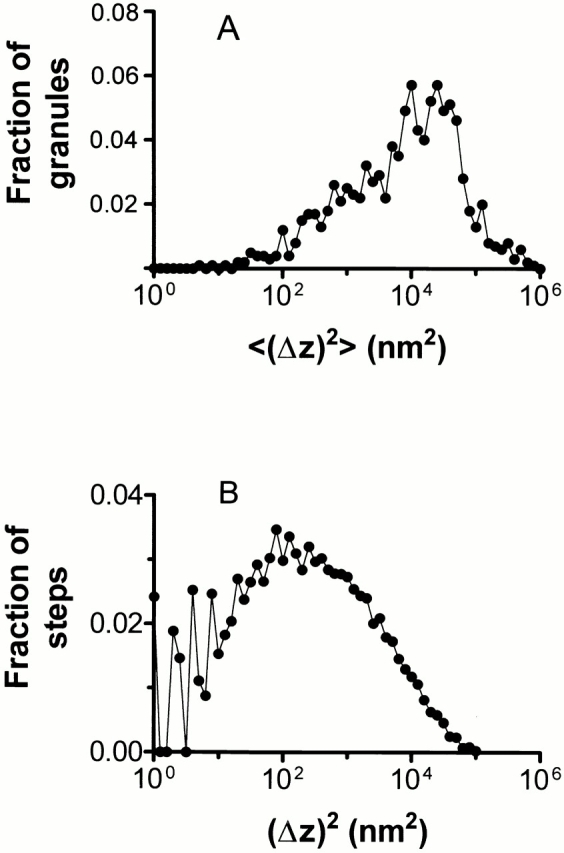
Histograms of step sizes. (A) For each granule that could be tracked for at least five consecutive frames (997 granules from 12 cells), <(Δz)²> was computed from an average of each interframe step size for that granule, and then allocated into bins of 10^0.1 width on a log scale of <(Δz)²>. Note that the absolute magnitudes shown on the abscissa can also be read as diffusion coefficients in view of , where the interframe time T = 0.5 s. (B) For all granules appearing in at least two consecutive frames (12 cells, 21,530 individual granule motions), all the individual (Δz)² values were pooled (regardless of their granule of origin), and then allocated into bins of 10^0.1 width on a log scale of (Δz)². Both of these histograms show that there are no distinct groups of slow and fast granules, but rather a broad continuum.

Granule Steps Tend to Reverse

Pure unrestricted Brownian velocities should exhibit zero persistence from frame to frame (apart from inertial effects that are on time and distance scales many orders of magnitude smaller than relevant here). A positive persistence (measured as a positive velocity autocorrelation) reports a tendency for a granule to keep moving in the same direction it was already moving, a possible indicator of directed movement. A negative persistence (measured as a negative autocorrelation) reports a tendency for the granule to reverse its direction, a possible indicator of caging or tethering (the two of which cannot be distinguished from each other). The calculated G(jT) based on granule Δz movements in the 0.5-s interframe time () shows a significantly negative value by the first τ, indicating that the movement was negatively correlated over a period of 0.5 s (Fig. 10 A). When a granule moves in a particular direction, there is a tendency in the next 0.5 s for the granule to move in the reverse direction. This result is complimentary to the data shown in Fig. 7 regarding restriction of long-term motion (on the 10-s time scale); the negative autocorrelation shows a restriction of short-term motion (on the 0.5-s time scale) as well. This negative correlation appears even for the subsets of granules that, based on their fluorescent intensities, are interpreted to be farther away (up to at least 250 nm) from the plasma membrane (data not shown). In neither basal nor stimulated cells is there any evidence of unidirectional motion, which would be detected as a positive autocorrelation for some times τ > 0.

Figure 10.

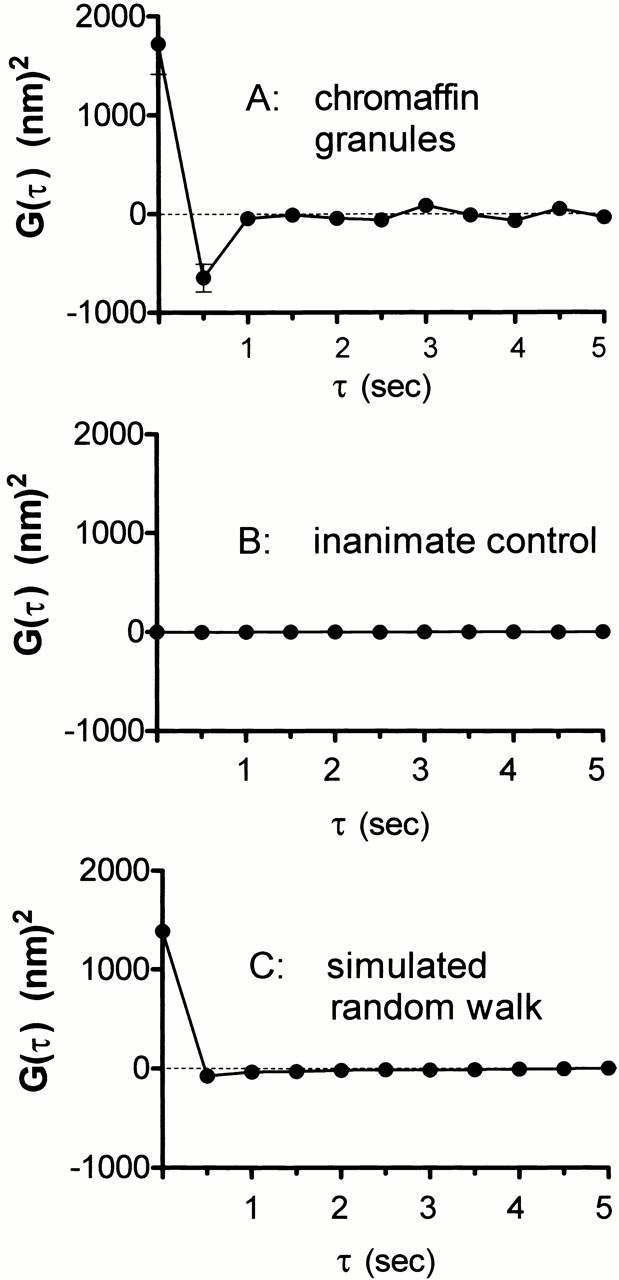
Autocorrelation of granule velocities. For each granule tracked in two or more consecutive frames, the time sequence of Δz displacements were autocorrelated as in Materials and Methods. The graphs show the mean ± SEM of G(τ) for: (A) granules in basal cells (128 granules from 12 cells), (B) constant intensity light scattering produced by immobile dust particles on a glass coverslip illuminated by an incoherent steady light source (i.e., flashlight), as a test for possible artifactual correlations generated by the instrumentation, and (C) simulated motion of 8,000 “granules” obtained using a random number generator, with the average <(Δz)²> adjusted to match the experimental granule results. Basal and stimulated granules show a tendency (more than would be expected from pure diffusion or a random walk) to reverse direction in the displacement of one interframe step to the next.

The negative correlation is not an artifact of instrument or software design nor of the finite exposure time. To determine whether the CCD camera was responsible for this negative correlation effect, light (from a battery-operated flashlight) scattered by stationary dust particles on a glass coverslip was followed over 50 images taken at a frequency of 2 Hz. The resulting autocorrelation function has a value very close to zero at all τ values and does not show a strongly negative value at the first τ (= 0.5 s) (Fig. 10 B). As a check against software artifacts in the autocorrelation program, an array of random numbers representing Δz values of 8000 “granules” over 100 “frames” was generated using a random number generator function. When the autocorrelation function is calculated for these values, the function immediately and correctly decays to zero by the first τ (Fig. 10 C). As a check against finite exposure time artifacts, cumulative simulated z positions can be generated by summing sequences of random Δz values, and then converting these sums to equivalent optical “intensities,” averaging the intensities over finite exposure times, and finally converting the sequence of averaged intensities back to simulated Δz values. The autocorrelation functions of sequences of such Δz values show no negative-going artifacts.

Effects of Latrunculin on the Cortical Actin Cytoskeleton and Granule Motion

The actin cytoskeleton is located immediately adjacent to the plasma membrane and may account for the restricted diffusion of chromaffin granules detected in the above experiments. Latrunculin B binds g-actin and thereby reduces cellular f-actin. Cells were incubated with or without 10 μM latrunculin B for 10 min, and then stained for f-actin using Alexa-phalloidin. In the absence of latrunculin, distinct cortical f-actin could be seen on the majority of chromaffin cells in a field of view (data not shown). The effect of latrunculin B on actin disruption was variable, but overall resulted in a 61% (P = 0.0092) decrease in the cortical actin ring when the fluorescence at the cell's periphery was compared with that inside the cell (data not shown). To determine whether the cortical actin cytoskeleton was responsible for the restriction and/or tethering of granules near the plasma membrane, cells were incubated with latrunculin B and imaged using TIRFM. Although there is evidence for a small increase in the rate of granule motion, the tendency of granule motion to become strongly restricted close to the plasma membrane is not altered. However, these experiments need to be interpreted with caution. Chromaffin cells became rounded and lifted from the glass coverslip upon treatment with latrunculin B, and there were relatively few survivors. It is possible that granule motion was determined only in those cells where the cytoskeleton was least affected by latrunculin B.

Effects of Clostridial Neurotoxins on Granule Motion

Another possible regulator of granule motion and position close to the plasma membrane is the SNARE complex, which is composed of syntaxin and SNAP-25 on the plasma membrane, and VAMP2 on the granule membrane. Clostridial neurotoxins are a family of potent inhibitors of exocytosis that act by proteolysis of the three SNARE proteins. The effects on secretion and granule motion of two of these toxins, TeNT (cleaves VAMP2) and BoNT/A (cleaves SNAP-25) were examined by cotransfecting plasmids encoding the light chain of either toxin with human GH or ANP-GFP.

Human GH secretion from cells expressing TeNT or BoNT/A was inhibited 99 or 49%, respectively, upon stimulation with the nicotinic agonist DMPP for 2 min (data not shown). The ability of transient transfection of the toxin light chains to inhibit secretion indicates physiologically significant proteolysis of VAMP-2 or SNAP-25. The partial inhibition of secretion in chromaffin cells by BoNT/A has been previously observed (Bittner et al. 1989), and is a characteristic of cleavage of a small carboxyl terminal peptide on SNAP-25.

Expression of TeNT or BoNT/A caused a small (although not statistically significant) increase in the total number of granules visualized by TIRFM per μm² (Fig. 5 C). There was little change in the population distribution of granules at different distances from the plasma membrane when all the granules are considered (Fig. 5 B). On the other hand, a particular subpopulation of granules (those granules that were present in at least 40 successive frames and moved through a range of at least 100 nm) was tracked to characterize the motion histories of individual granules. Granules in that particular subpopulation spent a smaller fraction of time near the plasma membrane in toxin-expressing cells than did granules in a similarly defined subpopulation in control (basal) cells (Fig. 6 B). The difference in the percentage of time that those granules spent at (uncorrected) distances of 120 nm or less (denoted as α₁₂₀) in toxin-expressing cells compared with nontoxin cells is highly statistically significant: for control cells, α₁₂₀ = 53 ± 4% (n = 57); for TeNT cells, α₁₂₀ = 33 ± 3% (n = 54, P < 0.0002); and for BoNT cells, α₁₂₀ = 39 ± 2% (n = 149, P < 0.0005). Because the plasma membrane may spatially undulate in distance from the substrate (see Materials and Methods), the influence of SNARE proteins very near the plasma membrane will appear to be spread over a wider range of z distances from the substrate. The relative reduction in time spent by granules in toxin-expressing cells within the closest 120 nm from the substrate is thereby consistent with the notion that SNARE proteins are important in mediating granule–plasma membrane interactions.

Neither TeNT/A nor BoNT/A altered the precipitous decrease in short-term diffusion coefficients of granules upon approaching the plasma membrane (Fig. 8 B). It is likely that the mechanisms involved in slowing granules as they approach the plasma membrane do not involve VAMP2 or SNAP-25. The toxins also had no effect on the restriction of granule motion with time. Plots of <Δz ²> versus time are nearly identical for granules in toxin-transfected and control cells (data not shown, see Fig. 7 A for control cells).

Discussion

We have used TIRFM microscopy to study quantitatively the motion and distribution of secretory granules near the plasma membrane of living bovine chromaffin cells. By several criteria, it is shown that the z-directed motion (i.e., in the direction normal to the membrane) is severely and increasingly restricted as the granule approaches the membrane. We discuss the possible causes and significance of the finding and the technology used in the studies.

Chromaffin Granules Are Concentrated Close to the Plasma Membrane

Within the very thin region probed by the evanescent field, granules are preferentially concentrated at the closest distances to the membrane, and they spend more time in that zone than slightly farther into the cell. This result supports the observations of Steyer et al. 1997 concerning the granule density at various distances d from the plasma membrane in unfixed, quickly frozen chromaffin cells. They found that ∼0.3 granules/μm² were at d = 0, and that the density of granules abruptly dropped off to between 0.1 and 0.05 granules/μm² 50 nm from the plasma membrane. In contrast, Plattner et al. 1997, also using cryofixation, did not observe a concentration of granules in close proximity to the plasma membrane. In fact, Plattner et al. 1997 reported a decrease in granule density as the plasma membrane was approached, and this decrease, or “wall effect,” was supported by Monte Carlo simulations of the data based on size distribution of granules. While these two previous studies used thin-section electron microscopy of cells obtained by cryofixation, our experiments measure the distribution and position of granules in live cells.

Chromaffin Granules Seem to be Caged

In our studies, we observed a wide variety of motions including but not limited to granules that approached the membrane, and then receded back into the cell as above. In fact, examples of almost any type of behavior could be seen. We took a statistical approach that evaluated the movements in a much larger population of tracked granules than previous studies, finding that granules were ever more restricted in motion as they approached the plasma membrane; that large movements in the x–y plane were rare; and that, on average, granules do not engage in any unidirectional motion. Despite the dominant randomness of the motions, two features were inconsistent with a purely Brownian model: (a) the apparent caging of long-distance motion, and (b) a tendency to reverse directions (contrary to unidirectional motion), as shown by the negative autocorrelation of granule z velocity at early times.

Granules Closest to the Plasma Membrane Have the Least Mobility

Granules closest to the plasma membrane were found to move at least two orders of magnitude more slowly than those further away from the membrane. The histogram showing the frequency of occurrence of D values, and the continuous, graded monotonic nature of the D versus z curve, both showed no evidence for a division of granules into two distinct classes, such as immobile at the membrane and fully mobile away from it. Proximity to the plasma membrane was inferred from brightness, but the D versus z dependence remained strong even after mathematical correction for the observed range of intrinsic granule brightness. Importantly, the decreased mobility near the membrane was observed for individual granules as well as deduced from the average motion of all granules. Granules were generally not permanently trapped as they approached the membrane; they merely moved more slowly when they were nearby and more rapidly when they were farther away. This behavior argues against the possibility of a photofixation-induced artifact.

Regardless of the z position, the average diffusion coefficient is much lower than would be expected for a granule-sized sphere of radius a = 150 nm undergoing free Brownian motion in a barrier-free medium of viscosity η ≈ 0.1 poise (i.e., 10× more viscous than water but what might be expected in cytoplasm: see Swaminathan et al. 1996). According to the Einstein hydrodynamic equation (D = kT/6πηa), we would expect such free diffusion to have D = 1.4 × 10⁻⁹ cm²/s. The fastest average z-diffusion coefficient we measure, that for the most distal granules, is still 15× slower than this “free” diffusion prediction. A more complete prediction of Brownian diffusion of a sphere must take into account the hydrodynamic effect of the planar surface with a no-slip boundary (Brenner 1961). Because viscosity disallows fluid motion right at the surface, the sphere's z-directed diffusion should approach zero there. However, the shape of the curve of this theoretical D versus z is completely different from what we observe for chromaffin granules (see Fig. 8 B, dashed line).

Another effect, this one purely geometrical, might be conjectured to suppress apparent motion at the surface. If a granule's average displacement in a given time interval is similar to its distance from the surface, then some of those granules will “reflect” at the surface and thereby report a smaller-than-expected (Δz)². However, a Monte Carlo simulation of this geometrical effect shows at most a 30% dip in (Δz)² for granules that have starting z positions near the surface, and the slight dip in (Δz)² disappears for granules starting at both z = 0 and z very large. Therefore, purely geometrical considerations do not account at all for the several orders-of-magnitude decrease of D suffered by actual cytoplasmic granules near the membrane surface.

A finite exposure time clearly averages random motions that necessarily occur in diffusive systems at shorter time intervals. However, a computer simulation of granule motion (by random number generator) and conversion to simulated fluorescence intensity, followed by a simulation of finite-exposure time averaging just as in the actual experimental data, showed that there is no bias or systematic error in the correct estimation of diffusion coefficients that are inferred from the size of (Δz)².

The detailed macromolecular structure in the submembrane region is probably responsible for the relationship of D versus z. Tethering or entrapment in a heterogeneous gel (perhaps with z-dependent pore size) or specific, reversible binding to proteins near the membrane are possible explanations. We were particularly interested in whether disruption of actin would result in an increase in granule motion. It is known that chromaffin cells contain an f-actin layer just inside the plasma membrane that extends ∼150–200 nm into the cytoplasm (Nakata and Hirokawa 1992). The role of the actin cytoskeleton in exocytosis has not been resolved. There is evidence for its disruption during secretion (Sontag et al. 1988; Nakata and Hirokawa 1992; Zhang et al. 1995), and that this rearrangement of actin increases the size of the readily releasable pool (Vitale et al. 1995). However, it is unclear whether actin is disrupted as a prelude to exocytosis or as a consequence of chromaffin granule membrane insertion into the plasma membrane. After exposure of cells to latrunculin B for 10 min, which resulted in a significant reduction of cortical f-actin, a small increase (∼50%) in granule diffusion coefficients were observed, with the strong D versus z dependence still preserved. A consequence of disruption of the actin cytoskeleton is that the cells have a tendency to round up off the glass. It may be that cells selected for TIRFM were less affected by latrunculin, and therefore did not have complete f-actin disassembly. While there is evidence that disruption of actin results in slightly increased granule motion, we are unable to determine whether actin is responsible for the highly restricted granule motion adjacent to the plasma membrane.

A recent study in PC12 cells investigated possible correlations between the state of actin and the motion of secretory granules (labeled with a GFP-protein hybrid) in the x–y plane (Lang et al. 2000). In contrast to the present study, treatment by latrunculin B caused a 50% reduction in the x–y diffusion coefficient of granules.

Effects of Cleavage of SNARE Proteins by Tetanus Toxin and Botulinum Toxin A

Transient expression of tetanus toxin and BoNT/A strongly inhibited secretion, thus indicating significant cleavage of VAMP and SNAP-25, respectively. An analysis of the fraction of time granules close to the plasma membrane is consistent with VAMP and SNAP-25 tethering the granule to the plasma membrane, presumably through SNARE complex formation. The analysis was performed on granules that could be followed for at least 20 s (40 frames) and that moved at least 100 nm (Fig. 6). This population of granules in toxin-expressing cells spend less time immediately adjacent to the plasma membrane, suggesting a reduction in the frequency and duration of granule interaction with the plasma membrane. The granules may be spending less time “sampling” the plasma membrane, a possible priming process for exocytosis.

Expression of tetanus toxin and BoNT/A had little effect on the decreased mobility of chromaffin granules upon approach to the plasma membrane (i.e., D versus z, Fig. 8). Thus, although VAMP and SNAP-25 are required at a late stage in the secretory pathway, and may contribute to the tethering of granules to the plasma membrane, they are unlikely to play a significant role in the restricted motion of granules approaching the plasma membrane.

Comparison with Other Studies

In most previous studies in chromaffin cells using TIRFM, chromaffin granules were labeled by the weak base acridine orange (Steyer et al. 1997; Oheim et al. 1998, Oheim et al. 1999; Steyer and Almers 1999; Oheim and Stuhmer 2000). We have compared granule labeling with acridine orange and by transfection with ANP-GFP. Because acridine orange accumulates in all acidic compartments, it does not specifically label chromaffin granules. In fact, incubation of cultures with acridine orange strongly labels punctate structures in contaminating cells in the culture (Johns, L.M., and R.W. Holz, unpublished observations). When acridine orange is removed from the medium after labeling (which is the protocol described in previous publications), the dye slowly exits the granules and cells. In our experiments with acridine orange following this protocol, only a small amount of punctate fluorescence remained despite considerable background fluorescence. The image quality after washing out acridine orange was not as high as in cells expressing ANP-GFP, and there was a tendency for granules to “explode” upon continuous excitation, an indication of potentially toxic effects of illuminating the chromophore.

Because of the enormous variability in chromaffin granule motion, both within and among cells, we developed software that automatically locates granules, tracks them through a time sequence of images, and analyzes their motion. The program permitted the analysis of hundreds of granules with thousands of motions, and reduced the chance of experimental bias in granule selection. The software allowed new types of analyses (population densities, time fraction, and diffusion coefficients versus z, all corrected for the spread of intrinsic granule brightness, and autocorrelations of granule motions) to be readily performed.

In one series of studies using acridine orange, some vesicles appeared to move steadily toward the membrane accompanied by motion in the x–y plane (parallel to the plasma membrane) such that the labeled vesicles approached the membrane at an angle in a directed rather than random manner (Steyer et al. 1997; Steyer and Almers 1999). Upon reaching the membrane, the vesicles ceased movement over several seconds and then moved back into the cell. The authors concluded that docking was observed, and that this process was transient and reversible. Steyer and Almers 1999 appropriately emphasized x–y motion because accurate quantitation in the z direction was reduced by the large evanescent field depth (or even highly oblique but subcritical angle illumination) that they employed. They found that long-term two-dimensional [(Δx)² + (Δy)²] motion versus time tended to exhibit a downward concavity, much as does (Δz)² versus time here. This decrease in motion as granules approach the plasma membrane is consistent with our results, although we focused mainly on the z motion that (by using TIRF) is measurable over distances two orders of magnitude smaller than the x–y Raleigh resolution limit of the microscope.

We observed a smooth continuum of D (in the z direction) versus z, and a smooth population distribution peaking at the smallest z, rather than distinct classes. In contrast, Oheim et al. 1999 reported diffusion coefficients (representing a three-dimensional motion without separating out the z direction) that suggested the presence of two distinct groups of granules consisting of bright ones (interpreted as membrane-proximal) that were 100-fold less mobile than a group of dimmer ones (interpreted as more distal). Recently, another study by the same group (Oheim and Stuhmer 2000) presented an extensive study of granule motion in chromaffin cells with acridine-orange–labeled granules. Similar to our results, they determined that the granules moved significantly less than what would be predicted for free diffusion, and that granules closer to the plasma membrane were ∼100× less mobile than those further away. Oheim and Stuhmer 2000 analyzed an impressive number of cells and granules, and again they identified two distinct pools of granules: immobile, near-membrane granules that they called “docked” granules, and mobile granules that were ∼60 nm further into the cell. An ambiguity in that study is the method by which granule position in the z axis was determined, which was based upon the ratio of vesicle intensity to local background fluorescence.

One possible reason for the identification of a broad continuum population of ANP-GFP–labeled granules (as judged by rate of motion) in our studies and the identification of two distinct populations of acridine-orange–labeled granules in previous studies is the greater specificity of labeling inherent in GFP-granule protein transfection. Alternatively, there may be differences between the pure one-dimensional z motion measured here and the three-dimensional motion reported in previous studies or in the manner in which z positions were estimated.

Oheim and Stuhmer 2000 identified a very small population of granules, ∼3% of the total population, that displayed large seemingly directed or transport-mediated motion in the plane parallel to the plasma membrane, which is similar to our findings.

Confocal microscopy (Burke et al. 1997) and TIRFM (Han et al. 1999) of granule motion in growth cones of nerve growth factor–treated PC12 cells demonstrated that ∼30% of granules under basal or stimulatory conditions are mobile. During stimulation of secretion, there was a preferential depletion of mobile rather than immobile granules near the plasma membrane, suggesting that the mobile pool is the one that is competent to undergo exocytosis. This observation is in direct contrast to those in chromaffin cells, in which Oheim and Stuhmer 2000 observed a preferential release of granules from the immobile or docked pool. (Recall that our results also show the slowest granules reside closest to the membrane, although in a broad continuum rather than two distinct classes.) The data suggest that granule motion differs significantly in chromaffin cells and in growth cones of nerve growth factor–treated PC12 cells.

In summary, we have exploited the ability of TIRFM to measure small motions in the z direction to investigate chromaffin granule motion within 300 nm of the plasma membrane. Chromaffin granules labeled with transiently expressed ANP-GFP move much more slowly than would be expected from free Brownian motion, and most surprisingly have short term diffusion coefficients that decrease by two orders of magnitude in a continuous fashion within less than a granule diameter of the plasma membrane. Granules tend to reverse direction within 0.5 s. The SNARE proteins VAMP and SNAP-25 are not required for the restricted mobility, although they may influence interaction with the plasma membrane. The automated image processing and quantitative approaches developed in the study combined with the ability to express proteins of interest together with ANP-GFP will facilitate the future investigation of the biochemical and physiological processes that control granule motion and, thereby, influence exocytosis.