Reduced intracellular ionic strength as the initial trigger for activation of endothelial volume-regulated anion channels

Abstract

Most mammalian cell types, including endothelial cells, respond to cell swelling by activating a Cl⁻ current termed I_Cl,swell, but it is not known how the physical stimulus of cell swelling is transferred to the channels underlying I_Cl,swell. We have investigated the precise relation between cell volume and I_Cl,swell in endothelial cells by performing whole-cell current recordings while continuously monitoring cell thickness (T_c) as a measure for cell volume. The time course of T_c was accurately predicted by a theoretical model that describes volume changes of patch-clamped cells in response to changes in the extracellular osmolality (OSM_o). This model also predicts significant changes in intracellular ionic strength (Γ_i) when OSM_o is altered. Under all experimental conditions I_Cl,swell closely followed the changes in Γ_i, whereas I_Cl,swell and cell volume were often found to change independently. These results do not support the hypothesis that Γ_i regulates the volume set point for activation of I_Cl,swell. Instead, they are in complete agreement with a model in which a decrease of Γ_i rather than an increase in cell volume is the initial trigger for activation of I_Cl,swell.

All living cells are programmed to activate a series of cellular processes to counter the harmful effects of cell swelling. One of the first detectable effects of cell swelling in most vertebrate cells is an increase in the plasma membrane permeability to anions, through the opening of anion channels (1). Although different types of swelling-activated anion currents have been functionally described, one phenotype seems to be predominant. This outwardly rectifying current, which under normal conditions is mainly carried by Cl⁻, has been termed I_Cl,swell for swelling-activated Cl⁻ current, and the underlying channel has been termed VRAC for volume-regulated anion channel. The biophysical and pharmacological properties of I_Cl,swell/VRAC have been extensively studied (for recent reviews, see refs. 2–4), but the precise activation mechanism of I_Cl,swell is still not resolved. Particularly, it remains unclear how the cell “senses” changes in its volume and translates this physical stimulus into the opening of VRAC.

Hypotonicity-induced cell swelling is accompanied by a dilution of the intracellular medium, resulting in a decrease of Γ_i, the intracellular ionic strength. Interestingly, it was recently shown that Γ_i modulates I_Cl,swell, independent of the molecular nature of the intracellular ions. A model was proposed in which Γ_i regulates the volume set point for activation of VRAC, by modulating a putative “volume sensor” (5–7).

In the present study we tested this model by investigating the relation between cell volume, Γ_i, and I_Cl,swell in endothelial cells. To this end, we set up a combined system that enables the simultaneous measurement of whole-cell currents and cell thickness (T_c). A theoretical model was developed that accurately predicts the osmotically induced volume changes and the concomitant changes in Γ_i. We demonstrate that I_Cl,swell is tightly coupled to Γ_i but not to cell volume. Our present results are discussed in the framework of a model in which a decrease of Γ_i rather than an increase in cell volume is the initial trigger for activation of I_Cl,swell.

MATERIALS AND METHODS

We used single endothelial cells from an established cell line from calf pulmonary artery (cell line CPAE; American Type Culture Collection). Cells were grown in DMEM (Life Technologies/GIBCO) with 20% fetal calf serum, 2 mM l-glutamine, 100 mg⋅ml⁻¹ streptomycin, and 100 mg⋅ml⁻¹ penicillin and were seeded on gelatin-coated coverslips 2–4 days before use.

The standard isotonic extracellular solution contained (in mM) 150 NaCl, 6 KCl, 1 MgCl₂, 1.5 CaCl₂, 10 glucose, and 10 Hepes, pH 7.4 with NaOH (320 mOsm). During the experiments, cells were perfused with a solution containing (in mM) 85 NaCl, 6 CsCl, 1 MgCl₂, 1.5 CaCl₂, 10 glucose, 10 Hepes, pH 7.4 with NaOH, and the appropriate amount of mannitol to reach the indicated osmolality (between 200 and 400 mOsm). In most experiments, a pipette solution was used containing (in mM) 40 CsCl, 100 cesium aspartate, 1 MgCl₂, 1.93 CaCl₂, 5 EGTA, 4 Na₂ATP, and 10 Hepes, pH 7.2 with CsOH (290 mOsm). The ionic strength of this pipette solution (Γ_p) is 155 mM. The concentration of free Ca²⁺ in this solution was buffered at 100 nM, which is below the threshold for activation of Ca²⁺-activated Cl⁻ currents (8) but sufficient to fully activate I_Cl,swell (9) in CPAE cells. For pipette solutions with a different Γ_p, the concentration of cesium aspartate was either increased or decreased. When necessary, sucrose was added to obtain the desired osmolality. We have chosen to use extra- and intracellular solutions containing Cs⁺ salts instead of K⁺ salts to minimize the contribution of an inwardly rectifying K⁺ current present in these cells.

Currents were monitored with an EPC-7 (List Electronic, Lambrecht/Pfalz, Germany) patch-clamp amplifier. Patch electrodes had dc resistances between 2 and 6 MΩ. Whole-cell membrane currents were measured in ruptured patches. Currents were sampled at 2-ms intervals and filtered at 200 Hz. The following voltage protocol was applied every 15 s from a holding potential of −20 mV: a step to −80 mV for 0.6 s, followed by a step to −100 mV for 0.2 s and a 2.6-s linear voltage ramp to +100 mV. Time courses of the whole-cell current were obtained by averaging the current in a 10-mV window around +95 mV and normalizing to the cell membrane capacitance (C_m). C_m values were obtained by using the analog compensation circuitry of the EPC7 amplifier. Except when mentioned otherwise, time zero corresponds to the rupture of the membrane. Our experimental conditions were designed such that measured whole-cell currents represent almost exclusively currents through VRAC. Therefore, all whole-cell currents are denominated I_Cl,swell. Cells showing any indication of other membrane and/or leak currents (e.g., changes in reversal potential and/or current rectification) were discarded from analysis.

The Cell surface area (CSA) of single cells was quantified from digital images recorded with a video camera (model CF 6, Kappa, Gleichen, Germany). Cell borders were traced manually and the surface of the traced region was determined by using the ImageTool 1.25 software (University of Texas Health Science Center, San Antonio). CSA was calculated as the average of three independent tracing procedures.

T_c was monitored with a slightly modified version of the method described by Van Driessche et al. (10). Gelatin-coated coverslips containing nonconfluent CPAE cells were incubated for about 30 min with 4 μl/ml Red Neutravidin-labeled microbeads (F-8775, Molecular Probes), followed by a 15-min washing with microbead-free solution. The microbeads were visualized by using a Xenon lamp and the XF40/E filter set (Omega Optical, Brattleboro, VT), which consists of a broadband excitation filter (maximal at 560 nm) and a 600-nm long-pass emission filter. Fluorescent images at different vertical positions were recorded with the CF 6 video camera, digitized, and displayed on a video monitor. The controlled vertical displacement of the objective was achieved by using a low-voltage piezoelectric translator (PIFOC P-721; Physik Instrumente, Waldbronn, Germany). The vertical position of preselected beads was determined as the position at which the fluorescent light intensity was maximal (10). T_c was calculated as the vertical distance between beads on the gelatin surface and on the cell surface. Home-written software was used to control the piezoelectric translator and perform the on-line image analysis.

Numerical solutions for the differential equations that describe changes in cell volume and Γ_i were generated by using the mathcad plus 6.0 software (Mathsoft, Cambridge, MA). The origin 5.0 software (Microcal Software, Northampton, MA) was used for statistical analysis and graphical presentation of the data. Whenever possible, a single experiment is shown representative of at least four similar experiments. Pooled data are given as mean ± SEM from n experiments.

RESULTS

The first aim of this work was to establish a system for measuring changes in endothelial cell volume during whole-cell patch-clamp measurements. In previous reports showing volume changes in patch-clamped cells, cell volume was mostly estimated from measurements of the cell diameter or cell surface area by using off-line image analyzing techniques (11–13). However, such volume measurements are restricted to cells with a simple spherical or cylindrical morphology and cannot be applied to flat cells such as endothelial cells. Here, we have combined the whole-cell patch-clamp technique with an optical method that monitors changes in cell thickness T_c by using fluorescent beads (10). This method combines an accuracy of <100 nm with a sampling rate of about 0.2 Hz. In comparison with the above-mentioned methods, it has the additional advantage that it enables on-line monitoring of cell volume.

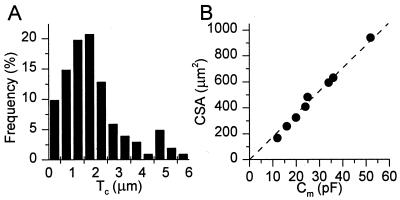
Fig. 1A shows a histogram of T_c values of single CPAE cells under isotonic conditions. Assuming a random distribution of the fluorescent beads over the whole cell surface, we obtain an average cell thickness of 1.86 ± 0.13 μm (n = 101). T_c values >3.5 μm were obtained exclusively from the region of the nucleus. Measurements of the cell surface area (CSA) of CPAE cells yielded an average value of 584 ± 63 μm² (n = 12). Therefore, we estimate the average cell volume of a CPAE cell to be around 1 pl. The average cell membrane capacitance (C_m) in this study was 32.5 ± 2.2 pF (n = 62). As shown in Fig. 1B, CSA correlated very well (r = 0.996) with C_m. From the linear fit we obtain that CSA (μm²) = 17.6⋅C_m (pF). Given a specific membrane capacitance of ≈1 pF per 100 μm² (14), it follows that, depending on the contribution of the basal membrane to C_m, CSA measurements underestimate total membrane area by a factor of 3–6. This probably indicates a high level of membrane folding in CPAE cells.

Figure 1.

Dimensions of CPAE cells. (A) Histogram of T_c values of nondialyzed CPAE cells in isotonic solution. Pooled data from 101 T_c determinations on 76 cells. (B) Correlation between CSA and C_m for eight whole-cell patch-clamped cells. The broken line represents the best linear fit, with a slope of 17.6 μm²/pF (r = 0.996). Note that these cells cover the whole range of CSA and C_m values observed in this study.

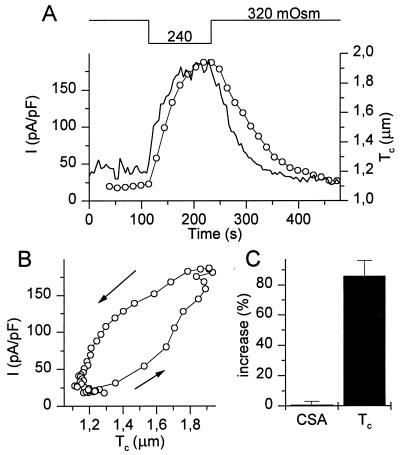
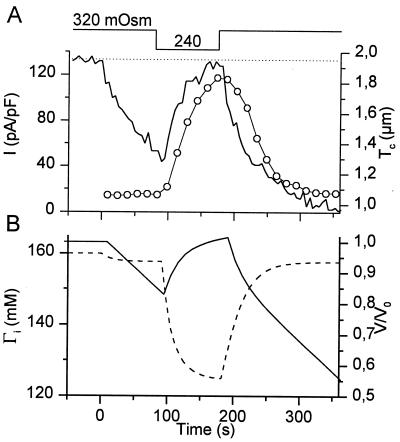
Fig. 2A shows a typical example of a simultaneous measurement of T_c and whole-cell current in a CPAE cell. Reducing the extracellular osmolality (OSM_o) from 320 to 240 mOsm causes a rapid increase in T_c and the activation of an outward current, identified as I_Cl,swell. Both cell swelling and activation of I_Cl,swell were fully reversible. Fig. 2B shows the relation between T_c and I_Cl,swell for the experiment in Fig. 2A. The hysteresis between I_Cl,swell and T_c indicates that cell swelling and cell shrinking precede activation and deactivation of the current. To establish a relation between T_c and cell volume, we measured the relative increase of T_c and CSA after decreasing OSM_o from 320 to 240 mOsm for 200 s. Fig. 2C shows that this maneuver induces an almost doubling of T_c without significantly changing CSA. Moreover, the relative increases in T_c measured at various spots on the cell surface were not significantly different (not shown). We can therefore conclude that T_c is a good measure of cell volume.

Figure 2.

Simultaneous measurement of T_c and whole-cell currents. (A) Changes in T_c (solid line) and whole-cell currents (circles) induced by the indicated changes in OSM_o. The whole-cell current was identified as I_Cl,swell. (B) Correlation between T_c and I_Cl,swell during the experiment shown in A. (C) Average increase in CSA and T_c in dialyzed cells (n = 8) after 200 s in hypotonic solution (240 mOsm).

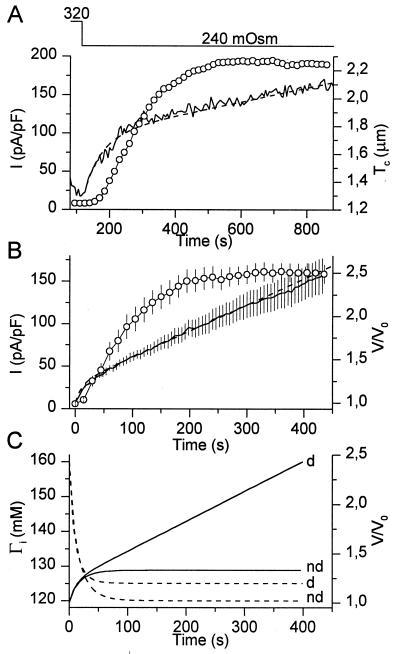
To further establish the relation between I_Cl,swell and cell volume, we performed experiments whereby I_Cl,swell and T_c were measured during prolonged hypotonic shocks. As illustrated in Fig. 3A, the increase in T_c during such a hypotonic challenge is biphasic, with a rapid initial swelling followed by a slower but persistent swelling. CPAE cells tolerated increases in T_c to ≈3 times the initial value before cell bursting occurred. We consistently observed that I_Cl,swell reached a plateau value, in spite of the fact that V/V₀ continued to increase (Fig. 3B). This could indicate either that I_Cl,swell saturates at a level where all VRAC channels in the plasma membrane are activated, such that further swelling can no longer increase I_Cl,swell, or that some other parameter secondary to changes in cell volume triggers the activation of I_Cl,swell. What follows is an attempt to discriminate between these two possibilities.

Figure 3.

Changes in T_c and I_Cl,swell during a prolonged reduction of OSM_o. (A) Changes in T_c (solid line) and I_Cl,swell (circles) as OSM_o was lowered from 320 to 240 mOsm. (B) Average current density (circles) and relative volume V/V₀ (solid line) during a 450-s reduction of OSM₀ from 320 to 240 mOsm (n = 10). The broken line in A and B represents the best fit of the model. In this panel, time 0 corresponds to the time at which OSM_o was reduced. (C) Model prediction of V/V₀ (solid lines) and Γ_i (broken lines) for dialyzed (d) and nondialyzed (nd) cells.

We propose a simple mathematical model to predict changes in cell volume (V) and in intracellular ionic strength (Γ_i) when the extracellular solution and the intracellular pipette solution have a different osmolality. First, we assume that there is no pressure built up in a cell. This assumption is supported by the finding that CPAE cells that are not intracellularly dialyzed behave almost as perfect osmometers (15). This first assumption also implies that there is neither a pressure difference nor net water flux between pipette and cell. Additionally, we assume that the net flux of solutes across the plasma membrane is negligible compared with the exchange of solutes between pipette and cytosol. To achieve this, cells were held at a potential close to the reversal potential of I_Cl,swell (≈−20 mV under the ionic conditions used). Hence, changes in V equal the net influx or efflux of water across the plasma membrane (J_m), which is linearly dependent on the transmembrane osmotic gradient:

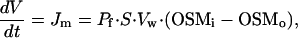1

where OSM_i is the osmolality of the intracellular medium, P_f is the osmotic water permeability of the membrane, S is the cell membrane surface, and V_w is the partial molar volume of water (1.8⋅10⁻⁵ m³⋅mol⁻¹). Osmolality can be estimated as the total concentration of solutes multiplied by the osmotic coefficient φ (≈0.93 for the osmolytes used). For simplicity, we also assume that the diffusion rate from the pipette into the cell is the same for all solute species in the pipette. Therefore, we use C_i and C_p as the global concentration of solutes in the cell and in the pipette, respectively. C_i changes due to solute exchange with the pipette and due to variations in the cell volume:

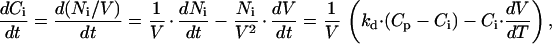2

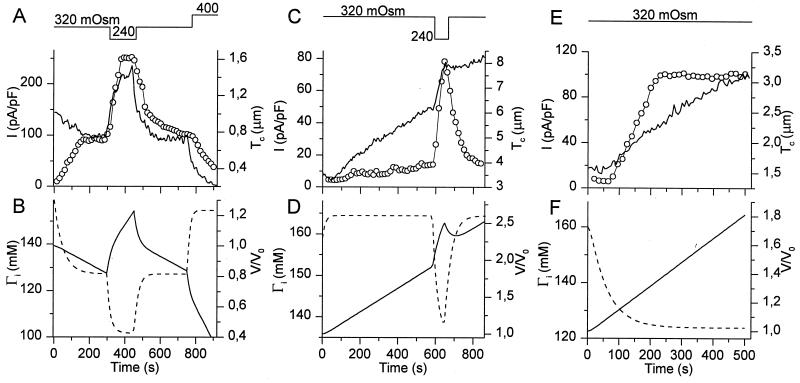
where k_d is a constant (m³/s) describing the rate of the diffusion of solutes from pipette to cell. The model essentially consists of two differential equations with two variables, C_i and V, and two unknown constants, P_f and k_d. We used home-written software employing a Stoer–Bullirsch algorithm (16) to numerically solve the differential equations for each set of values for P_f and k_d. A simplex method was used to determine the values of P_f and k_d that gave the best fit to the experimental volume measurements. Examples of such fits are shown in Fig. 3 A and B, from which we obtained average values for P_f and k_d of 2.53⋅10⁻⁵ m/s and 1.94⋅10⁻¹⁷ m³/s. The P_f value agrees very well with the value of 3⋅10⁻⁵ m/s, obtained from transmembrane fluxes of tritiated H₂O in calf pulmonary endothelial cells (17). For a cell with a volume of 1 pl the obtained k_d value corresponds to a diffusion time constant of 51.5 s. This is well in agreement with experimentally obtained time constants for the diffusion of solutes such as Fura-2, Ca²⁺, or Cs⁺ from the pipette into CPAE cells, which were found to range from 30 to 120 s. The above-mentioned constants were subsequently used to predict changes in V and C_i (or Γ_i) during osmotic challenges. Interestingly, the model predicts that Γ_i decreases significantly during an osmotic challenge and, like I_Cl,swell, reaches a plateau value, in spite of the continuous increase in V (Fig. 3C). Note that the decrease in Γ_i is even more pronounced in nondialyzed cells (Fig. 3C).

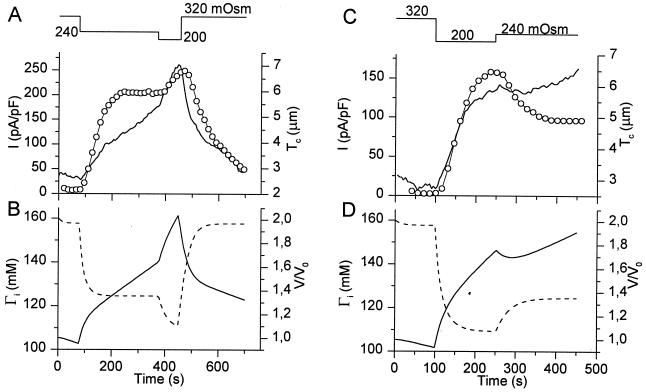
To further evaluate the relations between V, Γ_i, and I_Cl,swell, we have simultaneously measured T_c and I_Cl,swell in cells that were subjected to stepwise changes in extracellular osmolality, and we compared the experimental data with the model predictions of V and Γ_i. The experiment shown in Fig. 4A nicely illustrates how I_Cl,swell reaches a plateau during exposure to a 240-mOsm solution, in spite of the continuous increase in T_c. A subsequent decrease of the extracellular osmolality to 200 mOsm causes a higher rate of increase in T_c and a further increase of I_Cl,swell. The model predictions for T_c and Γ_i for this experiment are shown in Fig. 4B. It can be seen that the predicted values of V are in good agreement with the changes in T_c, whereas the predicted values of Γ_i closely mirror I_Cl,swell. This experiment also shows that the plateau level of I_Cl,swell during the 240-mOsm stimulus cannot be attributed to a saturated activation of all VRAC channels. Fig. 4C shows an experiment in which I_Cl,swell reaches a plateau value during exposure to a 200-mOsm solution. A subsequent increase in the extracellular osmolality to 240 mOsm causes only a transient decrease in T_c but a permanent decrease of I_Cl,swell to a lower plateau value. Again, the model accurately predicts the changes in V, and Γ_i closely mirrors I_Cl,swell (Fig. 4D).

Figure 4.

Comparison of experimental data of T_c and I_Cl,swell with model predictions of V/V₀ and Γ_i during stepwise changes in OSM_o. (A) T_c (solid line) and I_Cl,swell (circles) as OSM_o is stepped first to 240 mOsm and thereafter to 200 mOsm. (B) Model prediction of cell volume (solid line) and Γ_i (broken line) for the experiment shown in A. (C) T_c (solid line) and I_Cl,swell (circles) as OSM_o is stepped first to 200 mOsm and thereafter to 240 mOsm. (D) Same as B for the experiment shown in C.

As the above experiments indicate that I_Cl,swell follows the decrease in Γ_i, we measured I_Cl,swell and T_c in cells where Γ_i was directly reduced by dialysis with a pipette solution of low salt content but normal osmolality (Γ_p = 125 mM; 290 mOsm). As shown in Fig. 5A, such a maneuver activates I_Cl,swell in spite of a slight decrease in T_c. A subsequent decrease in extracellular osmolality causes an increase in T_c and a further increase in I_Cl,swell. Finally, I_Cl,swell was fully deactivated by using a hypertonic extracellular solution, which is expected to increase Γ_i to basal levels (Fig. 5B). Fig. 5C shows an experiment where Γ_i was increased by using a pipette solution with a high salt content (Γ_p = 195 mM; 365 mOsm). This hypertonic pipette solution induces cell swelling but does not significantly activate I_Cl,swell. A short reduction of OSM_o to 240 mOsm is still able to activate I_Cl,swell. As shown in Fig. 5D, the model accurately predicts the volume changes, whereas I_Cl,swell nicely mirrors Γ_i. It has to be noted that in 4 of 9 experiments using high-salt pipette solutions, I_Cl,swell was transiently activated but then returned to basal levels. In contrast, I_Cl,swell was consistently activated in cells dialyzed with a pipette solution that was made hypertonic by addition of sucrose (Γ_p = 155 mM; 365 mOsm) (Fig. 5E). In these cells, a significant reduction in Γ_i is expected (Fig. 5F).

Figure 5.

T_c and I_Cl,swell in cells dialyzed with pipette solutions with altered osmolality and/or salt content. (A) Activation of I_Cl,swell (circles) without any increase in T_c (solid line) in a cell dialyzed with a low-salt pipette solution (Γ_p = 125 mM; 290 mOsm), further activation of I_Cl,swell by reducing OSM_o to 240 mOsm and inactivation of I_Cl,swell by increasing OSM_o to 400 mOsm. (B) Model prediction of V/V₀ (solid line) and Γ_i (broken line) for the experiment shown in A. (C) Increase in T_c (solid line) without significant activation of I_Cl,swell (circles) in a cell dialyzed with a high-salt pipette solution (Γ_p = 195 mM; 365 mOsm). Reducing OSM_o to 240 mOsm causes further cell swelling and activation of I_Cl,swell. (D) Same as B for the experiment shown in C. (E) Increase in T_c (solid line) and activation of I_Cl,swell (circles) in a cell dialyzed with a hypertonic pipette solution with normal salt content (Γ_p = 155 mM; 365 mOsm). (F) Same as B for the experiment shown in E.

An alternative way to affect the volume of whole-cell patch-clamped cells is to apply pressure to the patch pipette. Our attempts to measure whole-cell currents while inducing cell swelling by application of positive pressure were, however, unsuccessful, as this approach most often resulted in activation of nonselective leaks and/or loss of the whole-cell configuration. In contrast, persistent application of a negative pressure to the patch-pipette was generally well tolerated by the endothelial cells. As illustrated in Fig. 6A, such a maneuver induced extensive shrinkage of the cells without affecting the activation of I_Cl,swell by a reduction of OSM_o. Under this condition, the model assumption of no net flux of water between cell and pipette is no longer valid. We have therefore introduced the parameter J_p, the net flux of solution from the cell to the pipette, yielding the following modifications to Eqs. 1 and 2:

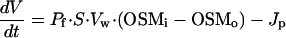3

and

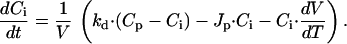4

As we have no means to quantify J_p, we performed model simulations with J_p ranging from 0 to 5⋅10⁻²¹ m³/s (= 5 fl/s) and evaluated the effect of J_p on V and Γ_i. It was found that J_p, while strongly affecting V, has little effect on the time course of Γ_i and no effect on steady-state Γ_i. For the simulation shown in Fig. 6B, we used a value for J_p of 2⋅10⁻²¹ m³/s, which yielded a time course for V comparable with the experimental data in Fig. 6A. Again, activation and deactivation of I_Cl,swell nicely follow the changes in Γ_i, whereas cell volume remains below the resting value during the whole experiment.

Figure 6.

Application of negative pressure to the patch pipette does not affect activation of I_Cl,swell. (A) After break-in (time 0), a constant negative pressure was applied on the patch pipette, causing extensive shrinkage of the cell. Reducing OSM_o to 240 mOsm causes an increase of T_c (solid line) to levels that remain below the resting T_c (indicated by the broken line). Neither activation nor deactivation of I_Cl,swell (circles) is affected by the negative pressure. (B) Model prediction of V/V_o (solid line) and Γ_i (broken line) for the experiment shown in A.

DISCUSSION

A swelling-activated, outwardly rectifying anion current termed I_Cl,swell has been detected in a wide range of vertebrate cell types, and its biophysical and pharamacological properties have been thoroughly described (for recent reviews, see refs. 2–4). It remains, however, obscure how the cell couples cell swelling to the opening of VRAC, the underlying volume-regulated anion channel. Several authors have proposed a mechanism whereby changes in cell volume are detected by a putative “volume sensor,” which directly or indirectly regulates the opening of VRAC. A change in Γ_i was supposed to alter the properties of this “volume sensor,” such that, at lower Γ_i, smaller increases in cell volume are sufficient to activate I_Cl,swell (5–7, 18). On the basis of our present results, we argue against such a mechanism in endothelial cells. First, all maneuvers that cause a reduction in Γ_i were found sufficient to activate I_Cl,swell, even when cell volume was at or far below the resting volume (Figs. 5A and 6), whereas cell swelling up to 200% of the initial volume did not activate I_Cl,swell at constant Γ_i (Fig. 5C). Second, once activated, I_Cl,swell was not sensitive to changes in cell volume but remained modulated by Γ_i (Figs. 3 and 4). Finally, in all experiments the time course of I_Cl,swell almost perfectly mirrored the time course of Γ_i, whereas such a correlation between I_Cl,swell and cell volume did not exist. We therefore propose a model in which the swelling-induced decrease in Γ_i, and not cell swelling itself, is the pivotal signal that regulates the opening of VRAC under anisosmotic conditions.

In accordance with this conclusion is a recent paper by Guizouarn and Motais (19) on swelling-activated transport pathways in trout erythrocytes. These authors show that fish erythrocytes can activate two distinct transport pathways in response to cell swelling: a channel of broad specificity with properties reminiscent of VRAC, and a K⁺–Cl⁻ cotransporter. Whereas the K⁺–Cl⁻ cotransporter seemed to be activated by the cell swelling itself, the VRAC-like channel was activated only when cell swelling was accompanied by a reduction of the intracellular ionic strength. In contrast, two recent studies proposed that VRAC activation is triggered by cell swelling as such, and not by a swelling-induced reduction in Γ_i (6, 7). Two arguments were used to support this conclusion. First, both studies state that in the whole-cell patch-clamp mode Γ_i is unlikely to change during water influx and cell swelling, because of the constant dialysis from the patch-pipette solution. We have, however, disproved this argument by showing experiments in which Γ_i deviates from Γ_p by up to 45 mM (≈30%). Second, Cannon et al. (7) reported activation of I_Cl,swell in CHO cells under conditions of apparently constant Γ_i, after the application of positive pressure to the patch pipette, in line with observations in other cell types (20–22). In contrast, we found no activation of I_Cl,swell after a >100% increase in cell volume under conditions of constant Γ_i (Fig. 5C). Several explanations can be given to explain this discrepancy. First, in most studies the osmolality of the pipette solution is lower than the osmolality of the “isotonic” bath solution. This leads to a constant efflux of water from the cytoplasm. According to our present data, the dialysis by the pipette solution may be too slow to compensate for this efflux, resulting in a Γ_i higher than Γ_p. Consequent application of positive pressure to the patch pipette leads to a faster dialysis of the pipette solution, causing a decrease in Γ_i which might be sufficient to activate I_Cl,swell in some cell types. Second, application of positive pressure to the cytoplasm may directly activate stretch-sensitive (anion) conductances, which may superficially resemble I_Cl,swell (23, 24). Third, although many of the properties of I_Cl,swell are similar in a wide range of mammalian cells, there seem to be important differences in the regulation of the current by intracellular pathways (for recent reviews, see refs. 2–4). Particularly, swelling-induced rearrangements of cytoskeletal elements regulate the opening of VRAC in some cell types (25–27), whereas a complete disruption of the cytoskeleton did not affect activation of I_Cl,swell in endothelial cells (28).

Okada (2) recently postulated that membrane unfolding would be a necessary step in the activation of VRAC. Membrane unfolding is indeed likely to occur during swelling of endothelial cells, given the high level of membrane folding that we estimated. However, the finding that reducing Γ_i per se activates VRAC without any cell swelling (see also ref. 7) argues against a critical role for such membrane unfolding. Similarly, intracellular γ-thio-GTP was found to activate I_Cl,swell without inducing changes in cell volume (T.V., unpublished observation).

It is important to note that nondialyzed cells swell to a much lesser extent than dialyzed cells when OSM_o is reduced, whereas the concomitant drop in Γ_i is more pronounced (Fig. 3C). Therefore, smaller decreases in OSM_o are expected to open VRAC under in vivo conditions. This explains why flux measurements in endothelial cells revealed significant activation of VRAC after reduction of OSM_o by only 7% (29), whereas the same reduction of OSM_o is mostly without effect in whole-cell patch-clamped cells (our unpublished results).

It remains unclear how Γ_i regulates VRAC, the channel underlying I_Cl,swell. A direct effect of Γ_i on VRAC seems unlikely, as activation of the current by lowered Γ_i remains dependent on protein tyrosine kinase activity (6, 30). We favor the idea that Γ_i acts similar to a second messenger, and directly or indirectly regulates the activity of the intracellular enzyme(s) that mediate the activation of I_Cl,swell. It will be of great interest to determine whether src-like tyrosine kinases such as p56^lck, which directly activates I_Cl,swell in lymphocytes (31), or small G proteins such as p21^rho, which is required for the activation of I_Cl,swell in intestine 407 cells (27), are directly influenced by Γ_i.

ABBREVIATIONS

I_Cl,swell

swelling-activated Cl⁻ current

T_c

cell thickness

OSM_o extracellular osmolality

Γ_i, intracellular ionic strength

Γ_p

ionic strength of the pipette solution

VRAC

volume-regulated anion channel

CSA

cell surface area

C_m

membrane capacitance