Abstract
Biological systems provide a complex environment that can be understood in terms of its dielectric properties. High concentrations of macromolecules and cosolvents effectively reduce the dielectric constant of cellular environments, thereby affecting the conformational sampling of biomolecules. To examine this effect in more detail, the conformational preference of alanine dipeptide, poly-alanine, and melittin in different dielectric environments is studied with computer simulations based on recently developed generalized Born methodology. Results from these simulations suggest that extended conformations are favored over α-helical conformations at the dipeptide level at and below dielectric constants of 5–10. Furthermore, lower-dielectric environments begin to significantly stabilize helical structures in poly-alanine at ɛ = 20. In the more complex peptide melittin, different dielectric environments shift the equilibrium between two main conformations: a nearly fully extended helix that is most stable in low dielectrics and a compact, V-shaped conformation consisting of two helices that is preferred in higher dielectric environments. An additional conformation is only found to be significantly populated at intermediate dielectric constants. Good agreement with previous studies of different peptides in specific, less-polar solvent environments, suggest that helix stabilization and shifts in conformational preferences in such environments are primarily due to a reduced dielectric environment rather than specific molecular details. The findings presented here make predictions of how peptide sampling may be altered in dense cellular environments with reduced dielectric response.
Abbreviations used: CHARMM, chemistry at Harvard molecular mechanics (program); CMAP, correlation map; DNA, deoxyribonucleic acid; DPPC, dipalmitoylphosphatidylcholine; GB, generalized Born; GBMV, generalized Born with molecular volume; HFA, hexafluoroacetone hydrate; HFIP, 1,1,1,3,3,3,hexafluoro-2-propanol; LMP2/cc-Pvqz, local Møller-Plesset 2/correlation-consistent polarized valence quadruple ζ; MD, molecular dynamics; MMTSB, molecular modeling tools in structural biology; PMF, potential of mean force; PPII, poly-proline II; REX, replica exchange; TFE, 2,2,2-trifluoroethanol
Introduction
Biological cells provide highly complex environments at the molecular level of detail (1–3). The resulting physicochemical properties play a critical role in determining the structure and dynamics of proteins and nucleic acids, thereby controlling their biological function (4). As prominent examples, cellular environments allow proteins to fold into unique native conformations (5,6) and provide the necessary level of solvation to stabilize the biologically most relevant B-form of DNA (7,8). Conformational preferences are modulated further through varying concentrations of cosolvents, in particular osmolytes (9–11), through the presence of other biomolecules such as chaperones (12,13), specific ligands that may induce conformational change upon binding (14,15), and macromolecular crowding in general (16–20). These cases can be understood in terms of specific molecular interactions, entropic effects due to confinement (19–22), and from a purely thermodynamic perspective as deviations from ideal solution behavior (23).
Another view of how cellular environments may affect the conformational sampling of biomolecules is based on electrostatic theory where different solvent environments are characterized primarily by their dielectric properties. Although cellular interiors largely consist of aqueous solvent, the dielectric properties may vary substantially. At one extreme, the phospholipid tails in the interior of biological membranes provide an extremely hydrophobic environment with a static dielectric constant near 1 (24). However, most biological cosolvents and high concentrations of peptides also lower the static dielectric response from pure water (25). Proteins occupy 20–40% of the cellular volume (2) and have a dielectric constant between 2 and 20 (26–28). Furthermore, high concentrations of cosolvents such as sugars lower the dielectric constant of aqueous solvent to values between 30 and 70 (25), whereas the dielectric response of water itself is also reduced simply by the presence of hydrophobic compounds in its vicinity (29). Consequently, one may estimate that the average effective dielectric constant of dense cellular environments lies between 10 and 40. This is in contrast to many experimental or computational studies of biological macromolecules that are carried out in dilute solutions with a dielectric constant close to 78, the value for pure water (25). A focus on a single, macroscopic dielectric environment greatly simplifies the highly dynamic heterogeneity that is present in cellular systems on the molecular level. It also neglects entropic effects that may arise due to crowding or mixing (20). However, the dielectric continuum view offers the advantage of a more general perspective without any further assumptions about the specific molecular nature of a given cellular environment. A few cases of structural changes in biomolecules in the presence of low-dielectric environments have been previously documented (30,31), but more general insight is still incomplete.
Electrostatic theory predicts that a reduction of solvent polarizability enhances charge-charge interactions and diminishes the advantage of sequestering hydrophobic components away from solvent. However, it is not obvious how this is reflected in altered biomolecular conformational preferences as a function of the dielectric constant of the environment. Experimental and computational studies of proteins and peptides in aqueous solvent with significant concentrations of organic cosolvents have offered some insight into this question (32–36). Alcohol-based cosolvents such as TFE (32,34), HFIP (33,37,38), and HFA (39) have been found to stabilize the helical contents of peptides compared to pure aqueous solution. The helix stabilization would be expected from a strengthening of the hydrogen-bonding interactions in lower dielectric environments. However, β-sheets or β-hairpins are also stabilized in some cases (40,41). In another example, simulations of surfactant protein C suggest that helicity present in higher dielectric solvents is lost in low-dielectric chloroform solvent at the expense of more extended structures (42). Other studies of proteins in nonaqueous, low-dielectric environments have suggested that the dynamics of enzymes is significantly altered in nearly dry organic solvent media (43,44), which has significant implications for their catalytic efficiencies in such environments (45).
Although experimental methods always examine specific chemical environments, computational methods can explore the conformational sampling of biomolecules as a function of the dielectric environment by employing continuum dielectric models (46). Such models have been successfully used for a long time to study biological systems in aqueous solvent (47) and also more recently in the context of biological membranes that can be described by multiple layers with different dielectric constants (48–50). Interactions of an explicit solute with partial charges from a classical molecular mechanics force field with a dielectric continuum are rigorously described by the Poisson equation (51,52). The resulting implicit model of the environment is easily coupled with standard molecular dynamics techniques, especially when the computationally highly efficient generalized Born (GB) approximation to the solutions of the Poisson equation is used (53). Recent modifications to the standard GB implementations extend its applicability to the entire range from low- to high-dielectric environments (54,55). As a result, it has become possible to carry out extensive conformational sampling with an implicit solvent model that accurately reflects the effect of different dielectric environments. In the study described here, such implicit solvent simulations were applied to explore the conformational sampling of three small peptides (alanine dipeptide, poly-alanine, and bee venom melittin) as a function of the dielectric environment.
Blocked alanine dipeptide serves as the prototypical model of peptide backbone thermodynamics and kinetics. Alanine dipeptide has been studied extensively, especially with theoretical methods (36,56–62). The potential of mean force (PMF) as a function of the two main degrees of freedom, the peptide torsion angles φ and ψ, is well established in vacuum and aqueous solvent (57,60–64). Although there are variations depending on the theoretical model that is applied, the general consensus is that alanine dipeptide in aqueous solvent has dominant minima at torsion angles corresponding to α-helical and extended C5/poly-proline II(PPII) conformations. Additional important local minima are located at the αL and C7ax conformations. In vacuum, the dominant minima shift to the extended C5 and C7eq conformations (64,66,67). In aqueous solution, a debate remains as to whether the global minimum in alanine dipeptide is located at the poly-proline II conformation (68–70). However, the conformational preference of alanine dipeptide at intermediate dielectric constants is not well characterized. In particular, it is unclear at which dielectric constant α-helical conformations become destabilized relative to extended conformations.
In poly-alanine, the conformational preference of the peptide backbone from alanine dipeptide is combined with the ability to form backbone C=O/N-H hydrogen bonds and consequently secondary structure elements. There is a long history of experimental and computational studies of poly-alanine (46,71–78). Results from these studies have established strong helical propensity upon addition of low-dielectric solvents such as TFE (79) and methane (80). In aqueous solvent the helical propensity of short poly-alanine peptides is reduced (75,77,81), but the exact amount of helicity depends on the peptide length, whereas results from previous studies also vary as a function of the force field in theoretical studies (46,73,82), experimental peptide capping (83), and the interpretation of experimental data (84).
Melittin from bee venom is a 26-residue amphiphilic peptide with the sequence GIGAVLKVLTTGLPALISWIKRKRQQ that is known to be very sensitive to the environment (85). Melittin forms a slightly bent helix when associated with phospholipid membranes (86–90), but retains a high fraction of helical conformations in aqueous solvent only when it aggregates to a tetramer under conditions of high salt concentration and high pH (91,92) or in the presence of dielectric-lowering cosolvents such as TFE, HFIP, HFA, methanol, or ethanol (37). In aqueous solution with low pH, melittin is monomeric and lacks helical structure due to the highly charged KRKR segment at the C-terminal (93). NMR structures determined in 35% v/v HFIP (94), in 50% v/v hexafluoroacetone (95), in methanolic solution (96), and in perdeuterated dodecylphosphocholine micelles (97) have found helical structures even at low pH. Melittin has also been studied through computer simulations with different explicit solvents (34,35,89,98,99). The results are generally consistent with the experimental findings and suggest increased helicity in lower dielectric media. In aqueous solution, melittin has been reported to be partially helical (35,99), or β-hairpin like (98) depending on the force field that was used. Furthermore, partially helical, V-shaped conformations were observed in moderately polar HFIP/water mixtures (98).
Extensive simulations of alanine dipeptide, poly-alanine, and melittin in different continuum dielectric environments are presented here. They generally confirm the findings from experiment and theory. However, rather than being simply confirmatory, these results suggest that the variation in conformational sampling in different solvent environments is in fact primarily due to the dielectric properties of the surrounding medium rather than specific molecular interactions. Furthermore, significant changes in conformational sampling are observed when the dielectric environments changes only by a relatively modest amount from dilute aqueous solution. It is possible that similar changes in conformational preferences also occur in dense cellular environments. The results are described and discussed in more detail in the following sections.
Methods
Molecular dynamics (MD) simulations of three small peptides: blocked alanine dipeptide, poly-alanine (A15), and melittin from bee venom were performed. To describe the effect of solvent dielectric constant on structure and dynamics of the three peptides, an implicit solvent representation was used. In this model, the solvation free energy of a given solute is decomposed into electrostatic contributions from a dielectric continuum model and nonpolar contributions ():
| (1) |
The electrostatic solvation free energy was obtained according to the generalized-Born (GB) formalism (100):
| (2) |
where is the solute cavity dielectric constant, is the solvent dielectric constant, is the atomic charge of the ith atom in electron units, is the interatomic distance between the ith and the jth atoms in Ångstroms, is the so-called effective Born radius of the ith atom in Ångstroms, and F is a dimensionless empirical parameter set to 8 in this study. The GBMV variant (101,102) was used to calculate the Born radii to obtain accurate solvation energies in close agreement with direct solutions of the Poisson equation (103).
A recent extension to the GBMV method was applied that allows reproduction of solvation energies from Poisson theory for different dielectric environments (54). This is achieved by calculating the effective Born radius as a function of the solvent dielectric constant according to the expression:
| (3) |
where C0, C1, D, and E are dimensionless free parameters, and
| (4) |
| (5) |
The integration is performed over the interior space of the solute except for the spherical region of a radius Ri centered at the ith atom (Ri is the van der Waals radius of the ith atom).
In all of the simulations, the dielectric constant was set to a value of 1 inside the solute cavity and to values ranging between 2 and 80 for the surrounding medium. All GBMV parameters were set as described in the original GBMV references (101,102) except for and , which were changed to improve the numerical stability of the simulations (104). The GBMV method also provides an estimate of the solvent-accessible surface area that was used to calculate the nonpolar solvation free energy according to the standard solvent-accessible surface area model (105). In all cases, the same value of 5.42 cal/(mol Å2) was used as the surface tension parameter (γ) to focus this study on a comparison of different dielectric environments.
Standard molecular dynamics simulations at 300 K were carried out for alanine dipeptide, whereas the replica exchange method (106,107) was used to enhance conformational sampling of poly-alanine and melittin. All simulations were carried out with CHARMM (108), version c32a2 for alanine dipeptide and melittin and version c33a2 for poly-alanine. The Multiscale Modeling Tools for Structural Biology (MMTSB) tool set (109) was used to facilitate the replica exchange molecular dynamics (REX-MD) simulations in conjunction with the CHARMM program and to analyze the simulation results. VMD was used to generate molecular graphics (110).
The CHARMM22 all-atom force-field parameters (111) were employed in combination with the CMAP φ/ψ torsion potential correction (64,112,113). Based on a recent comparison between implicit and explicit solvent sampling of the Ramachandran map, a slightly modified CMAP potential was used to better match the explicit solvent results at ɛ = 80 (61). Because the peptide systems are small, no cutoff was applied for calculating nonbonded interaction energies. An integration time step of 1 fs was used for the alanine dipeptide simulations and a time step of 1.5 fs was used for the simulations of poly-alanine and melittin. The SHAKE algorithm (114) was applied to constrain bonds involving hydrogen atoms. The temperature of the system was controlled by using Langevin dynamics (115). For simulations of alanine dipeptide and poly-alanine, a friction coefficient of 5 ps−1 for all nonhydrogen atoms was used except for backbone oxygen and nitrogen atoms where friction coefficients were set to 20 and 10 ps−1, respectively, according to previous tests (61). For melittin, a uniform friction coefficient of 10 ps−1 was used for all nonhydrogen atoms.
Alanine dipeptide was acetylated at the N-terminal and blocked with N-methylamide at the C-terminal. Initial peptide torsion angles were set to values of and in the α-basin. MD simulations were equilibrated for 2 ns and then continued to a total length of 500 ns : ɛ = 2, ɛ = 5,ɛ = 10, ɛ = 20, and ɛ = 80.
Poly-alanine, which was also acetylated at N-terminal and blocked with N-methylamide at the C-terminal, was folded from a fully extended conformation with the replica exchange algorithm. Eight temperatures spaced exponentially between 300 and 500 K were used. Each replica exchange cycle consisted of 500 steps (0.75 ps) of molecular dynamics simulation. A total of 59,000 cycles (44 ns) were completed, of which the last 22.5 ns were used for analysis to allow sufficient time to establish an ensemble of folded conformations. Poly-alanine was simulated with solvent dielectric constants of ɛ = 5,ɛ = 20, and ɛ = 80.
Monomeric melittin from bee venom was simulated starting from the crystallographic structure (Protein Data Bank (PDB) code 2MLT (92)) with an acetylated N-terminus and methylated C-terminus. The replica exchange algorithm was used with eight temperatures spaced exponentially between 300 and 400 K. A total of 110,000 cycles (82.5 ns) each with 500 molecular dynamics steps were carried out for each for solvent dielectric constants of ɛ = 5,ɛ = 20, ɛ = 40, and ɛ = 80. The last 60,000 cycles (from 37.5 to 82.5 ns) were used for analysis to allow for sufficient equilibration. As part of the analysis, conformations of melittin were clustered based on mutual similarity with the K-means method implemented in the MMTSB Tool Set (109) with a clustering radii of 3 and 4 Å.
PMFs were calculated from the replica exchange simulations with weighted histogram analysis (116,117) to take advantage of the conformational sampling at higher temperatures. The percentage of successful replica swaps between adjacent temperatures was 35–40% in the poly-alanine simulations and 40–45% in the melittin simulations indicating significant overlap only between adjacent temperatures. As a consequence, the weighted histogram analysis of the melittin simulations carried out at 300 K effectively only includes sampling from replicas at 300 and 313 K.
The analysis of poly-alanine includes a calculation of helicity as a function of residue number. An O(i) − H-N(i + 4) distance of <2.6 Å was used as the criterion to determine the presence of a helical residue following previous work (118). In the analysis of melittin, a bending angle between the N- and C-terminal helices was calculated as the angle between the average O(i) − H-N(i + 4) vectors for residues 2–5 and residues 16–20.
Results
Alanine dipeptide
Molecular dynamics simulations of alanine dipeptide (Fig. 1 A) were carried out over 500 ns in implicit solvent with different dielectric constants. PMF at 300 K calculated as a function of peptide backbone angles φ (C-N-Cα-C) and ψ (N-Cα-C-N) are shown in Fig. 2. Fig. 2 also includes an adiabatic map in vacuum for comparison that was obtained from the implicit solvent energies after minimizing the molecular geometries while restraining φ and ψ angles to grid points across the entire map. At a dielectric constant of 80 (Fig. 2 A), the energy surface shows the familiar features of the Ramachandran map with minima at the right-handed α-helix conformations (αR/α′), the extended β-forms (C5 and PPII), the seven-atom ring form C7ax, and the left-handed α-helix αL in agreement with previous theoretical studies (56–61). At ɛ = 80, the αR and PPII conformations have the lowest energies and are essentially equienergetic. These results reflect recent modifications of the CHARMM force field to match high-level ab initio data as well as the distribution of φ/ψ torsions from the PDB (64,113,119).
Figure 1.
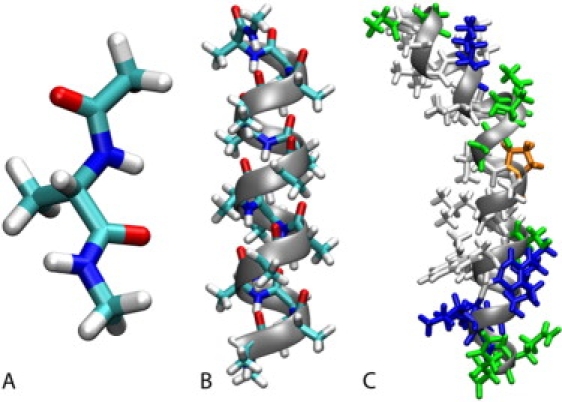
Structures of simulated systems in this study: blocked alanine dipeptide (A), poly-alanine A15 (B), bee venom melittin from PDB 2MLT with hydrophobic residues in white, polar residues in green, basic residues in blue, and proline in orange (C). Graphics were generated with VMD. (110)
Figure 2.
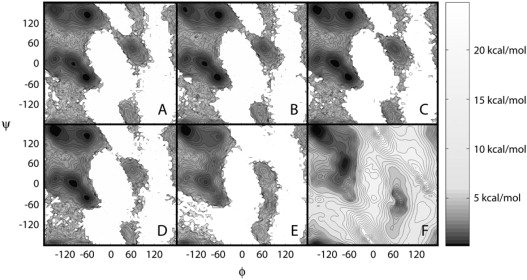
Potential of mean force (ΔG) as a function of φ/ψ dihedral angles in alanine dipeptide from implicit solvent simulations with different dielectric environments: ɛ = 80 (A), ɛ = 20 (B), ɛ = 10 (C), ɛ = 5 (D), ɛ = 2 (E). The adiabatic map of alanine dipeptide in vacuum (ɛ = 1) is shown for comparison (F). Contour levels are in increments of 0.25 kcal/mol up to 5 kcal/mol and in 1 kcal/mol increments thereafter. Additional color shading as a function of energy follows the scale indicated on the color bar.
When the dielectric constant of the environment is reduced, the relative conformational preferences shift from PPII to fully extended C5 conformations, from αR to α′ and also from the α-basin to the β-basin. These effects are subtle for intermediate dielectric constants but dominate at ɛ = 2, where only a single global minimum is located at fully extended conformations. In vacuum (ɛ = 1), the global minimum remains at extended conformations, whereas a second minimum appears at C7eq. Previous studies have reported the global minimum of alanine dipeptide at C7eq, but the relative stability of extended β-conformations compared to C7eq is sensitive to the level of theory in ab initio calculations. In high-level LMP2/cc-pVQZ calculations, C5 and C7eq were found to have comparable stability, although the minimum at C7eq is still lower in energy (119). To balance gas phase energetics with condensed phase properties in a fixed charge model, the entire β-region was lowered further relative to the α-region to match PDB distributions of φ/ψ angles and reproduce equilibrium structures of protein test systems in the final version of the CMAP version of the CHARMM force field (119). As a result, fully extended conformations are slightly lower than C7eq in vacuum. Significant changes are also observed on the right-hand side of the Ramachandran map (αL, C7ax) as a function of the dielectric environment. The relative stability of the αL basin decreases at ɛ = 5 and below. At the same time, a new minimum appears around φ = 80, ψ = −60 at the transition state between αL and C7ax.
To further quantify the results, the relative free energies of selected minima with respect to the αR conformation are tabulated in Table 1. The data show that at the initially slight preference for α-conformations shifts to the C5/PII minimum, whereas the C7eq and αL-C7ax transition states are reduced significantly at .
Table 1.
Relative free energies of selected alanine dipeptide conformation in different dielectric environments from potentials of mean force (ɛ > 1) and adiabatic map (ɛ = 1)
| φ | ψ | ɛ = 80 | ɛ = 20 | ɛ = 10 | ɛ = 5 | ɛ = 2 | ɛ = 1 | |
|---|---|---|---|---|---|---|---|---|
| αR | −65 | −40 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| α′ | −100 | 0 | 0.43 | 0.36 | 0.24 | 0.07 | −0.47 | −1.31 |
| C7eq | −75 | 75 | 3.50 | 3.19 | 2.77 | 2.20 | 0.28 | −2.73 |
| PPII | −60 | 145 | 0.18 | 0.11 | 0.09 | 0.05 | −0.26 | −1.08 |
| C5 | −155 | 160 | 0.61 | 0.42 | 0.17 | −0.20 | −1.51 | −3.52 |
| αL | 60 | 50 | 1.40 | 1.36 | 1.34 | 1.98 | 1.83 | 2.26 |
| αL-C7ax | 80 | −60 | 4.83 | 5.00 | 4.63 | 4.30S | 1.51 | −1.08 |
| C7ax | 50 | −150 | 2.92 | 2.66 | 2.53 | 3.07 | 2.29 | 1.75 |
All values are given in kcal/mol.
The long timescale of the simulations also allows the analysis of kinetic rates for conformational transitions between the selected basins. The corresponding results are given in Table 2. They indicate that the kinetic rates of transitions between the α and β (C5/PPII) basins are significantly accelerated as the dielectric constant is decreased from ɛ = 80. This is a direct consequence of the lowered relative free energy of the C7eq transition state. In contrast, the kinetic rates for transitions between the β and αL basins are reduced in less polar environments. Only few transitions between and with are observed at ɛ = 5 and below.
Table 2.
Kinetic rates from implicit solvent simulations of alanine dipeptide between selected conformational basins
| ɛ = 80 | ɛ = 20 | ɛ = 10 | ɛ = 5 | ɛ = 2 | |
|---|---|---|---|---|---|
| α → β | 3.87 (881) | 5.01 (1043) | 6.36 (1280) | 11.12 (2035) | 84.42 (8581) |
| β → α | 4.01 (883) | 4.25 (1039) | 4.99 (1275) | 7.21 (2038) | 24.07 (8581) |
| β → αL | 0.24 (52) | 0.20 (49) | 0.14 (36) | 0.03 (8) | 0.00 (1) |
| αL → β | 4.21 (52) | 3.86 (46) | 3.05 (34) | 3.21 (10) | 0.53 (1) |
All values are given in ns−1. Number of observed transitions are given in parentheses.
Although the changes in thermodynamic and kinetic properties in reduced dielectric environments can be translated into modified secondary structure propensities and altered backbone flexibility at the level of proteins, large changes are not observed unless the dielectric constant is reduced to ɛ = 5 or below.
Poly-alanine
The study of alanine dipeptide only considers the backbone propensities at the level of a single pair of peptide groups. It neglects the significant energetic contributions from hydrogen bonding that vary to a great extent as a function of the dielectric environment due to electrostatic screening effects. To examine the change in conformational preferences in a longer peptide that can form hydrogen bonds, folding simulations of poly-alanine (A15; Fig. 1 B) were carried out in different dielectric environments. As would be expected from a strong helix-promoting amino acid, only helical or largely disordered conformations were observed. The results in Fig. 3 show a preponderance of helical conformations at 300 K, the lowest temperature of the replica exchange simulations, but also the expected increased stability of helical conformations in lower dielectric environments. The average helicity is found to be 91.6% at ɛ = 80 92.4% at ɛ = 20 and 95.0% at ɛ = 5 As temperature increases, helical conformations are lost above ∼360 K with ɛ = 80 and above 380 K with ɛ = 20 whereas the helical form persists until close to 500 K with ɛ = 5. The statistical significance of these results was tested by examining block averages over three intervals between 10.5 and 44 ns. The results in Supplementary Table S1 show that convergence is clearly not achieved after 22 ns, but the variations are generally small between the third and fourth intervals. Hence, the interval from 22 to 44 ns was used for the above analysis. The remaining fluctuations in helicity between the second and third interval may be used to estimate errors in the average values over the entire 22- to 44-ns segment.
Figure 3.
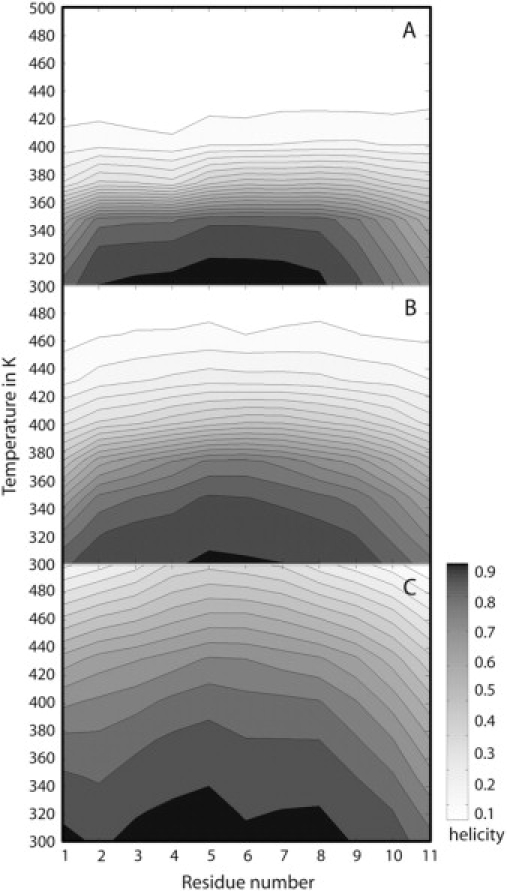
Per-residue helical propensity as a function of temperature for poly-alanine (A15) from replica exchange implicit solvent simulations with different dielectric environments: ɛ = 80 (A), ɛ = 20 (B), ɛ = 5 (C). The presence of helical structure is determined as a distance of <2.6 Å between backbone O (i) and N-H (i + 4) atoms.
Melittin
Bee venom melittin (Fig. 1 C) was simulated in different dielectric environments to examine how conformational sampling of a peptide with a more diverse amino acid sequence is affected by a change in environment. Results obtained from the last 45 ns of the replica exchange simulations are given in Figs. 4 and 5 as well as Table 3. Conformations of melittin are conveniently analyzed in terms of their radius of gyration and the bending angle between the N- and C-terminal helical sections. Fig. 4 shows the two-dimensional PMF maps at 300 K as a function of these two reaction coordinates. Each PMF map is augmented with a plot of the dominant conformational clusters obtained according to mutual structural similarity between structures extracted from the replicas at 300 K with a maximum clustering radius of 3 Å. Corresponding representative conformations from the dominant clusters are shown in Fig. 5.
Figure 4.
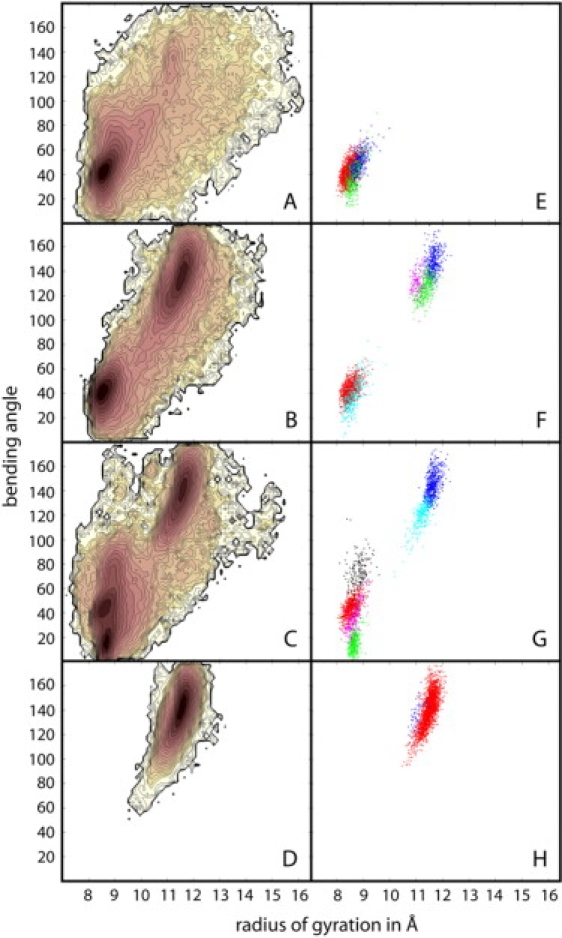
Conformational sampling of bee venom melittin in different dielectric environments with ɛ = 80 (A and E), ɛ = 40 (B and F), ɛ = 20 (C and G), and ɛ = 5 (D and H) from replica exchange simulations. Left side panels (A–D) show potentials of mean force (ΔG) at 300 K from WHAM analysis as a function of radius of gyration and helical bending angle. Contour levels are at 0.25 kcal/mol increments from 0 to 5 kcal/mol and in 1 kcal/mol increments from 5 to 10 kcal/mol. Color shading is similar to Fig. 2. Right side panels (E–H) indicate largest clusters based on mutual structural similarity that are populated at least 5% of the time. Color coding corresponds to relative cluster size in the following order: red > blue > green > cyan > magenta > black.
Figure 5.

Representative conformations of bee venom melittin from the most populated clusters shown in Fig. 4 in different dielectric environments with ɛ = 80 (A), ɛ = 40 (B), ɛ = 20 (C), and ɛ = 5 (D). Numbers indicate major conformational families. Hydrophobic residues are shown in white, polar residues in green, and basic residues in blue. All structures are aligned at the C-terminal helix. Graphics were generated with VMD (110).
Table 3.
Percentage of dominant conformations of bee venom melittin (see Fig. 5) sampled in different dielectric environments at 300 K during the last 45 ns of the respective replica exchange simulations
| Conformation | ɛ = 80 | ɛ = 40 | ɛ = 20 | ɛ = 5 |
|---|---|---|---|---|
| 1 | 0.0 (0.0) | 33.5 (6.8) | 36.7 (5.7) | 97.4 (2.1) |
| 2 | 1.8 (1.8) | 10.3 (6.8) | 0.0 (0.0) | 2.6 (2.1) |
| 3 | 80.9 (4.3) | 42.5 (13.9) | 30.6 (1.9) | 0.0 (0.0) |
| 4 | 10.8 (1.7) | 13.2 (1.1) | 24.5 (7.4) | 0.0 (0.0) |
| 5 | 3.2 (2.1) | 0.0 (0.0) | 8.0 (0.2) | 0.0 (0.0) |
Errors of the averages given in parentheses are estimated according to from ±SD σ of N = 3 block averages (see Supplementary Table S2).
At ɛ = 5, conformations of melittin are mainly α-helical with large bending angles between 120 and 160°. Most of structures are found in a single cluster with a slightly kinked long helix that is highly reminiscent of previously observed conformations of melittin when associated with phospholipid bilayers (89,99) and when forming tetramers in aqueous solvent (92). This conformation is similar to the x-ray structure of the tetrameric form (with a bending angle of 120°) in aqueous solution with pH = 5.0 (92), to the NMR structure in perdeuterated dodecylphosphocholine micelles (with a bending angle of 120°–160°) (97), and to conformations from simulations in an explicit DPPC bilayer (99) (bending angle 180°) and in an implicit membrane environment (90) (bending angle near 155°). An alternate minor conformation identified by the cluster analysis is also largely extended but has a more pronounced kink at the central P14 residue.
In contrast, with a high dielectric environment, ɛ = 80, melittin predominantly samples mostly compact conformations. The dominant minimum has a bending angle of around 40°, which actually corresponds to three slightly different V-shaped conformations according to the cluster analysis. Similar conformations have been reported previously from explicit water simulations of melittin (99) and in HFIP/water solvent (98). The compact structures found at the higher dielectric environment also match NMR data of melittin in 35% v/v HFIP (dielectric constant ɛ = 57(38)), consistent with two helical segments bent by an angle of 73 ± 15° (94). As shown in Fig. 6, the compact conformations involve formation of a hydrophobic core at the expense of backbone hydrogen bonding that is lost at the turn when compared to a fully extended structure. Based on the structures from the simulation, the W19 residue (shown in orange) is predicted to play a central role in stabilizing this particular conformation. This matches experimental results where mutations of W19 have resulted in lower helical populations in aqueous solvent (120,121). Extended conformations are also sampled at ɛ = 80, but with lower probability. In addition, there is broad conformational sampling of a variety of different conformations including partially unfolded conformations with large radii of gyration.
Figure 6.
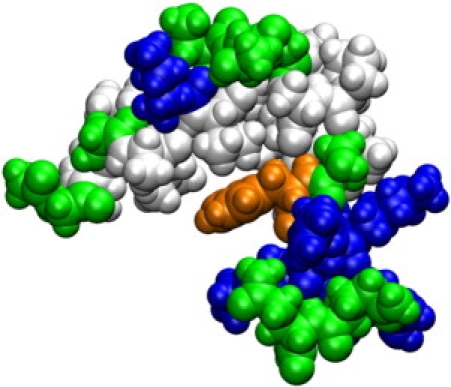
Dominant conformation of bee venom melittin at ɛ = 80 highlighting the formation of a hydrophobic core. Residues are colored according to type as in Fig. 5. Trp-19 is shown in orange. Graphics were generated with VMD (110).
At intermediate dielectric constants of ɛ = 20 and ɛ = 40 (Fig. 4, B and C), compact and extended conformations appear to be in equilibrium. However, at ɛ = 20 a third minimum appears with a very small bending angle of 20° that leads to a nearly parallel helix arrangement. Furthermore, conformational sampling of extended conformations with ɛ = 40 includes the minor conformation also seen at ɛ = 5, but that structure is essentially missing at ɛ = 20. The differences in conformational sampling between ɛ = 40 and ɛ = 80 and between ɛ = 40 and ɛ = 20 are remarkable and indicate that even modest changes in the dielectric environment can have significant consequences.
To better compare the conformational sampling of melittin at different dielectric constants, conformations from all values of ɛ were clustered together with a clustering radius of 4 Å. The resulting five major families are indicated in Fig. 5. Conformation No. 1 is the nearly fully extended conformation, No. 2 is extended but with a more pronounced kink, No. 3 is a compact V-shape structure, No. 4 is bent further with nearly parallel helices, and in conformation No. 5 the two helices lie in orthogonal planes with an angle of 90°. Table 3 shows how each of these conformations are sampled at different dielectric environments. To estimate sampling convergence and reliability of the reported percentages, a block average analysis was carried out. Block averages of the cluster population percentages were calculated for three time intervals during the last 45 ns of the replica exchange runs. The individual results given in Supplementary Table S2 indicate substantial variations in some cases. From the standard deviations, it is possible to calculate error estimates for the overall averages as reported in Table 3. The data clearly shows that the two major conformations Nos. 1/3 decrease/increase with increasing dielectric constant. However, the other three conformations vary with the dielectric constant in a less predictable fashion. Conformation No. 4 appears to become increasing stable with decreasing dielectric constant but disappears abruptly at ɛ = 5. Conformation No. 5 appears to be preferred at ɛ = 20, but is also observed with ɛ = 80. Conformation No. 2 is populated most significantly at ɛ = 40, but the statistical error is large indicating that its population could in fact be more similar to the other dielectric values with more extensive sampling.
Discussion
Extensive simulations of three peptides with continuum dielectric environments using different dielectric constants are presented in this study. As a whole, these simulations show significant changes in the conformational sampling of peptides between high (ɛ = 80), intermediate (ɛ = 10–40), and low dielectric (ɛ = 2–5) environments. The main findings are a shift to extended conformations and reduction of kinetic barriers at the level of a single dipeptide and an increased propensity to form backbone hydrogen bonds at lower dielectric environments that lead to increased helicity in poly-alanine and the preference of straight conformations versus compact, highly bent conformations in melittin. By essentially confirming previous studies of peptides in different explicit solvent environments, these results suggest that the dominant effect determining peptide stability in different environments does in fact stem from the degree of polarizability in the surroundings rather than specific molecular interactions. Molecular details remain relevant, however, in determining the effective dielectric constant of a given environment.
The focus on dielectric properties offers the advantage of conceptual simplicity but neglects other important physicochemical effects. The nonpolar contribution to the solvation free energy captures van der Waals interactions and the cost of cavity formation. A solvent-accessible surface-area-dependent nonpolar solvation energy term was included in these calculations but not adjusted as a function of dielectric constant to emphasize the electrostatic effect of a change in solvent polarizability. A less polar environment with a lower dielectric constant would be expected to incur a lower energetic penalty for forming solute cavities. However, dense cellular environments may have the opposite effect of disfavoring larger molecular cavities through macromolecular crowding.
The view followed here essentially emphasizes the change in enthalpic interactions with a crowded cellular environment. This is in contrast to past analyses of molecular crowding that have focused on the essentially entropic effect of reducing the number of accessible conformations for a given molecule through steric hindrance and confinement in the presence of nearby macromolecules (20,122,123). However, a full account of cellular crowding ultimately needs to incorporate both aspects. The dielectric treatment of cellular environments presented here could be extended easily to include the repulsive effect of steric hindrance through a standard cost-of-cavity nonpolar term proportional to the solvent-accessible surface area of a given molecule (105). The best choice for the proportionality constant is not immediately clear, but could be determined from test simulations of peptides and proteins in confined environments or environments with explicit spherical crowding agents as proposed in previous studies (122–124). This approach would assume that molecular crowding is isotropic in nature, however, anisotropic environments could in principle be accommodated as well.
The implicit description of the environment also may neglect specific interactions of the studied peptides with the solvent environment. In particular, the structuring of water due to molecular crowding may not be reflected fully with an implicit model. However, previous simulations of proteins and nucleic acids with implicit solvent have been found to be in excellent agreement with explicit solvent simulations despite the lack of specific solvent interactions (61,125). This is especially remarkable in the case of nucleic acids that are well known to interact with solvent in a highly specific manner (126), suggesting that specific solvent interactions are captured at least in part through local solvent polarization in the mean-field model. It is therefore likely that the additional effects of water structuring, apart from lowering the environmental dielectric constant, are not neglected to a significant extent compared to a fully explicit treatment.
The presented results invariably depend on the underlying force field and its limitations. Solvent polarizability is implicitly taken into account, but the lack of polarizability in the peptide force field that was used may not fully reflect the energetic implications in response to a change from a polar to a hydrophobic environment. Overall, the results are within the range of previous studies, but it may appear that helical structures are slightly too favorable compared to experimental data, although further experimental and computational studies are needed to more clearly address this issue. Possible causes include the underlying φ/ψ torsion potential and the previously reported tendency of generalized Born methods to possibly overstabilize salt-bridge formation (127). An overstabilization of strong electrostatic interactions would favor helix formation to maximize the number of hydrogen bonds. However, because of overall good agreement of the presented data with other experimental and computational studies, any such limitations do not appear to significantly affect the qualitative and semiquantitative predictions made here.
Since all amino acids except glycine and proline exhibit similar angle maps (128), the results for alanine dipeptide are key in understanding peptide backbone propensities as a function of the dielectric environment. Based on results from this study, a preference for extended conformations versus α-helical conformations is present at dielectric constants below ɛ = 5. α-Helical backbone conformations are stabilized in solution by the interaction of a relatively large dipole moment with the polar solvent (66). The destabilization of α-helical backbone conformations in low-dielectric environments can be understood based on increased electrostatic repulsion of the carbonyl oxygen atoms and amide hydrogen atoms due to decreased screening. The fully extended C5 conformation avoids such repulsion and offers an electrostatically favorable C=O/N-H interaction between neighboring peptide groups. Furthermore, the extended conformation is entropically more favorable (66). At very low dielectric constants (ɛ = 1–2), the C7eq conformation begins to dominate where an intramolecular hydrogen bond is essentially formed between C=O and N-H of adjacent peptide groups. At the same time, the other C=O/N-H pair is at larger distance but also contributes favorably to the electrostatic energy. Because C7eq is at the transition point between α- and β-conformations, the change in relative stabilities increases kinetic rates of α/β interconversions at lower dielectric constants. Although the changed conformational preferences in alanine dipeptide in low dielectric environments are expected to have implications for secondary structure formation in proteins, we generally do not see a strong effect until the dielectric constant is lowered below ɛ = 10. Such environments may be encountered in the interior of proteins or in biological membranes, but dense cellular environments may not be sufficient to strongly shift the conformational preferences according to our data.
The introduction of the possibility of longer-range intramolecular hydrogen bonds changes the preferences in peptide conformations as a function of the solvent dielectric constant. Poly-alanine is predominantly α-helical at the low dielectric constant and becomes less structured as the solvent dielectric constant increases due to increased competition between intramolecular hydrogen bonding and interactions with the polar solvent. At the same time, nonhelical structures partially reduce the exposure of the hydrophobic methyl groups of alanine to polar solvent. Reports of the helicity of poly-alanine in aqueous solution vary widely between 10 and 80% (46,73,75,77,81,82,129,130). Although our study with A15 clearly shows the destabilization of helical conformations in high-dielectric versus low-dielectric environments, our estimate of 84% for A15 at 300 K is at the high end of previous estimates. However, similar amounts of helicity were found experimentally for only slightly longer A22 peptides (81). Interestingly, a change from ɛ = 80 to ɛ = 20 increases helicity at the termini but does not appear to affect thermal stability to a significant extent. In contrast, a change from ɛ = 20 to ɛ = 5 dramatically increases stability to the extent that partial helical structures are still present at the highest temperature, 500 K, of the replica exchange simulation. Because the force-field parameters and implicit solvent model have limited applicability at such high temperatures, the actual folding temperature cannot be reliably estimated. Nevertheless, the trends described here are expected to remain valid. Our results qualitatively agree with increased stability of helical poly-alanine in less polar solvents such as TFE/water mixtures (79), confirming that helix destabilization in water can be understood primarily as a dielectric effect.
The most interesting case studied here is melittin. It was found that even relatively modest changes in the dielectric constant can significantly shift conformational preferences. Melittin has been reported to be in random coil form except for residues 5–9 and 14–20 in aqueous solution with a low pH near 4.0, although the labile proton exchange measurements cannot easily distinguish between mostly disordered conformations and rapid exchange between multiple ordered conformations (93,131). Furthermore, the addition of salt or phosphates, slightly increased temperature, and increased pH are known to shift the equilibrium to a tetrameric form of helical melittin (131). Increased pH is assumed to neutralize the N-terminus and K23 thereby reducing charge repulsion (131). The simulations presented here were carried out with an acetylated, neutral N-terminus. Consequently, it may be expected to find a larger degree of helicity at ɛ = 80 than for the zwitterionic form. The analysis of sampled conformations at ɛ = 80 suggests large conformational variability including many different partially helical, extended, and disordered structures. However, the helical V-shaped structure shown in Fig. 6 represents the dominant conformer with a break in helicity around residue 14. Because only a single copy of melittin was simulated, tetrameric aggregation as in the experiments could not be observed. Burial of hydrophobic residues is a central feature of the tetrameric form of melittin (92) and also appears to play a role in the stability of the V-shaped structure that was observed here. Compact, mostly helical structures of melittin similar to the V-shaped structure found here were also identified in recent explicit water simulations along with significant structural fluctuations over the course of a 30-ns trajectory (99). These simulations are in contrast to another recent simulation study of melittin that reported a nearly complete loss of helicity in aqueous solvent with a significant fraction of β-sheet formation (98). However, the findings of the latter simulations may be explained by the use of the GROMOS96 force field (132), which is known to favor β-sheets over α-helices compared to other force fields (133). In low-dielectric environments, melittin is predominantly helical with large bending angles. NMR structures of melittin obtained in micelles (97) or explicit simulations in lipid bilayers (89,99) show similar structures despite the more heterogeneous character of biological membranes. Furthermore, NMR structures in 50% v/v HFA (39) or methanolic solution (96) and studies of melittin in other alcohols (37,38) also find helices with larger bending angles. Based on the data presented here, all of these experiments can be interpreted in terms of the low-dielectric constants in such environments.
At intermediate dielectric constants of ɛ = 20 and ɛ = 4 the PMFs in Fig. 4 show an equilibrium between extended and compact helical structures. This can be compared with the NMR structure of melittin in 35% v/v HFIP (94) with a dielectric constant of 57 (38), which indicates two helical segments with a bending angle of 73 ± 15° and significant flexibility. The average conformational sampling at ɛ = 40 closely matches the NMR data, although our simulations suggest the presence of two major conformations with bending angles smaller and larger than 73° rather than a single, flexible conformation.
In mixtures of less polar cosolvent and water, the cosolvent may preferentially associate with a given peptide. An example is the preferential solvation by alcohol seen in NMR experiments (94) and explicit simulation studies (98). Although molecular details are neglected in the continuum dielectric approach followed here, the preferential solvation of lower dielectric cosolvents effectively reduces the dielectric constant even further from the value for bulk mixtures with water. This effect might explain the similarity of the NMR results for melittin in 35% v/v HFIP to our simulation results at a lower dielectric constant than bulk HFIP/water solutions.
The data presented here offer new insights into how different dielectric environments affect the conformational sampling of peptides. In particular, extended conformations are favored over α-helical conformations at the dipeptide level at and below dielectric constants of 5–10. Furthermore, lower-dielectric environments begin to significantly stabilize helical structures at ɛ = 20 and below as observed in poly-alanine. In more complex peptides such as melittin, different dielectric environments may result in altered conformational preferences with some conformations only populated to a significant extent at intermediate dielectric constants.
The results are generally in good agreement with previous studies of different peptides in less-polar solvent environments. This suggests that helix stabilization and shifts in conformational preferences in such environments are primarily due to a reduced dielectric environment rather than specific molecular details. Molecular details appear to be crucial only insofar as they determine the effective solvent polarizability near the peptide. The findings presented here are expected to be relevant for dense cellular environments, where the effective dielectric constant may be significantly reduced from dilute aqueous solvent. However, further studies are clearly needed to examine the effect of complex cellular environments on the sampling and dynamics of biomolecules in a more complete manner.
Supplementary material
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Appendix A.
Supplement
Acknowledgments
Calculations were carried out in part at the Michigan State University High Performance Computing Center.
We acknowledge financial support from National Science Foundation CAREER grant 0447799, the Alfred P. Sloan Foundation, and a Strategic Partnership Grant from Michigan State University.
Footnotes
Editor: Gregory A. Voth.
References
- 1.Alberts B., Johnson A., Lewis J., Raff M., Roberts K., Walter P. Garland Science; New York: 2002. Molecular Biology of the Cell. [Google Scholar]
- 2.Zimmerman S.B., Minton A.P. Macromolecular crowding—biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 3.Fulton A.B. How crowded is the cytoplasm. Cell. 1982;30:345–347. doi: 10.1016/0092-8674(82)90231-8. [DOI] [PubMed] [Google Scholar]
- 4.Ladbury J.E., Williams M.A. The extended interface: measuring non-local effects in biomolecular interactions. Curr. Opin. Struct. Biol. 2004;14:562–569. doi: 10.1016/j.sbi.2004.08.001. [DOI] [PubMed] [Google Scholar]
- 5.Onuchic J.N., Wolynes P.G. Theory of protein folding. Curr. Opin. Struct. Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 6.Dill K.A. Theory for the folding and stability of globular proteins. Biochemistry. 1985;24:1501–1509. doi: 10.1021/bi00327a032. [DOI] [PubMed] [Google Scholar]
- 7.Drew H.R., Dickerson R.E. Structure of a B-DNA dodecamer. III. Geometry of hydration. J. Mol. Biol. 1981;151:535–556. doi: 10.1016/0022-2836(81)90009-7. [DOI] [PubMed] [Google Scholar]
- 8.Makarov V., Pettitt B.M., Feig M. Solvation and hydration of proteins and nucleic acids: a theoretical view of simulation and experiment. Acc. Chem. Res. 2002;35:376–384. doi: 10.1021/ar0100273. [DOI] [PubMed] [Google Scholar]
- 9.Rosgen J., Pettitt B.M., Bolen D.W. Protein folding, stability, and solvation structure in osmolyte solutions. Biophys. J. 2005;89:2988–2997. doi: 10.1529/biophysj.105.067330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Street T.O., Bolen D.W., Rose G.D. A molecular mechanism for osmolyte-induced protein stability. Proc. Natl. Acad. Sci. USA. 2006;103:13997–14002. doi: 10.1073/pnas.0606236103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yancey P.H., Clark M.E., Hand S.C., Bowlus R.D., Somero G.N. Living with water stress: evolution of osmolyte systems. Science. 1982;217:1214–1222. doi: 10.1126/science.7112124. [DOI] [PubMed] [Google Scholar]
- 12.Hartl F.U., Hayer-Hartl M. Protein folding—molecular chaperones in the cytosol: from nascent chain to folded protein. Science. 2002;295:1852–1858. doi: 10.1126/science.1068408. [DOI] [PubMed] [Google Scholar]
- 13.Takagi F., Koga N., Takada S. How protein thermodynamics and folding mechanisms are altered by the chaperonin cage: molecular simulations. Proc. Natl. Acad. Sci. USA. 2003;100:11367–11372. doi: 10.1073/pnas.1831920100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bishop G.R., Ren J.S., Polander B.C., Jeanfreau B.D., Trent J.O., Chaires J.B. Energetic basis of molecular recognition in a DNA aptamer. Biophys. Chem. 2007;126:165–175. doi: 10.1016/j.bpc.2006.07.009. [DOI] [PubMed] [Google Scholar]
- 15.Carlson H.A. Protein flexibility is an important component of structure-based drug discovery. Curr. Pharm. Des. 2002;8:1571–1578. doi: 10.2174/1381612023394232. [DOI] [PubMed] [Google Scholar]
- 16.Bernado P., e la Torre G., Pons M. Macromolecular crowding in biological systems: hydrodynamics and NMR methods. J. Mol. Recognit. 2004;17:397–407. doi: 10.1002/jmr.694. [DOI] [PubMed] [Google Scholar]
- 17.Ping G., Yuan J.-M., Sun Z., Wei Y. Studies of effects of macromolecular crowding and confinement on protein folding and protein stability. J. Mol. Recognit. 2004;17:433–440. doi: 10.1002/jmr.710. [DOI] [PubMed] [Google Scholar]
- 18.Ellis R.J. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 2001;11:114–119. doi: 10.1016/s0959-440x(00)00172-x. [DOI] [PubMed] [Google Scholar]
- 19.Zhou H.X. Protein folding and binding in confined spaces and in crowded solutions. J. Mol. Recognit. 2004;17:368–375. doi: 10.1002/jmr.711. [DOI] [PubMed] [Google Scholar]
- 20.Minton A.P. How can biochemical reactions within cells differ from those in test tubes? J. Cell Sci. 2006;119:2863–2869. doi: 10.1242/jcs.03063. [DOI] [PubMed] [Google Scholar]
- 21.Friedel M., Sheeler D.J., Shea J.E. Effects of confinement and crowding on the thermodynamics and kinetics of folding of a minimalist β-barrel protein. J. Chem. Phys. 2003;118:8106–8113. [Google Scholar]
- 22.Brinker A., Pfeifer G., Kerner M.J., Naylor D.J., Hartl F.U., Hayer-Hartl M. Dual function of protein confinement in chaperonin-assisted protein folding. Cell. 2001;107:223–233. doi: 10.1016/s0092-8674(01)00517-7. [DOI] [PubMed] [Google Scholar]
- 23.Davis-Searles P.R., Saunders A.J., Erie D.A., Winzor D.J., Pielak G.J. Interpreting the effects of small uncharged solutes on protein-folding equilibria. Annu. Rev. Biophys. Biomol. Struct. 2001;30:271–306. doi: 10.1146/annurev.biophys.30.1.271. [DOI] [PubMed] [Google Scholar]
- 24.Stern H.A., Feller S.E. Calculation of the dielectric permittivity profile for a nonuniform system: application to a lipid bilayer simulation. J. Chem. Phys. 2003;118:3401–3412. [Google Scholar]
- 25.Akhadov Y.Y. Pergamon Press; Oxford, UK: 1981. Dielectric Properties of Binary Solutions. [Google Scholar]
- 26.Gilson M.K., Honig B.H. The dielectric-constant of a folded protein. Biopolymers. 1986;25:2097–2119. doi: 10.1002/bip.360251106. [DOI] [PubMed] [Google Scholar]
- 27.Antosiewicz J., McCammon J.A., Gilson M.K. The determinants of pK(a)s in proteins. Biochemistry. 1996;35:7819–7833. doi: 10.1021/bi9601565. [DOI] [PubMed] [Google Scholar]
- 28.Schutz C.N., Warshel A. What are the dielectric “constants” of proteins and how to validate electrostatic models? Proteins. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
- 29.Despa F., Fernandez A., Berry R.S. Dielectric modulation of biological water. Phys. Rev. Lett. 2004;93:228104. doi: 10.1103/PhysRevLett.93.228104. [DOI] [PubMed] [Google Scholar]
- 30.Elcock A.H., McCammon J.A. The low dielectric interior of proteins is sufficient to cause major structural changes in DNA on association. J. Am. Chem. Soc. 1996;118:3787–3788. [Google Scholar]
- 31.Jaaskelainen S., Verma C.S., Hubbard R.E., Caves L.S.D. Identifying key electrostatic interactions in Rhizomucor miehei lipase: the influence of solvent dielectric. Theor. Chem. Acc. 1999;101:175–179. [Google Scholar]
- 32.Buck M. Trifluoroethanol and colleagues: cosolvents come of age. Recent studies with peptides and proteins. Q. Rev. Biophys. 1998;31:297–355. doi: 10.1017/s003358359800345x. [DOI] [PubMed] [Google Scholar]
- 33.Dwyer D.S. Molecular simulation of the effects of alcohols on peptide structure. Biopolymers. 1999;49:635–645. doi: 10.1002/(SICI)1097-0282(199906)49:7<635::AID-BIP8>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- 34.Roccatano D., Colombo G., Fioroni M., Mark A.E. Mechanism by which 2,2,2-trifluoroethanol/water mixtures stabilize secondary-structure formation in peptides: a molecular dynamics study. Proc. Natl. Acad. Sci. USA. 2002;99:12179–12184. doi: 10.1073/pnas.182199699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Liu H.L., Hsu C.M. The effects of various alcohols on the stability of melittin: a molecular dynamics study. J. Chin. Chem. Soc. 2003;50:1235–1240. [Google Scholar]
- 36.Nguyen H.D., Marchut A.J., Hall C.K. Solvent effects on the conformational transition of a model polyalanine peptide. Protein Sci. 2004;13:2909–2924. doi: 10.1110/ps.04701304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hirota N., Mizuno K., Goto Y. Group additive contributions to the alcohol-induced α-helix formation of melittin: implication for the mechanism of the alcohol effects on proteins. J. Mol. Biol. 1998;275:365–378. doi: 10.1006/jmbi.1997.1468. [DOI] [PubMed] [Google Scholar]
- 38.Hong D., Hoshino M., Kuboi R., Goto Y. Clustering of fluorine-substituted alcohols as a factor responsible for their marked effects on proteins and peptides. J. Am. Chem. Soc. 1999;121:8427–8433. [Google Scholar]
- 39.Bhattacharjya S., Venkatraman J., Balaram P., Kumar A. Fluoroalcohols as structure modifiers in peptides and proteins: hexafluoroacetone hydrate stabilizes a helical conformation of melittin at low pH. J. Pept. Res. 1999;54:100–111. doi: 10.1034/j.1399-3011.1999.00088.x. [DOI] [PubMed] [Google Scholar]
- 40.Shibata A., Yamamoto M., Yamashita T., Chiou J.S., Kamaya H., Ueda I. Biphasic effects of alcohols on the phase transition of poly(L-lysine) between α-helix and β-sheet conformations. Biochemistry. 1992;31:5728–5733. doi: 10.1021/bi00140a006. [DOI] [PubMed] [Google Scholar]
- 41.Searle M.S., Zerella R., Williams D.H., Packman L.C. Native-like β-hairpin structure in an isolated fragment from ferredoxin: NMR and CD studies of solvent effects on the N-terminal 20 residues. Protein Eng. 1996;9:559–565. doi: 10.1093/protein/9.7.559. [DOI] [PubMed] [Google Scholar]
- 42.Kovacs H., Mark A.E., Johansson J., van Gunsteren W.F. The effect of environment on the stability of an integral membrane helix: molecular dynamics simulations of surfactant protein C in chloroform, methanol and water. J. Mol. Biol. 1995;247:808–822. doi: 10.1016/s0022-2836(05)80156-1. [DOI] [PubMed] [Google Scholar]
- 43.Hartsough D.S., Merz K.M. Protein flexibility in aqueous and nonaqueous solutions. J. Am. Chem. Soc. 1992;114:10113–10116. [Google Scholar]
- 44.Affleck R., Haynes C.A., Clark D.S. Solvent dielectric effects on protein dynamics. Proc. Natl. Acad. Sci. USA. 1992;89:5167–5170. doi: 10.1073/pnas.89.11.5167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Clark D.S. Characteristics of nearly dry enzymes in organic solvents: implications for biocatalysis in the absence of water. Philos. Trans. R. Soc. B. 2004;359:1299–1328. doi: 10.1098/rstb.2004.1506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Vila J.A., Ripoll D.R., Scheraga H.A. Physical reasons for the unusual α-helix stabilization afforded by charged or neutral polar residues in alanine-rich peptides. Proc. Natl. Acad. Sci. USA. 2000;97:13075–13079. doi: 10.1073/pnas.240455797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sharp K.A., Honig B. Electrostatic interactions in macromolecules—theory and applications. Annu. Rev. Biophys. Biophys. Chem. 1990;19:301–332. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- 48.Feig M., Tanizaki S. Development of a heterogeneous dielectric generalized Born model for the implicit modeling of membrane environments. In: Naidoo K., editor. Modelling Molecular Structure and Reactivity in Biological Systems. Royal Society of Chemistry; Cambridge, UK: 2006. pp. 141–150. [Google Scholar]
- 49.Lin J.-H., Baker N.A., McCammon J.A. Bridging implicit and explicit solvent approaches for membrane electrostatics. Biophys. J. 2002;83:1374–1379. doi: 10.1016/S0006-3495(02)73908-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Roux B. Influence of the membrane potential on the free energy of an intrinsic protein. Biophys. J. 1997;73:2980–2989. doi: 10.1016/S0006-3495(97)78327-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gilson M.K., Sharp K.A., Honig B.H. Calculating the electrostatic potential of molecules in solution: method and error assessment. J. Comput. Chem. 1987;9:327–335. [Google Scholar]
- 52.Baker N.A. Improving implicit solvent simulations: a Poisson-centric view. Curr. Opin. Struct. Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 53.Feig M., Brooks C.L. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr. Opin. Struct. Biol. 2004;14:217–224. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 54.Feig M., Im W., Brooks C.L. Implicit solvation based on generalized Born theory in different dielectric environments. J. Chem. Phys. 2004;120:903–911. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- 55.Sigalov G., Scheffel P., Onufriev A. Incorporating variable dielectric environments into the generalized Born model. J. Chem. Phys. 2005;122:094511. doi: 10.1063/1.1857811. [DOI] [PubMed] [Google Scholar]
- 56.Hassan S.A., Mehler E.L. A critical analysis of continuum electrostatics: the screened Coulomb potential-implicit solvent model and the study of the alanine dipeptide and discrimination of misfolded structures of proteins. Proteins. 2002;47:45–61. doi: 10.1002/prot.10059. [DOI] [PubMed] [Google Scholar]
- 57.Smith P.E. The alanine dipeptide free energy surface in solution. J. Chem. Phys. 1999;111:5568–5579. [Google Scholar]
- 58.Wan S.Z., Wang C.X., Xiang Z.X., Shi Y.Y. Stochastic dynamics simulation of alanine dipeptide: including solvation interaction determined by boundary element method. J. Comput. Chem. 1997;18:1440–1449. [Google Scholar]
- 59.Chekmarev D.S., Ishida T., Levy R.M. Long-time conformational transitions of alanine dipeptide in aqueous solution: continuous and discrete-state kinetic models. J. Phys. Chem. B. 2004;108:19487–19495. [Google Scholar]
- 60.Swope W.C., Pitera J.W., Suits F., Pitman M., Eleftheriou M., Fitch B.G., Germain R.S., Rayshubski A., Ward T.J.C., Zhestkov Y., Zhou R. Describing protein folding kinetics by molecular dynamics simulations. 2. Example applications to alanine dipeptide and β-hairpin peptide. J. Phys. Chem. B. 2004;108:6582–6594. [Google Scholar]
- 61.Feig M. Kinetics from implicit solvent simulations of biomolecules as a function of viscosity. J. Chem. Theory Comput. 2007;3:1734–1748. doi: 10.1021/ct7000705. [DOI] [PubMed] [Google Scholar]
- 62.Drozdov A.N., Grossfield A., Pappu R.V. Role of solvent in determining conformational preferences of alanine dipeptide in water. J. Am. Chem. Soc. 2004;126:2574–2581. doi: 10.1021/ja039051x. [DOI] [PubMed] [Google Scholar]
- 63.Hu H., Elstner M., Hermans J. Comparison of a QM/MM force field and molecular mechanics force fields in simulations of alanine and glycine “dipeptides” (Ace-Ala-Nme and Ace-Gly-Nme) in water in relation to the problem of modeling the unfolded peptide backbone in solution. Proteins. 2003;50:451–463. doi: 10.1002/prot.10279. [DOI] [PubMed] [Google Scholar]
- 64.MacKerell A.D., Feig M., Brooks C.L. Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 65.Reference deleted in proof.
- 66.Brooks C.L., Case D.A. Simulations of peptide conformational dynamics and thermodynamics. Chem. Rev. 1993;93:2487–2502. [Google Scholar]
- 67.Kaminski G.A., Friesner R.A., Tirado-Rives J., Jorgensen W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B. 2001;105:6474–6487. [Google Scholar]
- 68.Shi Z.S., Olson C.A., Rose G.D., Baldwin R.L., Kallenbach N.R. Polyproline II structure in a sequence of seven alanine residues. Proc. Natl. Acad. Sci. USA. 2002;99:9190–9195. doi: 10.1073/pnas.112193999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Makowska J., Rodziewicz-Motowidlo S., Baginska K., Vila J.A., Liwo A., Chmurzynski L., Scheraga H.A. Polyproline II conformation is one of many local conformational states and is not an overall conformation of unfolded peptides and proteins. Proc. Natl. Acad. Sci. USA. 2006;103:1744–1749. doi: 10.1073/pnas.0510549103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Kim Y.S., Wang J.P., Hochstrasser R.M. Two-dimensional infrared spectroscopy of the alanine dipeptide in aqueous solution. J. Phys. Chem. B. 2005;109:7511–7521. doi: 10.1021/jp044989d. [DOI] [PubMed] [Google Scholar]
- 71.Ooi T., Oobatake M. Prediction of the thermodynamics of protein unfolding: the helix-coil transition of poly (L-alanine) Proc. Natl. Acad. Sci. USA. 1991;88:2859–2863. doi: 10.1073/pnas.88.7.2859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Takano M., Yamato T., Higo J., Suyama A., Nagayama K. Molecular dynamics of a 15-residue poly(L-alanine) in water. Helix formation and energetics. J. Am. Chem. Soc. 1999;121:605–612. [Google Scholar]
- 73.Ohkubo Y.Z., Brooks C.L. Exploring Flory's isolated-pair hypothesis: statistical mechanics of helix-coil transitions in polyalanine and the C peptide for Rnase A. Proc. Natl. Acad. Sci. USA. 2003;100:13916–13921. doi: 10.1073/pnas.2334257100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Daggett V., Kollman P.A., Kuntz I.D. A molecular dynamics simulation of polyalanine: an analysis of equilibrium motions and helix-coil transitions. Biopolymers. 1991;31:1115–1134. doi: 10.1002/bip.360310911. [DOI] [PubMed] [Google Scholar]
- 75.Miller J.S., Kennedy R.J., Kemp D.S. Solubilized, spaced polyalanines: a context-free system for determining amino acid α-helix propensities. J. Am. Chem. Soc. 2002;124:945–962. doi: 10.1021/ja011726d. [DOI] [PubMed] [Google Scholar]
- 76.Levy Y., Jortner J., Becker O.M. Solvent effects on the energy landscapes and folding kinetics of polyalanine. Proc. Natl. Acad. Sci. USA. 2001;98:2188–2193. doi: 10.1073/pnas.041611998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Ingwall R.T., Scheraga H.A., Lotan N., Berger A., Katchals E. Conformational studies of poly-L-alanine in water. Biopolymers. 1968;6:331–368. doi: 10.1002/bip.1968.360060308. [DOI] [PubMed] [Google Scholar]
- 78.Garcia A.E., Sanbonmatsu K.Y. α-Helical stabilization by side chain shielding of backbone hydrogen bonds. Proc. Natl. Acad. Sci. USA. 2002;99:2782–2787. doi: 10.1073/pnas.042496899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Cammers-Goodwin A., Allen T.J., Oslick S.L., McClure K.F., Lee J.H., Kemp D.S. Mechanism of stabilization of helical conformations of polypeptides by water containing trifluoroethanol. J. Am. Chem. Soc. 1996;118:3082–3090. [Google Scholar]
- 80.Olivella M., Deupi X., Govaerts C., Pardo L. Influence of the environment in the conformation of α-helices studied by protein database search and molecular dynamics simulations. Biophys. J. 2002;82:3207–3213. doi: 10.1016/S0006-3495(02)75663-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Spek E.J., Olson C.A., Shi Z., Kallenbach N.R. Alanine is an intrinsic α-helix stabilizing amino acid. J. Am. Chem. Soc. 1999;121:5571–5572. [Google Scholar]
- 82.Roe D.R., Okur A., Wickstrom L., Hornak V., Simmerling C. Secondary structure bias in generalized Born solvent models: comparison of conformational ensembles and free energy of solvent polarization from explicit and implicit solvation. J. Phys. Chem. B. 2007;111:1846–1857. doi: 10.1021/jp066831u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Miller J.S., Kennedy R.J., Kemp D.S. Short, solubilized polyalanines are conformational chameleons: exceptionally helical if N- and C-capped with helix stabilizers, weakly to moderately helical if capped with rigid spacers. Biochemistry. 2001;40:305–309. doi: 10.1021/bi0019500. [DOI] [PubMed] [Google Scholar]
- 84.Kennedy R.J., Tsang K.-Y., Kemp D.S. Consistent helicities from CD and template t/c data for N-templated polyalanines: progress toward resolution of the alanine helicity problem. J. Am. Chem. Soc. 2002;124:934–944. doi: 10.1021/ja016285c. [DOI] [PubMed] [Google Scholar]
- 85.Dempsey C.E. The actions of melittin on membranes. Biochim. Biophys. Acta. 1990;1031:143–161. doi: 10.1016/0304-4157(90)90006-x. [DOI] [PubMed] [Google Scholar]
- 86.John E., Jahnig F. Aggregation state of melittin in lipid vesicle membranes. Biophys. J. 1991;60:319–328. doi: 10.1016/S0006-3495(91)82056-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Dempsey C.E., Butler G.S. Helical structure and orientation of melittin in dispersed phospholipid membranes from amide exchange analysis in situ. Biochemistry. 1992;31:11973–11977. doi: 10.1021/bi00163a003. [DOI] [PubMed] [Google Scholar]
- 88.Sessions R.B., Gibbs N., Dempsey C.E. Hydrogen bonding in helical polypeptides from molecular dynamics simulations and amide hydrogen exchange analysis: alamethicin and melittin in methanol. Biophys. J. 1998;74:138–152. doi: 10.1016/S0006-3495(98)77775-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Berneche S., Nina M., Roux B. Molecular dynamics simulation of melittin in a dimyristoylphosphatidylcholine bilayer membrane. Biophys. J. 1998;75:1603–1618. doi: 10.1016/S0006-3495(98)77604-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Im W., Feig M., Brooks C.L. An implicit membrane generalized Born theory for the study of structure, stability, and interactions of membrane proteins. Biophys. J. 2003;85:2900–2918. doi: 10.1016/S0006-3495(03)74712-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Terwilliger T.C., Eisenberg D. The structure of melittin. I. Structure determination and partial refinement. J. Biol. Chem. 1982;257:6010–6015. doi: 10.2210/pdb1mlt/pdb. [DOI] [PubMed] [Google Scholar]
- 92.Terwilliger T.C., Eisenberg D. The structure of melittin. II. Interpretation of the structure. J. Biol. Chem. 1982;257:6016–6022. [PubMed] [Google Scholar]
- 93.Lauterwein J., Brown L.R., Wuthrich K. High-resolution 1H-NMR studies of monomeric melittin in aqueous solution. Biochim. Biophys. Acta. 1980;622:219–230. doi: 10.1016/0005-2795(80)90033-1. [DOI] [PubMed] [Google Scholar]
- 94.Gerig J.T. Structure and solvation of melittin in 1,1,1,3,3,3-hexafluoro-2-propanol/water. Biophys. J. 2004;86:3166–3175. doi: 10.1016/S0006-3495(04)74364-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Gerig J.T. Structure and solvation of melittin in hexafluoroacetone/water. Biopolymers. 2004;74:240–247. doi: 10.1002/bip.20085. [DOI] [PubMed] [Google Scholar]
- 96.Bazzo R., Tappin M.J., Pastore A., Harvey T.S., Carver J.A., Campbell I.D. The structure of melittin. A 1H-NMR study in methanol. Eur. J. Biochem. 1988;173:139–146. doi: 10.1111/j.1432-1033.1988.tb13977.x. [DOI] [PubMed] [Google Scholar]
- 97.Inagaki F., Shimada I., Kawaguchi K., Hirano M., Terasawa I., Ikura T., Go N. Structure of melittin bound to perdeuterated dodecylphosphocholine micelles as studied by two-dimensional NMR and distance geometry calculations. Biochemistry. 1989;28:5985–5991. [Google Scholar]
- 98.Roccatano D., Fioroni M., Zacharias M., Colombo G. Effect of hexafluoroisopropanol alcohol on the structure of melittin: a molecular dynamics simulation study. Protein Sci. 2005;14:2582–2589. doi: 10.1110/ps.051426605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Glättli A., Chandrasekhar I., van Gunsteren W.F. A molecular dynamics study of the bee venom melittin in aqueous solution, in methanol, and inserted in a phospholipid bilayer. Eur. Biophys. J. 2006;35:255–267. doi: 10.1007/s00249-005-0033-7. [DOI] [PubMed] [Google Scholar]
- 100.Still W.C., Tempczyk A., Hawley R.C., Hendrickson T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990;112:6127–6129. [Google Scholar]
- 101.Lee M.S., Feig M., Salsbury F.R., Brooks C.L. New analytical approximation to the standard molecular volume definition and its application to generalized Born calculations. J. Comput. Chem. 2003;24:1348–1356. doi: 10.1002/jcc.10272. [DOI] [PubMed] [Google Scholar]
- 102.Lee M.S., Salsbury F.R., Brooks C.L. Novel generalized Born methods. J. Chem. Phys. 2002;116:10606–10614. [Google Scholar]
- 103.Feig M., Onufriev A., Lee M.S., Im W., Case D.A., Brooks C.L. Performance comparison of generalized Born and Poisson methods in the calculation of electrostatic solvation energies for protein structures. J. Comput. Chem. 2004;25:265–284. doi: 10.1002/jcc.10378. [DOI] [PubMed] [Google Scholar]
- 104.Chocholousova J., Feig M. Balancing an accurate representation of the molecular surface in generalized Born formalisms with integrator stability in molecular dynamics simulations. J. Comput. Chem. 2006;27:719–729. doi: 10.1002/jcc.20387. [DOI] [PubMed] [Google Scholar]
- 105.Sitkoff D., Sharp K.A., Honig B. Accurate calculation of hydration free-energies using macroscopic solvent models. J. Phys. Chem. 1994;98:1978–1988. [Google Scholar]
- 106.Hansmann U.H.E., Okamoto Y. New Monte Carlo algorithms for protein folding. Curr. Opin. Struct. Biol. 1999;9:177–183. doi: 10.1016/S0959-440X(99)80025-6. [DOI] [PubMed] [Google Scholar]
- 107.Sugita Y., Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999;314:141–151. [Google Scholar]
- 108.Brooks B.R., Bruccoleri R.E., Olafson B.D., States D.J., Swaminathan S., Karplus M. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 109.Feig M., Karanicolas J., Brooks C.L. MMTSB tool set: enhanced sampling and multiscale modeling methods for applications in structural biology. J. Mol. Graph. Model. 2004;22:377–395. doi: 10.1016/j.jmgm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 110.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 111.MacKerell A.D., Bashford D., Bellott M., Dunbrack J.D., Evanseck M.J., Field M.J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., KuchnirF L. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 112.MacKerell A.D., Feig M., Brooks C.L. Improved treatment of the protein backbone in empirical force fields. J. Am. Chem. Soc. 2004;126:698–699. doi: 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
- 113.Feig M., MacKerell A.D., Brooks C.L. Force field influence on the observation of pi-helical protein structures in molecular dynamics simulations. J. Phys. Chem. B. 2003;107:2831–2836. [Google Scholar]
- 114.Ryckaert J.P., Ciccotti G., Berendsen H.J.C. Numerical-integration of Cartesian equations of motion of a system with constraints—molecular-dynamics of N-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 115.Brooks C.L., Berkowitz M., Adelman S.A. Generalized Langevin theory for many-body problems in chemical-dynamics—gas-surface collisions, vibrational-energy relaxation in solids, and recombination reactions in liquids. J. Chem. Phys. 1980;73:4353–4364. [Google Scholar]
- 116.Kumar S., Bouzida D., Swendsen R.H., Kollman P.A., Rosenberg J.M. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 117.Kumar S., Rosenberg J.M., Bouzida D., Swendsen R.H., Kollman P.A. Multidimensional free-energy calculations using the weighted histogram analysis method. J. Comput. Chem. 1995;16:1339–1350. [Google Scholar]
- 118.Chen J.H., Im W.P., Brooks C.L. Balancing solvation and intramolecular interactions: toward a consistent generalized Born force field. J. Am. Chem. Soc. 2006;128:3728–3736. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Mackerell A.D. Empirical force fields for biological macromolecules: overview and issues. J. Comput. Chem. 2004;25:1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 120.Zhu J., Xie L., Honig B. Structural refinement of protein segments containing secondary structure elements: local sampling, knowledge-based potentials, and clustering. Proteins. 2006;65:463–479. doi: 10.1002/prot.21085. [DOI] [PubMed] [Google Scholar]
- 121.Blondelle S.E., Simpkins L.R., Perezpaya E., Houghten R.A. Influence of tryptophan residues on melittins hemolytic activity. Biochim. Biophys. Acta. 1993;1202:331–336. doi: 10.1016/0167-4838(93)90024-l. [DOI] [PubMed] [Google Scholar]
- 122.Cheung M.S., Thirumalai D. Effects of crowding and confinement on the structure of the transition state ensemble in proteins. J. Phys. Chem. B. 2007;111:8250–8257. doi: 10.1021/jp068201y. [DOI] [PubMed] [Google Scholar]
- 123.Cheung M.S., Thirumalai D. Nanopore-protein interactions dramatically alter stability and yield of the native state in restricted spaces. J. Mol. Biol. 2006;357:632–643. doi: 10.1016/j.jmb.2005.12.048. [DOI] [PubMed] [Google Scholar]
- 124.Cheung M.S., Klimov D., Thirumalai D. Molecular crowding enhances native state stability and refolding rates of globular proteins. Proc. Natl. Acad. Sci. USA. 2005;102:4753–4758. doi: 10.1073/pnas.0409630102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Chocholousova J., Feig M. Implicit solvent simulations of DNA and DNA-protein complexes: agreement with explicit solvent vs experiment. J. Phys. Chem. B. 2006;110:17240–17251. doi: 10.1021/jp0627675. [DOI] [PubMed] [Google Scholar]
- 126.Feig M., Pettitt B.M. Modeling high-resolution hydration patterns in correlation with DNA sequence and conformation. J. Mol. Biol. 1999;286:1075–1095. doi: 10.1006/jmbi.1998.2486. [DOI] [PubMed] [Google Scholar]
- 127.Geney R., Layten M., Gomperts R., Hornak V., Simmerling C. Investigation of salt bridge stability in a generalized born solvent model. J. Chem. Theory Comput. 2006;2:115–127. doi: 10.1021/ct050183l. [DOI] [PubMed] [Google Scholar]
- 128.Petsko G.A., Ringe D. New Science Press; London, UK: 2003. Protein Structure and Function. [Google Scholar]
- 129.Marqusee S., Robbins V.H., Baldwin R.L. Unusually stable helix formation in short alanine-based peptides. Proc. Natl. Acad. Sci. USA. 1989;86:5286–5290. doi: 10.1073/pnas.86.14.5286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Yang S., Cho M. Thermal denaturation of polyalanine peptide in water by molecular dynamics simulations and theoretical prediction of infrared spectra: helix-coil transition kinetics. J. Phys. Chem. B. 2007;111:605–617. doi: 10.1021/jp0649091. [DOI] [PubMed] [Google Scholar]
- 131.Wilcox W., Eisenberg D. Thermodynamics of melittin tetramerization determined by circular dichroism and implications for protein folding. Protein Sci. 1992;1:641–653. doi: 10.1002/pro.5560010510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.van Gunsteren W.F., Billeter S.R., Eising A.A., Huenenberger P.H., Krueger P., Mark A.E., Scott W.R.P., Tirono I.G. Vdf Hochschulverlage AG an der ETH Zürich; Zurich, Switzerland: 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. [Google Scholar]
- 133.Yoda T., Sugita Y., Okamoto Y. Secondary-structure preferences of force fields for proteins evaluated by generalized ensemble simulations. Chem. Phys. 2004;307:269–283. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplement


