A Geometric Principle May Guide Self-Assembly of Fullerene Cages from Clathrin Triskelia and from Carbon Atoms

Abstract

Clathrin triskelia and carbon atoms alike self-assemble into a limited selection of fullerene cages (with n three connected vertices, 3n/2 edges, 12 pentagonal faces, and (n−20)/2 hexagonal faces). We show that a geometric constraint—exclusion of head-to-tail dihedral angle discrepancies (DADs)—explains this limited selection as well as successful assembly into such closed cages in the first place. An edge running from a pentagon to a hexagon has a DAD, since the dihedral angles about the edge broaden from its pentagon (tail) end to its hexagon (head) end. Of the 21 configurations of a central face and surrounding faces, six have such DAD vectors arranged head-to-tail. Of the 5770 mathematically possible fullerene cages for n ≤ 60, excluding those with any of the six configurations leaves just 15 cages plus buckminsterfullerene (n = 60), among them the known clathrin cages. Of the 216,739 mathematically possible cages for 60 < n ≤ 84, just the 50 that obey the isolated-pentagon rule, among them known carbon cages, pass. The absence of likely fullerenes for some n (30,34,46,48,52–58,62–68) explains the abundance of certain cages, including buckminsterfullerene. These principles also suggest a “probable roads” path to self-assembly in place of pentagon-road and fullerene-road hypotheses.

Introduction

Although the term “fullerene” was applied initially by chemists to closed cages assembled from carbon atoms in 1985 (1), biologists were already familiar with fullerene cages (2,3) assembled from the protein clathrin (4,5). Such cages have n three-connected vertices, 3/2n edges, 12 pentagonal faces, and (n − 20)/2 hexagonal faces. Moreover, both carbon atoms, each just 12 Daltons, and clathrin trimers (triskelia) (6–8), each with mass ∼50,000 times as much (6–11), self-assemble into fullerene cages of a variety of sizes and shapes (2–5,12,13). Carbon does this from the gas phase at temperatures around 1200°C (14–16). Clathrin does this inside cells, where it self-assembles around inwardly budding patches of membrane (13,17) to encapsulate vesicles of different sizes (2,3,5,18,19). It does so at two sites: It withdraws such patches from successive compartments of the trans-Golgi network and from the plasma membrane (5,13,20,21). At the latter site, the area of synaptic vesicle membrane taken up by clathrin-mediated endocytosis determines the size of neurotransmitter-filled synaptic vesicles and the amount of neurotransmitter in each quantum that is subsequently released at the synapse (22).

Fig. 1 A shows stereoviews of four fullerene cages. Fig. 2 A shows the same four cages but in a more convenient form, a two-dimensional representation called a Schlegel diagram. Clathrin self-assembles into these (2,3,12,19,23) and larger cages. Cage 28-2 is the second of two cage isomers with 28 vertices. Cages 36-14 and 36-15 are the 14th and 15th of 15 cage isomers with 36 vertices (24). Cage 60-IPR-1 is the best known fullerene cage, the soccer ball with 60 vertices, long known to mathematicians as the truncated icosahedron. The truncated icosahedron is the smallest fullerene cage that has no adjacent pentagons, so it is the smallest isolated-pentagon rule (IPR) cage (25,26). Carbon famously self-assembles into this C₆₀ cage, which the chemists named “buckminsterfullerene” or the “buckyball” (1). Carbon also self-assembles into many larger cages, including the one IPR isomer of C₇₀ (27), very large, elongated nanotubes (28), and the small 36-15 cage (29,30). Clathrin also self-assembles into nanotube-type structures (31).

Figure 1.

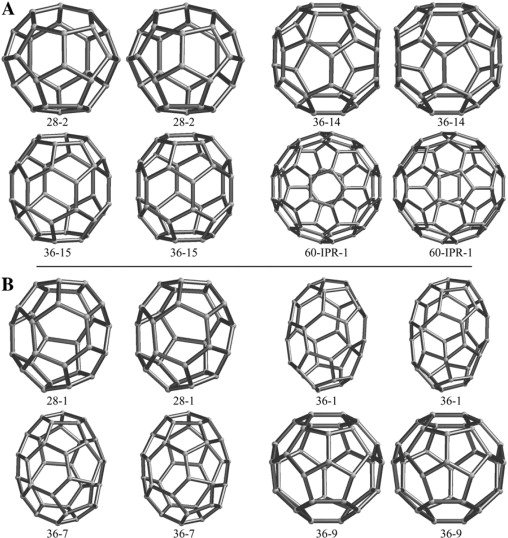
Stereopairs of fullerene cages. The recipes for these fullerenes are found in Fowler and Manolopoulos (24). (A) Probable fullerenes 28-2, 36-14, 36-15, and 60-IPR-1. Cage 28-2, the second of two cage isomers with 28 vertices (19) and 4 hexagons, has tetrahedral (T_d) symmetry. Cage 36-14, the 14th of 15 cage isomers with 36 vertices and 8 hexagons, has D_2d symmetry and is the second (II) with that symmetry of the 15. Cage 36-15, the 15th of the 15 cage isomers with 36 vertices and 8 hexagons, has D_6h symmetry. Cage 60-IPR-1 is the only IPR cage of 1812 isomers with 60 vertices. The clathrin versions of the first three have been called the “mini-coat”, the “tennis ball”, and the “hexagonal barrel” (3,11). The last one has the shape of a soccer ball. Mathematicians call it the truncated icosahedron, and it has icosahedral (I) symmetry (40). (B) Improbable fullerenes 28-1 (D₂), 36-1 [C₂(I)], 36-7 [C₁(II)], and 36-9 (C_2v).

Figure 2.

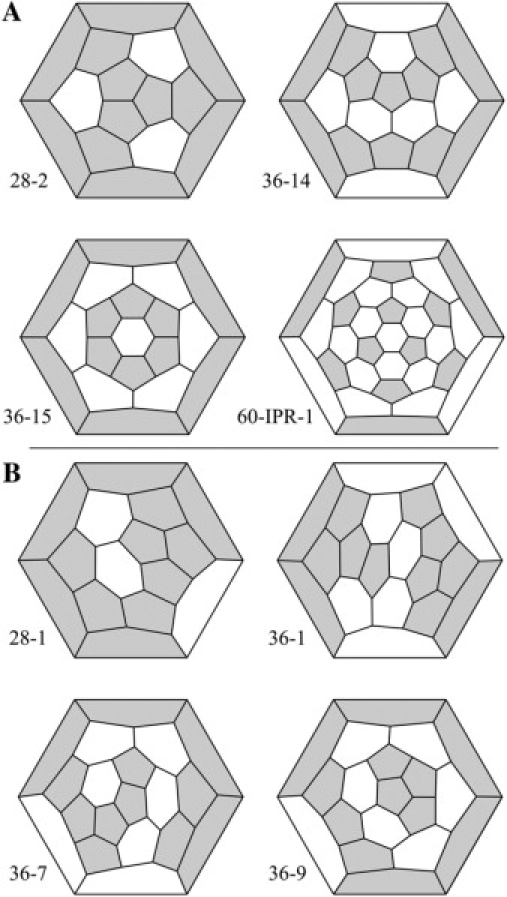
Schlegel diagrams for the probable (A) and improbable (B) fullerene cages shown in Fig. 1.

We refer to the fullerene cages in Figs. 1 A and 2 A, the ones that clathrin triskelia and carbon atoms have been shown to form, as probable. One can draw another isomer with 28 vertices—the 28-1 cage in Figs. 1 B and 2 B—and another 13 isomers with 36 vertices, three of which (36-1, 36-7, and 36-9) are also shown in Figs. 1 B and 2 B (24). We refer to these other cages, ones not observed experimentally, as “improbable”.

Here we pose and answer two questions. First, why do certain fullerene isomers self-assemble but others do not? Second, how is it possible for carbon and clathrin to successfully assemble into closed fullerene cages in the first place when so many paths lead to defective structures?

Fowler and Manolopoulos (24) number fullerenes in order of production by the pentagon spiral algorithm (32) that is able to produce a complete set of cage isomers for n < 100 (33), ordered so that low numbered isomers (e.g., 36-1 in Fig. 2 B) have the most bunched pentagons, whereas high numbered isomers (e.g., 36-15 in Fig. 2 A) have the most dispersed pentagons. For cages with 60 vertices, the highest numbered isomer is 60-1812 (34). It is also the first (and only) IPR isomer among the 1812 mathematically possible cages with 60 vertices, so it may be numbered 60-IPR-1 as well. The next larger IPR cage has 70 vertices, and then IPR cages are possible for every even n > 70 (Table 1) (24).

Table 1.

Characteristics of fullerenes with 20 ≤ n ≤ 84 vertices

									IDs of probable cages
n	Faces	Hexs	Graphically possible Cages	IPR cages	Lowest Np for each n	Number of lowest Np isomers	IDs of isomers with lowest Np	Number of probable cages	FM	Schonflies
20-60			5770	1		35		16
20-70			30,579	2		56		17
60-84			218,551	51		71		52
20-84			222,509	51		105		66
20	12	0	1	0	30	1	1	1	1	Ih
24	14	2	1	0	24	1	1	1	1	D6d
26	15	3	1	0	21	1	1	1	1	D3h
28	16	4	2	0	18	1	2	1	2	Td
30	17	5	3	0	17	1	3	0
32	18	6	6	0	15	1	6	1	6	D3
34	19	7	6	0	14	1	5	0
36	20	8	15	0	12	2	14, 15	2	14, 15	D2d(II), D6h
38	21	9	17	0	11	1	17	1	17	C2(V)
40	22	10	40	0	10	2	38, 39	2	38, 39	D2(III), D5d(II)
42	23	11	45	0	9	1	45	1	45	D3
44	24	12	89	0	8	2	75, 89	2	75, 89	D2(III), D2(VI)
46	25	13	116	0	8	7	99,103,107,108,109,114,116	0
48	26	14	199	0	7	4	171, 196, 197, 199	0
50	27	15	271	0	5	1	271	1	271	D5h(II)
52	28	16	437	0	5	1	422	0
54	29	17	580	0	4	1	540	0
56	30	18	924	0	4	4	843, 864, 913, 916	0
58	31	19	1205	0	3	1	1205	0
60	32	20	1812	1	0	1	1812 (IPR-1)	2	1784, 1812 (IPR-1)	D6h(II), Ih
62	33	21	2385	0	3	3	2184, 2377, 2378	0
64	34	22	3465	0	2	3	3451, 3452, 2378	0
66	35	23	4478	0	2	3	4169, 4348, 4466	0
68	36	24	6332	0	2	11	6073,6094,6146,6148,6149,6195, 6198,6269,6270,6290,6328	0
70	37	25	8149	1	0	1	All IPR	1	All IPR
72	38	26	11190	1	0	1	All IPR	1	All IPR
74	39	27	14246	1	0	1	All IPR	1	All IPR
76	40	28	19151	2	0	2	All IPR	2	All IPR
78	41	29	24109	5	0	5	All IPR	5	All IPR
80	42	30	31924	7	0	7	All IPR	7	All IPR
82	43	31	39718	9	0	9	All IPR	9	All IPR
84	44	32	51592	24	0	24	All IPR	24	All IPR
86	45	33	63761	19	0	19	All IPR
88	46	34	81738	35	0	35	All IPR
90	47	35	99918	46	0	46	All IPR
92	48	36	126409	86	0	86	All IPR
94	49	37	153493	134	0	134	All IPR
96	50	38	191839	187	0	187	All IPR
98	51	39	231017	259	0	259	All IPR
100	52	40	285913	450	0	450	All IPR

The number of hexagons (hexs) is (n - 20)/2. With 12 pentagons, the number of faces is 12 more. The number of graphically possible cages and graphically possible cages that obey the isolated pentagon rule (IPR cages) were counted by use of the Fullgen program or the CaGe program, which use a productive algorithm (38). For each n, the isomer with the lowest number of pentagon pairs (N_p) is listed according to the (FM) isomer numbering in Fowler and Manolopoulos (24). These lowest N_p values are listed in Table 4.1 of Fowler and Manolopoulos. Probable cages have no improbable Rings, and the number and identify of these are listed for each n. Cages with 84 < n ≤ 100 were not investigated with respect to improbable rings.

Until the 36-15 carbon cage was isolated and identified in 1998 (16), all of the isolated empty carbon cages before (and since) have been IPR cages (35). Therefore, the best known rule for predicting which fullerenes can self-assemble and which cannot is the isolated pentagon rule itself (25,26). The self-assembly of small fullerenes, clathrin with n = 28 and 36 triskelia and others (18) and more recently carbon with n = 36 (29) and perhaps 32, 44, and 50 (36,37), shows that the isolated pentagon rule is not the answer to the first question, at least not the whole answer.

However, the isolated pentagon rule is a specific instance of a more general rule that for each n favors those isomers with the smallest number N_p of pentagon pairs. This number is also equal to the number of edges between adjacent pentagons (Fowler and Manolopoulos (24)). For example, the (probable) cages in Figs. 1 A and 2 A have the lowest N_p among all cages with their number n of vertices: Probable cage 28-2 has 18 pentagon pairs, whereas improbable cage 28-1 has 20. Likewise, probable cages 36-14 and 36-15 have 12 pentagon pairs, whereas improbable cages 36-1, 36-7, and 36-9 have 16, 14, and 13, respectively. (For IPR cages, N_p = 0.) Not surprisingly, the highest numbered isomers (e.g., 36-14 and 36-15), the ones with the most dispersed pentagons, generally—but not always—have the lowest N_p. (See Table 4.1 in Fowler and Manolopoulos (24).)

Among carbon cages of any n, it is argued that the isomers with the fewest pentagon pairs (Table 1) are the most stable (25,26) on purely steric or geometric grounds (24), so the least-N_p rule could apply to clathrin as well as carbon. However, the differences, 18 vs. 20 and 12 vs. 13–16 pentagon pairs, are small. Moreover, the existence of probable small clathrin cages 28-2, 36-14, and 36-15 and the probable small carbon cage 36-15 (Fig. 2 A) demonstrate that pairs of adjacent pentagons (as found in 36-14 and 36-15) or even triplets of adjacent pentagons (as found in 28-2), configurations that are associated with high discrete curvature and steric strain (24,25), do not rule out self-assembly. Nonetheless, the least-N_p rule raises the hope that a single geometric rule could select for both carbon and clathrin which fullerene isomers can self-assemble.

Here, we propose such an explanation—a geometric constraint or rule—for why the cages we describe as improbable are not observed. The new rule is also based purely on geometric considerations and appears to apply to both clathrin and carbon fullerenes. Specifically, we propose that those configurations of a pentagonal or a hexagonal face and its five or six surrounding faces that generate head-to-tail dihedral angle discrepancies (DADs) are unlikely to self-assemble. This geometric rule is consistent with the least-N_p rule but is more restrictive, allows self-assembly of just 15 (small) non-IPR cages and all (large) IPR cages, provides a purely geometric explanation for the isolated pentagon rule for large (n > 60) fullerenes, and accounts for the abundance of the C₆₀ buckyball.

The head-to-tail exclusion rule also answers the second question: how carbon and clathrin successfully assemble into closed fullerene cages in the first place. Fig. 3 illustrates the problem. Fig. 3 A shows a spiral of pentagons and hexagons added in the order 55656665556555566565 to produce cage 36-15. When we generated random lists of 20 faces and selected 10 with exactly 12 pentagons, not one produced a closed fullerene cage. Fig. 3 B shows an example of one of those failures. The failures are not surprising, since random addition of 20 faces, each a pentagon or a hexagon, would generate 2²⁰ = 1,048,576 different lists, very few of them specifying any of the 15 closed fullerene cages with 36 vertices. Constraining the process to random orderings of 12 pentagons and 8 hexagons helps but still generates an overwhelmingly large number of lists, 20!/(12! × 8!) = 125,970 (32), nearly all unproductive. The head-to-tail exclusion rule answers this second question by permitting self-assembly only along pathways that lead to probable cages, all of which are closed fullerene cages. We therefore propose a probable roads hypothesis that provides insight generally into the nature of successful self-assembly.

Figure 3.

Random growth is unlikely to produce a closed fullerene cage. (A) The order for spiral addition of faces for cage 36-15 is 55656665556555566565, where “5” specifies a pentagon and “6” specifies a hexagon. This list, which comes from a “recipe” for making 36-15 (Fowler and Manolopoulos (24)) that consists of the positions of the 12 pentagons (1,2,3,4,8,9,10,12,13,14,15,18,20). Lists for 36-15 could start on any of the 20 faces and go backward as well as forward, in this case without any replicates, a total of 40 lists. The 36-15 cage shown by this Schlegel diagram is the same as the one shown by the Schlegel diagram in Fig. 2 A but centered on a different face. (B) An example of a random order for spiral addition of faces with 12 pentagons and 8 hexagons is 66555656566655555556. After addition of the 20th face, the two circled vertices are not three-connected, and no further addition of faces could produce a closed fullerene.

Methods

The pentagon spiral algorithm (32) produces all of the possible fullerene cages for all n < 100 vertices but misses one with n = 100 vertices (33). Based on a productive algorithm (38), the Carbon Generator (CaGe) program (www.mathematik.uni-bielefeld.de/∼CaGe/) can produce all of the fullerenes for any n without exception. We used the CaGe program to generate postscript versions of Schlegel diagrams and then Adobe Illustrator (Adobe Systems, Mountain View, CA) to make figures from these postscript files.

We also used the CaGe program to generate Protein Data Bank (pdb) files that contain three-dimensional coordinates of vertices and their connectivity. We created carbon fullerene cage frameworks from these pdb files with PC Spartan Pro (Wavefunction, Irvine, CA).

We computed equilibrium geometry for carbon cages and clathrin-analogous cages. The vertices in carbon cages were carbon atoms. In that case, we maximized the assignment of double bonds first to edges between adjacent hexagons (66 edges), then to 56 edges, and lastly to 55 edges, and then we used Spartan04 to compute the equilibrium geometry of these cages with semiempirical (PM3) quantum mechanical calculations. For clathrin-analogous cages, we used Molecular Mechanics (MMFF94 (39–43)) to compute equilibrium geometry, where each vertex was a customizable “X atom” with the Van der Waals radius and single-bond length (1.5 Å) of carbon and with an equilibrium bond angle of 116°. With only three bonds, these tetravalent, carbon-like X atoms were charged, so we also set the coefficients for electrostatic interactions to zero. Spartan04 and Spartan06 also produced three-dimensional coordinates of vertices, bond lengths, and bond angles of these cages with equilibrium geometry.

We made these carbon and X cages for a heuristic purpose, to gain insight into the cage structure that follows from competing constraints: bonding patterns, location of single and double bonds, ideal bond lengths, ideal bond angles, and force field constants. As the results show, different atoms and different energy minimization algorithms make little difference. In the context of constrained bond lengths and bond angles, connectivity of vertices in fullerene cages—the geometry—dominates the structure. Based on pure geometry, we computed the three dihedral angles about the three edges emerging from a vertex from the three bond angles at that vertex.

We used the Fullgen program (http://cs.anv.edu.au/(bdm/plantri/), written by Gunnar Brinkmann (Gent University, Belgium) and Brendan McKay (Australian National University) and a modification written by Gunnar Brinkmann to produce a list of all the “Rings”, one for each face, coded with numbers like 6555656 as described in the section “DADs in fullerenes” (see below) for each of the 222,509 fullerene cages with 20 ≤ n ≤ 84 vertices. We used Microsoft Excel (Microsoft, Redmond, WA) to translate these codes into Ring types with numbers like 643, as described in the section “Improbable paths”.

Results

Bond angles are close to 108° and 120°

Faces in fullerene cages are either hexagons or pentagons. The bond angles in regular hexagons and pentagons are 120° and 108°, respectively. The only fullerenes with regular faces—equal side lengths and equal bond angles—throughout are the dodecahedron with 20 vertices, 1 of the 5 Platonic or regular polyhedra, and the truncated icosahedron or soccer ball with 60 vertices, one of the 13 Archimedean semiregular polyhedra (44). All other fullerenes have some irregular faces, where the bond angles might deviate considerably from these ideal values. More particularly, it might be supposed that the bond angles in improbable cages deviate considerably more from ideal values than those in probable cages. Using Spartan, we modeled probable cages 28-2, 36-14, 36-15, and 60-IPR-1 (Figs. 1 A and 2 A) and improbable cages 28-1, 36-1, 36-7, and 36-9 (Figs. 1 B and 2 B) as carbon cages, with carbon atoms and optimal placement of double bonds, and as clathrin-analogous cages, with customizable X atoms and exclusively single bonds.

As shown by the unfilled bars in Fig. 4 A, all of the bond angles in probable carbon cages 28-2, 36-14, and 36-15 were close to ideal values. Means were close to 108° and 120°, and standard deviations were small, ∼1° in pentagons and up to 1.7° in hexagons. The greatest deviations from the ideal 108° in pentagons were 3.51°, 1.30°, and 1.67°, respectively. The greatest deviations from the ideal 120° in hexagons were 1.35°, 2.82°, and 2.56°.

Figure 4.

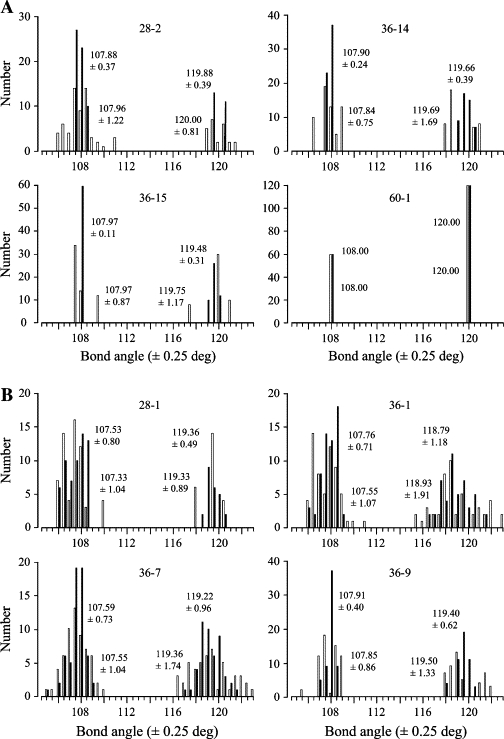
Bond angles in both probable fullerene cages (A), and improbable fullerene cages (B) were close to 108°, the bond angle in a regular pentagon, and 120°, the bond angle in a regular hexagon. The data represented by unfilled and filled bars were obtained from cages composed of carbon atoms and of clathrin-analogous atoms, respectively. To compute equilibrium geometry of carbon cages, we used semiempirical (PM3) quantum mechanical calculations after maximizing assignment of double bonds first to edges between adjacent hexagons (66 edges), then to 56 edges, and lastly to 55 edges. To compute equilibrium geometry of clathrin-analogous cages, we used molecular mechanical (MMFF94) calculations on cages with exclusively single bonds. Bins in the histograms are 0.5° wide; for example, the 108° bin contains angles x such that 107.75° < x ≤ 108.25°. Mean ± 1 SD is shown for each group of angles centered near 108° in pentagons and near 120° in hexagons. Values placed lower in each part correspond to the unfilled (carbon) bars, values placed higher to the filled (clathrin-analogous) bars.

As shown by the unfilled bars in Fig. 4 B, bond angles in improbable carbon cages 28-1, 36-1, 36-7, and 36-9 were also close to ideal. Means were close to 108° and 120°, and standard deviations were similarly small, ∼1° in pentagons and up to 1.9° in hexagons. The greatest deviations in pentagons were 2.22°, 2.95°, 3.16°, and 2.36°, respectively. The greatest deviations in hexagons were 2.09°, 4.31°, 3.36°, and 2.12°.

As shown by the filled bars in Fig. 4, A and B, angles in clathrin-analogous cages deviated even less from the ideal 108° in pentagons and 120° in hexagons.

Bond angles routinely vary by 12°, the difference between a bond angle in a pentagon and a bond angle in a hexagon, so these deviations may be regarded as minor. Thus, a significantly greater deviation in bond angle does not explain why improbable cages do not self-assemble whereas probable cages do.

Dihedral angles at a vertex

That bond angles vary by so little from ideal values suggests that it would be productive to investigate fullerene cages with the assumption that bond angles in hexagons and pentagons are the ideal 120° and 108°. Since all of the faces in fullerene cages are hexagons (6) or pentagons (5), and all of the vertices are trivalent, fullerenes have just four types of vertex: 666, 566, 556, and 555 (Fig. 5).

Figure 5.

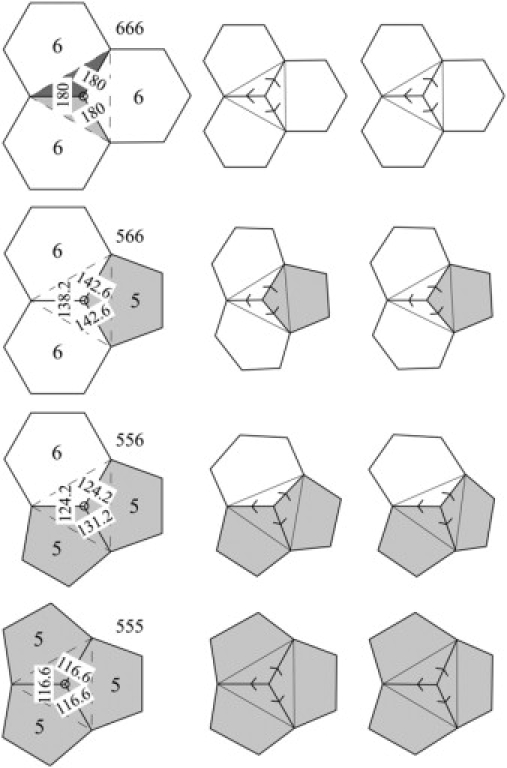
Four kinds of vertex: 666, 566, 556, and 555. A plane is defined by three points. Two planes intersect at each of the three edges emerging from a vertex. The angle that the two planes make with one another is a dihedral angle. Assuming regular hexagons (bond angles = 120°) and pentagons (bond angles = 108°), the nature of the three faces (5 or 6) about a vertex fully determines the three dihedral angles noted in the left column about the three edges emerging from that vertex. These dihedral angles may be appreciated from the stereofigures to the right.

Each triplet of bond angles at a vertex determines the three dihedral angles at that vertex. For example, the dihedral angle between the two filled planes associated with one of the edges emerging from the 666 vertex in the uppermost left part of Fig. 5 is 180°. Hexagons thus tile a plane. At the other extreme, the dihedral angles about the edges emerging from the 555 vertex in the lowermost part of Fig. 5 are 116.6°. (Compare the stereoversions of these vertices on the right side of Fig. 5.) All of the vertices in a dodecahedron (n = 20), with 12 pentagons and no hexagons, are 555 vertices, and all of the dihedral angles are 116.6°, so this smallest fullerene is close to spherical in shape. The dihedral angles about a 566 vertex are 138.2° about the 66 edge and 142.6° about the each of the two 56 edges (Fig. 5, second row). All of the vertices in buckminsterfullerene are of this type, and all of the dihedral angles are thus close to 140°, so this fullerene is also close to spherical in shape, a useful property for a soccer ball. Insofar as the bond angles are ideal, dihedral angles in fullerenes are fully determined by the types, pentagon or hexagon, of the three faces at each vertex.

The two dihedral angles about one edge may be different

Each edge in a fullerene is related to a quartet of faces. The central (bold) edge in Fig. 6 A, for example, is coded 66-56, the first pair of numbers representing the two end faces (6 and 6), the second pair the two side faces (5 and 6). The dihedral angle about the central edge at its left end is 142.6°, marked on the left side of Fig. 6 A. We show the same (central) edge on the right side of Fig. 6 A, but here we mark the dihedral angle about its right end, also 142.6°. They are the same because the two vertices necessarily have the same side 5 and 6 faces and happen to have the same end faces, a 6 for the left vertex and a 6 for the right. Because the dihedral angles about the central edge at its left and right vertices are the same, the upper left, center, and upper right edges may be coplanar, in which case the lower left, center, and lower right edges would be coplanar as well.

Figure 6.

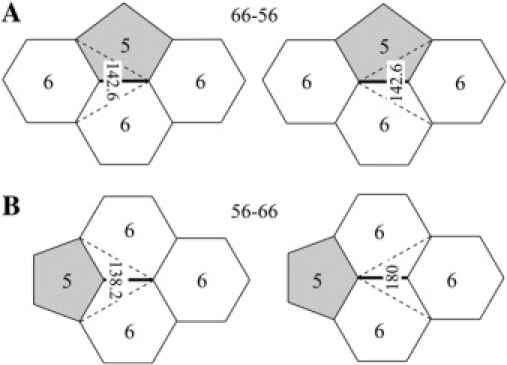
If the faces at the ends of an edge are different, the dihedral angle about the edge at one end is different from the dihedral angle about the edge at the other end. (A) If the faces at the ends of the central edge are the same, 6 and 6 in this case, the dihedral angles about the central edge are the same at its left and right ends, 142.6° in this case, so there is no DAD along this edge. This edge is labeled 66-56, the 66 for the two end faces, the 56 for the two side faces. (B) If the faces at the ends of the central edge are different, 5 and 6 in this case, the dihedral angles about the central edge are different at its ends, 138.2° on the left, 180° on the right. Therefore, the DAD is 41.8°, increasing and therefore broadening from left to right, from the pentagon-end face to the hexagon-end face. This edge is labeled 56-66, the 56 for the two end faces, the 66 for the two side faces.

The central edge illustrated in Fig. 6 B is coded 56-66. Again, the same (central) edge is represented on the left and right sides of the figure. The dihedral angle about the central edge at its left end is 138.2°, whereas the dihedral angle about the central edge at its right end is 180°. The difference arises because, even though the left and right vertices necessarily have the same side (6 and 6) faces, they have different end faces, 5 on the left and 6 on the right. The dihedral angle about the central edge thus increases by 41.8° from the left (5-end) to the right (6-end). This DAD has a direction, so it is drawn as a vector that points from the 5-end to the 6-end in later figures. Physically, then, the (dihedral) angle between pairs of planes about the central edge increases from the 5-end to the 6-end.

Just nine different types of edge, that is, just nine different types of face quartet, are possible (Fig. 7). Three of them, 56-66, 56-56, and 56-55, the ones in the center column of Fig. 7, have different end faces and thus a DAD. The other six have the same end faces, 5 and 5 or 6 and 6, and thus do not have a DAD.

Figure 7.

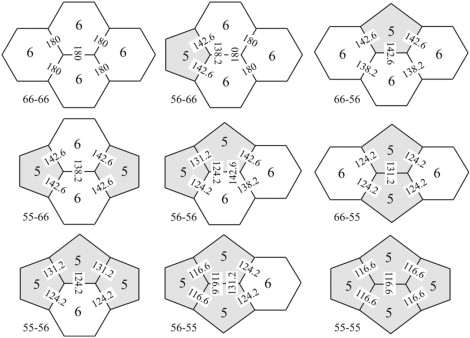
The nine kinds of edge include six with the same types of face (5 and 5 or 6 and 6) at the ends, hence no DAD, and three with different types of face at the ends, hence a DAD.

Fig. 8 A shows the three edges with a DAD again: The 56-66 edge discussed above (Fig. 6 B), with a DAD of 41.8° (180°–138.2°), is colored green. The 56-56 edge, with a DAD of 18.4° (142.6°–124.2°), is colored red. The 56-55 edge, with a DAD of 14.6° (131.2°–116.6°), is colored blue. In Fig. 8 A, these colored edges are drawn as vectors pointing from the 5-end to the 6-end, from the end with a smaller (narrower) dihedral angle to the end with a larger (broader) dihedral angle. The DAD vector thus points in the direction of the broadening of the dihedral angles about an edge.

Figure 8.

Types of Ring. (A) DAD is a vector, pointing from the pentagon end to the hexagon end, in the direction of broadening of the dihedral angle about that edge. The three types of DAD are colored green, red, and blue. (B) The eight pent-Rings. The numerical codes are explained in the text. The two pent-Rings with head-to-tail DADs are marked with an asterisk. (C) The 13 hex-Rings. The numerical codes are explained in the text. The four hex-Rings with head-to-tail DADs are marked with an asterisk.

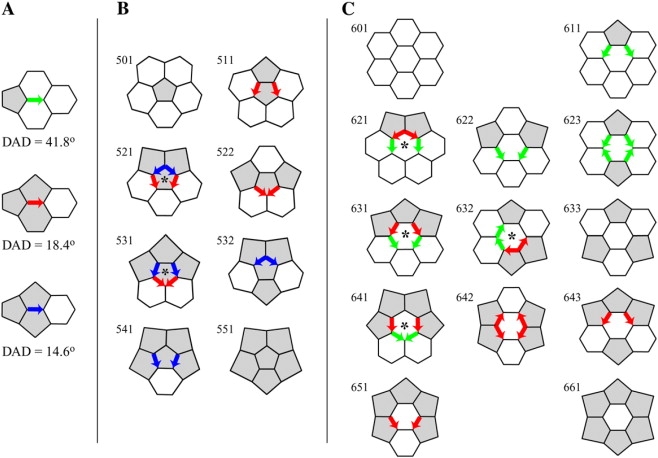
Improbable paths

We refer to a face plus the faces around it as a Ring. Fig. 8 B proves by construction that there are eight types of pentagon-centered Ring (pent-Ring). Fig. 8 C proves by construction that there are 13 types of hexagon-centered Ring (hex-Ring). We number the Rings in combinatorial order. For example, Ring 642 refers to a hexagon (6) with four pentagons around it arranged in the second of the three different ways, as shown for Rings 641, 642, and 643 in Fig. 8 C.

A face is fully described by a) the whole set of bond angles about its five (or six) vertices, and b) the dihedral angles about its five (or six) edges. Insofar as bond angles are ideal, 108° in pentagons and 120° in hexagons, the dihedral angles about each of the center face's edges are completely determined by the quartet of faces related to that edge, as was shown in Fig. 7. Therefore, for each of the Rings in Fig. 8, B and C, all of the bond angles and all of the dihedral angles associated with a center face are completely determined by the type (5 or 6) of the center face and the types (5 and 6) and arrangement of the surrounding faces. This property of Rings is a great virtue and makes them particularly useful for geometric investigation.

Below, after some additional explanation focusing on the edges of each Ring's center face, we suggest that the two pent-Rings marked with asterisks in Fig. 8 B and the four hex-Rings marked with asterisks in Fig. 8 C are unlikely to self-assemble in the first place, or if they do assemble, are unlikely to remain. As a result, self-assembly of fullerene cages that contain any of these six improbable Rings would be improbable, and paths of self-assembly that avoid these improbable Rings would avoid producing failed cages like the one in Fig. 3 B.

DADs in Rings

The 501 and 551 pent-Rings and the 601, 633, and 661 hex-Rings have no DADs (Fig. 8, B and C). The only structures composed entirely of pentagons and hexagons that can be constructed with these Rings are the dodecahedron (n = 20) with just twelve 551 Rings, the truncated icosahedron (n = 60) with twelve 501 Rings and twenty 633 Rings, and a plane of hexagons with just 601 Rings. Therefore, the only fullerenes with no DADs are the dodecahedron and the truncated icosahedron.

Most Rings do have DADs. Six of the eight pent-Rings in Fig. 8 B have DADs, blue (56-55), red (56-56), or both. Ten of the 13 hex-Rings in Fig. 8 C have DADs as well, red (56-56), green (56-66), or both. Fig. 8 provides a proof by construction that both pent-Rings and hex-Rings in fullerene cages can have zero, two, or four edges with a DAD but not one, three, five, or six edges with a DAD.

The existence of small fullerenes other than the dodecahedron—like the ones in Figs. 1 A and 2 A that self-assemble from clathrin and carbon, and all of the IPR fullerenes other than the truncated icosahedron that self-assemble from clathrin and carbon, including the famous IPR C₇₀ cage—proves that Rings with DADs are not forbidden. In some Rings adjacent DADs point in opposite directions (e.g., the 623 and 642 Rings), so broadenings and narrowings may compensate for one another.

Compensation is not possible in cases where adjacent DADs point in the same direction, where a broadening is followed directly by another broadening. The improbable Rings that harbor these head-to-tail DADs are the 521 and 531 pent-Rings that are marked with asterisks in Fig. 8 B and the 621, 631, 632, and 641 hex-Rings that are marked with asterisks in Fig. 8 C. Both of the starred pent-Rings and three of the four starred hex-Rings have two sets of head-to-tail DADs; the 632 hex-Ring has just one set. The physical justification for calling these Rings improbable, that their assembly would have to complete severely nonplanar surround faces, is presented in detail in the companion work (45).

DADs in fullerene cages

We apply these concepts to whole fullerene cages in Fig. 9. As in Fig. 8 A, we code each 56-66, 56-56, and 56-55 edge with a green, red, or a blue vector, ideally representing 41.8°, 18.4°, or 14.6° of DAD. We also label each face with an asterisk if it contains head-to-tail DADs among its edges. The probable fullerene cages in Fig. 9 A (28-2, 36-14, 36-15, and 60-IPR-1) have no head-to-tail DADs and thus none of the improbable Rings. By contrast, the improbable fullerene cages in Fig. 9 B (28-1, 36-1, 36-4, and 36-9) have head-to-tail DADs and thus improbable Rings.

Figure 9.

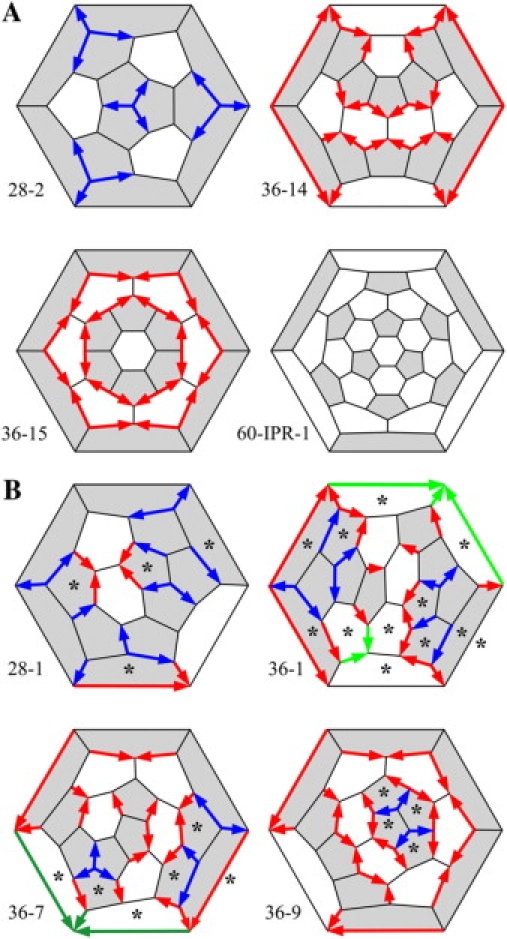
Schlegel diagrams for probable fullerenes (A) and improbable fullerenes (B) with color-coded DADs. Faces with head-to-tail DADs are marked with an asterisk.

To search among large numbers of fullerene cages for those that have improbable Rings and those that have none, it is convenient to identify all of the faces in a fullerene by their type of Ring, as we have done in the examples shown in Fig. 10. Table 2 shows the results for the two fullerene cages with n = 28 and the 15 cages with n = 36 vertices. In this table only the 28-2, 36-14, and 36-15 cages have no improbable Rings, exactly the three small cages into which clathrin self-assembles. Table 2 also shows that among the improbable fullerene cages with n = 28 and n = 36, the smallest number of improbable Rings is not one but two, and the smallest number of head-to-tail DADs is four.

Figure 10.

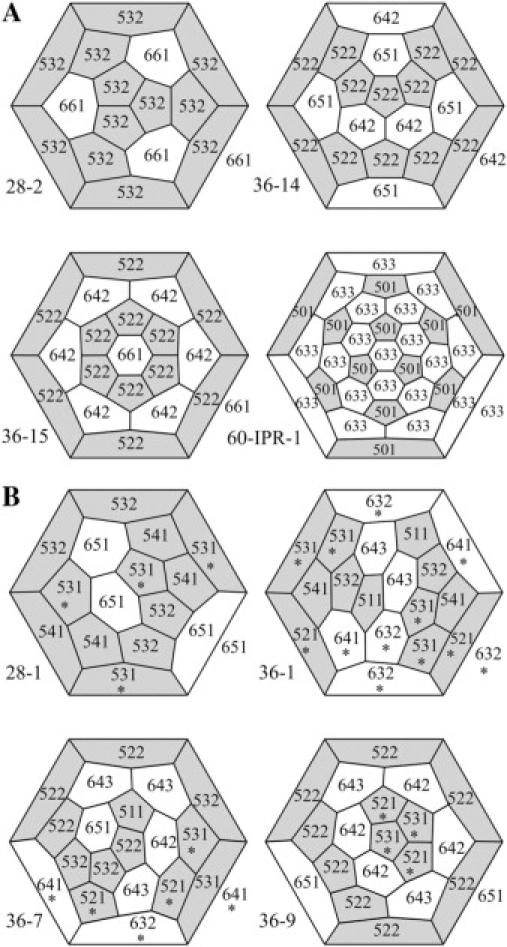
Schlegel diagrams with each face labeled according to its type of Ring for probable fullerenes (A) and improbable fullerenes (B). Faces with improbable Rings, that is, those that have head-to-tail DADs, are also marked with an asterisk.

Table 2.

The content of Ring types for both fullerenes with n = 28 and all 15 fullerenes with n = 36

n	28	28	36	36	36	36	36	36	36	36	36	36	36	36	36	36	36
Isomer ID	1	2	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
No. of Rings	16	16	20	20	20	20	20	20	20	20	20	20	20	20	20	20	20
Improb Rings	4	0	12	16	10	15	12	4	7	7	4	8	2	4	12	0	0
501	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
511	0	0	2	0	1	0	0	4	1	1	0	0	2	0	0	0	0
521*	0	0	2	4	5	5	0	0	2	5	2	2	2	4	6	0	0
522	0	0	0	0	0	0	4	0	4	1	8	6	4	6	0	12	12
531*	4	0	4	4	2	4	4	4	2	2	2	0	0	0	6	0	0
532	4	12	2	0	3	2	4	4	3	3	0	4	4	2	0	0	0
541	4	0	2	4	1	1	0	0	0	0	0	0	0	0	0	0	0
551	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
601	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
611	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
621*	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
622	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
623	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
631*	0	0	0	4	0	0	4	0	0	0	0	0	0	0	0	0	0
632*	0	0	4	4	2	4	0	0	1	0	0	2	0	0	0	0	0
633	0	0	0	0	1	0	0	0	0	1	0	0	0	0	2	0	0
641*	0	0	2	0	1	2	4	0	2	0	0	4	0	0	0	0	0
642	0	0	0	0	1	1	0	0	1	2	4	0	0	2	6	4	6
643	0	0	2	0	2	1	0	8	3	4	2	0	6	4	0	0	0
651	4	0	0	0	1	0	0	0	1	1	2	2	2	2	0	4	0
661	0	4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	2

The FM isomer numbering follows Fowler and Manolopoulos (24). The rows with bold numbers represent the improbable Rings, that is, the ones with head-to-tail DADs. A fullerene with 28 vertices has 12 pentagons and 4 hexagons, hence 12 pent-Rings and 4 hex-Rings. A fullerene with 36 vertices has 12 pent-Rings and 8 hex-Rings.

To be able to characterize the organization of DADs in the 222,509 graphically possible fullerene cages for 20 ≤ n ≤ 84, as enumerated in Table 1, we took several steps. First, we encoded every Ring in Fig. 8 by the type of center face (5 or 6) and the type of every surrounding face (5 or 6) in order. For example, hex-Ring 643 in Fig. 8 C is a hexagon (6) surrounded by four pentagons and two hexagons in this order, clockwise from the pentagon at the top left: 5, 5, 5, 6, 5, and 6. Thus, hex-Ring 643 could be encoded by the seven-digit number, the center face type followed by the surrounding face types, hence 6555656. Because the encoding of the surrounding faces could start on a different face, still in clockwise order, it also could be encoded by these seven-digit numbers: 6556565, 6565655, 6656555, 6565556, and 6655565. Finally, the order of the surrounding faces could be counterclockwise, producing another six encodings: 6565655, 6656555, 6565556, 6655565, 6555656, and 6556565.

Likewise, pent-Ring 511 in Fig. 8 B is a pentagon (5) surrounded by one pentagon and four hexagons and could be encoded by any of five six-digit numbers. In clockwise order these are 556666, 565666, 566566, 566656, or 566665; the counterclockwise order produces the same encodings.

Second, for each fullerene cage, we used the Fullgen program and a modification written by Gunnar Brinkmann to produce a list of all of its Rings encoded as above, each hex-Ring by a seven-digit number and each pent-Ring by a six-digit number. Third, we converted the list of Rings (e.g., 6555656 or 556666) so encoded to a list of Rings by type (e.g., 643 or 511).

Geometrically probable fullerene cages

The smallest fullerene, a dodecahedron with just 12 pentagons, has 20 vertices. The largest fullerenes we investigated have 84 vertices, moderately large cages with 12 pentagons and 32 hexagons. We investigated every one of these 222,509 fullerene cages to identify those without any improbable Rings. As was true for n = 28 and 36, the smallest number of improbable Rings in those cages that have any is not one but two, making these fullerene cages even more improbable.

Among these graphically possible fullerene cages for n from 20 to 84, only 66 are geometrically probable (Table 1). Fifteen are small cages (20 ≤ n ≤ 60) with adjacent pentagons, the ones shown in Fig. 11 A, and 51 are large cages (60 ≤ n ≤ 84) that obey the isolated pentagon rule (Table 1). The largest of the small non-IPR cages, 60-1784, has 60 vertices. The smallest of the IPR cages, the truncated icosahedron (60-IPR-1), also has 60 vertices.

Figure 11.

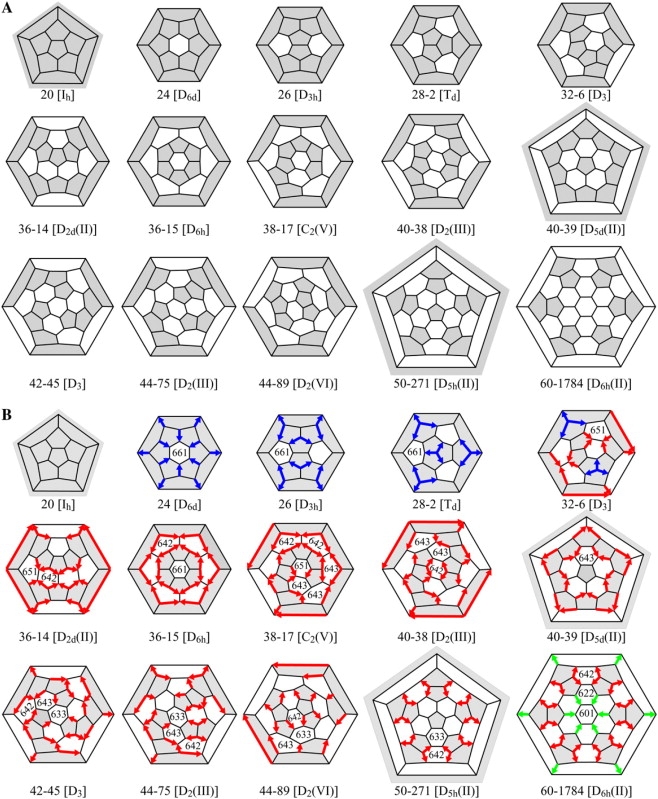
The 15 small, geometrically probable fullerene cages. (A) These fullerenes have adjacent pentagons but no improbable Rings. (B) Except for 20 (I_h), all of the small, geometrically probable fullerene cages have DADs. Some of these cages have DADs of just one color. Some have DADs of two colors, but none have Rings with two colors, which would have meant head-to-tail DADs.

Small, geometrically probable fullerene cages

Excepting the truncated icosahedron, all of the other 5,769 mathematically possible small (n ≤ 60) fullerenes have adjacent pentagons. We call this set of 15, including the non-IPR 60-1784, the small, geometrically probable fullerene cages (Fig. 11 A). There are two geometrically probable cage isomers for each n = 36, 40, and 44. There are no geometrically probable fullerene cages for n = 30, 34, 46, 48, 52-58, and 62-68; correspondingly, no fullerene cages with these n have been identified in carbon or clathrin. There are thus gaps, with no geometrically probable fullerenes for n immediately below and above n = 32, 50, and 60, none immediately below n = 36, and none immediately above n = 44.

Cages 24, 26, and 28-1 have two, three, and four isolated hexagons, respectively, isolated by virtue of being surrounded by pentagons. Cage 36-15 also has two isolated hexagons. Others of the small geometrically probable cages have strings of 2 hexagons (32-6), 3 hexagons (40-38), 4 hexagons (36-14), 9 hexagons (38-17), and 10 hexagons (40-38). Still others have loops of five hexagons (40-39) and six hexagons (36-15).

Cage 50-271 has two isolated pentagons. Other cages have strings of 2 pentagons (60-1784, 50-271, and 44-75), 3 pentagons (44-89), 4 pentagons (44-75 and 42-45), 6 pentagons (40-38), and 12 pentagons (38-17). Still others have loops of 6 pentagons (36-15), 10 pentagons (40-39), and 12 pentagons (36-14).

As noted above, the one cage with n = 20 has no DADs. The next three larger cages, 24, 26, and 28-1, have only blue DADs (Fig. 11 B). The nine cages 36-14 to 50-271 have only red DADs Two of the cages have DADs of two types: 32-6 has blue and red, and 60-1784 has red and green; of course, the two types of DADs in these probable cages are not arranged head-to-tail.

Large geometrically probable fullerene cages

By definition, IPR cages have no adjacent pentagons. Among pent-Rings, the only one without adjacent pentagons is the 501 pent-Ring (Fig. 8 B). Among hex-Rings, the only ones without adjacent pentagons are the 601, 611, 622, 623, and 633 hex-Rings (Fig. 8 C). Therefore, IPR cages can contain only these Rings.

Pent-Ring 501 has no DADs. Hex-Rings 601 and 633 have no DADs; the other three hex-Rings—611, 622, and 623—have edges with a DAD, but none has a head-to-tail DAD. Therefore, none of these five IPR hex-Rings is improbable. Since none of the pent-Rings and hex-Rings from which IPR fullerene cages are constructed is improbable, all IPR cages are geometrically probable. Specifically, 51 of the fullerenes cages for 60 ≤ n ≤ 84 are IPR, and all of these are necessarily geometrically probable.

Besides IPR cages, there are no other geometrically probable fullerenes for 60 < n ≤ 84. Conversely, at least for 60 < n ≤ 84, the only geometrically probable fullerene cages are the IPR ones. This finding was a great surprise. We address the question of whether geometrically probable non-IPR cages might exist for n > 84 in another work (S. Schein and T. Friedrich, unpublished).

The pent-Rings in IPR cages are all 501, which has no DADs. The fullerene with n = 20 is the dodecahedron. It contains only 12 faces, and all of them are 501 pent-Rings. Therefore, the dodecahedron has no DADs. The only hex-Rings in IPR cages with no DADs are 601 and 633. The hex-Rings in the IPR truncated icosahedron are all 633 (Fig. 10 A); therefore, this IPR cage has no DADs (Fig. 9 A). All other IPR cages—indeed, all other fullerene cages—have DADs; for example, the IPR cage with n = 70 has 20 green DADs, as shown in Fig. 1 of the companion work (45).

Vertices in probable cages

All of the 20 vertices in the dodecahedron are 555. All of the 60 vertices in the truncated iscosahedron are 566. Since a DAD requires two types of vertex—from 555 to 556 to make a blue DAD, from 556 to 566 to make a red DAD, and from 566 to 666 to make a green DAD (Fig. 8 A)—the dodecahedron and the truncated icosahedron have no DADs. Indeed, they are the only fullerene cages with no DADs. Only one other structure of pentagonal and hexagonal faces, a plane of hexagonal faces, has only one type of vertex (666) and thus no DADs, but that structure is not a cage.

All other cages have two, three, or four types of vertex. In order of the four vertex types 555, 556, 566, and 666, the sequence of numbers of each type in a cage with 36 vertices could be two in a row (e.g., the 24 and 12 in this sequence: 0 of the 555, 24 of the 556, 12 of the 566, and 0 of the 666), three in a row (e.g., 4, 16, 16, 0), or four in a row (e.g., 8, 12, 12, 4). Because neighboring vertices share two faces, no cage can have a sequence with a gap (e.g., 4, 20, 0, 12).

A head-to-tail arrangement of DADs has two types of DAD, blue and red, which require three types of vertex (555, 556, and 566 (Fig. 8 B)) or red and green, which requires three types of vertex (556, 566, and 666 (Fig. 8 C)). Except for cages 32-6 and 60-1784, with three types of vertex and two types of DAD, all of the other 13 small, probable, non-IPR cages in Fig. 11 B have just one or two types of vertex, not enough to have any head-to-tail DADs. Likewise, large (n > 60) IPR cages have no adjacent pentagons, ruling out 555 and 556 vertices, leaving them with exactly two types of vertex, 566 and 666, also not enough to have any head-to-tail DADs. Outside of the 13 small, probable, non-IPR cages and all IPR cages, are there any other cages with just two types of vertex? The answer must be no, or they would have been identified by our exhaustive search among 222,509 cages for 20 ≤ n ≤ 84 as a probable cage.

The exceptional cages 32-6 and 60-1784 prove that it is possible for a cage to have three types of vertex and two types of DAD but still no head-to-tail DADs. Are there any other such cages? Again, the answer must be no, or it too would have been identified in our exhaustive search of probable cages. Remarkably, apart from the two exceptional cages 32-6 and 60-1784 among the infinite universe of fullerene cages, the group of cages with just one or two types of vertex is identical to the group of cages that have no head-to-tail DADs, the probable cages.

The weak version of the head-to-tail exclusion rule

Five of the improbable Rings (521, 531, 621, 631, and 641) have two sets of head-to-tail DADs. Hex-Ring 632 has only one. For that reason hex-Ring 632 may be less improbable than the other five Rings. Table 3 lists cages that have none of the five highly improbable Rings but do have hex-Ring 632s. For n ≤ 60, there are 99 such cages. Fig. 12 shows the 1 such cage for n = 42, the 2 for n = 44 and n = 46, the 6 for n = 48, and the 10 for n = 50.

Table 3.

Additional fullerene cages with n ≤ 50 could self-assemble if hex-Ring 632 were not so improbable

n	Number of cages	IDs of cages
42	1	41
44	2	80, 87
46	2	99, 116
48	6	169, 171, 196-199
50	10	226, 242, 260-266, 270
52	8	333, 335, 417, 419, 420-422, 437
54	11	535, 537-540, 560-563, 579-580
56	20	641, 822, 824, 854-855, 862, 864-865, 913-924
58	13	1058-1059, 1190, 1193, 1195-1199, 1201, 1203-1205
60	26	1123, 1220, 1496, 15801581, 172, 1776-1779, 1783, 1787-1790, 1794, 1796-1797, 1799, 1803-1806, 1808-1810
62	23
64	28
66	24
68	48
70	29
72	48
74	60
76	69
78	57
80	139
82	92
84	146

These fullerene cages have none of the five Rings with two pairs of head-to-tail DADs (pent-Rings 521 and 531 and hex-Rings 621, 631, and 641) but do have hex-Ring 632s with just one pair of head-to-tail DADs.

Figure 12.

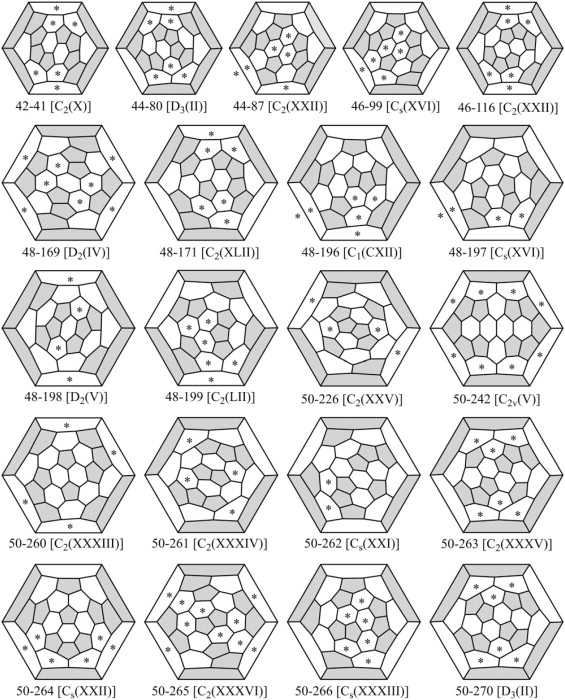
These additional fullerene cages with n ≤ 50 could self-assemble if hex-Ring 632 were not so improbable. Asterisks mark faces that are hex-Ring 632s.

The strong version of the head-to-tail exclusion rule excludes all six of the Rings with head-to-tail DADs, permitting just the 15 small (n ≤ 60) non-IPR fullerene cages in Fig. 11, buckminsterfullerene (n = 60), and IPR cages (n > 60). The weak version of the rule excludes all five or the Rings with two sets of head-to-tail DADs but permits hex-Ring 632 with one set; therefore, it additionally permits the fullerene cages for n ≤ 84 listed in Table 3, with the ones for n ≤ 50 shown in Fig. 12.

Discussion

The protein clathrin provides the three connected vertices and edges from which fullerene cages of different sizes self-assemble, from the one with 28 vertices to the truncated icosahedron with 60 (Figs. 1 A and 2 A) to still larger ones (3,12,19). Another protein, COPII, provides the edges and four connected vertices from which cages of different sizes (47) self-assemble, including the cuboctahedron (48). By contrast, viral capsid proteins provide surface tiles—not vertices—from which spherical virus shells self-assemble, typically geodesic spheres with icosahedral symmetry (49–51). Nonetheless, depending on the amount of nucleic acid or other “cargo” to be encapsulated, the same capsid proteins can also assemble virus shells of different sizes (52–54). All of these biological examples reveal a flexibility in accommodating loads of different sizes, afforded by the simple rules (e.g., fullerenes have three connected vertices and pentagonal and hexagonal faces) under which self-assembly operates.

However, although these simple rules admit an infinite number of graphically possible structures, rather few have been observed. Even more problematic, these simple rules by themselves are far more likely to produce defective structures (e.g., fullerene cages that cannot close, like the one in Fig. 3 B). Here we uncover a geometric constraint that greatly limits the range of fullerene structures to a small group of probable cages that includes the ones that have been observed.

We began by showing that the dihedral angles about the two ends of an edge may be different, rising from the pentagon (tail) end of the edge to the head hexagon end of the same edge. This rise, a DAD, is thus a vector characterizing an edge. We investigated Rings—a center face and its surrounding faces—because in that structure all of the dihedral angles and thus all of the DADs about the edges of the center face have been determined by the nature—hexagon or pentagon—of the faces. We found that the different Rings have different arrangements of DADs. In the companion work (45) we show that the surrounding faces of Rings with DADs arranged head-to-tail would be severely nonplanar, making self-assembly or maintenance of those Rings highly unlikely. Since such Rings with DADs arranged head-to-tail would be unlikely to self-assemble or last, self-assembly of cages that harbor such Rings is improbable. After exclusion of graphically possible cages with Rings that contain head-to-tail DADs in the range of 20 ≤ n ≤ 84, only a few cages remain as probable, specifically the 15 small, non-IPR ones (20 ≤ n ≤ 60) in Fig. 11, the truncated icosahedron (n = 60), and all of the 50 IPR ones (60 < n ≤ 84).

The head-to-tail exclusion rule admits both more and fewer fullerenes than standard rules

Like the IPR and the least-N_p rule, the head-to-tail exclusion rule is based purely on geometry and relies on the relationship between a face and its adjacent faces. It is therefore not surprising that the group of geometrically probable fullerenes is partly consistent with these previously proposed rules. Indeed, we show here that the isolated pentagon rule (25,26), the least-N_p rule (24), the typically high degree of symmetry among the cages that self-assemble (25,26,55), and the abundance of certain isomers, all follow from—and thus are explained by—the head-to-tail exclusion rule.

For example, all of the large fullerenes in our sample (60 < n ≤ 84) that are geometrically probable follow the IPR. Moreover, among the 15 small, non-IPR fullerenes with n ≤ 60, all but 60-1784 of the geometrically probable isomers are among those with least-N_p for their n (Table 1).

There are, however, important exceptions to those empirical rules. For example, the isolated pentagon rule permits only buckminsterfullerene with n = 60 and the small number of IPR isomers with n ≥ 70. The existence of small probable fullerene cages 28-1, 36-14, and 36-15 in clathrin, 36-15 in carbon (29), and perhaps 32-6, 44-75, 44-89, and 50-271 in carbon (36,37), all necessarily non-IPR, shows that the isolated pentagon rule is not inviolate. In addition, a recent report (18) provides unspecified fullerene cages from clathrin with n = 36, 38, 40, 44, and 50, numbers of vertices that are represented in Fig. 11, consistent with the predictions of the head-to-tail exclusion rule.

The related rule, selecting cages for any n with the lowest number N_p of edges between pentagons, has an inherent flaw: It requires selection of at least one isomer for any n (Table 1). The head-to-tail exclusion rule that we propose is both more discriminating and less. It is more discriminating in that all but one isomer, 60-1784, of the 15 non-IPR isomers that it selects are on the list of those with least-N_p, but it excludes many on that list. For example, it excludes all fullerene cages with n = 30, 34, 46, 48, 52-58, and 62-68. The rule is less discriminating in that it does include the 60-1784 cage with N_p = 6 pentagon pairs, a number only bettered because of the presence of the IPR buckminsterfullerene with 60 vertices and N_p = 0.

Symmetry is a consequence of the exclusion rule

Symmetry itself has been supposed to be a selection rule (55). However, the 15 small geometrically probable cages (Fig. 11) span a wide range of symmetry order. The symmetry order of point group I_h (cage 20) is 120 (Table 5.1 of Fowler and Manolopoulos (24)). That of point group T_d (cage 28-2), D_6d (cage 24), and D_6h (cages 36-15 and 60-1784) is 24. That of D_5h (cage 50-271) and D_5d (40)-(39) is 20. That of D_3h (cage 26) is 12. That of D_2d (cage 36-14) is 8. That of D₃ (cages 32-6 and 42-45) is 6. That of D₂ (cages 40-38, 44-75, and 44-89) is 4. That of C₂ (38)-(17) is 2. Moreover, although some of these cages possess a high symmetry order, so do other geometrically improbable cages with the same n. Thus, probable cage 50-271 is a member of the D_5h point group, but so is improbable cage 50-1 (Fowler and Manolopoulos (24)). Probable fullerene 40-39 is a member of the D_5d point group, but so is improbable cage 40-1 (Fowler and Manolopoulos (24)). Probable cage 44-89 is D₂, but so are five other improbable cage isomers with 44 vertices (Fowler and Manolopoulos (24)). Probable cage 60-1784 is the second of two cages with 60 vertices in the D_6h point group. Therefore, our results suggest that symmetry among the small, non-IPR, geometrically probable fullerenes is a consequence of the head-to-tail exclusion rule rather than a selection rule in its own right.

The strong and weak versions of the head-to-tail exclusion rule

Although we have not distinguished carbon and clathrin with respect to self-assembly of fullerene cages, there are differences. Carbon self-assembles almost exclusively into IPR cages, whereas small clathrin cages with adjacent pentagons are common. Carbon forms fullerene cages with hexagons and 12 pentagons, whereas clathrin can also form nonfullerene cages with heptagons (18,56). It is therefore possible that self-assembly by clathrin triskelia follows less strict rules than carbon.

For example, we have supposed that self-assembly by carbon excludes all of the six Rings with head-to-tail DADs, thus explaining assembly of IPR cages and C₃₆-15 from carbon. We call this rule the strong version of the head-to-tail exclusion rule. However, if clathrin were less strict, it might permit the hex-Ring 632 that has just one set of head-to-tail DADs. This weak version of the head-to-tail exclusion rule would permit self-assembly of not only the 15 non-IPR cages in Fig. 11 and all IPR cages but also the cages in Fig. 12 for n ≤ 50 and the larger ones listed in Table 3. The smallest of these weak version cages has 42 vertices, so the only remaining unrepresented n for clathrin would be 30 and 34. However, even if hex-Ring 632 were somewhat improbable rather than very improbable, we would expect to find relatively few of the weak version cages.

Probable vertices and cages of different sizes

If 555, 566, or 666 vertices were favored, then the dodecahedron, the truncated icosahedron, or the plane of hexagons, respectively, would be the lowest energy structures. However, no fullerene cage can be constructed from only 556 vertices (57), so if that vertex were favored, an argument has been made that the lowest-energy combinations of vertices 555, 556, and 566 would be found in the 28-2, 36-14, and 36-15 cages (57). Clearly, this argument does not apply to carbon cages, and since clathrin has been shown to self-assemble into non-IPR cages with more than 36 vertices (18), the truncated icosahedron (2,58), still larger cages (19), and planes of hexagons (56,59), this argument cannot be correct.

However, a simplification of the argument in Katsura (57), focusing on the curvature at a vertex, is instructive. For a discrete surface, curvature is equal to the angle deficit (D) at a vertex, 360° minus the sum of the three bond angles. For example, an ideal 556 vertex would have an angle deficit of 360° − 108° − 108° − 120° = 24°. A least-energy angle deficit at a vertex in the range from 36° to 24° would favor 555 and 556 vertices—just two types of vertex—and thus the small probable cages 24, 26, and 28-2. A least-energy angle deficit in the range from 24° to 12° would favor 556 and 566 vertices—just two types—and thus the small probable cages in Fig. 11 A with 36 ≤ n ≤ 50. And, a least-energy angle deficit in the range from 12° to 0° would favor 566 and 666 vertices—just two types—and thus the IPR fullerene cages with n > 60. These results and others are listed in Table 4.

Table 4.

Different least-energy angle deficits (D) at a vertex favor different types of vertex and different cages, all of them probable cages

	Favored vertices
Least-energy angle deficit (D) at a vertex	555	556	566	666	Favored cages
D ≥ 36°	x				20
36° > D > 24°	x	x			24, 26, 28-2
D = 24°	x	x	x		32-6
24° > D > 12°		x	x		36-14, 36-15, 38-17, 40-38, 40-39, 42-45, 44-75, 44-89, 50-271
D = 12°		x	x	x	60-1784
			x		60-IPR-1
12° > D > 0°			x	x	large (n > 60) IPR cages
D = 0°				x	planes of hexagonal faces

This table also shows how the least-energy angle deficit could favor the two exceptional cages, 32-6 and 60-1784, the only ones with three kinds of vertex: If the least-energy angle deficit were equal to 24°, then 556 vertices would be most favored, but since no cage has only 556 vertices, 555 and 566 vertices would also appear, leading to the exceptional 32-6 cage. Likewise, if the least-energy angle deficit were equal to 12°, then 566 vertices would be most favored, and including 556 and 666 vertices would produce the exceptional cage 60-1784. However, in the latter case, there is a cage with 566 vertices exclusively, the truncated icosahedron, so that cage would also be favored.

Cargo of different sizes, like the transferrin molecule (small), the low density lipoprotein molecule (intermediate), and the reovirus particle (large), elicit endocytosis employing clathrin cages over a wide range of size in one and the same cell (19). No single least-energy angle deficit would be suitable. However, if the preferred least-angle deficit at a vertex were determined by the curvature of the cargo, cage size could be instructively determined (19). However as shown in Table 4, the cages would still be limited to the probable ones described here.

A model for self-assembly: the probable roads hypothesis

According to the pentagon-road hypothesis, carbon fullerenes grow by addition of carbon to dangling bonds at the growing rim of unstable, IPR fragments of cages (cups), ultimately producing complete IPR cages like C₆₀ and C₇₀ (60,61). Because the fragments obey the IPR, identification of complete, small cages—necessarily non-IPR cages—like C₃₆-15 (16) would be inconsistent with this hypothesis (62). Of course, many clathrin cages are small and necessarily non-IPR, so the pentagon-road hypothesis is not particularly useful for clathrin fullerene cages.

According to the fullerene-road hypothesis, IPR carbon fullerenes result from addition (and deletion) of carbon to complete, small (and thus non-IPR) fullerene cages at interior sites in a manner that eliminates pentagon adjacencies (62), followed by further Ring rearrangement (63) to eliminate remaining pentagon adjacencies (24,64). The paucity or possible absence of evidence for complete small (n < 60) carbon fullerenes (on the way to assembling the carbon buckminsterfullerene) and the absence of evidence for complete carbon fullerenes for 60 < n < 70 (on the way to assembling the abundant IPR C₇₀ cage) create difficulties (65) for this hypothesis but not insurmountable ones (64).

The fullerene-road hypothesis permits backward as well as forward growth, along with internal reorganization. This hypothesis thus assumes thermodynamic equilibrium. The “pentagon road” does not permit internal reorganization and thus appears more closely allied with a kinetic description; however, at growing points along the rim, deletion as well as addition may be possible, suggesting reversibility and thus thermodynamic equilibrium. Thus, more fundamental than kinetics versus equilibrium is the issue of internal reorganization or not, with support for both positions for carbon cages.

The same issue confronts understanding of the growth of clathrin cages. Clathrin cages may grow monotonically (19), consistent with steady addition that could be confined to the rim (66). However, in clathrin-coated pits blocked from fission in permeabilized cells, all of the clathrin triskelia are capable of exchanging, requiring uncoating as well as growth mechanisms (67–69). Indeed, the nature of the physical interaction between a triskelion and its neighbors suggests that deletion and insertion of a triskelion are less awkward than might have been supposed (11,58,70). However, exchange due to deletion and insertion, if it were just one vertex out and one vertex back into the same spot, does not constitute internal reorganization, which requires insertion or deletion of pairs of vertices (71). The advantage of internal reorganization (13,58,71–73) in addition to exchange at the growing rim would be that curvature-generating pentagonal faces could be placed as needed (instructed) to fit the cage around cargo of different sizes (19,74).

The head-to-tail DAD exclusion rule suggests an alternate description of growth of both carbon and clathrin cages, the geometrically “probable roads” hypothesis: After the binding of single-carbon atoms or clathrin triskelia at the growing rim or pairs of carbon atoms (16,62,64) or clathrin triskelia ions (71) internally, nascent faces on a path to producing any of the Rings with head-to-tail DADs would be highly nonplanar (45), fail to complete, and then disassemble. Growth therefore leaves exclusively probable Rings in place and thus generates only probable cages, the small (n ≤ 60) non-IPR cages in Fig. 11 from smaller non-IPR fragments as well as buckminsterfullerene (n = 60) and large (n > 60) IPR cages from smaller IPR fragments.

The starting point for self-assembly is obviously a single carbon atom or clathrin triskelion. Nonetheless, a road map might be drawn starting with a hexagon or pentagon. However, to keep it even less cluttered, the roadmap in Fig. 13 shows only probable roads that begin with the included hex-Rings that are marked in the cages in Fig. 11 A, hex-Rings that already have 19–24 vertices. Also, Fig. 13 shows only a tiny sample of the probable roads that originate from those hex-Rings. The roads in the top half of the figure begin with non-IPR hex-Rings and lead (downward) to non-IPR cages. The roads in the bottom half begin with IPR hex-Rings and lead (downward) to IPR cages as well as switching into the top half to lead to non-IPR cages.

Figure 13.

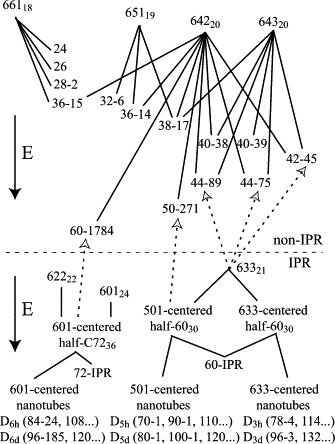
Part of a probable roads roadmap for fullerene structures, starting from some of the hex-Rings and leading to some of the fullerene cages permitted by the head-to-tail exclusion rule. Non-IPR hex-Rings and cages are above the dashed line; IPR hex-Rings and IPR cages are below it. IPR cages with N ≤ 84 are numbered among IPR cages according to Fowler and Manolopoulos (24); larger cages are numbered according to the order in which they are produced by CaGe. Bound carbon atoms or clathrin triskelia are lower in energy than free monomers, so the potential energy E of the system is lower for larger fullerene fragments or cages.

Roads may converge. For example, hex-Ring 633 with 24 vertices may grow into buckminsterfullerene via a hexagon-centered half-buckyball with 30 vertices or via a pentagon-centered half-buckyball with 30 vertices. Roads may diverge. For example, the pentagon-centered half of a buckyball may grow into 50-271, the buckyball itself, or nanotubes with a pentagon-centered half-buckyball as a cap. And, although we have emphasized the limited number of probable cages among the many mathematically possible fullerene cages, the vast majority of random additions of vertices would be unable to grow into any mathematically possible cage (e.g., Fig. 3 B) and end up having to reverse course and disassemble (19).

The probable roads hypothesis thus may rely on both kinetic and equilibrium-thermodynamic mechanisms. For example, only probable Rings might be completed because of kinetic limitations due to geometry, with the roads bounded by high (activation energy) walls. Alternatively, only probable Rings might last, reflecting a deep local energy trough that favors probable Rings over improbable Rings in an equilibrium situation. Within each road—bounded by walls (kinetics), or within each trough bounded by walls (equilibrium)—addition (growth) and deletion may occur, reflecting an equilibrium-thermodynamic process.

Indeed, as growth occurs along a probable road, the potential energy of the system falls as each monomer is withdrawn from a high-energy reservoir of unbound monomers and recruited to a lower-energy bound state as part of a growing cage, as indicated by the arrows in Fig. 13. In short, the more vertices, the larger the cage, the lower the potential energy of the system (75). The largest cage is thus a plane of hexagonal faces. Clathrin can form such a plane (2,56,59), and carbon commonly comes in the form of graphite. However, for clathrin cages, the pucker of the triskelions, an intrinsic angle deficit, promotes formation of curvature-inducing pentagonal faces (58,73,76,77). Insofar as pentagonal faces form with some probability anyway, the cage curves inward, ultimately closing with 12 of them, thus limiting cage size of both clathrin and carbon (16). Moreover, the binding of adaptor proteins into growing clathrin cages promotes assembly of cages with smaller radius and fewer vertices (13,22).

The absence of any probable path that would produce cages with vertex numbers both above and below n = 32, 50, and 60 and on one side of n = 36, 44, and 70 reduces the variety of fruitful roads and funnels self-assembly to the geometrically probable cage isomers at these n. Indeed, the presence of large gaps on both sides of n = 60, with no probable cages for 52 ≤ n ≤ 58 and 62 ≤ n ≤ 68 can explain the particularly great abundance of the C₆₀ buckminsterfullerene.

Self-assembly is the very basis for life. Small multisubunit proteins, the shell of a virus particle, the complex molecular factory that is the ribosome, and even large structures like organelles can be regarded as products of self-assembly; so, for that matter, can the folding of an individual protein molecule. The usual outcome in these examples is a single structure. By contrast, both carbon atoms and clathrin triskelia self-assemble into a variety of sizes and shapes of (fullerene) structures, so the many completed, probable cages at the ends of probable roads must occupy local energy minima rather than a global energy minimum. Thus, probable roadmaps—actually potential energy landscapes (78) that combine kinetics and equilibrium thermodynamics to guide self-assembly and equilibrium thermodynamics to drive it—may be able to describe a broad range of self-assembly processes.