Exploring the Parameter Space of Complex Self-Assembly through Virus Capsid Models

Abstract

We use discrete event stochastic simulations to characterize the parameter space of a model of icosahedral viral capsid assembly as functions of monomer-monomer binding rates. The simulations reveal a parameter space characterized by three major assembly mechanisms, a standard nucleation-limited monomer-accretion pathway and two distinct hierarchical assembly pathways, as well as unproductive regions characterized by kinetically trapped species. Much of the productive parameter space also consists of border regions between these domains where hybrid pathways are likely to operate. A simpler octamer system studied for comparison reveals three analogous pathways, but is characterized by much lesser sensitivity to parameter variations in contrast to the sharp changes visible in the icosahedral model. The model suggests that modest changes in assembly conditions, consistent with expected differences between in vitro and in vivo assembly environments, could produce substantial shifts in assembly pathways. These results suggest that we must be cautious in drawing conclusions about in vivo capsid self-assembly dynamics from theoretical or in vitro models, as the nature of the basic assembly mechanisms accessible to a system can substantially differ between simple and complex model systems, between theoretical models and simulation results, and between in vitro and in vivo assembly conditions.

Introduction

Self-assembly, a process by which collections of molecules spontaneously assemble into some structure or molecular machine under appropriate conditions, is an essential process for many of the key activities of living cells. These include the formation of protein and nucleic acid complexes necessary to protein, RNA, and DNA synthesis and degradation as well as pathological conditions such as the formation of prions and viral particles (1–3). An accurate understanding of complicated self-assembly reactions is therefore an important step in advancing the field of systems biology, which aims to build predictive models of the interactions of large numbers of components in living systems (4). Among the many examples of extremely sophisticated self-assembly in biology, virus capsid assembly has emerged as perhaps the most important model system for understanding complex self-assembly in general, in large part because of its relative experimental tractability and because the high symmetry of the structures makes them more amenable to theoretical analysis than are more heterogeneous systems. Nonetheless, our knowledge of capsid assembly and other complex self-assembly systems remains limited by the experimental challenges in directly observing rapid reactions on nanometer scales, particularly under in vivo conditions. Simulation methods have thus been essential to developing an understanding of the detailed dynamics of these systems.

Some of the key open questions about virus capsid assembly concern the nature of assembly pathways. Experimental examination of in vitro assembly systems suggests a great deal of diversity in assembly pathways among viruses. For example, the T = 7 phage P22 shows evidence of assembly through nucleation of a pentamer followed by accretion of coat protein monomers (5). HK97 (6), another T = 7 phage, and the human pathogen papillomavirus (7) both appear to assemble in a process involving an initial formation of capsomers (pentameric or hexameric components of the capsid), which then assemble into icosahedral shells. We define such an assembly process, in which capsid assembly proceeds through an initial aggregation reaction of coat monomers into a defined oligomer that then acts as the basic subunit for nucleation-limited capsid growth, as a “hierarchical assembly process”. This definition is in contrast to the oligomer-oligomer binding pathways that were found in prior simulation work (8,9) to provide a partial rescue pathway from kinetic trapping under conditions where nucleation-limited growth breaks down due to excessively high rate or concentration. Hepatitis B virus (HBV) (10) and cowpea chlorotic mottle virus (CCMV) (11) assemble through a different hierarchical process in which coat monomers first accumulate into dimers, then these dimers assemble via a nucleation-limited growth process involving a trimer-of-dimers nucleus. This diversity of assembly mechanisms raises several questions. Why have different assembly pathways evolved, even for viruses with superficially very similar final assembled geometries? Are there advantages or disadvantages to one pathway over another or is the choice simply arbitrary? How is the selection of pathways controlled at the level of protein-protein binding interactions? The answers to these questions could have important implications for human medicine, where attempts are being made to treat viral diseases by disrupting key steps in the assembly (12–14); for nanotechnology, where principles underlying virus capsid assembly and other complex biological assemblies are likely to prove valuable in learning how to design artificial self-assembly systems (15,16); and for basic research into the function and evolution of viruses.

Theoretical and simulation studies are proving crucial in interpreting these experimental results and gaining some understanding of the nature of assembly pathways in icosahedral capsids. Endres et al. (17) have applied a master equation approach, showing in simplified capsid models that a small number of critical intermediates can account for almost all of the pathways in a model system. A similar master equation technique was used by the same group to distinguish between different models of overall reaction pathways for hepatitis B virus assembly (10). This approach was generalized by Keef et al. (18) to study possible pathways and critical intermediates for the simian virus 40 (SV40) capsid and by Endres and Zlotnick (17) to provide general tools for interpreting experimental data on assembly kinetics to study overall pathways. In more recent work, our group has used stochastic simulations to study conditions under which these simplifying assumptions might break down. These studies found that high concentrations or conditions promoting high binding rate can bias the favored assembly pathways, promoting use of oligomer/oligomer interactions neglected under more simplified models (8). Furthermore, these effects become substantially more pronounced as we move from simpler to more complex capsid models (19). Coarse-grained molecular-dynamics-like models of capsid assembly have also proven useful for examining the effects of several parameters, such as solution temperature, concentration, and binding energy, on models of capsid assembly (1,20).

In this study, we apply stochastic discrete event simulations of icosahedral capsid assembly to attempt to answer some of the open questions about the nature of the assembly parameter space of complex self-assembly systems. Like Schwartz et al. (1), Endres and Zlotnick (17), Keef et al. (18), and Nguyen et al. (20), we are interested in studying the “phase space” of a complex assembly system as a whole as a function of its low-level binding interactions. We wish to understand what kinds of assembly pathways are accessible, what advantages or disadvantages they might have relative to one another, and how parameter variations produce transitions among them. For this purpose, we employ stochastic discrete event simulation, a simulation type that implements a kinetically correct model of all possible assembly pathways implied by a given set of binding rules, specifically excluding those pathways that would involve binding interactions that do not conform exactly to the binding rules. By kinetically correct, we mean that all possible pathways in the model will be sampled with probability proportional to their overall rates, provided the subunit-subunit binding rates are valid. The approach thus has the advantage of allowing a single simulation system to be used for a broad range of parameter values, regardless of which dominant pathways or combinations of pathways any particular parameter set produces. We use this method to explore accessible regions of the parameter space defined by varying two rate constants, comparing different points in space by their overall rates and yields, and by their intermediate distributions over time. To our knowledge, this is the first attempt to elucidate the space of assembly pathways as functions of coat-coat binding rates for a model of capsid assembly. We perform analogous experiments on a simpler octamer system to understand how the larger icosahedral system might behave in ways that would be unexpected from experience with simpler model systems. These results provide a basis for understanding the diversity of pathways available in a complex self-assembly system and the means by which transitions between them can be controlled.

Methods

Simulator design

Our simulations are based on a previously developed simulation tool (21) for coarse-grained simulation of complex self-assembly systems. The tool implements stochastic discrete event simulations using the model of Gillespie (22), a representation of stochastic reaction chemistry that is based on a continuous time Markov model (23) of the possible reaction trajectories of a system with finite numbers of intermediate species. The Gillespie model is implemented with a queue-based algorithm for fast, memory-efficient simulation of systems with large numbers of distinct intermediates (24). The simulator specifies model systems with a local rules representation (1,25), in which each assembly subunit is characterized by a set of binding sites with allowed neighbor sites and associated reaction rate constants. These subunit rules implicitly specify all of the structures and reactions that are possible in the system. To correct for the greatly reduced dissociation rate we would expect for multiply bound subunits, the simulator was run with an option disallowing dissociation of any subunit held in an assembly by multiple binding interactions unless all but one of that subunit's neighbors first dissociates from the assembly. This option has the effect of treating “loops” of subunits as infinitely stable over the time course of a simulation. The reader is referred to Zhang et al. (21) for details on the simulator implementation.

The simulator can optionally institute a correction for diffusion rates of oligomer species based on that of Lok and Brent (26). When this correction is used, the rate of a given binding interaction between two oligomers of size N₁ and N₂ is adjusted from the rate implied by its base binding rule by a factor of

$$\sqrt{\frac{N_1+N_2}{2N_1{N}_2}}\text{.}$$

Compared to the model without such a correction, this correction would be expected to yield a slower overall binding rate, yet yield more accurate binding rates for oligomer-oligomer interactions in a diffusion-limited system. The correction is not used for the majority of the simulations described below, but is enabled for a series of comparative simulations to determine the degree to which altered diffusion rates would affect our results for a diffusion-limited system.

Model systems

Two model systems were applied in this study. The study is primarily concerned with capsid assembly and relies on a 60-mer icosahedral capsid model for this purpose. The icosahedron was chosen because it is the simplest representation of spherical virus capsid assembly at the monomer level. Similar icosahedral model systems have been used in several prior simulation studies of capsid assembly (1,19,20,27,28). Previous studies by our group (8,19) have suggested several important qualitative differences in assembly behavior between such complex models and simpler, more experimentally tractable systems. To learn whether these complexity effects are also important to pathway selection, we also modeled a simpler octameric system. Although this latter system is too simple to be a realistic model of virus capsid assembly, it is sufficiently complex to exhibit several possible assembly mechanisms analogous to those found in the capsid models. Fig. 1 shows screen snapshots from these two model systems alongside the local rules specifying interactions between two binding sites of two different monomers. Fig. 1, a–d, show the complete octamer, two important intermediates in its assembly, and the local rules defining particle interactions in the system. The rules establish three binding interactions at 90° angles to one another. Two of them (colored green and yellow) yield an asymmetric binding interaction that produces square “capsomer” intermediates. We refer to these as the “intracapsomeric” bonds by analogy to the binding interactions producing pentameric capsomer substructures in icosahedral capsids. The other interactions (colored blue) form perpendicularly to the square capsomers through what we call “intercapsomeric” binding. To distinguish the tetrameric square (Fig. 1 c) involving two intercapsomeric and two intracapsomeric binding interactions from the capsomer (Fig. 1 b) formed only through four intracapsomer binding interactions, we refer to the former structure as a heterogeneous tetramer and the latter as a homogeneous tetramer. Two homogeneous tetramers can bind to one another by their four free binding sites each to create the full cube-shaped octamer. Fig. 1, e–h, show screen snapshots for the icosahedron and capsomer and trimer-of-dimer intermediates and the local rule defining the monomer binding interactions. A pair of asymmetric intracapsomer binding sites at 108° angles to one another produce a pentameric capsomer structure (Fig. 1 f). Intercapsomer binding sites bind symmetrically to one another to link 12 pentamers into the complete icosahedron.

Figure 1.

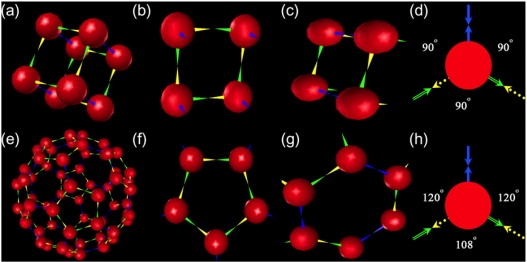
Model systems, key intermediates, and the local rules that produce them. The top row corresponds to the octamer system and the bottom row to the icosahedron system. (a) Complete octamer. (b) Homogeneous tetramer (capsomer) intermediate. (c) Heterogeneous tetramer intermediate. (d) Local rule describing the coat protein interactions in the octamer. The yellow and green arrows represent the asymmetric intracapsomer binding interactions and the blue arrows represent the symmetric intercapsomer interactions. (e) Complete icosahedron. (f) Pentamer (capsomer) intermediate. (g) Hexamer (trimer-of-dimers) intermediate. (h) Local rule describing the coat protein interactions in the icosahedron. The yellow and green arrows represent the asymmetric intracapsomer binding interactions and the blue arrows represent the symmetric intercapsomer interactions.

Experiments

Each system is parameterized by two forward rate constants and two reverse rate constants for the two binding interaction types. We denote these four rate constants by k_a+ (intracapsomer forward rate constant), k_a− (intracapsomer reverse rate constant), k_r+ (intercapsomer forward rate constant), and k_r− (intercapsomer reverse rate constant). We fixed a constant rate of 10³ (in arbitrary units) for both k_a− and k_r− in our two modeling systems and varied the two forward rates independently for each of the two systems. For the octameric system, we varied both k_a+ and k_r+ from 10⁻³ to 10⁵ in 10-fold increments. For the icosahedral system, we varied k_a+ over the range of 10⁻²–10⁵ and k_r+ over the range of 10⁻⁴–10³ in 10-fold increments. Each simulation run was initialized with 100N subunits, where N is the number of monomers in the complete structure (eight for octamer, 60 for icosahedron). Given such initial conditions, a maximum number of 100 complete structures could be achieved for each model system.

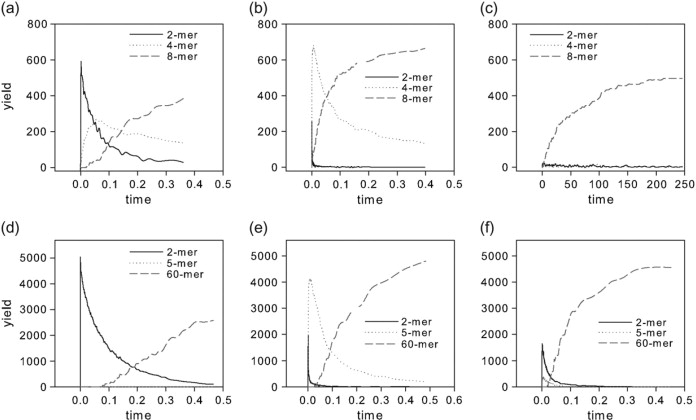
Each simulated assembly reaction was run until a pseudoequilibrium was achieved. Pseudoequilibrium was manually verified by determining whether all well-populated reactant species had reached stable counts in the simulation. We recorded the final yield (Y) of assembled complete structures in each system. We also recorded the time at which the amount of complete assembled structures reached Y/2. This time, which we call T₅₀, is used as a measure of the overall assembly rate. We also recorded the time courses of several important intermediate reactant species: 2-mer, 4-mer, and 8-mer intermediates for the octamer system and 2-mer, 5-mer, and 60-mer for the icosahedral system. These distributions are used to identify the pathways involved in each assembly reaction. These simulations were repeated with the diffusion rate correction described under “Simulator design” above.

Results and analysis

Fig. 2 shows the final yield (Y) of complete products (octamer or icosahedron) at equilibrium and the time to reach half of this yield (T₅₀) for each of the systems as functions of the inter- and intracapsomer binding rates. Fig. 2, a and c, depicts the yields and times for the octamer model. The figure displays several distinct regions of interest. When both binding rates are high (fronts of the figures), we observe a region of low yield, consistent with prior evidence of high kinetic trapping in the presence of high binding affinity (8,19). Although yield is low in this region, the overall assembly rate is rapid, as implied by the low T₅₀ in the front region of Fig. 2 c. Conversely, when both rates are low (backs of the figures), we observe nearly 100% yield but longer assembly time, as expected (8). Two distinct flat regions of high yield are observable in the left and right portions of the figures, with the right side corresponding to a low rate of intracapsomer binding but a high rate of intercapsomer binding and the left side corresponding to a high rate of intracapsomer binding but a low rate of intercapsomer binding. The slower of the two binding rates is limiting in each of these domains, because assembly yield and T₅₀ are insensitive to further increases in the higher rate. Yield appears essentially constant within either the left or right region over the parameter ranges examined, although the left region has a noticeably higher yield than the right. There is a continuous transition between these two regions through a third region of high yield where rates are similar for the two interaction types (back of the figures). Rate and yield are sensitive to changes in either parameter within this region. There is a gradual decline in yield and T₅₀ as parameters increase toward the fronts of the figures.

Figure 2.

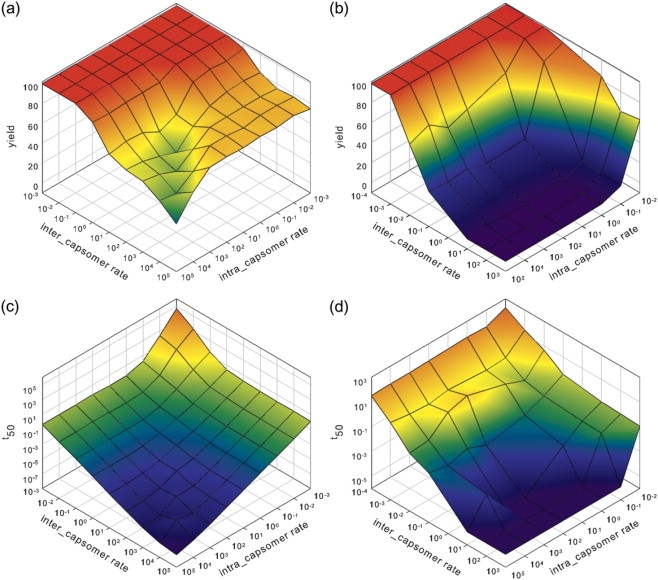
Changes of assembly yields (a and b) and assembly time needed to reach half the equilibrium level (T₅₀) (c and d) with intracapsomer and intercapsomer binding rate constants. A fixed breaking rate constant of 1000 is used across all the simulation experiments. (a) Yield of final assembled 8-mer (cube) structures for the octamer model. (b) Yield of final assembled 60-mer structures (icosahedron) for the capsid model. (c) T₅₀ for the octamer model. (d) T₅₀ for the icosahedral capsid model.

We can partially interpret this figure in terms of major pathways we would expect at different points in the parameter space. Fig. 3 a illustrates the pathways we would anticipate for the octamer assembly system. Where intercapsomer rates are much higher than intracapsomer rates, we would expect a hierarchical assembly mechanism, in which we rapidly accumulate dimers made by intercapsomer bonds before assembling octamers from the dimers through a second-order tetramer nucleation followed by first-order elongation. We call this a type I hierarchical assembly. This pathway corresponds to the right-side plateau region of Fig. 2, a and c. Since rapidly produced dimers are the building blocks for the formation of octamers, some population of hexamers would be formed and would continue to exist at pseudoequilibrium when no more dimers are available to further extend them to octamers. These hexamers would then become kinetically trapped, causing the observed lower octamer yield in that parameter domain. Where intracapsomer rates are higher, we would expect rapid accumulation of tetrameric “capsomers” in a fourth-order reaction, followed by accumulation of pairs of tetramers into octamers in a single additional step. We call this a type II hierarchical assembly. It would correspond to the left-side plateau region of Fig. 2, a and c. When rates are approximately balanced, we would expect a standard single-stage nucleation-limited assembly, where fourth-order nucleation of tetramers is followed by a second-order elongation through monomers. The nuclei could be capsomers or heterogeneous tetramers. We call this nonhierarchical mechanism a type III assembly. It would correspond to the region toward the middle of the plots. Despite their distinct assembly pathways, both type II and type III domains are capable of reaching the same end state of nearly complete conversion of monomers into octamers. The type II assembly provides a more efficient path to that end state, however. The type III assembly is also susceptible to kinetic trapping when both binding rates are high. Such kinetic trapping has been observed in many prior simulation and experimental studies of such systems (5,8). Note, though, that this pathway analysis is a significant oversimplification. It can approximately explain the behavior of the system at the extremes of rates in terms of three discrete mechanisms. The empirical data, though, shows a smooth transition in yield and rate as we move between these domains. Much of the parameter space thus appears to be occupied by regions where combinations of the three major assembly types or hybrid reactions not contained in any of them would be expected.

Figure 3.

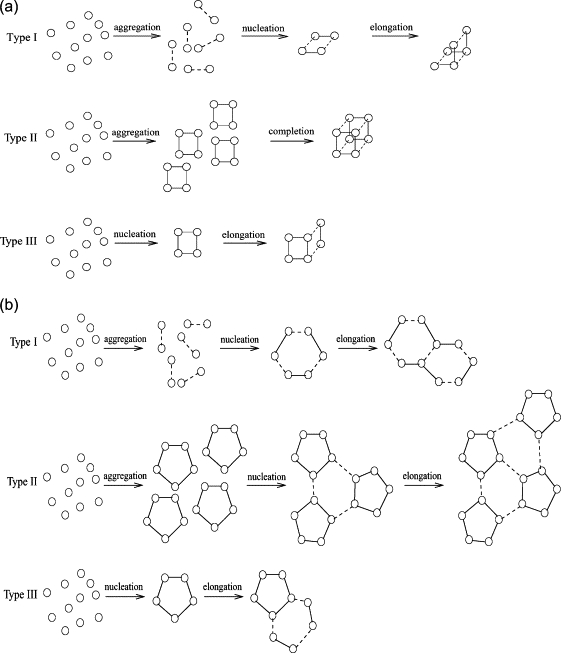
Predicted pathway domains for the two model systems. Each system is predicted to have three major pathways: two distinct hierarchical pathways (types I and II) and one nonhierarchical pathway exhibiting classic nucleation-limited growth (type III). (a) Octamer pathways. (b) Icosahedron pathways.

Fig. 2, b and d, depict the variation in yield and T₅₀ for the icosahedron. As with Fig. 2, a and c, we can identify three productive assembly regions in the parameter space: the type I region (back right), the type II region (back left), and the type III region (back center). Fig. 2 b shows high yield areas all along the back of the figure, corresponding to low rate in either parameter. High intercapsomer rates relative to intracapsomer rates result in a region of moderate yield at the back right of the figures. High intracapsomer rates relative to intercapsomer rates results in a region of high yield at the back left. Although these features are qualitatively similar to those observed for the octamer system, there are some notable contrasts. The icosahedron shows a precipitous drop off each region of high yield as the limiting rate increases. The octamer, by contrast, shows only gradual decreases in yield. The right region for the icosahedron achieves maximum yield at a noticeably higher overall assembly rate than is possible in the left region. The left region is significantly broader and subject to a more gradual decrease in yield and increase in rate with increasing intercapsomer binding rate. For example, the right region drops from nearly 100% yield to zero yield over approximately a 100-fold change in intracapsomer rate in contrast to the ∼10,000-fold change in intercapsome rate needed to cause a similar shift in yield in the left region. The right region thus appears to be the optimal domain for maximizing the rate of peak yield under highly controlled conditions, whereas the left region may be superior at achieving a robustly high yield under unpredictable conditions. There is once again a smooth transition between these regions through an intermediate region where the two binding rates are roughly proportional. Rates and yields are sensitive to both binding rates within this middle region, but largely insensitive to the larger of the two rates beyond it.

We can again interpret the figure in terms of three likely binding pathways. Fig. 3 b shows three pathways expected for the icosahedron system. Type I again corresponds to rapid intercapsomer binding, resulting in production of dimers that then assemble into complete shells through the nucleation of heterogeneous hexamers. Type II is again a hierarchical mechanism produced by rapid intracapsomer binding. For the icosahedron, though, type II assembly proceeds by aggregation into pentamers then to a nucleation-limited growth through a trimer-of-pentamers nucleus. The asymmetry in sensitivity to rate change between these regions can be largely explained by the differences in the number of required elongation steps after the aggregation stage. Both regions have third-order nucleation rates after aggregation, but the type II has many fewer elongation steps than the type I because it grows by pentamers rather than dimers. The long elongation phase would make the type I domain relatively less resistant to kinetic trapping and rate changes in the presence of small parameter variations. A nonhierarchical type III region is again predicted where there is a rough balance of rates. In this case, the nonhierarchical nucleation-limited assembly would be expected to proceed by slow pentamer nucleation followed by monomer accretion. All three regions would be expected to exhibit nucleation-limited growth after the aggregation reaction, making them vulnerable to kinetic trapping when binding rates are high. The trapped intermediate species may, however, differ between the three domains. The higher orders of most of the key assembly steps for icosahedron relative to octamer would explain the overall greater sensitivity of icosahedron rates and yields to small parameter variations. Note that these three pathway types are a result of the particular pattern of binding interactions used in our capsid model. A model allowing for more types of binding interactions with independent rates, as in Hagan and Chandler (9), could potentially open up additional pathway types not accessible to our two-parameter model.

To validate our interpretation of the rate and yield plots in terms of assembly mechanism, we conducted an additional analysis of intermediate distributions at three selected points in parameter space for each system. Fig. 4 shows curves of selected intermediate distributions over time for one point in parameter space believed to be representative of each of the three pathway domains for each system. The product of yield of each species at any time point and with its size is used here to quantify its distribution. The specific points in parameter space chosen are marked on Fig. 5 by capital letters A–F. Boundaries between the assembly domains were manually marked on Fig. 5 by looking for points at which the overall assembly rate becomes insensitive to further increases in the rate of the aggregation reaction. Fig. 4, a–c, show results for the octamer system, where we monitored time distributions of dimers, tetramers, and octamers. Fig. 4 a shows the point k_a+ = 10⁻², k_r+ = 10, believed to lie in the type I domain and marked by the letter A in Fig. 5 a. As expected, the graph shows a rapid production of symmetric dimers, which are slowly consumed to assemble heterogeneous tetramers and octamers. Fig. 4 b shows the point k_a+ = 10, k_r+ = 10⁻², believed to lie in the type II domain and marked by the letter B in Fig. 5 a. It shows a more pronounced early spike of tetrameric capsomers, which is accompanied by a lower peak of dimers. These early dimers are believed to be asymmetric dimers necessary for the early production of capsomers. These dimers are rapidly consumed into capsomers, which are then converted into octamers. Since only two capsomers are required to form an octamer, there is no possibility of kinetic trapping with this mechanism. Fig. 4 c shows the point k_a+ = 10⁻², k_r+ = 10⁻², believed to lie in the type III nonhierarchical domain and marked by the letter C on Fig. 5 a. This point shows minimal transient accumulation of either dimers or tetramers, consistent with the nucleation-limited assembly by monomer accretion predicted for a type III assembly.

Figure 4.

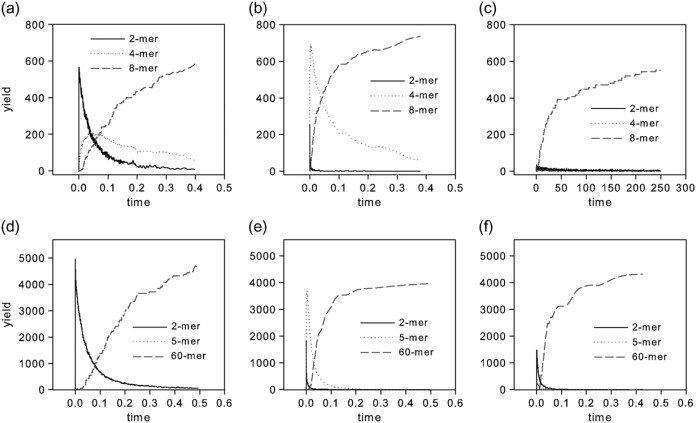
Weighted intermediate species distributions over time for regions of interest. (a) Octamer simulation for k_a+ = 10⁻², k_r+ = 10, belonging to the type I region. (b) Octamer simulation for k_a+ = 10, k_r+ = 10⁻², belonging to the type II region. (c) Octamer simulation for k_a+ = 10⁻², k_r+ = 10⁻², belonging to the type III region. (d) Icosahedron simulation for k_a+ = 10⁻², k_r+ = 10, belonging to the type I region. (e) Icosahedron simulation for k_a+ = 1, k_r+ = 10⁻², belonging to the type II region. (f) Icosahedron simulation for k_a+ = 10⁻¹, k_r+ = 10⁻¹, belonging to the type III region.

Figure 5.

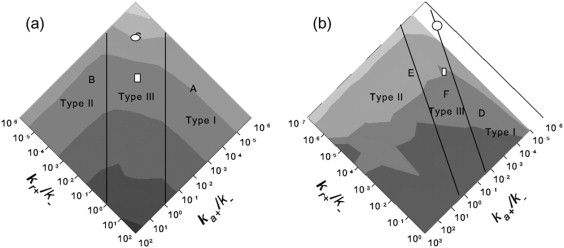
Phase diagrams mapping the predicted regions of assembly to plots of T₅₀. Darker intensities correspond to shorter times to assembly or to regions in which no productive assembly occurs. The slopes of the boundary lines are based on the orders of the aggregation events for the two hierarchical domains whereas the exact positions of the lines are based on visual identification of the region for which further change in the higher rate produces negligible overall increases in reaction rate. Consensus parameter values from capsid assembly estimates in the literature are marked assuming a 10-μM concentration typical for an in vitro system (circles) or assuming 500 μM concentration more likely to be representative in vivo (squares). Letters A–F mark points in the parameter domain at which intermediate distributions over time are surveyed in Fig. 4. (a) Octamer system. (b) Icosahedral system.

Fig. 4, d–f, show the time distributions for the icosahedron system, where we monitored distributions of dimers, pentamers, and icosahedra (60 mers) over time. Fig. 4 d shows the point k_a+ = 10⁻², k_r+ = 10, believed to lie in the type I domain and marked by the letter D on Fig. 5 b. As expected, the graph shows rapid formation of a high concentration of dimers followed by their gradual decrease as they assemble into 60 mers. There is negligible transient accumulation of pentamers. These observations are consistent with the predicted type I assembly pathway. Fig. 4 e shows the point k_a+ = 1, k_r+ = 10⁻², believed to lie in the type II domain and marked by the letter E on Fig. 5 b. It shows an early peak of pentamers, although also a small, short-lived peak of dimers. The pentamers are consumed as the reaction progresses, coincident with the appearance of 60 mers. These observations are consistent with the predicted type II pathway. Fig. 4 f shows the point k_a+ = 10⁻¹, k_r+ = 10⁻¹, believed to lie in the type III nonhierarchical domain and marked by the letter F on Fig. 5 b. Although this point does exhibit some early production of both dimers and pentamers, neither accounts for more than a small fraction of the total monomers present. This lack of well-populated intermediates is consistent with the expected type III pathway, although possibly with limited use of type I and type II reactions.

We finally sought to determine the degree to which accounting for altered diffusion rates might affect the results of our model. This correction would tend to yield more accurate results for a system in which binding rate is diffusion limited. Fig. 6, a–f, shows the results of simulations conducted with identical parameters to those of Fig. 4, a–f, but with the diffusion rate correction option described in Methods enabled. Intermediate distributions over time show that the three pathway types are all conserved at all six parameter values examined, although there are small quantitative differences in the curves. Assembly tends to be slightly slower with the correction but also to reach a slightly final higher yield at equilibrium. The correction therefore appears to produce some modest quantitative effects but to yield no significant qualitative change in any of the three pathway regions for either model system.

Figure 6.

Weighted intermediate species distributions over time for regions of interest with the simulator's diffusion rate correction option enabled. (a) Octamer simulation for k_a+ = 10⁻², k_r+ = 10, belonging to the type I region. (b) Octamer simulation for k_a+ = 10, k_r+ = 10⁻², belonging to the type II region. (c) Octamer simulation for k_a+ = 10⁻², k_r+ = 10⁻², belonging to the type III region. (d) Icosahedron simulation for k_a+ = 10⁻², k_r+ = 10, belonging to the type I region. (e) Icosahedron simulation for k_a+ = 1, k_r+ = 10⁻², belonging to the type II region. (f) Icosahedron simulation for k_a+ = 10⁻¹, k_r+ = 10⁻¹, belonging to the type III region.

Discussion

We have used stochastic discrete assembly simulations to characterize the space of assembly pathways for simple models of spherical virus capsid assembly. The simulations reveal three major pathway domains capable of producing nontrivial amounts of complete structures for each model system. One exhibits a nonhierarchical nucleation-limited assembly corresponding to slow formation of a nucleus followed by elongation by monomer addition. The others correspond to two hierarchical assembly mechanisms for which growth is preceded by aggregation into a multimer that acts as the principle unit of assembly. Although pathway phase diagrams are qualitatively similar between the two systems, the icosahedral system is characterized by a comparatively smaller productive parameter space and a much greater sensitivity to parameter changes in moving between domains or between productive and kinetically trapped regions of a given domain. Although the abstraction of discrete pathway domains is useful for understanding the systems, it is important to note that the boundaries between them are largely an artificial construct. The quantitative results show smooth transitions in overall assembly rates and yields as we move across the boundaries, suggesting that much of the productive parameter space likely represents mixtures of the dominant pathways and hybrid pathways accessible to the simulator but difficult to model theoretically.

One application of this work is to explore how we might alter binding rates to improve a self-assembly system by any given measure, an important question for understanding selective pressures on viral evolution and for using viral capsids as models for self-assembling nanotechnology. We could similarly ask how we might best interfere with an assembly system to disrupt normal growth. We can adopt the somewhat imprecise definition that a “good” system is one that leads to simultaneous high yield and short assembly time. In the octamer case, there then appears to be a slight advantage to the type II domain. The type III pathway can also achieve nearly complete yield, but at lower rates than the type II. The type I pathway is a poor choice by this criterion because it cannot achieve a peak yield for any parameters and generally has lower yield for a given rate than either type II or type III. The type II domain accomplishes this by effectively decoupling the octamer assembly pathway into two distinct simpler reaction pathways acting on different timescales: capsomer formation and dimerization of capsomers. Each of these pathways is protected from kinetic trapping, the first because none of its intermediates are stable and the second because it has only a single step. By contrast, the type III assembly is susceptible to kinetic trapping when binding rates are high enough for its second-order elongation rate to approach its fourth-order nucleation rate. The type I assembly is always vulnerable to kinetic trapping because its nucleation and elongation reactions have the same order and thus comparable rates for any binding rates. For the icosahedron, though, the answer is more complicated. The type I domain appears to be optimal for achieving peak yield at the highest assembly rate. Yet the type II domain's lower sensitivity to parameter variations may make it superior for achieving a robustly high rate and yield under more unpredictable assembly conditions. The nonhierarchical type III domain achieves a balance between these two tradeoffs, with border regions between the domains providing further room to tune the characteristics to particular assembly conditions. This observation might explain why the natural virology world appears to offer examples of all three kinds of assembly; the “best” domain could be any of the three or anywhere in between, depending on how predictable the assembly conditions are or what other mechanisms are employed to make them more predictable.

This observation leads to a second question: where might actual capsid assembly systems sit in this phase space? The prior literature provides some approximate estimates of the free energy of binding during capsid assembly. Model-based inferences from experimental data establish a range from ∼−2.9 to −4.4 kcal/mol per contact for HBV assembly (29) and ∼−3.8 kcal/mol, including coat and scaffold contributions, for P22 assembly (30). If we use −3.8 kcal/mol per contact as a consensus value, that would imply that the ratio k₊/k₋ is ∼680 M⁻¹ at 20°C for each binding site. Where this value would map on our phase diagrams depends on what we assume the units of concentration of our simulations to be, using an equivalence theorem sketched out in a previous study (8). If we assume our simulations represent 10 μM, a typical concentration for in vitro capsid assembly, then the k₊/k₋ needed to yield a free energy of −3.8 kcal/mol would be 8.5 × 10⁻⁶ particle⁻¹ for the octamer system or 1.1 × 10⁻⁶ particle⁻¹ for the icosahedron system. We can thus very roughly map real capsid assembly rates to this phase space by assuming k_a+/k_a− = k_r+/k_r− ≈ 8.5 × 10⁻⁶ particle⁻¹ for the octamer and k_a+/k_a− = k_r+/k_r− ≈ 1.1 × 10⁻⁶ particle⁻¹ for the icosahedron system. Fig. 5 identifies the corresponding points (represented with circles) in the parameter spaces for the two systems. For the octamer assembly, the consensus point lies in the middle of the type III nonhierarchical region. Our rate estimates would need to be perturbed by ∼3 orders of magnitude in either parameter (ΔΔG ≈ 4.0 kcal/mol) to produce hierarchical assembly by either mechanism. For the icosahedron, on the other hand, the consensus point lies approximately on the boundary of the type I and type III regions. Only a small error in either rate estimate would be needed to push it clearly into the type I or type III regions. A change of ∼2 orders of magnitude (ΔΔG ≈ 2.7 kcal/mol) in either parameter would be needed to produce type II assembly.

Our conclusions are very different if we assume our simulation represents a concentration of 500 μM, a level likely to be unachievable in vitro but realistic for the local concentration of coat protein at sites of capsid assembly in vivo (30). A free energy of binding −3.8 kcal/mol would then imply k₊/k₋ = 4.3 × 10⁻⁴ particle⁻¹ for the octamer and k₊/k₋ = 5.7 × 10⁻⁵ particle⁻¹ for the icosahedron. For the octamer, assuming k_a+/k_a− = k_r+/k_r− = 4.3 × 10⁻⁴ particle⁻¹ would still produce type III assembly with nearly complete yield, although the rate would be increased ∼50-fold relative to the 10-μM concentration. For the icosahedron, though, the higher concentration would move the system from the border of type I and type III domains well into the type III domain. These points are marked by squares in Fig. 5. The concentration change from the in vitro to the in vivo range would thus result in a substantial shift in the favored assembly pathways of the system. A slight loss in yield but a sizeable increase in rate would accompany the change in overall assembly pathway.

In drawing conclusions from such a simulation study, we must ask how the observed results might have been biased by the limitations of the model. The stochastic simulation method we used assumes a uniform reaction space in which times between reaction events are sufficiently long that spatial arrangements of particles can be assumed random. These assumptions are shared by ordinary differential equation (ODE) models of capsid assembly (17,31) but not required by Brownian dynamics capsid assembly models (1,9,20,27) or spatial Monte Carlo models (32). It is not possible to directly duplicate this study with any of these spatially aware models because all of them either used smaller symmetric 20-mer capsid models that cannot exhibit the hierarchical pathways of interest to us (20,32) or required concentrations above typical in vitro (1,20) or even in vivo levels (9,27,28) for systems to approach completion in reasonable timescales. We must therefore extrapolate from studies of simpler assembly systems to judge under what conditions explicit consideration of spatial arrangements of assemblies would lead to significant differences in quantitative performance. This question has been extensively studied in the literature on modeling macromolecular crowding effects on assembly reactions. These studies have suggested that models explicitly accounting for spatial effects will produce results virtually identical to space-independent ODE models under low concentration conditions, where particle diffusion is relatively unimpeded and long times elapse between collisions, but that the two will markedly diverge under conditions of high concentration. See, for example, Minton (33,34) and Zimmerman and Minton (35) for reviews of this issue. Models of other assembly systems suggest that a divergence between space-independent and space-free models will occur between typical in vitro and in vivo concentrations. For example, hard-sphere models of sickle-cell hemoglobin polymerization have suggested a modest 7% deviation from idealized space-free models at 20 g/L (1.25 mM) Hb_S, with the deviation rapidly increasing with higher concentrations. Space-aware lattice models of actin-like filament assembly suggested an ∼10% deviation from idealized kinetics at 250 μM, with a rapid increase beyond that point (36,37). We can therefore suggest that simulations of in vitro capsid assembly systems are unlikely to be significantly quantitatively altered by the lack of an explicit spatial model. This conclusion is supported by the fact that Zlotnick et al. (10) achieved a high-quality fit to a hepatitis B assembly system with their space-free ODE model over a broad range of in vitro concentrations and solution conditions.

Conclusions about results at in vivo concentrations where crowding effects become significant may be less trustworthy, especially if we account for the general crowding of the cell in addition to the higher concentration of coat monomers in vivo. Macromolecular crowding is generally observed to enhance assembly reactions (33) and crowding agents have been successfully used to promote assembly in several capsid assembly systems (38–41). We can therefore suggest that the shift our model predicts between in vitro to in vivo conditions in Fig. 5 is likely to understate the true magnitude of the change in rates and, thus, in pathways due to high concentrations of capsid proteins themselves and due to generalized crowding in the cell environment. Although one can in principle correct for crowding effects in an idealized model by adjusting rate constants (35), there is no general way to determine the amount of adjustment from first principles. These extremely high concentrations happen to be precisely where Brownian capsid assembly models become computationally tractable, and we might therefore suggest that the two model types might be treated as complementary sources of information, each more appropriate for modeling certain parameter domains.

A related issue in considering the reliability of our model is the fact that it excludes the possibility of malformed growth, which might lead to trapped malformed states or to rate changes due to reversible unproductive assembly. Whether this limitation is problematic depends on the degree to which off-pathway assembly occurs in the reaction system modeled. We are unaware of any attempt to quantify in vivo accuracy of assembly of any virus under normal conditions of host infection, but anecdotal evidence suggests assembly malformations are rare in wild-type conditions. Accuracy for in vitro systems depends a great deal on the system and the specific assembly conditions. For example, Zlotnick et al. (42) report no detection of misassembled forms in hepatitis B virus under ideal in vitro conditions whereas Moore and Prevelige (43) report only a minimal (but not quantified) fraction of misassembled species in a phage P22 in vitro assembly system. These and other capsids can produce high degrees of malformed growth under a variety of artificial conditions, including absence of key scaffold proteins (41,44), unusual ion concentrations during assembly (10), or changes in the stoichiometry of other assembly factors (43). Other in vitro systems, such as those for phage P4 (39) and phage φ29 (41), produce a large fraction of malformed species. The lack of a malformation mechanism in our study might be expected to lead to overestimates of yield and possibly assembly rate if it is applied to a system with an appreciable fraction of malformed structures. Our space-independent stochastic model can allow for exploration of malformed states (19), but with a much more computationally intensive method that would also be infeasible for this study.

Brownian models and similar discretized spatial Monte Carlo models also provide a straightforward way to simulate malformed growth, a capability used by Schwartz et al. (1,45), Hagan and Chandler (9), Nguyen et al. (20), and Wilber et al. (32), but are again also computationally infeasible for much of the parameter domains of interest in this study. We can, nonetheless, use the results of these other models to estimate where and how the conclusions of this study might be compromised by the lack of a malformation model. Schwartz et al. (1), Hagan and Chandler (9), and Wilber et al. (32) all found that malformed structures became the dominant assembly type under conditions of high concentration, but the exact amount depended on other parameters approximately corresponding to the energy of attraction of binding sites and the geometric flexibility of binding. All found malformations dominant with their default binding parameters only for concentrations in millimolar ranges, assuming a 4-nm particle in the case of Wilber et al. (32). With the most permissive binding parameters, though, malformations could become prominent at concentrations as low as 250 μM for Schwartz et al. (1). Nguyen et al. (20) had similarly found that with sufficiently strong binding interactions (low temperature), misassembled structures could become a common species across a wide range of concentrations, although malformed structures were never the dominant species in the 5.41- to 173-μM parameter range they examined. They further found, though, that temperatures yielding predominantly misassembled structures were strictly separated from those yielding predominantly complete assemblies by a wide region of kinetic trapping. Their results would appear to suggest that malformed growth competes with kinetically trapped growth and not with productive growth. We can therefore suggest that the lack of malformation pathways in our model is likely to lead to inaccurate assembly kinetics only within a subset of the kinetically trapped region of our parameter space corresponding to exceptionally high rates or concentrations. This region might extend more widely if coat-coat binding interactions are significantly stronger or more flexible than past capsid assembly models have assumed.

Finally, our use of a model that assumes infinite stability for structures held together by multiple binding interactions will limit the range of parameters in which the model is applicable. Experimental evidence from phage P22 (30,46) suggests that monomers exchange with free coat protein, allowing eventual equilibration of kinetically trapped states. This equilibration occurs on a timescale of weeks, however, in contrast to the timescale of minutes of the assembly process itself. Infinite loop stability would therefore be expected to have little impact on simulations such as those presented here that track the assembly process over the time required to exhaust free monomers. The assumption would not be valid for simulations several orders of magnitude longer, however, that attempted to capture the equilibration process of these kinetically trapped forms. Likewise, the assumption of infinite stability would become problematic for simulations run close to the critical concentration of capsid assembly, where the nucleation rate is comparable to the reverse rate of looped structures. Estimates in the literature for critical concentrations of capsid assembly systems are highly variable depending on solvent conditions and availability of auxiliary scaffolding molecules, but vary approximately from a low of ∼2 μM for CCMV (47) to a high of ∼5–6 μM for phage P22 with excess scaffold (30,46,5). The slowest simulations presented here correspond to concentrations approximately an order of magnitude above these estimates, suggesting that the assumption of infinite loop stability should have a minor effect on the most extreme points in our parameter space and a negligible effect elsewhere. This assumption would become problematic if we were to expand these simulations to lower rates, comparable to or below likely critical concentrations.

These analyses lead to several general conclusions about our ability to understand capsid assembly, whether by theory, simulation, or in vitro experiments. First, results from in vitro model systems may not be reliable guides to the pathways in use in the in vivo system. Although it is well established from theoretical and experimental studies that in vitro viral assembly systems can transition between productive and kinetically trapped domains within feasible in vitro concentration ranges (1,10,8,30,48), our results go further to say that feasible changes in concentration between in vitro and in vivo systems could produce transitions between entirely different productive pathways. As noted above, our model may in fact understate the magnitude of these shifts because of its neglect of spatial crowding effects on assembly rates. Second, results from simple model systems on the scale of the octamer may substantially mislead us about more complex systems, even an icosahedron representing only the simplest T = 1 spherical capsids. The icosahedral system exhibits much greater parameter sensitivity in rate, yield, and choice of assembly pathways. Thus, a change in assembly conditions corresponding to 50-fold concentration increase can produce a substantial change in pathways and assembly rate for the icosahedron while producing only modest changes in rate and no change in pathways or yield for the octahedron. These effects of system size on pathway control are consistent with prior modeling work showing that several unexpected qualitative properties of capsid-like assembly become apparent only with relatively complex models (19). Third, our theoretical tools for understanding these systems provide an incomplete picture that is reasonable only for limited portions of the parameter space. Our theory is best developed for understanding the type III domain, which is well described by tools of classic nucleation theory (49). Much of the actual parameter domain, though, is occupied by hierarchical mechanisms that are more difficult to model theoretically. Even those hierarchical models simplify the true picture considerably, as a large part of the parameter space appears not to lie cleanly in any of these three discrete domains, but rather to lie in boundary regions that are even more poorly described by existing theory. Furthermore, even a single system can transition between these domains in response to modest changes in parameter values or assembly conditions. Collectively, these observations suggest that we may not know nearly as much as we think we do about complex self-assembly. Neither our theoretical models, nor our knowledge from simple model systems, nor even our experimental studies of capsid assembly in vitro can necessarily be relied upon to characterize complex capsid assembly in vivo. Addressing these problems will likely require new theory, improved simulations, and new experimental methods for probing complex reactions in vivo or better mimicking in vivo conditions in vitro.