Ligand Binding to the Voltage-Gated Kv1.5 Potassium Channel in the Open State—Docking and Computer Simulations of a Homology Model

Abstract

The binding of blockers to the human voltage-gated Kv1.5 potassium ion channel is investigated using a three-step procedure consisting of homology modeling, automated docking, and binding free energy calculations from molecular dynamics simulations, in combination with the linear interaction energy method. A reliable homology model of Kv1.5 is constructed using the recently published crystal structure of the Kv1.2 channel as a template. This model is expected to be significantly more accurate than earlier ones based on less similar templates. Using the three-dimensional homology model, a series of blockers with known affinities are docked into the cavity of the ion channel and their free energies of binding are calculated. The predicted binding free energies are in very good agreement with experimental data and the binding is predicted to be mainly achieved through nonpolar interactions, whereas the relatively small differences in the polar contribution determine the specificity. Apart from confirming the importance of residues V505, I508, V512, and V516 for ligand binding in the cavity, the results also show that A509 and P513 contribute significantly to the nonpolar binding interactions. Furthermore, we find that pharmacophore models based only on optimized free ligand conformations may not necessarily capture the geometric features of ligands bound to the channel cavity. The calculations herein give a detailed structural and energetic picture of blocker binding to Kv1.5 and this model should thus be useful for further ligand design efforts.

Introduction

Voltage-gated K⁺ (Kv) channels are of fundamental importance for the function of excitable cells, such as neurons and muscle cells (1). In the human heart, Kv channels are specifically assigned the task of repolarizing the cell membrane at the end of the action potential, by means of the three delayed rectifier currents: I_Kr, I_Ks, and I_Kur. Prolongation of the action potential duration is a possible way of preventing cardiac arrhythmia—therefore, blocking of channels that perform the repolarization (i.e., lowering the net repolarization current) can generally be expected to have antiarrhythmic effects (2). The single most common serious cardiac arrhythmia is atrial fibrillation (AF), with a prevalence of almost 9% in ages 80–89 years (3). AF is known to be a major risk factor for stroke and at present treatment of AF is associated with potentially lethal side effects in the form of ventricular proarrhythmia (4–8). A majority of the available antiarrhythmic drugs target either I_Kr or both I_Kr and I_Ks, which are present not only in the atria but in the ventricles as well. Thus, the development of atrial-specific antiarrhythmic drugs is of the utmost medical importance. Among the three delayed rectifier currents, I_Kur is the only one present exclusively in the atrium (9–11). The ion channel associated with I_Kur is Kv1.5, and inactivation of Kv1.5 by antisense RNA has been found to lower I_Kur by as much as 50% (11–14). Kv1.5 is therefore considered a promising target for atrial-specific antiarrhythmic drugs.

Like for most other known potassium channels, the functional form of Kv1.5 is a homotetramer, with each subunit consisting of six membrane-spanning helices, S1–S6 (15). Helices S1–S4 make up the voltage sensor, which reacts to potential changes across the membrane and regulates the gating of the channel through a still-debated mechanism (16–18). The highly conserved selectivity filter is located between S5 and S6, and is connected to S5 via the pore helix and a short loop located outside the membrane (Fig. 1 A). Together, S5, S6, the filter, and the pore helix make up the pore of the channel, whose intracellular part is arranged in what has been dubbed an “inverted teepee” cavity (19). The surface of this cavity is highly hydrophobic—the only hydrophilic residues on the cavity surface are T479 and T480, which are located at the intracellular entry to the selectivity filter. T479 and T480 are also the only residues on the surface of the cavity that are not located in the inner helix (S6). This intracellular pore cavity has been identified as the binding site for a number of Kv1.5 blockers (20–26), and ligands of the type studied here have been shown to bind to, and block, the open state of the channel. This conclusion is based on the rapid block of current during a depolarization pulse and the enhancement by higher rates of stimulation (26). Mutational experiments have identified the S6 residues V505, I508, V512, and V516 along with T479 and T480, as important residues for binding of N-benzyl-N-pyridin-3-yl-methyl-2-(toluene-4-sulfonylamino)-benzamide hydrochloride (S0100176) and 2′-{[2-(4-methoxy-phenyl)-acetylamino]-methyl}-biphenyl-2-carboxylic acid (2-pyridin-3-yl-ethyl)-amide (AVE0118) (25,26). Additionally, the S6 residues T507, L510, and V514, as well as T479, have been identified as potential binding sites for quinidine, bupivacaine, and benzocaine (22–24), and V505, I508, L510, V512, and V516 have been shown to be involved in binding of Kvβ1.3 subunits (27).

Figure 1.

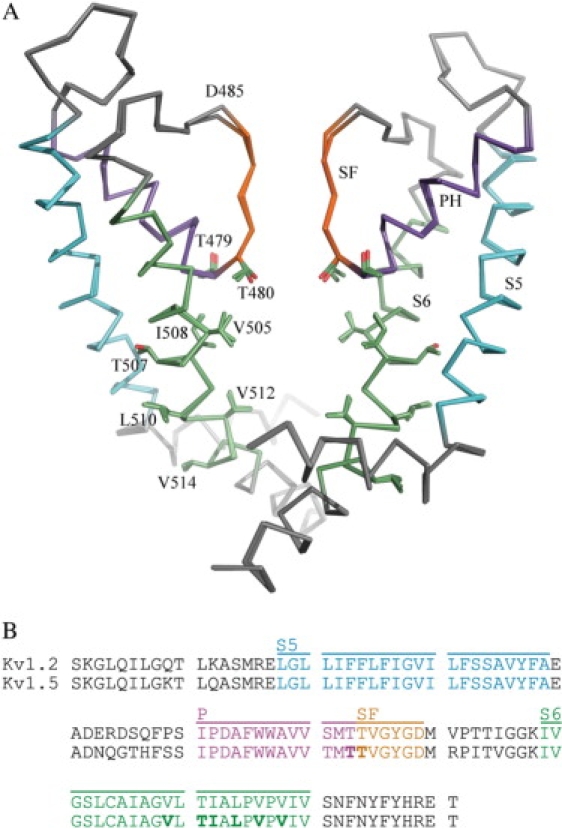
The 3D homology model of Kv1.5, superimposed on the Kv1.2 crystal structure (28) used as a template is shown in panel A. The pore helix, selectivity filter, and the membrane-spanning helices S5 and S6 are shown in purple, orange, cyan, and green, respectively. The side chains of the residues proposed to be involved in ligand binding (22–26), i.e., T479, T480, V505, T507, I508, L510, V512, and V514, are shown as sticks. Only two subunits of the tetramer are shown for clarity. Panel B shows the sequence alignment of the amino acid sequences of the pore region of Kv1.2 (PDB accession code 2A79) and Kv1.5 (Swiss-prot entry P22406). The color coding follows that in panel A. Residues in bold face have been identified as potentially involved in binding of a number of blockers (22–26).

With the recent publication of the open state Kv1.2 crystal structure (28), it became possible to construct a very reliable three-dimensional (3D) homology model of the selectivity filter and pore of Kv1.5, since the sequence identity between the two is ∼90% in this region (Fig. 1 B). Using such a model, computational methods can be used to investigate and characterize the interactions between potential blockers and the ion channel. Computational models for binding of bupivacaine, S0100176, and AVE0118 to Kv1.5 have been published earlier using the crystal structure of the much less similar KcsA channel (∼30% sequence identity in the filter and cavity regions) as a template for the homology modeling of Kv1.5 (25,26,29). The results from these studies are also somewhat ambiguous, with fairly different binding modes for the different ligands—in the study of S0100176, the ligand conformation is very compact and it is predicted to bind close to the selectivity filter (25), whereas the results from the bupivacaine and AVE0118 studies indicate a more stretched-out conformation of the ligand bound to the lower part of the cavity, near the characteristic PVP motifs (26,29). To our knowledge, no structural studies of Kv1.5 have been published to date where the binding of several ligands are addressed, and where calculated binding free energies are compared to experimental values. The fundamental question of what makes a potent Kv1.5 blocker thus remains unanswered.

The work presented here aims to further develop our knowledge of the binding of ligands to the Kv1.5 ion channel, in a manner similar to the work of Österberg et al. on the hERG channel (30). Binding modes and affinities of several ligands to the Kv1.5 channel are investigated in detail by a combination of computational methods, using blocking compounds and experimental binding data published by Peukert et al. (31). Besides homology modeling of Kv1.5, the procedure (Fig. 2) involves subsequent docking of ligands to the model and, finally, refinement of ligand poses and free energy calculations using molecular dynamics (MD) simulations together with the linear interaction energy (LIE) method (29,30). This type of combination of automated docking with force-field-based free energy calculations has become widely used for ligand binding predictions (32). The calculated binding affinities are in very good agreement with experimental results, with a near-perfect correlation in ranking of the ligand potencies. Furthermore, the results indicate that the key ligand-protein interactions are the same for all the studied ligands, and that they all bind in a similar pose. Desolvation of the hydrophilic linkers of the ligands is predicted to be the main discriminating factor separating the strong blockers from the weaker blockers.

Figure 2.

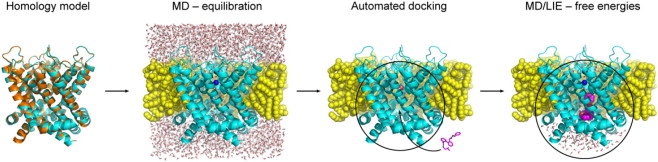
Overview of the computational procedure. In the first step, a homology model of Kv1.5 (cyan) is constructed using a template structure (orange). An octane membrane model (yellow) is then built around the ion channel and the system is equilibrated in water. In the next step, the water molecules are removed and automated docking is used to fit the ligands (purple) into the pore cavity. Finally, the complexes are solvated again for refinement and free energy calculations by molecular dynamics simulations, utilizing more efficient reduced spherical systems.

Materials and methods

Homology modeling

The modeling software Modeller 7v7 (33–35) was used to generate a 3D homology model of the open state of the Kv1.5 channel, using the 2.9-Å crystal structure of the Kv1.2 channel (Protein Data Bank (PDB) accession code 2A79 (28)) as a template. Helices S5 and S6 together with the selectivity filter and the pore helix were included in the model. In this region, the sequence identity between Kv1.2 and Kv1.5 is ∼90%, and they align without any gaps at all, which allows a very reliable homology model to be constructed. The system was then prepared for docking and MD simulations according to the procedure in Luzhkov et al. (36). An ∼35-Å-thick layer of octane molecules was subsequently built around the model, using Packmol (37), to emulate the membrane in which the ion channel is normally situated. The octane layer/ion channel assembly was then solvated with TIP3P water molecules (38) in a cubic periodic box with box length 77 Å, and allowed to equilibrate for 500 ps in an MD simulation at 300 K. During this relaxation all heavy atoms of the protein were subjected to 10 kcal/mol Å² harmonic positional restraints, to relieve possible bad contacts but keeping the structure of the ion channel model intact, while allowing the solvent and octane molecules to equilibrate around the channel assembly. This procedure was thus employed to prepare a relaxed system for docking.

Docking

All ligands were energy minimized with the OPLS all atom force field (39) before docking. Automated docking of the ligands was performed using the GOLD 3.0 software (40,41). GOLD uses a genetic algorithm (GA) in combination with scoring functions to predict binding poses for flexible ligands in a rigid binding site. In the work described here, the ChemScore scoring function was used exclusively (42). In addition to predicting the binding pose, ChemScore also estimates the binding free energy of each ligand pose, allowing the docking results to be compared directly with experimentally determined binding affinities. The active site radius was set to 22 Å, centered around a point on the symmetry axis of the channel ∼10 Å below the “roof” of the cavity—slightly above the PVP bend of the S6 helix. This positioning of the docking sphere enables the ligands to explore different docking conformations within the entire cavity, which is rather large and open at its intracellular side. Fifty GA runs were performed for each ligand, where all variables for the GA were set to their default values. GOLD was set to terminate the docking if the top three poses for a ligand were within 1.5 Å root mean-square deviation (RMSD). The docking procedure was performed with a water molecule present in the fourth position of the selectivity filter, which is the only position that is relevant for the cavity shape as seen by the docking algorithm (this position is also occupied in the majority of crystal structures of potassium channels). All other solvent molecules were thus removed from the system in the docking calculations and, after poses for the bound ligands had been obtained, the complexes were again solvated for molecular dynamics and free energy calculations (Fig. 2).

Molecular dynamics and binding free energy calculations

Binding affinities were calculated using molecular dynamics in combination with the linear interaction energy method, which uses simulations of the ligand free in solution as well as of the protein–ligand complex to calculate the change in free energy associated with binding to the protein (43). In the LIE method, the difference in interaction energies between the ligand and its surroundings is used to calculate the free energy of binding through the equation

$$\Delta G_{\text{LIE}}^{\text{bind}}=\alpha \Delta \langle V_{\text{l}-\text{s}}^{\text{vdW}}\rangle +\beta \Delta \langle V_{\text{l}-\text{s}}^{\text{el}}\rangle +\gamma \text{.}$$ (1)

Here, $\langle V_{\text{l}-\text{s}}^{\text{vdW}}\rangle$ and $\langle V_{\text{l}-\text{s}}^{\text{el}}\rangle$ are MD averages of the ligand-surrounding van der Waals and electrostatic interaction energies, respectively, and Δ denotes the difference between these averages in the bound and free states. The empirical parameter α is used to scale the van der Waals energies, and in earlier studies performed in our laboratory, an α-value of 0.18 has been able to reproduce the binding free energies of ligands in a number of different systems. The value of the ligand-dependent electrostatic parameter β is determined by a simple set of rules (44). According to these rules, the value of β is 0.43 for all ligands present in this study. To be able to reproduce absolute binding free energies, a constant term γ may be required, which has been shown to be related to binding site hydrophobicity (45).

All MD calculations were carried out using the program Q (46) with the OPLS all atom force field (39). Partial atomic charges were assigned to the ligands in analogy with the charges specified in the OPLS fragment library. A 25-Å simulation sphere was used for both simulations in the bound and free states. The 1010 loading state was used for the ion channel, i.e., a potassium ion was present in the first and third position of the selectivity filter, in accordance with earlier results (29,47–49). The same sphere center as described for the docking procedure was used, and the channel/ligand/octane systems were again solvated with TIP3P water (38) (Fig. 2). Only one ionizable residue per subunit (E433) was situated within 20 Å of the sphere center. These were modeled in their negatively charged form, yielding a net charge of −2 e for all simulations of the ligands in the bound state. Note that the ligands are neutral so that the energetic contributions from additional charged (and surface-exposed) residues farther away is negligible.

All atoms outside the 25-Å sphere were tightly restrained throughout the entire simulations. Water molecules at the surface of the sphere were subjected to radial and polarization restraints to mimic the properties of bulk water (50). Before data collection, each simulation system was heated in a stepwise manner from 10 to 300 K with all solute heavy atoms subject to strong (10–25 kcal/mol Å²) harmonic positional restraints. All simulations of the ligands in the bound state were then equilibrated without restraints for 500 ps, followed by 250 ps of production phase MD. To assess the problem of conformational sampling when simulating the ligands in the free state in water, 10 replicate water simulations of 1 ns each were performed for each ligand, with starting conformations generated by high temperature MD. For all production phase MD, a 1-fs time step was used along with the SHAKE procedure for all solvent bonds (51). Nonbonded interactions across the simulation sphere boundary were excluded. A nonbonded cutoff of 10 Å was used, with electrostatic interactions outside the cutoff treated with the local reaction field multipole expansion (52), except for the ligand, which had no cutoff applied to any of its interactions.

Results and discussion

Binding of eight ortho,ortho-disubstituted bisaryl compounds (Table 1) to the open state of the Kv1.5 channel was investigated using a three-step procedure, consisting of homology modeling, automated docking, and binding free energy calculations from molecular dynamics simulations. This enables a detailed structural analysis of binding modes and identification of the key ligand-protein interactions that contribute to the free energy of binding. The simulated compounds are a subset of the ligands for which experimental binding affinities have been published by Peukert et al. (31), and were chosen to include both the least and most potent inhibitors from that series, as well as displaying a fairly wide variety of structural features. All ligands share a common central biphenyl group, with substituents consisting of aliphatic and aromatic hydrocarbons, pyridyl rings, and primary amides, attached to the biphenyl group by amide, carbamate, ester, and sulfonamide linkers.

Table 1.

Compounds used in the simulations along with the corresponding experimental IC₅₀-values for human Kv1.5 (31)

Compound	Structure	Human Kv1.5 IC50 (μM)
7b		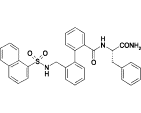9.1
7c		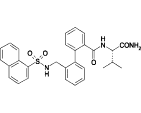11.2
15a		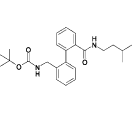3.5
17a		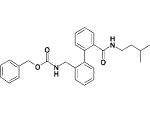0.8
17c		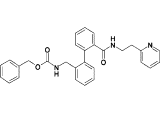0.7
17f		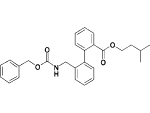8% inhibition at 10 μM
17g		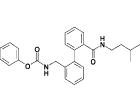3.3
17o		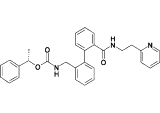0.16

The ligand numbering is the same as in Peukert et al. (31).

Homology modeling

The homology model of Kv1.5 is structurally more or less identical to the template, i.e., the pore region of the crystal structure of Kv1.2 (PDB accession code 2A79), which is not surprising, given the very high sequence identity in this region (Fig. 1 B). Residues 417–527 (Kv1.5 numbering) were included in the model, and the RMSD for the backbone atoms of the model compared to the template was 0.35 Å, when a single subunit of the model was superimposed on the crystal structure. For the residues that form the surface of the pore cavity, and thus can be expected to be important for correct docking and molecular mechanics interactions, the RMSD of the model compared to the crystal structure is 0.34 Å. The modeled structure is shown, together with the template in Fig. 1 A, and as can be clearly seen in this figure, the only part of the structure where the backbone of the Kv1.5 model differs significantly from the template is in the immediate surroundings of D485. This is most likely caused by the fact that the Cγ, Sδ, and Cɛ atoms of the adjacent methionine residue are missing in the crystal structure, forcing the modeling software to displace D485 somewhat to accommodate the side chain of M486. However, these residues are >20 Å away from the ligand binding site, and are, in fact, outside the simulation sphere in both the automated docking and molecular dynamics simulations. It should also be emphasized here that Kv1.5 and the template Kv1.2 have identical sequences in the cavity region so that the problem of arbitrarily modeling initial (before MD) side-chain rotamers does not really exist in this case. The situation is, for example, much more difficult in the case of the hERG channel (30) where the rotameric states of several aromatic residues have to be modeled in a more arbitrary way.

Automated docking

Each docking simulation generated 50 docked conformations of each ligand, except the docking of compound 17a, for which the three top-ranked solutions were within 1.5 Å RMSD of each other after 37 poses had been generated. The docking procedure generally generated slightly more diverse docking poses for the compounds containing sulfonamide groups (i.e., 7b and 7c), and to a lesser extent for the compounds containing pyridyl rings (i.e., 17c and 17o). Encouragingly, out of these 387 (=7 × 50 + 37) poses generated, only a handful fall outside of a consensus orientation where the biphenyl part of the ligand is positioned in the PVP region of the cavity, in close proximity to V512, P513, and V516. One of the substituents (generally the largest one) is then pointing toward the selectivity filter, typically in close contact with V505, I508, and A509. Mutational studies have identified residues V505, I508, V512, and V516 as important for Kv1.5 binding of two other ligands, S0100176 and AVE0118 (25,26). However, the results from the studies of S0100176 and AVE0118 indicate little or no effect from mutations of A509 or P513.

Out of the top 10 ranking solutions for any given ligand, taking only heavy atoms into account, the average RMSD compared to the top-ranked solution was 2.5 Å, with few poses deviating >4 Å from the top-ranked pose. Typical results are shown for ligand 17a in Fig. 3. Conformations that deviated more did so because the orientation of the substituents was flipped with respect to the other poses, whereas the biphenyl part remained in the same position. Even for ligand 7b, which showed relatively large diversity in the suggested binding poses, the positioning of the biphenyl part of the ligand is very well determined—the positions of the biphenyl carbons for all but seven poses (all of which are among the 10 lowest ranked) are all situated within the van der Waals surface of the top-ranked pose. The smallest compound, 15a, showed the least deviation between docking poses. The heavy atoms of the top 20 docking poses were in this case all within 2.6 Å RMSD of the highest-ranked pose, with a corresponding average RMSD of 1.6 Å. Note that because of the fourfold symmetry of the ion channel cavity, all RMSD values for the docking poses were calculated after rotating (in 90° increments) the docked poses around the symmetry axis of the cavity to find the orientation with the maximum overlap with respect to the top-ranked pose of the studied ligand.

Figure 3.

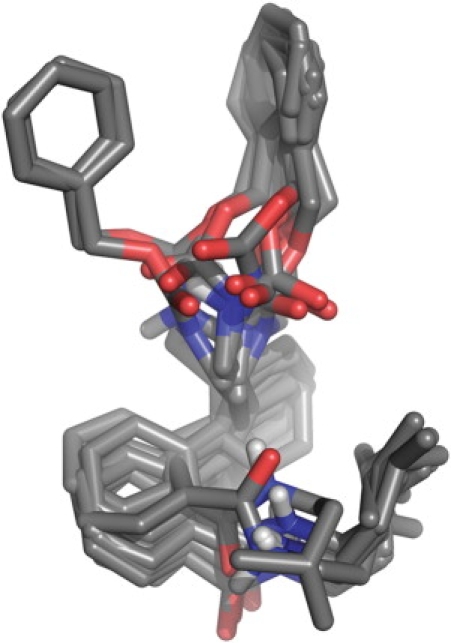
Top 10 docking solutions for compound 17a. The average heavy atom RMSD relative to the top-ranked pose is 1.4 Å. Note that some of the solutions have been rotated 90°, 180°, or 270° around the symmetry axis of the pore, because of the fourfold redundancy introduced by the symmetry of the ion channel.

Fig. 4 shows the correlation between the free energies of binding for each ligand as estimated by Chemscore, and the binding free energies derived from the experimentally determined IC₅₀-values of the ligands. The correlation between the fitness score and the estimate of the free energy of binding is not entirely straightforward in Chemscore, therefore, the top-ranked pose (with respect to fitness score) may not be associated with the lowest estimate of the free energy of binding. In Fig. 4, the lowest of the binding free energy estimates of the top five ranked poses for each ligand is plotted against the differences in binding free energy calculated from their experimentally determined IC₅₀-values (31). That is, we use here the common approximation $\Delta G_{\text{obs}}^{\text{bind}}\simeq RT\text{ln}I{C}_{50}$, which can be expected to yield reliable relative free energies whereas the absolute values are usually somewhat too positive (i.e., $I{C}_{50}>K_{\text{d}}$). A constant offset, analogous to the LIE γ-parameter, has been added to the binding free energy estimates from Chemscore to obtain the least-squares fit with respect to $\Delta G_{\text{obs}}^{\text{bind}}\text{.}$ The Spearman rank correlation coefficient is 0.12, indicating a very weak positive correlation between the calculated and observed values of the binding free energies. If compound 7b is left out of the calculation, the Spearman rank correlation coefficient increases to 0.43, which is significantly stronger, but still indicates a fairly weak positive correlation.

Figure 4.

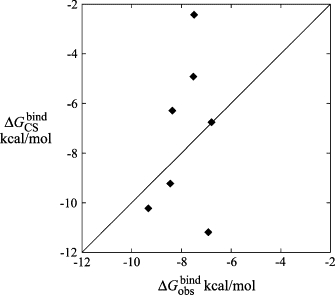
The correlation between the free energies of binding of ligands 7b–17o as calculated by Chemscore ($\Delta G_{\text{CS}}^{\text{bind}}$) (42) versus those experimentally determined by Peukert et al. ($\Delta G_{\text{obs}}^{\text{bind}}$) (31).

Molecular dynamics

For each ligand, the top five binding poses from the automated docking experiments were chosen for further investigation using molecular dynamics. Out of these 40 poses, all but one had the biphenyl part of the ligand positioned in the PVP region of the cavity. Generally, the ligand positions are stable during MD simulation, and the average structures from the production phase MD deviates relatively little from the docked positions (Figs. 5 and 6). The average RMSD of the heavy atoms of the poses shown in Fig. 5, compared to their corresponding docked poses, is 2.1 Å. The hydrophilic linkers have little or no specific interactions with the protein, and are thus fairly flexible during the MD simulations, whereas the hydrophobic parts of the ligand are typically more stable in their positions—sometimes alternating between equivalent sites on the tetrameric channel assembly (consider, e.g., the pyridyl group of ligand 17c in Fig. 5, which is rotated roughly 90° about the symmetry axis of the cavity between the docked and MD average poses).

Figure 5.

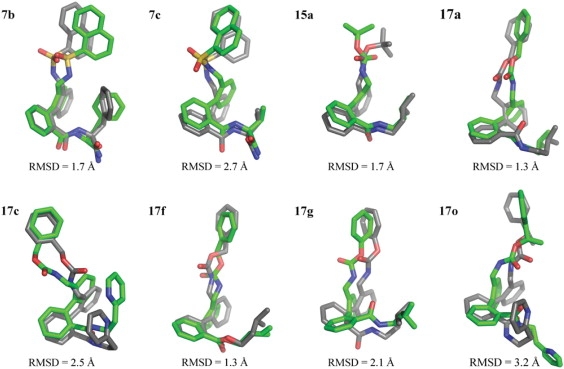
Comparison between the average structures from the production phase MD simulations in the bound state (green) and the corresponding docking poses (gray) used as starting conformations for the MD simulations. The average structures shown are from the simulations that yielded the lowest estimated free energy of binding.

Figure 6.

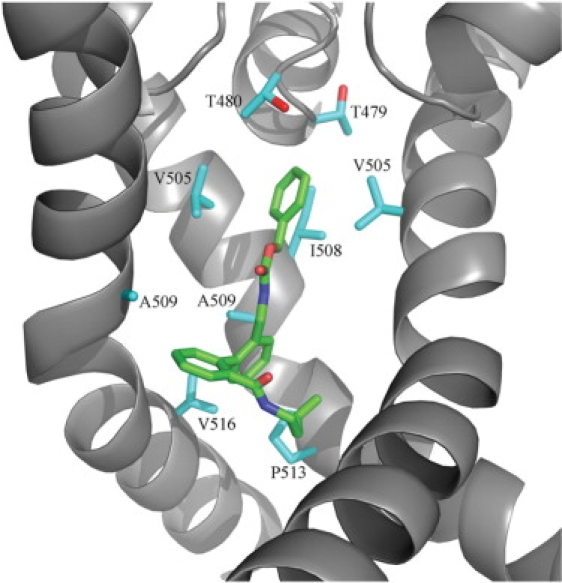
Molecular dynamics average structure of ligand 17a bound to the Kv1.5 ion channel. Protein residues within 4 Å of the ligand are shown as sticks. One channel subunit has been removed for clarity.

For each ligand, the nonpolar ligand-protein interactions were calculated and grouped by contributions from each residue of the protein (Fig. 7). On the one hand, the results of these calculations strongly support the earlier alanine scanning results of Decher et al. (25,26)—that V505, I508, V512, and V516 are important for Kv1.5 ligand binding. On the other hand, the results indicate that for all of the ligands, the largest or second largest contribution to the nonpolar interaction energy comes from either A509 or P513. This might at first appear to be at variance with the results presented by Decher et al., where the A509V and P513A mutants had little or no effect on binding of the compound AVE0118 (26). However, our model suggests that both of these mutations can be accommodated without displacing the bound ligands (Fig. 6), consistent with the possibility that both the native and mutant channels have favorable contributions from these residues.

Figure 7.

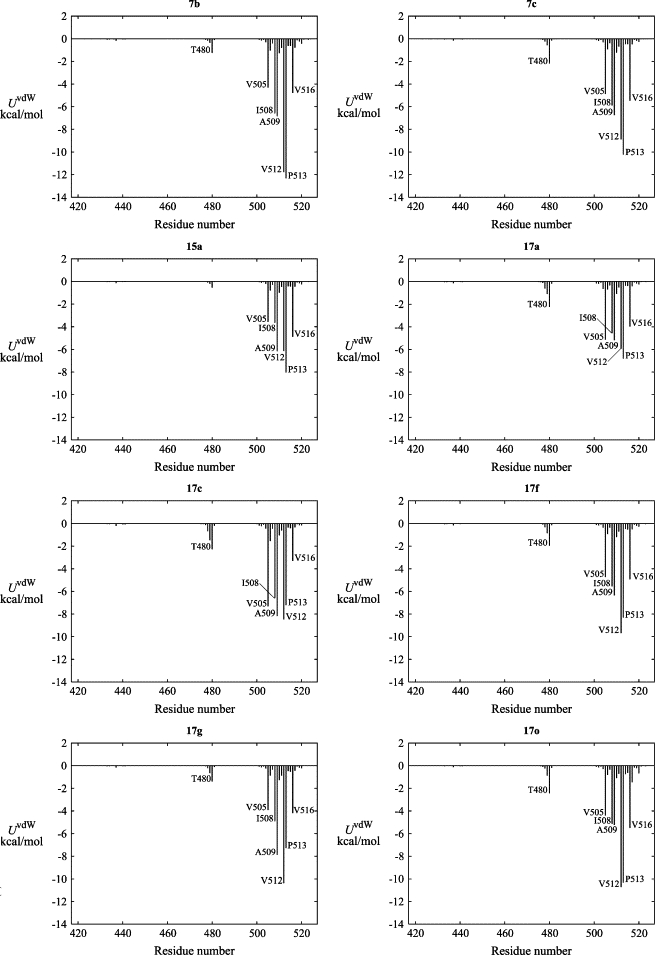
The contribution of each protein residue to the ligand-protein Lennard-Jones interaction energy. Because of the fourfold symmetry of the ion channel, the value of the interaction energy for a given residue number is the sum of the contributions from each of the four corresponding protein residues.

Also, T480, which was the single most important residue for binding in both previous studies (25,26), shows some contribution to the nonpolar ligand-protein interactions, but smaller than the other residues mentioned above. This is perhaps not surprising, considering that the threonine residues do not present many possibilities for significant hydrophobic contributions. However, the polar interactions between the ligands and T480 are equally weak, refelecting the fact that these ligands all bind with a nonpolar moiety pointing toward T480. This is in contrast to the most similar compound examined by Decher et al. (26), AVE0118, which according to our model would have its methoxy group in contact with the threonine side chains. All high-ranking solutions from additional dockings of that ligand consistently places the methoxy group in such a way. Hence, the large effect of the T480A mutation may reflect interactions with this specific group of the AVE0118 blocker, which is not present in any of the compounds in our set. It is also evident (Fig. 6) that the T480 side chains contribute in defining the upper part of the ligand binding cavity. This could mean that their contribution to ligand binding is mainly steric and that the T480A mutation would remove key restrictions leading to our consensus binding mode.

It is also interesting to note that the polar interactions between the ligands and the protein are generally much weaker than the nonpolar interactions. This is mainly due to the hydrophobic nature of the cavity and to the fact the ligands are neutral and only weakly dipolar. Among all of the ligands the only electrostatic interaction energy stronger than −2 kcal/mol is the interaction between compound 17a and residue I508. It is further noteworthy that throughout all of the 40 MD simulations, not a single stable hydrogen bond is formed between either of the ligands and the protein.

Binding free energies

The correlation between the lowest calculated free energy of binding (obtained from LIE and MD) for each ligand and the relative free energy differences derived from the experimentally determined IC₅₀-values is very good (Table 2 and Fig. 8 A). Using the standard values of the α- and β-parameters in the LIE equation (44), the average unsigned error of the calculated binding free energies is 0.7 kcal/mol. The ranking of the ligands is also in very good agreement with experiment, with a Spearman rank correlation coefficient of 0.83. Compound 17f is excluded from Fig. 8 and in the calculation of the average unsigned error, but included in the calculation of the Spearman rank correlation coefficient since the results in Peukert et al. (31) indicate that 17f is a weaker blocker than both 7b and 7c, although no IC₅₀-value was reported. If 17f is left out of the ranking according to binding free energies obtained by LIE, the Spearman rank correlation coefficient increases slightly to 0.86.

Table 2.

Ligand-surrounding energies and calculated binding free energies from the MD simulation resulting in the lowest binding free energy for each ligand

	${\langle V_{\text{l}-\text{s}}^{\text{vdW}}\rangle }_{\text{f}}$	${\langle V_{\text{l}-\text{s}}^{\text{vdW}}\rangle }_{\text{b}}$	${\langle V_{\text{l}-\text{s}}^{\text{el}}\rangle }_{\text{f}}$	${\langle V_{\text{l}-\text{s}}^{\text{el}}\rangle }_{\text{b}}$	$\Delta G_{\text{LIE}}^{\text{bind}}$	$\Delta G_{\text{obs}}^{\text{bind}}$ (31)
7b	−38.4 ± 0.3	−67.3 ± 0.4	−78.5 ± 1.5	−70.4 ± 1.2	−5.2 ± 1.3	−6.9
7c	−34.8 ± 0.2	−62.7 ± 0.1	−73.6 ± 1.7	−68.0 ± 0.1	−6.1 ± 0.8	−6.8
15a	−35.5 ± 0.2	−53.6 ± 0.4	−27.6 ± 0.5	−31.1 ± 0.8	−8.2 ± 0.6	−7.5
17a	−38.5 ± 0.3	−60.8 ± 1.2	−32.3 ± 0.9	−36.6 ± 0.6	−9.4 ± 0.9	−8.4
17c	−40.0 ± 0.3	−65.0 ± 0.0	−38.7 ± 0.7	−39.9 ± 0.4	−8.5 ± 0.5	−8.4
17f	−38.9 ± 0.3	−66.4 ± 0.2	−24.5 ± 0.9	−22.4 ± 0.2	−7.5 ± 0.5	N/A*
17g	−36.7 ± 0.2	−61.7 ± 0.7	−28.7 ± 0.3	−29.3 ± 0.5	−8.3 ± 0.5	−7.5
17o	−42.4 ± 0.4	−69.9 ± 0.4	−40.7 ± 0.8	−42.8 ± 0.2	−9.3 ± 0.5	−9.3

All values are in kcal/mol. ${\langle \rangle }_{\text{f}}$ and ${\langle \rangle }_{\text{b}}$ denote interaction energy averages for the free and bound states of the ligand, respectively. Errors are calculated as half of the difference between the averages of the first and second half of the data collection trajectory. Observed binding free energies are derived from $\Delta G_{\text{obs}}^{\text{bind}}\simeq RT\text{ln}I{C}_{50}$, with a 1 M standard state. A γ-value of −3.47, obtained from a least-square fitting of the calculated binding free energies (not including 17f) to $\Delta G_{\text{obs}}^{\text{bind}}$, was used to calculate $\Delta G_{\text{LIE}}^{\text{bind}}$.

^*No IC₅₀-value is available for compound 17f in Peukert et al. (31); see also Table 1.

Figure 8.

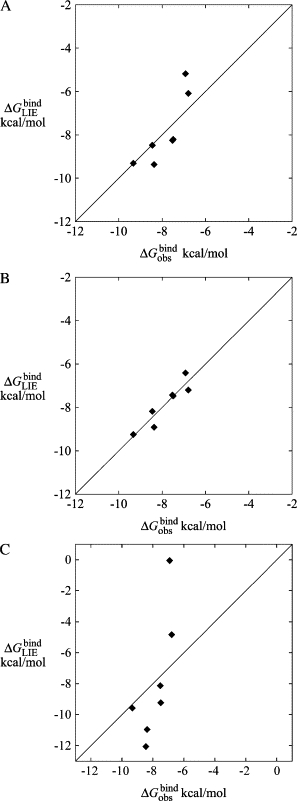
The correlation between the free energies of binding of ligands 7b–17o as calculated by molecular dynamics in combination with the LIE method ($\Delta G_{\text{LIE}}^{\text{bind}}$) versus those derived from the experimental data of Peukert et al. ($\Delta G_{\text{obs}}^{\text{bind}}$) (31). Two different LIE models are shown where panel A is the standard model of Hansson et al. (44), whereas the model in panel B has the electrostatic coefficient β for the protein optimized against the experimental data (see text). The lowest binding free energy estimate from the five different poses simulated for each ligand is plotted against the corresponding value calculated from experimentally determined IC₅₀-values (31). Panel C shows the corresponding correlation for the calculated binding free energies from simulations of a homology model based on KcsA. Note that a significantly lower value of the constant γ of −7.85 is needed to fit these data to $\Delta G_{\text{obs}}^{\text{bind}},$ indicating considerably weaker absolute binding.

The correlation between the calculated and experimental binding free energies may be further improved by using separate β-parameters for the electrostatic interaction energies in the bound and free states (44,53). Using the standard β-value of 0.43 for the free state and allowing the β-value for the bound state to be treated as a free parameter and performing a least-squares optimization with respect to the experimental values yield a bound state β of 0.48. The fit is somewhat improved (Fig. 8 B) and the average unsigned error decreases to 0.3 kcal/mol, whereas the Spearman rank correlation coefficient increases to 0.93. The increased Spearman rank correlation coefficient is largely a result of the calculated binding free energy of ligand 17f decreasing from −7.5 to −6.4 kcal/mol when using a bound state β of 0.48, resulting in a drop in ranking from the third least potent to the least potent compound. It is interesting to note that although the data for compound 17f are not used in the optimization of β, since there is no explicit experimental data to fit to, the effect of using a bound state β of 0.48 when calculating its free energy of binding is consistent with the experimental results in Peukert et al. (31).

It is also interesting to examine how predicted binding free energies are affected by the quality of the homology model of the Kv1.5 channel. To address this issue we constructed a homology model based on the crystal structure of KcsA (PDB accession code 1K4C) (54) using the same procedures as for the Kv1.2-based model. The sequence alignment with respect to KcsA is given in Luzhkov et al. (29). Docking and MD simulations were then carried out for the entire ligand data set as described above. It was immediately apparent from the new docking calculations that these solutions generally showed a larger spread with higher RMSD values than for the more accurate Kv1.2 model (for which an example is given in Fig. 3). This indicates that the binding modes become less well defined for a channel model based on KcsA, which would also be the expectation for an erroneous model. Furthermore, the calculated binding free energies from subsequent MD simulations show almost no correlation with the experimental values, even if the constant term (γ) is optimized to fit the absolute experimental values (Fig. 8 C). Also, a 4 kcal/mol more negative constant term is required in that case, suggesting significantly weaker absolute binding affinities than for the Kv1.2-based model. The average unsigned error of the calculated binding free energies, in fact, increases by >300% with the less accurate model based on KcsA (data not shown). These results thus serve as a negative control for our Kv1.2-based model and demonstrate that the quality of the homology modeling template is indeed important for obtaining reliable binding free energies.

Although, as noted in the previous section, the electrostatic interactions between the protein residues of the channel cavity and the ligands are relatively weak, they play a key role in determining the binding affinities of the ligands. In fact, the ranking according to $\Delta \langle V_{\text{l}-\text{s}}^{\text{el}}\rangle$ is identical to the ranking according to $\Delta G_{\text{LIE}}^{\text{bind}}$, with the exception of compound 15a. This ligand also has significantly less hydrophilic substituents compared to the other ones and the electrostatic interactions may thus be expected to contribute relatively more to binding. That is to say, although the nonpolar interactions give a larger overall contribution to the calculated binding free energies, that contribution is relatively uniform for the different ligands. In contrast, the larger differences in the electrostatic or polar contributions are more important in determining the relative potency of the ligands. If only ligand-water interactions are taken into account, a clear picture emerges where the two sulfonamide-containing compounds 7b and 7c both lose ∼15–20 kcal/mol in electrostatic interaction energy with water when going from the free state to the bound state, whereas the rest of the ligands have roughly as strong polar interactions with water both in the free and the bound state. The two ligands with the highest calculated binding affinities, compounds 17a and 17o, even have stronger electrostatic ligand-water interactions in the bound state than in the free state. It is obvious that the sulfonamide groups of compounds 7b and 7c, which have hydrogen bond donors and acceptors pointing in three different directions in addition to being shielded by a bulky naphthalene group, have a hard time finding enough solvent or protein hydrogen bond partners in the hydrophobic cavity. It is perhaps less obvious how the amide, carbamate, and ester groups of compounds 15a–17o manage to maintain their interactions with cavity waters in the bound state, but they are clearly sufficiently small and solvent exposed to do so. From this point of view, the relatively high calculated binding affinity for compound 17f is not surprising, given its similarity to 17g and 17a, and the similar binding poses suggested by the docking procedure. In fact, based solely on the differences in structure between 17a, 17f, and 17g one might even suggest that, given the nature of the binding site, 17f would be expected to be the best blocker of the three. Since 17a and 17f are identical apart from the amide linker in 17a and the ester linker in 17f, and the binding site is a highly hydrophobic but water-filled cavity, the less polarized ester linker would be less sensitive to desolvation than the amide linker.

Conclusions

Herein, we have reported homology modeling, automated docking of ligands, and binding free energy calculations from molecular dynamics simulations of the open state of the human Kv1.5 K⁺ ion channel. The 2.9-Å crystal structure of the very closely related Kv1.2 channel was used as a template for the homology modeling. Automated docking of eight ortho,ortho-disubstituted bisaryl compounds with known binding affinities was performed using the resulting 3D model. For the top five docking solutions for each ligand, the structural and thermodynamic stabilities of the docked complexes were further investigated using the LIE method in combination with MD simulations. The results from these simulations strongly suggest that all of the ligands bind to the Kv1.5 channel in a similar manner—with the biphenyl group of the ligands situated near the PVP bend of the S6 helices in the channel pore, and the larger of the two substituents pointing toward the selectivity filter. Out of the 387 suggested docking poses generated by automated docking, only a handful are positioned in a significantly different manner than the top-ranked poses—and the deviating poses are typically among the lowest ranked for that ligand. Furthermore, the ligands are found to be structurally stable in their docked positions during unrestrained MD simulations.

Although the binding free energy estimates and the implied ranking of the ligands obtained from the MD/LIE simulations are in very good agreement with experiment, the corresponding binding free energies and ligand ranking as estimated by the Chemscore function during the docking procedure shows little correlation with experimental data. This highlights the usefulness of the combination of automated docking and MD/LIE where the latter method will typically yield reliable binding free energy estimates, provided that the docking procedure generates reasonable binding poses. The reasons for why the simplified LIE approach is able to accurately describe binding in complex systems has been discussed in several recent works (45,53,55,56,57) and derive from a sound physical model of the (solvation) free energies of ligands in their bound and free states. It should, however, be noted that the more rigorous free energy perturbation and thermodynamic integration methods, that for many years have been considered too impractical and time consuming for binding calculations, have recently reemerged as promising tools (58–60). This is due both to increasing computational power and algorithmic development.

Although the simulations confirm the proposed significance of residues V505, I508, V512, and V516 for binding of ligands to Kv1.5, there is an apparent disagreement between the results presented herein and those of Decher et al. regarding mutations of A509 and P513 (25,26). That is, the results from alanine-scanning experiments of the pore region of Kv1.5 showed that the mutations A509V and P513A caused only very slight changes in ligand affinity for the compounds S0100176 and AVE0118. Although the former blocker is significantly different from those studied herein, AVE0118 shares the same scaffold and would most likely adopt the same binding mode as predicted by our calculations (additional dockings of AVE0118 confirm this result). This does, however, not necessarily mean that the interactions between the ligand and residues A509 and P513 are unimportant for binding. Since both A–V and P–A mutations are relatively moderate changes with respect to the possibilities of hydrophobic interactions with the side chains, it could be possible for a ligand to have nearly equally strong hydrophobic interactions with all three types of side chains. That is to say, while mutating large hydrophilic or charged residues into alanine will obviously have a significant effect on the affinity of a ligand if the mutated residue is specifically involved in binding, this may not be the case for residues whose side chains are more structurally similar to the single methyl group of alanine. Furthermore, our model suggests that the A509V and P513A mutations can be accommodated without actually displacing the ligands. Thus, it is perhaps not surprising that these mutations do not result in a significant loss of affinity as the mutated side chains may be similar enough to maintain hydrophobic interactions with the ligand. The T480A mutation, on the other hand, was found experimentally to have a large effect on the binding of AVE0118, but the threonines give rather modest contributions to the binding free energy in these simulations. Our model, however, predicts that the methoxy group of AVE0118, which is not present in any of the compounds studied here, would indeed be in contact with the threonines.

Based on the type of ligands studied herein, as well as meta-substituted benzene sulfonamides, a pharmacophore model for lead identification of Kv1.5 blockers has been suggested by Peukert et al. (31,61). This pharmacophore model consists of three hydrophobic centers in a triangular arrangement, with the distances between the hydrophobic centers being 12.62, 6.56, and 6.58 Å. For the ligands investigated in this work, this pharmacophore corresponds to a fairly stretched-out conformation, where the large hydrophobic groups of both substituents are roughly at an equal distance from the central biphenyl group. Indeed, the ligands do adopt this conformation in the free state (data not shown) but, as can be clearly seen in Fig. 5, the bound state conformations of the ligands are generally much less elongated. This illustrates a fundamental problem with deriving pharmacophores from optimized isolated ligand structures, as opposed to utilizing information regarding receptor-bound ligand conformations. The former type of pharmacophore model may fail to take into account conformational changes that the ligands undergo upon binding to the receptor. It is thus a general problem with “ligand-only” pharmacophore-based drug design that it is possible to imagine a compound that would satisfy the criterions of such a pharmacophore model, yet have little or no affinity for the binding site. Similarly, it is possible to envision a strong blocker that does not at all comply with the pharmacophore model. The conclusion is therefore that ligand-based pharmacophore searches for blocking compounds are likely to be hampered both by returning false positives and false negatives. A more fruitful strategy should thus be to utilize homology modeling together with docking to derive 3D pharmacophore models that incorporate information about the receptor.

In this work, the predicted binding modes to Kv1.5 are strongly supported by the following facts: i), the high sequence identity between Kv1.5 and Kv1.2 in the pore region, ii), a consensus docking pose for all compounds, which is also found to be stable during MD simulations, and iii), an excellent correlation between observed and calculated binding affinities, where the latter were obtained from detailed all-atom energetic calculations. Furthermore, a negative control, provided by simulations of the ligand series utilizing a less accurate homology model based on KcsA, showed that such a model does not yield good correlation with experimental binding affinities. This model for blocker binding to Kv1.5, based on the Kv1.2 template, is thus one of the few currently available examples of detailed 3D models for how drug-like compounds interact with ion channels.