Effects of Salt Concentrations and Bending Energy on the Extent of Ejection of Phage Genomes

Abstract

Recent work has shown that pressures inside dsDNA phage capsids can be as high as many tens of atmospheres; it is this pressure that is responsible for initiation of the delivery of phage genomes to host cells. The forces driving ejection of the genome have been shown to decrease monotonically as ejection proceeds, and hence to be strongly dependent on the genome length. Here we investigate the effects of ambient salts on the pressures inside phage-λ, for the cases of mono-, di-, and tetravalent cations, and measure how the extent of ejection against a fixed osmotic pressure (mimicking the bacterial cytoplasm) varies with cation concentration. We find, for example, that the ejection fraction is halved in 30 mM Mg²⁺ and is decreased by a factor of 10 upon addition of 1 mM spermine. These effects are calculated from a simple model of genome packaging, using DNA-DNA repulsion energies as determined independently from x-ray diffraction measurements on bulk DNA solutions. By comparing the measured ejection fractions with values implied from the bulk DNA solution data, we predict that the bending energy makes the d-spacings inside the capsid larger than those for bulk DNA at the same osmotic pressure.

Introduction

The interaction of counterions and added salts with the negatively charged phosphate backbone plays a major role in controlling the properties of DNA in solution. Under many conditions of biological significance DNA is highly compact, and this can occur only when the repulsions between the phosphate groups are largely compensated by counterions and/or screened by added salt (1). Furthermore, it is known that interaction of DNA with polyvalent ions such as the tetravalent amine spermine can cause double-stranded (ds) DNA to condense spontaneously into a toroid (1–3). Mono- and most divalent ions do not condense DNA; in fact, they are observed to raise the threshold concentration of polyvalent cations at which condensation occurs (4). Although such effects of counterions on DNA have been the subject of many experiments, theoretical investigations, and computer simulations, many issues remain open (5).

Insights into these ionic interactions can be obtained from direct measurements of the force required to compact or crowd DNA as a function of the ambient salt concentration. We describe here two complementary studies of this kind, one involving free dsDNA in solution and the other involving dsDNA constrained within a viral capsid.

The genome in many bacterial viruses (bacteriophages) is dsDNA. It is packaged in a rigid protein shell, the capsid, and is delivered to the host bacterium by ejection from this capsid (the phage “head”) through a hollow tubular “tail”. The DNA must be strongly crowded to be accommodated within the capsid. Bacteriophage-λ is typical; its 48.5-kbp genome, which has a contour length of 17 μm, is contained in a protein shell with an inner radius <29 nm. Thus the DNA within the capsid is highly stressed, because it has been bent along most of its length into a radius of curvature smaller than its 50-nm persistence length and crowded to a density (corresponding to an average interaxial spacing as small as 2.5 nm) at which the repulsions between neighboring portions of duplex are very large.

The genome delivery process, at least in its initial stages, is passive, requiring no energy input; it is driven by the energy stored in the DNA due to its confinement. The ejection force is therefore a measure of the stressed state of the DNA, due to both its crowding and bending. It has recently been shown that this force can be determined by experiments in which osmotic pressure is employed to inhibit the ejection (6). The results of these studies are consistent with the predictions of theory, not only for the magnitude of the initial force but also for the way it decreases as the genome is released (7,8). They also agree with direct single-molecule measurements (9) of the force as a function of packaged length. Recent investigations of the effect of mutant genome lengths on the ejection forces (10) also support the picture of capsid stress being dominated by short-range self-repulsion and bending elasticity of the strongly confined DNA chain.

When counterions are added to the buffer solution containing the phage, they permeate the capsid, where they can interact with the DNA and change the state of stress and hence the ejection force. For example, it was found that the osmotic pressure required to completely inhibit ejection in λ could be reduced by an order of magnitude by the presence of spermine in the buffer (6). Similarly, spermine has been shown to reduce the force of ejection in bacteriophage T5 (11).

This work investigates the relative contributions from repulsion and bending effects by using the osmotic stress technique (12) to measure directly the forces between DNA duplexes that are free of bending stress, i.e., bulk solutions of DNA. Here the interhelical repulsive forces are balanced by the osmotic pressure exerted by polymers such as high-molecular-weight polyethylene glycol (PEG) that are excluded from the DNA phase. The spacing between helices in the resulting macroscopic condensed DNA arrays is measured at each PEG concentration (osmotic pressure) by x-ray diffraction. (Note that these distances are determined not only by the direct electrostatic and hydration forces but also by the entropic repulsions arising from conformational fluctuations of the DNA helices (13)). The forces measured in phage ejection experiments are a consequence of these same DNA-DNA interactions although one expects some small corrections—especially in the undulation contributions—due to the average configuration being curved. The most important difference arises directly from the bending elastic stress, i.e., the “self energy” of the DNA associated with it being bent along all of its length (14). Accordingly, a comparison of the two measurements allows us to deduce the relative contribution of bending energy to viral capsid stress, as outlined in the following section. We discuss there as well the connection between the osmotic effects reported in this work and those explored in earlier studies by Serwer et al. (15) in which added osmolytes were shown to stabilize phage capsids (e.g., inhibit their thermal inactivation and their ability to be osmotically shocked).

In the experiments described here we examine the interaction of DNA with sodium (+1), magnesium (+2), and spermine (+4) ions by measuring the effect of these cations on the osmotic pressure inhibition of DNA ejection from λ-phage. We also carry out complementary measurements of interaxial spacings in bulk DNA solutions in equilibrium with the same osmotic pressure and involving the same salts. We find that the effect of monovalent cations is negligible up through physiological concentrations; for the di- and tetravalent salts, however, both sets of experiments show that DNA-DNA repulsions first decrease with added salt and then go through a minimum. We also study the dependence of DNA-DNA interactions on the nature of the coions, for the case of MgSO₄ and MgCl₂. In all cases the elastic bending energy is shown to make a significant contribution to the state of stress of phage-packaged DNA, in agreement with earlier theoretical predictions (7,8). In particular, we predict that the d-spacings in the capsid—when it has come to equilibrium with an external osmotic pressure—are significantly larger than those that characterize a bulk DNA solution at the same pressure.

Theory

The bulk solution case

Consider a situation, depicted schematically in Fig. 1 a, in which DNA is confined at concentration $c_{\text{DNA}}^{(\text{o})}$ inside a rigid, immovable, semipermeable membrane (mimicking a phage capsid, for example, but not so small) permeable to water and salt but not to DNA or PEG. The “outside” (upper) solution, containing PEG, is open to the atmosphere and is hence at a hydrostatic pressure of 1 atm, independent of the PEG concentration (c_PEG). The situation c_PEG = 0 corresponds to the “usual” situation of a phage capsid in buffer solution to which no osmolyte has been added, i.e., a solution that contains no component like PEG to which the capsid is impermeable; in turn, $c_{\text{DNA}}^{(\text{o})}$ corresponds to the DNA concentration in a fully packaged, not-yet-opened, capsid. Because of this high concentration of osmolyte (DNA) inside the capsid, water is drawn into the fixed volume and a large hydrostatic pressure is developed to equalize the chemical potential of the water throughout the system (in the “inside” and “outside” solutions). This hydrostatic pressure due to the compressed water inside the rigid volume (and withstood by the rigid walls of the container) is often described as a DNA repulsion pressure. For simplification, assume that the DNA is hexagonally packed. It follows that a fixed concentration of DNA inside the rigid walls, $c_{\text{DNA}}^{(\text{o})}$—associated with a fixed amount of DNA and a fixed confining volume—corresponds to a particular fixed value of interaxial spacing, $d^{(\text{o})}$. Suppose we now add PEG to the outside solution. Water will be drawn out of the DNA volume (with the d-spacing necessarily remaining constant), reducing the water density and the hydrostatic pressure inside. Let $c_{\text{PEG}}^{\ast }$ be the concentration of PEG that brings the pressure inside down to 1 atm. For this special value of c_PEG, water-exchange equilibrium corresponds to zero osmotic (hydrostatic) pressure difference and a net force of zero on the rigid walls confining the DNA. Equivalently, the osmotic pressure associated with the concentration $c_{\text{PEG}}^{\ast }$ is equal to the osmotic pressure exerted by the confined DNA at concentration $c_{\text{DNA}}^{(\text{o})}$ (spacing $d^{(\text{o})}$). As a consequence, even if the DNA were allowed the opportunity to “escape” from its confinement, it would not because there is no thermodynamic driving force for this process.

Figure 1.

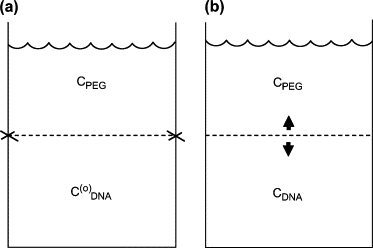
(a) Schematic diagram of osmotic equilibrium of a stiff polyelectrolyte confined in a fixed, rigid volume. (b) Same, for osmotic equilibrium of a stiff polyelectrolyte confined by a movable semipermeable membrane.

For any lower value of c_PEG there is a pressure difference and hence a net force (outward) on the confining walls, because an insufficient amount of water has been drawn out of the DNA solution to lower its hydrostatic pressure to 1 atm. Let c_PEG be such an intermediate value: $0<c_{\text{PEG}}<c_{\text{PEG}}^{\ast }$. Suppose we again consider the possibility of DNA “escape”; more precisely, we imagine being able to adjust (lower) the DNA concentration, either by removing DNA (e.g., by ejecting DNA from the capsid) or by increasing the walled-off volume (e.g., by expansion of the DNA phase in the bulk solution osmotic stress experiment—see Fig. 1 b and discussion immediately below). Let c_DNA ($<c_{\text{DNA}}^{(\text{o})}$), with corresponding $d(>d^{(\text{o})})$—dependent on c_PEG—be the concentration (d-spacing) that allows enough additional water to be drawn out of the DNA solution to lower its hydrostatic pressure to 1 atm.

The associated “mapping”, d(c_PEG), is precisely the function measured in the osmotic stress experiment depicted schematically in Fig. 1 b. Here the dotted line depicts a movable semipermeable membrane, so that the volume of the lower solution is not fixed and the DNA concentration can adjust in response to any imposed PEG concentration. In fact, because of the immiscibility of PEG and DNA, an experimental realization of this scenario need not involve any membrane whatsoever. Indeed, in the osmotic stress experiments that have been used to measure forces in a large number of systems involving lipid bilayers (in lamellar states) and biopolyelectrolytes like DNA (in hexagonal states), one simply varies the PEG concentration and measures the d-spacing in the coexisting phase of lipid or DNA, with d(c_PEG) implying Π(d) via the calibration Π(c_PEG) (12).

The small system case

The above discussion refers of course to well-known osmotic effects. We have outlined them here to provide a basis for highlighting the new effects that arise in the case relevant to comparing the two experiments reported in this work, namely: (1) measurement of the fraction of DNA ejected from a phage capsid in a solution of fixed osmolyte concentration as a function of salt concentration; and (2) measurement of d-spacing in a bulk solution of DNA at fixed osmotic activity as a function of salt. The latter experiment corresponds to the situation depicted in Fig. 1 b, as argued just above, whereas the former is described by Fig. 1 a in the case where DNA is confined to a sufficiently small volume.

It turns out, as argued below, that “sufficiently small volume” of confined DNA means that finite-size effects cannot be neglected. In particular, if the linear dimensions of the confining volume (the radii of phage capsids are generally no more than ∼30 nm) are not large compared to the DNA persistence length (50 nm), then the resulting bending of the DNA must be directly taken into account. More explicitly, as discussed quite extensively in earlier work (8), the total energy of a length L of DNA packaged in a phage capsid of radius R_c, is given by the sum of three contributions: one, E_int, due to the DNA-DNA interactions; a second, E_bend, to the bending of the DNA; and a third, E_surf, to surface terms. The first two terms have been referred to already in the Introduction, and will be written out explicitly and calculated below in the context of comparing our two osmotic stress experiments. The third arises from the packaged DNA being a small finite system (as opposed to a bulk solution of concentrated DNA) with a surface “tension” due to its interaction with the capsid; we neglect this term since earlier analyses have shown it to be the smallest of the three (8).

What, then, is the effect of the bending energy (E_bend) on the water-exchange equilibria described in the preceding section? Consider the $c_{\text{PEG}}<c_{\text{PEG}}^{\ast }$ case studied in the current experiments, i.e., phage capsids in a solution containing insufficient PEG to balance the osmotic pressure exerted by the confined DNA genomes. More precisely, the hydrostatic pressure inside the capsids is significantly higher than 1 atm, even though it is significantly lower than the value that would obtain were there no PEG outside. This pressure difference drives the ejection of DNA when it is given the chance to escape, e.g., upon opening of the capsids via addition of the phage receptor protein. According to the above discussion, the ejection will proceed until the DNA concentration inside drops to a value c_DNA sufficient to raise the chemical potential of the water inside to that of the water outside; at this point enough water will have been drawn out of the capsid to lower the inside hydrostatic pressure to 1 atm. But now, because of the bending energy leading to a higher level of stress for the confined DNA—specifically, due to DNA being bent into radii of curvature smaller than its persistence length—the d-spacing in the capsid will rise to a value larger than that measured in the bulk-solution osmotic stress experiment (Fig. 1 b) for the same PEG concentration c_PEG.

Note that the situation where c_PEG is insufficient to balance $c_{\text{DNA}}^{(\text{o})}$ is relevant to the usual situation in which purified, infectious, phage capsids are stored in buffer solution. Indeed, the concentration of osmolyte in the buffer is essentially zero, i.e., the capsids are permeable to most if not all of the components of the buffer. Consequently, the hydrostatic pressure inside the capsids is on the order of tens of atm, and this accounts for the loss of infectivity with time. More explicitly, under these conditions the phage capsids experience a high degree of “in-plane” (lateral) stress due to the large outward pressure exerted on them. Accordingly, the protein shells are only in metastable equilibrium, and thermal fluctuations eventually lead to their demise, i.e., to the relief of stress via the nucleation of cracks in the capsid (16). (Note that internal osmotic stress due to genome confinement can also work to stabilize the phage capsid if it is subjected to a small-scale, local, force from outside. More explicitly, recent measurements (17) of the response of phage capsids to AFM nanoindentation has shown that this internal pressure gives rise to a radially outward force that helps limit the extent of local deformation and hence decrease the chance of rupture.) At elevated temperatures capsid failure due to the internal osmotic pressure is all the more dramatic, and indeed it is common to “inactivate” phage by simply heating them. If a high enough concentration of osmolyte is present in the buffer solution, however, the arguments outlined above suggest that the hydrostatic pressure inside the capsids can be reduced significantly toward 1 atm. This effect was shown by Serwer et al. (15) almost 25 years ago when they inhibited the thermal inactivation of several phages by addition of various osmolytes. Similarly, they showed that the osmotic-shock inactivation of phages like T4, induced by incubation in high salt followed by rapid dilution, was significantly inhibited by addition of high concentrations of osmolyte to the dilution shock buffer. Even more interestingly, they demonstrated that the efficiency of in vitro packaging of several phages was enhanced by as much as a factor of 10 in the presence of osmolyte. This effect is directly related to the situation we discuss here in which the presence of added PEG results in the inhibition of phage ejection (or equivalently, to the concentrating of DNA in the corresponding bulk experiment). In addition to the PEG helping to “pull in” the DNA due to lowered hydrostatic pressure inside the capsid, it can also increase directly the efficiency of the packaging motor.

Calculation of DNA repulsion and bending energies

Here we quantify the above arguments by using measured values for the bulk-solution osmotic effects and the elastic (bending) moduli. In particular, we verify the prediction that d-spacings inside open capsids in PEG solution are necessarily larger than those observed for bulk solutions of DNA in osmotic equilibrium with PEG at the same c_PEG and investigate these effects as a function of ionic conditions.

For the DNA-DNA contribution, we start with the purely repulsive case appropriate to Na⁺ and Mg⁺² salts, for which the measured osmotic pressure Π versus interaxial distance d takes the approximate form (12)

$$\Pi (d)=F_{\text{o}}\text{exp}(-d/c)\text{.}$$ (1)

(Note that this Π(d) function corresponds precisely to the mapping $d(c_{\text{PEG}})\leftrightarrow c_{\text{PEG}}(d)$ discussed in the preceding section, as soon as one uses the calibrated relation between PEG concentration c_PEG and Π.) The repulsion energy per unit length, at spacing d, associated with two neighboring (and parallel) portions of DNA, is obtained from integrating Π(d) over the hexagonally packed DNA area per unit length ($\sqrt{3}/2d^2$), from d to ∞; multiplication by the packaged length L gives $E_{\text{int}}$. Similarly, the bending contribution is obtained by integrating the one-dimensional elastic energy per unit length, $\xi k_{\text{B}}T1/R^2(s)$, over the full length of packaged DNA; here ξ is the DNA persistence length and R(s) is the local radius of curvature at the contour distance $s(0\le s\le L)$ along the chain.

If the packaged chain is modeled as a hexagonally packed “spool” with spherical outer surface (of radius R_o = R_capsid, the internal radius of the capsid) and cylindrical empty core (of radius R_in), the energy of packaging can be written (7,8):

$$\begin{array}{l}E(d;L)=E_{\text{int}}+E_{\text{bend}}=\sqrt{3}{F}_{\text{o}}(c^2+cd)L\text{exp}(-d/c)+\\ \frac{4\pi \xi k_{\text{B}}T}{\sqrt{3}{d}^2}{\int }_{{\text{R}}_{\text{in}}}^{{\text{R}}_{\text{o}}}dr\frac{\sqrt{R_{\text{o}}^2-r^2}}{r},\end{array}$$ (2)

with

$$R_{\text{in}}=\sqrt{R_{\text{o}}^2-(\frac{3\sqrt{3}{d}^{2}L}{8\pi }}{)}^{2/3}\text{.}$$

Note that R_in, the radius of the empty core, is dependent on L and d, as indicated in the last line above. Recent computational work (18–21) has suggested the likelihood of packaged configurations quite different from the above-assumed spool structure, but these effects cannot easily be accommodated within our analytical theory and, in any case, do not change our qualitative conclusions.

The DNA energy as a function of L follows from minimizing E(d;L) in Eq. 2 with respect to d, for each value of L. Substituting the resulting d(L) into E(d;L) then gives E(L) and the ejection force for an arbitrary packaged length: $f_{\text{ej}}(L)=-dE(L)/dL$. Finally, the fraction ejected against an osmotic pressure difference Π is determined by finding the value of L that gives an ejection force equal to the osmotic resisting force, $f_{\text{res}}$, corresponding to Π. For the osmotic pressure associated with a PEG concentration of 15% w/w (the value used in our experiments; see below), we estimate this force to be ∼1.3 pN. More explicitly, we equate this force with the product of the PEG pressure Π and the volume of a unit length of DNA with cross-sectional area $\pi {(d_{\text{DNA}}/2)}^2$, where $d_{\text{DNA}}$ is the diameter of duplex DNA and its hydration shell: $f_{\text{res}}=\Pi (\pi /4)(d_{\text{DNA}}{)}^2=(3.5\text{atm}=0.35\text{pN}/\text{n}{\text{m}}^2)(\pi /4)(2.25\text{nm}{)}^2=1.3\text{pN}$. Note that $f_{\text{ej}}(L)=-dE(L)/dL$, as formulated here, is a sum of contributions from DNA-DNA repulsion (“int”) and DNA elasticity (“bend”) terms—see Eq. 2, whereas the $f_{\text{res}}(\leftrightarrow {\Pi }_{\text{PEG}}\pi {(d_{\text{DNA}}/2)}^2)$ that balances it is associated with the osmotic pressure of the PEG solution.

To carry out the calculations outlined above, we need to know how the DNA-DNA interaction depends on this concentration; i.e., we need F_o and c in Eq. 1 as functions of [Na⁺] and [Mg⁺²]. In principle we also need to know how the DNA persistence length ξ varies with added salt. The other quantities appearing in Eq. 2 for the DNA energy—R_o = 29 nm, and k_BT = 4 × 10⁻²¹ J—are fixed. For purposes of simplicity, i.e., to illustrate the basic qualitative point that stress in the capsid (and hence ejection fraction against a given osmotic pressure) is reduced by added salt and that bending energy leads to capsid d-spacings larger than those observed in bulk solutions of DNA at the same osmotic pressure, we take both c and ξ to be independent of added salt concentration. In fact, the decay length c is expected to vary with concentration of added salt over the 100 mM ranges of NaCl, MgCl₂, and MgSO₄ considered in our experiments, and similarly for the persistence length ξ. As emphasized below, however, we neglect these variations since we are not interested in quantitative details of the comparison between theory and experiment. Accordingly, we use a constant value of ξ = 40 nm for the persistence length, since our calculations are done for a range of Mg²⁺ concentrations up through 100 mM (i.e., high enough to lower the canonical persistence length of 50 nm to an electrostatically screened value of 40 nm) and since even our “zero-added-salt” solution (50 mM Tris plus 10 mM MgSO₄) involves a significant amount of Mg²⁺. Similarly, we use a constant value of c = 0.28 nm for the DNA-DNA repulsion decay length, determined from the slope of lnΠ vs. d (see Eq. 1) as measured for a 0.5 NaCl DNA solution (12). Then, from the assumption that only F_o varies with [Mg⁺²], it follows from Eq. 1 that

$$\frac{F_{\text{o}}([M{g}^{2+}])}{F_{\text{o}}([10\text{mM}])}=\text{exp}(\{d_{\Pi \ast }([M{g}^{2+}])-d_{\Pi \ast }(10\text{mM})\}/c)\text{.}$$ (3)

Here $d_{\Pi \ast }([M{g}^{2+}])$ is the measured d-spacing at Π* when the salt concentration is [Mg²⁺]; the buffer solution contains Mg²⁺ at a concentration of 10 mM, so 10 mM corresponds to the situation of no added magnesium salt.

To determine the value of F_o at this starting concentration we use Eq. 1 with the value of d = 3.70 nm measured with no added Mg²⁺ at the osmotic pressure Π* = 3.5 atm = 0.35 pN/nm²; we find $F_{\text{o}}(10\text{mM})=0.35\text{pN}/\text{n}{\text{m}}^2\text{exp}(3.70/0.28)=1.9\times {10}^5\text{pN}/\text{n}{\text{m}}^2$. From Eq. 3 we then obtain the F_o values for added MgSO₄ concentrations of 10, 40, and 90 mM, corresponding to our measured d-values of 3.52, 3.44, and 3.51 nm. Note that (see Fig. 3 a and discussion in the following section), as mentioned earlier, we find that the measured d-spacings first decrease with [Mg²⁺] and then increase, implying first a decrease in the strength of DNA-DNA repulsions (i.e., one has to go to smaller separation distances to find the same osmotic pressure, Π*) and then an increase in these interactions, consistent with our finding that the ejection fraction first decreases and then increases (see Fig. 2 a).

Figure 3.

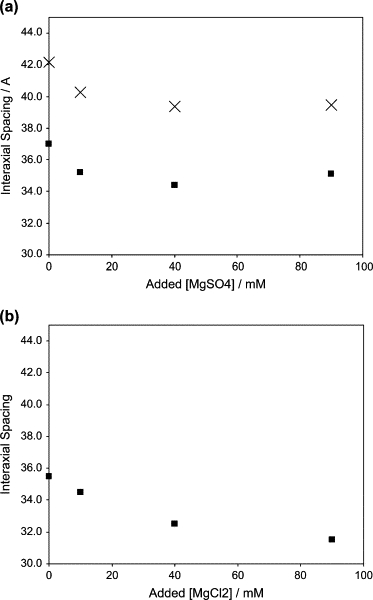
Measured d-spacings (solid squares) of a DNA solution in osmotic equilibrium with a 3.5 atm PEG solution, as a function of added Mg²⁺, showing the effect of changing coion from $\text{S}{\text{O}}_4^{2-}$ (a) to Cl⁻ (b). The zero of the abscissa corresponds to 10 mM Mg²⁺ already present in the buffer solution. The experimental uncertainties in the d-spacings are typically ±0.15 Å, comparable in size to the data points. Calculated d-spacings in the capsid, at the same osmotic pressure, are shown by × in Fig. 3 a, using the same theory (Eq. 2) as for the estimates of ejection fraction shown in Fig. 2 a.

Figure 2.

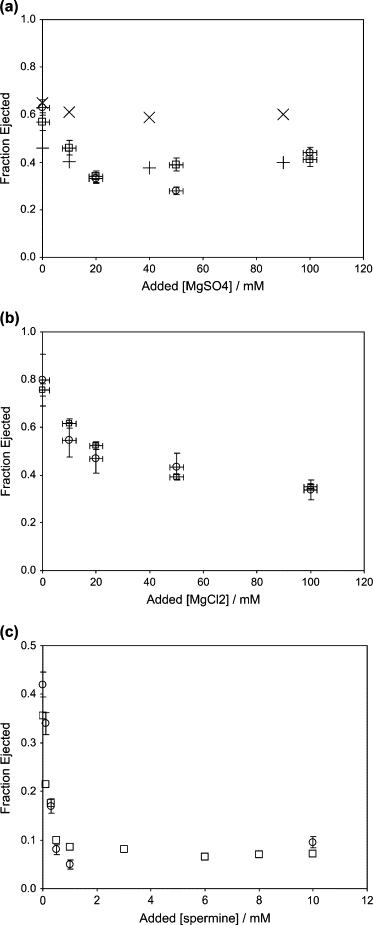
Measured ejection fractions as a function of added salt concentration, against an osmotic pressure (3.5 atm) induced by PEG8000 solution. Note that the zero of the abscissa corresponds to 10 mM Mg²⁺ already present in the buffer solution. (a) Added MgSO₄. (b) Added MgCl₂. (c) Added SpCl₄. In panel a we show two sets of data, for two different phage batches (open circles and squares, with associated error bars estimating the experimental uncertainties); results from a calculation of repulsion and bending energies (×); and estimates from neglect of bending energy, using measured d-spacings (+). The data in panels a and b refer to wild-type λ-samples, whereas panel c involves a shorter-genome-length (94%) mutant.

For the case of the added salt being tetravalent (spermine), a qualitatively new feature arises, namely the effective DNA-DNA interactions become attractive at large distances for sufficiently high (>1 mM) concentrations. More explicitly, instead of the single-exponential osmotic pressure given by Eq. 1, we have (B. A. Todd, V. A. Parsegian, A. Shirahata, T. J. Thomas, and D. C. Rau, private communication, 2007):

$$\Pi (d)=F_{\text{o,rep}}\text{exp}(-d/c^{\prime })-F_{\text{o,att}}\text{exp}(-d/2c^{\prime })\text{.}$$ (4)

The ranges c′ and 2c′ and the preexponential factors for the repulsive $F_{\text{o,rep}}$ and attractive $F_{\text{o,att}}$ contributions are determined from combining DNA repulsion data from osmotic stress measurements with attraction force data from single-molecule experiments for spermine concentrations in the millimolar range. Here $c^{\prime }=0.22nm$, as compared with c = 0.28 nm in Eq. 1; note that at high osmotic pressures c for Mg²⁺ is also found to be 0.22 nm, with the force curves becoming independent of Mg²⁺ concentration up to 100 mM. Furthermore, $F_{\text{o,rep}}$ and $F_{\text{o,att}}=7.1\times {10}^5\text{pN}/\text{n}{\text{m}}^2$ and $1.2\times {10}^3\text{pN}/\text{n}{\text{m}}^2$, as compared with $F_{\text{o}}=1.9\times {10}^5\text{pN}/\text{n}{\text{m}}^2$. As before, we neglect changes in the persistence length due to added counterions; accordingly the bending energy contribution is the same as that used in Eq. 2 and the calculation of ejection fraction follows through exactly as before. More explicitly, we obtain the new form for E_int by integrating Π(d) from Eq. 4 over $\sqrt{3}/2d^2$ and multiplying by L. Then, just as described above for the purely repulsive case, we proceed to determine the ejection force $f_{\text{ej}}(L)=-dE(L)/dL$ and thereby deduce the value of L (and corresponding ejection fraction $[(L_{\text{o}}-L)/L_{\text{o}}]$ that gives a value for f_ej equal to the fixed f_res = 1.3 pN. In this way we find that the ejection fraction for Sp⁴⁺ concentrations >1 mM should be 0.05, in excellent agreement with our osmotic suppression measurements (see Fig. 2 c).

Note that the balance of forces calculated immediately above involves an interaxial spacing of d = 2.79 nm, corresponding in turn to a packaged length of L = 14,700 nm. In the absence of PEG, i.e., for a resisting force of zero, we predict that the ejection will proceed down to L = 14,200 nm, with an interaxial spacing of d = 2.81 nm; because of the attractive interaction mediated by spermine, the ejection is highly incomplete even when there is no resisting force. For wild-type (48.5 kbp) λ (L_o = 16,500 nm), for example, L = 14,200 nm corresponds to as much as 85% of the genome remaining in the capsid after it is opened. Furthermore, the packaged DNA will be present inside as a toroidal condensate, free of any effects of confinement, i.e., its outside diameter is just smaller than the inner diameter of the capsid. A cryoelectron micrograph picture of this situation is shown in Fig. 4 (22).

Figure 4.

Cryoelectron micrograph of toroidally condensed DNA remaining unstressed in the capsid (wild-type phage, 48.5 kbp), following ejection at zero “external” osmotic pressure in the presence of spermine. Reprinted in part with permission from Evilevitch (22).

In the experiments described below we demonstrate the importance of bending energy contributions to the packaging stress in phage capsids by comparing the ejection fractions measured at fixed osmotic activity as a function of salt concentrations with those inferred (assuming packaged DNA volumes to be constant) from measured d-spacings in bulk DNA solutions under the same osmolyte and salt concentrations. By applying the theory outlined above the two sets of experiments are reconciled with one another and shown to corroborate the relative roles of DNA elasticity and self-repulsion in phage ejection.

Materials and methods

Osmotic suppression

The method for quantifying the amount of DNA ejected has been described in detail (6). In brief, the phage (λ) and its receptor (LamB) were incubated in the presence of DNase I in appropriate buffer. After incubation, the reaction mixture was centrifuged at 200,000 × g in a TLA 110 rotor (Beckman/Coulter, Fullerton, CA) to pellet the capsids. The ejected and digested nucleotides, remaining in the supernatant, were quantified by ultraviolet absorbance (Abs) at 260 nm (8453 spectrophotometer; Hewlett Packard, Palo Alto, CA). For each set of experiments, there is one positive control and two negative controls. In the positive control, no PEG8000 is in the buffer so the phage undergoes complete genome ejection upon binding of LamB (6). In the two negative controls (one with no PEG, and one in 15% w/w PEG), LamB is not added and no ejection occurs. In experiments with 15% w/w PEG, only a part of the genome is ejected due to osmotic inhibition by PEG (6); the fraction ejected is determined from [Abs(phage + 15% w/w PEG + DNase I + LamB) − Abs(phage + 15% w/w PEG + DNase I)] / [Abs(phage + LamB + DNase I) − Abs(phage + DNase I)], where (phage + 15% w/w PEG + DNase I) and (phage + DNase I) correspond to the two negative controls and (phage + LamB + DNase I) to the one positive control.

Sample preparation

Lyophilized deoxyribonuclease I was purchased from USB (Cleveland, OH), and PEG8000 from VWR (Westchester, PA). All chemicals were used without further purification. Bacteriophage-λ cI60 (48.5 kbps genome length) was grown and isolated from an infected culture of Escherichia coli strain c600. The isolated phage was dialyzed twice against 1000-fold volumes of buffer to remove cesium chloride and other impurities. The shorter genome deletion λ-mutant with 45.7 kbp DNA (corresponding to 94% of the wt-DNA length) was produced by thermal induction of lysogenic E. coli strain AE2 derived from S2739 strain (kindly provided by Stanley Brown, University of Copenhagen, Denmark). The phage receptor protein LamB was expressed and purified from E. coli strain pop154, which is transduced with the Shigella sonnei lamB gene (23,24). We use the S. sonnei LamB because—unlike the LamB from wild-type E. coli—it has been shown to induce ejection of bacteriophage-λ in vitro without requiring the addition of chloroform (25,26).

Osmotic stress

The method for direct force measurement by osmotic stress has been described in detail by Parsegian, et al. (12). In brief, condensed DNA arrays are equilibrated against a larger volume of coexisting polymer solution, typically high-molecular-weight polyethylene glycol, PEG, of known osmotic pressure. PEG (molecular weight of 8000) is excluded from many condensed macromolecular arrays, DNA in particular. Water and salt are free to exchange between the PEG and condensed DNA phases. After equilibrium is achieved, the osmotic pressures in both the polymer and macromolecular phases are the same, as necessarily are the chemical potentials of water and all other permeating species. If the condensed DNA phase is sufficiently ordered, the intermolecular distance can be determined as a function of the applied PEG stress by Bragg scattering of x-rays.

Sample preparation

High-molecular-weight chicken blood DNA was prepared as described previously (27). Polyethylene glycol (average molecular weight of 8000) and spermine·4HCl (SpCl₄) were purchased from Fluka Chemical, Milwaukee, WI (micro-select grade). All chemicals were used without further purification.

Precipitated DNA samples for x-ray scattering were prepared in several ways. Samples equilibrated against PEG solutions with either MgCl₂ or MgSO₄ were prepared by ethanol precipitation of ≈200 μg of chicken erythrocyte DNA in 0.3 M NaAcetate. The fibrous samples were centrifuged, washed with 70% (v/v) ethanol, and the DNA pellets transferred to PEG-salt solutions (1–1.5 ml) in screw cap microtubes. For DNA samples equilibrated against SpCl₄, concentrated (≈100 mM) SpCl₄ was added to 150 μl of 1.35 mg/ml chicken erythrocyte DNA (≈2 mM bp) in 10 mM TrisCl (pH 7.5) in steps of 0.4 mM with mixing to a final concentration of 2 mM. The condensed DNA pellet was centrifuged and transferred to PEG solutions containing 5 mM SpCl₄, 10 mM MgSO₄, 50 mM TrisCl (pH 7.5). Samples were equilibrated for several days with occasional vigorous mixing before transferring to fresh solutions. Samples were considered equilibrated after 1–2 weeks of incubation.

X-ray scattering

An Enraf-Nonius Service (Bohemia, NY) fixed copper anode Diffractis 601 x-ray generator equipped with double focusing mirrors (Charles Supper, Natick, MA) was used for x-ray scattering. DNA samples were sealed with a small amount of equilibrating solution in the sample cell, and then mounted into a temperature-controlled holder at 20°C as described by Mudd et al. (28). The sample to film distance was ∼16 cm. The scattered x-rays pass through a helium-filled Plexiglas cylinder with Mylar windows to minimize background scattering. Diffraction patterns were recorded by direct exposure of Fujifilm (Stamford, CT) BAS image plates and digitized with a Fujifilm BAS 2500 scanner. The images were analyzed using FIT2D (A. P. Hammersley, European Synchrotron Radiation Facility) and SigmaPlot 9.01 (Systat Software, San Jose, CA). The sample-to-image plate distance was calibrated using powered p-bromobenzoic acid. Mean pixel intensities between scattering radii r − .05 mm and r + .05 mm were averaged over all angles, 〈I(r)〉, and used to calculate radial intensity profiles, 2πr〈I(r)〉. The sharp, intense ring corresponds to interaxial Bragg diffraction from DNA helices packed in a hexagonal array.

Experimental results

The effect of Mg²⁺ concentration on ejection fraction was studied by increasing [Mg²⁺] up to 100 mM in the buffer solution containing 50 mM TrisCl (pH 7.5) and 10 mM MgSO₄. The measurements were carried out at a 15% w/w concentration of 8000 molecular weight PEG, corresponding to an osmotic pressure at 37°C of 3.5 atm. As discussed in detail in earlier work (6,10), the ejection faction is determined by measuring the 260-nm absorbance in the supernatant, after spinning down the sample following its incubation with receptor and nuclease. Fig. 2, a and b, show the results of measurements on several different phage samples that are nominally at the same concentration. The data for MgSO₄ show an initial decrease in the fraction ejected and a minimum at ∼50 mM added salt, whereas the data for MgCl₂ do not exhibit this “turnaround”. The addition of spermine, Fig. 2 c, leads to a very sharp initial drop in the ejection fraction, which then appears to go through a shallow minimum at ∼5 mM. Note that the measured ejection fractions from Fig. 2, a–c, can be compared directly at zero-added salt since they all correspond to the same ionic conditions (50 mM Tris, 10 mM MgSO₄). The measured fractions in the absence of added salt, i.e., at 10 mM Mg²⁺, are ∼20% higher than those previously measured (6,10). Despite many efforts to determine the cause of this systematic difference, including changing the preparation of the phage, we are unable to explain it. For the purposes of this study, however, only the changes in ejection fractions as the ion concentration is changed are of importance. We note also that the uncertainties in the present ejection fraction data are larger than many of those reported earlier at lower and higher osmotic pressures, because of a previously noted phenomenon (10), i.e., the presence of a minimum between 1.5 and 3.5 atm in the plot of observed ejection fraction versus osmotic pressure; this nonmonotonic behavior makes the fraction ejected in this range more sensitive to small uncertainties in the PEG concentration.

In Fig. 2 a we also plot the ejection fractions calculated from the theory outlined in “Calculation of DNA repulsion and bending energies”, showing qualitative agreement with the experimental values. The zero-added-Mg²⁺ result is nicely accounted for (i.e., the predicted ejection fraction matches those measured for different phage batches), and we also obtain the experimentally observed nonmonotonicity. The predicted magnitude of the variation with added salt is weaker than the measured one, because we have not bothered to include dependence of either the interaction decay length or the chain persistence length on added salt concentration. Even a small (few percent) decrease in decay length with added salt, for example, will give a significantly stronger decrease in calculated ejection fraction with added salt, since this length scale appears in the exponent of the DNA-DNA repulsion (see Eq. 1); but it is not interesting to try to fit the data in this way.

The x-ray diffraction measurements on macroscopically condensed and ordered DNA for varying concentrations of MgSO₄ are carried out at the same temperature and osmotic pressure (corresponding to 15 w/w% PEG8000. The results are shown in Fig. 3 a, where the interaxial spacing d is seen to decrease at first and then go through a shallow minimum near 50 mM added salt. Also plotted there are the d-spacings calculated from the theory based on Eqs. 1–3 discussed above, i.e., the interaxial distances that obtain inside the capsid when the packaged DNA has come to osmotic equilibrium with the external PEG. Note that the measured d-spacings, which pertain to a bulk DNA solution in osmotic equilibrium at the same pressure, are consistently lower than those that characterize the DNA inside. This is because of the effect of bending energy discussed in “The small system case” and calculated in “Calculation of DNA repulsion and bending energies”. Note also that a decrease in spacing at a fixed osmotic pressure, upon addition of divalent salt, means that the repulsive force is smaller, consistent with the decrease in the DNA ejection fraction seen in Fig. 2 a. Similar results are found for the case of added spermine, i.e., diffraction measurements carried out at spermine concentrations ranging from 1 to 5 mM show a very large decrease in the interaxial spacing, again in good qualitative agreement with the osmotic suppression studies.

An estimate of the ejection fraction can also be obtained directly from the interaxial spacing if one assumes that the volume d²L occupied by DNA in the capsid remains constant as ejection proceeds—as would be the case, say, if there were no bending energy cost and the self-repelling chain is free to fill the volume available in the capsid. More explicitly, let d_o be the spacing for the fully packaged genome; for wild-type (L_o = 48.5 kbp) λ this has been measured by Earnshaw and Harrison (29) to be 2.77 nm, thereby implying a value of $d_{\text{o}}^2{L}_{\text{o}}$, and hence of $d^{2}L$. It follows that the ejection fraction $(L_{\text{o}}-L)/L_{\text{o}}=1-L/L_{\text{o}}=1-{(d_{\text{o}}/d)}^2$ first decreases and then goes through a minimum, since the measured values for d in bulk solution (Fig. 3 a) behave in precisely this way; see the +'s in Fig. 2 a. As we discuss below, however, this assumption of constant occupied volume neglects the effect of the bending energy on the packaging within the capsid (8). Note that the +'s in Fig. 2 a appear to agree better with experiment than the ×'s from our theory, but—as emphasized above—this is because we have described the bending and repulsion contributions and their dependences on added cation concentrations in the simplest and (deliberately) crudest ways. Our intent has been to provide a conceptual basis for interpreting the experiments rather than a quantitative fit to the data. The constant-volume-assumption +'s, on the other hand, are not “spoiled” by any theoretical input; rather, they simply follow from measured bulk-solution d-spacings at the corresponding added cation concentrations.

As shown in Fig. 3 b, the diffraction measurements reveal substantial differences in the interaxial spacing of the DNA accompanying a change in the Mg²⁺ coions from $\text{S}{\text{O}}_4^{2-}$ to Cl⁻, the difference increasing with salt concentration. Consistent with these x-ray results, our data (not shown) on osmotic suppression of ejection fraction at a Mg²⁺ concentration of 100 mM show that the ejection with the chloride coion is 10% smaller than with the sulfate. The effect of the coion on ejection force can be understood as primarily due to solution nonideality. Measurements of the mean ion activity coefficient γ for Mg²⁺ as a function of coion have been tabulated (30); in a 100 mM solution, γ_S = 0.150 for $\text{S}{\text{O}}_4^{2-}$ and γ_C = 0.528 for Cl⁻. If we assume the complexation of Mg²⁺ with DNA to be equilibrated, then the relative concentrations of the complex with the different coions is given by the ratios of their activity coefficients, γ_C/γ_S = 3.5. Thus, considerably more Mg²⁺ is bound to DNA when the coion is chloride than when it is sulfate and the electrostatic repulsion between the chains is therefore smaller, in accord with the observation that the fraction of DNA ejected is lower in the chloride solutions.

We also performed ejection fraction measurements to determine the effect of monovalent salt (NaCl), added to the same 10 mM MgSO₄ and 50 mM TrisCl buffer solution, but the variation was not significant over a range of added salt up to 300 mM. The osmotic stress experiments show a change in d-spacing of <10% over a similar range of NaCl concentrations.

Fuller et al. (31) have recently reported single-molecule measurements in which they determine the velocities and forces associated with packaging a phage (φ29) genome in the presence of added mono-, di- and trivalent cations; from these data they deduce the packaging forces as a function of length in the capsid. They find, as expected, that these forces decrease with increasing concentration and valence of the added salts; they also find interesting effects of the particular cations on the function of the motor itself (e.g., Mg²⁺ is specifically needed to initiate packaging).

Discussion

The measurements and analyses presented here provide further elucidation of phage capsid pressures being determined by a combination of DNA self-repulsions and bending elasticity, and provide a quantitative account of how these forces depend on different counter- and coions.

We have measured the extent of DNA genome ejection from phage, against a fixed osmotic pressure mimicking that in the bacterial cytoplasm, as a function of the ambient concentrations of di- and tetravalent cations, Mg²⁺ and Sp⁴⁺. We find that the ejection fraction varies with each of these added salts, first decreasing and then increasing. To test recent theoretical analyses of DNA packaging in phage, we also measured directly the strength of DNA-DNA repulsions as a function of Mg²⁺ concentration and used these results to calculate the d-spacings of packaged DNA and the extent of genome ejection, each as a function of added salt; good agreement is found with measured values. In particular, our calculated d-spacings turn out to be significantly larger than those measured for bulk DNA solutions at the same osmotic pressure, thereby confirming the qualitative importance of bending energy (chain persistence).

The nonmonotonic variation of ejection fractions and d-spacings with the concentration of added divalent cations is related to the fact that higher concentrations of coions lead to a shift in the ion-association equilibrium in bulk solution (32); this possibility is suggested in particular by the differences found for MgCl₂ and MgSO₄ in both of our (ejection fraction and osmotic stress) experiments. The nonmonotonicity is consistent as well with all-ion computer simulations in which the force between two parallel charged rods is calculated as a function of the number of added multivalent counterions (33). For example, in the presence of +1 counterions and +1/−1 salt, adding +3/−1 salt leads first to a weakening of the repulsions between the rods and then to an attraction that is first enhanced and then decreased by further increase in +3 ions. This nonmonotonic behavior is attributed to the fact that the +3s first saturate the region between the two rods and then are forced—at higher +3 concentrations—to congregate on the “back” sides of the rods, resulting in a weakening of the attractive interaction. In this case, instead of a pair of rods (modeling the DNA duplexes) we have the situation of essentially “bulk” DNA that is locally hexagonally packed. And instead of the interaxial spacing being allowed to vary, it is fixed at a small value that corresponds to strong repulsions, even in the presence of polyvalent cations (+4). Upon initial increase in +4 concentration the repulsions decrease, as the polyvalent cations move into regions most advantageous for the local interactions between duplex portions; but then above a certain concentration of +4 in the bulk solution the cations are forced into regions that begin to increase the effective repulsions. These effects are addressed analytically in the correlated electron gas theory of Shklovskii and co-workers (34). As an alternative explanation for the nonmonotonicity associated with the addition of multivalent cation, competing Gibbs-Donnan equilibria have been suggested (35).

The two physical situations explored in this work both involve concentrated DNA in osmotic equilibrium with an “external” solution. In one, the DNA-containing capsid is opened in a solution containing a fixed concentration of PEG, corresponding originally (before the capsid is opened) to an osmotic pressure difference Π* between the inside and outside of the capsid; the fraction of DNA ejected is measured. In the other situation, an unconstrained, bulk, solution of DNA is equilibrated with a PEG solution characterized by osmotic pressure Π*; the d-spacing in the DNA solution is measured. Osmotic pressure equality is attained by ejection of DNA in the former case and by expansion of the DNA phase in the latter. The key to understanding the role of bending energy in determining the phage DNA packaging stress is to note that if there were no bending elasticity—i.e., if the only energy cost associated with packaging the DNA were the interactions between neighboring portions of duplex—then the d-spacing inside the capsid would be identical to that in the bulk DNA solution in osmotic equilibrium at the same pressure Π*. When, on the other hand, there is an energy cost associated with bending the DNA in the capsid, the d-spacing inside will increase beyond the value measured in bulk (d_capsid > d_bulk), consistent with the higher state of stress (osmotic activity) of the confined DNA and confirmed by the comparison between theory and experiment in Fig. 3 a.

Another example of the role played by bending energy is the fact that the volume occupied by the packaged DNA—proportional to d²L through a numerical factor of order unity—is not constant; rather, it increases with L. More explicitly, by calculating d(L) as outlined above (i.e., minimizing Eq. 2 with respect to d for each value of L), it is straightforward to show that d²L decreases significantly when L is decreased from its full length L_o; conversely, when the bending energy contribution is dropped from Eq. 2, the volume d²L remains constant. Indeed, this “prediction” was confirmed 30 years (!) ago by Earnshaw and Harrison (29), whose x-ray diffraction measurements yielded the mean Bragg distances (proportional to d-spacings) for a series of λ-phage mutants with decreasing genome lengths. They reported results for genomes as long as 1.05 (times wild-type length) and as short as 0.78; the associated Bragg spacings increased from 2.35 to 2.62 nm for this 25% decrease in L, corresponding to an 8% decrease in d²L; indeed they noted that the volumes occupied by their successively shorter packaged DNAs decreased in just this way. If the volumes had remained constant, the spacings would have been found to have a significantly larger range, increasing as $L^{-1/2}$ upon decrease in genome length.

Note that one could further test these same ideas by an additional, alternative, set of experiments. Instead of measuring the extent of ejection against a particular osmotic pressure, one could measure—by x-ray diffraction—the d-spacing inside the phage capsid as a function of osmotic pressure. More explicitly, the first measurement of d-spacing in the capsid would be performed at the osmotic pressure—determined earlier (6) to be 20 atm for λ in 50 mM Tris/10 mM MgSO₄—just large enough to completely inhibit DNA ejection; this d-spacing is the same as what one would find in the unopened capsid. The d-spacings for each of the successively smaller osmotic pressures would be measured and compared with the d-spacings calculated from theory (8), as outlined above. The differences between these d-spacings and those measured for bulk DNA solutions equilibrated against decreasing PEG pressures (as in Fig. 3) would again reflect the competing roles played by interaction and bending energies in the capsid confinement of DNA.