Phase Behavior of a Model Bilayer Membrane with Coupled Leaves

Abstract

We discuss the thermodynamic behavior of a bilayer composed of two coupled leaves and derive the Gibbs Phase Rule for such a system. A simple phenomenological model of such a system is considered in which the state of the bilayer is specified by the relative number of ordering lipids in the outer leaf, and in the inner leaf. Two cases are treated. In the first, both inner and outer leaves could undergo phase separation when uncoupled from one another. The bilayer can exist in four different phases, and can exhibit three-phase coexistence. In the second case, an outer layer which can undergo phase separation by itself is coupled to an inner leaf which cannot. We find that when the coupling is weak, the bilayer can exist in only two phases, one in which the outer layer is rich in ordering lipids and the inner leaf is somewhat richer in them than when uncoupled, and another in which the outer layer is poor in ordering lipids and the inner leaf is poorer in them than when uncoupled. Increasing the coupling increases the effect on the inner leaf composition due to small changes in those of the outer leaf. For sufficiently large coupling, a phase transition occurs and the bilayer exhibits four phases as in the first case considered. Our results are in accord with several observations made recently.

Introduction

There has been great interest in the idea that the lipids in the plasma membrane are not uniformly distributed, but rather that saturated lipids, such as sphingomyelin, aggregate with cholesterol in “rafts” that float in a sea of unsaturated lipids. It was first thought that such rafts served as platforms for signaling proteins (1); later they were implicated in a host of other processes. The hypothesis remains controversial, as discussed in recent reviews (2–6). One puzzling feature which must be understood is that artificial membranes whose composition mimics that of the outer leaf of the plasma membrane, rich in sphingomyelin, phosphatidylcholines, and cholesterol, readily show phase-separation into saturated-lipid-rich and saturated-lipid-poor domains (7–11). However, those whose composition mimics that of the inner leaf of the plasma membrane, where most of the phosphatidylethanolamine and phosphatidylserine is found in addition to cholesterol, do not exhibit such phase separation (12,13). The two leaves of the plasma membrane are almost certainly coupled in some way, either by the interdigitation of hydrocarbon tails or the rapid exchange of cholesterol (14–16). As a consequence, it has been hypothesized that domain formation in one leaf induces domain formation in the other (13,17,18). In fact, it is relatively easy to show that in such a coupled system, the onset of more ordered domains in one leaf must induce more ordered domains in the other (19). However, the degree of the increase in order in the two leaves depends on their composition, and need not be the same at all. Clearly visible domains have been induced in one leaf of an asymmetric bilayer by the presence of such domains in the other (13,20). But when the composition of one leaf is significantly altered, a bilayer can be observed to have visible domains in one leaf, but not the other (12,20). Clearly visible domains in both leaves can be brought about by changing either the components of the less-ordered leaf (13) or the relative composition of the same components of that leaf (20). Even when the domains are clearly visible in only one leaf, however, the concentration of ordered lipids in the other leaf is predicted (19) to be enhanced over what it would have been in the absence of coupling.

To clarify the nature of the phases of the bilayer, we have solved a simple phenomenological model of coupled leaves, one which is simpler than that considered earlier (19). When the coupling is weak, the model can be solved analytically; when the coupling is stronger, the model is solved numerically. We focus particularly on the situation in which one leaf, labeled the outer leaf, can undergo liquid-liquid phase separation when it is uncoupled from the other, inner, leaf. Two cases are considered.

In the first case, the inner leaf is such that it, too, can undergo phase separation even when uncoupled from the other leaf. We find that the bilayer can exist in four different phases. Two of them are characterized by an outer leaf rich in ordering lipids; in one it is paired with an inner leaf also rich in ordering lipids, while in the other it is paired with an inner leaf which is poor in them. In the other two phases, the outer leaf is poor in ordering lipids and is either paired with an inner leaf which is also poor in them, or is rich in them.

In the second case, the inner leaf does not, at the temperature of interest, undergo phase separation when uncoupled from the outer leaf. We find that for weak coupling, the bilayer exists in only one of two phases. In one, the outer leaf is rich in ordering lipids while the inner leaf is somewhat richer in them than when it was uncoupled from the outer leaf. In the other phase, the outer leaf is poor in ordering lipids while the inner leaf is somewhat poorer in them than when uncoupled. As the coupling increases, we find that small changes in the composition in the outer leaf can have large effects on the composition of the inner leaf. At sufficiently large coupling, a phase transition occurs and the bilayer now can exist in four phases, just as in the first case considered. Again, an outer leaf rich in ordering lipids can be paired with an inner leaf which is either richer or poorer in them, and similarly for an outer leaf poor in ordering lipids. The fact that separation in one leaf can induce separation in another which, by itself, would not separate, has been observed in experiment (20).

In the process of obtaining these results, we also make some general remarks by way of deriving the Gibbs Phase Rule for the bilayer system of coupled leaves.

Thermodynamics of the bilayer system

A bilayer is very much like the elementary system described in texts on thermodynamics, such as the excellent book of Callen (21), in which a wall, adiabatic and impermeable to matter, separates two closed systems. One asks about the equilibrium state of the system as the properties of the wall are changed; e.g., as the adiabatic coating is removed from the wall, so that energy can flow between the two systems, or as the wall is made permeable to some components, so that matter can flow between them, etc. In the bilayer, the two systems are the inner and outer leaves, and energy certainly flows between them, but few of the lipid components do, at least over timescales relevant to experiment. In contrast, cholesterol is one component that is exchanged freely between the two leaves (14–16). Thus the bilayer is like two systems separated by a membrane permeable to only some of the molecular species. Let the number of molecules of component k which are confined to the inner leaf be denoted by N_i,k, $k=1,2,\dots C_{\text{i}},$ the number of molecules of component l which are confined to the outer leaf by N_o,l, $l=1,2,\dots C_{\text{o}},$ and the number of molecules of component m which can be exchanged freely between leaves as N_x,m, $m=1,2,\dots C_{\text{x}}\text{.}$ Note that a particular molecular species, say palmitoyl-oleoyl-phosphatidylcholine, can be present in both leaves and not undergo significant interchange between them. In this case, this one species would contribute both to the number of components $C_{\text{i}}$ confined to the inner leaf and to the number $C_{\text{o}}$ confined to the outer leaf.

The internal energy of the system, U(S, N_i,k, N_o,l, N_x,m, A) can be written

$$U=TS+\sum _{\text{k}}{\mu }_{\text{i,k}}{N}_{\text{i,k}}+\sum _{\text{l}}{\mu }_{\text{o,l}}{N}_{\text{o,l}}+\sum _{\text{m}}{\mu }_{\text{x,m}}{N}_{\text{x,m}}+\gamma A,$$ (1)

where it has been assumed that both leaves are flat and of area A. The entropy is denoted S, the temperature T, and the surface tension γ. The chemical potentials of the k^th component confined to the inner leaf, of the l^th component confined to the outer leaf, and of the m^th component which can exchange between leaves, are denoted μ_i,k, μ_o,l, and μ_x,m, respectively. The differential of the internal energy is

$$dU=TdS+\sum _{\text{k}}{\mu }_{\text{i,k}}d{N}_{\text{i,k}}+\sum _{\text{l}}{\mu }_{\text{o,l}}d{N}_{\text{o,l}}+\sum _{\text{m}}{\mu }_{\text{x,m}}d{N}_{\text{x,m}}+\gamma dA\text{.}$$ (2)

Differentiating Eq. 1 and comparing with the above differential, we obtain the Gibbs-Duhem equation

$$d\gamma =-sdT-\sum _{\text{k}}{n}_{\text{i,k}}d{\mu }_{\text{i,k}}-\sum _{\text{l}}{n}_{\text{o,l}}d{\mu }_{\text{o,l}}-\sum _{\text{m}}{n}_{\text{x,m}}d{\mu }_{\text{x,m}},$$ (3)

where s ≡ S/A, n_{i, k} ≡ N_{i, k}/A, etc. For convenience, we note that the Helmholtz free energy per unit area, f ≡ (U – TS)/A, follows from Eq. 1,

$$f=\sum _{\text{k}}{\mu }_{\text{i,k}}{n}_{\text{i,k}}+\sum _{\text{l}}{\mu }_{\text{o,l}}{n}_{\text{o,l}}+\sum _{\text{m}}{\mu }_{\text{x,m}}{n}_{\text{x,m}}+\gamma \text{.}$$ (4)

Its differential, simplified with the use of the Gibbs-Duhem equation, Eq. 3, is

$$df=-sdT+\sum _{\text{k}}{\mu }_{\text{i,k}}d{n}_{\text{i,k}}+\sum _{\text{l}}{\mu }_{\text{o,l}}d{n}_{\text{o,l}}+\sum _{\text{m}}{\mu }_{\text{x,m}}d{n}_{\text{x,m}}\text{.}$$ (5)

We want to consider the coexistence between phases at which the $C_{\text{i}}$ components can interchange freely within the inner leaf between phases, the $C_{\text{o}}$ components can interchange freely in the outer leaf between phases, the $C_{\text{x}}$ components can exchange freely within and across leaves between phases, and heat can be exchanged. To do so, it is natural to make a Legendre transform to the thermodynamic potential γ(T, μ_i,k, μ_o,l, μ_x,m),

$$\gamma =u-Ts-\sum _{\text{k}}{\mu }_{\text{i,k}}{n}_{\text{i,k}}-\sum _{\text{l}}{\mu }_{\text{o,l}}{n}_{\text{o,l}}-\sum _{\text{m}}{\mu }_{\text{x,m}}{n}_{\text{x,m}},$$ (6)

where u ≡ U/A. This thermodynamic potential is simply the surface tension, whose differential is given above (Eq. 3).

It is now straightforward to derive the Gibbs Phase Rule for the bilayer. Suppose that there are ℘ phases in coexistence. The chemical potentials of all components, those confined to either leaf as well as those which are exchanged between leaves, must be the same in all phases. These conditions provide $(C_{\text{i}}+C_{\text{o}}+C_{\text{x}})(\wp -1)$ equations. Furthermore, phase coexistence comes about when the thermodynamic potential, γ, the surface tension, takes the same value in each phase. This provides another $(\wp -1)$ equation, so that there are, in all, $(C_{\text{i}}+C_{\text{o}}+C_{\text{x}}+1)(\wp -1)$ equations of coexistence. The unknowns are the values of the areal densities, n, of all components in each phase, and the temperature of the system at coexistence. Thus, there are $\wp (C_{\text{i}}+C_{\text{o}}+C_{\text{x}})+1$ unknowns. That the number of unknowns must be greater than, or equal to, the number of equations yields the phase rule

$$\wp \le C_{\text{i}}+C_{\text{o}}+C_{\text{x}}+2\text{.}$$ (7)

This inequality is applicable in those cases in which the value of the surface tension in the coexisting phases is unknown. This occurs, for example, if the area of the system is fixed, as is often the case in supported bilayers.

If the surface tension of the system is specified, however, either because the area of the system is free to adjust itself to minimize the free energy so that the tension vanishes, or because the tension is externally controlled, then this provides one additional equation so that in this case

$$\wp \le C_{\text{i}}+C_{\text{o}}+C_{\text{x}}+1surfacetensionspecified\text{.}$$ (8)

In a ternary system in which one component is cholesterol, which is free to exchange between leaves, and the other two are lipids confined to the leaves, $C_{\text{i}}=C_{\text{o}}=2,C_{\text{x}}=1,$ and there can exist up to six independent phases in a bilayer whose area is free to vary so that its surface tension vanishes.

In the simple model we will employ below, the compositional state of each leaf is characterized by a single number, an order parameter representing the difference between “ordered” components like saturated lipids and cholesterol, and “disordered” components, like the unsaturated lipids. Thus, in our model, $C_{\text{i}}=C_{\text{o}}=1,C_{\text{x}}=0,$ so that $\wp \le 4$ if the surface tension is not specified, as it was not in Allender and Schick (19), and $\wp \le 3$ if it is. In the latter case, a triple point is constrained to occur at a single temperature only. This illustrates one reason for a membrane to evolve to have multiple lipid components; it is not that the additional components permit the membrane to exist in additional phases. After all, membranes are known to display only a handful of distinct thermodynamic phases. Rather the presence of additional distinct components gives the membrane many additional degrees of freedom which can be manipulated to bring itself into one of the few useful phases.

The model

The description of the system can be simplified by characterizing each leaf by a single order parameter only. To see what this approximation entails, we consider a particular system, one in which each leaf contains a saturated (s) and an unsaturated (u) lipid which are not free to exchange between leaves, and cholesterol (c) which is free to exchange. In this case there are five independent areal densities: n_i,1 ≡ n_i,s, n_i,2 ≡ n_i,u, n_o,1 ≡ n_o,s, n_o,2 ≡ n_o,u, and n_x,1 ≡ n_x,c. It is convenient to introduce five independent linear combinations of these densities

$$n_1\equiv n_{\text{i,s}}-n_{\text{i,u}},$$

$$n_2\equiv n_{\text{o,s}}-n_{\text{o,u}},$$

$$n_3\equiv n_{\text{x,c}}+n_{\text{i,s}}+n_{\text{i,u}}+n_{\text{o,s}}+n_{\text{o,u}},$$

$$n_4\equiv n_{\text{i,s}}+n_{\text{i,u}}-n_{\text{o,s}}-n_{\text{o,u}},$$

$$n_5\equiv n_{\text{x,c}}-\frac{1}{4}(n_{\text{i,s}}+n_{\text{i,u}}+n_{\text{o,s}}+n_{\text{o,u}})\text{.}$$

The physical meaning of these combinations is clear. The first is the differences in areal densities of the saturated and unsaturated lipids in the inner leaf and the second is the analogous quantity in the outer leaf. The third combination is simply the total areal density of all components, the fourth measures the difference between the total lipid content in the two leaves, and the last measures the difference between the cholesterol density and the average of the lipid densities. In terms of these variables, the Helmholtz free energy per unit area, Eq. 4, is

$$f=\sum _{\text{j}=1}^5{\mu }_{\text{j}}{n}_{\text{j}}+\gamma ,$$ (9)

$$df=-sdT+\sum _{\text{j}=1}^5{\mu }_{\text{j}}d{n}_{\text{j}}\text{.}$$ (10)

We now make the observation that the total areal density of lipid bilayers, n₃, does not vary much, so that we do not lose crucial information about the phase behavior of the system by ignoring this variable. Equivalently this approximation can be viewed as restricting the system to a particular constant value of the total areal density. Similarly we assume that the areal differences described by n₃ and n₄ are not so important in describing the phase behavior, and can be fixed at particular values; that is, we assume that an adequate description of the system can be obtained by focusing only on the differences between the areal densities of the saturated and unsaturated lipids in the two leaves. Thus we approximate the description of the system of five areal densities by a two-dimensional cut in the five-dimensional space; i.e., we reduce the description to one entailing only two independent densities. We define order parameters x and y to be linearly related to n₁ and n₂, respectively. The excess Helmholtz free energy per unit area now reduces to a function of three variables only,

$$f(T,x,y)={\mu }_{\text{i}}x+{\mu }_{\text{o}}y+\gamma ,$$ (11)

$$df=-sdT+{\mu }_{\text{i}}dx+{\mu }_{\text{o}}dy,$$ (12)

where μ_i and μ_o are the fields conjugate to x and y, respectively. The Gibbs-Duhem equation, Eq. 3, reduces to

$$d\gamma =-sdT-xd{\mu }_{\text{i}}-yd{\mu }_{\text{o}}\text{.}$$

From the Gibbs-Duhem equation, one easily derives a useful Clausius-Clapeyron equation for the slope of the boundary between coexisting phases as follows. Because the surface tension γ is equal in coexisting phases, the difference between surface tensions in coexisting phases is always zero and does not change as one moves along a phase boundary. Hence

$$(s_{\text{a}}-s_{\text{b}})dT+(x_{\text{a}}-x_{\text{b}})d{\mu }_{\text{i}}+(y_{\text{a}}-y_{\text{b}})d{\mu }_{\text{o}}=0,$$ (14)

where the subscripts a and b denote the two coexisting phases. In particular, at constant temperature, the above gives a Clausius-Clapeyron equation

$$d{\mu }_{\text{i}}=-\frac{y_{\text{a}}-y_{\text{b}}}{x_{\text{a}}-x_{\text{b}}}d{\mu }_{\text{o}},$$ (15)

which has the consequence that the tie line connecting coexisting phases in the x,y (or composition) plane has a slope which is perpendicular to that of the phase boundary at the corresponding point in the μ_i,μ_o (chemical potential) plane.

To make further progress, we now consider a particular form of the Helmholtz free energy per unit area of the bilayer, f(T, x, y), a Landau expansion of it, which is

$$f(T,x,y)=c_{\text{i}}(T)x^2+x^4+c_{\text{o}}(T)y^2+y^4-\alpha xy\text{.}$$ (16)

There are several things to note. First, we have ignored linear terms in x and y as they only contribute to a shift in the conjugate fields μ_i and μ_o. This also shifts the zeros of the order parameters x and y from those of the areal densities n₁ and n₂ to which they are linearly related. Second, the quadratic part of this form is the same as that of Eq. 8 of Allender and Schick (19) except that we have taken the freedom of normalizing the order parameters to set the coefficients of the fourth-order terms to unity. This sets the constants of proportionality between the order parameters x and y and the areal densities n₁ and n₂. The variables which describe the specific mechanism coupling the leaves, whether by interdigitation of lipid tails or the interchange of cholesterol, have been integrated out, producing the last term in the free energy, −αxy, which couples the two leaves. It is assumed that α is positive so that ordering in one leaf promotes ordering in the other, and similarly absence of order in one promotes absence of order in the other. Third, this term is assumed to be the only one which couples the two leaves. This is in contrast to Allender and Schick (19). There the quadratic part of the free energy was diagonalized by transforming to the linear combinations σ ≡ y cos θ + x sin θ, τ = −y sin θ + x cos θ and a quartic free energy containing only σ⁴ and τ⁴ terms was considered. Expressed in the original order parameters, such terms contain the quartic couplings x³y, x²y², and xy³. When the coupling is weak and the order parameters are small, as assumed in a Landau expansion, these terms are certainly smaller than the quadratic coupling. Finally we stress that the values of both order parameters, x and y, must be given to specify a particular phase of the bilayer system.

At the coexistence of two phases, one has the condition of the equality in both phases of the chemical potential in the inner leaf, μ_i ≡ ∂f(T, x, y)/∂x, of the chemical potential in the outer leaf, μ_o ≡ ∂f(T, x, y)/∂y, and of the surface tension γ(T, x, y) ≡ f – μ_ix – μ_oy:

$${\mu }_{\text{i}}(T,x_1,y_1)={\mu }_{\text{i}}(T,x_2,y_2),$$ (17)

$${\mu }_{\text{o}}(T,x_1,y_1)={\mu }_{\text{o}}(T,x_2,y_2),$$ (18)

$$\gamma (T,x_1,y_1)=\gamma (T,x_2,y_2)\text{.}$$ (19)

With the free energy of Eq. 16, these functions are

$${\mu }_{\text{i}}(T,x,y)=2c_{\text{i}}(T)x+4x^3-\alpha y,$$ (20)

$${\mu }_{\text{o}}(T,x,y)=2c_{\text{o}}(T)y+4y^3-\alpha x,$$ (21)

$$\gamma (T,x,y)=-c_{\text{i}}(T)x^2-c_{\text{o}}(T)y^2-3x^4-3y^4+\alpha xy\text{.}$$ (22)

We shall consider separately two cases of interest, and both in the regimes of weak and of strong coupling. In the first, the temperature is such that each uncoupled leaf could, by itself, undergo a phase separation. This is the case in some of the experiments of Collins and Keller (20). In the second, we shall consider the case of possible biological interest, when the temperature is such that one uncoupled leaf, the outer one, could undergo a phase separation, but the other could not.

Leaves which can each phase separate when uncoupled

The assumption that each leaf, when uncoupled from the other, can undergo phase-separation implies that the temperature is such that c_i(T) < 0 and c_o(T) < 0. It is useful to obtain first the solutions of the equations of coexistence when the leaves are uncoupled (i.e., α = 0). These solutions are immediate. The coexisting values of x and y are

$$x=\pm \widehat{X},\widehat{X}(T)\equiv {(|c_{\text{i}}(T)|/2)}^{1/2},$$ (23)

$$y=\pm \widehat{Y},\widehat{Y}(T)\equiv {(|c_{\text{o}}(T)|/2)}^{1/2}\text{.}$$ (24)

Both chemical potentials vanish and the surface tension takes the value $-({\widehat{X}}^4+{\widehat{Y}}^4)\text{.}$

There are four possible phases which can coexist. Each phase is characterized by the values taken by the order parameters in each leaf:

• 1.$(x_1=\widehat{X},y_1=\widehat{Y}),$ which we denote (R,R′), the R for “rich” in ordering lipids;
• 2.$(x_2=-\widehat{X},y_2=-\widehat{Y}),$ which we denote (P,P′), the P for “poor” in ordering lipids;
• 3.$(x_3=-\widehat{X},y_3=\widehat{Y}),$ which we denote (P,R′); and
• 4.$(x_4=\widehat{X},y_1=-\widehat{Y}),$ which we denote (R,P′).

We now assume that the coupling is weak, and expand the order parameters x and y about the values they take when the leaves are uncoupled, denoted X and Y, where X either takes the value $\widehat{X}$ or $-\widehat{X},$ depending upon which phase is being described, and similarly Y either takes the value $\widehat{Y}$ or $-\widehat{Y}\text{.}$ We write

$$x=X+\delta x,$$ (25)

$$y=Y+\delta y,$$ (26)

and expand the chemical potentials and surface tension, Eqs. 20–22 to first-order in the small quantities α, δx, and δy,

$${\mu }_{\text{i}}(T,x,y)\approx 8X^2\delta x-\alpha Y,$$ (27)

$${\mu }_{\text{o}}(T,x,y)\approx 8Y^2\delta y-\alpha X\text{.}$$ (28)

$$\gamma (T,x,y)\approx -(Y^4+X^4)-8Y^3\delta y-8X^3\delta x+\alpha XY\text{.}$$ (29)

The three equations of coexistence, Eqs. 17–19, are now linear equations in four unknowns; the two values of δx in the coexisting phases, and the two values of δy.

For example, let us consider coexistence between phase 1, (R, R′), for which $X=\widehat{X},Y=\widehat{Y},$ and phase 2, (P, P′) for which $X=-\widehat{X},$ and $Y=-\widehat{Y}\text{.}$ With the approximate functions of Eqs. 27–29, the equations of coexistence become

$$8{\widehat{X}}^2\delta x_1-\alpha \widehat{Y}=8{\widehat{X}}^2\delta x_2+\alpha \widehat{Y},$$ (30)

$$8{\widehat{Y}}^2\delta y_1-\alpha \widehat{X}=8{\widehat{Y}}^2\delta y_2+\alpha \widehat{X},$$ (31)

and

$$\begin{array}{l}-({\widehat{Y}}^4+{\widehat{X}}^4)-8{\widehat{Y}}^3\delta y_1-8{\widehat{X}}^3\delta x_1+\alpha \widehat{X}\widehat{Y}\\ =-({\widehat{Y}}^4+{\widehat{X}}^4)+8{\widehat{Y}}^3\delta y_2+8{\widehat{X}}^3\delta x_2+\alpha \widehat{X}\widehat{Y}\text{.}\end{array}$$ (32)

From these equations, we readily obtain three of the order parameters in terms of the fourth,

$$\delta x_1=-\frac{{\widehat{Y}}^3}{{\widehat{X}}^3}\delta y_2,$$ (33)

$$\delta x_2=-\frac{{\widehat{Y}}^3}{{\widehat{X}}^3}\delta y_2-\frac{\alpha \widehat{Y}}{4{\widehat{X}}^2},$$ (34)

$$\delta y_1=\delta y_2+\frac{\alpha \widehat{X}}{4{\widehat{Y}}^2},$$ (35)

and, from Eqs. 27–29, the chemical potentials and surface tension

$${\mu }_{\text{o}}=8{\widehat{Y}}^2\delta y_2+\alpha \widehat{X},$$ (36)

$${\mu }_{\text{i}}=-\frac{8{\widehat{Y}}^3}{\widehat{X}}\delta y_2-\alpha \widehat{Y},$$ (37)

$$\gamma =-({\widehat{X}}^4+{\widehat{Y}}^4)-\alpha \widehat{X}\widehat{Y}\text{.}$$ (38)

Once either of the chemical potentials and temperature is specified along the phase boundary, the change in order parameter δy₂ can be obtained from the above along with the values of the other changes δx₂, δx₁, and δy₁. By eliminating δy₂ from these equations, we obtain the phase boundary

$${\mu }_{\text{o}}({\mu }_{\text{i}},T)=-\frac{\widehat{X}}{\widehat{Y}}{\mu }_{\text{i}},$$ (39)

where both chemical potentials will be small, of order α. From the results of Eqs. 33–35, it is straightforward to calculate the tie lines

$$\frac{y_2-y_1}{x_2-x_1}=\frac{-2\widehat{Y}+\delta y_2-\delta y_1}{-2\widehat{X}+\delta x_2-\delta x_1},$$ (40)

$$=\frac{2\widehat{Y}+(\alpha \widehat{X}/4{\widehat{Y}}^2)}{2\widehat{X}+(\alpha \widehat{Y}/4{\widehat{X}}^2)},$$ (41)

$$\approx \frac{\widehat{Y}}{\widehat{X}}\left[1+\frac{\alpha \widehat{X}}{8\widehat{Y}}\frac{({\widehat{X}}^2-{\widehat{Y}}^2)}{{\widehat{X}}^2{\widehat{Y}}^2}\right]\text{.}$$ (42)

One sees from the slope of these tie lines and from the slope of the phase boundary (Eq. 39) that the Clausius-Clapeyron equation (Eq. 15) is satisfied to lowest order in α. The reason that Eq. 39 is not correct to first-order in α is because both chemical potentials are, themselves, of order α so that a correction is of order α², which has not been included.

Proceeding in a similar fashion, we obtain the phase boundaries and tie lines between other phases. We find that the three phase boundaries meet at a triple point located at

$$({\mu }_{\text{i,t}1},{\mu }_{\text{o,t}1})=(-\alpha \widehat{Y},\alpha \widehat{X}),$$ (43)

at which the surface tension is ${\gamma }_{\text{t}1}=-({\widehat{Y}}^4+{\widehat{X}}^4)-\alpha \widehat{X}\widehat{Y}\text{.}$ By symmetry, there is another triple point at

$$({\mu }_{\text{i,t}2},{\mu }_{\text{o,t}2})=(\alpha \widehat{Y},-\alpha \widehat{X}),$$ (44)

at which γ_t2 = γ_t1. Before presenting a phase diagram, we must completely specify the system by giving the strength of the coupling, which we do in the dimensionless ratio β ≡ α/2|c_o|, and also the ratio r ≡ |c_i|/|c_o|. As c_i is proportional to (T – T_c,i) and c_o to (T – T_c,o), where T_c,i and T_c,o are the critical temperatures of the uncoupled inner and outer leaves respectively, the ratio r compares how far, at a given temperature, the two leaves are from their respective uncoupled critical temperatures.

In Fig. 1 a, we show a phase diagram in the x, y, plane for the case of identical leaves, r = 1, and for weak coupling β = 1/2. The dimensionless areal densities $x/\widehat{X}$ and $y/\widehat{Y}$ are plotted. The tie lines are those of the coupled system, and were obtained by numerical solution of the equations of coexistence. They agree very well with those of the weak-coupling theory given above. They end, by definition, on the binodals shown by the solid lines. The two regions of three-phase coexistence are clear. The dot-dashed lines show the binodals of the uncoupled system, one in which the tie lines are strictly horizontal or vertical. The square represents four-phase coexistence of the uncoupled system which, due to the coupling, breaks into the two three-phase coexistence regions joined by a region of two-phase coexistence.

Figure 1.

(a) Phase diagram in the x,y plane of the bilayer for r = 1, so that the leaves are essentially identical, and a weak coupling β = 0.5. The order parameter, y, of the outer leaf is shown in units of $\widehat{Y},$ and that of the inner leaf, x, is shown in units of $\widehat{X}=r\widehat{Y}\text{.}$ The tie lines end on the binodals of the coupled system shown with solid lines. The dashed-dotted lines denote the binodals of the uncoupled system. There are four possible phases of the bilayer; one in which the order parameters in both leaves are positive, (R,R′), one in which they are both negative, (P,P′), and two phases in which the order parameter in one leaf is positive while that in the other leaf is negative. Note that the region of four-phase coexistence in the uncoupled system breaks into two regions of three-phase coexistence connected by a region of two-phase coexistence between (R,R′) and (P,P′). (b) Phase diagram in the x,y plane of the bilayer for r = 1, and a stronger coupling β = 3.0. The point AA represents the state of a bilayer which consists of coupled, identical, leaves such that the system is in the one-phase region (P,P′); BB represents a bilayer of coupled, identical, leaves of a different composition such that the system is well within the coexistence region between (R,R′) and (P,P′), while the bilayer CC is barely within this two-phase region. The point AB represents the result of making a bilayer with one leaf of A and the other of B. It is within the coexistence region. The point AC represents the result of making a bilayer with one leaf of A and the other of C. It is within the one-phase region (P,P′).

For a system which is coupled strongly, the equations of coexistence must be solved numerically. The phase diagram for a system of identical leaves, r = 1, and coupling β ≡ α/2|c₀| = 3.0 is shown in Fig. 1 b. There is little qualitative difference from that of the weak coupling case. The greater deviation of the tie lines from being strictly horizontal or vertical reflect the effect of the coupling.

Leaves of which only one phase-separates when uncoupled

This case, in which the outer leaf can undergo phase separation at biological temperatures while the inner leaf cannot, is the one that might be of biological relevance.

The phase diagram of the uncoupled system is simple and is shown in Fig. 2 a. There are two phases; one in which the outer leaf is rich in ordering lipids while the inner leaf is disordered, (d,R′), and the other in which the outer leaf is poor in ordering lipids and the inner leaf is disordered, (d,P′). There is phase coexistence in the outer leaf at a specific value of μ_o = 0 irrespective of μ_i. In composition space, the order parameter of the outer leaf, y, takes the specific values $Y_1=-Y_2=\widehat{Y}=(-c_{\text{o}}{/2)}^{1/2}$ in the coexisting phases, irrespective of the order parameter in the inner leaf, x, which varies with the chemical potential μ_i. The tie lines are vertical and end on the binodals represented by solid lines. The dashed lines show the loci of the spinodals between which the system is unstable. They are given by the values of x and y which satisfy the equation

$$\left(\frac{{\partial }^{2}f}{\partial x^2}\right)\left(\frac{{\partial }^{2}f}{\partial y^2}\right)-{\left(\frac{{\partial }^{2}f}{\partial x\partial y}\right)}^2=0,$$ (45)

or equivalently

$$\left(\frac{\partial {\mu }_{\text{i}}}{\partial x}\right)\left(\frac{\partial {\mu }_{\text{o}}}{\partial y}\right)-\left(\frac{\partial {\mu }_{\text{i}}}{\partial y}\right)\left(\frac{\partial {\mu }_{\text{o}}}{\partial x}\right)=0\text{.}$$ (46)

(Of course ∂μ_i/∂y = ∂μ_o/∂x.)

Figure 2.

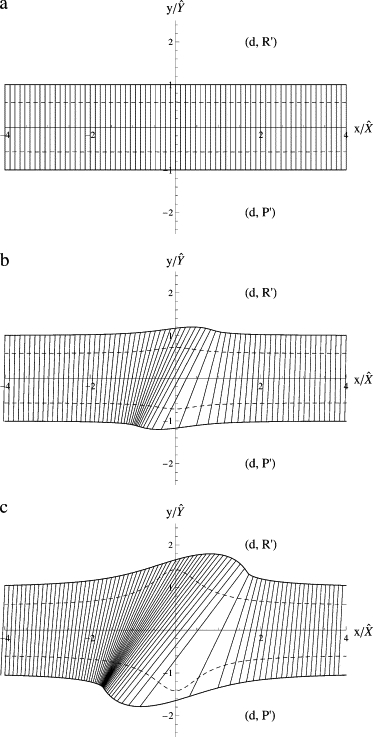
Phase diagrams for a system at a temperature at which the outer leaf can undergo phase separation when uncoupled from the inner leaf, but the inner leaf cannot undergo a phase separation when uncoupled from the outer leaf. The value of r = 1. (a) Phase diagram of the uncoupled system, i.e., β = 0. Solid lines and dashed lines denote the binodals and spinodals, respectively. (b) Same but for β = 0.75 and (c) for β = 2.25. For all three values of the coupling, the bilayer can exist in only two phases; that in which the inner leaf is disordered while the outer leaf is rich in ordering lipids (d,R′), and that in which the inner leaf is disordered while the outer leaf is poor in ordering lipids, (d,P′).

When the coupling between phases is turned on and treated as weak as before, one finds that the tie lines between the two phases are now given by

$$\frac{y_2-y_1}{x_2-x_1}=\frac{2c_{\text{i}}}{\alpha }\text{.}$$ (47)

They have a positive slope, so that the inner leaf in one phase is more ordered due to the ordered outer leaf, and is more disordered in the other phase due to the coupling to the disordered outer leaf. This is the expected behavior (19). From the Clausius-Clapeyron equation, Eq. 15, we obtain the phase boundary in the chemical potential space

$${\mu }_{\text{o}}=-\frac{\alpha }{2c_{\text{i}}}{\mu }_{\text{i}}\text{.}$$ (48)

The behavior of the tie lines is illustrated in Fig. 2, b and c, for the cases in which r = c_i/|c_o| = 1 and the couplings β = 0.75 and 2.25, respectively. Tie lines are drawn which begin at equal intervals along the upper boundary. One sees that with increasing coupling the spinodals become closer to the binodals, which indicates that the osmotic compressibility increases and the system, while still stable, is less so. As the quantity on the left-hand side of Eq. 46 is positive when the system is stable, and the first two terms of this equation are positive, one sees that the source of decreasing stability is either the effect of changes in the composition of the outer leaf on the chemical potential of the inner leaf, or the reverse.

This tendency grows with increasing coupling until the osmotic compressibility diverges at a phase transition. Now the bilayer can, as in the case treated previously, exist in any of four phases: two with an outer leaf rich in ordering lipids paired either with an inner leaf richer in ordering lipids, (R,R′), or with an inner leaf poorer in ordering lipids, (P,R′), and the other two with an outer leaf poor in ordering lipids paired either with an inner leaf richer in them, (R,P′), or poorer in them, (P,P′). Of course beyond the critical point, the distinction between these latter two phases is lost and one can only distinguish the single phase previously labeled (d,P′). A similar remark applies to the distinction between phases (R,R′) and (P,R′). A phase diagram for a coupling β = 4.0, which is larger than that needed to produce the separation, is shown in Fig. 3 a in the x,y plane, and in the plane of chemical potentials μ_o,μ_i in Fig. 3 b. In the vicinity of the critical point, of course, the osmotic compressibility is very large. Again this implies that small changes in the areal density of the outer leaf can have large effects on the areal density of the inner leaf.

Figure 3.

Phase diagrams for a system at a temperature at which the outer leaf can undergo phase-separation when uncoupled from the inner leaf, but the inner leaf cannot undergo a phase separation when uncoupled from the outer leaf. The value of r = 1, and the coupling is β = 4.0. (a) Phase diagram in the x,y plane. There is now an additional coexistence region between one phase in which the outer leaf is rich in saturated lipids as is the inner leaf, (R,R′), and another in which the outer leaf is rich is such lipids and the inner leaf is poor in them, (P,R′). (b) Upper-left quadrant of the phase diagram in the chemical potential plane. The chemical potentials μ_i and μ_o are given in units of ${\widehat{X}}^3$ and ${\widehat{Y}}^3,$ respectively. The lower-right quadrant follows by symmetry, and the other two display no phase boundaries.

Finally we have considered values of r ≡ |c_i|/|c_o| different than unity, that is, leaves which at T are at different temperature intervals from their critical temperatures in the uncoupled system. The results differ only quantitatively from those presented above for r = 1.

Discussion

We have employed a simple model free energy to study the effect of a coupling between the leaves of a bilayer, and have determined its phase diagram for both weak and strong couplings.

In the case in which leaves could each undergo phase separation even when uncoupled, the phase diagrams of Fig. 1, a and b, apply and display some of the phenomena which have been observed recently.

First, as observed in Kiessling et al. (13), a system which displays visible phase separation in the outer leaf but not in the inner leaf can be made to display visible separation in both leaves by replacing the components in the inner leaf with more ordering ones while keeping the components in the outer leaf fixed. This is understood in Fig. 1, a and b, in which one sees that an increase in the order parameter of the inner leaf, x, with no change in that of the outer leaf, y, can take the system from the phase (P,R′) to the phase (R,R′).

Second, one sees that the large region of four-phase coexistence of the uncoupled system becomes two large regions of three-phase coexistence in the coupled system. One should note that the magnitudes of the order parameters in the various coexisting phases are not the same; that is, the positive value of the order parameter in the outer leaf of the phase (R,R′) is larger than the positive value of the order parameter in the outer leaf of the phase (P,R′). Similar statements apply to the magnitudes of the negative order parameters in the inner leaves of the phases (P,R′) and (P,P′). As all order parameters are different in all three coexisting phases, one would expect each of the phases to appear differently under fluorescence microscopy. Just such a region of coexistence of three different phases has been observed (20).

Third, let us consider two different symmetric bilayers. One consists of identical, coupled, leaves with compositions such that the bilayer is in the one phase region (P,P′). Such a system is labeled AA in Fig. 1 b. The other consists of identical, coupled, leaves such that the bilayer is deep into the region of two-phase coexistence between (P,P′) and (R,R′). This system is labeled BB in Fig. 1 b. We now ask what happens when we form the bilayer AB which consists of one leaf of A and the other of B? From Fig. 1 b, one sees that the bilayer is in two-phase coexistence between the phases (R,R′) and (P,P′). Hence, both leaves show visible phase separation. That is, coupling a leaf which strongly separates to one that does not separate can cause both leaves of the coupled system to exhibit visible separation. This is precisely the behavior observed in Collins and Keller (20). To show that the opposite can also occur, we consider a third symmetric bilayer, one consisting of identical, coupled, leaves and which is only slightly within the region of two-phase coexistence between (P,P′) and (R,R′), a system marked CC in Fig. 2. If one now forms a mixed bilayer AC, one sees that the coupled system is now in the one-phase region (P,P′). Thus a leaf which does not phase-separate when coupled to another which separates only weakly can cause the coupled system to show no phase separation. This is again what was observed in experiment (20).

The results for the case which could be of biological interest, in which one leaf can order by itself while the other does not, are also interesting. When the coupling is weak, the results are similar in spirit to that of Allender and Schick (19). There are only two phases; in one the outer leaf is rich in ordering lipids while the inner leaf is somewhat richer in them than it would be when uncoupled. In the other phase, the outer leaf is poorer in the ordering lipids, and the inner leaf is somewhat poorer in them also. As the coupling is increased, we observe that there are compositions at which small changes in the amount of ordering lipids in the outer leaf can have large effects on their amount in the inner leaf; that is, the osmotic compressibility of the system increases. When the coupling exceeds a temperature-dependent amount, a phase transition occurs and there are now four possible phases just as in the first case discussed above. There is a critical point in the neighborhood of which the osmotic compressibility of the system can be very large. In this region, small changes in the composition of the outer leaf can cause very large changes in the composition of the inner leaf. As this difference in areal densities of ordered lipids in the inner leaf could provide a means by which proteins anchored to the inner leaf by an acylated chain could distinguish one region from another, it is possible that small changes in the composition of the outer leaf could have a large effect on partition coefficients of proteins attached to the inner leaf.

Finally we comment on the alignment of domains in one leaf with domains in the other. In the first case which we have considered, that in which each leaf could undergo phase separation even when uncoupled from the other, it is obvious that when uncoupled the domains in each leaf would be uncorrelated. As the coupling is turned on, the domains will tend to be correlated by the cost of the line tension between different phases of the bilayer. Nonetheless, because they can fluctuate independently when uncoupled, one expects that domain correlation will not be strong when the coupling is weak. For strong coupling, of course, one expects the domains to be very well correlated. This seems to be the case in the experiments of Collins and Keller (20). The situation is completely different in the case when the inner leaf would not undergo phase separation when uncoupled to the outer. Then, the fact that the inner leaf can exist in two phases, slightly richer or slightly poorer in ordering lipids, only comes about because of the coupling to the outer leaf, a coupling which acts like a chemical potential for the order parameter of the inner leaf. Therefore one expects the domains in the inner leaf to be very well correlated with those in the outer leaf. This, too, could clearly be of biological relevance.