A Biological Interpretation of Transient Anomalous Subdiffusion. II. Reaction Kinetics

Abstract

Reaction kinetics in a cell or cell membrane is modeled in terms of the first passage time for a random walker at a random initial position to reach an immobile target site in the presence of a hierarchy of nonreactive binding sites. Monte Carlo calculations are carried out for the triangular, square, and cubic lattices. The mean capture time is expressed as the product of three factors: the analytical expression of Montroll for the capture time in a system with a single target and no binding sites; an exact expression for the mean escape time from the set of lattice points; and a correction factor for the number of targets present. The correction factor, obtained from Monte Carlo calculations, is between one and two. Trapping may contribute significantly to noise in reaction rates. The statistical distribution of capture times is obtained from Monte Carlo calculations and shows a crossover from power-law to exponential behavior. The distribution is analyzed using probability generating functions; this analysis resolves the contributions of the different sources of randomness to the distribution of capture times. This analysis predicts the distribution function for a lattice with perfect mixing; deviations reflect imperfect mixing in an ordinary random walk.

Introduction

Earlier work (1) described a trapping model that predicts anomalous subdiffusion at short times and normal diffusion at long times for diffusion in the presence of a finite hierarchy of traps. We argued that the trap hierarchy is biologically reasonable. Abundant shallow traps correspond to nonspecific binding sites; the rare deepest trap corresponds to the biological target site of the diffusing particle; and the binding energies of intermediate traps depend on the similarity of the traps to the target site. We showed that for anomalous subdiffusion to occur, the diffusing particle must not be in thermal equilibrium with the traps; there must be some biological event that turns on the interaction of the diffusing particle with the traps and targets. The earlier article described the model qualitatively; here we consider it quantitatively. We consider the effect on reaction kinetics, specifically the search time required for the diffusing particle to find its target. Later work will examine transient anomalous subdiffusion. The kinetics problem provides a well-defined timescale to characterize the crossover times for anomalous subdiffusion.

Many workers have discussed reaction kinetics in terms of random walks; see, for example, den Hollander and Weiss (2) and Kozak (3). Reactions in bilayers are reviewed by Melo and Martins (4). The effect of traps and fractal substrates on kinetics is summarized by Barzykin et al. (5) and ben-Avraham and Havlin (6). Biochemical applications are discussed by Berry (7), Dewey (8), and Savageau (9).

We characterize reaction kinetics in terms of the time for a diffusing particle starting at a random position to first arrive at an immobile target site. We show that for a single target, the capture time can be described analytically in terms of two known quantities, the first passage time for a target without traps, and the average escape time from the set of traps. The capture time for multiple targets differs from the capture time for a single target by a numerical factor of order one; this correction factor is obtained from Monte Carlo calculations. The entire range of target numbers is of biological interest; targets may be a single gene or an abundant protein structure such as coated vesicles.

Methods

Monte Carlo calculations were carried out as described earlier (10) except that the ran2 random number generator (11) was used. General Monte Carlo techniques for diffusion problems are discussed elsewhere (12). Here triangular and square lattices were used for the two-dimensional case and the simple cubic lattice for the three-dimensional. Periodic boundary conditions were used. Initially a prescribed concentration of immobile traps and targets were placed at random sites on the lattice. A single tracer was placed at a random nontarget lattice site, and carried out a random walk until it first reached a target site. When the tracer was on a trap site, it would try to escape at each time step, with a prescribed probability of success. For the calculations with multiple sets of traps plus target, typically 1024 or 1000 sets were used, and the system size was chosen to give the required concentration. As will be discussed in detail, the capture time is sensitive to the number of sets, and 1000 sets is reasonably close to the asymptotic limit. For most of the runs, results were averaged over 500 random trap configurations and 1000 tracers per configuration. For runs with low escape probabilities or runs on very large systems, fewer repetitions were used, and for some runs many more repetitions were used to get smoother curves for publication, as indicated in the captions. Averages of various quantities are given as the mean ± SD for the stated number of points.

Results

The trap hierarchy model is potentially applicable to two-dimensional diffusion in the plasma membrane and three-dimensional diffusion in the nucleus and cytoplasm, so we will treat two-dimensional diffusion on triangular and square lattices and three-dimensional diffusion on a simple cubic lattice. The triangular and cubic lattices have coordination number 6, and as we shall see the results in two dimensions and three dimensions are surprisingly similar. It is well known that random walks are sensitive to dimensionality due to differences in the efficiency of diffusional mixing. One extreme, the complete graph, is the infinite-dimensional case. Here every lattice point is directly connected to every other lattice point so a tracer can move from any point to any other point in a single time step (13). Mixing is thus perfect in the sense that the system loses all memory of its previous state at every time step. A random walk on a three-dimensional lattice gives good mixing; a random walk on a two-dimensional lattice gives poor mixing; and anomalous subdiffusion on a two-dimensional lattice gives even worse mixing (7,14,15).

As an intuitive way of quantifying this, consider the probability of return, a key quantity in the understanding of random walks (16). A tracer starts a random walk at the origin of an infinite lattice. What is the probability that the tracer will return to the origin? In two dimensions and below, the probability is 1; for the cubic lattice, 0.341; for the four-dimensional hypercubic lattice, 0.193 (see (16) p. 153); and for the complete graph, 0. But for the finite systems and the timescales considered here, the difference between two-dimensional and three-dimensional systems is well represented by the known difference in capture times for a target in a trap-free system.

The discrete hierarchy of traps is shown schematically in Fig. 1. It is defined by the number of levels, the ratio of the number of traps from level to level, and the escape probability P_ESC per time step from the first level. The escape time from a trap of a given level is the reciprocal of the escape probability per unit time. As discussed elsewhere (1), it is assumed that for the diffusing particle to escape a trap it must have enough thermal energy to reach the ground state. The escape time is thus independent of the energy of the site to which the particle is moving. We write the hierarchy of Fig. 1 as 16/8/4/2/T, P_ESC = 0.1. This hierarchy will be used as the standard.

Figure 1.

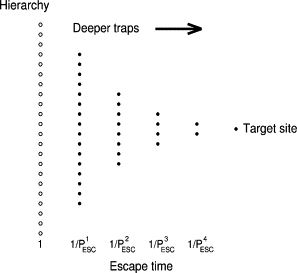
A typical hierarchy of discrete traps and target, written as 16/8/4/2/T.

Mean capture time

We consider reaction kinetics in the presence of a hierarchy of traps. A mobile particle starts at a random position on a finite lattice with periodic boundary conditions and carries out a random walk on the lattice until it first reaches an immobile target site. How many time steps are required? This first passage time can be regarded as a simple example of a reaction rate or as the time required for a mobile species to find its biological target. We examine the mean number of time steps until capture and the distribution of capture times.

To obtain the theoretical mean capture time, we adapt a key idea from the work of Harder et al. (17). They noted that in a system with traps, a diffusing particle carries out an ordinary random walk, with the ordinary distribution of paths from a random initial position to the target, and the ordinary distribution of revisits to sites (which depends on dimensionality). The only effect of the traps is to change the timescale for the random walks. This increase in time gives the transient anomalous subdiffusion found for a finite hierarchy (1), and the pure anomalous subdiffusion over all times found for an infinite hierarchy (17).

In quantitative terms, for any individual random walk in the presence of a single target, the capture time t_capt can be written as the sum of the diffusion times t_{diff ij} from trap i to trap j and the escape times t_{esc i} from the i^th trap. We have

$$t_{\text{capt}}=t_{\text{diff}01}+t_{\text{esc}1}+t_{\text{diff}12}+t_{\text{esc}2}+\dots$$ (1)

so that

$$t_{\text{capt}}=t_{\text{diff}}+t_{\text{esc}},$$ (2)

where t_diff is the sum of the diffusion times from trap to trap and t_esc is the sum of the excess escape times from all the traps encountered. The excess escape time does not include the single time step required for a visit to a site in the absence of traps, so that if no traps are present, t_capt = t_diff as required. Importantly, t_diff is the same as in the trap-free case.

We average this over many random walks. (Means are indicated by capitalized subscripts.) The mean t_DIFF is just the Montroll first passage time t_M(N), which gives the capture time for a single target in a finite system with no traps as a function of the number of lattice points N. The mean excess time in the traps is the product of the mean excess time per trap and the mean number of time steps until capture, that is

$$t_{\text{ESC}}=(\langle t_{\text{ESC}}\rangle -1)t_{\text{M}}\text{.}$$ (3)

Here 〈t_ESC〉 is the mean escape time averaged over all sites in the system, trap and nontrap, but excluding target sites because target sites do not delay the diffusing particle but immediately stop the random walk. (This definition must be changed when the reaction probability of the diffusing particle with the target is <1.) Both t_M and 〈t_ESC〉 are dimensionless, expressed as a number of time steps. The average of Eq. 2 then becomes

$$t_{\text{CAPT}}=\langle t_{\text{ESC}}\rangle t_{\text{M}}(N)\text{.}$$ (4)

Eq. 4 holds in the case of a single target. If there are a total of S targets we use the first passage time t_M(N/S), calculated for the average number of lattice points per target. This is a mean-field approximation so as discussed in detail later a correction factor A(S, C_T) is necessary and the final equation is

$$t_{\text{CAPT}}=A(S,C_{\text{T}})\langle t_{\text{ESC}}\rangle t_{\text{M}}(N/S)\text{.}$$ (5)

Here the number fraction of targets is C_T, the number fraction of traps is C_t, and the number fraction of traps plus targets is C_Tt. These are defined in terms of the total number of points in the lattice N = L² or L³ where L is the lattice edge. We define ${C^{\prime }}_{\text{T}}$ to be the number fraction of traps based on the number N′ of nontarget sites in the lattice. Note that A and t_M depend on the lattice and dimensionality but 〈t_ESC〉 does not. When Eq. 5 is applied to a physical system, the dimensionless capture time would be converted to a physical time by a factor Δt given by ℓ² = 2dD₀Δt, where ℓ is the lattice constant, d is dimensionality, and D₀ is the diffusion coefficient in the trap-free system. Values of ℓ and Δt would be chosen to resolve the spatial separation of the binding sites and the differences in escape times from the binding sites.

The Montroll first passage time is the mean number of time steps for a random walker to go from a random initial site to a prescribed immobile target site. It depends on the size, lattice, and dimensionality of the system. For two-dimensional lattices, the asymptotic formula for the first passage time is

$$t_{\text{M}}(2D)=\frac{N}{N-1}[A_{1}N\text{ln}N+A_{2}N+A_3+A_4/N+\dots ],$$ (6)

where the A_i are lattice-dependent constants. The capture time was introduced by Montroll (18) in work on the kinetics of photosynthesis. Arithmetic errors for the square lattice were corrected by den Hollander and Kasteleyn (19). The theoretical results were compared with exact numerical results by Kozak ((3) pp. 262–265). This review includes a convenient summary (Table III.4 in (3)) of the corrected numerical coefficients for various lattices. For the triangular lattice we use $A_1=\sqrt{3}/2\pi =0.275664448,A_2=0.235214021,A_3=-0.251407596$, and A₄ = −0.044 485 7. The first three coefficients are exact theoretical values from Montroll (18) and A₄ is the numerical value of Kozak (3). The effect of the A₄ term is negligible here. For the square lattice we use the theoretical values of den Hollander and Kasteleyn (19), A₁ = 1/π = 0.318 309 886, A₂ = 0.195 062 532, A₃ = −0.116 964 779, and A₄ = 0.484 065 704. For the square lattice, Kozak (3) found that if A₁, A₂, and A₃ are fixed at their theoretical values and A₄ is fit to exact numerical results, the value of A₄ is shifted by only 0.44%. The Monte Carlo results and Eq. 6 agree quantitatively. For the range of systems considered, N = 4² to 300², the ratio of the Monte Carlo value to the calculated value was 1.00003 ± 0.00048 (mean ± SD for 19 points) for the triangular lattice and 1.00007 ± 0.00124 (18 points) for the square lattice.

Finding an analytical expression for the simple cubic lattice is more problematic. Montroll (18) proved that t_M(3D) = a₀N + O(N^1/2) with a₀ = 1.516 386…. Kozak (3) obtained exact numerical results for a centrosymmetric trap with periodic boundary conditions for the seven odd cubes N = 3³ to 15³ and fit them to a two-term curve of Montroll's form. The fit was good over a limited region but was bad for small N and the asymptotic value was incorrect. Using that form to fit the Monte Carlo data obtained here gave a poor fit. Extending the series in inverse half-powers of N through $1/N\sqrt{N}$ gave reasonable least-squares fits at the data points themselves but was unacceptable because at intermediate points the fit showed spurious structure, including a parabolic minimum. A more satisfactory empirical description of the Monte Carlo data was a fit to a quotient of polynomials

$$\frac{t_{\text{M}}(3D)}{N}=\frac{N}{N-1}\frac{a_0+A_1/\sqrt{N}+A_2/N}{1+B_1/\sqrt{N}+B_2/N},$$ (7)

where a₀ is the exact asymptotic value from Montroll (18) and the factor of N/(N – 1) accounts for the fact that in the Monte Carlo calculations the initial position cannot be a target. Montroll (20) showed how this factor is included in the formalism.

The Monte Carlo data set contains 29 points with N from 2³ to 300³, so we are making heavy demands on an asymptotic formula. The results agree well with Kozak's exact results for the seven odd cubes N = 3³−15³; the ratio of the Monte Carlo to the exact capture times was 0.9992 ± 0.0006 for traps at random positions and 1.0009 ± 0.0013 for centrosymmetric traps. The Monte Carlo simulations went to much higher N than would be practical with Kozak's exact method. For small N the Monte Carlo results were highly reproducible. Five independent runs for N = 3³ gave t_CAPT = 30.474 ± 0.033, and for 15³, 4811.48 ± 4.84. Independent runs for N = 14³ with 0.5, 0.5, 5, and 50 million repetitions gave t_CAPT = 3899.14 ± 2.60; a run with 0.05 million repetitions gave 3878.1, −8.1 SD from the others, suggesting that 0.5 million repetitions was sufficient but 0.05 million was not. More repetitions for large systems would be better (note the outlier at N = 150³ in Fig. 2 b) but were impractical.

Figure 2.

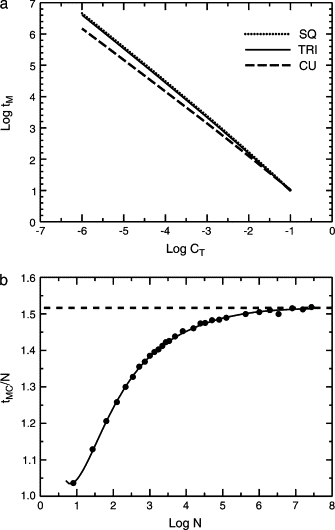
Capture times for a random walker in the presence of one target but no traps. (a) Log-log plot of the Montroll capture time t_M as a function of the target concentration C_T = 1/N for the two-dimensional case (triangular and square lattices) and the three-dimensional case (simple cubic lattice), from Eqs. 6 and 7 with coefficients given in the text. For the two-dimensional lattices, the theoretical results and the numerical results of Kozak are indistinguishable on the scale of this figure. (b) Scaled Monte Carlo capture times for the cubic lattice t_M(3D)/N as a function of log N, and least-squares fit Eq. 7. Horizontal line, theoretical asymptotic limit imposed by Eq. 7.

The least-squares fit to the Monte Carlo data gave the coefficients in Eq. 7 as a₀ = 1.516 386 = constant, A₁ = 190.340 805, A₂ = 60.901 235, B₁ = 133.054 765, and B₂ = 289.573 263. This function fit the entire range well; the ratio of the Monte Carlo to the calculated value was 0.99979 ± 0.00224, n = 29. The curve still showed a spurious parabolic minimum but the minimum was below N = 2³. Asymptotic expansion of this function gave $t_{\text{M}}(3D)\sim 1.516386N-11.4216\sqrt{N}+1141.49-148574/\sqrt{N}+\dots \text{.}$ All these coefficients are for a system with periodic boundary conditions; the effect of boundary conditions on capture times is examined in detail by Walsh and Kozak (21). Fig. 2 a shows the capture times from Eqs. 6 and 7 as a function of the target concentration C_T = 1/N in a log-log plot. Fig. 2 b shows the scaled Monte Carlo data for the cubic lattice and the fit of Eq. 7.

The effect of traps is taken into account by the mean escape time. In general,

$$\langle t_{\text{ESC}}\rangle =\frac{1}{N^{\text{'}}}{\sum _{\text{i}=0}^{\text{m}}}^{\text{'}}{n}_{\text{i}}{t}_{\text{ESC}\text{i}}=\frac{1}{N^{\text{'}}}{\sum _{\text{i}=0}^{\text{m}}}^{\text{'}}\frac{n_{\text{i}}}{P_{\text{ESC}}^{\text{i}}}\text{.}$$ (8)

Here the prime indicates that target sites are excluded from the sum, n₀ is the number of nonbinding sites, t_ESC0 = 1, n_i is the number of binding sites in the i^th level, $t_{\text{ESC}\text{i}}=1/P_{\text{ESC}}^{\text{i}}$ is the mean escape time from an i^th-level binding site, m is the total number of trap levels, and N′ is the total number of lattice points excluding targets. For the standard hierarchy 16/8/4/2/T with P_ESC = 0.1,

$$\langle t_{\text{ESC}}\rangle =(1-{C_{\text{t}}}^{\text{'}})1+{C_{\text{t}}}^{\text{'}}\left[\frac{16}{30}\times 10+\frac{8}{30}\times {10}^2\right)\left(+\frac{4}{30}\times {10}^3+\frac{2}{30}\times {10}^4\right],$$ (9)

giving for a 32 × 32 lattice with a single set of target and traps 〈t_ESC〉 = 25.3695 and for a 10 × 10 × 10 lattice 〈t_ESC〉 = 25.9550.

If only one target is present, these factors account for the capture time quantitatively, as shown in Fig. 3, where t_CAPT = t_M (curve ST). If traps and one target are present, t_CAPT = t_M〈t_ESC〉 (curve STt). The corresponding plot for data for the square lattice gives results scarcely distinguishable from Fig. 3 a, as the small difference between the first passage times for the triangular and square lattices in Fig. 2 a suggests. Monte Carlo calculations for a variety of trap hierarchies showed good agreement of the Monte Carlo capture time t_{CAPT MC} with the capture time from Eq. 5. The ratio t_{CAPT MC}/t_CAPT for ST curves has already been given. For the STt curves, for the triangular lattice the ratio is 1.00065 ± 0.00143, n = 12; for the square lattice, 0.99870 ± 0.00187, n = 12; and for the cubic lattice, 0.99911 ± 0.00171, n = 11. Maximum concentrations here are 0.0625 for ST curves and 0.0278 for STt curves in two dimensions, and 0.125 for ST curves and 0.0156 for STt curves in three dimensions.

Figure 3.

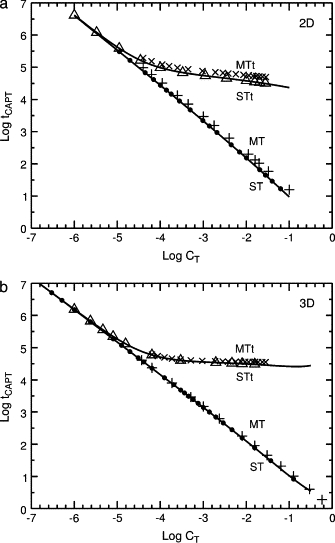
Monte Carlo capture times for the standard trap hierarchy. Log-log plots of t_CAPT as a function of the target concentration C_T. (a) Triangular lattice. (b) Cubic lattice. Points: Monte Carlo results for single targets (ST, circles), multiple targets (MT, +), a single set of traps and target (STt, triangles), and multiple sets of traps and targets (MTt, ×). Lines: theoretical values, t_CAPT = t_M for single targets (ST) from Eqs. 6, 7 and t_CAPT = t_M〈t_ESC〉 for a single set of traps and targets (STt). In these examples the total concentration of traps and targets C_Tt = 31C_T, so the total concentrations can be high; in the MTt series the maximum concentrations are C_T = 0.02861, C_Tt = 0.8868 in panel a and C_T = 0.02827, C_Tt = 0.8764 in panel b.

Fig. 3 shows that if multiple targets are present, the capture time increases by a small factor; compare curve MT with ST, and curve MTt with STt. This effect is quantitated in Fig. 4, giving the correction factor A(S, C_T) as a function of the number S of sets of traps and targets, at several target concentrations C_T. If t_{CAPT MC} is the capture time from Monte Carlo calculations, then we define A as

$$A(S,C_{\text{T}})=\frac{t_{\text{CAPT}\text{MC}}(S,C_{\text{T}})}{t_{\text{CAPT}\text{MC}}(1,C_{\text{T}})\langle t_{\text{ESC}}\rangle }\text{.}$$ (10)

Figure 4.

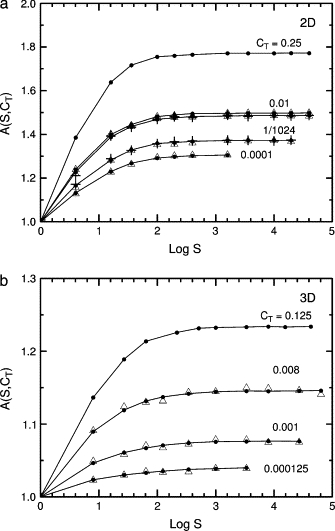
Dependence of the capture time on the number S of targets or sets of targets and traps for fixed target concentrations C_T. Values of A(S, C_T) are defined in Eq. 10. (a) Triangular and square lattices. (b) Cubic lattice. Note the changes in scale and C_T. Circles and lines, targets but no traps; triangles, traps and targets. The standard hierarchy of traps is used, 16/8/4/2/T, P_ESC = 0.1. In panel a for C_T = 0.01, the upper line is for the square lattice and the lower line is for the triangular lattice. Panel a also shows results for two alternative trap distributions on the triangular lattice, + for C_T = 0.01, the continuous distribution of Eq. 11, and + for C_T = 1/1024, the uniform discrete distribution 7/7/7/7/T. Runs were set up so that all concentrations and values of S were exact, although this limited the concentrations used. For example, when C_T = 0.01, the first series of runs had only target sites at a fixed concentration and the system size was varied. There was one target in a 10 × 10 grid, four targets in a 20 × 20 grid, and so forth to 3600 targets in a 600 × 600 grid. The second series used the same target concentrations and grids but one set of 30 traps per target, so the total concentration was C_Tt = 0.31. For runs with targets and traps, 500 trap configurations were used, and 1000 tracers per trap configuration. For runs with traps alone, to get smooth curves 1000 trap configurations were used and 10,000 tracers per trap configuration.

For the three runs with C_T ≤ 0.01, the calculated t_M could be used instead of the Monte Carlo value. But in two dimensions for C_T = 0.25, the Montroll capture time for S = 1 is off by 15%; it is hardly surprising that an asymptotic formula breaks down for N = 4. In two dimensions the multiple trap effect contributes a factor of 1.0–1.75, and in three dimensions, a factor of 1.00–1.25. The effect is independent of the number of sets of traps and targets after a few hundred sets are included, as Fig. 4 shows. Systems of targets alone and systems of targets and traps fall on the same curves, indicating that 〈t_ESC〉 accounts for the effects of traps on the means.

The reason for the dependence on the number of sets is random fluctuations in the trap density. For multiple targets we use the Montroll capture time per set t_M(N/S). This is a mean-field approximation, which takes into account the mean number of lattice sites per target but neglects fluctuations in the arrangements of targets. Periodic boundary conditions are used in all the Monte Carlo calculations, so the system is always infinite in that sense, but the size of the unit cell limits the scale of the fluctuations in target spacing. This effect is similar to well-known results in the kinetics of the annihilation reaction A + B → 0, where the particles in areas of average density vanish rapidly but the long-time kinetics is determined by areas enriched by chance in one species (22,23). These results imply that there will be a slow increase in the capture time as the size of the unit cell is increased, to give a singular limit in an infinite system. To test for this slow increase would require further Monte Carlo calculations beyond the scope of this work.

The results do not depend on the discrete hierarchical structure of the traps, as shown by three controls in excellent agreement with Eq. 5 and Fig. 4. The first is a series of runs with a single target and a single level of traps at area fractions 0.01, 0.02, 0.05, 0.1, 0.2, and 0.5, and the corresponding series with 1024 traps at a trap concentration of C_T = 0.0001. The second is the uniform discrete distribution 7/7/7/7/T used previously (1). The third is a continuous random distribution in which the escape time is $P_{\text{ESC}}^{\text{x}}$ with x a uniformly distributed random variate between a and b. If τ = 1/P_ESC, the mean escape time from a trap site is then (1/ln τ)(τ^b – τ^a)/(b – a) by a standard transformation (24) so that the mean escape time for the lattice is

$$\langle t_{\text{ESC}}\rangle =(1-{C^{\prime }}_{\text{t}})1+{C^{\prime }}_{\text{t}}\frac{1}{\text{ln}\tau }\frac{{\tau }^{\text{b}}-{\tau }^{\text{a}}}{b-a}\text{.}$$ (11)

Here we use a = 1, b = 4, P_ESC = 0.1, and 30 traps so that the number of traps is the same as in the standard example of Fig. 1, and the range of escape times is the same. The 7/7/7/7/T and continuous cases give data very similar to the STt and MTt results of Fig. 3 a but with larger times because 〈t_ESC〉 is larger. Values of A for the uniform discrete and the continuous distributions are shown in Fig. 4 a.

Distribution of capture times

The simplest description of the scatter in the capture times is the standard deviation σ. It is convenient to scale σ by the mean t_CAPT; this accounts for most of the variation, and the range of σ/t_CAPT is a concentration-dependent factor between 0 and 1.5. Scaling by the Monte Carlo value of t_CAPT accounts for the effects of system size, traps, and multiple targets as in Eq. 5. The ratio σ/t_CAPT is a distinct factor showing the effect of traps and multiple targets on the standard deviation beyond their effect on the mean.

As the target concentration increases, σ/t_CAPT increases from 1 at small C_T, say 10⁻⁶, to a maximum at ∼C_T ≈ 0.01, and then levels off or decreases at higher concentrations. Table 1 shows values of σ/t_CAPT at fixed concentrations, C_T = 0.01 for the triangular lattice and C_T = 0.008 for the cubic lattice, for a specified system size L and number of sets of traps and targets S. For a pure exponential distribution, the standard deviation equals the mean, and indeed for the case of a single target, the Monte Carlo value of the ratio is very close to one. Both traps and multiple targets increase σ/t_CAPT; traps have more effect than multiple targets and the effect is greater in the triangular lattice than in the cubic.

Table 1.

Ratio σ/t_CAPT

	L	S	tCAPT MC	σ/tCAPT MC
Triangular lattice, CT = 0.01
Single target	10	1	151.74	1.0094
Multiple targets	316	1024	224.65	1.1537
Single set of traps and target	10	1	38396.	1.2858
Multiple sets of traps and targets	316	1024	57101.	1.4032
Cubic lattice, CT = 0.008
Single target	5	1	157.17	0.9993
Multiple targets	50	1000	180.14	1.0234
Single set of traps and target	5	1	31731.	1.2809
Multiple sets of traps and targets	50	1000	36481.	1.2954

The actual distribution is more informative. In this section we discuss the Monte Carlo results, and in the next we predict the distributions approximately from a perfect-mixing calculation. Several independent factors contribute to the scatter: the distribution of capture times in the absence of traps; the number and depth of traps visited in each random walk; and the random escape time from each trap at each visit. The relative contributions can be seen in the Monte Carlo results; features of the histograms are predicted qualitatively by the perfect-mixing approximation.

The starting point is the distribution of capture times for a single target with no traps. In a finite system the fraction of capture times is asymptotically

$$f_{\text{n}}=[\text{exp}(1/\tau )-1]\text{exp}(-n/\tau ),$$ (12)

the discrete form of an exponential decay with time constant τ, assuming that the initial position of the diffusing particle cannot be a target site (25,26). In the case of a complete graph the distribution is known exactly at all times. If there are N lattice sites of which one is a target site, at each step the tracer moves to the target site with probability 1/N (because in the program the tracer can move to its current location or a different site), so the probability of capture at the n^th time step is

$$P(n)={\left(1-\frac{1}{N}\right)}^{\text{n}-1}\frac{1}{N}\text{.}$$ (13)

The coefficients for the complete graph Eq. 13 and the discrete exponential Eq. 12 are identical if τ = −1/ln(1 − 1/N), so for N ≫ 1, τ = N.

In a plot of Monte Carlo values of ln f(t) versus t, the single-target curve ST of Fig. 5 a is consistent with Eq. 12, as confirmed by fitting many similar histograms of Monte Carlo results on the triangular, square, and cubic lattices and obtaining the time constant τ. In two dimensions for both triangular and square lattices, there were deviations from exponential decay for the first few bins and then exponential decay with time constant τ. Bin sizes were varied depending on the mean capture time so the initial deviations are only described qualitatively. For the cubic lattice the deviations were smaller and for the complete graph, the histogram was exponential even at the shortest times. The behavior in an infinite system is discussed at the end of this section.

Figure 5.

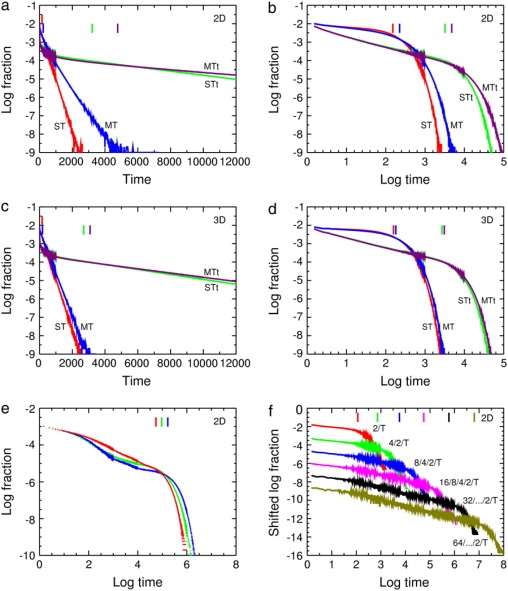
Distribution of capture times from Monte Carlo calculations for the standard example, 16/8/4/2/T but with P_ESC = 0.2 so that all the curves can be shown conveniently on the same scale. Changes in noise levels within a curve are due to changes in bin width. Vertical lines at top, means. Notation in panels (a–d): ST (red), single target but no traps; MT (blue), multiple targets but no traps; STt (green), single set of traps and target; MTt (purple), multiple sets of traps and targets. (a) Log fraction versus time for two dimensions, grid size 10 × 10 for the ST and STt curves, and 320 × 320 for the MT and MTt curves. (b) The same data versus log time to show the power-law region in the STt and MTt curves. (c) Log fraction versus time for three dimensions, grid size 5 × 5 × 5 for the ST and STt curves, and 50 × 50 × 50 for the MT and MTt curves. (d) The same data versus log time. The MT and MTt curves are for 1024 sets in two dimensions and 1000 in three dimensions. (e) The standard hierarchy 16/8/4/2/T (red) gives a power-law region but the uniform discrete distribution 7/7/7/7/T (green) and the continuous uniform distribution (blue) give more complicated curves. All three runs were on a 30 × 30 triangular lattice, and 5 million repetitions were used instead of the usual 0.5 million to separate the histograms more cleanly. (f) Increasing the number of levels in the hierarchy increases the size of the power-law region. The hierarchies used are 2/T, 4/2/T, 8/4/2/T, 16/8/4/2/T, 32/…/2/T, and 64/…/2/T with P_ESC = 0.1. For clarity the curves are shifted downward by 0, 1, 2, 3, 4, and 5 units, respectively. One target and set of traps was used on a triangular lattice. The system size was varied between 8 × 8 and 66 × 66 to keep the trap concentration as constant as possible, 0.02972 ± 0.00098; that is, an SD of 3.28% of the mean.

For multiple targets (curve MT, Fig. 5, a and c) the distribution is somewhat broader due to fluctuations in the local target density. When traps are present (curves STt and MTt), the distributions shift to much higher means and broaden considerably because each diffusing particle is likely to visit a different random sample of traps and the escape time from each trap visited is random, specifically, Poisson-distributed with mean $1/P_{\text{ESC}}^{\text{i}}\text{.}$ As further evidence that the presence of traps broadens the distribution, if the STt and MTt histograms are scaled by 〈t_ESC〉 (dividing t by 〈t_ESC〉 and multiplying the fraction by 〈t_ESC〉), the scaled distributions are still wider than the ST and MT distributions, respectively.

If the distributions are replotted in log-log form, in the presence of a hierarchy of traps (curves STt and MTt) in two dimensions there is an initial period of approximate power-law decay followed by slow exponential decay (Fig. 5 b). In three dimensions (Fig. 5 d) there is an initial transient followed by a period of approximate power-law decay and finally an exponential decay. The ST and MT curves here do not show power law decay; the ST curves are simply log-log plots of pure exponentials. A power-law distribution of first passage times is well known for anomalous subdiffusion (27); for example, in the continuous-time random walk (28), random walks on percolation clusters and Sierpiński gaskets with periodic boundary conditions (29), and weakly chaotic motion modeled as a random walk on a self-similar hierarchy of traps (30), though these examples are for somewhat different first passage time problems. So it is not surprising that here transient anomalous subdiffusion to a target results in a transient power-law distribution of capture times.

Fig. 5 e shows that the hierarchy yields a significant power-law region, but the uniform discrete distribution 7/7/7/7/T and the uniform continuous distribution of Eq. 11 give more complicated curves. The three curves coincide at small times, representing the time for the tracer to begin to see the differences in the structures of the sets of traps. Fig. 5 f shows that, as the depth of the hierarchy is increased, the power-law region increases considerably just as the region of anomalous diffusion does in Fig. 4 a of Saxton (1). The scaling of the exponential decay time with system size will be analyzed and compared to other characteristic times in later work.

These results are related to a large body of work begun by Rosenstock (31) on trapping of random walkers. This work is reviewed by ben-Avraham and Havlin (6) and Hughes (16), and extensively by den Hollander and Weiss (2). Note that the nomenclature in that literature is different from that in this article. There, for the reaction A + B → B, if A is immobile it is called a target and if B is immobile it is called a trap. Here we define targets as immobile reactive sites that terminate the random walk and traps as immobile nonreactive binding sites that delay the diffusing particle.

That literature uses the survival probability or decay law Φ_n, the probability that the diffusing particle has survived at least n steps without reaching the target. The decay law is found in terms of the number S_n of distinct sites visited at time step n in an infinite lattice. Assume the diffusing particle starts on a nontarget site. Then we have the exact result

$${\Phi }_{\text{n}}=\langle {(1-C_{\text{T}})}^{S_{\text{n}}-1}\rangle ,$$ (14)

because a particle captured at the n^th step must have been on S_n−1 nontarget sites previously. The average is over random walks and target configurations. This expression can be expanded in cumulants at short times to give

$${\Phi }_{\text{n}}=\text{exp}[-\lambda \langle S_{\text{n}}\rangle +{\lambda }^2\text{Var}{S}_{\text{n}}/2],$$ (15)

where λ = −ln(1 – C_T), 〈S_n〉 is the mean number of sites visited, and Var S_n is the variance of S_n. Here 〈S_n〉 and Var S_n can be found from Monte Carlo calculations. Alternatively one can use the exact series for 〈S_n〉 or simple approximations to the exact series (32,33), and a series for Var S_n ((16) section 6.2, (34)). The first-order term in Eq. 15 is the Rosenstock approximation (31), which is roughly correct in two dimensions and better in three. If the second-order term is included, agreement with Monte Carlo results is much better (35–37).

At long times the decay law is a stretched exponential, explained in physical terms by Balagurov and Vaks (38), Grassberger and Procaccia (22), Kayser and Hubbard (39), and Redner (40). This behavior is due to the existence of rare target-free regions. The probability that a tracer is in a target-free region is small but the escape time from the region is large, and the competition of these factors gives a stretched exponential. The crossover to a stretched exponential was examined by indirect methods (41–44). Direct attempts to find the crossover failed; it appears that one cannot reach the long-time limit in a practical finite system (25,42).

The decay law Φ_n is the cumulative distribution function of the probability distribution function used in Fig. 5. To compare the approaches we substitute Monte Carlo values of S_n and Var S_n into Eq. 15, and then find the probability distribution function at time $[t(n+1)-t(n)]/2\text{as}[\Phi (n+1)-\Phi (n)]/[t(n+1)-t(n)]\text{.}$

Eq. 15 is particularly useful in an infinite system because one can find S_n and Var S_n in a target-free system and predict Φ_n as a function of target concentration. The approach is less useful for finite systems because S_n and Var S_n depend on the system size. For a small system it is necessary to calculate S_n and Var S_n for each system size, but large systems are in the asymptotic region of the A(S, C_T) curve (Fig. 4) and a single set of values of S_n and Var S_n can be used. Thus in Monte Carlo calculations for C_T = 0.01, 0.02, 0.05, 0.10, and 0.20, Eq. 15 does not predict Φ_n well for a 10 × 10 triangular lattice but for a 320 × 320 lattice it predicts Φ_n well (data not shown).

Perfect-mixing distribution of capture times

If we assume perfect mixing, we can obtain the distribution of capture times by an exact numerical method based on probability generating functions (PGF). These generating functions are the sort used in the probability literature ((45) pp. 48–51, (46) pp. 31–33), not the generating functions based on the structure function of the lattice commonly used in analysis of random walks (and used by Montroll to derive the capture times) (2,16,26). In a PGF, escape probabilities are written as polynomials in z, and each power of z represents one time step. When different random processes are combined, the powers of z keep track of the number of time steps required; the coefficient of zⁿ gives the probability of n time steps.

We assume a single set of traps and a target. We consider the modified standard example, 16/8/4/2/T with P_ESC = 0.2 so that the mean escape time from the shallowest traps is τ = 1/P_ESC = 5. There are three contributions to the scatter in capture times: the distribution of capture times in the absence of traps, the distribution of traps encountered, and the distribution of escape times from each trap encountered.

The first contribution is the PGF for the capture times for a single target with no traps,

$$g_{\text{CAPT}}(z)=a_1{z}^1+a_2{z}^2+a_3{z}^3+\dots ,$$ (16)

where the coefficients a_i are obtained from theory (Eq. 12 or Eq. 13) or Monte Carlo calculations. There is no z⁰ term because it is assumed that the diffusing particle cannot start on the target. This contribution is shown in Fig. 6, a and b, on linear and logarithmic scales. The second contribution is from the distribution of trap depths; for the example considered, the PGF for the hierarchy of traps is analogous to Eq. 9,

$$g_{\text{HIER}}(z)=(1-{C_{\text{t}}}^{\text{'}})z+{C_{\text{t}}}^{\text{'}}\left[\frac{16}{30}{z}^5+\frac{8}{30}{z}^{25}+\frac{4}{30}{z}^{125}+\frac{2}{30}{z}^{625}\right]\text{.}$$ (17)

Figure 6.

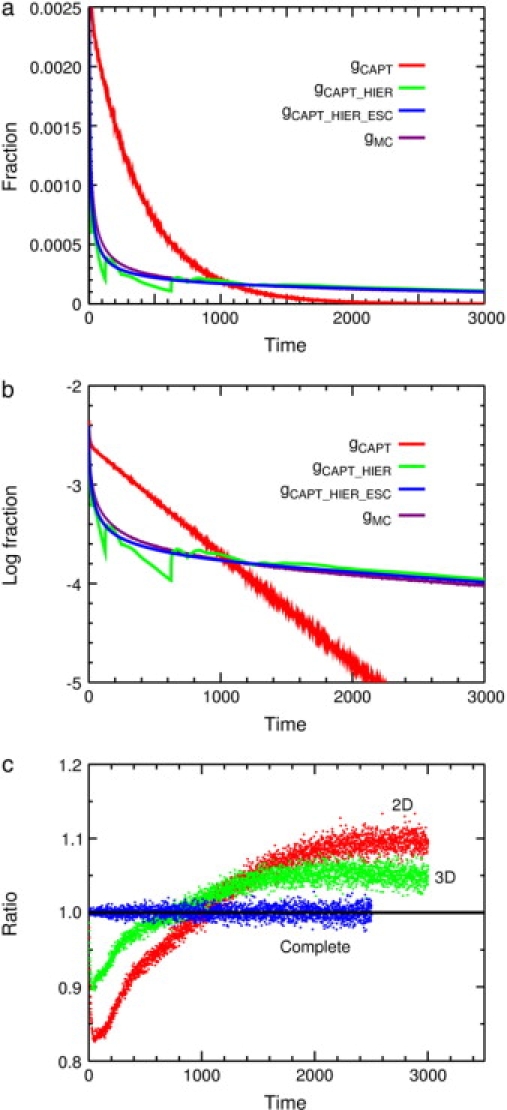
Probability distributions of capture times from the perfect-mixing approximation and Monte Carlo calculations. (a) Linear plot for the two-dimensional case. (b) Logarithmic plot for the two-dimensional case. Here g_CAPT is a histogram of Monte Carlo capture times for a single target and no traps, and g_{CAPT_HIER} (Eq. 19) combines g_CAPT with g_HIER to give the distribution for one set of traps and a target, assuming a fixed escape time from the traps. The final prediction, g_{CAPT_HIER_ESC} (Eq. 21), also takes into account the distribution of escape times from traps. The Monte Carlo result for one set of traps and target is given by g_MC. The distributions g_{CAPT_HIER} and g_{CAPT_HIER_ESC} are of significant magnitude well beyond 3000 time steps; the cumulative distribution functions for the Monte Carlo data at 3000 time steps are 0.568 in two dimensions and 0.654 in three. (c) Ratio of the Monte Carlo distribution to the calculated distribution log g_MC/log g_{CAPT_HIER_ESC} for the two-dimensional case, the three-dimensional case, and the complete graph. For the complete graph the ratio of the log coefficients was 0.9999 ± 0.0070 for 2500 time points. In all these calculations, to get smooth histograms large runs were used (10⁴ trap configurations and 10⁴ tracers per trap configuration).

The first term represents the single time step required to leave a nontrapping site, and the terms in brackets represent the mean number of time steps required to leave the four levels of traps in the hierarchy. The third contribution is from the random variation in the escape time from a trap. Let p = P_ESC be the escape probability in one time step, and let q = 1 – p. Then the probabilities of escape in the first three time steps are pq⁰, pq¹, and pq², respectively, and in general,

$$g_{\text{ESC}}(p,z)=\sum _{\text{n}=0}^{\infty }{z}^{\text{n}+1}p{q}^{\text{n}}=\frac{pz}{1-qz}\text{.}$$ (18)

This is a variant of the geometric distribution, and the mean is 1/p = τ. We use this PGF in the form g_ESC(τ, z). To combine PGFs, we use a standard result on stopped distributions: If S_N is the sum of a random number N of random variates, S_N = Y₁ + Y₂ + … + Y_N, and g_Y(z) is the PGF of Y, and g_N(z) is the PGF of N, then the PGF of S_N is g_N[g_Y(z)] ((45) p. 344, (46) pp. 16–18, 74–77).

To isolate the effect of the traps, we find the partial PGF $g_{\text{CAPT}\_\text{HIER}}(z)$ for capture in the presence of target and traps, but not including the variation in escape times,

$$\begin{array}{l}{g}_{\text{CAPT}\_\text{HIER}}(z)=g_{\text{CAPT}}[g_{\text{HIER}}(z)]\\ =a_1{[g_{\text{HIER}}(z)]}^1+a_2{[g_{\text{HIER}}(z)]}^2\\ +a_3{[g_{\text{HIER}}(z)]}^3+\dots \text{.}\end{array}$$ (19)

This curve is shown in Fig. 6, a and b. The distribution is much wider than the distribution with no traps, and there are sharp peaks and valleys due to specific sequences of traps.

To obtain the complete distribution, we combine all three PGFs. We combine g_HIER with g_ESC by substituting the four functions g_ESC(τ, z) from Eq. 18 for z in the second term of Eq. 17, giving

$$\begin{array}{l}{g}_{\text{HIER}\_\text{ESC}}(z)=(1-{C^{\prime }}_{\text{t}})z+\\ {C^{\prime }}_{\text{t}}\left[\frac{16}{30}{g}_{\text{ESC}}{(5,z)}^5+\frac{8}{30}{g}_{\text{ESC}}{(25,z)}^{25}+\right)\\ \frac{4}{30}{g}_{\text{ESC}}{(125,z)}^{125}+\frac{2}{30}{g}_{\text{ESC}}{(625,z)}^{625}]\text{.}\end{array}$$ (20)

We substitute $g_{\text{HIER}\_\text{ESC}}(z)$ for z in Eq. 16 to give

$$\begin{array}{l}{g}_{\text{CAPT}\_\text{HIER}\_\text{ESC}}(z)=a_1{[g_{\text{HIER}\_\text{ESC}}(z)]}^1+a_2{[g_{\text{HIER}\_\text{ESC}}(z)]}^2+\\ a_3{[g_{\text{HIER}\_\text{ESC}}(z)]}^3+\dots \text{.}\end{array}$$ (21)

We expand Eq. 21 in powers of z to give the PGF of the combined distribution. The first few terms of the expansion can be done by hand. The large-scale expansion was done in Mathematica (Wolfram Research, Champaign, IL). (To do the expansion, one chooses a maximum power, here 3000, and uses the Series function to expand the polynomials retaining terms through order z³⁰⁰⁰. Real coefficients are used, and integer exponents.) The resulting coefficients of z are exact numerical values.

We compare the distributions from Eq. 21 with histograms from Monte Carlo simulations. The dimensionality is varied to vary the efficiency of mixing. In all cases a single set of traps plus target is used, 16/8/4/2/T with P_ESC = 0.2 rather than the usual value of 0.1 to show the interesting structure more conveniently. System sizes are 15 × 15 in two dimensions, 6 × 6 × 6 in three dimensions, and 225 for the complete graph.

Results are similar in the three cases so detailed data are presented only for the two-dimensional case, where mixing is least efficient. Fig. 6 a shows a linear plot of the distributions, and Fig. 6 b shows a logarithmic plot of the same data. The g_CAPT curve is the histogram of Monte Carlo capture times for a system with a target but no traps. The distribution is exponential after ∼40 time steps. The g_{CAPT_HIER} curve includes the effect of the traps assuming that the escape times are equal to their means. This distribution decreases much more slowly than g_CAPT, and shows structure because g_HIER has only five powers of z. The obvious structure is at 125 and 625. The final curve g_{CAPT_HIER_ESC} brings in the distribution of escape times g_ESC, which smooths out the peaks and valleys from g_HIER. The g_MC curve is the observed Monte Carlo distribution for a single set of traps and target. The perfect-mixing curve agrees qualitatively but not quantitatively with the two-dimensional Monte Carlo results. For the three-dimensional case the results are similar but the g_CAPT curve becomes exponential after ∼15 points and the perfect-mixing curve is closer to the Monte Carlo curve. For the complete graph, the perfect-mixing distribution of capture times agrees with the Monte Carlo results quantitatively, as required; the complete graph was chosen to match the assumptions in the perfect-mixing approximation. Here the input capture times were from Eq. 13, not Monte Carlo values. The degree of agreement between the perfect-mixing approximation and the Monte Carlo distributions is shown in Fig. 6 c as the ratios log g_MC/log g_{CAPT_HIER_ESC} for the three cases. Agreement is qualitative for the two-dimensional and three-dimensional cases, but good enough to show that we understand the sources of the scatter. The deviations from the perfect-mixing approximation reflect known differences in mixing.

Lattice versus continuum models

The approximations in a lattice model of diffusion are reviewed in the literature (47,48). The main approximation is that the model averages out motion over distances of less than a lattice constant. The approximations involved in a lattice model of a reaction are beyond the scope of this article (see, for example, (4,49)) but we consider one aspect here, the continuum analog of the Montroll equation for the first passage time. This equation gives the time for a mobile particle initially at a random lattice point to reach an immobile target. An analogous continuum result in two dimensions is the first passage time for diffusion in an annular region (50). Here a target of radius s is at the center of a circular region b, with s ≪ b, and the reactant is initially distributed uniformly in the annulus. The mean capture time is

$$t_{2\text{D}}=\frac{b^2}{2D}\left(\text{ln}\frac{b}{s}-\frac{3}{4}\right)\text{.}$$ (22)

So if the number of lattice points N ∝ b², then to first order, t_2D ∝ N ln N, in agreement with the Montroll result Eq. 6. The continuum capture time for concentric spheres (50) t_3D = b³/3sD likewise gives t_3D ∝ N as in Eq. 7. These first-passage solutions are appropriate for the model used here (1) in which the interaction of the diffusing particle with traps and targets is turned on by some external event at t = 0.

Discussion

To a biophysicist, transient anomalous subdiffusion may be an interesting phenomenon or a useful probe of the equilibration of the diffusing species with cellular binding sites, reflecting the search of the mobile species for its biological target (1). But to a cell, the biological importance of transient anomalous subdiffusion is likely to be its effect on kinetics.

We have examined the effect of nonreactive binding sites on one of the simplest diffusion-mediated reactions, the reaction of a mobile particle with an immobile target, with reaction occurring with probability 1 on collision. If the system is simply one target, then the capture time is given by the Montroll first-passage time t_M (Eqs. 6 and 7), which depends only on the dimensionality, lattice, and size of the system. If nonreactive binding sites of finite depth are added, t_M must be multiplied by the mean escape time 〈t_ESC〉 (Eqs. 8 and 9), which depends on the trap concentrations and depths. If there are multiple targets, there is a numerical factor A between 1 and 2 obtained from Monte Carlo results (Fig. 4). This factor depends on the target concentration and the number of sets and reaches a constant value after a few hundred sets. Most of the difference between the two-dimensional and three-dimensional cases is given by t_M; there is a small difference in the correction factor A.

For reaction in the presence of a finite hierarchy of traps, the statistical distribution of capture times shows at short times the power-law region typical of anomalous subdiffusion and fractal systems, and at large times the exponential region expected in finite systems (Fig. 5, a–d). Similarly in plots of log 〈r²〉/t versus log t there is a crossover from anomalous to normal diffusion (1). An exact numerical method was presented to find the distribution for the perfect-mixing case. This method is qualitatively correct for the two-dimensional and three-dimensional cases, and shows that the main contribution to the width of the distribution is the distribution of traps visited in each random walk.

The model is highly general. It is applicable in two and three dimensions, provided the appropriate Montroll time and factor A is chosen. As pointed out in the paragraph at Eq. 11, the model applies to both continuous and discrete hierarchies of traps. The hierarchy is not required; the model applies to a single level of traps at various total trap concentrations and to a uniform distribution of traps 7/7/7/7/T. The effect of the hierarchy is to extend the interval of anomalous subdiffusion (1) and the power-law region in the distribution of capture times (Fig. 5 f). An important limitation is the use of a lattice model, and the extension to the continuum will be essential for applications.

A restriction of the model is the assumption that the initial position of the tracer is random. As discussed in detail earlier (1), this assumption implies that the system is in a nonequilibrium state and that some external event turns on the interaction of the tracer with the traps. The event could be the binding of a ligand to a receptor or the entry of a protein into the nucleus, for example. This assumption leads to the mean escape time 〈t_ESC〉 given by Eq. 8, in which all lattice sites are weighted equally. If the tracer is equilibrated with the traps, the mean escape time would be a Boltzmann-weighted average, weighting the deeper traps more heavily and increasing the mean escape time considerably.

Potential applications of the model are two-dimensional signaling reactions in the plasma membrane, three-dimensional signaling reactions in the cytoplasm, and three-dimensional reactions of proteins or subnuclear bodies in the nucleus. What is required to model one of these reactions is the number and depth of the traps, the number of target sites, and a correction for the effects of obstruction on diffusion. The most straightforward way to find the number and depth of the traps is to use single-particle tracking, as outlined earlier (1). It is appealing to try to apply proteomics to this problem. Genomics yields the abundance of DNA sequences and proteomics yields the abundance of proteins (51). Studies of the interactome (52) identify binding sites of soluble proteins to DNA (53–55), binding among soluble proteins (56), and binding among integral membrane proteins (57). Some of these studies simply classify interactions as binding or not; others examine the interactions more quantitatively. The interaction of transcription factors with DNA seems the most thoroughly characterized (53–55). The major difficulty is determining the fraction of physically accessible, unoccupied binding sites (58). The second quantity required, the number of copies of the target, can be obtained from biochemical, fluorescence, or genomic measurements. The final quantity required is the diffusion coefficient of a nonbinding mobile species as similar as possible to the reactive species. This can be obtained experimentally, or if enough information is available on the abundance, size, shape, and mobility of the obstacles, the effect on diffusion can be modeled.

Much work has been done recently on the role of statistical fluctuations in cellular dynamics given the low copy number of some species in cells (59–64). Spatially resolved modeling has shown that diffusion can be a significant source of noise in biological reactions. In a very simple model of gene expression by van Zon and ten Wolde (65), RNA polymerase binds reversibly to a promoter region to form a complex; the complex produces protein and dissociates; and the protein is degraded at a constant rate. When RNA polymerase binding is rate-determining, protein production occurred in bursts, with periods of rapid protein production followed by periods of pure decay. The spatially resolved model was much noisier than a well-stirred model because the arrival times of RNA polymerase at the promoter were broadly distributed in the spatially resolved model but more narrowly Poisson-distributed in the well-stirred model. We note that as Fig. 6 shows, the distribution of arrival times in a system with traps is even broader than in the trap-free diffusive system used by van Zon and ten Wolde (65). Later work from that laboratory (66) presented a spatially resolved continuum model of noise production in mRNA and protein synthesis by a gene controlled by a repressor. This model did not include one-dimensional diffusion of the repressor on DNA. Diffusion-induced noise was shown to be significant. Rapid rebinding of the repressor to the DNA upon dissociation was a key factor; the system could be described as well-stirred provided that reaction rates were renormalized by the average number of rebindings. If traps are added to this model, traps near the repressor binding site will slow the rapid rebinding and the trap hierarchy in general will slow longer-range transport. Interestingly, this model gave a distribution of repressor-DNA association times that is a power law at short times corresponding to rapid rebinding, and exponential at long times, as in a well-stirred system. The distribution is of the form found here (Fig. 6) for a much different model.

The results presented here show that if a mobile reactant has to search through a large number of nonreactive binding sites to find its target site, the variation in total trapping time may be a major contributor to diffusion-induced noise. The predicted wide statistical distribution of capture times must also be taken into account in comparing simulation with experiment.