Coarse-Grained Molecular Dynamics Simulations of Phase Transitions in Mixed Lipid Systems Containing LPA, DOPA, and DOPE Lipids

Abstract

The mechanisms that mediate biomembrane shape transformations are of considerable interest in cell biology. Recent in vitro experiments show that the chemical transformation of minor membrane lipids can induce dramatic shape changes in biomembranes. Specifically, it was observed that the addition of DOPA to DOPE has no effect on the stability of the bilayer structure of the membrane. In contrast, the addition of LPA to DOPE stabilizes the bilayer phase of DOPE, increasing the temperature of a phase transition from the bilayer to the inverted hexagonal phase. This result suggests that the chemical conversion of DOPA to LPA is sufficient for triggering a dramatic change in the shape of biomembranes. The LPA/DOPA/DOPE mixture of lipids provides a simple model system for understanding the molecular events driving the shape change. In this work, we used coarse-grained molecular dynamics simulations to study the phase transitions of this lipid mixture. We show that despite the simplicity of the coarse-grained model, it reproduces the experimentally observed phase changes of: 1), pure LPA and DOPA with respect to changes in the concentration of cations; and 2), LPA/DOPE and DOPA/DOPE mixtures with respect to temperature. The good agreement between the model and experiments suggests that the computationally inexpensive coarse-grained approach can be used to infer macroscopic membrane properties. Furthermore, analysis of the shape of the lipid molecules demonstrates that the phase behavior of single-lipid systems is consistent with molecular packing theory. However, the phase stability of mixed lipid systems exhibits significant deviations from this theory, which suggests that the elastic energy of the lipids, neglected in the packing theory, plays an important role.

Introduction

Cellular and subcellular trafficking are driven by two processes—fission, the budding of a vesicle from a donor compartment, and fusion, the integration of a vesicle thus formed into the membrane of an acceptor compartment (1). Both fission and fusion involve the formation of highly curved intermediates. As such, these processes cannot occur spontaneously. They must be catalyzed by proteins that somehow reduce the activation barrier for the formation of the curved intermediates.

In classical models, membrane deformation was thought to be driven exclusively by specific proteins. It was postulated that fission, for instance, is initiated by the recruitment of cytosolic coat proteins to the membrane (2). The stepwise assembly of these coat proteins then deforms the membrane into a spherical shape, and releases it as a vesicle along with its encased coat. Importantly, the lipids play no role in this mechanism—they are no more than passive targets of the membrane-deforming proteins.

Recent evidence suggests that lipids are active participants in the membrane deformation process. Indeed, the synthesis of certain lipids appears to be essential for both fission and fusion. However, the precise role of these lipids remains unknown.

One hypothesis states that the localized synthesis of these lipids serves to recruit the membrane-deforming proteins. For instance, phosphatidylinositol-4,5-phosphate is necessary for recruiting the proteins that catalyze the budding of clathrin-coated vesicles (3,4). Likewise, the enzyme phosphatidylinositol-3-OH kinase is essential for recruiting proteins that cause invagination of vesicles into late endosomes (5,6). Although this hypothesis allows the lipids to play a role, it is, in effect, identical to the classical models, inasmuch as the lipids serve to merely recruit curvature-generating proteins—they play no role in generating the curvature itself. That distinguished function is still attributed exclusively to proteins.

The second model postulates that localized synthesis of specific lipids, by itself, drives membrane deformation. This can happen because the lipid composition of a membrane influences its mechanical properties. The macroscopic (continuum) theory of membrane deformation identifies three such properties, namely, bending modulus, line tension, and tilt modulus (7–9). It implies, furthermore, that a significant change in any one of these properties can trigger a spontaneous change in the curvature of the membrane.

More recently, it has been argued that localization of lipids facilitates, rather than drives, membrane deformation (reviewed in (10)). This model is motivated by the following observations:

• 1.In vitro experiments show that the deformation of the membrane by specific proteins results in the formation of domains with different lipid compositions. Specifically, tubes pulled from giant vesicles containing dioleoylphosphatidylcholine, cholesterol, and sphingomyelin are enriched in dioleoylphosphatidylcholine, and depleted in cholesterol and sphingomyelin (11). It is conceivable that a similar phenomenon also occurs in vivo: COPI-coated Golgi vesicles have reduced levels of cholesterol and sphingomyelin (12).
• 2.The spatial segregation of lipids generates a line tension at the boundary between the domains (8), which can destabilize a nascent bud to such an extent that it ruptures, thus separating from the parent membrane (13).

Thus, in this model, membrane-deforming proteins initiate the process of membrane deformation, but lipids facilitate the rupturing process.

The last two models differ on the precise role of the lipids. However, in both cases, the lipids ultimately exert their effect by modulating a mechanical property of the membrane. As powerful as the macroscopic theory may be, it is incapable of predicting the manner in which these mechanical properties vary with the lipid composition. Thus, it seems desirable to construct a microscopic model capable of predicting this variation. This work is concerned with the development of such a microscopic model.

Given the length and timescales of membrane deformation, detailed atomistic models are impractical. Even with modern computing systems, the simulations would be extremely time-consuming. Simulations of lipid systems therefore often employ less detailed models, such as the Brownian dynamics simulations (14), dissipative particle dynamics (15), and coarse-grained molecular dynamics (CGMD) models (16–20). In this work, we use a CGMD model, which allows one to perform simulations on near-atomic length scales. Yet, it reduces the computational time by orders of magnitude, thus allowing a meaningful exploration of membrane dynamics. The CGMD models approximate small groups of atoms by a single united atom (bead). Several such models have been introduced and applied to simulations of various complex molecular systems (16,18–24), and further development of coarse-grained molecular models is a subject of active ongoing research. In this work, we use the coarse-grained model proposed by Marrink et al. (20).

It has been shown by Marrink et al. that this model adequately reproduces experimental data on phase behavior for mixtures of DOPE and DOPC, i.e., lipids with different headgroups but identical tails (25). Here, we show that this model also captures the behavior mixed-lipid systems containing lipids with different tail- as well as headgroups. To this end, we perform simulations of the extensive experimental data on the phase behavior of the LPA-DOPE and DOPA-DOPE systems obtained by Kooijman et al. (26). Among other things, they showed that these systems exhibit a temperature-induced transition from the lamellar phase (L_α) to the inverted hexagonal phase (H_II). The physical insights gained from our simulations of this phase transition could shed light on the mechanism of fusion and fission, since the geometry of the H_II phase is remarkably similar to the geometry of the highly curved intermediates formed in fusion and fission.

We demonstrate that CGMD simulations with the model proposed by Marrink et al. (20) agree qualitatively with the experimental results for both single-lipid and mixed-lipid systems. This suggests that the model can be used as a reliable tool for estimating the variation of mechanical properties of lipid systems. In addition, we investigate the role of molecular shapes in the phase behavior of the lipid systems and show that the phase behavior of the single-lipid systems is consistent with the molecular packing theory (27). However, the phase behavior of mixed lipid systems deviates from predictions of the packing theory due to subtle interactions between lipids neglected in this theory.

Methods

Coarse-grained model

For the sake of completeness, we summarize the coarse-grained model of Marrink et al. (20) used in this work. In this model, functional groups and molecules are represented by four types of beads, namely, polar (P), nonpolar (N), apolar (C), and charged (Q) beads. For example, three or four methyl/methylene groups of a lipid tail are represented by a single apolar bead C, and four water molecules are represented by a single polar bead P. The N and Q bead types have further subtypes which allow one to model different hydrogen-bonding capabilities of the corresponding groups of atoms. All the beads are assumed to have the same mass (72 amu) and van der Waals diameter (0.47 nm).

Interactions between nonbonded beads are modeled by the Lennard-Jones (LJ) 12-6 potential. The strength of this interaction is chosen depending on the nature of the interacting beads. The model does not explicitly account for the fine details of bead interactions, such as formation of hydrogen bonds. Instead, these bonds are modeled implicitly by adjusting the strength of the bead interactions to account for hydrophobic and hydrophilic effects caused by formation or breakage of hydrogen bonds. For example, the LJ energy parameter is 5 kJ mol⁻¹ for hydrophilic attraction between two polar (P) beads, and 1.8 kJ mol⁻¹ for a repulsive interaction between hydrophobic apolar (C) and hydrophilic polar (P) beads. The LJ potential is shifted smoothly to zero using the standard GROMACS shift function starting from 0.9 nm to the cutoff length of 1.2 nm (28,29). Electrostatic interactions between the charged beads are modeled by a shifted Coulombic potential. The shift mimics distance-dependent screening effects and is performed smoothly from 0 nm to zero at the cutoff length of 1.2 nm.

For chemically bonded beads, the bond length vibration is modeled by a harmonic potential with an equilibrium bond length of 0.47 nm and a force constant of 1250 kJ mol⁻¹ nm⁻². The bond angle vibrations are modeled by the harmonic potential of cosine type. The equilibrium force constant is 25 kJ mol⁻¹ for all bonds, except the cis double bond in the acyl chains of the lipid tail. The double bonds are modeled by a stiffer potential with an equilibrium force constant of 35 kJ mol⁻¹. The equilibrium bond angles depend on the geometry of the molecule, and the presence of double bonds in the acyl chain. For example, for a single bond in the alkyl chain, the equilibrium angle is 180°, whereas for a cis double bond the angle is 120°.

The coarse-grained models for water and DOPE were taken from the work of Marrink et al. (20). Coarse-grained models for Mg²⁺, Ca²⁺, DOPA, and LPA were developed by using the methodology of Marrink et al. (20) for mapping functional groups in a molecule to specific coarse-grained beads. Thus, Mg²⁺ and Ca²⁺ were modeled as single beads of type Qda (charged bead acting as a donor and acceptor of a hydrogen bond). The charge on these beads was reduced from 2.0e to 1.4e to account for the hydration shell surrounding the ion. This charge reduction is similar to that performed for the sodium ion in Marrink et al. (20).

Fig. 1 shows the atomistic structures and the corresponding coarse-grained models of DOPA and LPA. The models for the phosphate groups and the acyl tails in the two lipids are identical. The phosphate groups are modeled by beads of type Qa (charged beads acting as hydrogen-bond acceptors) with a net −1e charge, and the acyl tails, consisting of oleoyl fatty acid chains (18:1⁹), are modeled by five C beads. However, the models for the glycerol-ester linkages in DOPA and LPA are slightly different. Specifically, the glycerol-ester linkage in DOPA is modeled by two beads of type Na (nonpolar beads that act as a hydrogen-bond acceptor), which is similar to the glycerol-ester linkage in the model for DOPE proposed by Marrink et al. (20,25). In contrast, the glycerol-ester linkage in LPA is modeled by a single Nda bead (a nonpolar bead capable of being both donor and acceptor of hydrogen bonds). The latter choice is motivated by the fact that, unlike DOPA, the glycerol group in LPA has a hydroxyl group, which can act as a hydrogen-bond donor. We chose a single bead to represent the glycerol-ester linkage in LPA because results of simulations with the two-bead model contradict the experimental data. Specifically, this model predicts that LPA molecules dissolved in water in the absence of counterions will self-assemble into wormlike micelles, rather than the spherical micelles observed in the experiments (discussed in Results).

Figure 1.

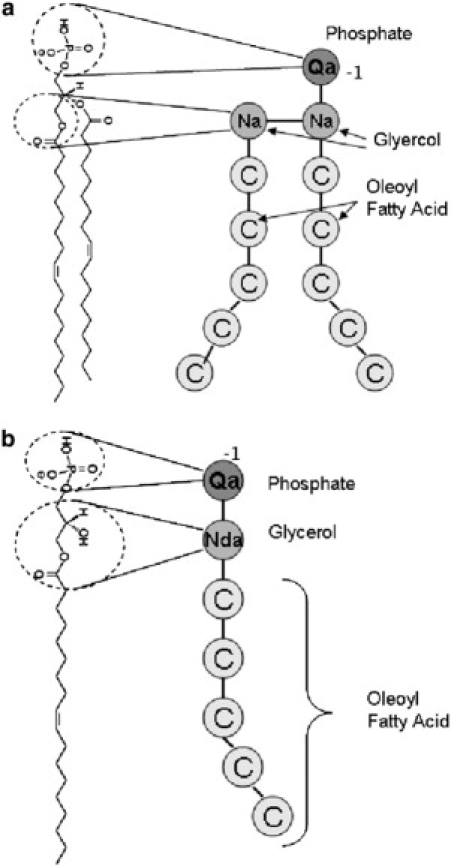
Detailed atomic structures and the corresponding coarse-grained models for (a) DOPA and (b) LPA lipid molecules. Mapping between different groups of atoms and the coarse-grained beads is shown for some groups. Note that double bonds are causing the kink in the tail chains. The bead types are denoted as follows: C, apolar; P, polar; Qa (Na), charged (nonpolar) groups acting as hydrogen-bond acceptor; and Nda, nonpolar groups acting as hydrogen-bond donor and acceptor (20).

It is worth noting two points regarding the possible extensions and modifications of this model. First, experimental studies show that the phase behavior of LPA is sensitive to pH (26). However, H⁺ ions are too small to be explicitly included into the coarse-grained model. In principle, the effects of changing pH can be modeled by modifying the effective charges of heavier ions and the screening lengths of the electrostatic potential. However, we have refrained from making these modifications, and confined our attention to the effect of heavy divalent cation concentration (Mg²⁺ and Ca²⁺). Moreover, to focus the current simulations on the effects of the heavy divalent cations, the charge balancing due to monovalent anions (e.g., Cl⁻ used in the experiments of Kooijman et al. (26)) is modeled implicitly via the screened electrostatic potential introduced in the CG model (20). This screening leads to a relatively short effective range (≈0.6 nm) for the electrostatic interactions, thus preventing an instability that would occur in a system with unbalanced charges and unscreened long-range electrostatic interactions.

Second, one can make fine adjustments to fit the model to the data. For instance, in a recent study of the mixed DOPE/DOPC systems, Marrink et al. modified the strength of interactions between lipid phosphate groups and water to increase the stability of the lamellar phase (25). In this study, we chose not to make these fine adjustments.

Simulation details

Molecular dynamic (MD) simulations were performed with the GROMACS MD simulations package (29). In all the systems, anisotropic Berendsen pressure coupling was used with a reference pressure of 1.0 bar. All systems were also coupled to a temperature bath using Berendsen coupling. The time step used in the simulations was 40 fs. Periodic boundary conditions were imposed in all three directions.

In the CG model, four water molecules are represented by a single CG particle. In what follows, references to the amount of water in the simulation correspond to the amount of “real” water molecules (which is four times the number of model water beads). Also, the dynamics predicted by the coarse-grained model is on average four times faster than the real dynamics (20). This conclusion is based on a comparison of diffusion coefficients obtained experimentally with those predicted by the CGMD simulations for various systems, including lateral diffusion of lipids in bilayers. This speedup of the dynamics is common to most CG models and occurs because CG interaction potentials are much smoother than the atomistic potentials. Therefore, the durations of the simulations are reported below in terms of real time (i.e., four times the simulation time).

Molecular shapes

In molecular packing theory (27), the geometry of amphiphilic molecules is characterized by the packing parameter

$$S=\frac{v}{l_{\text{c}}{a}_0},$$ (1)

where a₀ is the optimal headgroup area, v is the tail volume, and l_c is the length of the fully extended tail (which is independent of the temperature).

The optimal headgroup area a₀ accounts for the effective range of interactions between lipid headgroups. The value of a₀ corresponds to the minimum of the intermolecular interaction energy and represents a balance between 1), attraction between lipid molecules due to the surface tension at the interface between the hydrophobic tails and the hydrophilic headgroups; and 2), repulsion between headgroups due to various contributions, such as electrostatic, steric, and hydration forces. Therefore, we estimate the optimal lipid headgroup diameter d as the equilibrium distance between the headgroup centers of mass. The distance between headgroups is measured under the assumption that all headgroups belong to a well-defined surface and the displacements of the headgroups in the direction transverse to the surface are negligible. For example, for each leaflet of a bilayer, we compute the distances between the projections of the headgroups on the bilayer surfaces. For nonplanar surfaces, such as those of spherical micelles and inverted hexagonal phases, the distance between headgroups is computed along the geodesics of the corresponding surfaces. In the analysis of spherical micelles and inverted hexagonal phases, we approximate the surface containing lipid headgroups by spheres and cylinders, respectively.

To determine a measure of the headgroup size, we appeal to the distribution function, g(r). The first maximum of g(r) corresponds to the equilibrium (optimal) distance between the headgroups. For brevity, we shall refer to this distance as the headgroup size. In systems containing lipids of a single type, the headgroup size corresponds to the first maximum of the pair-correlation function g(r). In mixed lipid systems, the headgroup size is obtained from pair-correlation functions g_ij(r) between headgroups of the lipids of types i and j; i, j = 1, 2. The major and minor lipid components in the system are denoted by indices 1 and 2, respectively. In the current simulations, the fraction of the major component was relatively high (90%). Therefore, to the leading order, the headgroup diameter d₁ of the major lipid component was assumed to coincide with the location of the maximum of g₁₁(r). This assumption was validated by the fact that, in the considered mixed lipid systems, g(r) almost coincides with g₁₁(r), thus proving that the contribution of the minor component to the effective headgroup size of the major component is negligible. The headgroup diameter d₂ of the minor component was obtained from the pair-correlation function g₁₂(r) between the major and the minor components using the relationship r_12,max = (d₁ + d₂)/2, where r_12,max is the location of the first maximum of g₁₂(r).

There is no unique way to define volume v occupied by a fluctuating lipid tail. However, since the goal of this work is to assess effects of various factors on the change of the lipid shape, it is sufficient to focus on the relative magnitudes of the tail volumes, which should be insensitive to specifics of a particular definition. For this purpose, for each hydrocarbon chain of the lipid tails, we consider vector L connecting the first and last beads of the chain and compute the probability distributions of its length L and orientation cos φ with respect to the normal n to the monolayer surface (see Fig. 2). The monolayer surface is defined as the surface containing the headgroup centers of mass.

Figure 2.

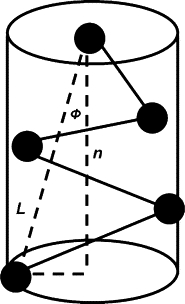
Schematic of the approximation (2) for the volume occupied by a lipid tail.

Relative increase in the tail volume corresponds to 1), increase in the magnitude of fluctuations of the tail beads, which is manifested by increase in variances of L and φ and/or 2), increase in the volume corresponding to the average tail configuration. To estimate the average tail volume we approximate the volume occupied by each of the tail chains by a cylinder with height L cos φ and the base of radius L sin φ, as illustrated in Fig. 2. Therefore,

$$v\approx N_{\text{c}}{v}_{\text{c}},v_{\text{c}}\approx \pi L^3\text{cos}\phi \text{si}{\text{n}}^2\phi ,$$ (2)

where v_c is the volume of an individual tail chain and N_c is the number of the chains in the lipid tail, N_c = 1 for LPA and N_c = 2 for DOPE and DOPA.

Below, we show that criteria 1 and 2, based on the magnitudes of the fluctuations and the averages of L and cos φ, lead to consistent results.

Results

As noted in the Introduction, Kooijman et al. studied the phase behavior of 1), pure LPA as a function of Mg²⁺ concentrations; 2), pure DOPA as a function of Ca²⁺ concentrations; and 3), mixtures of DOPE/LPA and DOPE/DOPA as a function of temperature (26). Furthermore, they argued that the observed phase behavior could be rationalized in terms of molecular shape changes and proposed specific mechanisms to explain these changes. We show below that the CG model successfully captures the experimentally observed phase behavior. In addition, the simulations allow us to check the validity of the mechanistic hypotheses proposed by Kooijman et al.

Phase behavior of LPA as a function of [Mg²⁺]

Kooijman et al. studied the shape change of LPA aggregates in response to increasing concentrations of Mg²⁺ (26). The experiments were performed at 310 K and a pH of 7.2. They observed that in the absence of Mg²⁺, LPA forms spherical micelles. However, as the ratio [Mg²⁺]/[LPA] is increased, the micelles aggregate to form bilayer disks.

To test the ability of the CG model to reproduce these observations, we conducted self-assembly simulations of the LPA lipids (shown in Fig. 1 b), water, and different concentrations of divalent ions (representing Mg²⁺). The simulations were performed at 310 K. The simulation box was randomly populated with 500 molecules of LPA, 192 molecules of water per LPA molecule, and varying amounts of Mg²⁺ corresponding to the three concentration ratios studied by Kooijman et al. ([Mg²⁺]/[LPA] = 0, 0.2, and 1.0). These random dispersions of LPA and Mg²⁺ in water rapidly self-assembled into micelles, and equilibrated within 800 ns.

Fig. 3 shows the equilibrium structures formed at the end of the simulation for the three values of the ratio [Mg²⁺]/[LPA] used in the experiments. The simulations show that in the absence of Mg²⁺, several small micelles are formed (Fig. 3 a). When the ratio [Mg²⁺]/[LPA] is increased to 0.2, the aggregation number of micelles increases, as is evident from the increased size and reduced number of micelles (Fig. 3 b). If the ratio [Mg²⁺]/[LPA] is increased further to 1.0, the lipids assemble into a single aggregate, the side and top views of which are shown in Fig. 3, parts c and d, respectively. It is clear from these two figures that the single aggregate is disk-shaped. The model simulations therefore agree nicely with the experiments: As the concentration of Mg²⁺ increases, so does the micellar size, until all the micelles fuse to form a single disk-shaped aggregate at sufficiently large [Mg²⁺]/[LPA].

Figure 3.

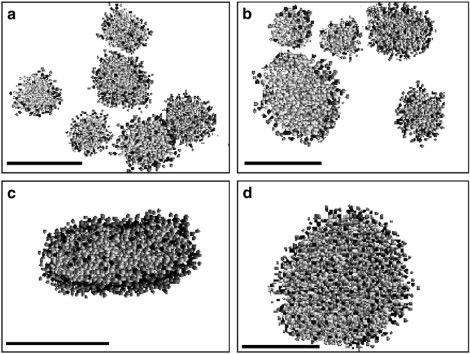
Dependence of the size and shape of LPA micelles on [Mg²⁺]: (a) Molar ratio [Mg²⁺]/[LPA] = 0. (b) Molar ratio [Mg²⁺]/[LPA] = 0.2. (c) Side view of aggregate formed at molar ratio [Mg²⁺]/[LPA] = 1.0 (d) Top view of aggregate formed at molar ratio [Mg²⁺]/[LPA] = 1.0. For the sake of clarity, water molecules and ions were removed from these plots. Scale bars represent 5 nm. The figures are created using the VMD software package (41).

To quantify the shape change of the LPA aggregates shown in Fig. 3, we calculated the three radii of gyration, R₁ ≤ R₂ ≤ R₃. The ratios R₂/R₁ and R₃/R₁ characterize the extent to which the shape of an aggregate deviates from that of a sphere. For a perfect sphere, both ratios are equal to one and for a disklike ellipsoid, R₂/R₁ = 1 and R₃/R₁ > 1 (see, e.g., (30)). Fig. 4 shows that as the concentration of Mg²⁺ increases, so does the asphericity of the lipid aggregates and, in particular, at [Mg²⁺]/[LPA] = 1, the micelle has an oblate shape.

Figure 4.

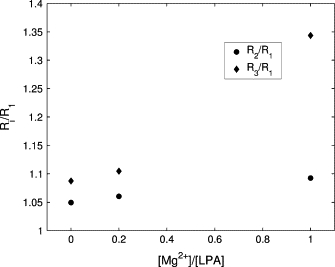
Ratio of the largest (R₃) and the second largest (R₂) radii of gyration to the smallest radius of gyration R₁ of the LPA micelles as a function of the molar ratio [Mg²⁺]/[LPA].

To explain the microstructural change of LPA from micelles to disk-shaped aggregates, Kooijman et al. (26) appealed to the theory of molecular packing, according to which microstructural changes reflect alterations in the shape of the individual molecules. Specifically, they argued that

• 1.In the absence of Mg²⁺, LPA molecules are inverted-cone-shaped. However, in the presence of Mg²⁺, they become cylinder-shaped because their headgroups contract.
• 2.This contraction of the headgroups is caused by interactions with the Mg²⁺ ions. Each Mg²⁺ ion binds to the headgroups of two LPA molecules, thus squeezing their heads together.

The simulations allowed us to test the validity of these two hypotheses.

To test the validity of the first hypothesis, we calculated the variation of the shape of LPA molecules as a function of the ratio [Mg²⁺]/[LPA]. Since the nonpolar tails are unaffected by any changes in the charge of the surrounding molecules, the change in the packing parameter S defined by Eq. 1 is due to the variation of the charged headgroup area.

The average headgroup diameter of LPA molecules, summarized in Table 1, was determined by calculating the correlation function, g(r), in the absence of ions and at the equimolar concentration of LPA lipids and Mg²⁺ ions. In the former case, the LPA micelles are approximated by perfect spheres. In the latter case, the micelles are approximated by bilayer disks and the pair correlation is computed between the lipid molecules within the same leaflet of the bilayer. Moreover, only lipid molecules located at a sufficiently large distance from the disk edges are taken into account in the calculation of g(r). The obtained correlation functions (Fig. 5) demonstrate that in the presence of Mg²⁺ ions, g(r) has the near-periodic profile characteristic of ordered structures. Furthermore, the headgroup diameter, corresponding to the first peak of g(r), decreases from 0.70 nm to 0.53 nm, which is consistent with the first hypothesis of Kooijman et al. (26).

Table 1.

Headgroup diameters of LPA and DOPA under various conditions; the headgroup diameter of DOPE remains the same (≈0.73 nm) under all considered conditions

System	dLPA	System	dDOPA
Pure LPA	0.70 nm	Pure DOPA	0.80 nm
LPA + Mg2+	0.53 nm	DOPA + Ca2+	0.78 nm
LPA + DOPE	0.53 nm	DOPA + DOPE	0.62 nm

Figure 5.

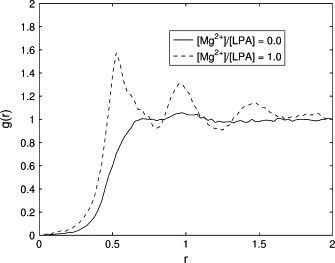
The pair correlation function for LPA molecules, g(r), calculated from simulations of pure LPA (solid line), and LPA + Mg²⁺ (dashed line). The correlation function shows that the headgroup diameter of LPA molecules decreases from 0.70 nm to 0.53 nm in the presence of Mg²⁺.

To check the second hypothesis, we calculated the number of LPA molecules bound to each Mg²⁺ ion. For this calculation, we chose the sphere of influence of each Mg²⁺ ion to be 0.6 nm. This choice was based on the observation that the screened electrostatic force between Mg²⁺ and LPA decays to near zero at an interparticle distance of 0.6 nm. The analysis showed that for the systems with equimolar Mg²⁺ concentration, on average 2.6 LPA molecules were within the sphere of influence of each Mg²⁺ ion. For the system with [Mg²⁺]/[LPA] = 0.2, we found that on average 2.2 LPA molecules were within the sphere of influence of each Mg²⁺. As expected, at the lower ion concentration, a smaller fraction of LPA lipids is affected by Mg²⁺. Specifically, 91% and 34% of the LPA molecules are strongly interacting with a Mg²⁺ ion at the equimolar concentration and at the lower Mg²⁺ concentration, respectively. Thus, the simulations support the second hypothesis of Kooijman et al. (26).

Phase behavior of DOPA as a function of [Ca²⁺]

Kooijman et al. (26) also studied the phase behavior of pure DOPA systems with respect to concentration of Ca²⁺ ions at neutral pH and a temperature of 310 K. They observed a lamellar phase both in the absence of ions and at the equimolar concentration of Ca²⁺ and DOPA.

We performed self-assembly simulations to test if the CG model reproduced these results. To this end, 500 DOPA molecules and 17,500 CG water particles were randomly placed in a simulation box. For the simulation of the phase behavior in the presence of Ca²⁺, 500 CG divalent cations were also added to the system. The systems were simulated at 310 K for 1.6 μs.

Consistent with the experiments of Kooijman et al. (26), we observed the formation of a lamellar phase both in absence and in the presence of Ca²⁺. The molecular packing theory implies that Ca²⁺ produces negligible change in the shape of DOPA molecules. Indeed, the pair correlation functions g(r) for DOPA headgroups, shown in Fig. 6, demonstrate that the diameter of the headgroup changes only slightly due to presence of the ions, from d ≈ 0.80 nm in the absence of the ions to d ≈ 0.78 nm in the presence of the ions. This decrease in the headgroup size is caused by the screening of electrostatic interactions between the negatively charged phosphate groups by the Ca²⁺ cations.

Figure 6.

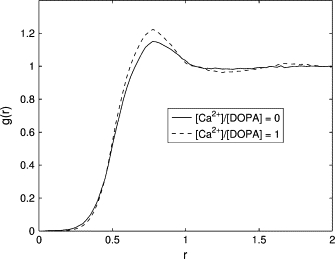
The correlation function, g(r), based on simulations of pure DOPA (solid line) and DOPA + Ca²⁺ (dashed line). The correlation function shows that the headgroup diameter of DOPA molecules slightly decreases from d ≈ 0.80 nm to d ≈ 0.78 nm in the presence of Ca²⁺.

Phase behavior of DOPE, DOPE-LPA, and DOPE-DOPA as a function of T

Kooijman et al. (26) observed that when the temperature is increased, pure DOPE undergoes a transition at T ≈ 280 K from the lamellar (L_α) phase to the inverted hexagonal (H_II) phase (see curve labeled with open triangles in Fig. 7). Upon addition of 10 mol % LPA to DOPE, the phase transition temperature increases to T ≈ 305 K (curve labeled with open circles in Fig. 7). The addition of 10 mol % DOPA to DOPE results in a very slight increase in the phase transition temperature to T ≈ 282 K (curve labeled with open squares in Fig. 7). The experiments therefore show that addition of LPA stabilizes the lamellar phase, whereas addition of DOPA has essentially no effect on the stability of the lamellar phase. The goal of the simulations discussed below is to study whether this transition is mirrored by the coarse-grained model and to elucidate the molecular basis of the stabilizing effect of LPA.

Figure 7.

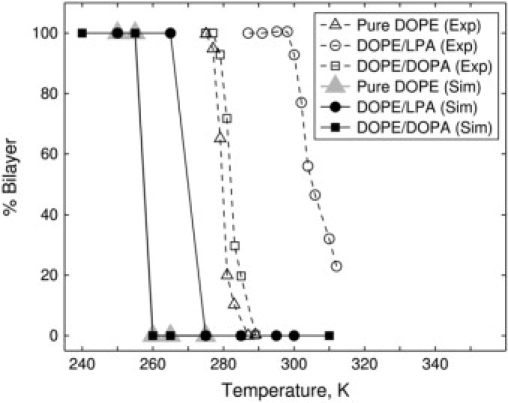
Temperature-induced phase transition between lamellar and inverted hexagonal phases in the mixed lipid systems: Comparison of experimental data (26) and simulations for pure DOPE (triangles), DOPE/LPA (circles), and DOPE/DOPA (squares) systems. The experimental data are shown by open symbols and the simulation results are shown by solid symbols. The lamellar phase corresponds to 100% bilayer and the inverted hexagonal phase corresponds to 0%. The composition of the mixed systems is 90% DOPE and 10% of a minor lipid (LPA or DOPA).

We investigated the stability of the lamellar phase in DOPE, DOPE/DOPA, and DOPE/LPA systems by using the simulation protocol similar to that used by Marrink et al. for studying the phase behavior of DOPE/DOPC mixtures (25). To this end, we prepared a perturbed lamellar phase of the lipid(s), and simulated its subsequent evolution at various temperatures. If the lamellar phase is stable at a particular temperature, the perturbation decays, and system returns to the lamellar phase. If the lamellar phase is unstable at that temperature, the perturbation grows, and the system evolves to the inverted hexagonal phase.

The perturbed lipid lamellar phase was prepared as follows:

• 1.A bilayer was first generated by simulating the self-assembly of randomly dispersed lipid-in-water system with a relatively low lipid concentration. The conditions used for generating the bilayers for the considered lipid systems are summarized in Table 2. For instance, in the case of the DOPE/LPA mixture, the bilayer was generated by simulating the self-assembly of 500 lipid molecules (with 10% LPA) at a water/lipid ratio of 80:1 and a temperature of 280 K. Bilayer formation was observed within 200 ns and the system was equilibrated for an additional 600 ns.
• 2.The bilayer was then dehydrated to a water/lipid ratio of 15:1, and two identical dehydrated bilayers were stacked on top of each other.
• 3.
  The two stacked bilayers were perturbed with planar sinusoidal perturbations of identical amplitude and wavelength but opposite phases, i.e., the perturbations were of the form

  $$\pm A\text{sin}(kx),A=\frac{L_{\text{z}}}{10},k=\frac{2\pi }{L_{\text{x}}},$$ (3)

  where L_x and L_z denote the dimensions of the simulation box in the x- and z-directions (the bilayers were normal to the z axis). Since the perturbations imposed on the two bilayers have opposite phases, the location of the maximum of the perturbation for one bilayer coincides with that of the minimum of the neighboring bilayer.
• 4.This perturbed configuration was then energy-minimized using the steepest descent method until a local minimum was reached. The obtained configuration was copied in the normal direction to obtain a system consisting of four bilayers.

Table 2.

Conditions used for generating the DOPE, DOPE/DOPA, and DOPE/LPA bilayers

	DOPE	DOPE/DOPA	DOPE/LPA
Number of lipid molecules	500	120 (10% DOPA)	500 (10% LPA)
Water/lipid ratio	80:1	120:1	80:1
Temperature	280 K	240 K	280 K
Bilayer formation time	200 ns	80 ns	200 ns
Additional equilibration time	600 ns	720 ns	600 ns

Fig. 8 a shows an example of the perturbed lamellar phase generated for simulating the phase transition of the DOPE/LPA mixture. The choice to impose the perturbation given by Eq. 3 with the wavelength equal to the width L_x of the simulation box is based on our preliminary simulations of phase transitions in unperturbed systems. The instability leading to the phase transition in these simulations is dominated by the mode with the wavelength L_x. Ideally, the wavelength of the perturbed mode should be chosen based on a stability analysis of a linear model. However, the linear elastic model for the lipid bilayer is neutrally stable (7) and therefore the linear stability analysis cannot predict the most unstable mode. To assess the onset of the instability of the lamellar phase it is necessary to perform a nonlinear stability analysis of the system. The latter is outside the scope of this article and therefore we use the perturbations based on the empirical observations of the unperturbed systems.

Figure 8.

Simulations of the temperature-induced transition of DOPE/LPA from lamellar to inverted hexagonal phases: (a) Initial perturbed configuration of the lamellar phase. (b) Final configuration of DOPE/LPA system at 250 K (lamellar phase). (c) Final configuration of DOPE/LPA system at 300 K (inverted hexagonal phase). The black, gray, and white spheres represent lipid headgroups, tail beads, and water beads, respectively. To illustrate the geometry of the systems more clearly, all the configurations were generated by copying the simulation cell three times in the lateral direction. The figures are created using the VMD software package (41).

To investigate the stability of the lamellar phase, the evolution of the perturbed lamellar phase was simulated at various temperatures. In the particular case of DOPE/LPA, the simulations were performed at temperatures between 250 K and 300 K. We found that at T ≤ 265 K, the perturbed lamellar phase returned to its original configuration, which remained stable for 4.0 μs (Fig. 8 b). In contrast, at T ≥ 275 K, the perturbed lamellar phase evolved to the inverted hexagonal phase (Fig. 8 c). These results are summarized in Fig. 7 by the curve labeled with solid circles. Analogous simulations were performed for pure DOPE and mixed DOPE/DOPA systems. In the case of DOPE, we found that at T ≤ 255 K, the lamellar phase remained stable for 7.2 μs, whereas at T ≥ 260 K, the system evolved to the H_II phase (gray triangles in Fig. 7). In the case of the DOPE-DOPA mixture, the system remained stable for 4.0 μs at T ≤ 255 K, and transitioned to the H_II phase at T ≥ 260 K (solid squares in Fig. 7).

It is evident from Fig. 7 that the simulations are in qualitative agreement with the experimental data. The phase transition temperature for the model DOPE/DOPA system is ∼12 K lower than that of the DOPE/LPA system. Thus, the coarse-grained model captures both the stabilizing effect of LPA and the absence of a significant effect of DOPA on the stability of the lamellar phase of DOPE.

However, the precise values of the phase transition temperatures predicted by the simulations are different from those observed in the experiments. The experiments show phase transition temperatures of 282 K and 305 K for DOPE/DOPA and DOPE/LPA, respectively, but the corresponding simulated values are ∼258 K and 270 K, respectively. In principle, quantitative agreement can be obtained by adjusting the model parameters (see, for instance, (25)). However, our goal was to determine whether the model shows reasonable agreement with the data. We have therefore refrained from making fine quantitative adjustments.

The temperature-induced phase transitions shown in Fig. 7 can be explained in terms of the molecular packing theory as follows (26,31):

• 1.At low temperatures, DOPE molecules are cylinder shaped, and hence, exist as a bilayer. As the temperature increases, the tails undergo more pronounced thermal fluctuations leading to increase of their volume. At sufficiently high temperatures, DOPE molecules become cone-shaped, thus triggering a transition from the lamellar to the inverted hexagonal phase.
• 2.The addition of a minor lipid to a DOPE bilayer increases or decreases the phase transition temperature, depending on the molecular shape of the minor lipid. If the minor lipid is inverted-cone or cylinder-shaped at temperatures above the L_α → H_II transition temperature for pure DOPE, its addition relaxes the stress within the DOPE bilayer by occupying the hydrophobic voids, thus resulting in an increase of the phase transition temperature, T_H. If the minor lipid is cone-shaped, its addition has no effect on T_H if its geometry is identical to that of the DOPE molecules, and decreases T_H if it is even more cone-shaped than DOPE.

Kooijman et al. (26) postulated that LPA molecules, which are inverted-cone-shaped in systems consisting of pure LPA, remain inverted-cone-shaped even in the presence of DOPE. Thus, addition of LPA increases T_H. In sharp contrast, DOPA molecules, which are cylinder-shaped in systems consisting of pure DOPA, somehow become cone-shaped in the presence of DOPE.

The above explanation rests upon two assumptions:

• 1.As the temperature increases, the volume v of the lipid tails increases due to more pronounced fluctuations, and
• 2.The shape of DOPA (respectively, LPA) molecules changes (respectively, does not change significantly) when they are exposed to an environment consisting of DOPE.

We checked the validity of both assumptions.

Tail volume

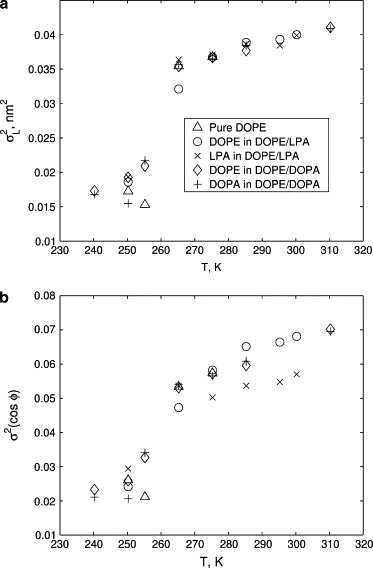
As discussed in Methods, the tail volumes are estimated using the distributions of the length L and the orientation cos φ of the vectors L connecting the first and last beads of tail chains (see Fig. 2). We observe that the temperature dependence of the tail shape distributions is consistent for all lipids in all considered systems. The mean and the variance of L and cos φ for the considered lipid systems at various temperatures are shown in Figs. 9 and 10. The estimates for the volume of a single tail chain v_c computed using the approximation (2) and the obtained mean values of L and cos φ are shown in Fig. 11. As temperature of the system increases, the mean values of L and cos φ decrease (see Fig. 9), leading to the increase in the chain volume v_c (see Fig. 11). An additional confirmation of the increase of the tail volume with temperature is provided by the growth of the fluctuation magnitude of the length and the orientation of the end-to-end vector L with the temperature increase (see Fig. 10).

Figure 9.

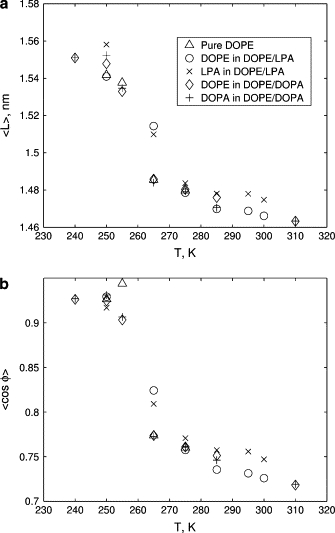
Temperature dependence of the mean of (a) length L and (b) orientation cos φ of the end-to-end vectors L of tail chains in the considered lipid systems (see legend).

Figure 10.

Temperature dependence of the variance of (a) length L and (b) orientation cos φ of the end-to-end vectors L of tail chains in the considered lipid systems. The notation is the same as in Fig. 9.

Figure 11.

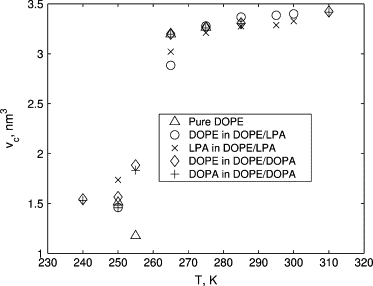
Temperature dependence of the estimate (2) for volume v_c of individual acyl chains of lipid tails. The notation is the same as in Figs. 9 and 10.

Furthermore, we observe a jump in the shape distribution of tails for temperatures between 255 K and 275 K, i.e., in the range corresponding to the L_α → H_II transitions. Our data suggests that the tail properties in this temperature range are affected both by the temperature and the geometry of the system. Specifically, for the DOPE and DOPE/DOPA systems, the jump takes place over a relatively narrow range 255 K ≤ T ≤ 265 K. For these systems, the lower boundary of this range corresponds to the L_α phase and the upper boundary corresponds to the H_II phase. On the other hand, for the DOPE/LPA system the jump is spread over a wider temperature range. Although there is a sharp change in the tail properties at T = 265 K, this change is not as large as that for the DOPE and DOPE/DOPA systems at this temperature. This indicates that although most of the jump in the tail properties can be attributed to the temperature change, the specific geometry of the phase (L_α for DOPE/LPA and H_II for DOPE and DOPE/DOPA) also affects the tail properties. The tail properties of the DOPE/LPA system undergo a near-discontinuous change at the phase transition temperature of T = 275 K, at which point they become almost identical to those of DOPE and DOPE/DOPA systems.

Headgroup size

The size of DOPE headgroups remains essentially unchanged as the minor LPA or DOPA components are added to a DOPE bilayer, as demonstrated in Fig. 12 a. On the other hand, the pair-correlation functions shown in Fig. 12 b imply that the headgroup sizes of the minor components in the mixed bilayers are significantly smaller than those in pure lipid systems. Specifically, LPA headgroup diameter decreases from 0.70 nm (see Fig. 5 and Table 1) to 0.53 nm in the presence of DOPE. Similarly, DOPA headgroup diameter decreases from 0.80 nm (see Fig. 6 and Table 1) to 0.62 nm in the presence of DOPE. This reflects the fact that in the presence of DOPE, the electrostatic repulsion between the negatively charged headgroups of LPA and DOPA is reduced due to the shielding effect of the surrounding zwitterionic headgroups of DOPE molecules.

Figure 12.

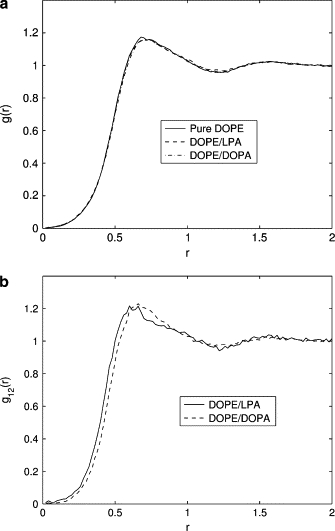
(a) The correlation function, g(r), for DOPE headgroups based on simulations with pure DOPE (solid line), DOPE/LPA (dashed line), and DOPE/DOPA (dash-dotted line). The correlation function shows that there is virtually no change in the headgroup diameter d of DOPE in the presence of small concentrations of DOPA or LPA (d ≈ 0.73 nm). (b) The correlation function, g₁₂(r), between major and minor components in mixtures of DOPE and LPA (solid line) and DOPE and DOPA (dashed line). The diameters of the minor components in these mixtures are d ≈ 0.53 nm for LPA and d ≈ 0.62 nm for DOPA.

The headgroup size change indicates that screening of electrostatic interactions between DOPA headgroups is performed more efficiently by the DOPE headgroups located in the same plane as the DOPA groups than the divalent cations dissolved in solution (see Phase Behavior of DOPA as a Function of [Ca²⁺]). On the other hand, the screening of LPA headgroup interactions is performed equally efficiently by the DOPE lipids within the bilayer and the divalent cations in solution (see Phase Behavior of LPA as a Function of [Mg²⁺]).

Packing parameter

Tail-groups of the considered lipids consist of one (for LPA) and two (for DOPE and DOPA) oleoyl fatty acid chains. Therefore, the length l_c of the fully extended tails is the same for these lipids. The volumes of the tail chains, summarized in Fig. 11, show that for the DOPE/LPA and DOPE/DOPA systems, v_c(DOPE)/v_c(LPA) ≈ 1 and v_c(DOPE)/v_c(DOPA) ≈ 1 at most temperatures. Equation 1 therefore implies that the ratio of the packing parameters for the major and minor components is inversely proportional to their optimal headgroup areas, i.e.,

$$\frac{S(\text{DOPE})}{S(\text{LPA})}\approx 2\frac{d_{\text{LPA}}^2}{d_{\text{DOPE}}^2}\approx 1.05,$$ (4)

$$\frac{S(\text{DOPE})}{S(\text{DOPA})}\approx \frac{d_{\text{DOPA}}^2}{d_{\text{DOPE}}^2}\approx 0.72\text{.}$$ (5)

Here, d_DOPE ≈ 0.73 nm is the headgroup diameter of DOPE (in all considered systems) and d_LPA and d_DOPA are the headgroup diameters of LPA and DOPA in the DOPE/LPA and DOPE/DOPA systems, respectively (see Table 1). The factor of 2 in Eq. 4 reflects the difference in the number of chains in the LPA and DOPE tails.

Equations 4 and 5 imply that in the mixed systems, the shapes of DOPE and LPA are effectively the same, and that DOPA is more cone-shaped than DOPE. Packing theory therefore implies that LPA should have a negligible effect on the stability of the DOPE lamellar phase, and DOPA should destabilize the DOPE lamellar phase. Both these results contradict the experiments of Kooijman et al. (26) and our observations (see Fig. 7). Nevertheless, the packing theory successfully explains the relative effects of DOPA and LPA on the stability of the DOPE lamellar phase, namely that the L_α → H_II phase transition temperature of the DOPE/LPA system is higher than that of the DOPE/DOPA system.

The above arguments ignore the contribution of the entropy of mixing to the free energy of the mixed lipid system, which could explain the inability of the packing theory to explain the shift (or lack thereof) of the transition temperature in the mixed DOPE/LPA and DOPE/DOPA systems relative to the pure DOPE system. However, our simulations indicate that both the lamellar and the inverted hexagonal phases of the DOPE/LPA and DOPE/DOPA systems are well mixed. Therefore, the contribution of the entropy of mixing to the free energies of these two phases is the same and the entropy of mixing does not affect the phase stability. This suggests that the molecular packing theory oversimplifies the behavior of mixed lipid systems. In the next section, we discuss a possible improvement of the theoretical analysis and propose a hypothesis that may explain the observed discrepancy.

Discussion

The results presented in the previous section indicate that the phase behavior of the considered single-lipid systems can be successfully explained by the packing theory. However, for the mixed lipid systems, the packing theory alone does not provide an adequate explanation for the changes in stability of the lamellar phase upon addition of a minor lipid (LPA or DOPA) to DOPE. Therefore, an analysis based on a more detailed theoretical description is required.

For bilayers, such a description is provided by the elastic model proposed by Helfrich (7). This model predicts the following free energy per unit area f_H of a lipid bilayer,

$$f_{\text{H}}=\frac{\kappa }{2}{(J-J_{\text{s}})}^2+\overline{\kappa }K,$$ (6)

where J and K are the total and Gaussian curvatures of the membrane, respectively; J_s is the spontaneous curvature; κ is the bending modulus; and $\overline{\kappa }$ is the Gaussian modulus. The spontaneous curvature directly corresponds to the molecular shape, e.g., J_s = 0 for cylindrical molecules.

The equilibrium configuration of a membrane corresponds to the particular shape that minimizes the total energy. It follows from Eq. 6 that a bilayer can be stable even if the spontaneous curvature is not zero, provided the energy required to form a bilayer ($\kappa J_{\text{s}}^2/2\text{per unit area of the bilayer}$) is lower than its energy in any other phase.

Hence, to determine whether molecules with nonzero spontaneous curvature form a stable bilayer, it is necessary to compare their energy in the lamellar phase with their energy in other phases. Neglecting the interbilayer interactions, the energy of the lamellar phase is given by the Helfrich model (6). However, this model cannot predict energies of nonlamellar phases because it does not account for the energy associated with the tilt of lipid molecules present in most nonbilayer phases.

This is accomplished by an extension of the Helfrich model (6) proposed by Hamm and Kozlov (9,32). The Hamm-Kozlov model accounts for the energy of tilt of the lipid molecules, which enables application of the elastic model to nonbilayer systems such as the inverted hexagonal phase (32) and the intermediate stalk formed in vesicle fusion (33,34). The tilt energy of lipid molecules is quantified by the tilt modulus κ_θ. With this model it is possible to predict phase stability of the lamellar phase and determine the transition temperature between the lamellar and the hexagonal phases. It was shown by Hamm and Kozlov (32) that the relative stability of the lamellar and inverted hexagonal phases is determined by two parameters: the spontaneous total curvature ${\tilde{J}}_{\text{s}}$ (which accounts for both the spontaneous curvature and the spontaneous lipid tilt) and the ratio of the bending and the tilt moduli, κ/κ_θ ≡ λ². In particular, if the lipid molecules are cone-shaped, i.e., ${\tilde{J}}_{\text{s}}<0,$ the L_α phase is more stable whenever $\lambda \left|{\tilde{J}}_{\text{s}}\right|<1/3\text{.}$

Therefore, we propose the following hypothesis to explain the effects of the LPA and DOPA lipids on the DOPE system. Due to the symmetry of the considered molecules, their spontaneous tilt is expected to be zero and therefore the total spontaneous curvature ${\tilde{J}}_{\text{s}}$ coincides with the spontaneous curvature J_s.

From Eqs. 4 and 5, it follows that

$$|J_{\text{s}}(\text{DOPE}/\text{LPA})|\approx |J_{\text{s}}(\text{DOPE})|,$$ (7)

$$|J_{\text{s}}(\text{DOPE}/\text{DOPA})|>|J_{\text{s}}(\text{DOPE})|,$$ (8)

where J_s(DOPE), J_s(DOPE/LPA), and J_s(DOPE/LPA) denote the spontaneous curvatures of the corresponding systems.

It is expected that the addition of the minor (DOPA or LPA) components to the DOPE system alters its bending and/or tilt moduli. We hypothesize that their ratio λ² is smaller in the mixed systems than in the pure DOPE system. This together with Eq. 7 implies that

$$\lambda (\text{DOPE}/\text{LPA})|J_{\text{s}}(\text{DOPE}/\text{LPA})|<\lambda (\text{DOPE})|J_{\text{s}}(\text{DOPE})|,$$ (9)

and the stability boundary of the L_α phase is shifted toward the higher temperature upon addition of LPA. In the case of DOPE/DOPA, we further hypothesize that the changes in λ and |J_s| upon addition of DOPA to DOPE balance each other so that

$$\begin{array}{l}\lambda (\text{DOPE}/\text{DOPA})|J_{\text{s}}(\text{DOPE}/\text{DOPA})|\\ \approx \lambda (\text{DOPE})|J_{\text{s}}(\text{DOPE})|\end{array}$$ (10)

and the net effect of the addition of DOPA to DOPE is that the phase transition temperature remains almost unchanged or slightly increases, as suggested by the experiments of Kooijman et al. (26).

To validate the hypotheses of Eqs. 9 and 10, it is necessary to obtain the bending and tilt moduli of the considered mixed systems. The procedure for calculating the bending modulus from MD simulations is well established (35–38). The procedure for the calculation of the tilt modulus has been recently proposed by the authors and applied to the analysis of a DPPC bilayer (39) and a mixed DPPC/PI4P bilayer (40). Calculation of these elastic parameters requires a sufficiently large system and, unfortunately, the systems considered in this study are too small to reliably compute the tilt and bending moduli. Simulations of larger systems and an accurate estimation of the dependence of the elastic parameters on the composition of the DOPE/DOPA and DOPE/LPA systems will be a subject of our future work.

Conclusions

We have shown that a coarse-grained molecular model can successfully simulate the phase behavior of single- and mixed-lipid systems containing LPA, DOPA, and DOPE. Specifically, the model predicts

• 1.The phase behavior of LPA and DOPA as a function of [Mg²⁺] and [Ca²⁺], respectively.
• 2.The phase changes of DOPE, DOPE/LPA, and DOPE/DOPA systems as a function of temperature.

Analysis of the molecular shapes shows that the phase behavior of the single-lipid systems can be understood in terms of the molecular packing theory. However, for the mixed lipid systems, namely, DOPE/LPA and DOPE/DOPA, the packing theory alone does not provide an adequate explanation for the changes in stability of the lamellar phase upon addition of LPA or DOPA lipids to DOPE. In these cases, an analysis based on a more detailed theoretical description is required. The elastic energy model proposed by Hamm and Kozlov offers one way of rationalizing the data for mixed lipid systems.