Molecular Mechanics of Filamin's Rod Domain

Abstract

Rearrangement of the actin cytoskeleton is integral to cell shape and function. Actin-binding proteins, e.g., filamin, can naturally contribute to the mechanics and function of the actin cytoskeleton. The molecular mechanical bases for filamin's function in actin cytoskeletal reorganization are examined here using molecular dynamics simulations. Simulations are performed by applying forces ranging from 25 pN to 125 pN for 2.5 ns to the rod domain of filamin. Applying small loads (∼25 pN) to filamin's rod domain supplies sufficient energy to alter the conformation of the N-terminal regions of the rod. These forces break local hydrogen bond coordination often enough to allow side chains to find new coordination partners, in turn leading to drastic changes in the conformation of filamin, for example, increasing the hydrophobic character of the N-terminal rod region and, alternatively, activating the C-terminal region to become increasingly stiff. These changes in conformation can lead to changes in the affinity of filamin for its binding partners. Therefore, filamin can function to transduce mechanical signals as well as preserve topology of the actin cytoskeleton throughout the rod domain.

Introduction

The actin cytoskeleton functions in cell migration and motility, cell shape, cell division, intracellular protein trafficking, and, most importantly, signal transduction. The actin cytoskeleton is not static and rigid but dynamic and constantly rearranging itself in response to the environment. For the actin cytoskeleton to carry out a variety of processes within the cell, multitudes of organizing factors exist (1). Organization factors are proteins that bind to actin and reorganize actin filaments. The purpose of reorganization can be to absorb, transduce, or transmit stresses, form protrusions in the cell membrane and cytoplasm, and regulate actin polymerization rate. Proteins that bind specifically to rearrange the organization of actin most often contain a conserved actin-binding domain (ABD) (2,3).

The function of an ABD is dictated by the mechanochemical properties of its rod domain. The actin-binding protein fimbrin is a monomer with multiple tandem repeats of the ABD (4). Fimbrin's almost nonexistent rod domain results in tight actin bundles (5). Parallel and less dense formations of actin are induced by α-actinin, an antiparallel homodimer containing only four rod domain repeats versus none in fimbrin (6,7).

Even more diverse are the filamins, containing a longer rod domain in addition to the ABD in each subunit of the antiparallel homodimer (8). The long rod domain, composed of immunoglobulin (Ig)-like fold tandem repeats, facilitates binding and stabilizing of actin into an orthogonal network of filaments (9). Orthogonal networks characterize lamellapodia formation in cells, large sheet-like protrusions found in epithelial cells, neuronal cells, and fibroblasts. Lamellapodia function in cellular migration across surfaces. In some forms of cancer, filamin is absent, which influences the ability of the cancer to migrate and metastasize, and thus the cancer is less invasive (10). In addition, filamin has been implicated in diseases of the brain, heart, and bone tissues (11–14).

There are multiple forms of filamins across species, mainly differing in the number of tandem repeats and the presence of hinge regions (15). Human filamins, in addition to the ABD, generally contain 24 tandem rod-domain repeats in each subunit of the dimer and three linking hinge regions contributing added flexibility (16). Structural biologists have only recently resolved the atomic coordinates of repeats 4, 5, and 6 of the rod domain of filamin from the slime mold Dictyostelium discoideum (8). Dictyostelium discoideum filamin (ddFLN) differs from human filamin in that it contains only six tandem repeats of ∼96 amino acids and lacks any hinge regions in the rod domain (8). Despite these differences, human filamin is remarkably similar to ddFLN, even with the organization at the dimer interface, suggesting similar mechanical properties (17).

Recent evidence reveals the diverse role filamins play in addition to cytoskeletal organization. There are over 20 proteins that are known to interact with vertebrate-type filamins, including chemoreceptors (18). Filamin can act as a director of the actin cytoskeleton, to embrace and localize receptors of the membrane, or as a scaffolding protein (19–21). In addition, filamin can influence down-regulation of receptors by translocation of receptors into the nucleus or influence membrane polarization by interacting with potassium rectifier channels (22,23). Filamins can also communicate with the extracellular matrix by binding to integrins (24).

The diversity of filamins means potential diversity in the composition of the repeats. Rod-domain tandem repeats are each evolutionarily specialized to a particular function. Within ddFLN, each tandem repeat is believed to contain coupled structural and biochemical properties that relate directly to function. The existence of an intermediate in the rod domain repeat has been proposed previously (25–28).

This study uses molecular dynamics (MD) simulations with bending moments (Fig. 1) and pulling forces (Fig. 2) to investigate a possible mechanism to explain how filamin-interacting protein (FIP) interacts with repeat 4. Similarly, the repeat containing the dimerization module (repeat 6, Fig. 2 A) should be mechanically unique and portray properties that support the lack of homology.

Figure 1.

The effect of bending the dimerized rod domain of filamin. To assess the universality of the pulling direction used in this study, the dimerized rod domain was bent by applying a bending moment to each N-terminal end. The resulting tension illustrates analogous conformational changes in each monomer and to the stretching simulations presented in the study. Removing the load and allowing the structure to relax result in the dimer returning to its original state before bending moment was applied, which is in agreement with the resolved crystal structure by Popowicz et al. (8).

Figure 2.

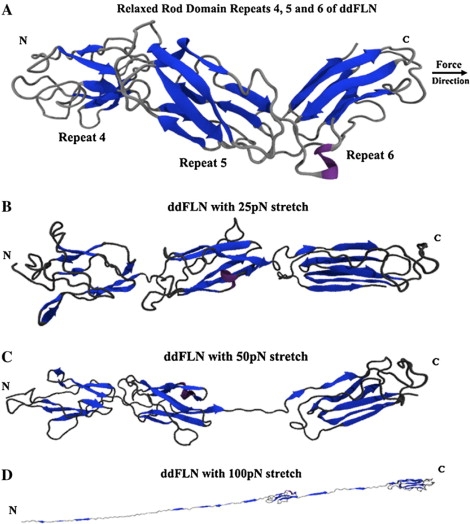
(A) The native conformation of Dictyostelium discoideum's rod domain repeats 4, 5, and 6. Force is applied to the C-terminal α-carbon away from the N-terminal α-carbon. This force approximates the physiological effect of stretching on the rod domain of filamin molecules. Note the staggered conformation and tertiary structure of the interrepeat region, which will be rapidly distorted and unfolded with force application. In addition, repeat 4 is in its closed state, concealing its core. (B) Within 30 ps at 25 pN of force, the staggered geometry is lost within the rod domain of ddFLN. Regions of the protein begin to become distorted: notice the strained geometry identified as a helical loop in repeat 5 and that the interrepeat of 5 and 6 begins to unfold. The repeats are aligned in line with the axis of the applied force. (C) After a minimum of 100 ps at 50 pN, the predicted weak linker region between repeats 5 and 6 unfolds completely. Unfolding this region can allow the rest of the rod domain to move more freely, whereas the dimer holds together tightly, and actin is still bound through ABDs. (D) Force >100 pN is required to unfold repeat 6. Repeat 5 still contains some detectable tertiary structure, but the majority of its β-strands have been pulled out of coordination. At 75 pN the linker region between repeats 4 and 5 is intact and unfolds only when the repeats themselves begin to lose large degrees of structure.

MD simulation is used to evaluate the potential role of filamin's rod domain in relation to stress transmission and mechanotransduction. MD is particularly powerful in simulating single-molecule experiments, and MD techniques have made consistent, accurate predictions of protein behavior (29,30). Computational (in silico) studies possess the ability to carry out single-molecule dynamics and predict the corresponding effects down to single atomic movements. Biophysical computation is ideal for identifying conformational changes in catalysis and enzyme-substrate binding dynamics. The user of MD can direct changes to the atomic coordinates that correspond to a physical event. For example, Mofrad et al. (31) simulated external forces applied to focal adhesion kinase and studied how the protein “deformation”, i.e., alteration of the molecular conformation, affected its binding partnership with paxillin, a potential mechanism for mechanotransduction at the focal adhesion proteins. In a more recent study, Lee et al. used MD simulations to discover a potential mechanism for force activation of talin's cryptic binding site with vinculin (32). Direct experimental measurements of such mechanotransducing events are not trivial, thus computations are of great importance.

MD studies ultimately aim to explain in vivo phenomena and thereby ensure that computational artifacts are held to a minimum, and MD results are often used to support existing experimental evidence or to direct experimental design. For example, structural integrity analysis of α-actinin's rod domain through MD has provided evidence to support experimental theories of its semiflexible nature (7). Other examples of MD application include the study of titin unfolding pathways (33), analysis of mechanical unfolding of fibronectin (34), and force-induced titin kinase activation (35). MD studies have provided insight on experimental data and allowed for clear and concise models of physiological phenomena.

Here, we use MD models to simulate the application of tensile forces to ddFLN rods and analyze the induced molecular conformational changes, examining filamin's structural attributes. The MD results are correlated with previous experimental data wherein structures of stretched repeats were not explicitly obtained (25–28). Simulations will shed light on how mechanical stresses may potentially alter the molecular conformations of the rod domain repeats. It is hypothesized that ddFLN rod domain repeats may serve as possible mechanosensors, communicating to protein partners, FIP, the stressed state of ddFLN. With MD techniques, the overall characteristics of the rod domain can be closely monitored. The tension forces applied to the ddFLN rod may induce reversible remodeling. One may speculate that this remodeling may function to absorb the applied stresses by unfolding at a given tension and dissipating stress during refolding. Stretched cells containing ddFLN homologs can therefore employ filamin analogously in absorbing stresses and mechanosignaling.

Methods

The atomic coordinates of repeats 4, 5, and 6 of a single subunit of ddFLN's rod domain were utilized. The all-atom coordinates were obtained through the Protein Data Bank (PDB), under PDB ID 1WLH. ddFLN's crystal structure was resolved by Popowicz et al. (8). The ddFLN monomer has 308 amino acids organized into three Ig-like folds.

MD simulations were performed using a commercially available software package CHARMm c32b1 (36,37), with CHARMm topology and parameter files top19.rtf and param19-1.2.prm used with the empirical potential energy function (37).

All of the simulations were performed with ddFLN in a continuum dielectric characteristic of the water model (38,39). Schaefer et al. (39) developed the analytical continuum electrostatics (ACE) potential implicit solvation model that accurately approximates both the electrostatic and nonelectrostatic contributions to the effective free energy. In this model, calculations of the electrostatic contribution to the free energy are carried out using analytical approximations to the solution of Poisson's equation (ACE model (39)). A pairwise potential then determines the approximate value for the nonpolar solvation free energy.

All MD simulations were carried out utilizing a 1-fs integration timestep, and the ACE parameters were set to 1.0 IEPS (dielectric constant utilized for the space occupied by the molecule), 80 SEPS (dielectric constant used to approximate solvent), ALPHA 1.3 (Gaussian density distribution that determines atom volume), and sigma 2.5 (hydrophobic contribution scaling value to ACE). A switching function with values between 12.0 Å and 13.0 Å was used to cut off nonbonding van der Waals and electrostatic interactions. The total number of atoms within the system was 2749.

The beginning of every MD run consisted of a base minimization in which defects in the crystal structure coordinates could be minimized (40). This run was carried out using the adopted basis-set Newton-Raphson method for 1000 steps with no atoms fixed, to minimum gradient root mean-square of 0.32. The crystal environment is substantially different from the physiological environment of the protein, and hence, certain torsions and inferior contacts can be introduced during the process of crystallization of the protein, and a minimization is needed to reduce ill-defined coordinates and locate a nearby local minimum in energy landscape.

Immediately after the base minimization, the system was heated linearly to 310 K in 1000 steps and then equilibrated for another 1000 steps to again determine a local minimum in the system.

Once physiological coordinates of ddFLN were approximated, the protein was again held in a 310 K environment with the α-carbon of the N-terminal end fixed. A pull force was applied to the α-carbon of terminal residue 308 in a direction corresponding to a vector from the N-terminus α-carbon to the C-terminus α-carbon described by the force arrow in Fig. 2 A. This pull direction results in a rod domain axial tension and corresponds to the physiological tension filamin experiences during actin filament stretching.

Electron microscopy data support the overall structure of filamin being V-shaped, and thus, initial extension will result in a bending moment on the molecule until the axis of the rod aligns parallel to the tension (41,42). To test whether the tensions applied in this study can describe filamin in the V-shape, a bending moment was applied to the original structure (see gray lines in Fig. 1). Interestingly, a bending moment of ∼60 pN·nm about the C-terminal α-carbon of each monomer is sufficient to bend the dimer into the configuration seen in Fig. 1. This situation is equivalent to fixing the C-terminal α-carbon and applying 5 pN of constant force to the N-terminal α-carbon of each monomer for 100 ps. Removing this bending moment results in a relaxation back to the original structure (gray lines in Fig. 1) nearly identical to the resolved crystal structure. The conformational state in gray lines in Fig. 1 and pictured in Fig. 2 A is therefore preferred in the absence of any bending moments. In addition, the resultant tension caused by bending induces conformational changes analogous to those presented in this study.

The tension forces used in this study are notably larger than the force required to induce bending; the V-shape will therefore be lost nearly instantaneously. Thus, these simulations explicitly apply to situations where V-shape is lost after tension. This study also assumes that given identical boundary conditions to each monomeric unit, each monomer behaves analogously with respect to the general conformational changes. To make the simulation more feasible computationally, only a single monomer is simulated.

Each tandem repeat in the filamin monomer must have tension applied initially to attachments at either end. This simulation takes advantage of this fact by applying the net force in the physiologically relevant direction along the rod domain axis.

Pulling forces were incrementally increased from 0 to 125 pN, all carried out over a total of 2,500,000 steps with a 1-fs integration step. This corresponds to a constant pull for 2.5 ns. The magnitude of force is chosen so as to produce a conformational change within attainable computational limits, and in some cases the velocity experienced or tensions applied to the ddFLN rod may be much larger than those a cell may experience. Much smaller forces can carry out entirely analogous conformational changes, but the tensions applied must hold for a longer duration. Even on the time scale of tens of nanoseconds, which is exceedingly demanding computationally, smaller and more physiologically common velocities can carry out the molecular changes presented here (32). Tertiary and secondary structure content were determined after every MD simulation utilizing the analytical options packaged with visual molecular dynamics software (43).

A constant force extension was chosen over constant velocity extension to allow for isolation of intermediates for longer periods of time. Intermediates isolated through constant-force simulations can be equilibrated under the applied load for long periods of time. This ensures that the intermediate is stable and is not transient in the unfolding pathway. Constant-velocity extension was also avoided to ensure that forces being applied were not abnormally large but were close to being physiologically relevant. A complete unfolding of ddFLN's rod domain was also not necessary, thus negating the need for constant-velocity simulations.

To visualize extension of ddFLN, end-to-end distance from the α-carbon of the amino terminus to the α-carbon carboxy terminus is calculated at every 100-fs interval. The distance between these two points is plotted versus time (see Fig. 5). In addition, solvent-accessible surface area was calculated through CHARMm utilizing the Lee and Richards surface (44).

Figure 5.

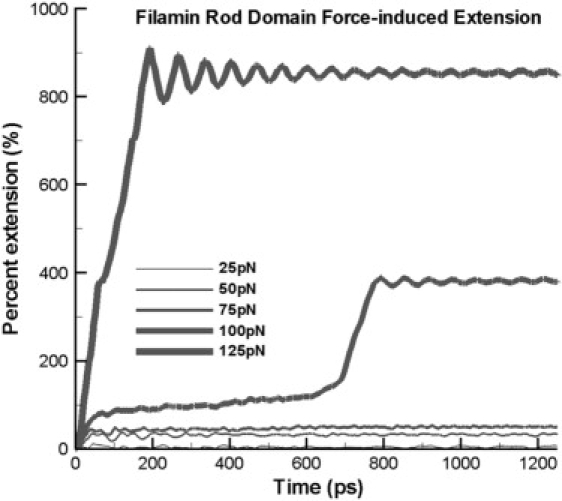
The percentage extension of the whole rod domain is calculated versus time during the application of a constant force. The presence of stable intermediates corresponds to areas where slope approaches zero. These structures correspond to those seen in Figs. 2 and 3.

In general the simulations here can apply only to situations in which ddFLN is stretched. Compression of filamin is plausible when a cell is forcibly stressed, but our models are limited to stretching forces.

Results

In general, pulling on the rod domain of filamin has unique effects at each tandem repeat or Ig-like domain. Results are organized by reviewing the effect of force on each repeat separately and, finally, the rod domain as a whole (see Fig. 5). The effect of force is to unwind and unfold force-dampening and stress-absorbing linker regions and to alter the conformations of the tandem repeats. In one case, repeat 5, force distorts tertiary structure sufficiently to destabilize the fold, and a stable intermediate is not observed. In the other two cases, tandem repeats 4 and 6 find stable intermediate conformations with different stiffness properties. All of these properties tie into their physiological roles in the actin-binding protein filamin, as discussed below.

Repeat 4

Repeat 4 contrasts appreciably from the other tested rod domain repeats in that it contains the shortest average β-strand length of 9 Å and the fewest number of β-strands, i.e., five. In comparison with repeats 5 and 6 the organization within repeat 4 is less compact. Repeat 4 is largely characterized by loops, and the β-strands contain varying degrees of axis wrap and intrastrand twist (Fig. 2 A). Each β-strand is a part of a twisted β-sheet that wraps loosely around the domain axis and is biased toward the C-terminal region toward repeat 5.

The rearward portion of repeat 4 contains side chains that are typically 3 Å distant from side chains extended from repeat 5. Analogously, these distances are a minimum 4 Å from repeats 5 and 6. A single Angstrom may not appear to be large, but this corresponds to a one-third increase in distance, and if the Lennard-Jones potential is considered, attraction is directly proportional to the radius to the sixth order, and a single Angstrom can attenuate attractive forces by over fivefold. This region is bridged by inflexible amino acids Pro⁶⁴⁷-Ala⁶⁴⁸-Pro⁵⁴⁹, and this follows that the linking region between repeats 4 and 5 is predicted to be inflexible (8,45).

When 25 pN is applied, the staggered orientation of the repeats is lost within 30 ps, and side chains extending into this region from repeat 5 physically pull on side chains within repeat 4. This new conformation results in two peripheral loop regions of repeat 4 to be pulled rearward toward its C-terminus and nearer repeat 5.

Residues in these two loops toward the N-terminus that originally anchored the loops to repeat 4 are pulled away. The increase in distance affords the activation barrier required for these side chains to induce a large conformational change within these two loops. The conformational change involves the peeling back of these loops onto themselves, resulting in a stabilizing of intraloop interactions (Fig. 3). Amino acids that facilitate this conformational change contain long flexible side chains with ionic or hydrogen bond character. These features allow multiple stable orientations of these side chains so long as ionic or polar partners are satisfied.These two loops are found at opposite sides of repeat 4 (Fig. 4). These two peripheral loops both contain key aspartate residues within the loop that direct the conformational change. During application of 50-pN force for 300 ps, the distance among donor partners and Asp⁶⁰⁷, Asp⁶¹⁰, and Asp⁶¹⁴ in one of these loops increases enough for the side chains to project into the solvent. At this point, the side chains are now free to find new partners, which they find within their own loop's amide backbone. This results in curling back of the loop (Fig. 3).

Figure 3.

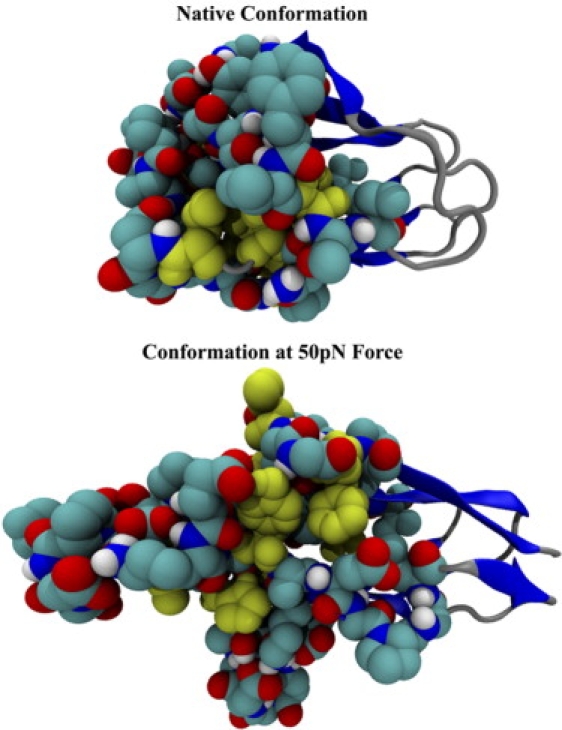
Force along the rod domain to the right induces a conformational change in repeat 4 within 300 ps at 50 pN of force. The conformational change involves peripherally located Asp-containing loops that rotate to hydrogen bond with their own intrastrand amide nitrogens. This causes the loops to curl back onto themselves and expose two large gaps in the hydrophobic core, colored in yellow.

Figure 4.

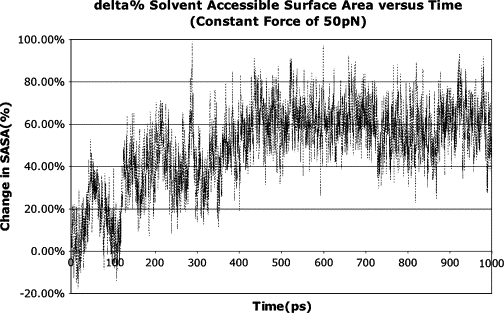
The change in the solvent-accessible surface area (SASA) is calculated for 10 hydrophobic core amino acids, Tyr⁵⁵⁵, Ile⁵⁷⁴, His⁵⁷⁵, Ala⁵⁷⁶, Val⁵⁷⁷,Phe⁵⁹¹, Val⁵⁹³, Leu⁶³¹, Val⁶³⁶, and Phe⁶³⁹, and plotted versus time. Within 450 ps, the SASA increases by 60%. Therefore, these amino acids are significantly exposed on force activation of repeat 4 of the rod domain.

On the opposite side of the molecule an entirely analogous mechanism occurs, where within 350 ps at 50 pN, Asp⁶³² and Asp⁶³⁴ are physically separated from their native partners and projected into the solvent. Their new partners are found after the loop is strained backward by interrepeat attraction rearward. This results in the interaction of each Asp⁶³² and Asp⁶³⁴ to hydrogen bond with backbone amide nitrogens (Fig. 3).

Movement of both loops alters the structure of the molecule significantly, but it remains stable until 100 pN of force has been applied (Fig. 2). This intermediate is reached quickly and remains stable between 25 and 75 pN for the total duration of each 2.5-ns simulation. The two loops pulled back expose hydrophobic areas of the core (Fig. 3). Core hydrophobic amino acids Tyr⁵⁵⁵, Ile⁵⁷⁴, His⁵⁷⁵, Ala⁵⁷⁶, Val⁵⁷⁷, Phe⁵⁹¹, Val⁵⁹³, Leu⁶³¹, Val⁶³⁶, and Phe⁶³⁹ all increase their solvent-accessible surface area by 60% within 450 ps at 50 pN of force (Fig. 4). Multiple simulations, including those with an explicit water model, all exhibit the existence of this stable intermediate with an exposed core.

The existence of a stable intermediate for repeat 4 has been postulated to exist on the basis of in vitro atomic force microscopy studies (25–28). Physiologically, it may also serve to bear stress. The existence of an intermediate breaks up the energy requirements into smaller discrete steps in the unfolding to absorb varying amounts of stress.

The evidence from these in silico experiments and previous in vitro observations supports the idea that intermediate structures observed may be relevant. In addition, comparable tensile loads on a ddFLN rod in vivo can lead to this conformational change in repeat 4 and may therefore be functional in a mechanotransduction pathway. The force-induced conformational changes may biochemically communicate the stretched state within the cell.

Repeat 5

Each repeat is classified by an Ig-like motif. The organizations within repeat 5 can be characterized generally as intermediately compact compared with repeats 4 and 6. Repeat 5 contains seven antiparallel β-sheets of an average approximate length of 14 ± 5 Å. Each β-strand within repeat 5 follows around the axis with an approximate 20° wrap. This forms a twisted antiparallel barrel-like structure biased toward an end closest to repeat 4 (Fig. 2 A).

There exists a sharper kink between rod domain repeats 5 and 6 at ∼105° versus 130° between 4 and 5. This correlates with the extensive contact surface between repeats 4 and 5 versus less contact between 5 and 6. The interactions between repeats 4 and 5 account for a less staggered geometry between these two repeats.

As force is applied, repeat 5 loses tertiary structure initially by losing its natural wrap and increasing the overall distance between antiparallel β-strands. This effect is most pronounced at larger forces approaching 75  pN (Fig. 2). Further unfolding of the barrel formed does not occur until much larger forces are applied and β-strands from both the N- and C-termini are removed. These gaps in the barrel further destabilize the overall structure of the β-strands, and after 2.5 ns of 100 pN, there no longer exists significant atomic β-strand geometry within repeat 5 (Fig. 2 D).

In the unfolding of repeat 5, no significantly stable intermediate exists. Unfolding follows with slight destabilization of the β-strand geometries, and there is immediate and complete unfolding when the threshold force is reached, at ∼100 pN. Complete unfolding of repeat 5 occurs at ∼3 ns when 100 pN or larger forces approaching 125 pN are applied. These larger forces can unfold not only repeat 5 but the entire molecule within 500 ps. At forces as large as 125 pN, the molecule does not unfold sequentially from most flexible to least flexible but instead unfolds from the site of force application to the opposite end. This can be a consequence of rapid unfolding pathways, where tension is so large equilibration is not achieved across the entire molecule.

Repeat 6

A highly ordered and compact structure characterizes repeat 6. The average length of the six antiparallel β-strands is 19 Å, and there exist little detectable twist and wraps of the strands. Instead, the β-strands in repeat 6 form two symmetrical β-sheets, each consisting of three β-strands facing one another (Fig. 2 A). The large surface area exposed to the solvent by just one of these sheets serves as the dimerization module for the physiologically active rod domain of ddFLN.

Of all the rod domain repeats tested, repeat 6 is the most resilient. Repeat 6 is the only domain remaining folded after multiple simulated 100-pN pulls for 2.5 ns. Only when forces as large as 125 pN are applied does repeat 6 unfold. Sufficient tertiary structure remains, conceivably, to keep the rod domain dimer intact when large forces are applied that unfold rod domain repeats 4 and 5. This can have potential physiological significance because repeats can unfold to absorb force and refold when force is absent (25–28).

Molecular stiffness of the rod domain increases with increasing average length of the β-strands and decreasing β-strand twist. Two tight, ordered β-sheets exist in this domain, forming stable intramolecular interactions.

Although repeat 6 appears conformationally stiff, remaining folded during the application of large forces, the linker region between repeats 5 and 6 is the weakest region as a whole. The weaker interactions serve as a basis for less structural integrity, but physiologically this may also play a role. As force is applied, this region unfolds rapidly under pulling forces between 50 and 75 pN (Fig. 2 C), extending 17 Å and exhibiting a rotational and angular flexibility relative to the rest of the rod domain (Fig. 3). Under force, the rod domain can actively become flexible, allowing for ddFLN to remain bound to the actin cytoskeleton, holding the cortical network together while absorbing exterior forces.

Interrepeat regions

When force is applied to repeats 4, 5, and 6 of the rod domain, the repeats lose their staggered topology within 30 ps at 25 pN (Fig. 2 B). This nearly instantaneous event can contribute 10% extension in the entire molecule (Fig. 5). Over the entire dimerized rod domain of ddFLN in Dictyostelium discoidium, this effect alone can contribute ∼40 Å in extension when force is immediately applied. If this is scaled up to a human ddFLN, the rod domain repeats losing staggered orientation can contribute ∼160 Å in extension from a single dimerized ddFLN molecule. This is independent of any potential unfolding within a repeat as a result of force application.

As the pulling force is increased, the interrepeat regions begin to unfold and lose tertiary structure. This unfolding can contribute further extension to the entire rod domain. Unfolding of the interrepeat region between repeats 5 and 6 occurs consistently within 100 ps of 50 pN of force (Fig. 2 C). A larger force of 75 pN does unfold this interrepeat region, but, surprisingly, not significantly faster than 50 pN, suggesting the presence of an activation barrier. Forces of 50–75 pN for 2.5 ns are insufficient to unfold any region of the molecule further.

A small α-helical loop exists between rod domain repeats 5 and 6, colored purple in Fig. 2 A. This small loop has a 50-pN threshold of unfolding completely and contributes additional extension in the direction of stretch, up to 14.0 Å. The helical loop epitomizes how regions of the rod domain specialize to absorb and dissipate stress at different thresholds.

The repeat region between 5 and 6 unfolds quickly and completely when 50–75 pN of force is applied. On the other hand, this area never unfolds at 25 pN for 2.5 ns. Because the unfolding is graded and contains multiple energy barriers, there is no single spring constant that can describe the rod domain's structural stiffness.

Interrepeat organization between repeats 4 and 5 changes by aligning the domains in the axis of force applied (Fig. 2 B). The region between repeats 4 and 5 is more resilient against deformation and can resist unfolding even when 75 pN of force is applied for 2.5 ns. Larger forces of 100 pN unfold the region between repeats 4 and 5 but also unfold the actual repeats themselves after 600 ps (Fig. 2 D). The interrepeat region between repeats 4 and 5 may influence the overall integrity of the repeats themselves.

Discussion

The dynamics of ddFLN's rod domain illustrates coupling between the mechanical and chemical properties governing activity within the cell. The staggered tandem repeat organization can potentially serve to facilitate both conformational changes within the repeat domains and serve as a means of bearing smaller forces within the cytoskeleton. The exact composition and interactions of the interrepeat regions serve as points of modularity where function or stress-bearing properties can be specialized to a particular role.

The interrepeat region between repeats 5 and 6 is flimsy and fully unfolds quickly with 50 pN. This can be a region specialized to absorb cellular stresses and keep the cortical network intact when stress is applied to the cell. The existence of multiple domains like this can increase the stress-bearing role of ddFLN in Dictyostelium discoidium.

On the other hand, the region between repeats 4 and 5 is stiff and actually influences the conformational flexibility of repeat 4. The stability of this repeat region correlates with the stability of repeats 4 and 5 themselves. Whether or not this region is actually responsible for their stability is unknown, but the existence of multiple salt bridges contributes free energy of stabilization to rod domains.

The free energy contribution to the salt bridge interactions between the rod domain repeats can serve as an energy sink when force is applied, pulling the molecule out of its staggered orientation. The staggered orientation not only compacts ddFLN into a tighter structure but also provides an initial role in the stress-absorbing mechanism. Extension in the rod domain afforded solely by loss of staggering can contribute a large percentage of the apparent flexibility of orthogonally linked actin-cytoskeletal networks. In addition, it serves as a means for removing strain at the ABD of ddFLN and the dimerization module.

One can speculate further based on the requirement of a bending moment to keep the molecule in the V-shape state (Fig. 1). The axial tension resulting from the bending of the rod domain can serve to unfold the linking regions of these repeats, imparting increased flexibility. The bending moment for in vivo filamins can either be brought on by having a long rod domain or induced by an actin-binding event. The actin binding may contort the rod domain into adopting tension and bending moment. The axial tension can increase flexibility, whereas the bending moment is responsible for keeping the molecule in the bent state. This can be a force-activated flexibility of filamins and can serve to explain why the crystal structure illustrates a stiffer molecule than predicted. The crystallography data do not support the flexibility imparted by a “beads-on-a-string behavior” hypothesis of filamins; however, in vivo filamin appears flexible (8,46). One can consolidate these two hypotheses by proposing that, under tension, filamins become flexible.

Another degree to which ddFLNs can functionally specialize is within the repeats themselves. Repeats can also be specialized to be load bearing, to serve as binding scaffolds, or to transduce mechanical signals. Repeat 6 is a highly ordered structure that serves the role of holding the entire rod domain dimer together. Stability of a homodimer is, in general, dependent on the surface area from which each subunit electrostatically interacts. It is logical, therefore, that maximizing contact area between the subunits involves the formation of a flat and ordered β-sheet to the periphery.

In addition, the stability of repeat 6 can serve to preserve electrostatic interactions of the dimer even when forces as large as 100 pN are applied to the rod domain. If repeat 6 of one subunit of the rod domain can withstand at least 100 pN, it is not then unfeasible if the dimer can withstand at least twice as much force in vitro before unfolding sufficiently for dissociation (25–28). Repeat 6 is the stiffest repeat, followed by repeat 5, which is intermediate in stiffness and affords no apparent conformational variability. The direct role of repeat 5 is not altogether apparent. Its relation to other repeats in ddFLN, namely 1, 2, and 3, should be assessed. Repeats 4 and 6 may be exceptions within the rod domain in that repeat 4 may serve as a point of variance through allowing conformational flexibility within a repeat, and repeat 6 may act as a cradle of dimerization. Indeed, repeat 6 contains no sequence homology to the other repeats of the rod domain. Repeat 5 may simply be load bearing and contribute no additional unique function.

Repeat 4's intermediate significantly increases the hydrophobic core's surface area to the solvent. The increase in solvent-accessible surface area is ∼60% after 450 ps at 50 pN. The large increase in effective hydrophobicity of the repeat can potentially drive association to other partners. Existence of this cryptic binding site is supported by variability in binding partners. ddFLN is a versatile partner for binding within the rod domain (17). A hydrophobic cryptic binding site can drive nonspecific association. This can account for the variability in binding partners to a single repeat (17).

Proteins that have been found to interact with repeat 4, FIP for example, have been shown to be involved in signal transduction events regulating cell tissue density (47). The data presented here support the concept that a cellular response to stress, for example migration, involves load being applied from the plasma membrane through the cytoskeleton and translation of that stress through filamin. Stretched filamin will then undergo conformational changes in repeat 4 to bind FIP, beginning the signal cascade to alter tactic behavior.

Human filamins contain repeats that are not confined to binding to cytoskeletal elements but can bind to chemoreceptors, for example (8). The stressed state of a cell can feasibly be communicated through similar unfolded intermediate pathways, signaling cell growth or arrest (48,49). These theories can directly support a mechanochemical basis for carcinogenesis or other onset of diseases such as HIV, where filamin has been implicated (48,49).

Future studies will include the simulations of more tandem repeats and, if possible, human filamins with their respective hinge domains, when structures are available. Studies should also aim to identify the molecular effects of ddFLN when exposed to compression forces. Simulations including the ABD of ddFLN in addition to its rod domain will reveal specifically what sort of stresses the network can withstand. The molecular effects attributable to organizing an orthogonal network still remain a mystery. ddFLN's ability to regulate more than just structural aspects of the cell is a marvelously intriguing process that may well reveal the mechanical relation to disease.