Equilibrium Dynamics of Spermine-Induced Plasmid DNA Condensation Revealed by Fluorescence Lifetime Correlation Spectroscopy

Abstract

The spermine-induced DNA condensation is a first-order phase transition. Here, we apply a novel technique fluorescence lifetime correlation spectroscopy to analyze this transition in a greater detail. We show that the method allows for the observation of the condensed and uncondensed molecules simultaneously based solely on different fluorescence lifetimes of the intercalating fluorophore PicoGreen in the folded und unfolded domains of DNA. The auto- and cross-correlation functions reveal that a small fraction of the DNA molecules is involved in the dynamic intramolecular equilibrium. Careful inspection of the cross-correlation curves suggests that folding occurs gradually within milliseconds.

One of the key steps of cell transfection is the condensation of DNA that enables the DNA to be transported into the target cells. The condensation of the large and negatively charged DNA is commonly achieved by molecules carrying several positive charges, such as spermine. During the spermine-induced condensation, a decrease of the hydrodynamic radius was observed followed by the formation of assemblies of several condensed DNA molecules (1). It was also shown that the condensation is a first-order phase transition, i.e., that the condensed and uncondensed molecules coexist in solution (2) until there is enough spermine so that all molecules collapse.

To explore the point of coexistence, we employ a novel technique—fluorescence lifetime correlation spectroscopy (FLCS) (3,4) that gives detailed insight into the condensation mechanism and the timescale of the process. FLCS is based on fluorescence correlation spectroscopy (FCS) (5), which analyzes fluorescence fluctuations arising from changing numbers of fluorescently labeled particles in ∼1 fL detection volume of a laser-excitation confocal microscope. FCS provides information on concentration and mean residence time of particles in the focus and, consequently, on their diffusion coefficient. FLCS additionally distinguishes between fluorophores with different lifetimes and similarly to dual-color FCS (6), enables one to calculate cross-correlation functions between two particles of different fluorescent lifetimes and thus reveals interactions between them.

Materials and methods

The 10-kbp pH βApr-1-Neo plasmid, PicoGreen (PG) and spermine were prepared and used as described elsewhere (1). We used the labeling ratio 1 PG/100 basepairs. Experiments were performed in a TE buffer (pH 7.95, 10 mM Tris, 1 mM EDTA) at 25°C.

FLCS measurements were performed on a MicroTime 200 inverted confocal microscope (PicoQuant, Berlin, Germany). We used a pulsed diode laser (LDH-P-C-470, 470 nm, PicoQuant) with 40-MHz repetition rate, dichroic mirror 490 DRLP and band-pass filter 515/50 (Chroma, Rockingham, VT), and a water immersion objective (1.2 NA, 60×) (Olympus, Tokyo, Japan). Low power of 4 μW was chosen to minimize photobleaching and saturation. The detector afterpulsing effects were prevented by correlating only photons from different single photon avalanche diodes (PDMs, Microphoton Devises, Bolzano, Italy) that were used simultaneously. Photon arrival times were stored in time-tagged time-resolved recording mode. All the data were acquired for 2 h to achieve good photon statistics.

Results and discussion

Free DNA

Since the size of DNA exceeds three times the diameter of the laser focus, the autocorrelation curve (ACF) for multiply labeled DNA molecules is difficult to model. The segmental motion and the Brownian motion of the whole molecule are superimposed (7), which typically causes additional fluctuations lowering the amplitude of ACFs and increases the apparent number of particles in the focus. For the sake of simplicity, the ACF of free DNA was fitted to a model taking into account one freely diffusing species in the detection volume:

$$G(\tau )=1+\frac{1}{PN(1-T)}\left(1-T\left(1-{\text{e}}^{\frac{\tau }{{\tau }_0}}\right)\right)\times \left(\frac{1}{1+(\tau /{\tau }_{\text{res}})}\cdot \frac{1}{{(1+(\tau /{\tau }_{\text{res}})({\omega }_0/{\omega }_{\text{Z}}{)}^2)}^{\frac{1}{2}}}\right)\text{.}$$ (1)

Being aware of the complexity of DNA movement, we assign the residence time τ_res to the lateral movement of the whole molecule. The triplet-like term containing the “triplet” parameters T and τ₀ describe here the effect of the segmental motion of the chain specific for our DNA. PN is an apparent number of particles in the detection volume. ω₀ and ω_Z are half-axes of the detection volume. Although Eq. 1 has a semiempirical character, it is sufficient for our purposes.

Point of coexistence—middle point

During the FCS experiment with increasing spermine/basepair ratio, apart from the step-like drop in τ_res and PN (the drop in PN is caused by formation of rigid point-like molecules much smaller that the size of the focal volume (8)), lifetime of PG undergoes shortening from 4.2 to 3.3 ns. Since the change appears simultaneously with the change in other parameters, it can be assigned to the formation of folded domains on the DNA chain with different microenvironment of PG. We regard the spermine/basepair ratio (close to 2), when the lifetime of PG equals 3.9 ns, to be the “middle point” of the condensation, where molecules of PG coexist in the unfolded and folded domains of DNA. This will be the subject of the further examination.

Using normalized decays of the 4-ns (4.2 ns) and 3-ns living fluorophores (3.3 ns), i.e., PG in the unfolded and folded DNA that can be measured separately (spermine/basepair ratio 0 and 6, respectively), the decay pattern of the compound signal at the middle point and uniform noise pattern, the filters (mathematical analogs of optical filters used in dual-color FCS) can be calculated as described in Gregor and Enderlein (3). Application of the filters to the measured fluorescence signal provides ACFs of the 4- and 3-ns lifetime fluorophores and two CCFs. The ACFs describe the behavior of the fluorophores in the unfolded or folded microenvironment, whereas the CCFs contain information on the interaction between them.

ACFs

The ACFs of the middle point correspond well to the ACFs of the free and condensed DNA measured independently (Fig. 1). There is a slight difference in the millisecond range in the case of free DNA, which is probably caused by the contribution of the intramolecular dynamics, which will be commented on later. The residence times and amplitudes of both the ACFs are well separated (Fig. 1, inset). The amplitude of the 4-ns ACF, corresponding to the free DNA molecules is an order of magnitude smaller than the amplitude of the 3-ns ACF corresponding to the condensed point-like particles. This confirms that, at the middle point, most of the molecules are either in a totally collapsed or noncollapsed state. Furthermore, it proves that FLCS can separate the signal from a single dye in two different microenvironments.

Figure 1.

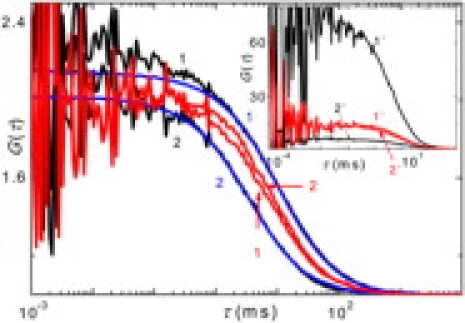
ACFs and CCFs obtained from filtering of the intensity trace at the middle point. Particle number-corrected ACFs of the 4-ns, 3-ns component (black curves 1, 2), amplitude-corrected CCFs, 3 × 4 ns, 4 × 3 ns (red curves 1, 2); particle number-corrected ACFs of the free and condensed DNA measured separately (blue curves 1, 2). (Inset) ACFs and CCFs (not corrected) obtained from filtering of the intensity trace at the middle point. ACFs of the 4-ns, 3-ns component (black curves 1′, 2′), and CCFs, 3 × 4 ns, 4 × 3 ns (red curves 1′, 2′).

CCFs

The nonone CCFs suggest that apart from the mere coexistence of folded and unfolded DNA, either the “static” coexistence of folded and unfolded states in one molecule (or molecule aggregates), or the presence of dynamic transitions between them can be expected. Since the system is rather complex, we focus on a qualitative explanation of the condensation on the molecular level.

The amplitudes of normalized CCFs are between the amplitudes of the ACFs, which can not arise only from the “static” coexistence of the states (6).

The consideration of the amplitudes and the presence of a slight maximum in the CCFs suggest a dynamic interchange between 4- and 3-ns living PG, i.e., an equilibrium dynamics between folded and unfolded DNA molecules or domains on the DNA chain.

Model for fast dynamics

The dynamics can be described by the following chemical reactions (4):

$$\begin{array}{l}\text{Unfolded DNA}\stackrel{{\text{k}}_1}{⟶}\text{Folded DNA}\\ \text{Folded DNA}\stackrel{{\text{k}}_2}{⟶}\text{Unfolded DNA.}\end{array}$$

Assuming that both occur on a timescale shorter than the diffusion, the expressions for normalized ACFs and CCFs can be derived (3) (triplet transition was neglected):

$$G_{\alpha \beta }(\tau )=1+\frac{1}{PN}(1+g_{\alpha \beta }{\text{e}}^{-\lambda \tau })D_{\text{Diff}},$$ (2)

where α and β denote either unfolded or folded DNA and g_αβ = −1 for α ≠ β, g_{unfolded,unfolded} = k₁/k₂, g_{folded,folded} = k₂/k₁, λ = k₁ + k₂. The term D_Diff stands for the long-time diffusion-dominated part of the correlation curves, i.e.,

$$D_{\text{Diff}}=\frac{1}{1+(\tau /{\tau }_{\text{average}})}\times {\left(\frac{1}{1+(\tau /{\tau }_{\text{average}})({\omega }_0/{\omega }_{\text{Z}}{)}^2}\right)}^{1/2},$$ (3)

where τ_average is the average residence time of the molecules in the detection volume. It should be noticed that for the given assumption, D_Diff is supposed to be the same for all four CFs. If the transition was fast enough, the molecule would change its diffusion properties many times during its stay in the focus, thus τ_average would depend on the diffusion coefficients of both the folded and unfolded states weighted by the time spent in each particular state. Our measured ACFs differ markedly in diffusion properties revealing free and condensed DNA molecules in coexistence. This suggests that the dynamics occur on the timescale of diffusion and/or the transition is undergone only by a relatively small fraction of molecules.

Residence times depicted in Fig. 1 follow the inequality: ${\tau }_{\text{res}}(3\text{ns}\text{ACF})\le {\tau }_{\text{res}}(\text{CCF})\le {\tau }_{\text{res}}(4\text{ns}\text{ACF})\text{.}$ It suggests that the system consists of folded and unfolded DNA molecules and of molecules dynamically undergoing the phase transition, which may occur either in one step or gradually in domains.

In both the cases, both the ACFs will consist of two contributions: the diffusion of free or condensed DNA and the dynamics of the phase transition-undergoing DNA. Fitting of the ACFs is rather complicated especially if the latter contribution is expected to be low. In the case of 4-ns ACF, we can see a slight decrease on a millisecond timescale (Fig.1), in the case of 3-ns ACF, the dynamics and the diffusion are probably intermixed as will be proved later. Thus, we did not perform further fitting of the ACFs and rather concentrate on CCFs where only events related to the lifetime changes contribute.

The CCFs clearly differ in shape in the range of milliseconds. This asymmetry may indicate that the mechanism of folding and unfolding differs in that particular time range. It confirms that the timescale of the dynamics and the timescale of the diffusion are not separated and the dynamics occur on the millisecond timescale.

Model corrected for multiple labeling

Although the timescales of the transition dynamics and diffusion are not separated, we attempted to compare the observed CCFs with the simple model. The theoretical increase of CCFs at short lag-times, where the diffusion does not interplay with the dynamics, would be close to the observed CCFs only if λ was in the range of 10³ ms⁻¹ (Fig. 2). The microsecond dynamics, however, contradict the previous conclusions.

Figure 2.

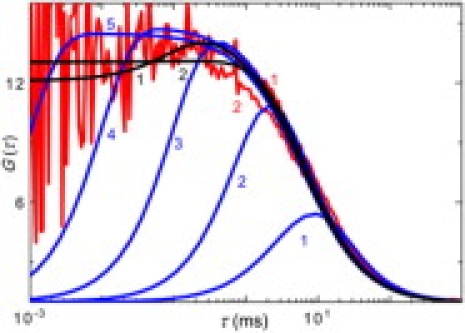
Experimental CCFs, 3 × 4 ns, 4 × 3 ns (red curves 1, 2); theoretical CCFs obtained from the model without multiple labeling are: τ_res = 6 ms, λ = 0.1, 1, 10, 100, 1000 ms⁻¹ (blue curves 1–5); CCFs obtained from the model including multiple labeling are: τ_res = 6 ms, N_F = 5.5, λ = 1, 10 ms⁻¹ (black curves 1, 2).

Thus, CCFs at the short lag-times are affected by another factor. The most probable one is the fact that the DNA molecules are multiply labeled. Provided that DNA collapses gradually in separated domains, individual fluorophores on the same DNA molecule behave differently. This phenomenon, so-called intrachain segregation, was reported by Yoshikawa et al. in a series of publications (9). We derived theoretical CCFs for the case of diffusion (much slower than the dynamics) of point-like molecules labeled by N_F fluorophores independently undergoing the transition between the 4-ns and 3-ns state with given rate constants (4):

$$G_{\alpha \beta }(\tau )=1+\frac{1}{PN}\left(1-\frac{1}{N_{\text{F}}}{\text{e}}^{-\lambda \tau }\right)D_{\text{Diff}}\text{.}$$ (4)

That model is in a good agreement with the observation at short lag-times of CCFs even for the concluded millisecond dynamics. For both the theoretical CCFs depicted in Fig. 2, we obtained the values of N_F around 5.5. Considering the labeling ratio, we can estimate that the average domain contains 1800 basepairs.

To sum up, the careful inspection of the CCFs, suggests that a small fraction of the DNA molecules undergoes the equilibrium intramolecular transitions between the condensed and uncondensed form, which occurs gradually in separated domains on a millisecond timescale.

Supplementary material

To view all of the supplemental files associated with this article, visit www.biophysj.org.