Diffusion of Glycerol through Escherichia coli Aquaglyceroporin GlpF

Abstract

The glycerol uptake facilitator, GlpF, a major intrinsic protein found in Escherichia coli, selectively conducts water and glycerol across the inner membrane. The free energy landscape characterizing the assisted transport of glycerol by this homotetrameric aquaglyceroporin has been explored by means of equilibrium molecular dynamics over a timescale spanning 0.12 μs. To overcome the free energy barriers of the conduction pathway, an adaptive biasing force is applied to the glycerol molecule confined in each of the four channels. The results illuminate the critical role played by intramolecular relaxation on the diffusion properties of the permeant. These free energy calculations reveal that glycerol tumbles and isomerizes on a timescale comparable to that spanned by its adaptive-biasing-force-assisted conduction in GlpF. As a result, reorientation and conformational equilibrium of glycerol in GlpF constitute a bottleneck in the molecular simulations of the permeation event. A profile characterizing the position-dependent diffusion of the permeant has been determined, allowing reaction rate theory to be applied for investigating conduction kinetics based on the measured free energy landscape.

Introduction

In the course of their evolution, living organisms have learned to adapt to inhospitable environments by perfecting their cell membrane to become impervious to toxic compounds, while allowing useful, innocuous chemical species to translocate selectively. The physiological processes that regulate the inward transport of water and nutrients across the cell barrier and the outward release of waste material are accomplished by highly specific membrane proteins; among them is the family of major intrinsic proteins. The glycerol uptake facilitator (1–3) (GlpF) constitutes a noteworthy member of this family, found among others in Escherichia coli. This aquaporin (4), ubiquitous in living organisms, is responsible for passive transport of water and small hydrophilic species, such as linear polyalcohols.

GlpF possesses a homotetrameric structure, each monomer forming an independently functional, 28 Å-long pore. Particularly important elements constituting the core of this protein are two half-membrane spanning repeats related by an essentially twofold symmetry (3). Approximately half of each repeat is α-helical, the remainder of the scaffold being clearly nonhelical. The narrowest section of the pore, known as the selectivity filter (SF), is located roughly 8 Å from the central plane of the lipid bilayer. The N-termini of the α-helical repeats convene roughly at the center of the channel, where the so-called Asn-Pro-Ala (NPA) motifs are located—motifs particularly well conserved among all aquaporins (5). With the high-resolution structures of GlpF at 2.2 Å (6–8), new light was shed on the sophisticated mechanisms developed by the cell machinery to survive in hostile, nutrient-poor surroundings. In Escherichia coli, for instance, glycerol is conveyed in a nonselective fashion across the outer membrane by porins, and then selectively across the inner membrane by aquaglyceroporins, like GlpF. Phosphorylation by glycerol kinase in the cytoplasm traps glycerol in the cell and initiates its consumption, hence, precluding diffusion back through the inner bacterial membrane. Among the remarkable structural features of GlpF, a periplasmic vestibule has been postulated to be conducive to efficient glycerol uptake (9), which promotes rapid bacterial growth in low-concentration glycerol solutions. The 2.2 Å crystallographic structure of GlpF offers an opportunity for elucidating the function of homologous transporters by means of site-directed mutagenesis experiments (10). An improved understanding of the underlying mechanisms that govern water and glycerol conduction in aquaporins is desirable both on a fundamental and an applicative level, because these major intrinsic proteins are implicated in critical inherited diseases. A mutation of aquaporin Aqp0, for example, has been linked to congenital cataract (11), although no molecular mechanism has yet been proposed.

Considerable effort has been invested in recent years to decipher the function of aquaporins by means of molecular dynamics (MD) simulations (8,12–15), in particular the conduction events of glycerol through GlpF (9,16). Due to the long timescales covered by the slow diffusion of glycerol in GlpF (17), currently not amenable to all-atom MD, investigation of the rare conduction events has been tackled using steered MD (18) (SMD), whereby permeation is accelerated through the application of an external force. Following an appropriate pulling regime, the equilibrium free energy profile across the conduction pathway may be recovered from an ensemble of independent irreversible transformations, employing the Jarzynski identity (19). Cognizant of the inherent limitations of nonequilibrium simulations to provide a realistic picture of the conformational and orientational relaxation phenomena in transmembrane channels, conduction of glycerol in GlpF was investigated at thermodynamic equilibrium, using an adaptive biasing force (20,21) (ABF) scheme to overcome the barriers and escape from the minima of the free energy landscape. The simulations reveal that the timescales spanned by the ABF-assisted transport of glycerol and its reorientation and isomerization in GlpF are comparable. The free energy profile averaged over the four different channels is smooth and features a single barrier, the height of which is consistent with experimental observables (17). Based on the free energy profile and the position-dependent diffusion coefficient, diffusional kinetic theory is applied to compute a mean first passage time for glycerol conduction across GlpF.

Theory and methods

Modeling

Solvation of the GlpF homotetramer in a fully hydrated palmitoyloleoylphosphatidyl-ethanolamine (POPE) bilayer is described in Jensen et al. (16). POPE constitutes a relevant model for the inner membrane of E. coli, which contains 70–80% of phosphatidylethanolamine lipids—palmitoyl and oleoyl moieties being the most abundant acyl tails (22). As was shown by Jensen et al., the thickness of this membrane model is consistent with the size of the protein (16). In this work, the z-direction of Cartesian space coincides with the normal to the water-membrane interface. To enhance the statistical information supplied by the simulations, the assisted transport of glycerol was investigated along that spatial direction, in the four channels of GlpF, through the definition of four independent reaction coordinates.

MD simulations

All simulations were performed using the NAMD simulation package (23) in the isobaric-isothermal ensemble. The pressure and the temperature were maintained at 1 bar and 300 K, respectively, employing the Langevin piston algorithm (24) and softly damped Langevin dynamics. The particle-mesh Ewald method (25) was utilized to compute electrostatic interactions. The r-RESPA multiple time-step integrator (26) was used with a time step of 2 fs for short-range and 4 fs for long-range forces. Covalent bonds involving a hydrogen atom were constrained to their equilibrium length. The GlpF homotetramer and its environment were described by the all-atom CHARMM27 force field (27,28).

ABF free energy calculations

To investigate the assisted transport of glycerol in GlpF, the reaction coordinate was chosen as the distance separating the center of mass of the former from the centroid of the channel in which it was confined, projected onto the z-direction of Cartesian space. Variation of the free energy, ΔG(z), along z was determined using the ABF method (20), which relies upon the integration of the average force acting on z. In the NAMD implementation of ABF (21), this force is evaluated within the classical thermodynamic integration formalism (29). The free energy derivative, dG(z)/dz, is estimated locally throughout the simulation, thus providing a continuous update of the biasing force. When applied to the system, this bias generates a Hamiltonian bereft of a net average force along z. Consequently, all values of the reaction coordinate are sampled with an equal probability, thereby improving significantly the accuracy of the computed free energies. To further increase the efficiency of the calculation, the interval connecting the cytoplasmic and the periplasmic sides of the membrane—that is, −20 ≤ z ≤ +15 Å—was divided into seven nonoverlapping windows, in which up to 30 ns of MD trajectory were generated. The initial Cartesian coordinates of the system for each window were obtained from the constant-velocity SMD simulations of Jensen et al. (9), with a preliminary equilibration stage of ∼1 ns. Instantaneous values of the force were accrued in bins 0.1 Å wide, which appears to constitute a reasonable choice for modeling transport phenomena (21). To understand how the measured free energy can be affected by the choice of the reaction coordinate, an alternate definition of the latter was examined, whereby the center of mass of the complete channel was replaced by that of the SF. To this end, a 20-ns ABF simulation was performed using a single, 10 Å broad window embracing the entire free energy barrier that arises between the periplasmic vestibule and the NPA filter. Moreover, increasing the width of the windows constitutes a possible route to fathom quasi-nonergodicity scenarios prone to occur in stratified approaches (30), in particular when the reaction coordinate is strongly coupled to slowly relaxing orthogonal degrees of freedom. Combining the statistical information accrued using both choices of a reaction coordinate, exploration of the reaction pathway characterizing the translocation of glycerol through GlpF was carried over a total simulation time equal to 0.12 μs.

Diffusion coefficient measurements

A set of independent simulations was performed at key positions along the conduction pathway, from which a profile of z-dependent diffusion coefficients, D(z), was computed. A convenient, concise expression for D(z) was derived by Hummer in the framework of an overdamped harmonic oscillator (31),

$$D(z)=\frac{\text{var}(z)}{{\tau }_{\text{z}}},$$ (1)

where the variance, var(z), is equal to 〈z²〉 − 〈z〉², and τ_z is the characteristic time of the normalized autocorrelation function of z:

$${\tau }_{\text{z}}=\frac{{\int }_0^{+\infty }\langle \delta z(t)\delta z(0)\rangle \text{d}t}{\text{var}(z)}\text{.}$$ (2)

Here, δz(t) = z(t) − 〈z〉. The autocorrelation functions were determined from 4-ns MD simulations, during which the vertical position of the glycerol molecules was restrained by means of a harmonic potential with a force-constant equal to 10 kcal/mol/Ų (21). Each simulation yielded four estimates of D(z), corresponding to distinct positions of the permeant in the four individual channels of GlpF. As a basis of comparison, the effective diffusion coefficient of glycerol in bulk water was estimated from its mean-square displacement measured in an independent, 20-ns simulation.

Results and discussion

Free energy of glycerol transport

As revealed in Fig. 1, the free energy profile delineating glycerol permeation through GlpF is remarkably simple. The constriction region is prefaced by a shallow vestibular minimum, substantially weaker than that determined from cv-SMD simulations (9). The SF consists of a single free energy barrier, the average height of which, ΔG^‡, is ∼8.7 kcal/mol, falling nicely within the error bar associated to the experimental activation energy of Borgnia and Agre, equal to 9.5 ± 1.5 kcal/mol (17). The remainder of the free energy landscape, in particular near the NPA motif, is essentially flat—suggesting that from this point on, glycerol diffuses rapidly toward the cytoplasm. This result is consistent with previous observations relying on unbiased simulations (16).

Figure 1.

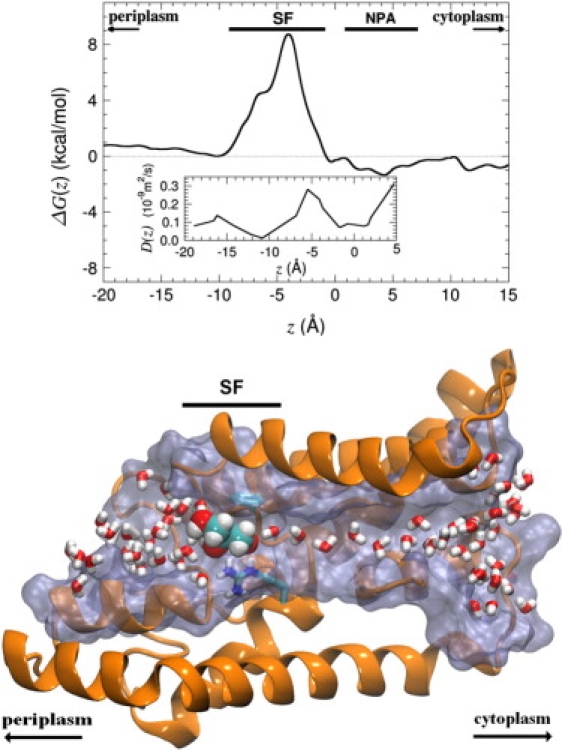
(Top) Free energy profile for glycerol conduction in the GlpF homotetramer obtained from equilibrium ABF simulations totaling 0.12 μs of sampling, via an integration of the force exerted on glycerol along the z-direction of Cartesian space. This potential of mean force corresponds to an average of the individual free energy profiles determined in the four channels forming GlpF. (Inset) Z-dependent diffusion of glycerol in GlpF was derived from additional simulations, wherein the permeant is confined in a harmonic potential. (Bottom) Cross-sectional view of a GlpF monomer. Pore-lining residues are rendered as a smooth surface, whereas a cartoon representation is used to depict the rest of the protein. The residues forming the SF and the water molecules contained in the pore are drawn in a licorice representation. The glycerol molecule located at the SF is highlighted in a space-filling representation. Image rendering was done with VMD (41).

In the hypothetical limit of infinite sampling, the free energy profiles delineating the translocation of glycerol in the four different channels of GlpF should superimpose perfectly. Even after 0.12 μs of sampling, this is, however, not completely the case. Whereas the individual potentials of mean force possess identical qualitative features, reaching a fully quantitative agreement constitutes a daunting task. The root-mean-square deviation of the average force, ${\langle F_{\text{z}}\rangle }_{\text{z}},$ is, nevertheless, moderate and peaks at ∼2.2 kcal/mol/Å in the entropically most challenging region of the conduction pathway, that is, its constriction section. This result, together with the qualitative understanding of convergence issues detailed in the following paragraphs, justifies the assertion that convergence of the free energy calculation has been attained.

It is important to underline that throughout the 0.12 μs of ABF simulations, only minute structural differences in GlpF have been detected. The distance root-mean-square deviation computed over the trace of the different channels never exceeds 2.2 Å. Furthermore, secondary structure analysis (32) does not unveil any unsuspected alteration or loss of structure. On the contrary, over the timescale explored by these simulations, the entire scaffold of TM α-helices forming the homotetramer remains utterly intact.

Choice of the reaction coordinate and nonequilibrium phenomena

To a large extent, the efficiency of the free energy calculation—albeit, in principle, not its accuracy—depends upon the choice of the reaction coordinate. Ideally, the latter ought to embrace all relevant slow degrees of freedom to guarantee rapidly converging free energy differences (33). In practice, however, efficiency of the calculation collapses when diffusion along the reaction pathway follows narrow valleys separated by high free energy barriers.

This shortcoming is further magnified in the event of a suboptimal selection of the reaction coordinate, incapable of mirroring the intricate topology of the molecular system. Whereas, in an average sense, the normal to the water-membrane interface—i.e., the z-direction of Cartesian space—constitutes a natural choice for modeling the permeation of glycerol in GlpF, well-localized distortions in the conduit demonstrate that a surrogate, one-dimensional reaction coordinate may not be able to capture fully the motion of the permeant as it crawls through the crooked and narrow regions of the channel. In particular, markedly different behaviors have been monitored between consecutive passages of glycerol at given heights of the channel, even though the time elapsed between these passages can span several nanoseconds. As illustrated in Fig. 2, local deviations of the pathway with respect to a hypothetically straight hollow tubular structure causes glycerol to collide against the walls of the SF. Alteration of the latter through isomerization of the participating amino acids may be viewed as the result of quasi-nonequilibrium effects, which are likely to be rooted in the application of the adaptive bias before the estimate of the average force is properly converged. The permeant is then thrusted artificially toward the edge of the channel, only because the choice of the reaction coordinate is locally inadequate. Although a one-dimensional description is formally correct, convergence of the free energy calculation can be severely impeded by quasi nonequilibrium phenomena requiring much longer sampling times to allow closely coupled, slow degrees of freedom to relax appropriately.

Figure 2.

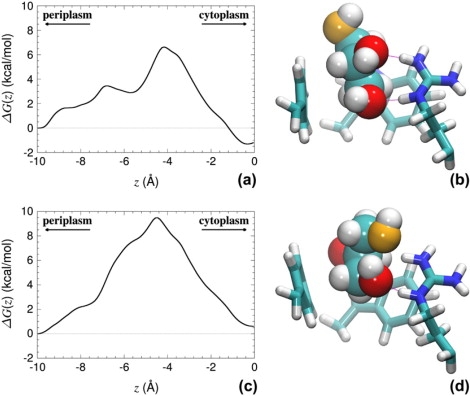
Energetics deduced from incomplete sampling of glycerol transport across the SF region of GlpF. One trajectory captures a local minimum (a) mirrored in a typical conformation of the permeant (b). Another trajectory samples a monolithic barrier (c) corresponding to an inadequate orientation and conformation of glycerol (d). (b and d) Glycerol is shown in space-filling representation, and protein side chains (Trp⁴⁸, Phe²⁰⁰, Arg²⁰⁶) are shown in licorice representation. Carbon atoms are shown in light blue, nitrogen atoms are in dark blue, hydrogen atoms are in white, and oxygen atoms are in red, except for atom O1 of glycerol, which is shown in orange. Image rendering (b and d) was done with VMD (41).

Orientation and conformational equilibrium of glycerol

At the experimental level, the activation energy measured for glycerol conduction through GlpF (17) involves an average over an ensemble of molecules entering the constriction region of the aquaglyceroporin with distinct conformations and orientations. On the timescale of the experiment, it is expected that glycerol reorients to optimize its induced fit in the SF and NPA regions, the exploration of which may be hardly amenable to equilibrium free energy calculations—and even less so to irreversible pulling simulations (34). A closer look at the four permeant molecules as they enter the SF sheds new light on the intimate relationship between orientation, isomerization, and free energy. From the latter, it may be understood that exaggeratingly short free energy calculations starting with a quasi-optimal orientation and conformation of glycerol may predict erroneously unhampered diffusion and the disappearance of the free energy barrier.

Analysis of the MD trajectories indicate that, when confined in the conduction pathway, glycerol may isomerize and adopt three possible conformations—i.e., gauche-gauche, gauche-anti, and anti-anti, as labeled after the configuration of the two O-C-C-O torsional angles. In bulk water, the anti-anti and gauche-anti conformers each account for roughly 45% of the population, while the probability for gauche-gauche is <10%. As indicated in Fig. 3, the relative population of these conformers varies dramatically as a function of the position of glycerol in the channel. Within the pore, conformational preferences are influenced by a balance of solvation by water and specific interactions with pore-lining residues. Anti-anti structures are slightly more frequent in regions of the pore where the solvation shell of glycerol is partly depleted (see Fig. 1). The anti-anti conformation, as the only one fully compatible with the formation of an intramolecular hydrogen bond, is favored in such regions due to the lack of competing hydrogen-bonding species. In the SF, in contrast, the gauche-gauche conformation is preferred because it promotes the formation of a network of hydrogen bonds with the neighboring Phe²⁰⁰ and Arg²⁰⁶ residues, as shown in Figs. 4 and 5, while the nonpolar face of the molecule forms favorable hydrophobic contacts with the side chains of Trp⁴⁸ and Phe²⁰⁰. In the same region, the anti-anti conformer is the least populated one on account of the lesser possibilities it offers for hydrogen-bonded motifs.

Figure 3.

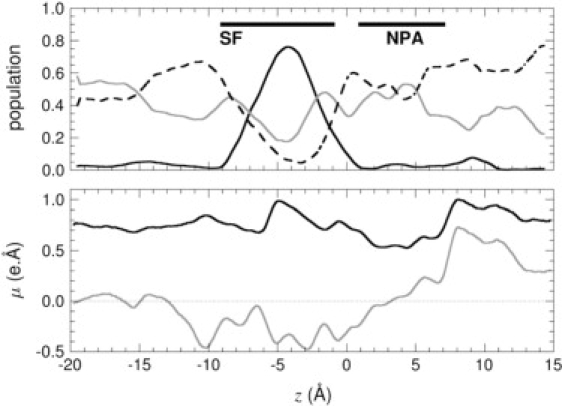
(Top) Conformational and orientational preference of glycerol in the GlpF homotetramer, as a function of the reaction coordinate, z: Population of gauche-gauche (dark, solid line), gauche-anti (light, solid line), and anti-anti (dark, dashed line) conformations. (Bottom) Total molecular dipole moment of glycerol (dark, solid line) and its projection along the z-direction of Cartesian space (light, solid line), averaged over the four channels of GlpF.

Figure 4.

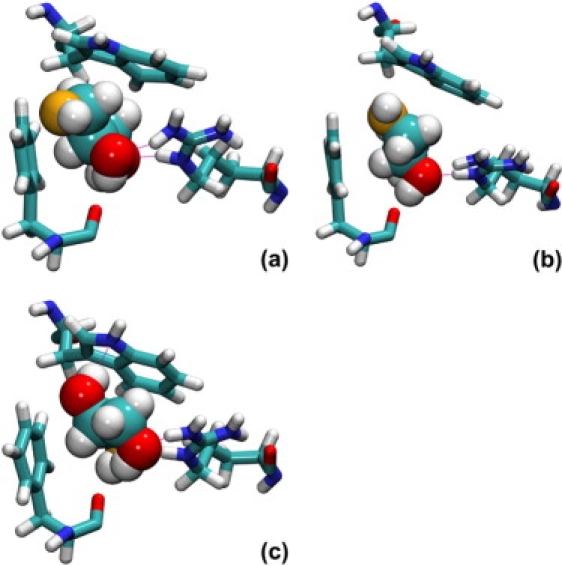
Conformational equilibrium of glycerol in the SF region of the GlpF homotetramer: gauche-gauche (a), gauche-anti (b), and anti-anti (c) conformations. Image rendering was done with VMD (41).

Figure 5.

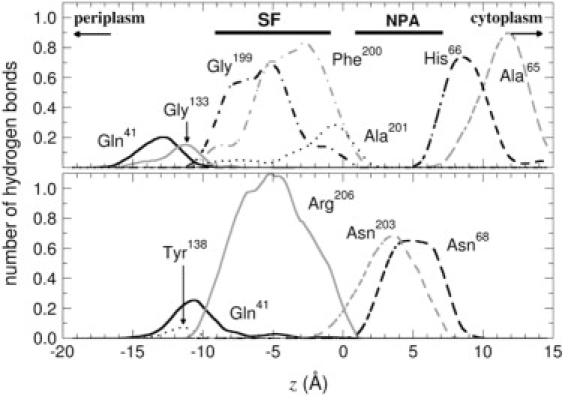
Evolution of the number of hydrogen bonds as a function of the reaction coordinate, z. (Top) Hydrogen-bond acceptors; (bottom) hydrogen-bond donors. Asn⁶⁸ and Asn²⁰³ belong to the NPA motif. Arg²⁰⁶ is able to form two hydrogen bonds simultaneously, hence an average number greater than unity.

Orientation of glycerol in the midst of the SF follows a two-state regime, whereby the vector joining the first and the last carbon of the molecule is either parallel or antiparallel to the normal to the water-membrane interface, $\widehat{\text{n}}\text{.}$ Noteworthily, the preferred parallel orientation is conducive to the emergence of the gauche-gauche conformer, hence, suggesting an intimate relationship between orientation and conformation. The marked propensity toward gauche-anti conformers for antiparallel orientations further illustrates the stereoselectivity of the channel, in which conformation is dictated by prochirality, as depicted in Figs. 3 and 4. Interestingly enough, the average orientation of the dipole moment, μ, obeys a mechanism reminiscent of water transport in GlpF, wherein μ is roughly antiparallel to $\widehat{\text{n}},$ before tilting to a parallel orientation near the NPA motif (14). Unlike water, however, inversion of the glycerol dipole moment is not strictly correlated with tumbling of the molecule, as it can happen through overall conformational changes and reorientation of individual hydroxyl groups. In addition to the specific interactions with pore-lining residues mentioned previously, this electrostatic effect thus introduces another type of coupling between the permeation process and the internal degrees of freedom of the permeant. Both mechanisms are likely to affect the permeation kinetics.

Capturing relaxation phenomena

SMD simulations associated with the Jarzynski identity (19), whereby a permeant molecule is pulled irreversibly in each monomer of GlpF, yielded a rugged free energy landscape (9), at variance with the smooth profiles depicted in Fig. 1. This marked discrepancy may be explained, at least in part, by the nonequilibrium nature of pulling experiments that do not allow the mutual adaptation of glycerol and the channel as the former is dragged along the conduction pathway. Of particular interest, the two peaks characteristic of the SF in the SMD simulations (9) merge into a single free energy barrier when turning to the ABF approach. This coalescence is likely to be rooted in the ensemble average over all possible orientations of glycerol in equilibrium free energy calculations, which does not favor any particular low-entropy arrangement in the SF. In sharp contrast, glycerol molecules are preoriented in irreversible pulling experiments, thereby mirroring the crystallographic structure and forming the expected hydrogen-bonding patterns.

In vivo, permeation of GlpF by one glycerol molecule seems to occur at least on the microsecond timescale or longer (1), which precludes a full sampling of the permeation pathway by means of unbiased atomistic simulations. Such a rare event may, nonetheless, be modeled by accelerating the natural process to a timescale compatible with the contingencies of MD-related approaches. Beyond the underlying principles of the methods, these ABF simulations differ from previous computational investigations in regard to the significantly longer timescales they cover. As illustrated in Fig. 6, isomerization of the permeant in the channel occurs on the multi-nanosecond timescale, flipping of the two torsional angles, φ₁ and φ₂, of glycerol being concerted. This phenomenon spans a somewhat shorter, yet appreciable timescale when glycerol is immersed in bulk water. The absence of concerted transitions in the aqueous environment suggests that coupling of the two angles in the SF of GlpF stems from conformational restrictions in that region. Similarly, reorientation of the permeant (see Fig. 6, c and d) is reasonably fast near the cytoplasm, but is slowed down dramatically in the SF region, where it may remain frozen, either parallel or antiparallel to $\widehat{\text{n}},$ for as long as ∼10 ns. Pulling experiments of glycerol at the constant velocity of 30 Å/ns are probably not able to capture relaxation phenomena that embrace significantly longer timescales.

Figure 6.

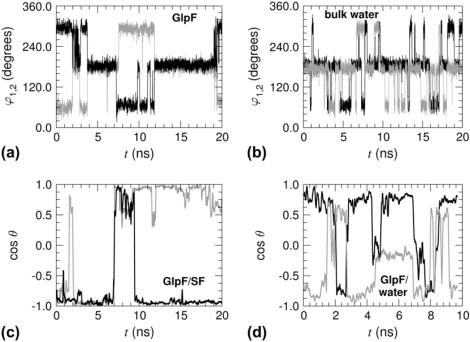
Conformational and orientational relaxation of glycerol in the GlpF homotetramer: Time-evolution of the two torsional angles of glycerol confined in the SF (a) and in bulk water (b). Time-evolution of the orientation of glycerol in the SF (c) and in the periplasmic vestibule (d). Monomer 1 (dark, solid line) versus monomer 2 (light, solid line).

Concurrent isomerization and reorientation of glycerol appears to act as the rate-limiting step toward permeation across GlpF. This concerted adaptation to the rough surface of the SF may be related to an induced fit in protein-ligand association. Similar in spirit to the exploration of conformational space by the ligand trying to find its way to the binding pocket, where it will be locked tightly, the permeant searches among all possible combinations of conformation and orientation for the particular one that will ensure passage through the SF. As glycerol slowly diffuses within the SF region, it is progressively stabilized by the formation of intermolecular hydrogen bonds with the channel. This is illustrated in the movie provided as Supplementary Material.

Intrinsic dynamics of glycerol and kinetics of permeation

Transport of glycerol in GlpF may be viewed as a diffusion process in an external potential of mean force created by the confined environment of the membrane channels. ABF reshapes the free energy landscape seen by glycerol as it progresses along z, removing kinetic traps and barriers, while keeping a quantitative account of these features. Application of the method requires one to choose an arbitrary parameter, z, as an a priori reaction coordinate, though ABF permits the permeant and the channel to adapt mutually as the former moves along z, conferring to the system significant freedom to find the actual reaction pathway. Convergence of the ABF calculation is optimal in the ideal case of a process involving a concerted motion coupling z to other degrees of freedom, with a single, slow degree of freedom, i.e., the ABF reaction coordinate, and a fast-relaxing orthogonal manifold. The ABF treatment is perfectly adapted to the reaction rate theory, which relies on this type of timescale separation—that is, the slow manifold being described explicitly, and the fast manifold being introduced as a mean field, in the form of the free energy profile.

The simulations of glycerol in a bulk aqueous environment yield an isotropic diffusion coefficient equal to 2.1 × 10⁻⁹ m²/s, in reasonable agreement with the experimental value of 1.1 × 10⁻⁹ m²/s determined at 298 K (35). Estimation of a position-dependent diffusion coefficient for the complex motion of glycerol in the confined environment of the channel is far more challenging. Lu et al. (36) report an attempt at measuring the diffusion coefficient of glycerol in GlpF based on the velocity autocorrelation functions. This approach yields a value of 2.2 × 10⁻⁹ m²/s, a somewhat unrealistic value considering that it is larger than the experimental estimate for glycerol in bulk water (35). Lu et al. concluded that long, nanosecond timescale sampling is required to quantify self-correlations of the fluctuations that drive glycerol diffusion in the channel. Indeed, as shown in Fig. 1, 4-ns measurements based on position autocorrelation functions yield values of the expected order of magnitude, slightly smaller than the diffusion coefficient for water in the same channel, determined by Tajkhorshid et al. (8) to be 4.6 × 10⁻¹⁰ m²/s.

It is remarkable that some of the highest values of D(z) within the channel are found in the region of the SF. Tight restrictions on the shape and orientation of glycerol in that highly constricted region (see Fig. 3 and discussion above) have the opposing effects of 1), smoothing locally the effective free energy surface—hence, the higher diffusion coefficient; and 2), imposing a high entropic penalty, thereby significantly reducing the thermal accessibility of that section of the channel. Not too surprisingly, the second effect is predominant, so that the SF acts as a barrier to glycerol permeation, as will be seen below.

The intrinsic diffusion coefficient may be used together with the free energy profile along the reaction pathway to infer the mean first passage time, τ(a→b), of glycerol from the periplasmic vestibule, a, to the cytoplasm, b (37):

$$\begin{array}{l}\tau (a\to b)={\int }_{\text{a}}^{\text{b}}\text{exp}[\beta \Delta G(z)]D^{-1}(z)\\ \times \left[{\int }_{\text{a}}^{\text{z}}\text{exp}[-\beta \Delta G(\zeta )]\text{d}\zeta \right]\text{d}z\text{.}\end{array}$$ (3)

Here β = (k_BT)⁻¹, where k_B is the Boltzmann constant, T is temperature, and D(z) is the z-dependent diffusion coefficient. As can be seen in Fig. 1, the latter varies between ∼0.02 and 0.3 × 10⁻⁹ m²/s—i.e., ten to a hundred times slower than the free diffusion of glycerol in an aqueous medium. The noteworthy fast diffusion in the region of the SF confirms that rare events are rare indeed, only because they occur after numerous failed attempts to overcome the free energy barrier, and not because climbing the latter is slow (38,39).

Applying Eq. 3 to the free energy and the position-dependent diffusion coefficient profiles of Fig. 1, it follows that τ(a → b) = 5 × 10⁻⁴ s, which corresponds to a rate constant of ∼2 × 10³ s⁻¹. This rate constant is approximately two orders-of-magnitude smaller than the per-channel turnover estimated by Heller et al. (1) based on the in vivo measurements by Alemohammad and Knowles (40). The theoretical estimates of Lu et al. (36), which account for the whole transport process from the periplasm to the cytoplasm, range from 4 × 10⁵ to 10⁶ s⁻¹, assuming a 0.5 M glycerol concentration.

Conclusion

Glycerol conduction in GlpF has been investigated from the perspective of unprecedented equilibrium free energy calculations executed over a timescale spanning 0.12 μs. Compared to shorter, irreversible pulling experiments, the length of these simulations and their reversible character allow the permeant to reorient and isomerize freely as it diffuses slowly through the conduction pathway. The simulations further illuminate that orientational and conformational relaxation of glycerol and its ABF-assisted transport along the tripathic channels span comparable timescales. The structure of the free energy profile characterizing GlpF permeation by glycerol is qualitatively simple and features a single free energy barrier located at the SF. The height of the free energy barrier separating the periplasmic vestibule from the NPA motif, initially modulated by the original orientation of glycerol in the channel, converges after appropriate sampling toward the experimentally determined activation energy (17). In this respect, these free energy calculations constitute an important, albeit still incomplete step toward the full understanding of glycerol diffusion in GlpF. Of particular interest are the symptomatic quasi-nonequilibrium effects that modulate the height of the free energy barrier in the SF region and can be ascribed to both the choice of the reaction coordinate and the convergence of the adaptive bias. These results imply that conduction in aquaglyceroporins does not exhibit complete timescale separation, but rather depends on fluctuations that are slow compared with the motion along the conduction pathway. Gating of membrane channels generally obeys such a reaction mechanism. Advancing our understanding of assisted transport phenomena across membranes necessarily requires better characterization of the slow fluctuations that are coupled to self-diffusion in aquaporins and other channels. Application of diffusional kinetic theory based on the measured free energy profile and position-dependent diffusion coefficient yields a predicted rate constant that appears to be overestimated compared to the available experimental value. Although the latter relies upon arguable assumptions and only provides a rough idea of the associated kinetics, this apparent discrepancy calls for additional investigations. Extending this approach to other transport phenomena, well-characterized experimentally, is envisioned to help assess whether mean-field models (that is, diffusion in a one-dimensional potential of mean force) describe in a reliable and effective way the statistical distribution of the permeation events that underlie the observable, macroscopic transport rate.

Supplementary material

To view all of the supplemental files associated with this article, visit www.biophysj.org.