Abstract
In the companion article, we proposed that fullerene cages with head-to-tail dihedral angle discrepancies do not self-assemble. Here we show why. If an edge abuts a pentagon at one end and a hexagon at the other, the dihedral angle about the edge increases, producing a dihedral angle discrepancy (DAD) vector. The DADs about all five/six edges of a central pentagonal/hexagonal face are determined by the identities—pentagon or hexagon—of its five/six surrounding faces. Each “Ring”—central face plus specific surrounding faces—may have zero, two, or four edges with DAD. In most Rings, the nonplanarity induced by DADs is shared among surrounding faces. However, in a Ring that has DADs arranged head of one to tail of another, the nonplanarity cannot be shared, so some surrounding faces would be especially nonplanar. Because the head-to-tail exclusion rule is an implicit geometric constraint, the rule may operate either by imposing a kinetic barrier that prevents assembly of certain Rings or by imposing an energy cost that makes those Rings unlikely to last in an equilibrium circumstance. Since Rings with head-to-tail DADs would be unlikely to self-assemble or last, fullerene cages with those Rings would be unlikely to self-assemble.
Introduction
When Kroto et al. (1) discovered carbon with 60 atoms in the form of a truncated icosahedron, the same shape as a modern soccer ball, they dubbed it “buckminsterfullerene” (60 IPR in Fig. 1 A). Triskelions (MW ∼60,000) (2), trimers of the protein clathrin (3–6), also self-assemble into this structure (7,8). Kroto et al. (1) gave the shorter name fullerene to the group of related cages that have n three-connected vertices, 3n/2 edges, 12 pentagons, and (n−20)/2 hexagons. The smallest fullerene is the dodecahedron with 20 vertices, composed of just 12 pentagons and no hexagons (20 in Fig. 1 A). The dodecahedron and the truncated icosahedron are special in that all of their faces are regular and thus planar.
Figure 1.
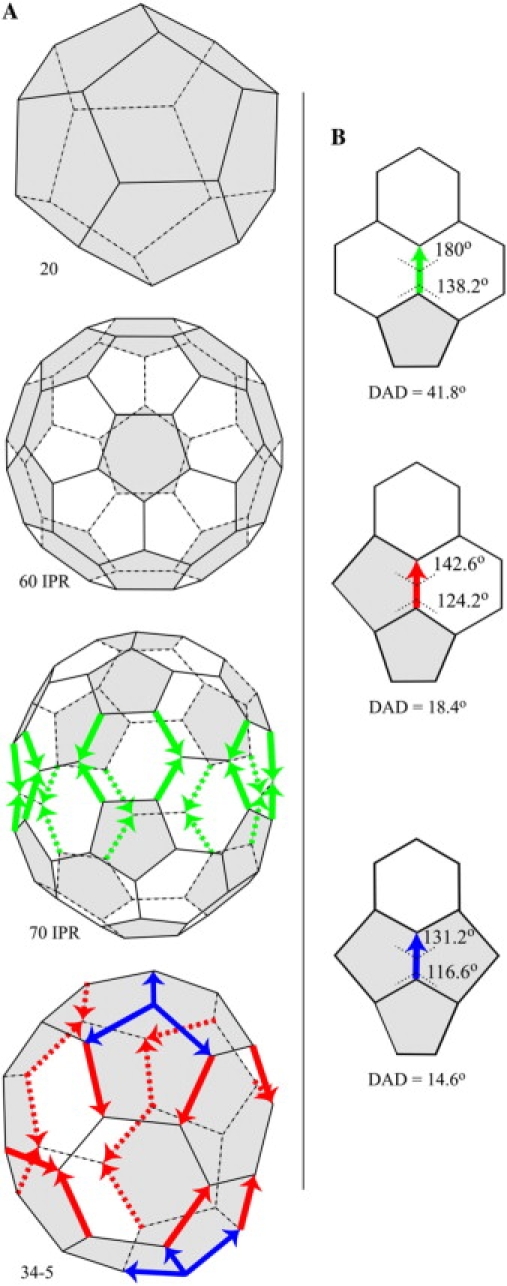
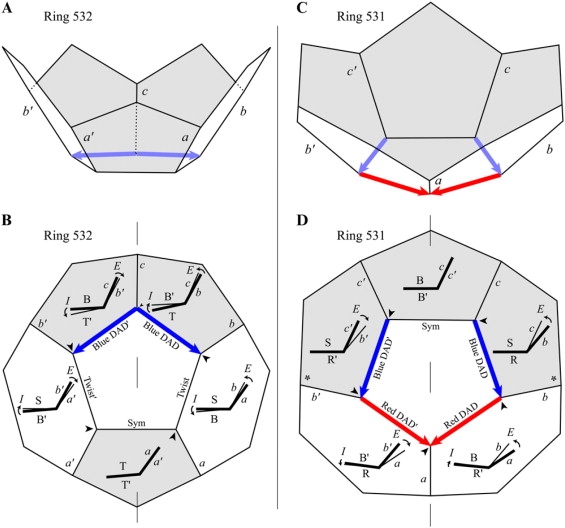
Fullerene cages and edges with DAD. (A) A fullerene cage has an even number (n ≥ 20) of three-connected vertices, 12 pentagonal faces, and (n-20)/2 hexagonal faces. 20: The smallest fullerene cage is the dodecahedron, with 20 three-connected vertices and 12 regular pentagonal faces. It is one of five Platonic solids. 60 IPR: The truncated icosahedron, with 60 three-connected vertices, 12 regular pentagonal faces, and 20 regular hexagonal faces, is one of 13 Archimedean solids. None of the pentagons are adjacent to one another, so the cage follows the isolated pentagon rule. 70 IPR: Only one fullerene cage with 70 three-connected vertices follows the isolated-pentagon rule. It has 12 pentagonal faces and 25 hexagonal faces. The 20 green arrows pointing from a pentagon at one end to a hexagon at the other end mark green DAD edges (see B) around the waist; the five hexagonal faces with four DAD edges each, and the 10 hexagonal faces with two DAD edges each are all nonplanar. 34-5: With 34 three-connected vertices, 12 pentagonal faces, and 7 hexagonal faces, this fullerene cage has two kinds of DAD edge, red and blue (see B). In two of the pentagonal faces, the heads of blue DAD edges meet the tails of red DAD edges, a total of four head-to-tail DADs. The isomer number 5 among cages with 34 vertices is from Fowler and Manolopoulos (9). (B) At any vertex, the dihedral angles are determined by the three internal angles (e.g., 108° in pentagons or 120° in hexagons) at the vertex. The dihedral angles about a green DAD edge at its top (hexagon) and bottom (pentagon) ends are 180° and 138.2°; respectively, a DAD of 41.8°. Corresponding values are also shown for the red and blue DAD edges as well.
The fullerenes are infinite in number. For 20 ≤ n ≤ 60 vertices, there are 5770 different, graphically possible, fullerene cages (9,10). For n = 60 alone, there are 1812 fullerene cage isomers (9,11). The number of isomers increases approximately exponentially for n > 60. Except for the dodecahedron and the truncated icosahedron, in all of the fullerene cages, like the one with 70 vertices in Fig. 1 A, the faces cannot all be regular or planar, and the vertices cannot all be identical. Such vertices are thus quasi-equivalent (12), in analogy with the tiles that make up the pentagonal and hexagonal faces of an icosahedral virus shell. The latter are described as quasi-equivalent because, although identical at the molecular level, the tiles are not identical in how they bind to neighbors, varying with geometric location within the shell.
Carbon atoms and clathrin triskelia both assemble into a variety of fullerene cages. Carbon atoms primarily make the truncated icosahedron (C60) (1) and larger cages (13) like the one with 70 vertices (14) in Fig. 1 A that obey the isolated-pentagon rule (IPR) (15,16), but carbon also self-assembles into a cage with 36 vertices (17). Clathrin triskelia self-assemble into specific fullerene isomers with 28, 36, 38, 40, 44, and 50 vertices (18,19) as well as with 60 and more (7,8). This limited number of outcomes is remarkable in two ways. Firstly, the vast majority of structures that result from random assembly of vertices into hexagons and pentagons are not closed cages (10). Why should self-assembly produce any closed cages at all? Secondly, with so many graphically possible fullerene cages, why should self-assembly produce so few, particularly the specific ones that have been observed?
To answer these two questions, we proposed in the companion article (10) the head-to-tail exclusion rule that focuses on dihedral angles about edges. Each edge has two dihedral angles about itself, one at one end and another at the other end. If the faces at the two ends of an edge are different, the two dihedral angles are different, hence a dihedral angle discrepancy (DAD). In Fig. 1 B we color-code the three types of DAD, each a vector with its tail at the edge's pentagon end and its head at the edge's hexagon end, thus pointing from the smaller to the larger dihedral angle.
The only fullerene cages that have no edges with DAD are the dodecahedron, with pentagons at both ends of every edge, and the truncated icosahedron, with pentagons at both ends or hexagons at both ends of every edge (60 IPR in Fig. 1 A). The existence of other carbon and clathrin fullerene cages, like the 70 IPR cage in Fig. 1 A, proves that the presence of edges with DAD is not in itself a barrier to self-assembly.
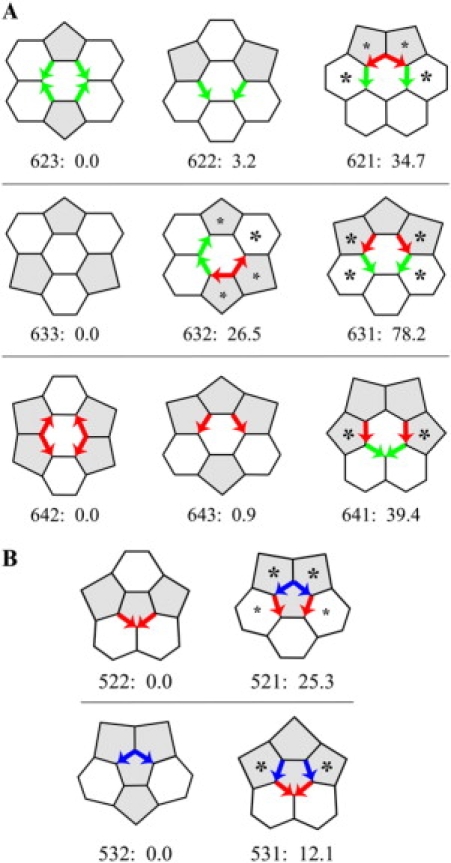
Instead, the head-to-tail exclusion rule states that fullerenes with a particular configuration of edges with DAD, arranged head of one DAD to tail of another DAD, are unlikely to self-assemble. One such unlikely cage (34-5) is shown in Fig. 1 A, with four instances of the head of a blue DAD edge meeting the tail of a red DAD edge. Here we explain the physical mechanism that underlies the head-to-tail exclusion rule. The explanation begins with a complete set of Rings, each comprising a central hexagonal face and its six surrounding faces (hex-Rings in Fig. 2 A) or a central pentagonal face and its five surrounding faces (pent-Rings in Fig. 2 B). We show that, in Rings with head-to-tail DADs (the ones in the fourth rows of Fig. 2, A and B, marked with asterisks), self-assembly of the set of surrounding faces would be improbable because some of those surrounding faces would be severely nonplanar. The physical reason for the severe nonplanarity will be summarized in Fig. 3 and justified in succeeding figures. Therefore, self-assembly of cages with Rings with head-to-tail DADs would be improbable.
Figure 2.
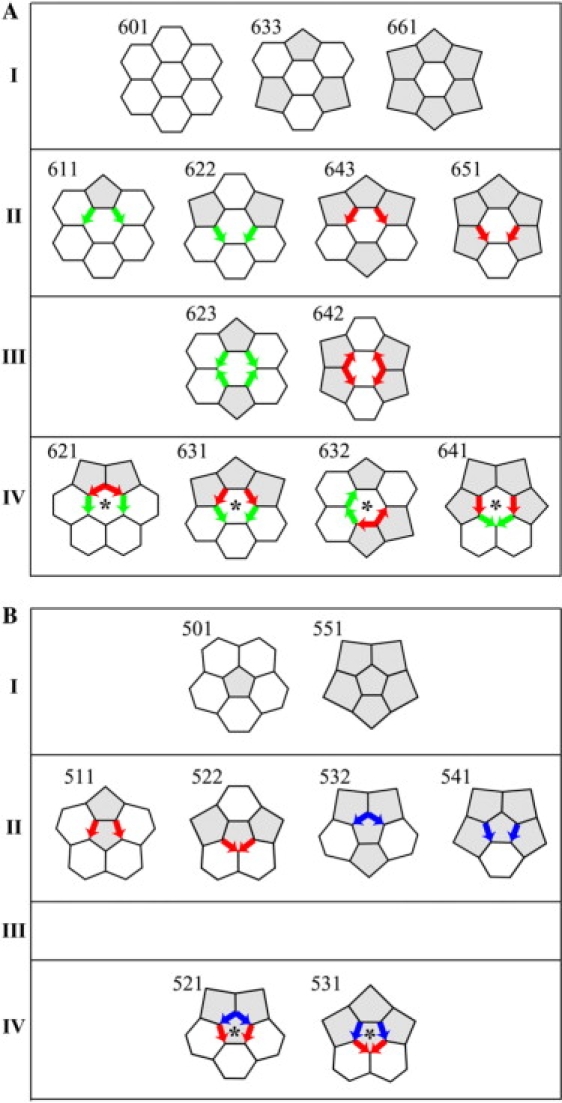
There are 13 hex-Rings (A) and 8 pent-Rings (B) that may be grouped by number and arrangement of DADs. I: Rings with no DAD edges. II: Rings with two DAD edges. III: Rings with four DAD edges, arranged head-to-head or tail-to-tail. IV: Rings with four DAD edges, with one or two head-to-tail arrangements of DADs. The latter Rings are marked with asterisks.
Figure 3.
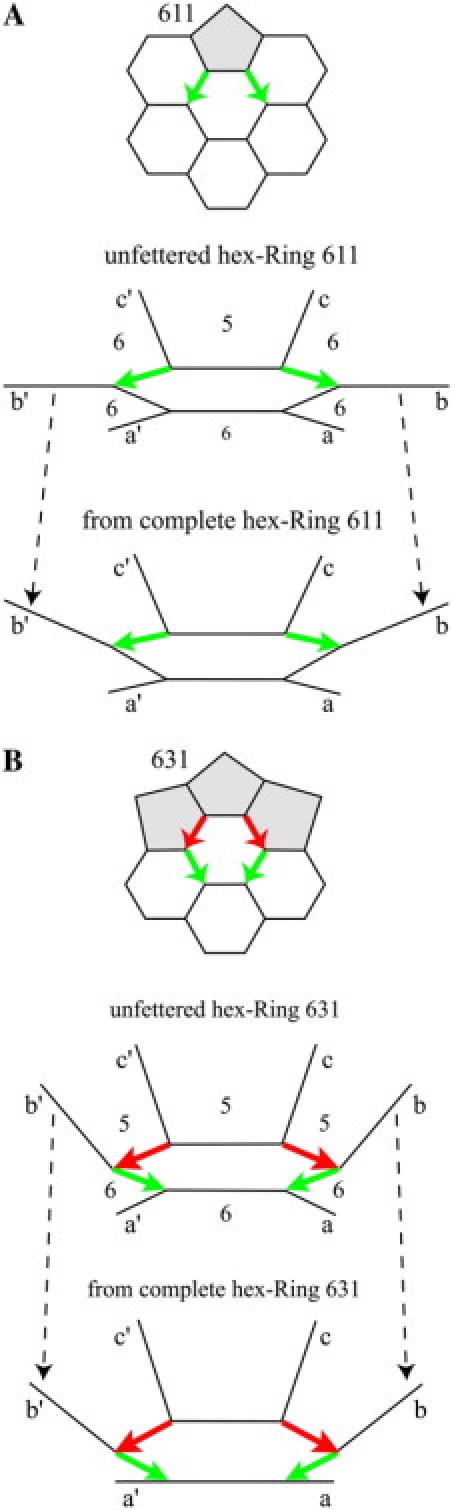
Unfettered versus complete versions of hex-Rings 611 and 631. (A, upper) Hex-Ring 611 with two green DADs. (A, middle) The three-dimensional structure of hex-Ring 611 but with incomplete surrounding faces. The number 5 marks a nascent surrounding pentagon, and the number 6 marks a nascent surrounding hexagon. Unfettered, the internal angles are ideal, 108° in nascent pentagons and 120° in nascent hexagons, the central hexagonal face is planar, and the dihedral angles are ideal. The four 666 vertices cause the front four external edges a, a′, b, and b′ and the central face to lie in a plane that we designate as horizontal. Due to the green DADs, the back two external edges c and c′ rise steeply from the horizontal plane. (A, lower) The same fragment as in the middle part but extracted from hex-Ring 611 after completion of the surrounding faces. By contrast with the unfettered structure in the middle part, external edges b and b′ rise from the horizontal plane approximately half as steeply as external edges c and c′. The dashed lines draw attention to the change in the angle of rise of external edges b and b′. (B, upper) Hex-Ring 631 with two pairs of head-to-tail, red-to-green DADs. (B, middle) The three-dimensional structure of hex-Ring 631 but with incomplete surrounding faces. Unfettered, the internal angles are ideal, the central hexagonal face is planar, and the dihedral angles are ideal. The two 666 vertices cause the front two external edges a and a′ and the central face to lie in a plane that we designate as horizontal. Due to the green DADs, external edges b and b′ rise steeply from the horizontal plane. Due to the red DADs, external edges c and c′ rise even more steeply. (B, lower) The same fragment as in the middle part but extracted from hex-Ring 631 after completion of the surrounding faces. External edges b, b′, c, and c′ rise nearly as steeply as they do in the unfettered structure in the middle part. The dashed lines draw attention to the absence of change in the angle of rise of external edges b and b′.
Methods
Types of rings
In the companion article (10) we order all of the possible hex-Rings and pent-Rings by label. Each Ring label has three digits. For example, 633 is a hex-Ring (6) with three (3) pentagons among the six surrounding faces, and it is the third (3) of three possible arrangements (after 631 and 632) of those pentagons among the surrounding faces, the arrangement with pentagons most spread out. For the present purposes, we order the Rings differently, by number and arrangement of DADs (Fig. 2), but the labels are the same. The Rings with head-to-tail DADs, marked with asterisks, are deemed “improbable”.
Molecular models of rings
We used Spartan ‘04 (Wavefunction, Irvine, CA) to create molecular models of the Rings in Fig. 2. We created two kinds of model, one from aluminum atoms and one from carbon atoms. We minimized energy by computing equilibrium structure with molecular mechanics (MMFF94 (20–24)), which takes into account deviation of bond (or internal) angle from its ideal value, deviation of bond (or edge) length from its ideal value, and torsion, related to nonplanarity of faces. Our use set the electrostatic force to zero, so the structure of aluminum models is unaffected by the charge on the (trivalent) aluminum atoms at the periphery of the ring that make only two bonds. Likewise, the structure of carbon models is unaffected by the charge on the (tetravalent) carbon atoms that have only two or three bonds. We constrained all bond lengths to 2.5 Å in aluminum and 1.43 Å in carbon. We constrained all internal angles in hexagonal faces to 120° and all angles in pentagonal faces to 108°. These constraints cannot all be satisfied perfectly (except in the dodecahedron with 20 vertices and the truncated icosahedron with 60), so energy minimization creates a structure that is a best (least energy) compromise.
We emphasize that the aluminum and carbon models should be regarded as heuristic, providing insight into the geometrical relationships that follow from imposition of the absolute constraint due to connecting the atoms in the face of weaker constraints on edge lengths and internal angles. As the results show, different atoms or energy minimization algorithms, that is, different models, produce similar geometry but differ in quantitative details; for this reason, we report data from both models.
Measurement of dihedral angle and rotations
We also used Spartan's dihedral angle function for two purposes. First, if we click on the points 1, 2, 3, and then 4 in the configuration shown in the top half of Fig. 4 A, we obtain the angle between the two planes 123 and 234, that is, the dihedral angle (138.2°) about edge 23 at its top end. If instead we click on the points 6, 3, 2, and then 5 in the configuration shown in the bottom half of Fig. 4 A, we obtain the angle between the two planes 632 and 325, that is, the dihedral angle (180°) about edge 23 at its bottom end. The difference, 180°–138.2° = 41.8°, is the green DAD. Second, if we click on the points 1, 2, 3, and then 4 in the configuration shown in Fig. 5 A, we obtain the angle of rotation (torsion angle) between edge 12 and edge 34 about their common edge 23 as shown in Fig. 5 D.
Figure 4.
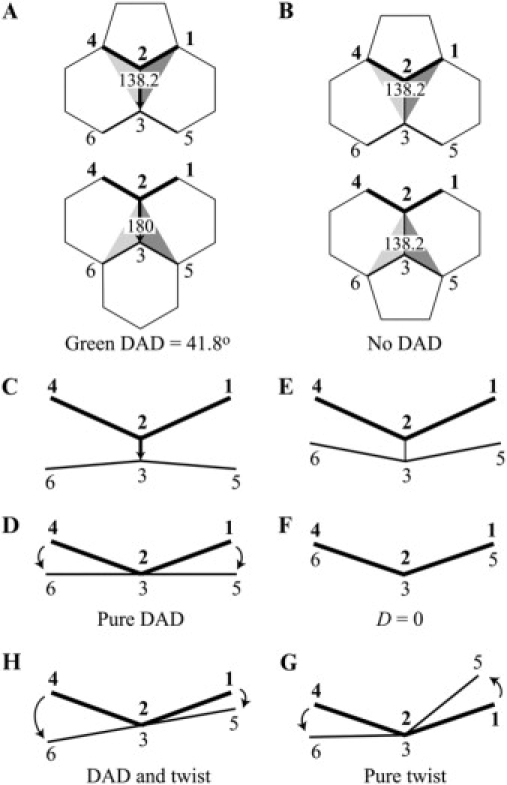
A physical description of DAD and twist. (A) The green DAD edge has two hexagonal side faces, a pentagon at the top, and a hexagon at the bottom. Focusing on the two end vertices one at a time, the dihedral angle about edge 23 at its top is 138.2° and at its bottom is 180°. The DAD is thus 41.8°, pointing from top to bottom. Bolded vertex numbers are in front; unbolded vertex numbers are in back. (B) This edge has the same end faces, both pentagons, so it is without DAD. Focusing on the two end vertices one at a time, the dihedral angle about edge 23 at its top is 138.2° and at its bottom is 138.2° as well. The DAD is thus 0°. (C) If the top of the figure in A is tilted forward and the bottom backward, then edge 23 is foreshortened. (D) If the top of the figure in C is tilted even farther forward, edge 23 appears as a point. The 138.2° angle between the near (thick) edges 24 and 21 is the dihedral angle about edge 23 at its top (vertex 2) end. The 180° angle between the far (thin) edges 36 and 35 is the dihedral angle about edge 23 at its bottom (vertex 3) end. The difference, a DAD of 41.8°, conveys broadening of the dihedral angle from the pentagon (near) end to the hexagon (far) end. The curved arrow on the left marks counterclockwise (negative) rotation of the far edge 36 from the near edge 24 about edge 23. The curved arrow on the right marks clockwise (positive) rotation of the far edge 35 from the near edge 21 about edge 23. The presence of equal and opposite rotations is a hallmark of an edge with pure DAD, that is, without any twist. (E) If the top of the figure in B is tilted forward and the bottom backward, then edge 23 is foreshortened. (F) If the top of the figure in E is tilted even farther forward, edge 23 appears as a point. The 138.2° angle between the near (thick) edges 24 and 21 is the dihedral angle about edge 23 at its top (vertex 2) end. The same 138.2° angle between the far (thin) edges 36 and 35 is the dihedral angle about edge 23 at its bottom (vertex 3) end. The difference is 0°, so this edge has no DAD. (G) Starting with the configuration in F, far (thin) edges 36 and 35 are both rotated counterclockwise, and edge 23 is said to acquire counterclockwise (negative) twist. The DAD is still zero. The left curved arrow marks the counterclockwise rotation of the left edges 36 from 24 about edge 23, and the right curved arrow marks the identical counterclockwise rotation of the right edges 35 from 21 about edge 23. The presence of identical rotations is the hallmark of an edge with pure twist. The dihedral angles between the front (thick) edges (138.2°) and between the back (thin) edges (138.2°) are unchanged, so DAD remains zero. (H) Starting with the configuration in D, if far (thin) edges 36 and 35 are both rotated counterclockwise, edge 23 is said to acquire counterclockwise (negative) twist. The DAD is still 41.8°. The left curved arrow marks a large counterclockwise rotation of the left edges 36 from 24 about edge 23, and the right curved arrow marks a small clockwise rotation of the right edges 35 from 21 about edge 23. The difference between the left and right rotations is the same as the difference between the left and right rotations in D because the difference represents the DAD, which is unchanged. The average of the two rotations is the twist. This edge has both DAD and twist.
Figure 5.
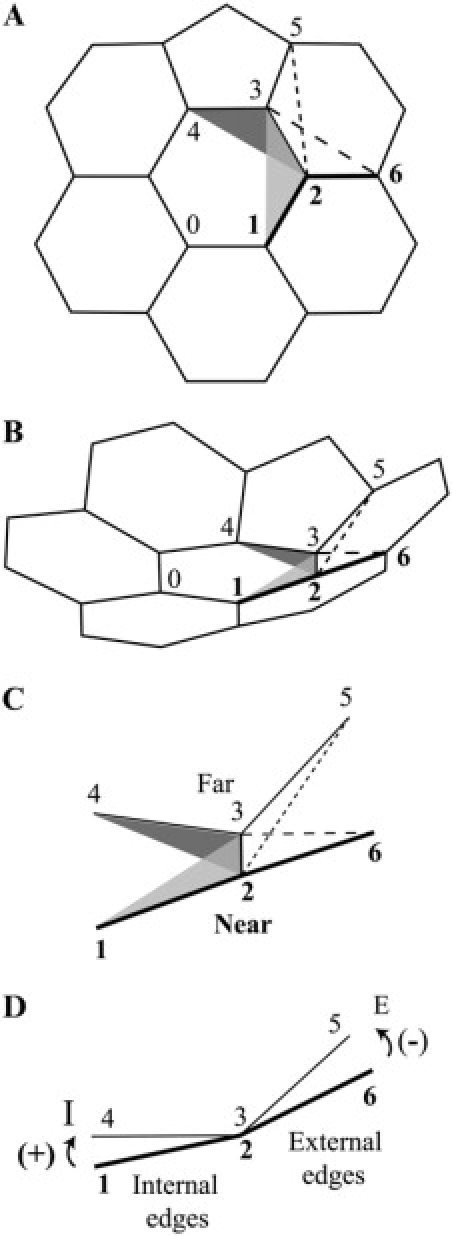
Development of the elevation diagram of the green DAD edge of hex-Ring 611. (A) With the four points 1, 2, 3, and 4 in this configuration, the dihedral angle between two planes 123 and 234 gives the angle of rotation of far (thin) edge 34 from near (thick) edge 12 about their common edge 23. Far edge 34 and near edge 12 are part of the central face and are thus internal edges. The angle through which far internal edge 34 is rotated from near internal edge 12 (about their common edge 23), the internal rotation about edge 23, is equal to the dihedral angle between the 123 and the 234 planes. Far edge 35 and near edge 26 are part of a surrounding face and are thus external edges. The angle through which far external edge 35 is rotated from near external edge 26, the external rotation about edge 23, is equal to the dihedral angle between the 623 and 235 planes. (B) Rotating the Ring in part A clockwise and then tilting the top of the Ring backward makes common edge 23 appear shorter. The near internal edge 21 and the near external edge 26 are thick, and the far internal edge 34 and the far external edge 35 are thin. (C) An enlargement of part of B. (D) Tilting the top of C farther backward shortens edge 23 even more, making it appear as a point and making the four planes appear as lines. In this elevation diagram, the change in dihedral angle of internal edges 34 from 12 provides the internal rotation I, and the change in dihedral angle of external edges 35 from 26 provides the external rotation E.
Results
Overview
Fig. 3, described in the next section, summarizes the physical basis for the head-to-tail exclusion rule, the chief point of this article: Of the 21 types of Ring in Fig. 2, those six with head-to-tail DADs would be unlikely to self-assemble because this arrangement of DADs produces highly nonplanar surrounding faces, more specifically external edges with large external rotation. The key quantity is thus external rotation, which we shall define below. Given that these six Rings are unlikely to self-assemble, then graphically possible cages with any of these six Rings would be unlikely to self-assemble. By contrast, the nonplanarity caused by DADs in other Rings is shared among surrounding faces and is thus reduced, generally halved.
To understand the physical basis, we had to invent three geometric quantities beyond the DAD that we first described in the companion article (10). The physical description of these quantities, DAD D, twist T, external rotation E, and internal rotation I, and the relationships among them, are presented in Figs. 4 and 5.
These data (D, T, E, and I) for all of the Rings, presented in Table 1 and Supplementary Material 1 Table 1, illustrated by Figs. 6–9and related by equations, led us to the physical explanation summarized in Fig. 3.
Table 1.
Representative aluminum models
| Ring | Edge type | Ext rot (E) | Int rot (I) | Dist of E (α) | DAD (D) | Twist (T) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 611 | ||||||||||||||||
| Pent | Sym | 0.00 | 0.00 | −31.51 | 0.00 | 0.00 | 0.00 | 31.51 | 15.76 | −15.76 | ||||||
| Hex | Green | −16.34 | 12.03 | 52% | 28.37 | −2.16 | ||||||||||
| Hex | Twist | −15.17 | −12.03 | 48% | 3.14 | −13.60 | ||||||||||
| Hex | Sym | 0.00 | 0.00 | 31.51 | 0.00 | 0.00 | 0.00 | −31.51 | −15.76 | 15.76 | ||||||
| Hex | Twist | 15.17 | 12.03 | −3.14 | 13.60 | |||||||||||
| Hex | Green | 16.34 | −12.03 | −28.37 | 2.16 | |||||||||||
| Sum | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||||||||
| 621 | ||||||||||||||||
| Pent | Red | −8.65 | 8.37 | −48.45 | −3.78 | 18% | 17.02 | −0.14 | 44.67 | 22.34 | −26.12 | |||||
| Hex | Green | −21.98 | 3.76 | 45% | 25.74 | −9.11 | ||||||||||
| Hex | Twist | −17.82 | −15.91 | 37% | 1.91 | −16.87 | ||||||||||
| Hex | Twist | 17.82 | 15.91 | 48.45 | 3.78 | −1.91 | 16.87 | −44.67 | −22.34 | 26.12 | ||||||
| Hex | Green | 21.98 | −3.76 | −25.74 | 9.11 | |||||||||||
| Pent | Red | 8.65 | −8.37 | −17.02 | 0.14 | |||||||||||
| Sum | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||||||||
| 623 | ||||||||||||||||
| Pent | Sym | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||||||
| Hex | Green | −12.90 | 14.55 | 27.45 | 0.83 | |||||||||||
| Hex | Green | 12.90 | −14.55 | −27.45 | −0.83 | |||||||||||
| Pent | Sym | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||||||
| Hex | Green | −12.90 | 14.55 | 27.45 | 0.83 | |||||||||||
| Hex | Green | 12.90 | −14.55 | −27.45 | −0.83 | |||||||||||
| Sum | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||||||||
| 631 | ||||||||||||||||
| Pent | Sym | 0.00 | 0.00 | −42.82 | 0.00 | 0.00 | 0.00 | 42.82 | 21.41 | −21.41 | ||||||
| Pent | Red | −16.65 | 0.03 | 39% | 16.68 | −8.31 | ||||||||||
| Hex | Green | −26.17 | −0.03 | 61% | 26.14 | −13.10 | ||||||||||
| Hex | Sym | 0.00 | 0.00 | 42.82 | 0.00 | 0.00 | 0.00 | −42.82 | −21.41 | 21.41 | ||||||
| Hex | Green | 26.17 | 0.03 | −26.14 | 13.10 | |||||||||||
| Pent | Red | 16.65 | −0.03 | −16.68 | 8.31 | |||||||||||
| Sum | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||||||||
| 632 | ||||||||||||||||
| Pent | Red | −14.94 | 3.57 | −18.91 | −0.11 | 18.51 | −5.69 | 18.80 | 9.40 | −9.51 | ||||||
| Hex | Green | −29.50 | 2.13 | 31.63 | −13.69 | |||||||||||
| Hex | Green | 25.53 | −5.81 | −31.34 | 9.86 | |||||||||||
| Pent | Twist | 3.89 | 3.85 | 19.00 | 0.16 | −0.04 | 3.87 | −18.84 | −9.42 | 0.07 | ||||||
| Hex | Twist | 2.81 | 1.84 | −0.97 | 2.33 | |||||||||||
| Pent | Red | 12.30 | −5.53 | −17.83 | 3.39 | |||||||||||
| Sum | 0.09 | 0.05 | −0.04 | 0.07 | −0.04 | −0.02 | −9.44 | |||||||||
| 531 | ||||||||||||||||
| Pent | Sym | 0.00 | 0.00 | |||||||||||||
| Pent | Blue | −15.05 | −1.24 | −31.01 | 0.76 | 49% | 13.81 | −8.15 | 31.77 | 15.89 | −15.13 | |||||
| Hex | Red | −15.96 | 2.00 | 51% | 17.96 | −6.98 | ||||||||||
| Hex | Red | 15.96 | −2.00 | 31.01 | −0.76 | −17.96 | 6.98 | −31.77 | −15.89 | 15.13 | ||||||
| Pent | Blue | 15.05 | 1.24 | −13.81 | 8.15 | |||||||||||
| Sum | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||||||||
| 532 | ||||||||||||||||
| Hex | Twist | −5.99 | −5.70 | −11.20 | 3.52 | 53% | 0.29 | −5.85 | 14.72 | 7.36 | −3.84 | |||||
| Pent | Blue | −5.21 | 9.22 | 47% | 14.43 | 2.01 | ||||||||||
| Pent | Blue | 5.21 | −9.22 | 11.20 | −3.52 | −14.43 | −2.01 | −14.72 | −7.36 | 3.84 | ||||||
| Hex | Twist | 5.99 | 5.70 | −0.29 | 5.85 | |||||||||||
| Pent | Sym | 0.00 | 0.00 | 0.00 | 0.00 | |||||||||||
| Sum | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||||||||
Angles of interest (in degrees) associated with all of the edges of representative hex-Rings and pent-Rings composed of aluminum atoms. Edge lengths were constrained to 2.5 Å, and internal angles were constrained to 108° in pentagonal faces and 120° in hexagonal faces. Electrostatic interactions were turned off. The equilibrium geometry of each Ring structure was determined by molecular mechanics calculations (MMFF94) (20–24) in Spartan ‘04. External rotation (E) and internal rotation (I) were measured. DAD (D) and twist (T) were calculated from E and I according to Eqs. 1 and 2.
Figure 6.
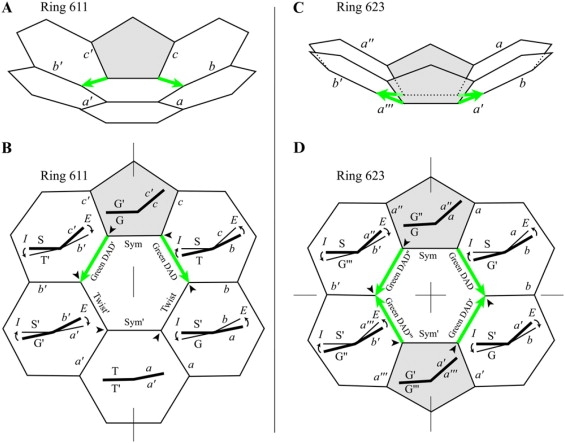
Internal and external rotations in the models of probable Ring 611 and Ring 623 composed of aluminum atoms. (A) In this view, the model of hex-Ring 611 from aluminum atoms appears as an upwardly curving bowl. The pentagon is at the back and rises above the floor, and two green DAD edges emerge from it. With reference to the a and a′ edges, nearly on the floor of the bowl, the b and b′ edges rise, and the c and c′ edges rise even more. (B) The central face in this aluminum model of Ring 611 has two Sym edges (S and S′) that cross the line of mirror symmetry. Each mirror-symmetric half also has a green DAD edge (G or G′) and a Twist edge (T or T′). Each of the central edges has an elevation diagram in its surrounding face. In each elevation diagram, the internal edges are shown on the left, the external edges on the right. This convention follows from looking end-on down each central edge from the point of view of its associated arrowhead. As in Fig. 5 D, a clockwise rotation from a front (thick) edge to a back (thin) edge is positive. The central edges are labeled S, G, and T—Sym, Green, and Twist—for the right side of the Ring and S′, G′, and T′ for the left side. The external edges are labeled a, b, and c for the right side of the Ring and a′, b′, and c′ for the left side. (C) Hex-Ring 623, here shown as an upwardly curving bowl, has four green DAD edges. (D) The elevation diagrams for Ring 623 follow the description in part B, except that the labeling of central edges (G, G′, G″, ) and of external edges (a, a′, a″, ) takes advantage of the two mirror-symmetric axes between left and right halves and between top and bottom halves.
Figure 7.
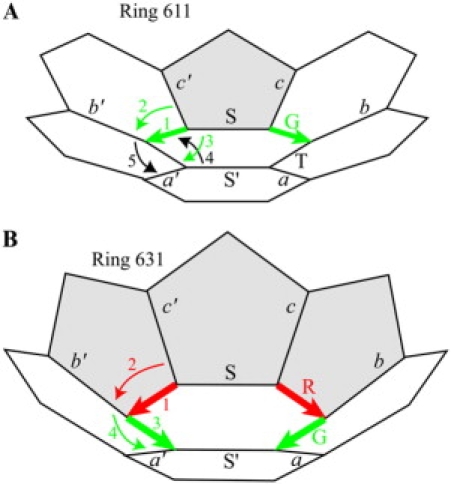
Sharing versus nonsharing of rotations. (A) In Ring 611, viewed cup-up, the green DAD 1 broadens the dihedral angle from the pentagon to the hexagon end of that edge by +D°, causing downward (counterclockwise, negative) external rotation 2 of ∼−D/2° and downward (clockwise, positive) internal rotation 3 of ∼+D/2°. Because the sum of the internal rotations in a symmetric half must be zero, internal rotation 4 must be equal and opposite that of inward rotation 3, thus −D/2°. Because the Twist edge T′ (not labeled but symmetrically placed to Twist edge T) has no DAD, external rotation 5 must be equal to the inward rotation 4, thus −D/2° as well. As a result, the external rotations 2 and 5 are each ∼−D/2°. (B) In Ring 631, viewed cup-up, the red DAD 1 broadens the dihedral angle by −R°, causing downward (counterclockwise, negative) external rotation 2 of ∼−R° and no internal rotation. Likewise, the green DAD 3 broadens the dihedral angle by −G°, causing downward (counterclockwise, negative) external rotation 4 of ∼−G° and no internal rotation.
Figure 8.
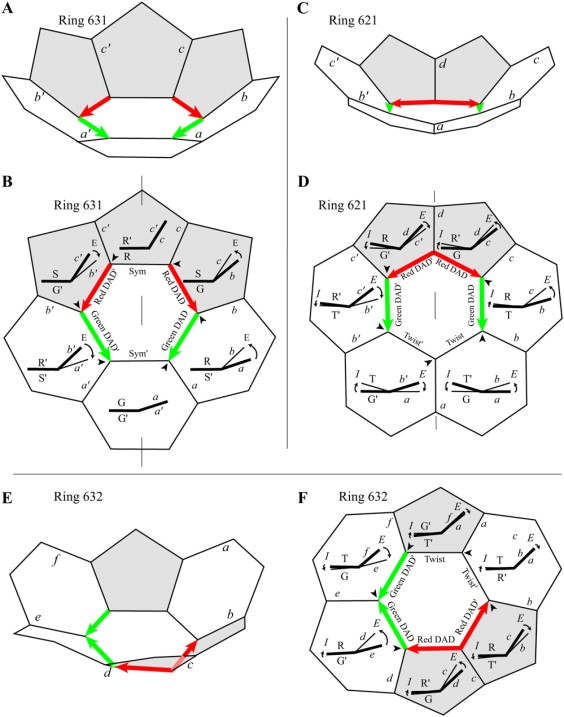
Internal and external rotations in the models of the improbable Row IV hex-Rings 631 (A and B), 621 (C and D), and 632 (E and F) composed of aluminum atoms. The diagrams follow the description in the legend of Fig. 6.
Figure 9.
Internal and external rotations in models of the probable pent-ring 532 (A) and the improbable pent-Ring 531 (B) composed of aluminum atoms. The diagrams follow the description in the legend of Fig. 6.
Some of our reasoning relies on the assumption that internal angles are ideal, 108° in pentagonal faces and 120° in hexagonal faces. Supplementary Material 2 Table 1 and Supplementary Material 2 Fig. 1 justify such reasoning even when internal angles are not ideal.
Finally, we describe why the highly nonplanar surrounding faces, like the one that would be built from external edges a and b at the bottom of Fig. 3 B, would be unlikely to self-assemble: By describing such a nascent surrounding face as nonplanar, we mean that the external rotation E between the two external edges (e.g., edges a and b) is very large. As a result, it is unlikely that another two vertices would be able to bridge the gap between the vertices at the ends of those two external edges a and b to complete the nascent surrounding hexagonal face. Likewise, it is unlikely that another one vertex would be able to bridge the gap between the vertices at the ends of external edges b and c to complete the nascent surrounding pentagonal face. Thus, those Rings would be unlikely to complete self-assembly. We complement this description with measurement of the high energy cost of Rings with head-to-tail DADs in Fig. 10.
Figure 10.
The energy cost of nonplanar faces in Rings with head-to-tail DADs. The criterion for a highly nonplanar surrounding hexagon is that its central edge has more than ∼20° of external rotation. The criterion for a highly nonplanar surrounding pentagon is that its central edge has more than ∼10° of external rotation. For a particular surrounding face, if the criterion is met for both aluminum and carbon models, the asterisk is large; if the criterion is met for only one model, the asterisk is small. The number to the right of each Ring label is the energy for that ring relative to the baseline Ring to the far left of that row. The energy was computed for carbon Rings with molecular mechanics, but all bonds were single bonds, and electrostatic interactions were turned off. The Rings in each row have the same number of atoms. (A) Hex-Rings. (B) Pent-Rings.
Overview of the physical basis
The dashed arrows in Fig. 3 mark the central concept of this article. The dashed arrows show that external edge b (or b′), essentially on the floor in the middle part of Fig. 3 A, rises to an angle intermediate between the angles of external edges a and c (or a′ and c′) in the lower part of Fig. 3 A after the surrounding faces have been completed. By contrast, the dashed arrows in Fig. 3 B show that the angle of external edges b (or b′) shows almost no change from the middle part of the figure to the lower part.
Hex-Ring 611, shown in the top part of Fig. 3 A, has only green DADs. Since it has no DADs arranged head-to-tail, we describe it as probable in the companion article (10). The middle part of Fig. 3 A represents the three-dimensional structure of a fragment of this hex-Ring unfettered by completion of surrounding faces. With no constraints, internal angles are ideal, 108° in putative pentagonal (5) faces and 120° in putative hexagonal (6) faces, and the central hexagonal face is planar. Because the dihedral angles about edges that emerge from a 666 vertex—vertices that join three hexagons—are all 180°, the front four 666 vertices place the front four external edges a and a′, b and b′, in the same (horizontal) plane as the central face. The back two vertices are 566, requiring a dihedral angle of 138.2° about the tail end of the green DAD, so the back two external edges c and c′ rise steeply. If completion of the surrounding faces left these external edges a, b, and c (or a′, b′, and c′) in the same position, then the hexagonal face that includes edges b and c (or b′ and c′) would be severely nonplanar. However, as illustrated in the lower part of Fig. 3 A, based on the data in Table 1, completion of the surrounding faces raises external edges b and b′, thus distributing the nonplanarity among surrounding faces and reducing the severity of the nonplanarity of the face that would include b and c (or b′ and c′).
Hex-Ring 631, shown in the top part of Fig. 3 B, has two pairs of head-to-tail DAD edges. We describe it as improbable (10). With no constraints, the fragment in the middle of the figure has ideal internal angles and a planar central hexagon. The two 666 vertices cause the front two external edges a and a′ to lie in the same (horizontal) plane as the central face. Due to the green DADs, external edges b and b′ rise steeply from the horizontal plane. Due to the red DADs, external edges c and c′ rise even more steeply. If completion of the surrounding faces left these external edges in the same position, then both the hexagonal face that includes edges a and b (or a′ and b′) and the pentagonal face that includes edges b and c (or b′ and c′) would be severely nonplanar. Based on the data in Table 1, after completion of the surrounding faces, external edge b (or b′) rises nearly as steeply as it does in the unfettered structure. The reason edge b (or b′) does not move is that if it rose more steeply, the hexagonal face that includes edges a and b (or a′ and b′) would then become more nonplanar, but if it rose less steeply, the pentagonal face that includes edges b and c (or b′ and c′) would become more nonplanar. Insofar as energy follows the square of deviations from ideal, energy would rise in both cases. Thus, completion of the surrounding faces leaves undiminished the severe nonplanarity of the surrounding faces bordering the green and the red DAD edges.
In the remainder of Results we show that hex-Ring 631 in Fig. 3 B is representative of Rings with head-to-tail DADs insofar as having surrounding faces with undiminished nonplanarity. We also show that hex-Ring 611 in Fig. 3 A is representative of the other Rings with DADs insofar as the nonplanarity of surrounding faces is distributed and reduced. We also show why this happens.
A physical description of DAD
As shown in Fig. 1 B, an edge with a green DAD has a pentagon at one end, a hexagon at the other, and two side hexagons. In Fig. 4 A, we pull the two ends apart to show that the dihedral angle about the top of vertical edge 23, at the 566 vertex 2, is 138.2°, whereas the dihedral angle about the bottom of edge 23, at the 666 vertex 3, is 180°. (Please note that we bold near-vertex numbers.) The difference, a DAD, is 41.8° (10). By contrast, if the faces at the two ends of an edge are the same, as is the case in Fig. 4 B for vertical edge 23, the end vertices are both 566, the dihedral angles (138.2°) at the two ends of the edge are the same, and the edge has no DAD.
To show the DAD physically, we tilt the top of Fig. 4 A forward, foreshortening edge 23 (Fig. 4 C). If the top of that figure is tilted farther forward to become Fig. 4 D, edge 23 appears as a point, showing near (thick) edges 24 and 21 and the 138.2° dihedral angle between them, along with far (thin) edges 36 and 35 and the 180° dihedral angle between them. In Fig. 1 B, we represented this change in dihedral angle, the green DAD, by the green vector with its tail at the narrow (pentagon) end and its head at the broad (hexagon) end. Thus, as shown by Fig. 4 D, the green DAD represents an increase of 41.8° in dihedral angle, a broadening from tail end (138.2°) to head end (180°).
Viewed along edge 23, the edge that appears as a point in Fig. 4 D, near edge 24 rotates counterclockwise (negative) into far edge 36, as shown by the curved arrow on the left. And, near edge 21 rotates clockwise (positive) into far edge 35, as shown by the curved arrow on the right. As will be described below, this rotation (in degrees of angle) on the one side minus this rotation on the other side measures the overall broadening from the front edges to the back edges, the DAD.
As was shown in Fig. 1 B, because the side faces may be two hexagons, a hexagon and a pentagon, or two pentagons, there are three types of DAD edge that we color green (41.8°), red (18.4°), and blue (14.6°), respectively, with the vectors always pointing from the pentagon (narrow dihedral angle) end of the edge to the hexagon (broad dihedral angle) end of the edge.
Edges may have twist as well as DAD
For an edge without any DAD, as in Fig. 4 B, the far edges could be directly behind the near edges, as shown by tilting the top of Fig. 4 B forward into Fig. 4 E and farther forward into Fig. 4 F, and then the near edges would obscure the far edges. However, even without any DAD, the far edges may not be directly behind the near edges due to twist of edge 23. For example, Fig. 4 G shows a rotation of both far (thin) edges 36 and 35 in the same (counterclockwise) direction from the near (thick) edges 24 and 21. The DAD is still 0°. Likewise, without altering the 41.8° DAD required by the arrangement of faces in Fig. 4 A, the broadening shown in Fig. 4 D may be accompanied by twist, as illustrated in Fig. 4 H. Because the twist of the near (thick) edges into the (thin) far edges is counterclockwise, the resulting rotation from near edge 24 into far edge 36 is no longer equal and opposite to the rotation from near edge 21 into far edge 35, as was the case in Fig. 4 D but the difference between the two rotations remains 41.8°.
Below, in Fig. 5, we place the sign and magnitude of the DAD (D) and the twist (T) in the context of Rings.
Row I hex-Rings
The hex-Rings in Row I of Fig. 2 A have no DAD edges. Hex-Ring 601 alone would form a plane of planar hexagons. All of the hexagons in the truncated icosahedron (Fig. 1 B) are Ring 633.
Row II hex-Rings
Sym edges
All of the hex-Rings in Row II of Fig. 2 A have two DAD edges. As can be seen in Ring 611, for example, each of these hex-Rings has a vertical line of mirror symmetry that bisects two Sym edges, the Sym edge at the top and the Sym′ edge at the bottom, splitting each hex-Ring into mirror-symmetric halves.
Internal and external rotation
Hex-Ring 611, shown in Fig. 5 A, is representative of the Row II hex-Rings. The pentagon is at the back (Fig. 5 B). The bowl-like structure of the tilted and slightly rotated Ring in Fig. 5 B curves upward because the pentagon pulls the back part of the structure up from the floor. In this figure, we can look down the foreshortened green DAD edge 23, one of the edges of the central face and therefore a central edge. The two edges 21 and 34 are internal edges with respect to their common central edge 23. (Edges 21 and 34 are also central edges, but when we focus attention on central edge 23, they become internal edges.) We call rotation from near (thick) internal edge 21 into far (thin) internal edge 34 about central edge 23 internal rotation (I).
The enlargement in Fig. 5 C focuses on this region of the Ring. After additional backward tilt into Fig. 5 D, an end-on view down the green DAD edge 23 makes that edge appear as a point and makes the associated internal planes 321 and 234 appear as internal edges 21 and 34. The right-hand screw rule determines the sign of the rotation between near edge 21 and far edge 34 about edge 23. It is positive in this case: If you point your right thumb into the page, from near vertex 2 to far vertex 3, you have to turn your fingers in the clockwise (positive) direction for their tips to go from near edge 21 to far edge 34. (The sign of the rotation is the same if you point your right thumb out of the page, from far vertex 3 to near vertex 2. In that case, you also have to turn your fingers clockwise for their tips to go from far edge 34 into near-edge 21.) Because the curved arrow on the left in Fig. 5 D represents the internal rotation (I) from near (thick) edge 21 to far (thin) edge 34 about their common edge 23, the curved arrow is clockwise when the rotation is positive. This is so in all of our figures.
The two edges 26 and 35 are part of surrounding faces. We call them external edges with respect to their common central edge 23, and we call rotation from near (thick) edge 26 to far (thin) edge 35 about central edge 23 external rotation (E). By the right-hand screw rule, this rotation E in Fig. 5 D is negative in sign. Because we draw the curved arrow representing external rotation E from near (thick) external edge 26 to far (thin) external edge 35, the counterclockwise rotation signified by the curved arrow is negative in sign.
In summary, for both internal and external rotations I and E, clockwise rotations are positive in sign, and counterclockwise rotations are negative in sign.
The relationship between DAD (D) and internal and external rotations I and E
We call the diagram in Fig. 5 D an elevation diagram. Sym edge 34 and Sym edge 01 in Fig. 5 A define the floor of the Ring and define the horizontal plane, so we draw edge 34 in Fig. 5 D as horizontal. The elevation diagram thus shows the elevation of the internal and external edges with respect to horizontal. It also shows the internal and external rotations I and E from near (thick) edges to far (thin) edges.
Table 1 and the complete Supplementary Material 1 Table 1A list the measured E and I with respect to each of the six central edges of Ring 611 modeled with aluminum atoms. Edge 23 is one of the edges of Ring 611 with a green DAD. The elevation diagram for this green DAD edge (Fig. 5 D) shows that the internal and external rotations edge appear to be nearly equal and opposite. For one of the green DAD edges of hex-Ring 611, I = +12.03° and E = −16.34°, confirming the impression that I and E are nearly equal and opposite. Corresponding measured values are listed for Rings modeled with carbon atoms in Supplementary Material 1 Table 1B. The values in the complete Supplementary Material 1 Tables 1A and 1B are qualitatively in complete agreement, so we cite data for just the aluminum models of Rings in the text and construct figures from the aluminum models.
The angle between the near (thick) external edge 26 and the near (thick) internal edge 21 in Fig. 5 D is the dihedral angle about the green DAD edge 23 at its vertex 2 end. The angle between the far (thin) external edge 35 and the far (thin) internal edge 34 is the dihedral angle about green DAD edge 23 at its vertex 3 end. The DAD is the difference, shown by the narrowing of the dihedral angle from the near (thick) hexagon end at vertex 2 of the green DAD edge 23 to the far (thin) pentagon end at vertex 3 of the green DAD edge 23. This narrowing (reduction, negative in sign) of the angle between the near (thick) edges to the angle between the far (thin) edges in Fig. 5 D is thus the very picture of a DAD in a Ring. Equivalently, we may speak of the broadening (increase, positive in sign) of the angles from the pentagon end to the hexagon end. Thus,
| (1) |
As given by Eq. 1, the magnitude calculated for the DAD (D) of this edge is (+12.03°) − (−16.34°) = +28.37°.
This value is not equal to the ideal 41.8° for a green DAD because the internal angles are not all equal to the ideal angles 120° in the hexagons or 108° in the pentagons. We discuss the effect on D of departures from ideal internal angles in The Effect of Internal Angles that Deviate from Ideal is Small in Supplementary Material 2. That section shows that the effect of nonideal angles on D is much greater when a 666 vertex is involved, as in a green DAD edge, than in a case where no 666 vertex is involved, as in a red or blue DAD edge (Fig. 1 B). Specifically, dropping one of the angles at a 666 vertex by 1° from the ideal 120° to 119° reduces dihedral angles from the ideal 180° by ∼11.5°. By contrast, dropping one of the ideal angles at 566, 556, and 555 vertices by 1° reduces dihedral angles from the ideal by 1.2°–1.9°, 0.7°–1.4°, and 0.5°–1.2°, respectively (essentially trivial amounts).
Complete sets of elevation diagrams
Fig. 6 A also shows the upwardly curving bowl created by Ring 611. In Fig. 6 B, the elevation diagrams for all six central edges are shown in the corresponding surrounding faces. For example, the elevation diagram outside the green DAD edge at the upper right is identical to that in Fig. 5 D. In Fig. 6 B, that green DAD edge has a small arrowhead at its lower right to specify where your eye would be as you sight down that edge, thus specifying near and far internal and external edges with respect to that central edge, just as they were in Fig. 5. All of the other central edges have small arrowheads as well to specify near and far edges in their elevation diagrams. All of the arrowheads point in the same counterclockwise direction. As a result, in all of the elevation diagrams, sighting down a central edge from its arrowhead puts internal edges on the left and external edges on the right.
As in Fig. 5 D, in each elevation diagram, near-internal and external edges are shown as thick line segments, and far internal and external edges are shown as thin line segments. Also as in Fig. 5 D, the signs of the rotations follow the right-hand screw rule, and our convention is to show curved arrows that point from near to far edges with respect to a central edge to represent I and E rotations. Thus, the sign of a curved arrow that points clockwise is positive.
The relationship among twist (T), DAD (D), and internal and external rotations I and E
Recalling Fig. 4 G, twist T is the average of the internal and external rotations about a central edge:
| (2) |
As already shown in Fig. 4, a central edge with I = E has D = 0 and twist T equal to I and to E. For example, the Twist edge on the right side of Ring 611 in Fig. 6 B should not have any D because its end faces are the same, both hexagons. When that edge is rotated and tilted to sight straight down it, as shown by its elevation diagram outside the Twist edge on the lower right of Fig. 6 B, the internal and external rotations can be seen to be nearly equal, I = −12.03° and E = −15.17° (Table 1), with curved arrows in the same counterclockwise direction. Twist T calculated by Eq. 2, the average of I and E, is −13.60° (Table 1). Because the internal angles are not all ideal, the D of this Twist edge is not zero, but it is small; by Eq. 1, D is just (−12.03°) − (−15.17°) = +3.14° (Table 1).
Because of nonideal internal angles, the green DAD edge with D of +28.37° does have some Twist T, but it too is small: [(+12.03°) + (−16.34°)]/2 = −2.16° by Eq. 2. Thus, the green DAD edge has predominantly D, and the Twist edge has predominantly T.
The total D in the right mirror-symmetric half of Ring 611 is 31.51°, the sum of 28.37° for the green DAD edge and 3.14° for the Twist edge.
Equations 1 and 2 lead to additional equations that reveal how internal and external rotations depend on DAD and twist:
| (3) |
| (4) |
Because of the pentagon, external edges c and c′ in Fig. 6 A have large angles with respect to the horizontal, as can be seen in the elevation diagram in the pentagon above the upper Sym edge in Fig. 6 B.
Because its end faces are the same, this Sym edge has no DAD; because of the overall symmetry of the Ring, it has no twist either. Due to symmetry and Eq. 3, there is also no internal rotation about this Sym edge. Due to symmetry and Eq. 4, there is no external rotation about this Sym edge either, and external edges c and c′ have the same angle with respect to horizontal. The same reasoning applies to the lower Sym′ edge. However, for the Sym′ edge, there is no adjacent pentagon, so the elevations of the external edges a and a′ from the horizontal plane are very small. In general, the D and T, I, and E about Sym edges are all zero.
Ideally, hex-Ring 611 has the two green DAD edges with D and no T (approximately correct), the two Twist edges with T but no D (also approximately correct), and two Sym edges with neither D nor T (exactly correct). The actual values of E, I, D, and T about all of the central edges in 611 are given in Table 1 and the Supplementary Material 1 Tables 1A and 1B. The Supplementary Material 1 Tables show qualitatively the same story for the other Row II hex-Rings.
Half hex-Rings
As can be seen in Fig. 6 A for hex-Ring 611, the Sym and Sym′ edges are parallel and thus form a plane that we define as horizontal. Therefore, within each right or left symmetric half of hex-Ring 611, the sum of the internal rotations I over the two non-Sym edges, that is, the DAD edge and the Twist edge, must be zero. Thus,
| (5A) |
If edge 1 refers to the DAD edge and edge 2 refers to the Twist edge, then
| (5B) |
Indeed, for Fig. 6 B on the right side, I1 = −12.03° and I2 = +12.03° (Table 1). This rule applies to all of the Row II hex-Rings, as can be verified in Table 1 and Supplementary Material 1 Table 1.
Incorporating Eq. 3 into Eq. 5B produces Eq. 6A:
| (6A) |
It follows that
| (6B) |
or
| (6C) |
Therefore, as can also be verified in Table 1 and the Supplementary Material 1 Table 1, the sum of the T values over the two non-Sym edges in each symmetric half-Ring of a Row II hex-Ring is half of the sum of the D values in that symmetric half-Ring but opposite in sign. For example, for the right symmetric half of Ring 611, and
The sum of the external rotations E in the symmetric half of a Row II hex-Ring is not equal to zero, but taking into account the zero external rotation about the Sym edges, we can derive a useful relationship by use of Eq. 4, again assigning edge 1 to the green DAD edge and edge 2 to the Twist edge:
| (7A) |
therefore,
| (7B) |
Applying Eq. 6C:
| (8) |
Equation 8 states three relationships that hold for Row II hex-Rings, relationships that can be verified in Table 1 and the Supplementary Material 1 Table 1. The most critical relationship is this one: In each (left or right) symmetric half of a hex-Ring, the sum of the external rotations is equal and opposite to the sum of the DADs. The DADs are responsible, quantitatively, for the external rotations. For example, for the right symmetric half of hex-Ring 611, and correspondingly Later, we show that the key to the physical mechanism of the head-to-tail exclusion rule is the distribution and magnitude of the external rotations that must sum to the total magnitude of the DADs in each half Ring.
Whole hex-Rings
Around any whole Ring, I generally sums to zero. This is so because a sequence of internal rotations from any one internal edge to the next, to the next … and ultimately back to itself must end up back in its starting position. This is also so for a sequence of external rotations from any one external edge ultimately back to itself, so around any whole Ring, E generally sums to zero as well. Thus, the sum of the internal and external rotations over the six edges of a hex-Ring is zero:
| (9) |
| (10) |
These two rules may be observed by following the full sequence of internal (or external) rotations on the left (or right) sides of the six elevation diagrams for hex-Ring 611 in Fig. 6 B. The data in Table 1 and the Supplementary Material 1 Table 1 confirm these rules for this and the other Row II hex-Rings. (In Nonzero Sum of Internal and External Rotations Around a Whole Ring, offered in Supplementary Material 2, we describe a minor exception to Eqs. 9 and 10.)
Because of mirror symmetry in the case of the Row II hex-Rings, the external and internal rotations I and E about mirror-equivalent edges, like the green DAD edge on the right (I = +12.03° and E = −16.34°) and the green DAD edge on the left (I = −12.03° and E = +16.34°) in Fig. 6 B, are equal and opposite, as may be confirmed in Table 1 and Supplementary Material 1 Table 1 as well. Also, the Ds of mirror-equivalent edges (like the green DAD edges) are equal and opposite (e.g., +28.37° and −28.37°), as are the Ts (e.g., −2.16° and +2.16°), as can be seen in Fig. 6 B. As a result, over the top half of each Row II hex-Ring (e.g., left green DAD edge, top Sym edge, and right green DAD edge in Fig. 6 B), the sums of the E, I, D, and T values are all zero. Likewise, the sums of these values over each bottom half (e.g., left Twist edge, bottom Sym′ edge, and right Twist edge in Fig. 6 B) are zero.
Equal sharing of external rotations between DAD and Twist edges
If the internal angles were all the ideal 120° and 108°, the DAD edges would have D but no T, and the Twist edges would have T but no D. In that case, the above Eqs. 3 and 4 would give the effects of the DAD rather simply: For the DAD edge, ID = +D/2 and ED = −D/2. For the Twist edge, IT = −D/2 and ET = −D/2. As demanded by Eqs. 5A and B and Eq. 8, the sum of the internal rotations in a symmetric half-Ring (+D/2 + −D/2) is zero, and the sum of the external rotations in a symmetric half-Ring (−D/2 + −D/2) is −D. Of particular importance, the external rotation ultimately due to a DAD of magnitude D would be distributed equally (−D/2) between the two non-Sym edges. In fact, E about the DAD edge and E about the Twist edge in each symmetric half of Ring 611 are close to equality (Fig. 6 B).
Fig. 7 A provides an equivalent description of the physical situation. Following the numbers in that diagram:
-
1.
The green DAD vector, running from its pentagon end to its hexagon end, has a DAD of magnitude D. The broadening of the dihedral angle from the pentagon end to the hexagon end causes
-
2.
counterclockwise external rotation E = −D/2 about the DAD edge, and
-
3.
equal but opposite—clockwise—internal rotation I = +D/2 about the DAD edge.
-
4.
Because the sum of the internal rotations must be zero in a symmetric half (Eqs. 5A and 5B), the clockwise internal rotation I = +D/2 about the DAD edge must be balanced by an opposite—counterclockwise—internal rotation I = −D/2 about the Twist edge.
-
5.
Because the Twist edge has no DAD, the counterclockwise internal rotation I = −D/2 about the Twist edge must be accompanied by an equal—also counterclockwise—external rotation E = −D/2 about the Twist edge.
Due to these relationships, the DAD and Twist edges share the external rotation due to the D of the DAD, each taking half (−D/2).
If the internal angles are not all ideal, the situation is a little more complicated. However, if the two halves are mirror-symmetric, the Sym edges are still parallel, and I and E rotations of the Sym edges are still zero. Also, the internal rotations about the DAD and Twist edges are still equal and opposite (ID = −IT). However, the DAD edge may have some T, and the Twist edge may have some D, so the external rotations do not necessarily distribute perfectly equally (−D/2) about each of the two edges. For Ring 611, the external rotation about the green DAD edge on the right is +16.34°, whereas that about the Twist edge is +15.17°. If α is the percent of total D about the DAD edge of a symmetric half, then (100−α) would be the percent of the total D about the Twist edge. In the ideal case, α would equal 50%. Table 1 and Supplementary Material 1 Table 1 show that α for the Row II hex-Rings is 52% for Ring 611, 63% for Ring 622, 45% for Ring 643, and 55% for Ring 651. Thus, the data show that the Row II hex-Rings do distribute the nonplanarity nearly equally between the surrounding face at the DAD edge and the surrounding face at the Twist edge.
The approximately equal sharing of nonplanarity makes sense with regard to minimization of energy. The Hookean energy cost of deviation from an ideal value goes as the square of the magnitude of the deviation: two deviations of magnitude cost less than 1 deviation of magnitude 0 and one of magnitude 1, thus 2 × ()2 = vs. 1 × 12 + 1 × 02 = 1. More simply, stretching two identical springs in series stretches each one by half of the total stretch.
This sharing of external rotation in hex-Ring 611 explains the difference between the middle and bottom parts of Fig. 3 A. In the middle, the surrounding faces are not completed, the central face is planar, only back external edges c and c′ rise (steeply) from the (horizontal) floor, and middle external edges b and b′ remain on the floor. Completion of the surrounding faces produces Fig. 6 B, in which edges b and b′ rise from the floor approximately half as steeply as edges c and c′. By extracting just the central face and the external edges from the completed Ring 611 in Fig. 6 B, the bottom of Fig. 3 A shows clearly this sharing of external rotation.
Row-III hex-Rings
Each of the two hex-Rings in Row-III of Fig. 2 A has two pairs of head-to-head green DAD edges (623) or two pairs of tail-to-tail red DAD edges (642), two Sym edges, and no Twist edges. All of the equations above for Row-II hex-Rings apply to Row-III hex-Rings. However, Row-III hex-Rings have mirror-symmetric top and bottom halves as well as mirror-symmetric left and right halves, so these have an additional simplifying constraint. From the upper to the lower green DAD edges of hex-Ring 623, each of the values of I, E, D, and T is equal and opposite (Table 1), as can be seen in Fig. 6 D. For example, for the green DAD edge on the upper right, these values are −14.55°, +12.90°, −27.45°, and −0.83°; for the green DAD edge on the lower right, all of these values are the same magnitude but have the opposite sign (Table 1). The same is true for the upper and the lower red DAD edges of hex-Ring 642 (Supplementary Material 1 Table 1). The sum of the Is, the Es, the Ds, and the Ts in each of the halves—left, right, upper, and lower—is thus zero.
Like the situation in hex-Ring 611, where E and I are nearly equal and opposite, the internal and external rotations about each of the green DAD edges in hex-Ring 623 are nearly equal and opposite (Fig. 6 D), with for example I = −14.55° and E = +12.90° for the green DAD edge on the upper right of Fig. 6 D (Table 1). Also, like the situation in hex-Ring 611, these green DAD edges in hex-Ring 623 have D (−27.45°) but almost no T (−0.83°). Of particular note, external rotation about each green DAD edge (+12.90° for the upper right in Fig. 6 D) is close to but slightly less than half of the magnitude of its green D (−27.45°). Internal rotation (−14.55°) takes up slightly more than half. In the IPR fullerene with 70 vertices in Fig. 1 C, all of the five hexagons with four green DADs are Ring 623s, and each behaves in this manner.
The situation in hex-Ring 642 is similar in that less than half of the DAD ends up as external rotation. At each red DAD edge, the internal rotation (+14.06°) takes up considerably more than half of its red D (+17.66°), so the external rotation (−3.60°) takes up considerably less than half of that red D. Because the internal rotation is larger than the external, the edge has T as well as D, but the T (+5.23°) has the same sign as the D (+17.66°).
Above, we showed that each DAD edge in a Row-II hex-Ring reduces its external rotation ideally 1), by splitting its D between internal rotation (+D/2) and external rotation (−D/ and 2), then the Twist edge repays the internal rotation (−D/2) and incurrs equal external rotation (−D/2). Ideally, each DAD edge in a Row-III hex-Ring reduces its external rotation by the same mechanism, splitting its D between internal rotation (+D/2) and external rotation (−D/2). However, in place of a Twist edge, the second edge in a Row-III hex-Ring is also a DAD edge, with the second DAD pointing in the opposite direction from the first. As a result, this second edge splits its −D between internal rotation (−D/2) (which automatically pays off the internal rotation of the first DAD edge) and external rotation (+D/2). Ideally, the external rotation at each DAD edge is reduced to half of the magnitude of its D for Ring 642. In fact, the data show that the external rotations of the green DAD edges in Ring 642 are reduced to even less than half.
Row-IV hex-Rings
Hex-Ring 631, with two Sym edges
Like the Row II hex-Rings, hex-Ring 631 (Fig. 8, C and D) has two Sym edges, and the above equations apply to the remaining two edges in each mirror-symmetric half. Also, like the Row-III hex-Rings, hex-Ring 631 has two DAD edges in each half. However, as shown in Fig. 8 A, these two DAD edges are in a head-to-tail arrangement, from head of red DAD edge with D = +16.68° to tail of green DAD edge with D = +26.14° (Table 1). The total D in the mirror-symmetric half is +42.82°.
In addition, the total external rotation in a half (equal to minus the sum of the two Ds by Eq. 8, hence −42.82°) must be taken up by just these two edges, the red DAD edge and the green DAD edge, since no Twist edge is available. The resulting very large external rotations, −16.65° and −26.17°, are visible in the elevation diagrams in Fig. 8 B. The reason for the absence of sharing of the external rotations is that any shifting of the D about one DAD edge into internal rotation would increase the external rotation about the next DAD edge. Indeed, because essentially all of the D is taken up exclusively by external rotation at these two DAD edges, the internal rotations are very small (+0.03° and −0.03°), as demanded by Eq. 1 and shown in the elevation diagrams in Fig. 8 B.
Fig. 7 B provides an equivalent description of the physical situation. Following the numbers in that diagram:
-
1.
The red DAD vector, running from its pentagon end to its hexagon end, has a DAD of magnitude R. The broadening of the dihedral angle from the pentagon end to the hexagon end causes
-
2.
a counterclockwise external rotation E = −R but no internal rotation about the red DAD edge.
-
3.
The green DAD vector, running from its pentagon end to its hexagon end, has a DAD of magnitude G. The broadening of the dihedral angle from the pentagon end to the hexagon end causes
-
4.
a counterclockwise external rotation E = −G but no internal rotation about the green DAD edge.
Because each of the external rotations about the red and green DAD edges takes up the entire broadening due to its DAD, there is no sharing of external rotations and no sharing of the broadening between external and internal rotations.
The absence of sharing of the external rotations explains the similarity between the middle and bottom parts of Fig. 3 B. The severity of the nonplanarity of the putative surrounding hexagonal face outside the green DAD edge and of the putative surrounding pentagonal face outside the red DAD edge is fully preserved in the completed Ring.
Because the internal rotations of the DAD edges in Ring 631 are so small, each of these DAD edges must therefore twist (−8.31° and −13.10°) by an amount equal to minus half of its D, as can be observed in Fig. 8 B. Thus, about each DAD edge, T is half of its D but opposite in sign (Table 1). With essentially no internal rotation, the central face is planar or nearly so (Fig. 8 A), but the external rotations are very large, and the faces external to the green DAD edge and to the red DAD edge are highly distorted (nonplanar).
Hex-Rings 621 and 641, with only one Sym edge
Unlike the situation of the hex-Rings in Rows I–III and of hex-Ring 631, the only line of mirror-symmetry in Row-IV hex-Rings 621 and 641 passes through two vertices (Figs. 2 A and 8 D). There are thus no parallel Sym edges, no requirement that the sum of the internal and external rotations in each right and left mirror-symmetric half equals zero, and Eqs. 5A and 5B and Eqs. 6A–6C do not apply. Addition of the third non-Sym edge in each half produces a revised form of Eqs. 7A and 7B for hex-Rings 621 and 641:
| (7A′) |
| (7B′) |
For example, in Table 1 for the right half of hex-Ring 621, and . Because the two terms on the right side of Eq. 7B′ turn out to be nearly equal, Eq. 8 is still approximately true, with ΣE = −ΣD in each symmetric half containing a green DAD edge, a red DAD edge, and a Twist edge (Fig. 8, C and D). With head-to-tail DADs, the D values add, the total D in a symmetric half is very large, and the total E in a half is correspondingly very large, as is apparent in the elevation diagrams of hex-Ring 621 in Fig. 8 D.
Unlike hex-Ring 631, the two hex-Rings 621 and 641 have a Twist edge to take up some of the external rotation (Fig. 8, C and D). For Ring 621, the red DAD edge on the right distributes the effect of its D half by external rotation (+8.65°) and half by internal rotation (−8.37°), so its T (+0.14°) is essentially zero (Fig. 8 D; Table 1). However, the external rotation of the green DAD edge (+21.98°) is very large, larger in magnitude than half of the green D (−25.74°) (Table 1) by virtue of a twist T (+9.11°) of opposite sign that increases the external rotation. (In this respect, having D and T of opposite sign (Table 1), the green DAD edge is similar to the two DAD edges of hex-Ring 631.) The external rotation in the Twist edge (+17.82°) is also quite large to satisfy Eq. 8, essentially balancing the internal rotation of the red DAD edge (Fig. 8 D). In summary, the external rotation about the red DAD edge is not severe, so the surrounding face at the red DAD edge is not so nonplanar, but the price is very large external rotation about the green DAD and Twist edges, causing more severe nonplanarity of the surrounding faces at those edges.
The situation in Ring 641 is similar to that in Ring 621, except that the external rotation about the Twist edge is unremarkable, whereas the red DAD edge has almost all external rotation and no internal rotation (Supplementary Material 1 Table 1). Correspondingly, the magnitude of the T is half of its D but of opposite sign. The external rotation about the green DAD edge is also more than half of the magnitude of its DAD, with T of sign opposite to its D. In summary, the surrounding face at the Twist edge is not so nonplanar, but the surrounding faces at the two DAD edges suffer extra nonplanarity.
Hex-Ring 632, with only one head-to-tail arrangement of DADs
Of all the 21 Rings, hex-Ring 632 is the only one without any line of symmetry (Figs. 2 A and 8, E and F). Also, all of the other excluded Rings have two head-to-tail arrangements of DADs, but Ring 632 has just one. Nonetheless, the external rotation about every one of the four DAD edges is more than twice the internal rotation (Fig. 8 F; Table 1). Indeed, the external rotation about the green DAD edge in the head-to-tail arrangement (+29.50°) is very large, partly because the green DAD edge has a large D (−31.63°) but partly because it has almost no internal rotation (−2.13°). The external rotation about the other green DAD edge (−25.53°) is also very large. Thus, all four of the surrounding faces would be nonplanar, and the ones at the green DAD edges would be highly nonplanar.
Pent-Rings
Each of the pent-Rings has a line of mirror-symmetry that bisects one Sym edge and one vertex (Fig. 2 B). Therefore, like Rings 621 and 641, none of the pent-Rings has parallel Sym edges, and Eqs. 5A and 5B, Eqs. 6A–6C, and Eq. 8 cannot be applied rigorously. Excluding the Sym edge, for which I = 0 and E = 0, each symmetric half has two working edges. Therefore, the original Eqs. 7A and 7B still apply. Moreover, Eq. 8 is still approximately true, that ΣE = −ΣD in each mirror-symmetric half (Table 1 and Supplementary Material 1 Table 1). All of the other equations above still apply to the pent-Rings.
Moreover, as described in the section of Supplementary Material 2 called The Effect of Internal Angles that Deviate from Ideal is Small, the dihedral angles at 566, 556, and 555 vertices are little affected by internal angles that deviate from the ideal. That is, the measured Ds about red and blue DAD edges remain very close to their ideal values 18.4° and 14.6°. For the same reason, the measured D about edges that are not supposed to have D, like Twist and Sym edges, remains zero or very close to zero. Thus, in these pent-Rings, the Twist edges have T but no D, the Sym edges generally have no D and no T, and virtually all of the D is restricted to the DAD edges (Table 1 and Supplementary Material 1 Table 1). In addition, each of the values of I, E, D, and T is generally equal and opposite from one mirror-symmetric half to the other.
Row I pent-Rings
The Row I pent-Rings in Fig. 2 B have no DAD edges. All of the pentagons in the dodecahedron (Fig. 1 A) are pent-Ring 551. All of the pentagons in any IPR fullerene, including the truncated icosahedron, are pent-Ring 501.
Row II pent-Rings
In the key characteristic, the Row II pent-Rings are similar to the Row II hex-Rings: The external rotation induced by the DAD edge is shared between the DAD and Twist edges. For example, as a percent (α) of the total external rotation in each mirror-symmetric half, the external rotation in the DAD edge in pent-Ring 532 in Fig. 9, A and B, is 47%, with the Twist edge taking up 53% (Table 1). (The I, E, D, and T about the Sym edge are all zero.) The corresponding percentages (α) for the DAD edges in pent-Rings 511, 522, and 541 are 60%, 58%, and 63% (Supplementary Material 1 Table 1A). With the exception of pent-Ring 511, the percentages are similar in the carbon models (Supplementary Material 1 Table 1B).
Row III pent-Rings
There are no Row III pent-Rings.
Row IV pent-Rings
Like the other pent-Rings, pent-Rings 521 and 531 have a line of mirror symmetry that bisects one Sym edge and passes through a vertex rather than another Sym edge (Fig. 2 B and Fig. 9, C and D). Therefore, Eqs. 5A and 5B and Eqs. 6A–6C do not apply, but Eq. 8 is approximately true, that ΣE = −ΣD in each mirror-symmetric half (Table 1). Specifically, for the right side of Ring 521, ΣE = +30.50°, whereas ΣD = −31.66°. Likewise, for the right side of Ring 531, ΣE = +31.01°, whereas ΣD = −31.77°. Like the other Rings with mirror-symmetry, the I, E, D, and T values are equal and opposite in the two halves. Like Row IV hex-Rings 621, 631, and 641, these two pent-Rings have in each mirror-symmetric half a head-to-tail arrangement of DAD edges, specifically blue head to red tail (Fig. 2 B).
Because these pent-Rings have a Sym edge, they are even more like hex-Ring 631, in that in each mirror-symmetric half, two edges—not three—share the external rotations due to their DADs (Fig. 9 D). Thus, as in hex-Ring 631, in the right side of pent-Ring 531 essentially all of the D (−13.81° and −17.96° for the blue and red DAD edges) must be taken up by external rotation (+15.05° and +15.96°) at these two DAD edges. Internal rotations are thereby minimized (+1.24° and −2.00°) (following Eq. 1), producing a nearly planar central face, as shown by the elevation diagrams for Ring 531 (Fig. 9 D). The external rotations are therefore large for three reasons: the total D in each half-Ring is the sum of two Ds; the internal rotations are nearly zero; and there is no third edge to share the external rotations. These large external rotations (Fig. 9 D) mean that the surrounding faces at the DAD edges would be highly nonplanar.
Head-to-tail DADs, nonplanar faces, and relative energy among Rings
In Fig. 10 we mark each highly nonplanar surrounding face with an asterisk, the criterion being an external rotation about a central edge of ∼20° or more for a surrounding hexagon or ∼10° or more for a surrounding pentagon. We justify the difference in criterion because completion of a surrounding hexagon is achieved by addition of two vertices beyond the external edges, whereas completion of a surrounding pentagon is achieved by addition of just one. We reason that two vertices would have twice the flexibility of one in attempting to bridge the gap between the ends of the external edges that are pointing off in different directions.
Molecular mechanics (20–24), which was used to obtain the structures of the carbon Rings that gave rise to the data in Supplementary Material 1 Table 1B, also provided energies of the Rings (Fig. 10). However, as described in Methods, electrostatic interactions were turned off, and all of the carbon-carbon bonds were single bonds. Nonetheless, comparison is possible among Rings with the same number of carbon atoms (e.g., 621, 622, and 623 in Fig. 10 A), providing data consistent with a severe energy cost associated with head-to-tail DADs.
As shown for hex-Rings in Fig. 10 A, with hex-Ring 623 as baseline, hex-Ring 621 with its two pairs of head-to-tail DADs is 34.7 kcal/mol higher in energy. With hex-Ring 633 as baseline, the energy of hex-Ring 632 with one pair is 26.5 kcal/mol higher, and the energy of 631 with two pairs is 78.2 kcal/mol higher. With hex-Ring 642 as baseline, hex-Ring 641with two pairs is 39.4 kcal/mol higher. For pent-Rings in Fig. 10 B, with pent-Ring 522 as baseline, the cost of two pairs of head-to-tail DADs is 25.3 kcal/mol, and with pent-Ring 532 as baseline, the cost is 12.1 kcal/mol. These energies are many RT, ∼0.6 kcal/mol at room temperature. (The ideal gas constant R is 2 cal K−1 mol−1, and the absolute temperature T is 298 K.) If equilibrium obtained, based on the Boltzmann equation, the ratio of the concentrations of a Ring with head-to-tail DADs to a Ring without would be between e−12.1/0.6 and e−78.2/0.6, very small ratios indeed.
Discussion
DADs generate nonplanar faces
All of the faces of a dodecahedron and of a truncated icosahedron can be planar because every edge has the same types of faces at its two ends: two pentagons in the case of the dodecahedron (20 in Fig. 1 A) and either two pentagons or two hexagons in the case of a truncated icosahedron (60 IPR in Fig. 1 A). All other fullerene cages, an infinite number of them (9), have some edges with a pentagon at one end and a hexagon at the other. Such an edge has different dihedral angles about its two ends, a DAD (Fig. 1 B) (10), so one or both of the two faces alongside the edge must be nonplanar. Thus, all other fullerene cages must have some faces that are nonplanar.
Many of these other fullerene cages exist in nature. Clathrin triskelia self-assemble into fullerene cages of different sizes, including ones with 28, 36, 38, 40, 44, 50, and >60 vertices (8,18,19). This flexibility enables clathrin to endocytose cargo over a very wide range of sizes (8). Carbon atoms self-assemble into cages with 36 (17), 60, 70 (14), and more (13) vertices. Therefore, the presence of DADs and nonplanar faces must be compatible with self-assembly of both clathrin and carbon.
However, the number of fullerene cages that has been identified is quite limited. We proposed the hypothesis that a head-to-tail arrangement of DADs in a cage precludes self-assembly of that cage (10). This rule excludes all but 66 fullerene cages out of 222,509 graphically possible cages with 20 ≤ n ≤ 84 vertices. All of the clathrin and carbon cages in this range of n whose structure has been identified are among this group of 66. The 66 cages are comprised of 15 small non-IPR fullerene cages for n ≤ 60, the truncated icosahedron (a.k.a. buckminsterfullerene) for n = 60, and all of the 50 large fullerene cages that obey the isolated pentagon rule for 60 < n ≤ 84. The last finding suggests that the head-to-tail rule provides a geometric explanation for the IPR rule for large carbon fullerenes (S. Schein and T. Friedrich, unpublished).
The geometric explanation of the head-to-tail exclusion rule
Here we show that that a Ring with a head-to-tail arrangement of DADs would have some severely nonplanar surround faces. This implicit geometric consequence may impose a kinetic barrier to prevent assembly of Rings with head-to-tail DADs or may impose an energy cost to make those Rings unlikely to last in a competitive (equilibrium) situation. For carbon fullerenes, investigators point out that the energy on a per-carbon basis of the less abundant C70 is lower than that of the more abundant C60, part of the reasoning that ascribes selection among carbon fullerenes to kinetics (26). By contrast, clathrin triskelia are not so tightly embedded in cages (27,28) and exchange with triskelia in the cytoplasm (29–31), so self-assembly of clathrin may be described in equilibrium terms (e.g., (32,33)). In either case, the geometric picture of head-to-tail DADs that we describe here would exclude cages with head-to-tail DADs.
To develop the geometric picture, we first had to discover the affect of a single DAD on a Ring, where a Ring is defined as a central face and its immediately surrounding faces. With our focus on one edge of the central face—a central edge—we define the two adjacent central-face edges as internal edges and the two adjacent surrounding-face edges as external edges (Fig. 5). A DAD arises if the face at one end of the central edge is a pentagon and the face at the other end is a hexagon (Fig. 1 B). In that case, the dihedral angle about the central edge at the pentagon end is less than the dihedral angle about the central edge at its hexagon end. Necessarily, the angle between the internal and external edges at the pentagon end is less than the angle between the internal and external edges at the hexagon end (Fig. 5 D).
For a Ring with one DAD in each symmetric half—the Ring placed cup-up—the broadening of dihedral angle caused by the DAD is shared approximately equally between 1), a downward rotation of the external edge at the hexagon end with respect to the external edge at the pentagon end; and 2), a downward rotation of the internal edge at the hexagon end with respect to the internal edge at the pentagon end. For example, the green curved arrow 2 on the left in Fig. 7 A shows the downward rotation from external edge c′ to external edge b′, and the green curved arrow 3 on the right shows the approximately equal downward rotation from the internal Sym edge S to the internal Twist edge T′. As a result, the black curved arrow 5 on the left in Fig. 7 A shows the downward rotation from external edge b′ to external edge a′, and the black curved arrow 4 on the right shows the approximately equal upward rotation from the internal green DAD edge G′ to the internal Sym edge S′.
In Rings with head-to-tail DADs in each symmetric half, the broadening about each DAD edge is not shared between external and internal rotation. Instead, the broadening is achieved largely or entirely by a downward rotation of the external edge at the hexagon end with respect to the pentagon end (Fig. 8 and Fig. 9 D). Inward rotation does not contribute at the first DAD edge because it would have to be paid back by additional downward external rotation at the second DAD edge. Likewise, inward rotation does not contribute at the second DAD edge because it would have to be paid back by additional downward external rotation at the first DAD edge. This standoff is most clearly seen in Fig. 7 B, which shows no internal rotation at either of the red or green DAD edges of Ring 631.
This geometric picture emerged after definition of four quantities, DAD D, twist T, internal rotation I, and external rotation E, followed by measurement of I and E and calculation of D and T for all of the central edges in molecular models of all of the 16 Rings with DADs (Fig. 2; Table 1, Supplementary Material 1 Table 1). These data revealed relationships among the quantities, led us to recognize the geometric bases for the relationships, and enabled us to write the equations that underlie those relationships.
External rotation and nonplanar surrounding faces
When the external edge at the hexagon end of a central edge is rotated downward with respect to the external edge at the pentagon end, the surrounding face at that central edge must be nonplanar. Therefore, we speak of surrounding faces as nonplanar because the term is familiar, but from the point of view of the assembling Ring or the assembled Ring, what we mean specifically is that the two external edges are not in the same plane. The nascent (nonplanar) surrounding face may never actually assemble because vertices are unable to bridge the gap between the ends of the external edges that are pointing in different direction—thus a kinetic barrier. Or, if the Ring can assemble at all, the Ring with severely nonplanar surrounding faces would be a high-energy structure that would be replaced by a lower energy Ring with which it is in equilibrium.
Ironically, in Schein and Sands-Kidner (10) we identified the Ring type of all of the faces in a fullerene cage merely as a convenient way to tally head-to-tail DADs. Now, we understand that the geometric relationships at issue require the Ring. The failure to complete (kinetics) or keep (equilibrium) those Rings with head-to-tail DADs is at the heart of the exclusion mechanism. The Rings with head-to-tail DADs are improbable, either in initial assembly (kinetics) or over time in competition with other Rings (equilibrium).
How improbable?
As just stated, the severe nonplanarity of a surrounding face suggests that a Ring with such a face is unlikely to self-assemble. In addition, all of the improbable Rings have multiple—two, three, or four—highly nonplanar surrounding faces (the ones marked by asterisks in Fig. 10), so the relative probability of an improbable Ring versus a probable Ring should be that low probability to the second, third, or fourth power. Moreover, among the 222,443 excluded cages out of the 222,509 mathematically possible fullerene cages with 20–84 vertices, the smallest number of improbable Rings is two (10), though most have more, lowering the probability of an excluded cage with such Rings by another power of two or more.
Quasi-equivalent vertices
The vertices in fullerene cages are similar in that they are all three-connected and join pentagons and hexagons. In a dodecahedron—a Platonic, regular polyhedron—all of the vertices are 555, joining three regular pentagons, so these vertices are equivalent. Likewise, all of the vertices in a truncated icosahedron—an Archimedean, semiregular polyhedron—are 566, each joining a regular pentagon and two regular hexagons, and are equivalent.
No other fullerene cage has a single type of vertex. The vertices in other fullerene cages include two or more of the four vertex types 555, 556, 566, and 666 (10). Triskelia at different vertex types in a single cage may be described as quasi-equivalent, in analogy with otherwise identical capsid protein tiles of virus shells that bond differently depending on geometric position in the surface of the shell (12). In addition, since internal angles are generally not exactly equal to the ideal 108° in pentagons or 120° in hexagons, potentially every vertex in a cage may be different from one another.
Flexible and reliable self-assembly
The challenge faced by clathrin is to be able to self-assemble about cargo of a wide range of sizes. Perfectly identical triskelia could produce only two fullerene cages, the dodecahedron with 20 vertices and the truncated icosahedron with 60. For both clathrin and carbon, relaxing the requirement for identical vertices permits cages with faces that are not regular and often nonplanar. However, were there no additional geometric constraints, addition of vertices to produce hexagons and pentagons at random would fail in the vast majority of cases to produce a closed, fullerene cage (10).
Fortunately, there is an implicit geometric constraint, the head-to-tail exclusion rule (10), which from the point of view of the physical mechanism described here might better be described as the no-Rings-with-head-to-tail-DADs rule. Because it is a geometric constraint, it may act as a kinetic barrier to prevent assembly of such Rings or as an energy penalty that prevents maintenance of such high-energy Rings under equilibrium assembly conditions.
This implicit geometric constraint has two consequences. First, it blocks random completion of hexagons and pentagons, permitting only a subset of paths of fullerene growth, along what we have called “probable roads” (10), in contrast to what investigators of carbon fullerenes have called the “pentagon road” (34,35) and “fullerene road” (36,37) hypotheses. Second, these probable paths lead to a limited repertoire of clathrin and carbon fullerene cage structures, specifically the 15 small, non-IPR cages for 20 ≤ n < 60, the truncated icosahedron (n = 60), and the IPR cages for n > 60 (10). This repertoire, though limited in structure, includes fullerene cages of a wide range of n: 20–28, 32, 36–44, 50, 60, and ≥70. In addition, clathrin can self-assemble into non-fullerene cages with heptagonal faces (19,38), so clathrin may be able to produce cages with the few missing n as well.
Icosahedral virus shells are also flexible in structure but much less so. Different icosahedral virus shells have 60T triangular subunits, with T taken from a series 1, 3, 4, 7, 12, 13, 19, 21… (12,39). The subunits associate into pentamers with five subunits and hexamers with six. The number n of vertices of equivalent icosahedral fullerene cages is 60 T/3 = 20 T. Thus, the T = 1 structure is the dodecahedron (n = 20), the T = 3 structure is the truncated icosahedron (n = 60), and the T = 4 structure is the icosahedral IPR fullerene isomer with n = 80. Moreover, in a few cases a particular virus may form shells of different T numbers (40–44). Clearly, though, the restriction to icosahedral structures limits virus structure to a very small number of isomers with quantal jumps in T number.
Therefore, in a single cell, to enclose cargo of different sizes, evolution has selected a caging system whose building blocks are vertices (as in clathrin) rather than tiles (as in viruses). This choice reflects both flexibility in cage size and reliability in cage assembly, the physical basis of which is an implicit geometric constraint, the head-to-tail exclusion rule.
Supplementary material
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Appendix A.
Supplement Supplement
Supplement Supplement
Acknowledgments
We are grateful to Kendall Houk, Peter Bentler, and Frederick Eiserling for their encouragement.
Footnotes
Editor: Robert Hsiu-Ping Chow.
References
- 1.Kroto H.W., Heath J.R., O’Brien S.C., Curl R.F., Smalley R.E. C60: Buckminsterfullerene. Nature. 1985;318:162–163. [Google Scholar]
- 2.Kirchhausen T., Harrison S.C., Chow E.P., Mattaliano R.J., Ramachandran K.L., Smart J., Brosius J. Clathrin heavy chain: molecular cloning and complete primary structure. Proc. Natl. Acad. Sci. USA. 1987;84:8805–8809. doi: 10.1073/pnas.84.24.8805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pearse B.M.F. Coated vesicles from pig brain: purification and biochemical characterization. J. Mol. Biol. 1975;97:93–98. doi: 10.1016/s0022-2836(75)80024-6. [DOI] [PubMed] [Google Scholar]
- 4.Pearse B.M.F. Clathrin: a unique protein associated with intracellular transfer of membrane by coated vesicles. Proc. Natl. Acad. Sci. USA. 1976;73:1255–1259. doi: 10.1073/pnas.73.4.1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ungewickell E., Branton D. Assembly units of clathrin coats. Nature. 1981;289:420–422. doi: 10.1038/289420a0. [DOI] [PubMed] [Google Scholar]
- 6.Kirchhausen T., Harrison S.C. Protein organization in clathrin trimers. Cell. 1981;23:755–761. doi: 10.1016/0092-8674(81)90439-6. [DOI] [PubMed] [Google Scholar]
- 7.Kanaeseki T., Kadota K. The vesicle in a basket. A morphological study of the coated vesicle isolated from the nerve endings of the guinea pig brain, with special reference to the mechanism of membrane movements. J. Cell Biol. 1969;42:202–220. doi: 10.1083/jcb.42.1.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ehrlich M., Boll W., Van Oijen A., Hariharan R., Chandran K., Nibert M.L., Kirchhausen T. Endocytosis by random initiation and stabilization of clathrin-coated pits. Cell. 2004;118:591–605. doi: 10.1016/j.cell.2004.08.017. [DOI] [PubMed] [Google Scholar]
- 9.Fowler P.W., Manolopoulos D.E. Clarendon Press; Oxford: 1995. An Atlas of Fullerenes. [Google Scholar]
- 10.Schein S., Sands-Kidner M. A geometric principle may guide self-assembly of fullerene cages from clathrin triskelia and from carbon atoms. Biophys. J. 2008;94:958–976. doi: 10.1529/biophysj.107.110817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Manolopoulos D.E. Comment on “Favorable structures for higher fullerenes”. Chem. Phys. Lett. 1992;192:330. [Google Scholar]
- 12.Caspar D.L.D., Klug A. Physical principles in the construction of regular viruses. Cold Spring Harbor Symp. Quant. Biol. 1962;27:1–24. doi: 10.1101/sqb.1962.027.001.005. [DOI] [PubMed] [Google Scholar]
- 13.Thilgen C., Diederich F. Structural aspects of fullerene chemistry—a journey through fullerene chirality. Chem. Rev. 2006;106:5049–5135. doi: 10.1021/cr0505371. [DOI] [PubMed] [Google Scholar]
- 14.Taylor R., Hare J.P., Abdul-Sada A.K., Kroto K.W. Isolation, separation and characterization of the fullerenes C60 and C70: the third form of carbon. J. Chem. Soc. Chem. Commun. 1990;1990:1423–1425. [Google Scholar]
- 15.Kroto H.W. The stability of the fullerenes Cn (n=24, 28, 32, 50, 60 and 70) Nature. 1987;329:529–531. [Google Scholar]
- 16.Schmalz T.G., Seitz W.A., Klein D.J., Hite G.E. Elemental carbon cages. J. Am. Chem. Soc. 1988;110:1113–1127. [Google Scholar]
- 17.Piskoti C., Yarger J., Zettl A. C36, a new carbon solid. Nature. 1998;393:771–774. [Google Scholar]
- 18.Crowther R.A., Finch J.T., Pearse B.M.F. On the structure of coated vesicles. J. Mol. Biol. 1976;103:785–798. doi: 10.1016/0022-2836(76)90209-6. [DOI] [PubMed] [Google Scholar]
- 19.Cheng Y., Boll W., Kirchhausen T., Harrison S.C., Walz T. Cryo-electron tomography of clathrin-coated vesicles: structural implications for coat assembly. J. Mol. Biol. 2007;365:892–899. doi: 10.1016/j.jmb.2006.10.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Halgren T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996;17:490–519. [Google Scholar]
- 21.Halgren T.A. Merck molecular force field. II. MMFF94 van der Waals and electrostatic parameters for intermolecular interactions. J. Comput. Chem. 1996;17:520–552. [Google Scholar]
- 22.Halgren T.A. Merck molecular force field. III. Molecular geometries and vibrational frequencies for MMFF94. J. Comput. Chem. 1996;17:553–586. [Google Scholar]
- 23.Halgren T.A. Merck molecular force field. IV. Conformational energies and geometries for MMFF94. J. Comput. Chem. 1996;17:587–615. [Google Scholar]
- 24.Halgren T.A. Merck molecular force field. V. Extension of MMFF94 using experimental data, additional computational data, and empirical rules. J. Comput. Chem. 1996;17:616–641. [Google Scholar]
- 25.Reference deleted in proof.
- 26.Taylor R. Imperial College Press; London: 1999. Lectures Notes on Fullerene Chemistry. [Google Scholar]
- 27.Fotin A., Cheng Y., Sliz P., Grigorieff N., Harrison S.C., Kirchhausen T., Walz T. Molecular model for a complete clathrin lattice from electron cryomicroscopy. Nature. 2004;432:573–579. doi: 10.1038/nature03079. [DOI] [PubMed] [Google Scholar]
- 28.Fotin A., Cheng Y., Grigorieff N., Walz T., Harrison S.C., Kirchhausen T. Structure of an auxilin-bound clathrin coat and its implications for the mechanism of uncoating. Nature. 2004;432:649–653. doi: 10.1038/nature03078. [DOI] [PubMed] [Google Scholar]
- 29.Wu X., Zhao X., Baylor L., Kaushal S., Eisenberg E., Greene L.E. Clathrin exchange during clathrin-mediated endocytosis. J. Cell Biol. 2001;155:291–300. doi: 10.1083/jcb.200104085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wu X., Zhao X., Puertollano R., Bonifacino J.S., Eisenberg E., Greene L.E. Adaptor and clathrin exchange at the plasma membrane and trans-Golgi network. Mol. Biol. Cell. 2003;14:516–528. doi: 10.1091/mbc.E02-06-0353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yim Y.-I., Scarselletta S., Zang F., Xufeng W., Lee D.-w., Kang Y.-s., Eisenberg E., Greene L.E. Exchange of clathrin, AP2 and epsin on clathrin-coated pits in permeabilized tissue culture cells. J. Cell Sci. 2005;118:2405–2413. doi: 10.1242/jcs.02356. [DOI] [PubMed] [Google Scholar]
- 32.Mashl R.J., Bruinsma R.F. Spontaneous-curvature theory of clathrin-coated membranes. Biophys. J. 1998;74:2862–2875. doi: 10.1016/S0006-3495(98)77993-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nossal R. Energetics of clathrin basket assembly. Traffic. 2001;2:138–147. doi: 10.1034/j.1600-0854.2001.020208.x. [DOI] [PubMed] [Google Scholar]
- 34.Heath J.R., O’Brien S.C., Curl R.F., Kroto H.W., Smalley R.E. Carbon condensation. Comm. Cond. Matter Phys. 1987;13:119–141. [Google Scholar]
- 35.Smalley R.E. Fullerene self-assembly. Acc. Chem. Res. 1992;25:98–105. [Google Scholar]
- 36.Heath J.R. Synthesis of C60 from small carbon clusters: a model based on experiment and theory. In: Hammond G.S., Kuck V.J., editors. Fullerenes: Synthesis, Properties, and Chemistry of Large Carbon Clusters, ACS Symp Ser. #481. American Chemical Society; Washington, DC: 1991. [Google Scholar]
- 37.Curl R.F. On the formation of the fullerenes. A postbuckminsterfullerene view of the chemistry, physics and astrophysics of carbon. Philos. Trans. Phys. Sci. Eng. 1993;343:19–32. [Google Scholar]
- 38.Heuser J., Evans L. Three-dimensional visualization of coated vesicle formation in fibroblasts. J. Cell Biol. 1980;84:560–582. doi: 10.1083/jcb.84.3.560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Baker T.S., Olson N.H., Fuller S.D. Adding the third dimension to virus life cycles: three-dimensional reconstruction of icosahedral viruses from cryo-electron micrographs. Microsc. Mol. Biol. Rev. 1999;63:862–922. doi: 10.1128/mmbr.63.4.862-922.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Crowther R.A., Kiselev N.A., Böttcher B., Berriman J.A., Borisova G.P., Ose V., Pumpens P. Three-dimensional structure of hepatitis B virus core particles determined by electron cryomicroscopy. Cell. 1994;77:943–950. doi: 10.1016/0092-8674(94)90142-2. [DOI] [PubMed] [Google Scholar]
- 41.Kenney J.M., von Bonsdorf C.-H., Nassal M., Fuller S.D. Evolutionary conservation in the hepatitis B core structure: comparison of human and duck cores. Structure. 1995;3:1009–1019. doi: 10.1016/s0969-2126(01)00237-4. [DOI] [PubMed] [Google Scholar]
- 42.Thuman-Commike P.A., Greene B., Jakana J., Prasad B.V.V., King J., Prevelige P.E., Chiu W. Three-dimensional structure of scaffolding containing phage P22 procapsids by electron cryo-microscopy. J. Mol. Biol. 1996;260:85–98. doi: 10.1006/jmbi.1996.0383. [DOI] [PubMed] [Google Scholar]
- 43.Thuman-Commike P.A., Greene B., Malinski J.A., King J., Chiu W. Role of the scaffolding protein in P22 procapsid size determination suggested by T=4 and T=7 procapsid structures. Biophys. J. 1998;74:559–568. doi: 10.1016/S0006-3495(98)77814-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dokland T.E., Lindqvist B.H., Fuller S.D. Image reconstruction from cryo-electron micrographs reveals the morphopoietic mechanism in the P2–P4 bacteriophage system. EMBO J. 1992;11:839–846. doi: 10.1002/j.1460-2075.1992.tb05121.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplement Supplement
Supplement Supplement


