The dynamics of mass migration

Abstract

We specify a set of equations defining a dynamic model of international migration and estimate its parameters by using data specially collected in Mexico. We then used it to project the a hypothetical Mexican community population forward in time. Beginning with a stable population of 10,000 people, we project ahead 50 years under three different assumptions: no international migration; constant probabilities of in- and out-migration, and dynamic schedules of out- and in-migration that change as migratory experience accumulates. This exercise represents an attempt to model the self-feeding character of international migration noted by prior observers and theorists. Our model quantifies the mechanisms of cumulative causation predicted by social capital theory and illustrates the shortcomings of standard projection methodologies. The failure to model dynamically changing migration schedules yields a 5% overstatement of the projected size of the Mexican population after 50 years, an 11% understatement of the total number of U.S. migrants, a 15% understatement of the prevalence of U.S. migratory experience in the Mexican population, and an 85% understatement of the size of the Mexican population living in the United States.

Social scientists have long noted that international migration is characterized by a strong internal momentum: Once a particular migration stream has been initiated, for whatever reason, it tends to persist and grow over time. Because of this persistence, core receiving areas accumulate identifiable sets of sending nations whose relative contributions to the total inflow remain fairly stable from year to year, yielding well structured migratory systems. In their comprehensive review of the global migration literature, Massey et al. (1) identified five principal international migratory systems operating in the world today, each focused on a different core receiving area: North America, Western Europe, the Persian Gulf, Asia and the Pacific, and the Southern Cone of South America.

The tendency for migration to persist and grow over time has been studied under a variety of rubrics. Economists refer to a process of “path dependence” whereby early migrants reduce costs and risks for later arrivals, thereby increasing movement along specific routes (2). Sociologists, in contrast, refer to a process of “cumulative causation” whereby social networks connecting migrants to nonmigrants make the process of migration “self-perpetuating” (3). Whatever one labels it, recent theoretical work suggests that the persistence of migration in space and time stems from two fundamental processes: human and social capital accumulation (4, 5). The former operates among individuals and the latter through the social networks in which they are embedded.

People may begin migrating for a variety of reasons. They may seek to relocate abroad permanently to earn higher lifetime incomes, as posited by neoclassical economics (6). They may seek to manage risks and overcome market failures by migrating abroad temporarily to accumulate savings or diversify sources of income, as specified by the new economics of labor migration (7). They may move in response to deliberate recruitment efforts by governments or employers, as argued by segmented labor market theorists (8), or they may emigrate because they have been displaced from a traditional livelihood by structural economic transformations, as predicted by world systems theorists (9).

Whatever the initial reasons for migration, once someone has lived and worked in a foreign setting, he or she is no longer the same person. The experience of work in an advanced industrial economy generates irreversible changes in individual motivations and personal attributes that make long-term settlement (of temporary migrants) or re-emigration (of returned migrants) very likely. Satisfaction of the wants that originally led to emigration creates new wants, and access to high wages creates new standards of material well being and instills new ambitions for upward mobility that did not before exist. As migrants grow accustomed to higher incomes, they alter their consumption patterns and adopt new lifestyles that cannot be maintained through local work, making additional trips necessary and stays abroad longer.

These shifting motivations signify a change in human capital—the personal qualities that make individuals productive and determine their value to potential employers (10). In addition to shifting motivations, migrants acquire other forms of human capital in the course of foreign labor migration. They gain a knowledge of the host country’s language, employment practices, job routines, and ways of life. They learn how to enter the country legally or illegally, find out where the jobs are, and discover how to manage life in a foreign setting. As a result of this new knowledge—this new human capital—the costs and risks of taking an additional trip (or staying on for an additional year) drop while the potential benefits rise.

Once it has been experienced, therefore, international migration tends to be repeated, becoming a familiar resource used again and again as new needs arise and motivations change. Having worked abroad once, people acquire knowledge that lowers the risks, raises the benefits, and reduces the costs of additional migration, which raises the odds that they take another trip, which yields still more knowledge and experience, which raises the odds of a third trip, generating still more knowledge, leading to a fourth trip, and so on. The more someone migrates, the more he or she is likely to continue migrating and the longer he or she will stay abroad, yielding a self-sustaining process of human capital accumulation that produces more trips of longer duration. The operation of such feedback loops explains why migrants recruited under various “guestworker” schemes invariably come to overstay their welcome (11).

Social capital refers to productive value arising from social relationships between people. According to Bourdieu and Wacquant (12), “social capital is the sum of the resources, actual or virtual, that accrue to an individual or a group by virtue of possessing a durable network of more or less institutionalized relationships of mutual acquaintance and recognition” (p. 119). The key characteristic of social capital is its convertibility—it may be translated into other forms of capital and income (13). People gain access to social capital by being in networks and institutions and then convert it into material resources to improve or maintain their position in society (14).

Among those considering international movement, a social tie to a current or former migrant is productive because one can draw on it to gain access to a high-paying foreign job. Potential migrants extract the social capital embedded in ties to migrants to lower the costs and risks and raise the benefits of international movement. Each act of migration thus creates social capital among those to whom the migrant is related. Once someone migrates, the costs and risks of international movement fall for that person’s friends and relatives, inducing some of them to migrate, which further expands the network of people with ties to migrants, yielding more social capital, which induces new people to migrate, further expanding the network, and so on. The steady accumulation of social capital through the progressive expansion of interpersonal networks yields another powerful feedback loop that results in the cumulative causation of migration over time.

The voluminous research literature reviewed by Massey et al. (1) clearly shows that having a tie to someone with migrant experience increases the likelihood of out-migration; that the odds of taking an additional trip rise with each trip taken; and that probabilities of emigration and settlement both increase as foreign experience accumulates. To date, however, no study has modeled the twin processes of human and social capital accumulation to demonstrate how they operate dynamically to perpetuate international migration. Our purpose here is to develop such a dynamic model—one that specifically captures the powerful feedbacks operating through human and social capital accumulation—to quantify the cumulative causation of international migration.

Modeling Mass Migration

The key feature of our theoretical argument is that migratory decisions taken at one point in time influence the context for decisions taken at a later date, making additional trips more likely and yielding a dynamic feedback process. Our purpose here is to construct a statistical model of that process by using empirical data from Mexico, the largest contributor of immigrants to the United States. Our simulation projects a typical Mexican community population forward in time under three scenarios: no international migration, constant international migration, and dynamically changing international migration.

Population Change in the Absence of Migration.

We begin by assuming a Mexican town of 10,000 inhabitants within which fertility and mortality are fixed and there is no in- or out-migration. We distribute the community’s inhabitants according to the 1990 age–sex structure for Mexico as a whole and hold age-specific schedules of fertility and mortality constant at their 1990 levels (15). Using standard component projection methods (16), we project this population ahead 110 years to generate a stable age and sex distribution (17). We then reset the total population to 10,000 inhabitants, distribute it according to the stable age distribution just derived, and project it ahead another 50 years to derive estimates of the future size and demographic structure of the community in the absence of migration.

Table 1 summarizes our baseline conditions. Given the demographic parameters observed in Mexico in 1990, a closed stable community population yields an age distribution skewed toward the young ages, a total fertility rate of 3.35 children per woman, an annual growth rate of 1.6%, and life expectancies at birth of 68.8 years for men and 74 years for women. After 50 years, the original community population of 10,000 would have grown to 22,730 inhabitants in the absence of in- or out-migration.

Table 1.

Basic assumptions about age composition, fertility, and mortality (in abridged form) for projection of baseline model used in simulation exercise

Age	Stable age distribution	Fertility rate	Mortality rate		Out-migration rate		In-migration rate
			Males	Females	Males	Females	Males	Females
0–4	0.114	—	0.0107	0.0009	0.0005	0.0001	0.0558	0.0439
5–9	0.104	—	0.0008	0.0006	0.0010	0.0002	0.1544	0.1242
10–14	0.096	—	0.0007	0.0004	0.0035	0.0009	0.1201	0.0958
15–19	0.088	0.085	0.0012	0.0005	0.0353	0.0089	0.1675	0.1350
20–24	0.081	0.181	0.0019	0.0007	0.0709	0.0184	0.2379	0.1950
25–29	0.074	0.169	0.0026	0.0009	0.0589	0.0151	0.2703	0.2233
30–34	0.067	0.124	0.0032	0.0012	0.0423	0.0107	0.2772	0.2293
35–39	0.061	0.076	0.0038	0.0017	0.0281	0.0071	0.3017	0.2511
40–44	0.056	0.030	0.0047	0.0024	0.0179	0.0045	0.3112	0.2596
45–49	0.050	0.006	0.0061	0.0036	0.0010	0.0024	0.3229	0.2701
50–54	0.045	—	0.0084	0.0054	0.0048	0.0012	0.3432	0.2885
55–59	0.039	—	0.0119	0.0084	0.0025	0.0006	0.3501	0.2948
60–64	0.034	—	0.0144	0.0129	0.0008	0.0002	0.4497	0.3881
65–69	0.029	—	0.0256	0.0201	0.0001	0.0000	0.4599	0.3979
70–74	0.023	—	0.0379	0.0312	—	—	—	—
75–79	0.018	—	0.0563	0.0488	—	—	—	—
80–84	0.012	—	0.0832	0.0739	—	—	—	—
85–89	0.006	—	0.1229	0.1132	—	—	—	—
90–94	0.003	—	0.1843	0.1748	—	—	—	—
95–99	0.001	—	0.2802	0.2717	—	—	—	—

Population Change with Static Migration.

Our projection is by no means the first to incorporate international migration. Official projections done by the U.S. Bureau of the Census have long incorporated assumptions about net immigration to the United States, and the mathematics of incorporating migration schedules into population forecasting have been well elaborated by others (18, 19). So far, however, demographic projections have assumed static rather than dynamic migration schedules, using constant age-specific migration rates and applying them mechanically to forecast the future size and composition of a population experiencing net migration. To facilitate such projections, Castro and Rogers (20) have developed model migration schedules to complement those developed earlier for fertility and mortality (21).

We illustrate projections done under the usual assumption of a fixed migration schedule by applying male and female schedules of age-specific out- and return-migration probabilities shown on the right side of Table 1. We derived these schedules for 1990 by using data obtained from the Mexican Migration Project, described below. As can be seen, the yearly likelihood of out-migration to the United States is considerably higher for men than women. Both curves rise to a peak in the age interval 20–24 and then decline steadily to age interval 50–54. The annual probability of return migration is also higher for men than for women, but, unlike the out-migration curve, it increases steadily with age. Using these constant schedules, we projected the population ahead 50 years to yield a new community population of 21,991 inhabitants, ≈2% smaller than the closed population because of the out-migration of some townspeople to the United States.

Population Change with Dynamic Migration Schedules.

Prior demographic projections have tended to forecast populations of receiving rather than sending countries; yet, it is the accumulation of human and social capital in the sending region that is primarily responsible for the self-feeding character of international migration (22). If demographers are to have any hope of understanding international migration and projecting it accurately, they must change the way they approach the problem of population forecasting. Rather than mechanically projecting a population ahead assuming constant migration schedules that vary only by age and sex, they must develop dynamic algorithms that capture the migration-inducing effects of migratory experience accumulated within the sending population. As the migratory experience of a community grows, the odds of out-migration rise for its members. What is required is an equation that expresses this dynamic feedback relationship. More specifically, we need an equation that relates an individual’s migration propensity at time t to the migratory experience he or she may have accumulated in prior years, as well as the to the amount of experience that has accumulated in the community by that date:

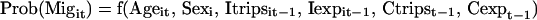1

where Prob(Mig_it) = person i’s probability of migrating in year t; Mig_it = 1 if i migrated in year t and 0 otherwise.; Age_it = the age of person i in year t; Sex_i = sex of person i; Itrips_{it − 1} = the number of trips made by person i in year t − 1; Iexp_{it − 1} = the migratory experience accumulated by person i in year t − 1; Ctrips_{t − 1} = the number of trips made by other community members in year t − 1; and Cexp_{t − 1} = the migratory experience accumulated by other community members in year t − 1.

In this specification, the rate of out-movement depends not only on the age and sex of the individual in question, but also on his or her prior migratory experience (i.e., on his or her accumulated human capital) and on the degree to which he or she is surrounded by other townspeople with migratory experience (the quantity of social capital). Once a migrant has emigrated abroad, of course, he or she is at risk of returning home. Whether one conceives of return migration as an instance of failure (where a migrant does not realize expected gains in income and returns home disappointed—the favored explanation of neoclassical economics) or as part of a deliberate strategy of temporary labor migration (where a migrant seeks to minimize risk or acquire capital—the favored explanation of the new economics of labor migration), it is clear that migration is a two-way street and that accurate projections need to incorporate processes of exit as well as entry. As before, the likelihood of return migration is influenced by prior accumulations of human and social capital. Thus, for any migrant present in the receiving nation at time t, the annual probability of going home is specified as

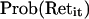2

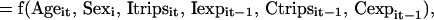where Prob (Ret_it) = the probability that migrant i returns to community in year t; Ret_it = 1 if the migrant returns to his or her community in year t and 0 otherwise; and the other variables are defined as before.

To simulate what would happen to our hypothetical community given rates of in- and out- migration that change dynamically in response to prior migratory experience, we first project the population ahead 1 year by using the constant fertility and mortality schedules described earlier (not yet allowing out-migration). Then we raise everyone’s age by 1 year, subtract the deaths, add in the births, and apply probabilities of out-migration by age and sex. Because no one has yet migrated, all of the measures of migratory experience are set to zero, so that, given the sex and age of each person in the population, we derive an individual probability of out-migration. We sum these predicted probabilities within 5-year age–sex categories to derive expected distributions of out-migrants. Within each age–sex category, we randomly designate certain people to migrate to the United States, up to the number of migrants expected for that category.

Once in the U.S., these international migrants are subject to the risk of return migration defined by Eq. 2. For the sake of simplicity, we assume that each out-migrant acquires 6 months of experience on entry to the United States. Inserting one trip and 6 months into the prediction equation along with age and sex, we generate individual probabilities of return migration, which are once again summed by sex and age to derive expected distributions of return migrants. Within each age–sex category, we randomly select people to return home, each with 6 months of experience and one trip under his or her belt.

We then move ahead to year 2, raise everyone’s age by 1 year, and once again add in births and subtract deaths. At this point, however, the community has been transformed not only by fertility and mortality, but also by migration: Some community members now have taken one trip to the United States and have acquired 6 months of U.S. experience, so they display higher probabilities of out-migration. At the same time, the total number of trips and the total stock of U.S. experience have risen in the community, generating new quantities of social capital to raise the odds of out-migration for all townspeople. We thus recompute individual probabilities of out-migration based on the new distribution of trips and migratory experience among individuals and within the community, and once again sum by sex and age to derive expected distributions of out-migrants, who we then randomly designate to leave for the United States. These out-migrants each are given 6 months of additional U.S. experience and another U.S. trip and are added to the population still remaining in the United States from the prior year who now have 12 more months of experience in addition to the 6 assumed from the prior year.

This operation yields a new U.S.-based population subject to the risk of return migration, but one with a greater diversity of migratory backgrounds. Some migrants remain on a trip begun in year 1 and have 18 months of U.S. experience; others have just left on their first trip in year 2 and only have 6 months of experience; and a few people are on their second trip with 12 months of total experience. The diversity of backgrounds yields a new diversity of return migration probabilities, which are grouped by age and sex to yield new distributions of returnees who are once randomly assigned to return and then are reinserted into the appropriate age–sex category within the Mexican community along with their accumulations of trips and experience.

As we move ahead to year 3, the community grows even more diverse with respect to U.S. experience: Some have no U.S. trips or experience; some have one trip and 6 months of experience; and some have two trips and 12 months of experience. After repeating the exercise and generating new predicted probabilities of out-migration, summing by age and sex to generate distributions of out-migrants, and randomly assigning people within age–sex groups to leave for the U.S., we produce another population of migrants in the U.S. who are then once more subject to the risk of return migration.

This U.S. population of Mexican migrants is still more heterogeneous than that observed in the previous cycle: Some have one trip and 6 months of experience; some have two trips and 12 months of experience; others have two trips and 18 months of experience; and a few have three trips and 30 months of experience, yielding a new set of return migration probabilities and new distributions of returning migrants who are reinserted into the community with their diverse accumulations of trips and U.S. experience, which, in turn, changes the distributions of human and social capital in the community, leading to new probabilities of out-migration, and so on.

Our dynamic projection of international migration proceeds sequentially in this fashion year-by-year for 50 years to produce an evolving binational population of community members in Mexico and the United States, each with a distribution of U.S. trips and migratory experience that gradually increases and diversifies over time to change the probabilities of out- and return-migration in the next cycle. What remains, of course, is for us to generate empirical estimates of the parameters for Eqs. 1 and 2 so that we can implement our dynamic projection algorithm.

Estimating the Dynamic Equations

Such dynamic equations make strong demands on data that national statistical systems are ill-equipped to handle. In most countries, a statistical office simply counts the number of foreign born persons and records the number of entries and exits to the national population. Statistical bureaus in receiving nations generally do not enumerate the number of people in other countries who have accumulated migratory experience within their borders. In the case of the United States and Mexico, for example, we know from official sources the number of Mexican-born persons residing in the United States, the number of U.S.-born persons residing in Mexico, and the number of Mexicans who arrive each year in the United States as legal visitors and permanent residents aliens; but we do not know with any certainty the number of Mexicans in Mexico who have been to United States or how this number has changed over time; nor do we know the total number of Mexicans who enter the United States each year because an unknown but presumably large number are undocumented. Because the United States maintains no exit controls, moreover, statistics on return migration do not exist, and the number of emigrants to Mexico and other countries can only be estimated indirectly (23).

In short, the information necessary to estimate the dynamic projection equations we have specified is unavailable from conventional sources. Fortunately, the requisite data are available from the database of the Mexican Migration Project, a binational study based at the University of Guadalajara and the University of Pennsylvania. With funding from the National Institutes of Health and the Hewlett Foundation, its investigators have worked since 1987 to compile a comprehensive set of accurate data on documented and undocumented Mexican migration to the United States. The data incorporate samples gathered on both sides of the border and include retrospective life histories of all household heads, yielding the longitudinal data necessary to estimate Eqs. 1 and 2.

Our data come from simple random samples of Mexican communities gathered during December and January of 1982–1983 and in successive years from 1987 to the present. As of this writing, the database contains 38 separate communities representing the states of Jalisco, Michoacán, Guanajuato, Nayarit, and Zacatecas, which together constitute a region (western Mexico) that historically has sent a majority of migrants to the United States (24). The database includes one additional community from the state of Guerrero, a newer migrant-sending located in the central region to the south of Mexico City (other communities from this region are in the process of being added to the file). The winter is generally the best time to locate and interview U.S. migrants within Mexico because seasonal migrants return home to spend the Christmas holidays with their families. The community samples are thus representative of dwelling units occupied in Mexico during the winter months of the survey year.

Within most communities, the sample size was 200 households, but in smaller settlements fewer households were chosen and in a few cases larger samples were compiled. Sampling frames were constructed by conducting a house-to-house census of each community. Usually an entire town or city was canvassed, but in large urban areas this was not possible and specific working-class neighborhoods were demarcated and sampled instead. Sampling fractions ranged from 0.029 to 0.803 and averaged ≈0.228. Across the communities, our procedures yielded a total sample of 4,853 households representing a hypothetical population of ≈2.3 million people. Detailed information on the community samples is available from the authors on request.

The Mexican data were supplemented with nonrandom samples of out-migrants located in the United States during the summer following each winter’s survey. From the Mexican samples, we determined where in the U.S. community members went and sent interviewers to those places to survey migrants who had settled abroad (generally people with 3 years of continuous residence north of the border). Snowball sampling methods were used to compile these samples (25). In most communities, 20 out-migrant households were surveyed, but in some cases smaller numbers were questioned, yielding a total sample size of 415 U.S. households. U.S. sampling fractions are estimated to range from 0.009 to 0.999 and to average 0.305 [see Massey and Parrado (26) for a description of the methods used to estimate U.S. sampling fractions].

In choosing Mexican communities for study, Mexican Migration Project investigators sought to include a range of population sizes, ethnic compositions, and economic bases. Communities were not chosen because they were thought to contain U.S. migrants, and, in fact, the dataset includes a wide range of migratory experiences, ranging from one community in which just 9% of adults have been to the United States to another in which 60% have ever migrated (27). Although the sample is not strictly representative of the states of western Mexico, it contains a broad cross-section of households and communities and yields a sample of migrants whose characteristics are remarkably similar to those enumerated in representative national surveys (28). Full documentation of these data, along with the datasets themselves, are publicly available from the Mexican Migration Project website at http://lexis.pop.upenn.edu/mexmig/.

Respondents were interviewed by using ethnosurvey methods (29). Within each household, investigators gathered basic information about the social, economic, and demographic characteristics of the head, the spouse, the head’s children, and other household members. From each household head, they collected a detailed life history that includes a labor history, a migration history, a property history, a marital history, and a fertility history. To estimate Eqs. 1 and 2, we selected male and female household heads and reconstructed their lives from birth onward to create an annual record of their age, migratory experience, and the migratory experience of other household heads living the community. We then used the resulting life history file to estimate two discrete-time event history models corresponding to Eqs. 1 and 2.

First, we estimated an equation linking the likelihood of taking a trip to the United States to an individual’s age, sex, number of prior trips, and months of prior experience, plus the number of trips and total U.S. experience accumulated by other heads in the community. For all person-years observed in Mexico, we used a logistic model to regress a dichotomous indicator of whether the respondent left for the United States in year t (1 if yes and 0 otherwise) on his or her set of personal and community characteristics in year t − 1.

The second model considers the process of return migration. It follows respondents year-by-year from the moment they enter the United States on any trip until they return home to Mexico. Given their characteristics in year t − 1 (age, sex, number of prior trips, months of prior experience, number of community trips, and months of community experience), we predicted whether the respondent left the US. to return to Mexico in year t (1 if yes and 0 otherwise).

Table 2 presents means and SDs of the variables we used in the estimation of these two equations. The data used to predict the out-migration equation consist of 316,928 person-years observed in Mexico from 1965 to the survey date (compiled from 6,797 separate respondents). In the average person-year, the typical subject was 26 years old and had accumulated 6.3 months of prior U.S. experience on 0.64 earlier trips. At any point in time, the average respondent lived in a community in which the average number of trips was 0.71 and the average months of U.S. experience was 9.4. Given the fact that the sample is composed of household heads, it is naturally skewed toward males, but there is more than enough variation to estimate the effect of gender.

Table 2.

Means and standard deviations of variables used to estimate migration equations for a dynamic simulation of Mexican migration to the United States

Variable	Out-migration: Person years spent in Mexico		Return migration: Person years spent in U.S.
	Mean	SD	Mean	SD
Age	25.9	18.1	33.5	12.0
Sex (=Male)	0.85	0.17	0.96	0.10
Number of prior U.S. trips	0.64	2.50	4.50	5.80
Months of prior U.S. experience	6.30	26.7	75.4	42.0
Number of U.S. trips in community	0.71	1.15	1.80	2.20
Months of U.S. experience in community	9.40	12.7	24.1	32.1
Person-years observed	316,928		28,811

The data used to estimate the equation predicting return migration includes 29,811 person-years spent by 2,961 migrants in the United States. Given that this sample is restricted to U.S. migrants, it is older (average age of 33.5) and more male (96%) than that used for the first equation, and, in the typical person-year, the average respondent had accumulated considerably more experience: 4.5 U.S. trips and 75 months (6.3 years) of migratory experience. During a typical person-year spent in the United States, moreover, other household heads in the community had accumulated a total of 1.8 trips and 24.1 months of total U.S. experience.

Table 3 presents the specific equation estimates. In every case, the size and direction of effects corresponds to theoretical expectations, and, given the large number of cases involved, all coefficients are highly significant. In general, the likelihood of international out-migration falls with age, is much higher for men than for women, and grows with the number of U.S. trips and months of U.S. experience (at both the individual and community levels). Likewise, the probability of return migration increases with age and is greater for men than for women, and it rises with the number of trips taken by individuals but falls with the total months of U.S. experience accumulated at the individual and community levels, as well as with the total number of trips accumulated within the community. These findings reinforce our basic theoretical argument that the odds of both out- and in-migration vary in response to changes in the accumulated stocks of social and human capital.

Table 3.

Estimates of equations used to predict out-migration and return migration in a dynamic simulation of Mexican migration to the United States

Variable	Out-migration		Return migration
	B	SE	B	SE
Age	−0.016	0.001	0.023	0.002
Sex (=Male)	1.468	0.055	0.292	0.103
Number of prior U.S. trips	0.259	0.004	0.018	0.005
Months of prior U.S. experience	0.007	0.001	−0.012	0.001
Number of U.S. trips in community	0.182	0.012	−0.066	0.020
Months of U.S. experience in community	0.011	0.001	−0.005	0.002
Constant	−4.791	0.146	−3.636	0.294
Person-years	316,928		28,811
−2 log likelihood	86,744		22,654

Coefficients for survey year are not shown; all coefficients shown are significant at P < 0.001. B, regression coefficient; SE, standard error. 

The Dynamics of Migration

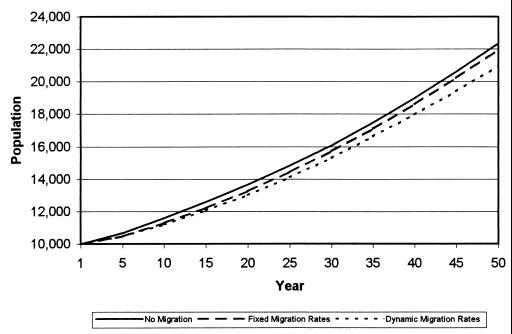
Fig. 1 compares the size of the community population projected forward under three assumptions: no migration, fixed migration, and dynamic migration. As can be seen, allowing for the dynamic effect of human and social capital accumulation yields a higher rate of out-migration and a lower rate of return migration that eventually produces a smaller community population in Mexico. After 50 years of dynamically changing migration rates, the community population is projected to be 20,984, ≈6% lower than the size of the closed population and ≈5% below that achieved with fixed rates of in- and out-migration.

Figure 1.

Mexican community population projected under three assumptions.

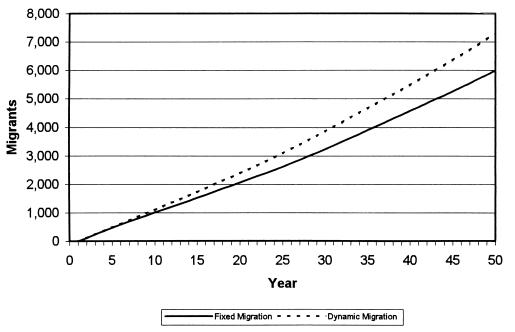
Although the percentage difference in the projected size of the Mexican community is modest given the large population base, dynamic and fixed migration schedules yield markedly different numbers of U.S. migrants over time. As Fig. 2 shows, after 50 years, the total number of U.S. migrants projected under fixed assumptions is 6,003 whereas, under dynamic assumptions, it is 7,286, a difference of 21%. In other words, by failing to incorporate migration’s dynamic feedback effects, standard projection algorithms substantially understate the number of people who ultimately go on to become international migrants.

Figure 2.

Total number of persons with U.S. experience assuming fixed and dynamic migration schedules.

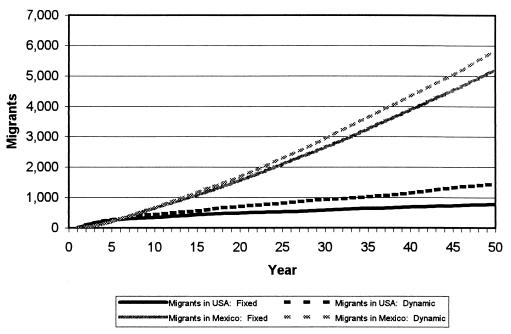
The migrant population may be further divided into two groups: those located in Mexico at any point in time and those located in the United States. Fig. 3 presents projections of these two populations over 50 years assuming fixed and dynamic migration schedules. Viewed from the Mexican side of the border, the failure to account for migration’s dynamic effects yields an 11% understatement of the number of people with U.S. migratory experience. Under fixed assumptions, the number of Mexicans projected to have been to the United States after 50 years is 5,211 whereas, under dynamic assumptions, it is 5,825. This discrepancy yields a substantially lower prevalence of U.S. migration among community members by year 50, with 23.7% of the community population estimated to have been to the United States under fixed assumptions compared with 27.8% under dynamic assumptions.

Figure 3.

Migrants in Mexico and the U.S. assuming fixed and dynamic migration schedules.

The discrepancy is even greater for the population of Mexicans projected to be living in the United States. Given fixed migration schedules, only 792 Mexicans are estimated to reside north of the border by year 50, but, with dynamically changing migration schedules, the number is projected at 1,461, almost double the baseline figure. If we were to rely on standard projection methods, in other words, and not model the dynamic effects of human and social capital accumulation, after 50 years, we would understate the number of Mexicans living in the United States by around 85%—hardly a trivial error from the viewpoint of U.S. citizens.

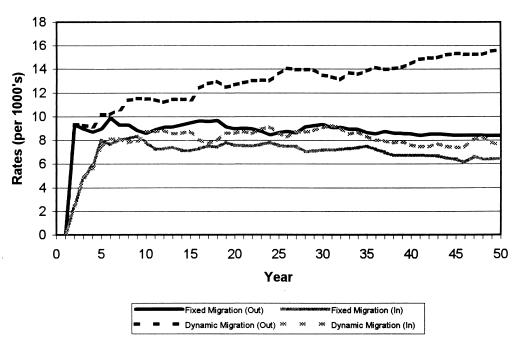
Fig. 4 shows the reason for this sizeable error by plotting crude rates of out- and return-migration under both fixed and dynamic assumptions. Incorporating dynamic feedback effects into the projection yields rates of out-migration that steadily rise over time and rates of return migration that trend slowly downward, reflecting the fact that human and social capital accumulate to increase the odds of out-migration and decrease the likelihood of returning home. As a result, the rate of net out-migration increases steadily over time. Under fixed assumptions, in contrast, rates of out and return migration do not diverge, but move roughly in tandem to yield a small, relatively constant rate of net-out migration. As a result, the assumption of fixed migration eventually comes to understate substantially the number of Mexican immigrants located north of the border.

Figure 4.

Out- and in-migration rates assuming fixed and dynamic migration schedules.

Discussion and Implications

By specifying equations that define dynamic schedules of international in- and out-migration, estimating their parameters empirically by using longitudinal data from Mexico, and using these estimates to project a hypothetical community population forward in time, we have confirmed the self-feeding character of international migration noted by field workers and theorists. Our simulation exercise began with a stable community of 10,000 inhabitants subject for many years to constant fertility and mortality and projected it ahead for 50 years under three alternative assumptions: that the community experienced no international migration; that it experienced constant probabilities of out- and in-migration varying only by age and sex; and that it experienced probabilities of out- and in-migration that changed dynamically in response to the accumulation of migratory experience over time.

Our model enabled us to quantify the dynamic feedback effects postulated by theorists who argue that migration is cumulatively caused by the steady accretion of migration-specific human and social capital. Using constant age- and sex-specific migration schedules instead of dynamically changing schedules yields a 5% overstatement of the projected size of the Mexican community after 50 years, an 11% understatement of the number of U.S. migrants, a 15% understatement of the prevalence of migratory experience in the sending population, and an 85% understatement of the size of the Mexican population living in the United States.

These conclusions are of more than academic interest because throughout its history the U.S. Bureau of the Census has used fixed migration schedules to project the future size and composition of the U.S. population. Our analysis suggests that, as long as projection methods fail to account for the dynamic effects that migration has in promoting the accumulation of human and social capital, they will be doomed perpetually to understate the effect of international migration on U.S. society.

In 1964, for example, the Census Bureau projected the U.S. population ahead assuming a net annual immigration of 300,000 persons distributed according to a fixed age and sex structure. This led to a projected total of 9.3 million immigrants by 1995, but observed legal immigration over the period was 19.2 million, nearly 50% higher. Although the latter figure does not take into account emigration, which seems to average about a third of the inflow (23), even discounting the gross figure by a third to allow for return migration yields a figure of 12.9 million, which is still 39% higher than that achieved under fixed assumptions. Moreover, that figure only captures the legal portion of the total net inflow. If we conservatively assume a net migration of just 100,000 undocumented migrants per year, total net immigration through 1995 rises back up to 15.9 million, yielding a 65% understatement by using the Census Bureau’s fixed assumption of 300,000 per year after 1964.

Although demographers did not realize it at the time, the figure of 300,000 net immigrants was already out of date when the Census Bureau established it. To be sure, the assumption seemed eminently reasonable at the time, given the history of immigration to the United States that had prevailed up to that point. Legal immigration had only exceeded 300,000 thrice over the past several decades (in 1956, 1957, and 1963), so the assumption of 300,000 migrants seemed safe, even conservative. Unfortunately, after 1965, the annual figure never again fell below 325,000 and by 1967 was running at 362,000 per year.

Government demographers soon realized that their assumed level of net immigration was too small, so in 1967 they increased it to 400,000 per year. Within 10 years, however, legal immigration had surpassed even this figure, never to return again. Despite this fact, the Census Bureau clung to an assumption of 400,000 net immigrants well into the 1980s, by which time legal immigration was actually running at ≈600,000 per year. In 1984, demographers raised the assumed level to 450,000 and by 1989 to 500,000. Unfortunately, by 1989 legal immigration was running in excess of one million per year. Indeed, the last year that U.S. immigration even approached 500,000 was 1980. By the early 1990s, Census Bureau demographers had come to their senses and raised the assumption to 880,000 net immigrants. Yet even this figure was unrealistically low: During the 1990s, legal immigrants arrived at rate of one million per year, and another 200,000 net undocumented migrants were estimated to be arriving as well.

It is thus clear from the record of the past two decades that the Census Bureau has been playing a game of catch-up in making assumptions about immigration to the United States. By the time that demographers get around to updating their assumptions based on recent trends, their information is already well on the way to being out of date. The fundamental weakness of the Bureau’s projection methodology is not the wisdom or responsiveness of its assumptions about immigration but the assumption that it is constant and invariant over time. As a result, its forecasts have consistently understated actual immigration, yielding figures that are modestly in error at the national level, seriously in error for subgroups affected by immigration (such as Hispanics or Asians), and spectacularly wrong for the principal immigrant-receiving states (California, New York, Florida, Illinois, Texas).

Rather than mechanically applying constant age- and sex-specific schedules of international migration, our analysis suggests that demographers would be better served by developing dynamic projection algorithms that take into account the fact that each cohort of migrants is preceded by others who have arrived before, yielding a stock of human and social capital that raises the odds of future movement to dynamize the flows. Although our own projection methodology makes strong data demands that are impractical for widespread application, we offer it to illustrate how the dynamics of international migration work and to quantify the feedback effects we have identified. A more practical approach to creating satisfactory forecast models might be to project future immigration flows in a way that is sensitive to the number of immigrants within the United States, as Walker and Hannan (30) have done in predicting immigrant destinations. This information is readily available from federal statistics, and, assuming that it correlates with the number and experience of migrants living abroad, it would provide a simple and effective means of incorporating the dynamic effects of human and social capital accumulation into demographic projection models.