Coupled prediction of protein secondary and tertiary structure

Abstract

The strong coupling between secondary and tertiary structure formation in protein folding is neglected in most structure prediction methods. In this work we investigate the extent to which nonlocal interactions in predicted tertiary structures can be used to improve secondary structure prediction. The architecture of a neural network for secondary structure prediction that utilizes multiple sequence alignments was extended to accept low-resolution nonlocal tertiary structure information as an additional input. By using this modified network, together with tertiary structure information from native structures, the Q₃-prediction accuracy is increased by 7–10% on average and by up to 35% in individual cases for independent test data. By using tertiary structure information from models generated with the rosetta de novo tertiary structure prediction method, the Q₃-prediction accuracy is improved by 4–5% on average for small and medium-sized single-domain proteins. Analysis of proteins with particularly large improvements in secondary structure prediction using tertiary structure information provides insight into the feedback from tertiary to secondary structure.

Many approaches for predicting secondary structure from sequence have been developed (1–13). The phd program published by Rost and Sander (14, 15) used multiple sequence–sequence alignments for the first time. The state-of-the-art psipred program by Jones (16) uses position-specific scoring matrices obtained in psiblast searches (17). The most accurate of these methods achieve a Q₃ score between 75% and 80%, where Q₃ is the percentage of amino acids correctly predicted as helix, sheet, or coil if all amino acids are classified in one of the three groups. Not only secondary structure but also supersecondary structural elements such as U-turns or β-hairpins can be predicted from sequence (18–22). In essentially all previous work, the prediction of the secondary structure at a given position i is based entirely on a local sequence window of 5–27 aa centered on the position; sequence information distant from position i is ignored, although, during folding, interactions with residues distant along the linear sequence but close in space are likely to influence the structure at position i.

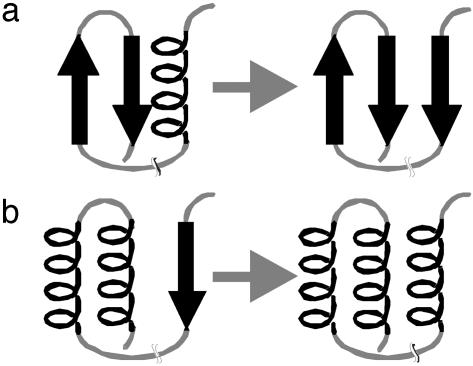
During the folding process of a protein, a certain fragment first might adopt a secondary structure preferred by the local sequence (e.g., an α-helix) and later be transformed to another secondary structure (e.g., a β-strand) because of nonlocal interactions with a segment distant along the sequence (Fig. 1). The structures of peptides corresponding to portions of complete native sequences have been investigated to identify parts of the sequence that adopt the native conformation early, as well as parts that undergo transitions (23, 24). Whereas some peptide fragments adopt stable conformations similar to those seen in the complete protein (25, 26), other peptides adopt different secondary structure in different contexts (27–33). As shown by Minor and Kim (34), the same local 11-aa sequence can adopt β-strand or α-helix structure, if inserted at two different positions in protein G. Also, for prion proteins, it appears that the same sequence can adopt different tertiary folds with different secondary structure (35–48). These results support the idea that the secondary structure in some portions of a protein sequence depends critically on tertiary interactions (49).

Fig. 1.

Two hypothetical folding pathways show the formation and subsequent transformation of secondary structure. (a) A preformed β-hairpin coming spatially close to a preformed α-helix. To form a three-stranded sheet, the α-helix needs to transform into a strand. (b) A β-strand distant in sequence coming spatially close to two helices packing against each other. The β-strand transforms into an α-helix to form a three-helix bundle.

Because of the indeterminacy of local sequence–structure relationships, the prediction of secondary structure from a local sequence window must fail in some cases. Secondary structure prediction is excellent (with Q₃ ≈ 90%) for many proteins but is as low as Q₃ = 50% for some sequences. Usually the mistakes in secondary structure prediction occur in regions with local sequences that do not clearly prefer the formation of α-helix, β-strand, or coil, where the choice may ultimately be dictated by quite nonlocal interactions. These nonlocal interactions, which result from the complex folding process, cannot be reproduced by a simple neural network, even if the complete sequence is provided as input. However, given a set of possible tertiary structure models, a neural network potentially could extract nonlocal information that in turn could help to predict the secondary structure of such regions more accurately and with a higher confidence level.

Given the amino acid sequence of a protein, possible tertiary structure models can be generated by de novo protein structure prediction methods. The rosetta de novo protein structure prediction method (50) has proven to be one of the most successful approaches. It can make good predictions for a large number of different folds, as demonstrated during CASP4 and CASP5 [Critical Assessment of Techniques for Protein Structure Prediction (51–53)]. The Protein Data Bank is screened for fragments that have a high primary-sequence homology and a secondary structure that matches the predicted secondary structure for each three- and nine-residue fragment of the query sequence. These fragments sample possible conformations for each local segment of the chain and are combined by using a Monte Carlo algorithm to generate possible tertiary structures.

In this article, low-resolution 3D information obtained from rosetta models is incorporated into a neural network secondary structure prediction method and found to decrease the number of critical mistakes. Going one step further, the improved secondary structure prediction is shown also to improve the structural models generated by rosetta when used for fragment selection. The procedure can be viewed as a mimic of the actual folding process: the secondary structure is formed based on local sequence preferences and later reevaluated based on the long-range interactions in frequently sampled tertiary structures.

Methods

Scoring Matrix-Based Secondary Structure Prediction. A previously described neural network approach for predicting secondary structure from a single sequence profile of seven amino acid properties over a window of 39 aa (13) was extended to process position-specific scoring matrices as additional input parameters. These matrices can be obtained from psiblast searches (17) and previously have been shown to be useful for secondary structure prediction (16). For this purpose, 20 additional input units were added per position. Thus, the number of input units was 1,053 [(7 + 20) × 39]: the number of hidden neurons in the standard three-layer feed-forward network was optimized to be 39, and three output neurons predicted three-state probabilities for an amino acid's being helix, sheet, or coil. The network was trained with ≈1,000 structures from the Protein Data Bank (54) selected to have a resolution better than 2.5 Å and a sequence identity of <50% as obtained from the Culled PDB Page (R. L. Dunbrack and G. L. Wang, Institute for Cancer Research, Fox Chase Cancer Center, Philadelphia) [now the Protein Sequence Culling Server (PISCES) www.fccc.edu/research/labs/dunbrack/pisces/)].

The training was performed by using the smart program (www.jens-meiler.de/index_soft.html), which performs back-propagation of errors. The learning rate was decreased from 10^–2 to 10^–4 during the training process, and the momentum was kept constant at 0.5. A monitoring set of 100 sequences was used to interrupt the training process as soon as its standard deviation was minimized. A second independent set of 100 sequences was used to evaluate the quality of the prediction. The training took 13,425 cycles (≈250 h on a 1.0-GHz Pentium III processor equipped with 2 gigabytes of memory). The prediction from sequence alone is accessible for academic users via the JUFO server (www.jens-meiler.de/jufo.html).

Incorporation of Tertiary Structure Information. To use rosetta models for secondary structure prediction, it is necessary to incorporate 3D structural information into the neural network input. Because many structural models (typically a few thousand) with different and partially wrong secondary structure are built by rosetta, an algorithm is desired that extracts information relevant for secondary structure prediction from a set of 3D models and combines it with sequence profile information. Because the local secondary structure at any sequence position might be wrong in the majority of the models, it is not used as input. Also, local sequence effects should be reflected in the primary-sequence information and should therefore not add new information to the input. The description of the 3D structure has to focus on the incorporation of interactions between parts of the molecule that are more distant in sequence and be robust in dealing with incorrect secondary structure in some of the models.

For incorporating low-resolution structural information, 90 input neurons were added to the neural network. The tertiary structure information fed to the network for a particular amino acid i was derived from all other amino acids j with C^α_i–C^α_j distances <8, 12, and 16 Å and a sequence separation of at least five amino acids [absolute (i – j) > 5]. For these amino acids, the number of helix, sheet, and coil residues (3 parameters), their average property profiles (7 parameters; compare ref. 13), and their averaged position-specific scoring matrices (20 parameters) in each of the distance bins were captured with 30 (3 + 7 + 20) input units. Thus, a total of 90 (3 distance bins × 30 input units) additional input neurons for the low-resolution structural information was added to the original network architecture. The network was trained in the manner described above for the sequence-alone network, by using the native structure of the proteins in the training, monitor, and independent data sets. The training took 14,775 cycles until the weights were optimized. The prediction from sequence in combination with a given tertiary structure is accessible for academic users via the JUFO3D server (www.jens-meiler.de/jufo3D.html).

Tertiary structure information was provided to the network from either the native structure or 1,000 rosetta models (50). We chose to use the network trained on native structures rather than retraining it with rosetta models. This choice allowed the use of as many native structures as possible for training, not only of proteins with <180 aa as foldable with rosetta. A “moving target” effect is avoided in which improvements in rosetta would require retraining. Also, the method is more general in the sense that it potentially can be applied to models generated with other protein structure prediction methods without prior retraining.

To obtain a single secondary structure prediction from a set of structural models, the three-state probabilities predicted by the neural network were averaged over all models. Before averaging, each model was weighted according to its score (a better score suggested a more probable 3D structure) and the internal consistency between the actual secondary structure of the model and the secondary structure predicted by the neural network using the model.

Results and Discussion

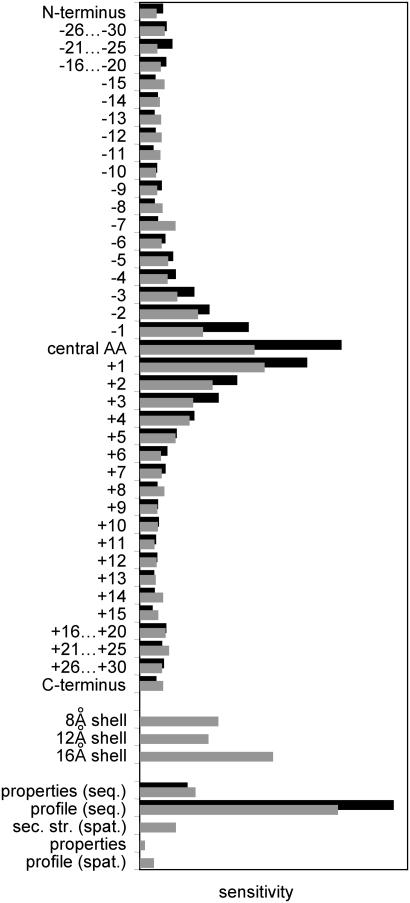
Analysis of the Artificial Neural Networks. The input-sensitivity profiles (defined as the first derivative of an output value with respect to a changing input vector) of the two neural networks (sequence-only versus sequence-plus-model) are similar over the sequence window (Fig. 2). Not surprisingly, the actual amino acid of interest and its direct neighbors had the largest influence on the prediction. The network that utilized tertiary structure information obtained ≈20% less information from the sequence than did the sequence-only network, as can be seen from the reduced sensitivities in the sequence profile. This part of the information was replaced by the low-resolution structural data. The most useful structural information was taken from the secondary structure of the spatially close amino acids, but position-based scoring matrices and the property profiles also contributed.

Fig. 2.

Comparative sensitivity analysis for the neural network that uses sequence alone (black bars) and the sequence-plus-model network (gray bars). On the horizontal axis, the sensitivity (numerical derivative of the output response with respect to a particular input) is plotted for all input parameters given on the vertical axis. In both cases, the relative increased importance of the central amino acid (central AA) and the decay for positions that are more distant in sequence can be seen. In the case of the sequence-plus-model prediction, the influence of the sequence data is reduced. About 20% of the overall information content is taken from the input data coding the spatial structure. The major influence of the scoring matrix in coding the sequence and the strong influence of secondary structure elements that are spatially close [sec. str. (spat.)] are evident.

Secondary Structure Prediction from Sequence-Only Network. The sequence-only neural network was tested on a set of 137 sequences with <150 aa that were not used for training. The trained neural network yielded prediction accuracy (Q₃) of 75% (SS1, Table 1), in agreement with the method of Jones (16) for this set of data (Q₃ = 75%).

Table 1. Comparison of secondary structure prediction results.

	Correctly predicted, %
		Helix	Sheet	Coil
SS1	Helix	28.9	0.8	7.2
	Sheet	1.2	11.8	7.5
	Coil	4.6	3.6	34.4
SS2	Helix	31.2	0.4	5.2
	Sheet	0.5	14.6	5.5
	Coil	4.5	4.4	33.7
SS3	Helix	30.7	0.1	6.0
	Sheet	0.2	15.7	4.7
	Coil	4.5	2.9	35.2

Results shown were obtained for 137 proteins with 10,127 aa by using sequence only (SS1; see ref. 13), sequence plus 1,000 rosetta models (SS2), and sequence plus native fold (SS3). SS1 yielded 78%, 58%, and 81% correctly predicted helices, sheets, and coils, respectively, with a correctly predicted average of 75%. SS2 yielded 85%, 71%, and 79% correctly predicted helices, sheets, and coils, respectively, with a correctly predicted average of 80%. SS3 yielded 83%, 76%, and 83% correctly predicted helices, sheets, and coils, respectively, with a correctly predicted average of 82%.

Secondary Structure Prediction Using Low-Resolution Information from Tertiary Structure. As expected, the Q₃ value improved (to 82%) for the independent set when using the correct 3D structures as input (SS3, Table 1). This value could be increased further by including higher-resolution 3D information. However, the low-resolution representation was chosen because it seemed most appropriate for the low-resolution structural models obtained from rosetta.

It is encouraging that including the low-resolution structural information from the true structures corrected serious mistakes in secondary structure prediction, where sheet, helix, and coil are interchanged. The gain of information naturally varies from sequence to sequence. Whereas, for many sequences, the nonmodified sequence-only setup yields already high Q₃ values of ≈90% and not much improvement is possible, some sequences perform rather poorly with only local information (Q₃ < 70%) and allow for a significant improvement. This possibility is particularly notable for β-strand prediction, which improved from 58% to 76% (Table 1). In contrast to α-helices, β-sheets are defined by nonlocal contacts and are therefore harder to predict from a local sequence window alone. Most of this lack of information already can be overcome by using a low-resolution description of tertiary structure as introduced here. Whereas the accuracy of helix and coil prediction increased by only 5% and 2%, respectively, the accuracy of sheet prediction increased by 18%.

Secondary Structure Prediction Using Predicted Tertiary Structure. Although the above results are encouraging, they require knowledge of the native structure and hence cannot be used for a protein of unknown structure. How much can be obtained from low-resolution and, often, low-accuracy de novo structural models?

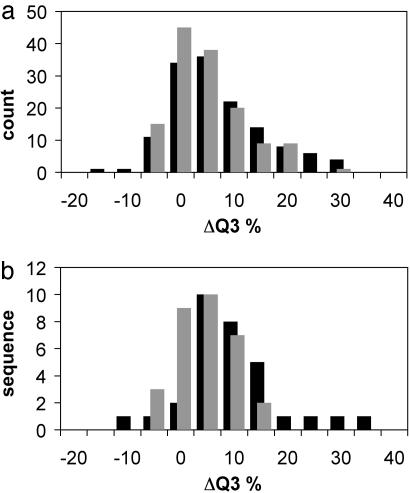
The results naturally will suffer when predicted structural models are used instead of the correct 3D fold. Nonetheless, on average, over the set of 137 proteins, an increase of 5% in the Q₃ value was obtained (SS2, Table 1). The Q₃ value increased from 75% to 80% when models were used and to 82% when the native structure was used as input for the neural network over a total of 10,127 aa. More important was the improvement of 13% in the prediction of β-sheets. A histogram of the changes in the Q₃ values for this set of proteins is given in Fig. 3a. Although many of the models have incorrect topologies and even coil or helix in place of a β-strand, if a second β-strand can come close in the majority of the models, the judgment of the network changes. Conversely, if no partner for a wrongly predicted β-strand can be found because of spatial restrictions, it can turn into a coil or helix.

Fig. 3.

Histogram of the change in secondary structure prediction accuracy (Q₃) resulting from inclusion of low-resolution tertiary structure information from the native structure (black bars) or rosetta models (gray bars) in the neural network secondary structure prediction. The change in Q₃ is shown on the horizontal axis, with count (a) or sequence (b) shown on the vertical axis. The average improvement for the independent set of 137 structures (a)is7% and 5%, respectively, and for the combined set of LIVEBENCH6 and CAFASP3 targets (b) is 10% and 4%, respectively.

The improvement that can be gained from the incorporation of low-resolution 3D models varies from case to case, depending on the quality of the sequence-only prediction and the variety and quality of the structural models. Of the set of 137 structures, a subset of 14 structures with differences in the sequence-only and sequence-plus-model prediction of >15% of the positions was selected. Table 2 gives an overview of this subset of proteins. The average sequence-only secondary structure prediction accuracy was 62%, significantly lower than the 75% seen for the complete set of data. The prediction accuracy achieved by including the structural models increased to 75%, which is only 3% lower than that achieved by using correct structure.

Table 2. Coupled prediction of secondary and tertiary structure.

PDB code	aa	Fold type	SS1	TS1	SS2	TS2	SS3
1ail_	70	α	54	6.0	64	6.0	67
1aoy_	78	αβ	76	6.2	89	5.7	82
1bm8_	99	αβ	60	9.3	72	8.8	76
1c8cA	64	β	53	7.6	67	5.0	64
1cc5_	76	α	70	6.4	86	6.2	84
1dtdB	61	αβ	51	6.7	69	5.7	71
1fwp_	66	αβ	56	8.0	68	7.3	77
1hz6A	67	αβ	70	4.1	87	3.4	79
1isuA	62	αβ	74	7.5	89	6.9	89
1sap_	66	αβ	53	7.3	65	6.6	74
1vie_	60	β	62	8.5	68	9.0	82
1vqh_	86	β	56	11.1	71	6.8	83
1wapA	68	β	57	8.3	68	7.7	82
2ezk_	93	α	74	7.0	85	6.6	83
Average	73		62	7.4	75	6.6	78

PDB, Protein Data Bank; aa, number of amino acids; SS1, percentage of secondary structure predicted from sequence only; TS1, rmsd with 1D secondary structure prediction given in angstroms; SS2, percentage of secondary structure predicted from models; TS2, rmsd with 3D secondary structure prediction given in angstroms; SS3, percentage of secondary structure predicted from native fold.

The improvement obtained for the sequence-plus-model prediction raises the question of how well the tertiary structure of the rosetta models alone reflects the true secondary structure of the protein. A secondary structure prediction from the tertiary structure of 1,000 models alone was obtained by computing the ratio of helix, strand, or coil conformation for every amino acid in the 137 proteins of the benchmark set. The Q₃ value achieved with this prediction method (71%) is significantly lower than the prediction from sequence alone (75%). Hence, the combination of sequence and tertiary information is critical to obtain an improvement in the predicted secondary structure.

CAFASP3 and LIVEBENCH6. The neural network was used to predict the secondary structure from models generated by the rosetta server during the CAFASP3 and LIVEBENCH6 (55) experiments. The results obtained for the 31 proteins modeled by using the rosetta de novo protocol are consistent with the numbers reported in Table 1 for the independent set of 137 proteins. The Q₃ value increased from 72% to 76% when using models and to 82% when using the native structure as input for the neural network over a total of 4,423 aa. The distribution over the protein sets is plotted in Fig. 3b. The average confidence level of the neural network decision increased from 45% (sequence-only) to 49% (sequence-plus-model) to 54% (sequence-plus-native structure) as the network came to a more definite decision by using the tertiary structure in regions where only an ambiguous prediction was made before.

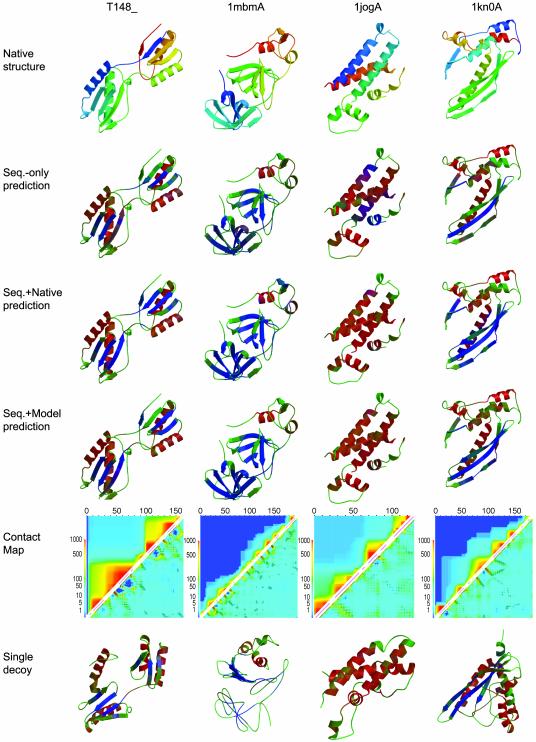
Fig. 4 illustrates ways in which tertiary structure can feed back to improve secondary structure prediction in four examples from LIVEBENCH6 and CAFASP3. T148 is a domain-swapped (the first strand lies in the second domain) ferredoxin fold that consists of two β-sheets, each of them packed with two helices on one side. The sequence-only prediction missed the first and the last strand completely, as indicated in green (which represents coil in Fig. 4). Also, the prediction of the helical and strand regions was rather ambiguous at some places. Virtually all of these mistakes were corrected when the native fold was used in the modified neural network. The Q₃ value increased from 74.1% to 87.7%. The spatial closeness of weakly predicted β-strands to a different β-strand in the 3D structure helped the neural network to draw the correct conclusion.

Fig. 4.

Examples of feedback from tertiary structure to secondary structure prediction taken from the CAFASP3 and LIVEBENCH6 experiments. The native structures are shown in the first row and are shown from the N terminus (blue) to the C terminus (red). In the second row, the predicted secondary structure from sequence-only prediction is shown, with predicted helix (red), predicted sheet (blue), and predicted coil (green). Mixtures of those colors represent ambiguously predicted regions. In the third row, the same color scheme represents the secondary structure prediction obtained by using the native structure as input for the modified neural network. The fourth row displays the secondary structure prediction obtained from the neural network by using rosetta models as input. The fifth row shows contact maps in which native contacts between an amino acid i and an amino acid j are indicated as black open squares in the right lower triangle matrix at position (j,i), and the frequency with which the models sampled a particular contact is shown in a gradient from never (dark blue) to always (red), on a logarithmic scale at the same position (j,i). The upper triangle matrix visualizes how frequently fragments of the 3D structure are correctly predicted in rosetta models; the color at position (i,j) indicates the number of models that have an rmsd 100 < 6 Å to the native structure for the fragment from amino acid i to amino acid j. The sixth row shows the lowest rmsd model in the ensemble color-coded with the secondary structure prediction obtained from the neural network by using only this model.

In this case as well as in the other three examples, rosetta was unable to predict the complete protein structure correctly. The two subdomains were built correctly in some of the models; however, their relative orientation was wrong, and the domain swap was very rarely suggested by rosetta. Still, those partial predictions allowed the neural network to improve the secondary structure significantly to achieve a Q₃ of 85.8%. The sampling of possible 3D structures and the analysis of the consistency of predicted and modeled secondary structure suggest that β-strands are more likely than coil or helix in the ambiguously predicted regions.

Domain A of the arterivirus nsp4 (1mbmA) (56) folds in three subdomains. The first two contain only β-sheet, whereas the latter one contains two α-helical regions. The single-state prediction was at 66.2% accuracy, mainly because some small secondary structure elements were missed and the length of the individual β-strands was wrongly predicted. When using the native structure as input to the neural net, many of the ambiguous regions were clearly predicted, which resulted in an increased Q₃ of 75.3% and an improved confidence level. Beside a better prediction of beginnings and endings of β-strands, two β-bridges in the third domain, as well as one additional strand in the second domain, were found correctly. The rosetta models did not capture the complex nonlocal topology of the two β-domains. Typical models contained three separate domains, two of them with a local β-sheet, one α-helical. However, even these models were sufficient to improve the prediction to a Q₃ of 75.8%, although they contained mainly β-hairpins instead of the less local strand contacts in the native structure.

The third example, domain A of HI0073/HI0074 protein pair from Haemophilus influenzae (1jogA) (57), is an all-helical protein. However, the sequence-only prediction gave the end regions of the first two helices a high strand probability. In addition, one short helix was predicted as strand, and the prediction for the last helix had significant coil probability. Still, the sequence-only prediction was at a high level of 71.3%. When the correct 3D structure was used, those mispredicted regions were mostly corrected. The strand signal vanished almost completely, and only at few places was a significant coil signal obtained, which was, however, still lower than the helix probability in those regions. The Q₃ value increased to 86.0%. rosetta was (correctly) unable to bring the regions of the molecule with an increased strand probability spatially close, and, hence, the strand regions were converted to helices, leading to an improved Q₃ of 87.6%.

In domain A of the homologous pairing domain from the human Rad52 recombinase (1kn0A) (58), only the middle strand of the three-stranded β-sheet was predicted from sequence alone with a high probability. The two neighboring strands that lie on the edge of the sheet were predicted as coil with a very low confidence level. Also, one strand of the small β-hairpin was missing, as well as one of the short α-helices. When using the 3D structure as additional input for the modified neural network, most of the strand amino acids were correctly predicted, and only the small helix was still predicted as coil. The Q₃ value increased from 69.0% to 81.0%. The prediction from models (Q₃ value of 79.9%) was not significantly worse. Interestingly, the best models built for this protein adopt a fold that appears to be the spatial inverse of the native structure. In the model shown in Fig. 4, the three-stranded sheet is properly formed, but the helix is packed on the opposite site compared with the native structure. In consequence, the small helix bundle sits on the opposite site. This model still has a relatively high rms deviation (rmsd) from the native structure (>10 Å); however, all C^α–C^α distances are close to the distances measured in the native structure, and these are the data used by the neural network.

Tertiary Fold Prediction. We investigated whether the tertiary structure–secondary structure feedback could be extended to generate improved 3D models using the improved secondary structure prediction as input to rosetta. One thousand structures were built with the sequence-only prediction (TS1, Table 2) and with the model-assisted prediction (TS2, Table 2) where the models were taken from the previous run.

The quality of the models produced was assessed by comparing the model native C^α–C^α rmsd of the tenth-most accurate model to avoid statistical artifacts that might be caused by looking at the best rmsd only. When using the model-assisted secondary structure prediction, the average rmsd decreased from 7.4 to 6.6 Å (TS2, Table 2). Whereas in many cases the rmsd did not change significantly (Δrmsd < 0.5 Å), it did improve for the majority of the problematic proteins (1c8cA, 1dtdB, 1fwp_, 1hz6A, 1isuA, 1sap_, 1vqh_, and 1wapA) between 0.6 and 4.3 Å. rosetta on average generates poorer models for these proteins than for the complete set of 137 structures, which might partially be caused by the ambiguous secondary structure prediction. However, the improvement of the secondary structure prediction is certainly more significant than the change in the quality of the predicted models. A second iteration of secondary structure prediction and generating rosetta models further improved neither the secondary structure prediction nor the 3D models.

The most significant improvement in the quality of the tertiary fold, which was accompanied by an improvement of the Q₃ prediction accuracy of 15%, was for 1vqh, an 86-residue, all-β protein. Only three of the eight β-strands were recognized, whereas a fourth was predicted to be a helix when using sequence-only prediction. After incorporating a set of 1,000 models (obtained by using this ambiguous secondary structure prediction) into the secondary structure prediction, the Q₃ value became 71%, and seven of the eight strands were recognized. When using the correct 3D fold as input, all eight strands were recognized and Q₃ was found to be 76%. In this particular case, the predicted structure improved drastically. The rmsd value of the tenth-best model by rmsd dropped from 11.1 to 6.8 Å.

Conclusion

Although very accurate for many proteins, secondary structure prediction from sequence alone can fail if the formation of secondary structure is strongly coupled to the formation of tertiary interactions. This is especially true for β-strands, where nonlocal partners are frequently necessary. Here we show that even very low-resolution tertiary structure information can improve the prediction of secondary structure.

A drawback of the new method is its dependence on rosetta models, which limits its application to single-domain proteins. Incorporation of very long-range interactions between domains and within single large domains will require improvements in de novo protein structure prediction methodology. Despite this currently limited applicability, the method does illuminate the ways in which tertiary structure can feed back on secondary structure. The characterization (Fig. 4) of the proteins for which the largest changes in secondary structure prediction were brought about by using tertiary structure models suggests that the most important influences are on regions with some β-strand propensity. Such regions are predicted to be β-strands if and only if there are nearby β-strands in plausible tertiary structures. This resolution of ambiguous β-strand propensity by the presence (or absence) of tertiary β-sheet interactions is likely to mirror the fate of segments of the polypeptide chain with weak β-strand propensity during the actual folding process.