Biomolecular hydration: From water dynamics to hydrodynamics

Abstract

Thermally driven rotational and translational diffusion of proteins and other biomolecules is governed by frictional coupling to their solvent environment. Prediction of this coupling from biomolecular structures is a longstanding biophysical problem, which cannot be solved without knowledge of water dynamics in an interfacial region comparable to the dry protein in volume. Efficient algorithms have been developed for solving the hydrodynamic equations of motion for atomic-resolution biomolecular models, but experimental diffusion coefficients can be reproduced only by postulating hundreds of rigidly bound water molecules. This static picture of biomolecular hydration is fundamentally inconsistent with magnetic relaxation dispersion experiments and molecular dynamics simulations, which both reveal a highly dynamic interface where rotation and exchange of nearly all water molecules are several orders of magnitude faster than biomolecular diffusion. Here, we resolve this paradox by means of a dynamic hydration model that explicitly links protein hydrodynamics to hydration dynamics. With the aid of this model, bona fide structure-based predictions of global biomolecular dynamics become possible, as demonstrated here for a set of 16 proteins for which accurate experimental rotational diffusion coefficients are available.

The translational and rotational motions of a protein molecule are three or more orders of magnitude slower than the relaxation of its linear and angular momenta and can therefore be described accurately by diffusion equations (1). Such global dynamics is thus characterized by isotropic translational (D_T) and rotational (D_R) diffusion coefficients, or by the corresponding tensors. The dynamic protein–solvent coupling is embodied in Einstein's fluctuation–dissipation theorem D_T,R = k_BT/ζ_T,R (2). When this equation is combined with the results of macroscopic continuum hydrodynamics (3) for the friction coefficients of a sphere of radius a undergoing steady translation or rotation in a solvent of shear viscosity η₀, one obtains the celebrated Stokes–Einstein (SE) relations

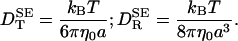[1]

More elaborate expressions have been derived for ellipsoidal solutes (4). When applied to globular proteins, these expressions severely overestimate the diffusion coefficients. As an example, consider the rotation of hen egg-white lysozyme (HEWL). By using either the crystal structure or the partial specific volume in solution, one obtains a molecular volume of 16 nm³. Inserted into Eq. 1, this yields D_R = 42 μs^–1 in H₂O at 20°C. If the elongated shape of HEWL is modeled by a prolate spheroid of aspect ratio 1.5, D_R is reduced to 40 μs^–1, still a factor 2 above the experimental value of 20 ± 1 μs^–1 (5). Early workers attributed such discrepancies to “bound” water that migrates with the protein and therefore contributes to its hydrodynamic volume (6, 7). Measurements of transport coefficients like D_T or D_R thus became established as a method for quantifying protein hydration.

Proteins, of course, do not have ellipsoidal shapes. Is the discrepancy between measured and calculated diffusion coefficients then simply a result of the different hydrodynamic properties of the real protein shape and the ellipsoidal model? To address this question, efficient numerical methods have been developed for computing the hydrodynamic friction tensors of rigid biomolecular structures described in atomic detail (8–12). Such realistic modeling of biomolecular shape brings theory much closer to experiment and also removes most of the variation in apparent hydration among different proteins. Nevertheless, even molecular hydrodynamics does not quite bridge the gap between theory and experiment. Typically, the calculated rotational diffusion coefficient is still 30% too large. This discrepancy, which exceeds the experimental uncertainty in D_R by an order of magnitude, is usually ascribed to about half a monolayer of “tightly bound” water molecules (9–17).

The putative role of “bound” water in this context is a higher-order effect: the perturbation of the bulk solvent by the protein reacts back and perturbs the motion of the protein itself. Nevertheless, it is an important and longstanding biophysical problem (6). Most biologically important molecular events take place at the biomolecule–solvent interface. All sources of information about the elusive properties of this interface are welcome, and any inconsistencies in our understanding should be confronted. Furthermore, from a more pragmatic point of view, an incomplete understanding of the hydration effect prevents us from using molecular hydrodynamics to make bona fide predictions of global protein dynamics with an accuracy that matches the experimental one.

What are the implications of attributing the 30% discrepancy in D_R to “tightly bound” water molecules? Because D_R is inversely proportional to volume (see Eq. 1), the volume of this “rigid” hydration shell is, in the case of HEWL, 0.30 × 16 = 4.8 nm³. If a water molecule occupies 25 ų at the protein surface, as suggested by Voronoi analysis of protein crystals (18), then this volume corresponds to ≈200 water molecules. If these water molecules were immobilized at the protein surface, they would contribute to the hydrodynamic friction in the same way as protein atoms. According to conventional wisdom, this will still be the case if these water molecules exchange with bulk water, so long as their residence times are longer than the rotational correlation time of the protein so they migrate with the rotating protein. The widely accepted interpretation thus implies that ≈200 water molecules on the surface of HEWL have residence times longer than the (rank-2) rotational correlation time, 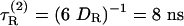, of HEWL. Hydration dynamics has been a controversial issue, but recent ¹⁷O magnetic relaxation dispersion (MRD) measurements (19, 20) and molecular dynamics simulations (21–24) demonstrate conclusively that water molecules at protein surfaces are highly mobile, with mean residence times in the range 10–50 ps (at room temperature) for nearly all hydration sites. Our principal aim here is to resolve this paradox.

Methods

Experimental Rotational Diffusion Coefficients. The theory proposed here was tested against a set of 16 proteins, for which D_R has been determined from measurements of the backbone ¹⁵N T₁ and T₂ relaxation times and the ¹⁵N—{¹H} steady-state nuclear Overhauser effect. The protocols used for such relaxation experiments and the associated data analysis are highly standardized. These D_R values are based on independent relaxation data from 50–200 residues (after exclusion of unresolved or highly disordered residues). The precision is therefore very high, with values as low as 0.2% frequently quoted. However, when systematic errors, arising from slow internal motions, rotational anisotropy, etc., are taken into account, the accuracy in D_R is probably on the order of a few percent. The NMR relaxation data yield the isotropic rank-2 rotational correlation time τ_R⁽²⁾ = (6 D_R)^–1, from which we extract D_R. The experiments were carried out at temperatures ranging from 22 to 41°C in water containing 5–10% D₂O (for the NMR lock signal). We have corrected all values to pure H₂O at 20°C, assuming that D_R is proportional to T/η(T) (see Eq. 1).

Calculated Rotational Diffusion Coefficients. With modern computing resources, hydrodynamic calculations can be performed routinely on realistic structural models of proteins and other macromolecules. The two most widely used computational approaches are the boundary-element (BE) Stokes flow method (10, 12) and the Kirkwood–Riseman–Bloomfield (KRB) method (8, 11). When applied to proteins, both methods use as structural input the coordinates of all nonhydrogen protein atoms, usually taken from a crystal structure. Because hydrodynamic friction originates at the protein–solvent interface, it is necessary only to model the external protein surface. Small-scale surface irregularities are computationally demanding but hardly affect the global hydrodynamic properties (12). In the BE method, surface smoothing is accomplished by rolling a probe sphere (typically 0.3-nm radius) over the van der Waals surface of the protein and then discretizing this probe-excluding surface by a triangulation algorithm. The hydrodynamic calculation is performed with stick boundary condition on the smoothed protein surface (10, 12). In the KRB method, the protein surface is defined by spheres, all with the same atomic radius σ₀, located at the positions of nonhydrogen protein atoms. This shell of overlapping spheres is filled by smaller spheres that act as point sources of hydrodynamic friction, and the radius of the small spheres is then extrapolated to zero.

For each of the 16 investigated proteins, we performed KRB calculations of D_R with the program hydropro ver. 5a (11). In these calculations, we used a bulk solvent viscosity η₀ = 1.002 cP (1 P = 0.1 Pa s), as for H₂O at 20°C. The effective atomic radius, σ_H = 0.30 nm, was chosen to minimize the difference between calculated and experimental D_R values for our set of proteins. The atomic coordinates were taken from high-quality x-ray crystal structures with R factor < 0.21 and resolution limit ≤ 0.2 nm for all but three proteins. To minimize the influence of any cryogenic artifacts, crystal structures determined at or near room temperature (as for the NMR studies) were preferred.

Results

Dynamic Coupling to a Perturbed Solvent. The dynamic coupling of a solute to a perturbed solvent was first investigated in connection with the limiting conductivity of electrolyte solutions (25). This problem has been addressed by continuum theory as well as by molecular theory and simulation. In continuum treatments, additional attributes, besides viscosity, are sometimes assigned to the solvent, such as compressibility, electric polarization, and nonlocal response (in space and time). Another extension of the primitive model is to allow for a nonuniform solvent viscosity; for example, the viscosity η_S in the first solvation shell might differ from the bulk solvent viscosity η₀. For solutes as small as monatomic ions, continuum theories can provide valuable physical insight but can hardly be expected to deliver quantitatively accurate results. In addition, the electric field of a small ion gives rise to a variety of electric effects (electrostriction, dielectric friction, dielectric saturation, and polarization diffusion) that overshadow the effect of the solute-induced perturbation of solvent dynamics. For proteins, on the other hand, these electric effects are unimportant. Moreover, because the first hydration layer of even a small protein contains hundreds of water molecules, the continuum treatment is more easily justified.

Let us then evaluate the rotational diffusion coefficient D_R of a spherical “protein” of volume V_P immersed in an incompressible solvent with viscosity η_S within a spherical shell of volume V_S and the bulk value η₀ elsewhere. By solving the linearized Navier–Stokes equations and computing the frictional torque from the stress tensor (3, 26, 27), one finds

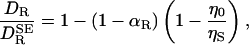[2]

where α_R = V_P/(V_P + V_S) and 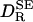, as given by Eq. 1, is the rotational diffusion coefficient in the absence of solvation effects. This result has the expected limits. In the absence of solvation, meaning η_S = η₀ and/or V_S = 0, Eq. 2 reduces to 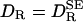. In the “solvent-berg“limit, where η_S » η₀ so that a negligible fraction of the viscous energy dissipation occurs in the solvation shell, we also recover the SE Eq. 1, but now with a hydrodynamic volume that includes the effectively rigid solvation shell.

The next step is to generalize Eq. 2 so that it can be applied to real proteins, which lack the spherical symmetry assumed in its derivation. That deformation of a sphere to a prolate spheroid of aspect ratio 1.5, as in the case of HEWL, reduces D_R by merely 6% shows that size matters much more than shape. Furthermore, the large drop in D_R in going from a smooth spheroid to a high-resolution model is not primarily due to atomic-scale surface roughness. Boundary-element calculations on HEWL show that D_R is insensitive to the finer details of protein shape (12). Instead, D_R is reduced because large-scale shape irregularities, such as the binding cleft in HEWL, make the rotating protein displace a larger amount of solvent than would a compact protein of the same volume. This phenomenon is well known in the field of polymer dynamics: according the the Rouse–Zimm theory, hydrodynamic interactions between polymer segments render a random coil hydrodynamically equivalent to a compact sphere with a radius determined by the coil's radius of gyration (28). Because the detailed protein shape is relatively unimportant, we expect that Eq. 2 can be applied also to real proteins. We can therefore replace the left-hand side of Eq. 2 by 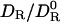, the ratio of the D_Rs of the real protein in the real perturbed solvent (D_R) to that in an unperturbed bulk solvent ().

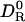As a further generalization, we must take into account the variation of the local viscosity over the structurally and chemically heterogeneous protein surface. Because the fluid velocity field involves the spatial integral of [η(r)]^–1, it is the inverse surface viscosity 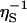, rather than η_S itself, that should be averaged. In Eq. 2, we therefore replace η₀/η_S by the spatial average 〈η₀/η_S〉 over the solvation shell volume V_S. This η_S^–1 averaging makes physical sense: even if η_S is very large in a small region, D_R should not be affected much, because most of the viscous dissipation occurs outside this small region in any case.

In the final step, we must relate the local viscosity η_S to a known dynamic quantity. All transport processes in water, including viscous flow and diffusive molecular motions, are governed by the hydrogen-bond lifetime, which sets the time scale for restructuring of the hydrogen-bond network that permeates the liquid (29). Because rotation is a localized motion, we use the rank-2 rotational correlation time, hereafter denoted by τ_S, as a measure of water dynamics in the solvation shell. More specifically, we assume that η_S is proportional to τ_S. This assumption is supported by the observation that bulk water rotation obeys Eq. 1 closely over a wide temperature range (30). In fact, from –10 to 60°C, the SE radius a varies by only 1.7%, whereas the viscosity changes by a factor 6. The same approximation has been used in studies of small-ion mobilities (31, 32).

Summing up, we have arrived at the following expression for the hydration effect on the rotational diffusion coefficient of a protein or other biomolecule:

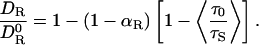[3]

The average can be expressed as

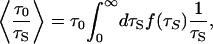[4]

where f(τ_S) is the normalized water correlation time distribution in the hydration shell. Water ¹⁷O MRD studies on seven globular proteins yield 〈τ_S〉/τ₀ = 4.9 – 6.4, with an average of 5.5 (19, 20). With τ₀ = 2.1 ps at 20°C (30), this gives 〈τ_S〉 = 12 ps. Physical considerations (20) and molecular dynamics simulations (33–35) suggest that the distribution f(τ_S) is skewed toward longer τ_S, and that it vanishes for τ_S values somewhat shorter than τ₀. A normalized distribution with these features is 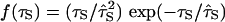, which peaks at and has 〈τ_S^–1〉 = 2 〈τ_S〉 ^–1. Accordingly, we adopt 〈τ₀/τ_S〉 = 0.35 as our best estimate. A small fraction of the several hundred water molecules at the protein surface, located in pockets and crevices and interacting strongly with the protein, have correlation times up to several hundred picoseconds. Such water molecules contribute disproportionately to the experimentally determined average 〈τ_S〉 but hardly affect the inverse average in Eq. 4. Recent low-temperature MRD studies (K. Modig, E. Liepinsh, G. Otting, and B.H., unpublished observations) show that the vast majority of surface waters behave in much the same way as water molecules hydrating free amino acids and other small molecules, for which 〈τ_S〉/τ₀ ≈ 2 – 3 (20, 36, 37).

To estimate the geometric quantity α_R in Eq. 3, we take the hydration shell volume V_S to be proportional to the molecular surface area A_P of the protein: V_S = λ_S A_P. The effective shell thickness λ_S should be slightly less than one water diameter (0.28 nm). With λ_S = 0.20 nm, the number of water molecules in the hydration shell of HEWL becomes 0.20 × 64/0.025 = 512, in accord with simulation-based estimates (35). This λ_S value should apply to any globular protein. For HEWL, we thus obtain α_R = 16/(16 + 0.20 × 64) = 0.56. Inserting this, along with 〈τ₀/τ_S〉 = 0.35, into Eq. 3, we find .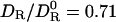

Molecular Hydrodynamics with Dynamic Hydration. Molecular hydrodynamics calculations on atom-resolution protein models typically yield D_R values 30% larger than experiment. Agreement with experiment can be forced if the atomic radius σ₀ is replaced by a larger effective hydrodynamic radius σ_H. The price for this agreement is loss of true predictive power. According to the standard interpretation, the difference σ_H – σ₀ represents the effect of rigidly bound water molecules. However, the physical significance of the adjustable parameter σ_H has not been established independently. In contrast to this ad hoc approach, our analysis showed that the 30% D_R discrepancy can be fully accounted for, at least in the case of HEWL, by an independently determined modest viscosity enhancement (longer τ_S) near the protein surface. To see whether this explanation is generally valid, we have examined a set of 16 monomeric globular proteins in the size range 6.5–27.7 kg mol^–1 (see Table 1, which is published as supporting information on the PNAS web site, www.pnas.org).

The results of this analysis are shown in Fig. 1 and Table 1. The linear (Pearson) correlation coefficient between and 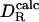is r = 0.968, and the ratio has a mean of 0.992 with standard deviation of 0.086. The optimum effective radius σ_H is therefore close to 0.30 nm. For 13 of 16 proteins, the theoretical prediction is within 10% of the experimental value 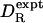. In a previous analysis of a set of 14 proteins (five of which occur in our set), KRB calculations with σ_H = 0.33 nm yielded for 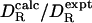a mean of 0.993 with a standard deviation of 0.112 (15). The larger effective radius obtained there may reflect differences in the experimental data. In the previous analysis, the remaining difference between and 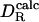was attributed to experimental error (15). We believe that two additional factors play a role here. First, side-chain conformations of some surface residues are affected by protein–protein contacts in the crystal, leading to small but real differences in the average protein structure between solution and crystal environments. Second, flexible polypeptide segments are treated as rigid in the hydrodynamic calculation. This is probably the main reason for the 17% underestimation of D_R for ubiquitin (the worst case in our set). In the crystal structure of ubiquitin, a four-residue segment at the C terminus extends out from rest of the protein, but in solution, this segment may fold back onto the protein at least part of the time. If three of these four protruding residues are deleted, is increased by 17% (38).

Fig. 1.

Correlation between rotational diffusion coefficents measured by ¹⁵N relaxation () and calculated by molecular hydrodynamics with σ_H = 0.30nm (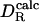, filled symbols) or one-half of that calculated from the SE relation with the partial protein volume (0.5 , open symbols). The data refer to H₂O at 20°C, and the 16 proteins are identified in Table 1. (Inset) The inverse rotational diffusion coefficient, 1/D_R (ns^–1), for HEWL and BPTI calculated by molecular hydrodynamics by using crystal structures 1HEL and 5PTI, respectively, and variable effective atomic radius σ_H (nm).

Table 1 also gives the (calculated) rotational anisotropy, defined in terms of the principal components of the rotational diffusion tensor as A = 2 D₁₁/(D₂₂ + D₃₃), with the principal axes labeled so that D₁₁ ≥ D₂₂ ≥ D₃₃. We thus have A = 1 for a spherical top, whereas A > 1 indicates a prolate-like symmetric top. With A = 1.42, HEWL exhibits the largest deviation from spherical-top behavior among the 16 proteins. Because ¹⁵N relaxation data are usually analyzed under the assumption of spherical-top rotation, one might expect the agreement between and 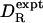to deteriorate with increasing rotational anisotropy. In our data set, however, the correlation between the deviation 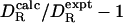and A is very weak (r = 0.44). It is also conceivable that the deviation correlates with protein size. For a small protein, global and internal motions will not be fully time-scale separated, which will affect the interpretation of the correlation time that we use to extract . Furthermore, the hydrodynamic calculation is based on a continuum description of the solvent, which should be less accurate for small proteins. For the investigated proteins, however, the deviation 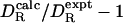shows no correlation with the molecular mass of the protein (r = –0.10).

The SE diffusion coefficient 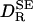in Table 1 was calculated from Eq. 1 in the form . The partial molar volume of the protein was obtained from , with the (nearly invariant) partial specific volume cm³ g^–1. As seen from Fig. 1, 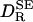is strongly correlated with 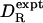(r = 0.975), but it is typically twice as large: the mean of 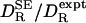is 2.014 with a standard deviation of 0.283. Dividing 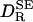by 2, we thus obtain a simple and surprisingly accurate estimate of the true rotational diffusion coefficient: (kg mol^–1) at 20°C.

The present calculations, like previous ones (11, 12, 15), demonstrate that molecular hydrodynamics calculations with a fixed (protein-independent) effective atomic radius σ_H can reproduce experimentally determined rotational diffusion coefficients. Our calculations yield σ_H = 0.30 nm. The important new element in our analysis is that we can now rationalize the value of σ_H in terms of hydration dynamics, as determined by independent experiments. To do this, we must relate the thickness λ_S of the perturbed layer of water molecules and the solvation dynamics in this layer, characterized by 〈τ₀/τ_S〉, to the thickness σ_S ≡ σ_H – σ₀ of a hydrodynamically equivalent rigid (η → ∞) solvation layer that reduces the rotational diffusion coefficient of the protein by the same amount. To this end, we derive an expression for (where 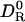refers to the bare unhydrated protein) for the equivalent protein (with a rigid solvation layer). This expression is then identified with Eq. 3, which expresses the same ratio for the real protein.

According to the SE Eq. 1 with V = V_P + σ_S A_P,

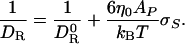[5]

This result is rigorously valid only for spherical solutes, but it remains a good approximation for globular proteins. To show this, we have calculated D_R as a function of the effective radius σ_H for two proteins. As seen from Fig. 1 Inset, 1/D_R does indeed increase linearly with σ_H (or with σ_S at fixed σ₀). Moreover, the slope is within 10% of that predicted by Eq. 5. For bovine pancreatic trypsin inhibitor (BPTI), with A_P = 34 nm², Eq. 5 predicts a slope of 51 s m^–1, whereas the fit in Fig. 3 yields 54 s m^–1. For HEWL, with A_P = 64 nm², Eq. 5 predicts 95 s m^–1, and the fit yields 86 s m^–1.

By combining Eqs. 3 and 5 and substituting, as before, λ_S A_P for V_S in the α_R term of Eq. 3, we obtain after rearrangement

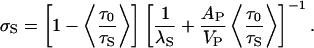[6]

In apparent contrast to the results of the KRB calculations, Eq. 6 implies that σ_S depends on protein size. By fitting the results of analytical geometric computations on a large set of protein crystal structures (39), we obtain the scaling relations A_P(nm²) = 7.43 [M_P (kg mol^–1)]^0.81 and V_P(nm³) = 1.02 [M_P (kg mol^–1)]^1.03. When these relations are inserted into Eq. 6, along with λ_S = 0.20 nm and 〈τ₀/τ_S〉 = 0.35 (see above), we find that σ_S varies from 0.097 to 0.104 nm for our set of 16 proteins. The size dependence in σ_S can therefore be neglected, and we adopt σ_S = 0.10 nm as a universal value.

If our analysis is correct, the resulting bare atomic radius, σ₀ = σ_H – σ_S = 0.20 nm must make physical sense. This value refers to the extended atoms (incorporating covalently attached hydrogens) used in the hydrodynamic model. Moreover, it refers to the contact that these extended atoms make with water molecules. The pair correlation functions between water-O and protein-C/S or protein-N/O atoms typically peak at 0.38 and 0.28 nm, respectively (40). Subtracting the water-O van der Waals radius of 0.14 nm, we obtain surface contact radii of 0.24 and 0.14 for nonpolar and polar extended surface atoms, respectively. Because a single radius is used in the hydrodynamic model, σ₀ should be regarded as an average over all solvent-exposed atoms at the protein surface. For native globular proteins, 57 ± 4% of the solvent-accessible surface is contributed by nonpolar atomic groups and the rest by polar or charged groups (41). Combining all this, we obtain σ₀ = 0.57 × 0.24 + 0.43 × 0.14 = 0.20 nm, in perfect agreement with our dynamic hydration model.

Translational Diffusion. Our analysis of the hydration effect on the global motion of proteins has focused on rotation. There are two reasons for this. First, the experimental database is more extensive and accurate for rotation than for translation. Second, rotation is more strongly affected by hydration, because the fluid velocity field around a rotating sphere decays as r^–2, whereas the velocity field around a translating sphere has a more long-ranged r^–1 component related to fluid displacement (3). As a consequence, the fraction of the viscous energy dissipation that occurs within the solvation shell of volume V_S is 1 – α_R for rotation (0.44 for HEWL), but only 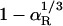for translation (0.18 for HEWL).

For translational motion, the solution to the Navier–Stokes equations is more involved but, to a good approximation, the ratio can be expressed on the same form, Eq. 2, as for rotation, with the only difference that α_R is replaced by (25, 26, 31, 32, 42). The steps leading up to Eq. 3 are valid also in the translational case. According to the SE Eq. 1, we have for the equivalent rigid-hydration-shell model used in molecular hydrodynamics calculations: 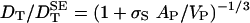. Proceeding as in the rotational case, we can express σ_S as a function of λ_S, 〈τ₀/τ_S〉, and A_P/V_P. For the same parameter values as before, we find a near-universal value σ_S = 0.11 nm, only 10% larger than in the rotational case. (For our set of 16 proteins, σ_S varies from 0.109 to 0.113 nm.) Because σ₀ should not depend on the type of motion, we predict that the optimum value for the effective atomic radius in KRB calculations of D_T is σ_H = 0.31 nm. Previous KRB calculations of D_T for 19 proteins are inconclusive in this regard; the reported σ_H values, adjusted to achieve agreement with experimental D_T values, have a mean of 0.28 nm, but a large standard deviation of 0.11 nm (15). Presumably, this scatter reflects inaccuracies in the experimental data. For HEWL, the experimental D_T value, from dynamic light scattering (43), is 1.06 (in units of 10^–10 m² s^–1) at 20°C. With V_P = 16 nm³ the SE prediction (1.37) is only a factor 1.3 larger (compared to a factor 2.1 for rotation) and is hardly affected (1.35) by deformation to a prolate of aspect ratio 1.5. A molecular hydrodynamics calculation (12) with the boundary element method and no hydration yields D_T = 1.19, indicating a hydration effect of 12% (compared to 30% for rotation).

Discussion

Hydrodynamics and Water Exchange. The effect of solute–solvent interactions on solute mobility has been explored theoretically along two roads: molecular theory and continuum hydrodynamics (25). As shown here, our hydrodynamic approach appears to provide a consistent theoretical framework for linking protein motion to hydration dynamics. The alternative, a truly molecular theory that predicts 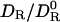from intermolecular forces and torques at the inhomogeneous protein–water interface, can hardly be pursued without drastic simplifications that would limit the predictive power of the theory.

A molecular theory has recently been proposed that describes the effect of hydration dynamics on protein rotation (17). As in most other molecular theories of solute mobility, the starting point is the second fluctuation-dissipation theorem (1), relating the rotational friction coefficient ζ_R to the time integral of the torque autocorrelation function (TACF). Rather than applying this rigorous result of linear response theory to the total friction ζ_R, the authors of ref. 17 use it to calculate the additional friction 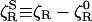attributed to solvation, which amounts to a corresponding decomposition of the torque and neglect of cross-correlations. A similar type of approximation, separating hard repulsive from soft attractive forces, has been used in a molecular theory of dielectric friction (44). In the protein hydration case, however, the physical significance of the decomposition remains obscure. After further approximation, the authors of ref. 17 proceed to model the hydration TACF in terms of the torque experienced by ≈ 500 water dipoles, each of which interacts with a nearby divalent protein charge in a low-dielectric medium. Furthermore, they identify the torque correlation time with an average water residence time at the protein surface. The result is a formula that expresses 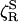in terms of 10 parameters, half of which are unknown or bear little relation to the real protein. According to this formula, increases without bound with increasing water residence, rather than approaching the expected “solvent-berg” limit. Nevertheless, by a suitable choice of parameter values, the authors of ref. 17 reproduce the factor-3 discrepancy in D for myoglobin: as determined by dielectric spectroscopy, vs. , as predicted by Eq. 1 for the molecular volume of myoglobin (V_P = 21 nm³). Actually, the discrepancy should only be a factor 2, as for most other proteins (see Table 1 and Fig. 1); a more accurate experimental value, determined by fluorescence depolarization (45), is 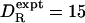μs^–1 (at 20°C). As discussed above, most of this factor-2 discrepancy should be attributed not to hydration but to the fact that myoglobin is not a compact sphere.

The proposed molecular theory (17) is an attempt to formalize the notion that the hydration effect on D_R is governed by the rate of exchange of water molecules between hydration layer and bulk. Although intuitively compelling, this notion is not entirely correct. Hydration affects D_R to the extent that it modifies the total rate of viscous energy dissipation (3). MRD studies of numerous proteins have shown that water molecules have long (>1 ns) residence times only if they are trapped in internal cavities or in deep surface pockets (19, 20). Whether rigidly bound or freely rotating, water molecules in such confined hydration sites do not contribute to viscous dissipation. Rather, it is the water molecules in contact with the exposed parts of the protein that are responsible for the hydration effect on D_R. For these unconfined and highly mobile water molecules, the residence time is governed by hydrogen-bond dynamics, just like their rotation (20, 35). We use water rotation as a viscosity indicator, because it is a more localized motion than translational diffusion (or molecular exchange).

Validity of the Continuum Approximation. Only the long-wavelength and low-frequency thermal fluctuations of a molecular liquid can be described rigorously in terms of a viscous continuum fluid (46). Although a typical protein is three orders of magnitude larger in volume than a water molecule, the volume of the interfacial region, where the solvent is significantly perturbed, is comparable to the dry protein volume. The effect of protein–solvent interactions therefore cannot simply be subsumed into a mathematical boundary condition, as in macroscopic hydrodynamics. In the molecular realm, geometry cannot be fully disentangled from interactions. Two strategies have been devised for dealing with this problem.

One possibility is to adjust the position of the frictional surface (σ_S > 0) and/or the nature of the fluid velocity field at this surface (partial slip boundary condition). Another is to allow the fluid viscosity to vary in space. In the case of small molecules and ions, the first strategy has been advocated because it makes little physical sense to speak about the viscosity of one or a few solvent molecules (47). For small solute molecules, it is also common to use a pure slip boundary condition for translational diffusion. The protein case is different, because there are now hundreds of water molecules interacting directly with the solute. The macroscopic stick boundary condition is appropriate, not because individual water molecules are attached to the protein for long periods, but because, statistically speaking, the lateral velocity component of a fluid element is averaged to zero rapidly on the time scale for appreciable changes in the position and orientation of the protein (48). In addition, the atomic-scale surface roughness of the protein drags the solvent along (49). The stick boundary condition emerges from molecular theories without the need for a long solvent residence time, so long as the solute–solvent interaction includes an attractive component (49, 50).

Hydrodynamics can be formally extended to short (but supramolecular) length scales by introducing a generalized viscosity η(k) that depends on the wavevector k = 2π/λ and reduces to the macroscopic viscosity in the long-wavelength limit: η(k 3 0) = η₀ (46). The leading-order correction to η₀ is of the form η(k) = η₀(1 – αk²). Molecular dynamics simulations of bulk water with a polarizable force field gives α = 4.2 × 10^–3 nm² (51), implying that 50% of the bulk viscosity is recovered already at a wavelength of 0.6 nm. In contrast to nonassociating liquids, the viscosity of water remains within a factor 3 of its bulk value when it is confined between hydrophilic surfaces to film thicknesses as small as 1 nm (52, 53). These properties are manifestations of the close connection between viscosity and the hydrogen-bond network in water and provide further support for our use of the water rotational correlation time as an indicator of local viscosity in an interfacial region that contains hundreds of water molecules.

The interaction of water molecules with the polar and ionic groups at the protein surface is essentially electrostatic in nature. Even the most long-ranged of these interactions, the orientationally averaged charge–dipole interaction, falls off as r^–4. Already in the second hydration layer, water–water interactions dominate strongly over water–protein interactions. As a result, water molecules not in direct contact with the protein surface behave very much like bulk water. However, the electric field generated by a charged protein decays asymptotically as r^–2 and therefore gives rise to weak polarization of a large number of water molecules. Because of the finite rotational correlation time of the water molecules, the polarization lags behind the time-dependent polarizing electric field emanating from the moving protein. In the case of rotation, this dielectric friction can be formally described by a position-dependent viscosity: η(r) = η₀[1 + (b/r)⁴] (25). Although important for small ions, this electrohydrodynamic effect can be shown to be negligible for proteins. This theoretical prediction is borne out by MRD experiments on the proteins BPTI and ubiquitin (54, 55), showing that D_R is nearly constant in the pH range 2–11. Moreover, the modest variation (20–30%) seen in D_R does not correlate with either the net protein charge or the total number of charged groups. Instead, it can be attributed to minor conformational changes and self-association (56).

X-ray and neutron solution scattering (57), analysis of protein crystals (18), and molecular simulations (58) all indicate that the first layer of water molecules at the protein surface has 10–20% higher density than bulk water. Although most of this density increase seems to be a trivial correlation effect (20, 58), also present for hard spheres next to a hard wall, it could conceivably influence the hydrodynamic behavior of proteins. A 10% increase in water density requires a pressure of ≈2 kbar but alters the viscosity by at most a few percent at ambient temperatures (59). A more elaborate treatment, where the hydrodynamic equations of motion are solved for a compressible fluid (42), yields a result analogous to Eq. 2 but with the viscosity ratio replaced by (η₀ρ_S)/(η_Sρ₀). In the case of HEWL, a 10% density increase (ρ_S/ρ₀ = 1.1) would change D_R/D⁰_R from 0.71 to 0.73. The hydrodynamic properties of proteins are therefore not significantly affected by solvent density variations.

Continuum hydrodynamics often makes surprisingly accurate predictions all the way down to the molecular level (60). The error cancellation underlying this success appears to be particularly favorable for water. Modeling a water molecule as a sphere of radius 0.14 nm (the standard van der Waals radius), the SE Eq. 1 yields D_R = 59 ns^–1 at 20°C, not very far from the experimental value, 79 ns^–1 (30). If we argue that friction is exerted at the solvent-accessible surface (0.28 nm), we obtain D_R = 7.3 ns^–1, an order of magnitude below experiment. And if we impose a slip boundary condition, we get an infinite D_R (no friction). Although we cannot exclude the possibility that the quantitative success of our dynamic hydration model is to some extent fortuitous, the model has the considerable merit of unifying a large body of experimental and theoretical data in a consistent way. Furthermore, the model can be tested by computer simulation, which should lead to further insights about the molecular details of solvation effects on global (61) as well as internal (62) protein dynamics.