Information exchange and the robustness of organizational networks

Abstract

The dynamics of information exchange is an important but understudied aspect of collective communication, coordination, and problem solving in a wide range of distributed systems, both physical (e.g., the Internet) and social (e.g., business firms). In this paper, we introduce a model of organizational networks according to which links are added incrementally to a hierarchical backbone and test the resulting networks under variable conditions of information exchange. Our main result is the identification of a class of multiscale networks that reduce, over a wide range of environments, the likelihood that individual nodes will suffer congestion-related failure and that the network as a whole will disintegrate when failures do occur. We call this dual robustness property of multiscale networks “ultrarobustness.” Furthermore, we find that multiscale networks attain most of their robustness with surprisingly few link additions, suggesting that ultrarobust organizational networks can be generated in an efficient and scalable manner. Our results are directly relevant to the relief of congestion in communication networks and also more broadly to activities, like distributed problem solving, that require individuals to exchange information in an unpredictable manner.

Information exchange is central to the performance of a wide range of networked systems, including infrastructures such as the Internet (1), airline, postal, and transportation networks, as well as peer-to-peer file sharing systems, communication networks, and organizations such as public bureaucracies (2, 3) and business firms (4, 5). Despite considerable recent exploration of the structure of real-world networks (6–8) and a long established organizational complexity literature in sociology (9–11), the dynamics of information exchange in networks has attracted limited attention (12, 13). In this paper, we introduce a model of what we call “organizational networks,” networks whose purpose is to organize and coordinate the decentralized exchange of information. In focusing on information exchange, our general aim is to construct a framework for exploring organizational robustness with respect to a range of environmental stresses.

The topic of optimal organizational architecture has long been of concern to economists (4, 14–17), but their emphasis has been on efficiency rather than robustness. As a result, the economics literature on organizations has focused almost exclusively on multilevel hierarchies: acyclic, undirected branching networks that originate at a single root node and descend through a series of levels or ranks to their terminal leaf nodes. By connecting N nodes together with the minimum required number of N- 1 links and creating a chain of command that is only L ∝ log N links in depth, hierarchies are almost as efficient as possible. Unlike hub-and-spoke networks (a special case of a hierarchy with a single subordinate level), multilevel hierarchies require each node to interact directly with, on average, only b other nodes, where b << N and is generally called the “span of control.” Hierarchies are therefore attractive, scalable architectures whenever individual capacity is bounded (e.g., managers in business firms) or else not easily augmented (e.g., terminals in airline networks). Numerous variations on this basic argument have been invoked to justify the optimality of hierarchical organizational networks for exerting control (2, 14, 18), performing decentralized computations (4), distributing processing load (16), making decisions (15), and accumulating knowledge (17).

However, a critical, and often unstated, assumption of this line of investigation is that the organization's task is decomposable into simpler subtasks, such that each subtask can be completed independently and therefore in parallel with others (19). Radner (4), for example, analyzes the case of summing a set of integers, a linearly associative task that is trivially decomposable. In contrast, most modern business firms and public bureaucracies face problems that are not only large and multifaceted but also ambiguous: objectives are specified approximately and typically change on the same time scale as production itself, often in light of knowledge gained through the very process of implementing a solution (9). As a result, problem solving is almost always a collective activity (20), embodied in strategies such as mutual monitoring (21, 22) and simultaneous design (23) in which initial designs or solutions are regularly adjusted on the basis of information-rich collaboration between individuals, teams, departments, and even different organizations.

Under these circumstances, the chief problem facing an organization is not efficiency, understood roughly as being maximized by minimizing the number of costly links needed to support a defined burden. Rather, the challenge is robustness: on the one hand, protecting individual nodes from being overtaxed by the direct and indirect effects of changing and unpredictable patterns of collaboration; and on the other hand, protecting the organization as a whole from disintegration in cases where individual failures occur regardless. More specifically, when task definitions are ambiguous, individual collaborators will often exchange information with other problem solvers (10), if only to ask after and obtain information about potential partners or to keep abreast of design changes relevant to their immediate task. In cases where the information is exchanged indirectly (e.g., via a superior), the relevant intermediaries incur an information processing burden. The burden imposed by any single coordinating message may be small, but high rates of message passing in combination with concentration of traffic will tend to overload key nodes. An analogous problem arises in other kinds of organizational networks, such as the Internet, airline networks, or the postal system, which must redistribute information, personnel, or materials while simultaneously minimizing the likelihood of overload. Organizational networks that minimize the probabilities of such failures exhibit what we call “congestion robustness.”

In addition to resisting failure at the level of individual nodes, contemporary organizational networks must continue to function even when individual elements do fail. The Internet, for example, suffers little performance loss in the event that individual routers fail. Business firms can display remarkable resilience with respect to (seemingly) catastrophic breakdowns in their supply chains (20), involving loss of key component producers, equipment, personnel, and office space (24, 25). In contrast, under conditions of environmental uncertainty and catastrophe recovery, hierarchies are extremely prone to cascading breakdowns because the failure of nodes near the top of the hierarchy effectively severs large subnetworks from the main organization, thereby impairing global coordination. Organizations that reduce the adverse consequences of externally driven failures exhibit what we call “connectivity robustness.” Finally, we call organizational networks that exhibit both congestion and connectivity robustness “ultrarobust.”

Our approach to the design of organizational networks through the lens of information exchange under conditions of ambiguity follows naturally from a long line of work in organizational sociology in which issues such as the interaction between an organization and its environment (9–11), the role of uncertainty in necessitating communication (9, 10), and the importance of adaptability to innovation and crisis management (9, 24, 26) have frequently been emphasized. By operationalizing the performance of organizations in ambiguous environments in terms of robustness, we hope to extend the optimality approach of the economics literature on firms to the richer domain of organizational sociology.

Modeling Organizational Networks

Our model requires four components: (i) an algorithm for constructing organizational networks, (ii) a specification of the task environment from which the requirement for information exchange is derived, (iii) a precise description of information exchange in terms of an algorithm for passing messages, and (iv) a well defined way of measuring congestion and connectivity robustness.

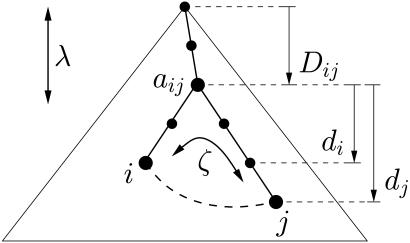
Network Construction Algorithm. Our algorithm takes as its point of departure the simplest version of an organizational network: a pure hierarchy with branching ratio b and L levels. The number of nodes is therefore N = (b^L- 1)/(b- 1), where the lth level possesses b^l nodes and l = 0,..., L- 1. The algorithm proceeds by sequentially adding links, chosen stochastically, until a prescribed total of m have been added. The probability P(i, j) that two nodes i and j will be connected depends on the depth D_ij of their lowest common ancestor a_ij in the backbone and also their own depths d_i and d_j, respectively, beneath a_ij (in Fig. 1, for example, D_ij = 2, d_i = 2, and d_j = 3). We choose links without replacement, and P(i,j) is therefore always normalized over all remaining pairs of unconnected nodes. We treat links that are added in this manner differently from links that are part of the hierarchical backbone: backbone links define a node's coordinates in the network and also transmit information; added links only transmit information. Thus, the hierarchical backbone may be thought of as the formal organization (chain of command), whereas added links correspond to the informal organization, a common distinction in the sociological literature of organizations (9, 10, 26, 27).

Fig. 1.

Schematic of the network construction algorithm. Links to be added are chosen stochastically according to Eq. 1 (without replacement) to a hierarchical backbone with L levels and branching ratio b. Eq. 1 takes as its arguments the organizational distance x_ij between two nodes i and j, as well as the depth D_ij of their lowest common ancestor a_ij. Organizational distance is defined as x_ij = 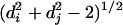, where d_i and d_j are measured relative to a_ij (see text for details). The two parameters λ and ζ set characteristic lengths in D_ij and x_ij, respectively, beyond which links are unlikely to form, thus embodying the influence of rank and homophily on link formation within an organizational network. Because links are chosen without replacement, links that are initially unlikely to be chosen will eventually be selected. This means that although λ and ζ control the order in which links are added, they do not have a simple interpretation in the resulting networks formed by the addition of many links. The alternative of choosing links with replacement and taking only the set of unique links so chosen would mean that the number of links added would no longer be conserved.

We thus map the theoretical problem of how organizational networks should be structured into the question of what is the corresponding functional form of P. Furthermore, whatever form of P that is appropriate for one kind of organization in a given environment (e.g., an early 20th automobile manufacturing firm) may well be inappropriate elsewhere (e.g., an early 21st century software manufacturer). We therefore seek a class of functions that is sufficiently general to explore a wide range of alternative topologies, but not so general that the resulting space of networks cannot be explored systematically.

To restrict the possible form of P, we make the following assumptions that we claim are plausible for the case of organizational networks. (i) Because it is a probability, we require that P is nonnegative for all values of D_ij, d_i, and d_j. (ii) Because immediate subordinates and superiors in the underlying hierarchy (d_i + d_j = 1) are connected by default, P is effectively constrained to be non-zero for values of d_i + d_j ≥ 2 (we disallow self-connections and duplicate links). (iii) We assume that individuals are identical aside from their relative position in the hierarchy; hence, P is symmetric with respect to d_i and d_j. (iv)All else being equal, we assume that individuals of the same rank are “closer” than individuals of different ranks; thus, for fixed d_i + d_j, distance is minimized when d_i = d_j. Incorporating assumptions i–iii, we define organizational distance x_ij between two nodes i and j to be x_ij = 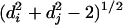(valid for d_i + d_j ≥ 2). (v) We assume that P decreases monotonically with increasing x_ij, a familiar property of social networks known generically as homophily (28), or the tendency of “like to associate with like” (we note that together, assumptions iv and v effectively incorporate two kinds of homophily that can be roughly attributed to similarity in class and profession, respectively). (vi) P is also assumed to decrease monotonically with respect to increasing lowest common ancestor rank D_ij; that is, all other things being equal, nodes of higher rank are more likely to interact. (vii) Because both homophily (assumption v) and lowest common ancestor rank (assumption vi) effects will apply to varying extents across different organizations, we introduce two tunable parameters, λ and ζ, that can be interpreted as characteristic lengths in x_ij and D_ij, respectively, beyond which connections become unlikely.

Incorporating assumptions i–vii, we propose the following stochastic rule governing the formation of new interactions:

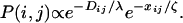1

We use Eq. 1 to choose (without replacement) the sequence of m links to be added to an initial hierarchical backbone, where different choices of λ and ζ will result in different network topologies for the same choice of b, L, and m (i.e., the same number of links added to the same backbone).

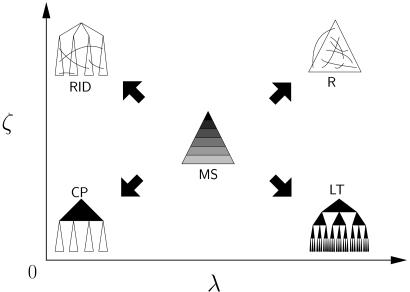
We immediately observe four stylized classes of organizational networks that arise for limiting values of (λ, ζ), as depicted in Fig. 2.

Fig. 2.

Classes of networks realized in different regions of (λ, ζ)-space. Multiscale networks occupy a broad interior region of space, whereas random (R), random interdivisional (RID), local team (LT), and core-periphery (CP) networks arise when one or both parameters approach their limiting values. Technically, the upper limit for both λ and ζ is ∞, and these limits would typically be approximated by numbers sufficiently larger than the maximums of x_ij and D_ij. However, because λ and ζ only set the order in which links are likely to be chosen, and hence are nontrivially related to the resulting networks, these parameters effectively reach ∞ at values less than the maximums of x_ij and D_ij.

Random: For (λ, ζ) → (∞, ∞), links are allocated uniformly at random; that is, neither lowest common ancestor rank nor homophily has any influence on link selection.

Local team: For (λ, ζ) → (∞, 0), links are allocated exclusively between pairs of nodes that share the same immediate superior, regardless of their superior's rank. Hence, homophily is important to link selection, but lowest common ancestor rank is not. The result is that “teams” form at all levels of the hierarchy.

Random interdivisional: For (λ, ζ) → (0, ∞), links are allocated exclusively between nodes whose lowest common ancestor is the single node at the top of the hierarchy. Links therefore only form between nodes in different “divisions” (the largest subunits) of the organization, but otherwise they are allocated randomly, meaning that lowest common ancestor rank is important but homophily is not.

Core-periphery: For (λ, ζ) → (0, 0), links are added exclusively between subordinates of the top node alone. The resulting networks are characterized by a fully connected central core from which pure branching hierarchies extend. For non-zero, but small, values of λ and ζ (i.e., in the vicinity of the origin in Fig. 2), the core-periphery dichotomy continues to pertain, but the core extends beyond the top layer. Hence, both homophily and lowest common ancestor rank matter.

Multiscale: Finally, we identify a fifth, qualitatively distinct class of networks that arise in the central region of Fig. 2 [i.e., intermediate values of (λ, ζ)]. We call this class multiscale networks because, unlike the four classes of networks defined above, whose connectivity is dominated by a single scale [either local (team) or global (random) ties], these networks display connectivity at all scales simultaneously. Multiscale networks, however, do not display uniform density of links at all scales: link density decreases monotonically with depth, such that the top rank (the core) exhibits the highest density, thus distinguishing multiscale networks from earlier “small-world” network models (29) in which random links are distributed homogeneously. This difference is critical for the problem at hand because, in a wide variety of environments, the hierarchical nature of organizational networks tends to place the burden of information exchange disproportionately on higher ranks. Thus multiscale networks and core-periphery networks have much in common. But by exhibiting connectivity across all other ranks as well, multiscale networks also embody the salient features of local team and random networks, a combination that, as we show below yields desirable robustness properties.

Task Environment. We specify the organization's task environment in terms of the rate and distribution of messages to be exchanged between individual problem solvers in the course of completing some global task. Stable environments correspond to a low rate of information exchange μ (defined as the average number of messages initiated by each individual at each time step), whereas volatile environments are equivalent to high μ. In addition to volatility, the environment may also allow for varying task decomposability: tasks that are nearly decomposable correspond to a pattern of message passing that requires only individuals within the same team (i.e., nodes with the same immediate superior) to communicate; tasks that cannot be decomposed even approximately require constant communication between remote, as well as nearby, individuals. In practice, for each message initiated at a node s at rate μ, a corresponding target node t is selected by weighting all nodes at distance x from s with a factor exp{-x/ξ}, normalizing appropriately, and then choosing t at random according to the resulting distribution. Thus, for ξ = 0 (local dependencies only), all messages are to be delivered to local targets, whereas for ξ = ∞ (global dependencies), t is chosen uniformly at random.

Information Exchange. Once initiated, a message is passed from source to target through a chain of intermediaries. Each node in the chain must process each message that it initiates or receives in the same time step by forwarding it to an immediate neighbor, choosing the neighbor who has the lowest common ancestor with the target node (in case of equally distant neighbors, one such neighbor is chosen at random). Thus each node i is assumed to have complete information regarding its own location in the hierarchy, as well as the locations of its neighbors. Each node also understands general information about targets beyond its immediate neighborhood, an assumption we call “pseudoglobal knowledge.” If node i is an indirect superior of t in the hierarchy, then pseudoglobal knowledge implies that i knows in which of the subunits t belongs but not specifically where (in which case i could send the message directly); similarly, if t is not beneath i but subordinate to one of i's neighbors along an informal link, i knows to send the message “across” the hierarchy to that neighbor; if neither of these cases hold, then i must pass the message up the hierarchy to its immediate superior. Pseudoglobal knowledge therefore embodies an inherent tradeoff between quantity and quality of information: high ranking nodes tend to possess general information about more subordinates than nodes in lower ranks but have less specific information about any one subordinate.

Pseudoglobal knowledge can also be interpreted in terms of distributed problem solving, where the target's address, rather than being the location of an individual in an organization, can be thought of instead as a complete description of the solution required by a particular problem (by analogy, the call number of a book in a library characterizes the knowledge contained therein). Neither the knowledge itself nor its address, however, is initially available to the problem solver (the sender) who must therefore poll his or her contacts in the organization for a relevant recommendation. The closer a contact is to the eventual target, the more accurately he or she can direct the problem solver, and the fewer subsequent intermediaries are required to conclude the search (we do not consider the case where the relevant knowledge does not exist in the organization). The progress of a message therefore corresponds to a problem solver acquiring increasingly specific knowledge about the problem to be solved; a process that can only succeed with the cooperation of increasingly knowledgeable intermediaries.

Measures of Robustness. The property of ultrarobustness requires an organizational network to exhibit both congestion robustness (the capacity to protect individual nodes from congestion) and connectivity robustness (the capacity to remain connected even when individual failures do occur). To measure congestion robustness, we initiate an average of μ messages per node each time step over a total of T time steps, where messages are removed from the system on reaching their designated target. Assuming that each node i can process a maximum of R_i messages per time step without failure, then an organizational network will, on average, remain free of failures only if R_i > r_i = μNρ_i for all i, where r_i is the rate of messages to be processed by node i and congestion centrality ρ_i is the probability that any given message will be processed by i. Although congestion centrality is similar to other centrality measures in graph theory (30) and social network analysis (31), it is more appropriate to the problem of information exchange in that it depends on task decomposability (ξ) and the message passing algorithm as well as a node's position in the network. [For example, when message passing is sufficiently global (ξ is large), high-ranking nodes will be more central than low-ranking nodes, as would be the case for betweenness centrality (31). But when message passing is purely local (ξ → 0), nodes at all ranks (other than the bottom rank) will be equally central.] Assuming that environmental volatility (μ) and individual capacities (R_i) are beyond the control of the organization, a robust architecture is one that reduces the congestion centrality, hence the likelihood of failure, of its constituent nodes. We therefore associate congestion robustness with the reduction of maximum congestion centrality ρ_max over the entire network (we have also considered <ρ>, obtaining qualitatively similar results).

Even a network that is highly robust with respect to congestion related failures can suffer failures, such as sickness, accidents, sabotage, attack, and natural disasters, that are imposed on it from the outside (20, 24, 25). In accordance with previous work (32–34), we therefore define connectivity robustness in terms of the fractional size C = S/(N- N_r) of the largest connected component (size S) remaining after the removal of N_r nodes. Because different removal strategies have previously been shown to yield dramatically different conclusions regarding the connectivity robustness of other classes of networks (32), we have examined a number of such strategies: preferential elimination of nodes by rank (top-down); elimination of nodes radiating out from a random start point (cascade); preferential elimination of highly connected nodes (hubs); and uniformly random elimination (random).

Results and Discussion

We now investigate the congestion and connectivity robustness of organizational networks as measured by ρ_max and C respectively, as a function of both environmental conditions (μ, ξ) and network topology (m, λ, ζ). Before commencing, we note that when μ = 0 (i.e., a static environment) and in the absence of exogenous failures, all networks perform identically. Efficiency arguments similar to those outlined above therefore dictate that pure hierarchies (m = 0) will be superior to all other network topologies. Thus, in the trivial limit of an unchanging environment, our model is consistent with the standard economics literature on organizations (e.g., refs. 4 and 14).

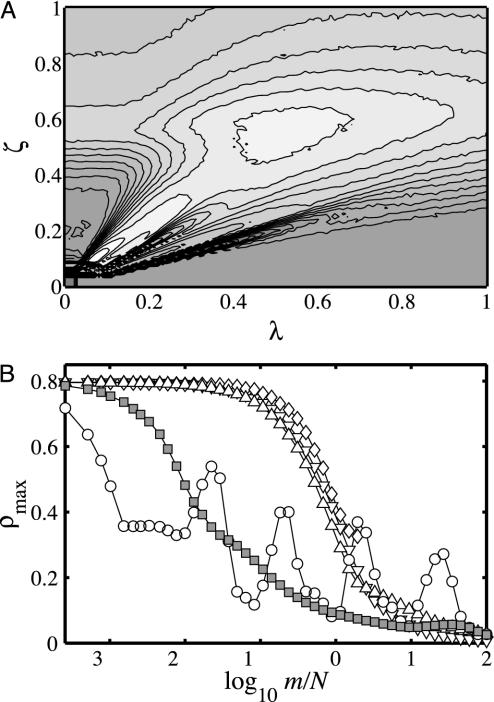
Congestion Robustness. We first consider information congestion associated with an intermediate level of task interdependency, ξ = 1. Fig. 3A shows ρ_max for a fixed network density m = N as a function of the network topology parameters λ and ζ. Equating the axes of Figs. 2 and 3A, we can infer that multiscale networks minimize congestion (hence maximize congestion robustness) at least as well, and generally much better than, the other four generic network classes. Furthermore, the congestion robustness property of multiscale networks persists over a broad region of the parameter space, ensuring that it is stable with respect to small changes in parameters. Core-periphery networks (Fig. 2, bottom left) can also exhibit desirable congestion properties. But because their performance depends so heavily on the relatively small population of nodes in the core, they suffer from extreme sensitivity to parameter selection, with the best and worst performing networks arising for almost identical choices of parameters (Fig. 3A, lower left).

Fig. 3.

Congestion centrality ρ_max as a function of the network parameters (m, λ, ζ). For both plots, the underlying hierarchy of the networks examined here has N = 3905 nodes with branching ratio b = 5 and depth L = 6. (A) Contour plot of ρ_max(λ, ζ) for ξ = 1 averaged over an ensemble of 100 networks. Lighter regions correspond to lower values of ρ_max(λ, ζ). For each parameter pair (λ, ζ), m = N links are added and the resulting network is tested by initiating messages at each node with probability μ = 2.561 × 10^-3 for T = 10³ time steps (i.e., an average of 10 messages are generated per time step). The broad local minimum centered around (λ, ζ) = (0.5, 0.5) corresponds to multiscale networks. (B) Change in ρ_max with the addition of links. The networks tested here are random (λ = ∞, ζ = ∞, ▿, local team (λ = ∞, ζ = 0, ⋄), random interdivisional (λ = 0, ζ = ∞, ▵), core-periphery (λ = 0.1, ζ = 0.15, ○), and multiscale (λ = 0.5, ζ = 0.5, □). Each data point is the average of 100 realizations. In the case of multiscale networks, most of the reduction of ρ_max is obtained by the addition of only m = N links (the same holds for <ρ>).

Fig. 3B generalizes the above result by comparing ρ_max for the different network classes over the full range of network density m (where particular choices of parameters have been used as proxies for each class). We note that ρ_max eventually decreases as a function of increasing network density m, regardless of the procedure used to add links, and that when m is sufficiently large, all networks perform similarly. However, Fig. 3B also points to some less obvious conclusions: (i) ρ_max does not necessarily decrease monotonically with m. In particular, the congestion experienced by the most congested node in a core-periphery network can increase significantly as more edges are added, before falling again, giving rise to oscillations periodic in log(m/N) (a consequence of the sensitivity to parameters noted above). (ii) The drop in ρ_max occurs an order of magnitude earlier for multiscale networks than for random, random interdivisional, and local team networks. In fact, almost all of the drop in ρ_max for multiscale networks occurs for m ≈ N, which for large N is negligible compared with m_max = O(N²).

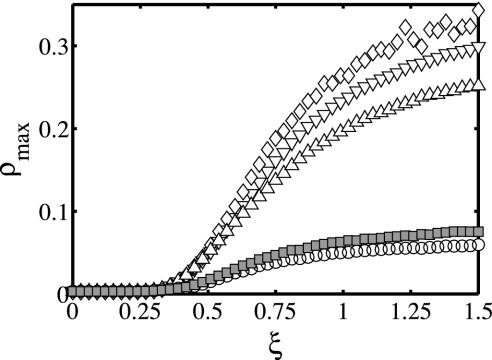
Fig. 4 continues the comparison between multiscale and other classes of organizational networks, extending it across the entire range of environmental complexity ξ, for fixed m = N and for the same representative choices of (λ, ζ) as in Fig. 3B. In the limit of full task decomposability ξ → 0, at which messages are passed exclusively between closely separated individuals, all types of organizational networks perform equally well. As decomposability decreases, however, large differences in congestion robustness manifest themselves, with multiscale networks always performing almost as well as any other class, and much better than most. Furthermore, although core-periphery networks can also perform well, outperforming multiscale networks for some parameter choices, they continue to exhibit the same sensitivity to parameter choices mentioned above (i.e., a slightly different choice of parameters would generate much worse core-periphery results, circles in Fig. 4). Multiscale networks display no such sensitivity; hence, they represent a more reliable solution to congestion robustness.

Fig. 4.

Variation of congestion centrality ρ_max as a function of ξ, where increasing ξ corresponds to decreasing task decomposability. Symbols correspond to the same parameter choices of (λ, ζ) as in Fig. 3B, with 100 samples per data point. Multiscale networks perform almost as well as core-periphery networks over the entire range of ξ, and significantly better than all other classes (random, random interdivisional, and local team) for any but completely decomposable (ξ → 0) tasks.

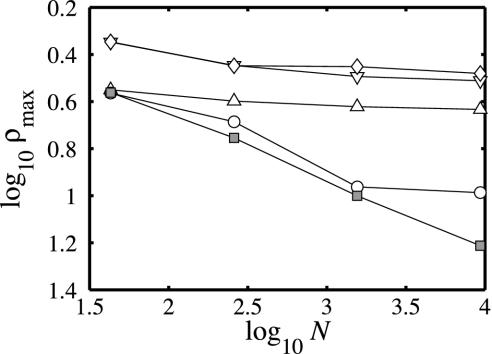
Finally, for fixed μ (volatility), congestion increases, regardless of topology, as a function of organizational size; that is, an organization can break simply under the burden of its own coordination requirements (35). However, the manner in which congestion increases with N can vary across different network topologies, leading to large differences in the maximum size that an organization can attain in any particular environment. In particular, for large N the maximum congestion r_max = μNρ_max at any one node scales linearly with N for random, random-interdivisional, local team, and core-periphery networks but scales sublinearly for multiscale networks. Thus, multiscale networks display the surprising property that maximum congestion centrality ρ_max actually decreases with the size of the system (while approaching a constant for the other network classes), a result we confirm in Fig. 5. Another way to interpret the scaling of r_max is in terms of the maximum size N_max attainable by an organization, given some constraint R_max above which failures become inevitable. In Fig. 5, for example, setting R_max = 570 yields estimates of N_max ≈ 1,600 for random networks, N_max ≈ 1,800 for local team networks, N_max ≈ 2,400 for random interdivisional networks, N_max ≈ 5,500 for core-periphery networks, and N_max ≈ 9,300 for multiscale networks. In other words, given the same individual-level capacities and the same environmental conditions, multiscale networks can grow to nearly twice the size of the next best class without incurring failures.

Fig. 5.

Scaling of ρ_max with increasing network size N. Symbols represent the same choices of (λ, ζ) as in Fig. 3B. The task environment is given by ξ = ∞ and constant μ (i.e., individual nodes send the same number of messages independent of network size), and N is increased by fixing the branching ratio b = 6 and increasing the number of levels L = 3, 4, 5, and 6 (i.e., N = 43, 259, 1,555, and 9,331). Congestion centrality ρ_max rapidly approaches a constant for local team, random, and random interdivisional networks, and also appears to approach a constant at large N for core-periphery networks, whereas for the multiscale example given, ρ_max decreases roughly as N^-0.28.

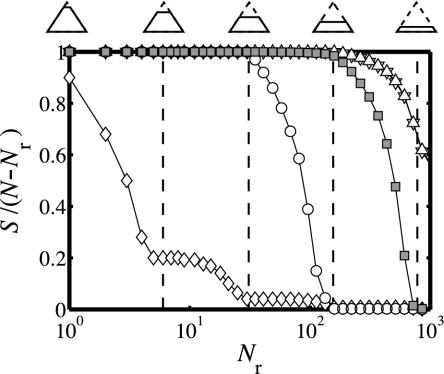
Connectivity Robustness. The second aspect of robustness that is of interest to organizational networks is their capacity to remain connected and thereby functional in the event of failures, whether induced endogenously (as with congestion) or exogenously. To quantify connectivity robustness we measure C = S/(N- N_r) after the targeted removal of N_r nodes, where we have studied a number of different targeting strategies, specified above. In Fig. 6, we present the results for the “top-down” elimination strategy, because it results in the most damaging choice of targets, and also is the most likely result of congestion-related failures (even in multiscale networks, congestion is concentrated in the top ranks). Local team networks are by far the least robust of the five classes, followed by core-periphery networks, whereas random and random interdivisional are the most robust. Multiscale networks, however, are almost as robust as random networks, performing measurably worse only after all of the organization but the bottom rank has been eliminated. The other targeting strategies yield similar results, except that all classes of networks perform better than in the top-down case, and that core-periphery networks replace local team networks as the worst performing class when the “hubs” strategy is used.

Fig. 6.

Connectivity robustness of multiscale networks as measured by the largest cluster size S after targeted removal of N_r nodes. Cluster size is normalized by the size of the remaining network N–N_r. The networks are the same as those described in Fig. 3B with 10 samples per data point. Nodes are removed according to a top-down targeting strategy (see text) where N_r is increased until the top five levels of a possible six have been eliminated. The hierarchies depicted and dashed vertical lines correspond to complete removal of nodes down to a depth of 1, 2,..., 5. Random and random interdivisional networks are the most resilient to this form of network degradation, whereas local team networks perform poorly. Multiscale networks, however, are almost as robust as random networks. In the case of (λ, ζ) = (0.5,0.5), disintegration of the remnant components begins only after four of the six levels of the hierarchy are removed.

Taken together, the above results suggest that multiscale networks display a remarkable combination of properties. (i) Over a wide range of environmental conditions, multiscale networks minimize the likelihood of congestion related failure. (ii) Even in the event that failures occur anyway, multiscale networks remain extremely resilient to disconnection. (iii) No other class of organizational networks studied exhibits both congestion and connectivity robustness: core-periphery networks handle congestion well but are easily disconnected; random and random-interdivisional networks are difficult to disconnect, but easy to congest; and local team networks are bad in both senses. Hence, multiscale networks are not only ultrarobust but appear to be uniquely so. (iv) Multiscale networks achieve ultrarobustness efficiently in the sense that most of the attendant benefits are generated by a relatively small number O(N) of additional links. (v) The superior robustness of multiscale networks also conveys better scaling properties than other classes of networks in that, for a given level of environmental volatility μ, multiscale networks can grow to much larger sizes before suffering failure. (vi) The properties of multiscale networks are themselves robust in the sense that they are insensitive to small (or even quite large) changes in the network parameters λ, ζ, and m. Networks resembling multiscale networks may therefore be expected to arise in real-world business firms and bureaucracies, at least some of which do appear to display properties that resemble our notion of ultrarobustness (20, 24, 25).