Stripe formation in juvenile Pomacanthus explained by a generalized Turing mechanism with chemotaxis

Abstract

Current interest in pattern formation can be traced to a seminal paper by Turing, who demonstrated that a system of reacting and diffusing chemicals, called morphogens, can interact so as to produce stable nonuniform concentration patterns in space. Recently, a Turing model has been suggested to explain the development of pigmentation patterns on species of growing angelfish such as Pomacanthus semicirculatus, which exhibit readily observed changes in the number, size, and orientation of colored stripes during development of juvenile and adult stages, but the model fails to predict key features of the observations on stripe formation. Here we develop a generalized Turing model incorporating cell growth and movement, we analyze the effects of these processes on patterning, and we demonstrate that the model can explain important features of pattern formation in a growing system such as Pomacanthus. The applicability of classical Turing models to biological pattern formation is limited by virtue of the sensitivity of patterns to model parameters, but here we show that the incorporation of growth results in robustly generated patterns without strict parameter control. In the model, chemotaxis in response to gradients in a morphogen distribution leads to aggregation of one type of pigment cell into a striped spatial pattern.

The coupling between growth and patterning, which is important in many developing systems (1–3), is particularly evident in the coloration patterns of the angelfish Pomacanthus (Fig. 1). Young angelfish of this genus display three vertical white stripes on a dark blue/black background, and as the fish grows, new stripes develop via gradual insertion between the preexisting stripes. This process repeats twice before the pattern undergoes a further transformation into its adult form. The first workers to suggest a mechanistic explanation for stripe doublings were Kondo and Asai (4), who proposed a Turing model (5) that predicts regular doubling of the number of morphogen peaks on a growing one-dimensional domain. Although their predictions are qualitatively consistent with the patterning sequence in the angelfish, there are several important observations that are not explained (6). In vivo, new stripes emerge gradually between preexisting stripes, first appearing faint and narrow, and then slowly widening, and the mature stripes are narrow in comparison with the region separating them. In contrast, the Kondo–Asai model predicts that the width of new stripes is nearly equal to that of mature stripes, and narrow stripes can only be obtained by choosing a threshold close to the peak of morphogen concentration, in which case stripe formation is unlikely to be robust to parameter variations. Furthermore, it is not known whether the one-dimensional peak doublings translate to two-dimensional stripe doublings. A Turing model on a geometrically realistic two-dimensional domain has been considered (7), but this model contains boundary sources that orient the pattern, in the absence of which only spots are obtained. Both groups of authors incorporate growth in an ad hoc fashion and do not consider cell movement.

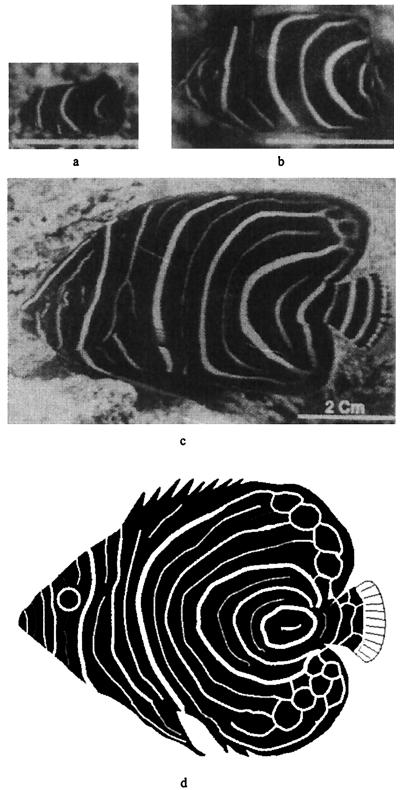
Figure 1.

Juvenile pattern sequence on Pomacanthus semicirculatus, showing the transition from 3 to 6 to 12 vertical stripes. (a) 2 months; (b) 6 months; and (c) 12 months. [Reprinted with permission from Nature (376, 765–768; copyright 1995, Macmillan Magazines Ltd.)]. Computer rendition of juvenile P. imperator shown at Bottom for comparison.

In all vertebrates, pigment cells, a population of cells that arises at the dorsal midline of the neural tube (8), are thought to originate in the neural crest. Pigment cell precursors in the zebrafish Danio rerio migrate from the neural crest to seed the dermal and epidermal layers for establishment of the larval pattern. Subsequent adult patterning is established through further migration and proliferation (9). A series of transplant experiments performed by Kirschbaum (10) has revealed that patterning in this and related species is controlled by unknown chemical factors in the dermal layer.

Model Development.

The dominance of a specific color in a region of the skin is indicative of an accumulation of pigment cells or chromatophores of the type producing that color (11). For example, the white bands of the clown anenome fish are caused by dense populations of iridophores. It is therefore reasonable to suppose that the dark pigmentation in Pomacanthus is the result of melanophores, whereas the white stripes are derived from iridophores. Both are particularly common types of chromatophore in fishes. In light of Kirschbaum’s results, we suppose that patterning is controlled by the spatial distribution of two morphogens that react together and diffuse in a two-dimensional subepidermal tissue layer comprising multiple cell types, including the chromatophores (12). In the absence of growth and division, the morphogen concentrations satisfy the reaction–diffusion equations

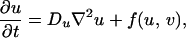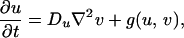1

where f and g represent the chemical kinetics. To model the early stages of angelfish patterning (Fig. 1a), we suppose that the morphogen distributions evolve on a rectangular domain of side lengths L and 2L, centered at the origin.

Slow coloration changes, such as stripe formation in fishes, are the result of either an increase in the number of pigment cells or the amount of pigment they contain (12), and it is likely that the former occurs in the growing juvenile. We assume nutrients are supplied to the subepidermal layer from the tissue below in a homogeneous manner and, to incorporate both growth of the tissue and growth in the number of pigment cells as simply as possible, we postulate that all cell types grow at the same rate. This produces a uniform dilation of the tissue about the central point, but nonuniform growth rates can easily be treated (2). Estimates of growth rates, derived from Fig. 1, are approximately 1.85 × 10⁻⁴ cm⋅hr⁻¹ in the rostral-to-caudal (RC, snout-to-tail) direction and 2.20 × 10⁻⁴ cm⋅hr⁻¹ in the dorsal-to-ventral (DV, top-to-bottom) direction.

To incorporate cell movement into the model, we suppose that the combined density of the cell types, as well as the density of the extracellular matrix, remain constant. This is reasonable, because cells are largely composed of water, and under this assumption, cells can only move by displacing a neighboring cell. We simplify the model by considering just two cell types, iridophores and melanophores. The balance equation for the density of the i^th cell type can be written

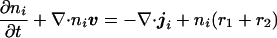2

where v = (r₁xi + r₂yj) is the uniform velocity field generated by growth, r₁ and r₂ are the growth rates in each direction, and j_i is the flux relative to the mass-average velocity. In early development, the path taken by pigment cells is likely to be controlled either by a chemotactic mechanism (13–17) or by guidance cues in the extracellular matrix (18). We postulate that the iridophore cells move chemotactically in response to one of the morphogens, and that the flux of these cells relative to the melanophore cells comprises both a diffusional component caused by random motion and a directed component that results from the tactic response. Of course, the connection between morphogen and movement may not be so direct: the morphogens may modify the matrix, which may in turn provide guidance to the cells. It is not crucial whether it is the melanophores or the iridophores that are chemotactic, and whether they are attracted or repelled; all combinations will give rise to similar phenomena. In addition, it is possible that undifferentiated pigment cells first respond to the morphogen distribution by differentiation, but chemotaxis is still necessary to maintain the integrity and forms of the stripes.

Under the assumption of constant growth and both diffusive and tactic contributions to the flux, the governing equation for the density of the iridophore cells can be written,

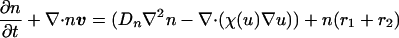3

The term χ(u) = χ₀/(k + u)² represents the local response of cells to the concentration of the chemotactic substance (19). In the simulations, we choose χ₀ < 0, which means that u is a repellent.§ A schematic showing the key assumptions made in deriving the model is shown in Fig. 2. For computational convenience, both the above equation and the equations for morphogen evolution with growth incorporated can be transformed from a growing domain into a fixed domain, at the expense of introducing additional terms. This results in the following system of equations,

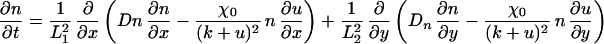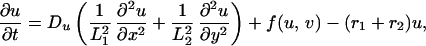4

where L₁(t) = L₁(0) exp r₁t and L₂(t) = L₂(0) exp r₂t represent the changing domain dimensions as a function of time. Pigment cells in larval Pomacanthus arcuatus initially form a uniform gray pigmentation when the fish is between 5 and 7 mm in length, and we take a uniform initial distribution of both types of pigment cells. The juvenile pigment pattern consisting of five vertical white bars subsequently develops from this uniform distribution (21).

Figure 2.

Schematic showing the key model features. We assume two types of pigment cells, represented here by the light and dark circles. (Top) When the underlying morphogen field is uniform, both cell types are spread uniformly throughout the two-dimensional tissue layer. The dark cell types dominate, resulting in dark pigmentation, although they are not necessarily the more numerous. (Middle) The formation of a spatial pattern in the morphogen (shown by underlying pattern) provides the information for organization of the white cell types. These cells move along gradients in the directions indicated by the arrows, displacing the black cells. The resulting cell density pattern, shown at Bottom, consists of a series of white stripes separated by the black cells. Because cell movement is relatively slow with respect to changes in the underlying field, the development of the stripes is a gradual process. As the tissue grows, the total number of pigment cells increases, yet the density remains constant. New stripes are formed through a combination of chemotactic movement and proliferation of chromatophores.

Numerical Simulations Producing Striped Patterns.

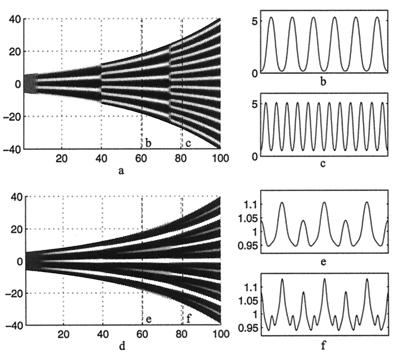
We first solve the equations on a one-dimensional growing domain with the piecewise linear kinetics used by Kondo and Asai. The morphogen evolution is independent of the cell movement, and the number of maxima of u and v double at regular intervals (Fig. 3 a–c). Hereafter we refer to this behavior as mode doubling. The doubling occurs via a mechanism of peak splitting: peaks bifurcate to troughs, whereas troughs maintain their spatial location. As a pattern in the morphogen distribution develops, iridophore cells accumulate at the minima (Fig. 3 d–f), which results in the formation of white pigment stripes (see also Fig. 2). Movement of the cells is much slower than diffusion of molecules, which leads to slow evolution of cell distributions as compared with the morphogens. The former evolve on the time scale of domain growth, and when the splitting in morphogen distribution occurs, new cell movement ensues, and cells begin to accumulate at sites of new minima. These new peaks develop via a combination of chemotactic movement and proliferation of the iridophore cells lying between the preexisting stripes. In the developing pigment pattern of the larval salamander, some xanthophore cells remain in the melanophore stripes (see Fig. 2 of ref. 20) and vice versa. Thus, it is certainly realistic that new stripes in Pomacanthus develop from the iridophore cells that had been “left behind” in the melanophore region. As a result, new peaks in cell density develop slowly between preexisting peaks. Chemotactic movement produces sharp aggregation peaks, and these peaks are narrow compared with the region separating them, which is consistent with how angelfish stripes grow. On scaling the value for the cell diffusion coefficient used in the simulation, we obtain a value for D_n on the order of 10⁻⁸ cm²⋅hr⁻¹. We have been able to scale both the cell diffusion coefficient and the chemotactic sensitivity coefficient by several orders of magnitude without qualitative differences in behavior. Sensitivity of the model to strength of the chemotactic component was tested by varying χ₀ with D_n held constant. Qualitatively similar behavior was observed when χ₀ was increased or decreased up to an order of magnitude from the value in Fig. 3. Further increases, however, disrupted the patterning. Stronger sensitivities to the chemical resulted in sharp aggregations of iridophores at the stripes: all of the iridophores are attracted to the region of stripe formation, and consequently no cells remain to form secondary stripes. Decreases in sensitivity by more than an order of magnitude would result in very broad iridophore stripes of low amplitude and, consequently, stripes would be faint or invisible on the macroscopic scale.

Figure 3.

(a) A space (vertical)—time plot showing the evolution of the morphogen u on a growing one-dimensional domain. (b and c) Cross sections showing the spatial pattern corresponding to the dashed lines in a. Peak doubling is rapid; there is no slow insertion of new peaks. Parameters selected to give rise to the three-peak pattern, corresponding to the number of stripes on the angelfish, Fig. 1a. (d) The corresponding plots of the cell density, showing the gradual insertion of new stripes on the same domain. We use f(u, v) = 0.08u − 0.08v + 0.05 − 0.03u, g(u, v) = 0.1u − 0.15 − 0.06, and set 0 ≤ 0.08 (u − v)+ 0.05 ≤ 0.18 and 0 ≤ 0.1u − 0.15 ≤ 0.5. We set D_u = 0.007, D_v = 0.1, D_n = 5.0 × 10⁻⁴, χ₀ = −1.0 × 10⁻⁴, k = 1 and the domain growth is given by L(t) = 11.0 exp(10⁻⁴ t). Initial conditions are small (±0.5%) random spatial perturbations about the homogeneous steady state for the morphogens and an initially uniform cell distribution, n(x, 0) = 1. Boundary conditions are taken as zero flux for both cells and morphogens.

An important question is how sensitive the mode doubling and peak insertion are to the kinetic scheme chosen. We examined this question for a number of other kinetic schemes, and found the following qualitative behavior for all schemes: when the ratio of chemical diffusion coefficients is low, mode doubling does not occur, but an increase in this ratio results in mode doubling (unpublished data, see also refs. 22 and 23). It is known that a large ratio of the diffusivities can be generated via binding of the activator chemical to a relatively immobile molecule (24), and a mechanism of this type is a key factor in experimentally obtained Turing patterns (25).

Because patterning in vivo occurs in two dimensions, we must determine whether the one-dimensional results on peak insertion apply in two dimensions as well. In Fig. 4 a–d, we display the u morphogen for a domain with an initial RC:DV ratio of 2:1 and growth rates as estimated above. The cell density shown in the sequence Fig. 4 e–h demonstrates the gradual insertion of stripes. Thus, the model can predict this important experimental observation. We have used the same piecewise linear kinetics as described in Fig. 3. More generally, the formation of stripes, as opposed to spots, which are the dominant patterns in two dimensions, has been shown to depended on nonlinear terms of the chemical kinetics (26–28). We have successfully obtained a regular sequence of stripe doublings under a number of nonlinear schemes, including the Lengyel–Epstein model (25), a mechanism proposed to account for the Turing patterns in the chlorite–iodide–malonic acid–starch reaction (29, 30), and a model proposed for the reaction between oxygen and uric acid in the presence of uricase (31). Neither of these reactions are proposed as the mechanistic basis for patterning within the skin itself; rather, our intention is to demonstrate the generality of the previous results.

Figure 4.

(a–d) The first three stages of stripe splitting for the chemical u. (a) t = 1,000; (a) t = 5,000; (c) t = 9,000; (d) t = 13,000. The RC:DV ratio is 1.9:0.95 initially, and the growth rate is 0.00018 in the RC and 0.00022 in the DV directions. The evolution of the cell density is shown in e–f. (e) t = 12,000; (f) t = 14,000; (g) t = 16,000; (h) t = 18,000. Insertion of new stripes is gradual. For convenience we have rescaled the domain to a fixed size. The equations are solved by using an Alternating Direction–Implicit scheme with 101 × 101 grid. Parameters, kinetics and initial and boundary conditions are as in Fig. 3.

The stability of the doubling sequence depends on several factors, as is shown in Fig. 5 for a domain that is initially twice that in Fig. 4. Initially the evolution is similar, but as the domain expands, stripes lose their one-dimensionality, first becoming wavy, and eventually highly convoluted. Similarly, increases in the growth rate can result in convoluted stripes. Such patterns are often seen in nature, for example, in the angelfish Chaetodontoplus duboulayi. Larger increases in the growth rate can disrupt all patterning and lead to stable spatially uniform morphogen distributions. The difficulty of controlling patterning on large, rapidly growing domains suggests an explanation for the fact that many large animals have uniform skin colors.

Figure 5.

(a–f) Breakup of the stripe-splitting sequence.(a) t = 4,000; (b) t = 7,200; (c) t = 7,600; (d) t = 8,000; (e) t = 10,000; (f) t = 12,000. We take the initial domain to have dimensions 3.8 × 1.9 and other data is as in Fig. 4.

The theory predicts that reliable patterning on the angelfish requires that the initial domain be small or narrow and the growth rate not too large. The growth rates used are derived from observations, and the size constraint on the domain is satisfied as well. The RC:DV ratio of larval Pomacanthae is approximately 3:1 (32), and if patterning is initiated at these stages, the theory predicts that the dominant patterns will be vertical stripes, as seen in Fig. 3.

More Complicated Patterns.

We have thus far considered a mechanistic basis for the generation of vertical stripes that are inserted between preexisting ones on a two-dimensional domain, yet observations suggest that the bars on juvenile angelfish curve away at the dorsal and ventral edges. This curvature is moderate for the majority of species, but is particularly pronounced on P. imperator, where a ring usually forms on the tail, and stripes close to this ring curve around it (33, 34) (see Fig. 1). The geometry of the two-dimensional domain itself has been suggested to play a role (7). In ref. 7, the authors use enhanced sources on certain boundaries, which subsequently forces patterning into a specific configuration, and they concentrate on aspects of patterning nearer the boundaries. Here we propose an alternate mechanism for generating the body patterns characteristic of juvenile P. imperator.

Under the initial conditions considered in the earlier simulations, the early pigment pattern arises more or less uniformly throughout the domain, but by triggering a disturbance of the initial morphogen field from different regions, curved patterns can be generated. The simulations shown in Fig. 6 demonstrate how modifications of the initial field disturbance can lead to different patterns. Biologically, this patterning could arise from an initial subpopulation of cells that are confined to a particular body region and which trigger the chemical reaction that subsequently spreads throughout the epidermis. Interspecies differences in patterning would arise from different body locations of this population. Thus, for the juvenile stripes of P. semicirculatus, the patterning is initiated at the tail, whereas for P. imperator, the patterning is initiated cranial to the tail. Stripe doubling has only been shown in the case where stripes form a regular pattern parallel to one of the boundaries (Fig. 4), and it is desirable to understand whether stripe insertion can occur between curved stripes such as those in Fig. 5. Fig. 7 b–d shows the evolving pattern as the domain grows for a portion of the pattern initially shown in Fig. 7a. Despite the high degree of curvature, stripe insertion occurs between the older stripes. Closer to the boundary, the patterning is less regular, a feature also seen in juvenile Pomacanthus. Stripe insertion also occurs when the pattern consists of concentric rings, as seen in P. imperator. The robustness of the patterning here may be reinforced under realistic geometries or by enhancement at the domain boundaries, as previously suggested (7).

Figure 6.

Variations in the initial disturbance of the initial morphogen field results in a number of patterns comparable with the different patterns seen in species of Pomacanthus. Initial disturbance is marked by the region within black rectangle. (a) A disturbance cranial to the tail result in formation of ring patterns, compare with P. imperator (Fig. 1d). The disruptions to the patterning close to the boundaries compares with the disruptions observed in juvenile P. imperator. (b) The disturbance occurs at the tail, resulting in semicircular stripes reminiscent of juvenile P. semicirculatus (Fig. 1 a–c). (c) Larger initial disturbances can result in stripes of little curvature, which occur in juveniles of the species P. striatus. (d) An even larger initial disturbance can robustly generate stripes. Simulations use same chemical kinetics and parameter values as in Fig. 3, however, similar patterns are obtained for nonlinear kinetic schemes. All plots show activator concentration (u).

Figure 7.

Numerical simulation showing stripe insertion between curved stripes. Initial conditions as shown in a, generated as in Fig. 6. As the domain grows, (b–d), new stripes develop and grow between the preexisting ones. Closer to the boundaries, the patterning is less regular, as is observed on juvenile Pomacanthus. For initial conditions consisting of a target pattern of concentric rings, stripe insertion has also been observed. Simulations use kinetics and parameter values as stated in Fig. 3, but with the bounds 0 ≤ 0.08 (u − v)+ 0.05 ≤ 0.21. This allows new stripes to occur via insertion as opposed to splitting.

Juvenile patterning is similar in a number of angelfish species, yet adult patterns can vary widely. For example, adult P. imperator display horizontal blue and yellow stripes, whereas P. semicirculatus exhibit a fine-grained spotted pattern. P. semicirculatus is only occasionally seen in its adult form when reared in an aquarium—usually, it retains the juvenile pattern of vertical stripes. Raising P. semicirculatus in an aquarium often limits the maximum size to which it can grow (34), thus reinforcing a potential link between growth and patterning. In Fig. 8, we demonstrate how the transformation from juvenile to adult patterning can occur through the model derived above. To reflect the decreasing rate of growth as the juvenile matures, a logistic growth has been applied. Thus, the domain grows in an exponential fashion during earlier stages and evolves to a constant size at larger time. The simulations demonstrate that a regular stripe-doubling sequence takes place during the early juvenile stages, yet as the domain approaches a constant size, these stripes lose stability to a spotted structure. A mixed spot/stripe pattern can be seen to occur as cells relocate during the transition.

Figure 8.

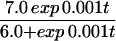Transformation from juvenile to adult pigment markings in the angelfish P. semicirculatus, for a logistic-type growth. We use L₁(t) = L₂(t) = to model a domain growing exponentially initially and approaching a constant size at large time. Simulation results for the cell density show the slow insertion of new stripes as the domain grows during initial stages (a and b), followed by a breakup into a pattern of spots as the domain approaches its maximum size. During the breakup into spots, an intermediate phase can be seen where the pattern is a combination of stripes and spots (d and e). We use the Lengyel–Epstein model of the (chloride/iodide/malonic acid reaction for the chemical kinetics,

with parameter values k₁ = 10.0, k₂ = 17.6, D_u = 0.01, D_v = 2.0, D_n = 5.0 ×10⁻⁵, χ₀ = 2.5 × 10⁻⁵, and an initial domain of dimensions [0,1.58] × [0,1.58]. To force a pattern of regular stripes, we have selected initial conditions of the form shown in Fig. 6d for the morphogens.

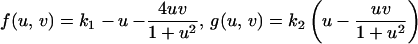DISCUSSION

A model has been developed that can account for aspects of pigment patterning in the growing marine angelfish, Pomacanthus. The schematic shown in Fig. 2 outlines the key components of the model and demonstrates how this mechanism leads to the observed behavior. Our model relies on a chemotactic mechanism for cell movement, which is thought to occur in other systems. For example, in mouse it has been suggested that melanocytes in the neural crest migrate onto the lateral pathway in response to the chemoattractant Steel, which diffuses from its site of production in the developing epithelium (15–17). Human melanocytes have been shown to be chemotactic to leukotrines, endothelin-1, and certain fibroblast growth factors (14). However, it is important to note that other mechanisms, for example haptotaxis or cell adhesion, can lead to a similar type of model and hence to similar patterning.

As mentioned above, the convoluted stripes (Fig. 5f) are regularly observed patterns in a variety of fish species. A relative of the zebrafish, Danio malabaricus, shows this pattern on the forebody despite an earlier (larval and young juvenile) patterning similar to the zebrafish, which has an adult pattern consisting of horizontal stripes. This species grows to a much larger size, and our results suggest that the observed changes in the pattern can be attributed to the differences in size. The hypothesis of “initiation centers” from which the pattern develops to form the curved stripes suggests possible experimental tests. By using excision of tissue at these centers just before pattern formation in our model, we could predict the disappearance of patterning. Transplantation experiments could also be performed, in which case we would expect a new site of pattern initiation.

Applications of Turing’s mechanism have been limited in the past because of the difficulty in generating the desired pattern robustly. For example, large numbers of regular stripes are unlikely to arise reliably without tight parameter control. In the present model, in which growth, cell movement, and patterning are coupled, this can be reliably achieved by initiating stripe formation on a small domain and relying on growth to generate regular stripes on larger domains (compare Fig. 4d). In the absence of growth, the resulting structures are closer to the convoluted patterns shown in Fig. 5f. Chemotaxis, which is an essential component of the model, produces the slow growth of new stripes. The positional information provided by the morphogen distributions is used here to direct cell movement and produce the pattern, rather than to trigger new gene expression and cell differentiation.

To facilitate understanding, the model presented here has been kept as simple as possible, but the processes occurring in the skin are undoubtedly more complex. For example, there exist multiple pigment cell types that are likely to interact with both each other and with the proposed morphogens. It is tempting to speculate that such interactions may lead to the more complex transformations of pigment patterning as the fish matures, for example the transformation from juvenile pigmentation to the horizontal yellow and blue stripes in P. imperator.