Abstract
A transcriptional module (TM) is a collection of transcription factors (TF) that as a group, co-regulate multiple, functionally related genes. The task of identifying TMs poses an important biological challenge. Since TFs belong to evolutionarily and structurally related families, TF family members often bind to similar DNA motifs and can confound sequence-based approaches to TM identification. A previous approach to TM detection addresses this issue by pre-selecting a single representative from each TF family. One problem with this approach is that closely related transcription factors can still target sufficiently distinct genes in a biologically meaningful way, and thus, pre-selecting a single family representative may in principle miss certain TMs. Here we report a method—TREMOR (Transcriptional Regulatory Module Retriever). This method uses the Mahalanobis distance to assess the validity of a TM and automatically incorporates the inter-TF binding similarity without resorting to pre-selecting family representatives. The application of TREMOR on human muscle-specific, liver-specific and cell-cycle-related genes reveals TFs and TMs that were validated from literature and also reveals additional related genes.
INTRODUCTION
Precise spatio-temporal regulation of gene expression is critical for normal functioning of all living organisms. Gene expression is controlled largely at the level of transcription. Transcriptional regulation is carried out by cooperatively interacting transcription factor (TF) proteins that bind to specific cis-regulatory regions in the relative vicinity of the gene, often in a sequence-specific manner (1,2). This cooperatively interacting group of TFs is termed the transcriptional module (TM) and the identification of TMs is important for elucidating the transcriptional control underlying a set of coordinately regulated genes (3–7).
The computational problem of TM identification can be stated as follows. Given a positive set of gene promoters (P) that are suspected to be transcriptionally co-regulated, as well as a negative control (N), identify the group(s) of TFs or DNA motifs as a proxy underlying the co-regulation. Numerous computational approaches for detecting TMs have been previously proposed that essentially detect groups of motifs that are enriched in P relative to N. Here, we focus specifically on the methods that use known motifs compiled in databases such as TRANSFAC (8) and JASPAR (9). Several tools, such as Toucan (10), CONFAC (11) and oPOSSUM (12), search for known and novel single motifs enriched in P. Certain other tools search for enriched TF pairs and are more relevant to TM identification. For example, oPOSSUM2 searches for TF pairs or triplets that are enriched in P relative to N using the Fisher exact test (13), and CREME searches for enriched groups of motifs within a pre-specified distance from each other (14).
TM identification methods, and indeed all sequence-based analysis of transcriptional regulation, suffer from one limitation. Structurally related TFs, usually classified as a family, recognize similar DNA motifs, and it is currently not possible to disambiguate TFs in the family from one another based on a DNA element or motif alone. One approach to address this ambiguity is to use a single representative for a group of TFs with similar binding motifs. Sandelin and Wasserman (15) have previously provided family-based positional weight matrices (PWM). In the TM detection tool oPOSSUM2, TFs are first clustered (through single linkage) based on their pairwise PWM similarities and then a single PWM is selected as the representative for each cluster. The arbitrariness of the pairwise distance threshold, as well as low accuracy of single-linkage clustering can be problematic. By considering TMs consisting only of the family representatives, oPOSSUM2 drastically reduces the computational time. Nevertheless, because assessing larger combinations of PWMs can be computationally prohibitive, oPOSSUM2 only assesses TMs consisting of at most three PWMs. The groups of family representatives that are enriched in P relative to N are expanded into their respective members, and all member combinations are finally assessed for enrichment. As we argue in the following, there may be problems with this approach of pre-selecting PWM cluster representatives. Other TM detection tools, such as CREME, that do not distinguish among highly similar PWMs, must account for overlapping binding sites of similar PWMs in order to avoid detecting invalid TMs.
We have previously shown that the binding sites for a TF often fall into distinct subtypes and a mixture of the subtype PWMs can better predict binding sites relative to an overall PWM (16). These clusters can be similar at a gross level but differ in subtle features. Thus, even when two TFs have similar binding sites at a gross level, these subtle differences may indeed be biologically relevant. Therefore, by reducing an entire family of TFs to a single representative PWM, we are likely to miss biologically relevant targets. On the other hand, if we incorporate similar PWMs in our analysis, we will be overwhelmed by largely overlapping binding sites that do not provide independent information, which is required by the statistical tests for enrichment. Hence, ideally we need a measure that automatically down-weighs such largely overlapping (i.e. high covariance) binding sites without completely eliminating them from consideration to avoid missing biologically relevant signals.
The ‘Mahalanobis distance’ measure was proposed precisely to estimate distances between two vectors of interdependent or co-varying variables (17). Given gene sets P and N, and a potential TM C = {c1, c2, … , cn}, for each gene, we first compute the TM vector and then compute its distance from a ‘Zero’ vector (see Methods section) using the Mahalanobis distance (MD). Given the |P| (where |•| represents the size of P) MD values for the positive genes and |N| MD values for the negative control genes, we estimate the TM enrichment using a non-parametric test. To address the combinatorial explosion when assessing large TMs, we iteratively search for TMs of increasing size up to five TFs. For each iteration, we consider all possible extensions of significant TMs from the previous iteration, and retain only those extended TMs that yield improvements over the smaller subsets of TMs that are contained within them. It should be noted that for the purposes of the analysis presented here, our only restriction on the spatial clustering of the binding sites within a TM is that they should be within the 1 kb promoter region in question. This definition of a TM may differ somewhat from other definitions, which sometimes require more stringent proximity of the binding sites comprising the TM.
We have applied our tool—TREMOR (this software will be made available upon request)—to detect TMs in three human datasets: genes involved in cell cycle, and genes specifically expressed in liver and in muscle. We detect several significant TMs involving the TFs known to be involved in relevant processes or tissue functioning. A genome-wide search of human promoters using the significant TMs reveals additional genes that are likely to be involved in a similar process.
METHODS
PWM match score computation
A positional weight matrix is a 4-by-m matrix representing the DNA-binding specificity of a transcription factor that binds to an m bases long DNA site. Given a DNA sequence, the PWM score S is computed by summing for each nucleotide in the sequence, the position-specific score for the nucleotide in the corresponding PWM. Let MIN and MAX be the minimum and the maximum scores respectively, achievable by a PWM. Thus, the percentile score for the DNA sequence is (S−MIN)/(MAX−MIN). Given a 1 kb promoter sequence, we compute the percentile score for every m long substring of the promoter (in both strands) and record the maximum of all substring scores as the promoter score.
Mahalanobis distance
Widely used in the statistical literature, the ‘Mahalanobis distance’ (17) is a distance measure in the Euclidian setting that takes into account the correlations among different coordinates. The distance is defined as
where x and y are two vectors of the same length, and V is a covariance matrix of coordinates. The introduction of the covariance matrix has two effects. First, the matrix normalizes the effects of coordinates: when the coordinates are independent, the distance reduces to the ‘normalized’ Euclidian distance 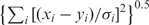 , where σi is the SD along coordinate i. Second, the Mahalanobis distance down weighs coordinates that are highly correlated. Consider the artificial example where we replicate one coordinate n times, add some small random numbers (to avoid singularity), and append them to the inputs x and y. Whereas Euclidian distance will inflate the influence of the coordinate by (n + 1)-fold, in Mahalanobis distance the weights of the replicated coordinates are adjusted by the covariance, so the total weight for the (n + 1) coordinates is (about) the same as a single coordinate. This feature is very useful when some coordinates are redundant due to the data collection procedures.
, where σi is the SD along coordinate i. Second, the Mahalanobis distance down weighs coordinates that are highly correlated. Consider the artificial example where we replicate one coordinate n times, add some small random numbers (to avoid singularity), and append them to the inputs x and y. Whereas Euclidian distance will inflate the influence of the coordinate by (n + 1)-fold, in Mahalanobis distance the weights of the replicated coordinates are adjusted by the covariance, so the total weight for the (n + 1) coordinates is (about) the same as a single coordinate. This feature is very useful when some coordinates are redundant due to the data collection procedures.
We formulate the TF set enrichment problem using the Mahalanobis distance as follows. Given positive gene set P and negative gene set N and a potential TM C = {c1, c2, … , cn}, for each promoter g in P and N, we first compute the vector of TM scores s(g) = [c1(g), c2(g), … , cn(g)], where ci(g) is the score of PWM ci on gene g. The reference vector is s* = (0, 0, … , 0), where 0 is the minimum achievable score for PWM ci. Let V be the covariance matrix for the PWMs (defined below), the score of TM on gene g is dv(s(g),s*).
Euclidian distance
For comparison purposes, we have also implemented the Euclidian distance measure. This step simply involves setting the covariance matrix for a TM of size n to an identity matrix of size n and repeating the same algorithm used for computing TMs based on Mahalanobis distance.
Covariance computation
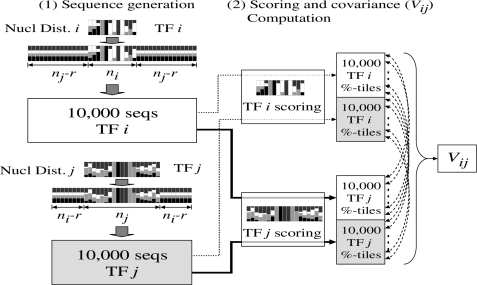
The Mahalanobis formulation requires us to compute, for each PWM pair, the covariance between the scores of the two PWMs. An analytical approach to computing the covariance between two PWMs seems difficult. This is because the PWMs can be of different lengths, and can be aligned in multiple ways. We have instead followed a sampling strategy. See Figure 1 for an illustration.
Figure 1.
Procedure for computing the covariance of the percentile scores of two TFs (see Methods section).
We score a sample of sequences using both PWMs resulting in matched pairs of scores, which is then used to compute the covariance. Complications arise because of unequal PWM lengths and a large sample space. Simple sampling strategies can lead to inaccurate covariances, as the number of high-scoring sequences is exponentially small. Instead, we devised a stratified sampling procedure by randomly generating sequences using the distributions dictated by the two PWMs in the following fashion. The generation requires a parameter r, the minimum overlap between the two PWMs; we used r = 4. Given any two PWMs Mi and Mj (mi and mj nucleotides long, respectively), we first generated 10 000 random sequences of mi + 2(mj−r) nucleotides each: the first and the last mj−r sites are sampled i.i.d. using distribution (A,T:0.3, C,G:0.2), corresponding to human genome composition, and the middle mi sites are sampled using the nucleotide distribution according to Mi. We then generated another 10 000 random sequences of length mj + 2(mi−r) by swapping Mi and Mj in our procedure. For each of the 20 000 sequences, we computed the maximum PWM scores using Mi and Mj and then transformed them into percentile scores: the percentile of a PWM score s using Mi is (s−smin)/(smax−smin) × 100, where smax and smin are the maximally and minimally achievable PWM scores using Mi. The covariance Vij was defined as the covariance using the 20 000 pairs of percentile scores.
The covariance as defined above should reflect the similarity between the binding motifs of the two TFs we compare, rather than other generic features such as GC richness. In other words, the covariance should be high only when the corresponding PWMs are similar, and the covariance becomes zero if we scramble the sites in the two PWMs to keep the sequence composition frequency but destroy the position-specific information. To demonstrate this property, we scrambled the PWMs by permuting the sites within each PWM, computed the covariance matrix using these random PWMs and then compared the result with the covariance matrix using the actual PWMs. In both cases, the majority of covariances are negative, meaning the respective pairs of PWMs are substantially different and sequences scoring high in one PWM tend to score low in the other. However, the number of positive covariances using actual PWMs (1.457%) is five times higher than that using permuted PWMs (0.310%), as expected (see Supplementary Figure S4).
The parameter r represents the minimum overlap between two PWMs. Two different transcription factors can bind to sites that overlap by 2 or 3 bases. To avoid this possibility while computing the covariance we required r to be at least 4. It is also possible that in the determination of DNA-binding sites for a transcription factor, there may be slight shift in motifs detected in different experiments. Thus to allow for this possibility, r should not be too high. Certainly for a higher value of r, fewer PWM pairs will achieve high covariance. Any measure of PWM pair similarity faces this choice (18) and while there is no objective way, ours is a reasonable choice.
Overview of TREMOR
Biologically, a TM is a set of transcription factors that coordinately regulate a set of genes. Formally, a TM C of size n is a set of n PWMs. A TM vector corresponding to a gene promoter is a vector of size n, where the ith value in the vector is the match score of the ith PWM against the promoter sequence. For the match score, we use the maximum percentile score of the PWM on the promoter sequence thus, each value in the vector is in the [0, 1] interval. Vector V0 is [0, 0, … , 0] with n zeros (see Methods). We use the Mahalanobis distance to compute the distance MD(C) between the TM vector and V0. This distance is an estimate of how well the promoter matches the TM. Let T = {1, … , 584} be the set of 584 vertebrate PWMs in TRANSFAC. Define Di to be the set of TMs of size i. Let P and N be the positive and negative promoter sets.
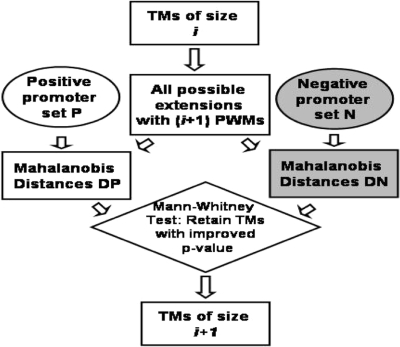
The iterative TM computation (Figure 2) proceeds as follows:
Figure 2.
A single iteration of the method for computing TMs. Starting with single PWMs (TM of size 1), in each iteration, the top scoring TMs are retained and all extensions are assessed in the next iteration. DP and DN refer to distances from vector V0 of positive and negative vectors. A Mann–Whitney test is performed with the null hypothesis that median (DP) ≤ median (DN).
Initialize
D1 = T. For each TM C in D1, and each promoter in P, compute MD(C). Call this set of distances DP. Repeat this for the promoters in N; call this set of distances DN. Using the Mann–Whitney two-sample test, we test the null hypothesis: median (DP) ≤ median (DN). This test yields a P-value for C. Retain in D1 only TMs with P-value ≤ 0.05.
Iterate for i = 2 through K
For each TM C in Di−1, create a new TM C′ = C∪{t} where t is from 1 to 584. Compute the P-value for C′ as above.
Of all TMs with i TFs, retain each C′ such that P-value (C′) is smaller than the P-values of ‘all’ subsets of C′. In other words, we only retain an extended TM if the extension improves the P-value. The 1000 TMs of size i with lowest P-values constitute Di.
Finally, the combined TM list after the ith iteration potentially includes not only all TMs of size i, but also all the smaller TMs that could not be extended; hence the list represents maximal TMs. In practice, not all TMs produced after the fifth iteration are of size 5 and in some cases, none of the size 4 TMs could be improved upon.
Recall that we do not remove any PWMs as a pre-processing step. Consequently, we may detect two (or more) TMs that are closely related. For instance, we may detect both (X, Y, Z) and (X, Y, Z′) for PWMs X, Y, Z and Z′, where Z is very similar to Z′. For brevity of presentation and interpretation, we remove such highly similar TMs as a post-processing step. This post-processing step should not be confused with the clustering of PWMs and pre-selecting cluster representatives as done by oPOSSUM2 (13). We refer to the final set of detected TMs after the post-processing step as the ‘non-redundant set’.
Removing highly similar TMs
This step is mainly for ease of reporting and interpretation of the results and should not be confused with pre-filtering of similar PWMs as is done by oPOSSUM2 (13). Because we do not remove similar PWMs as a pre-processing step, we may detect two TMs that are closely related. For instance, we may detect both (X, Y, Z) and (X, Y, Z′) for PWMs X, Y, Z, Z′ where Z is very similar to Z′. For brevity of presentation and interpretation, we remove such highly similar TMs as a post-processing step. Consider two TMs of sizes k and n, k ≤ n. We determine the overall similarity between the two TMs. We first form a complete bipartite graph of k and n vertices in the two parts, and set the weight of each edge (i, j) to be the covariance between the ith PWM in the first TM and the jth PWM in the second TM. We then compute the highest weighted matching of the k TFs into the n TFs. If the weight of each of the k edges in the matching is higher than a pre-determined threshold (we have used the 98th percentile of all covariance values as our threshold), then the two TMs are considered similar. In our iterative procedure, we retain the top 1000 TMs with smallest P-values. We scan this list and remove a TM if it is similar to another TM with a lower P-value.
Expression coherence
We used the ‘expression coherence’, or ‘EC’ (19,20) to indicate the level of correlation in gene expression. Given a set of genes G, the expression coherence is the fraction of all pairwise correlations of G exceeding the 95% of pairwise correlations of 1000 randomly chosen genes. We used the normalized cell cycle expression data from Ref. (21) with data averaged between the independent experiments, for the Affymetrix 6800 human gene arrays to compute the coherence score. Human expression data for the muscle- and liver-specific genes were based on Affymetrix Human U133A array, with gcRMA background correction (22). The background expectation of EC score is 5%.
RESULTS
Effect of TM size on the P-value
Our iterative extension of TMs is based on P-value comparisons across TMs of various sizes. This would be inappropriate if the P-value depended on the size of the TM. We explicitly tested this dependence as follows. The foreground and background labels for the gene promoters were randomly shuffled for each dataset. We then computed, for each size i from 1 to 5, P-values of 10 000 randomly generated TMs of size i. For size 1, all 584 PWMs (TMs of size 1) were used. Figure S1 shows the P-value distributions of the random TMs for the human cell cycle data. Two conclusions can be made from this analysis. First, there is no significant bias in P-value distribution (6.01% of all TMs have P-value ≤0.05, which is very close to 5% as expected), and second, there is no appreciable difference in P-value distribution between TMs of different sizes. The former observation justifies the use of P-values as a measure of significance and the latter observation justifies the comparison of P-values across different sizes in the iterative procedure. Next we apply our approach to three biological datasets.
Application to biological datasets
We have tested our approach on three human datasets—cell cycle genes, liver-specific genes and muscle-specific genes. The foreground set sizes are 246 for cell cycle data, 15 for liver data and 57 for muscle data. For the control (or negative) set, we use a randomly selected set of 1000 human gene promoters independently for each foreground set.
Because we assess a large number (in the order of 170–180 000) of TMs of sizes 1 through 5, it is critical to correct for multiple testing. During each iteration, we keep track of all TMs tested and their P-values. We then compute their respective false discovery rates (q-values) using a previously reported approach (23). All TMs of size greater than 1 detected by our procedure have significant q-values (≤0.05) except for TMs of size 2 in the liver dataset. For TMs of size 1 this is not always the case. Since there were only 584 tests of size 1 TMs and typically a number of these tests showed significance (7.5–26%), the q-value approach turns out to be conservative. Nevertheless, the size-1 TMs detected by our approach were supported by literature.
As an additional measure of stringency, for each dataset (foreground P and control N), we create another foreground (P′) and control (N′) by randomly permuting among P and N; the foreground and control sizes remain unchanged. We compute the TMs in (P′, N′) in parallel. For each TM of size >1 detected in (PN), we only report the TMs whose P-values are lower than the lowest P-value achieved in (P′, N′). Nonetheless, virtually all TMs in (P, N) have a P-value lower than the lowest P-value in (P′, N′). Thus, we report TMs that qualify the following two criteria: the TMs (i) must have a q-value ≤0.05 and (ii) must be more significant than all TMs in the corresponding permuted sets (P′, N′). The exception to this rule is size 1 TMs in which case we report all TMs with P-value ≤0.05.
For each dataset, along with the results obtained by TREMOR, we also discuss the results obtained by two other comparable programs—oPOSSUM2 (13) and CREME (24). The tool oPOSSUM2 is limited to TMs of sizes 2 and 3. The main site for oPOSSUM2 was not available so we used the developmental site (www.cisreg.ca/oPOSSUM2_dev/opossum2.php) instead. For a fair comparison with TREMOR, we used the following settings for oPOSSUM2. We used sequences 1 kb upstream and 0 bp downstream of transcription start sites, and binding sites that are among top 30% most conserved sites between human and mouse; we did not use any intersite distance constraint. oPOSSUM2 uses JASPAR PWMs, which cannot always be unambiguously mapped to TRANSFAC PWMs. Even for CREME, which is based on TRANSFAC PWMs, the exact PWMs that CREME selects depend on many parameters and a direct PWM-based comparison is difficult. We instead discuss general characteristics of the predictions as follows.
TMs in human cell cycle
Previous genome-wide studies have identified several cell cycle regulated genes in human (25). Whitfield et al. published a set of genes that show cyclic expression in their own microarray experiments as well as in a previous experiment reported in Ref. (21). They also reported an additional list of genes curated from the literature. We combined these two lists and mapped them to 246 human Refseq genes. This list constitutes our foreground set P. As a control, we randomly selected 1000 human Refseq genes. For the set of 246 foreground and 1000 control promoters of sizes 1 kb each, we applied TREMOR to compute TMs of sizes 1 through 4 (size-4 TMs could not be improved upon). The non-redundant sets of significant TMs at the end of each iteration are listed in the Supplementary Data. Recall that after the kth iteration, we retain non-extensible TMs of smaller sizes. We refer to a TM with n PWMs as TM-n.
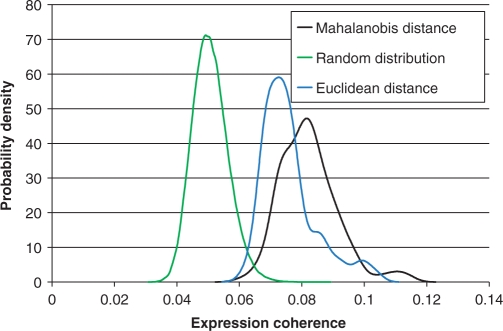
Table 1 summarizes the results, especially highlighting the known key regulators of cell cycle—E2F, CREB and NF-Y (26). Some of the differences between TREMOR and other programs may reflect the differences between the two programs in the way the promoter sequences were scored by a PWM. Unlike for single TFs, and to some extent for TF pairs, experimental data for higher order TMs is not available. In order to validate these higher order TMs, we took the approach in Ref. (24) as follows. For each TM-4, we scored each of the 7452 human gene promoters in the cell cycle dataset, using the Mahalanobis vector distance and selected the genes with top 100 scores. We then computed the ‘expression coherence’ (EC) (see Methods section) of these genes in human cell cycle data (21). EC is a previously described measure that quantifies the similarity in expression profiles among the genes in a set (19). Since there were only 23 genes in common between these 100 genes and the 232 genes used for TM identification, the proposed scheme can be considered as an independent validation. Results do not change when we remove the overlap. As control, we randomly sampled 100 genes and computed their EC. Figure 3 shows four distributions of coherence scores for the top 100 scoring genes for each of the 158 significant TM-4s computed using Mahalanobis distance. We have also presented other distributions of coherence scores as control. As a baseline expectation, we show the distribution of coherence scores for 100 000 random sets of 100 genes. Using a 95th percentile threshold from the baseline distribution (nominal false positive of 5%), 100% of the Mahalanobis distance-based coherence scores are significant. To highlight the benefits of using Mahalanobis distance, we have also implemented the Euclidian distance measure. We describe this analysis further in the simulation studies section. The figure also shows the coherence score distribution for the top 100 scoring genes for each of the 77 significant TM-3s computed using Euclidian distance (the algorithm using Euclidian distance did not achieve any improvement beyond size-3 TMs). The figure clearly indicates that the genes detected by significant TMs using Mahalanobis distance have a significantly greater EC in the cell cycle data relative to other controls.
Table 1.
Summary of the results for human cell cycle data
| TM-1 | TM-2 | TM-3,4 | ||
|---|---|---|---|---|
| TREMOR | • 41 significant TFs detected | • 98 TM-2s detected. | • 63 TM-3s detected. | |
| • 15 TFs have P-values lower than the lowest P-value in the randomly permuted set. | • 35 include E2F and 36 include NF-Y. | • All include NF-Y and 15 include E2F. | ||
| • NF-Y is at rank 1, E2F at rank 2 and CREB at rank 12 | • Rank-1 TM-2—(NF-Y c- Myc:Max). These TFs form a complex in cell cycle regulation. | • 158 TM-4s detected. | ||
| • Of the remaining 12, 7 have evidence of potential cell cycle involvement: HOXA7 (34) (the reference shows evidence of involvement of a close relative, Hoxa-10), Elk-1 (35), ETF (36) (ETF regulates p53 which mediates cell cycle arrest), AR (37), AP-2alpha (38), Ik-2 (39), v-Myb[v-Myb motif enrichment in cell cycle gene promoters was previously shown in Ref. (40) and direct involvement in cell cycle was shown for a close relative c-Myb in Ref. (41)]. | • Rank-3 TM-2—(NF-Y E2F).These TFs are are known to interact (42). | • Of these, 150 include NF-Y, and 71 include both E2F and NF-Y. | ||
| • (NF-Y AP-2) has a P-value = 1.1E−14. CDP and AP-2 function synergistically to regulate H3.2 during cell cycle and NF-Y and CDP bind to neighboring CAAT boxes in H3.2 promoter (43). | ||||
| OPOSSUM2 | TM-2 | TM-3 | ||
| • 20 significant (P ≤ 0.05) TM-2s. | oPOSSUM2 detected 33 size-3 TMs (64 by TREMOR). Surprisingly the | |||
| • Only two include E2F, in combination with NF-Y and Gfi. Both combinations are detected by TREMOR. | three cell cycle regulators—E2F, NF-Y or CREB—were not included in any of the TMs returned by oPOSSUM2, while a majority of TREMOR TM-3s include these key TFs. | |||
| • (CREB E2F) not detected. | ||||
| • Only two TM-2s include NF-Y. | ||||
| • In general, oPOSSUM detects fewer and more varied TMs while TREMOR TMs revolve around primary TFs- E2F, NF-Y and CREB. | ||||
| CREME | • On our gene set, CREME yielded a total of two TM-3s—(AREB6, STAT4, TCF1P) and (SRY, STAT4, TCF1P, EGR). These do not include the three well-known cell cycle TFs—E2F, CREB and NFY. | |||
| • CREME was applied to a slightly different cell cycle data in the original paper (19). CREME detected 47 TFs, compared to TREMOR's 41. CREME reports only seven significant non-redundant TMs. The three TM-2s are (ZF5 GR), (ZF5 HAND1E47) and (ZF5 USF2). The first two are detected by TREMOR. USF2 is an E-box TF and there are several TM-2s detected by TREMOR that link ZF5 with an E-box protein. The larger TMs detected by CREME were not detected by TREMOR. | ||||
For oPOSSUM2 and CREME, the results are compared to TREMOR. Unless otherwise specified, for TREMOR we only mention the TMs whose P-values were lower than the lowest P-value for the corresponding randomly permuted set (see text).
Figure 3.
Distributions (probability density functions) of expression coherence (at 95th percentile threshold; see Methods section) in cell cycle data. The plot (green) on the left based on random gene set provides a base line. The plot (black) to the right is for the top 100 target genes identified by each of the 158 significant cell cycle TMs of size 4. The blue plot in the middle is based on the target genes identified by the TMs using Euclidian distance.
TMs in human liver-specific gene promoters
Liver-specific gene expression is regulated by a combination of multiple TFs, most important among which are HNF-1,3,4 and c/EBP (27). Based on these four TFs, computational models have been proposed to predict promoters with liver-specific expression (28). This dataset was also used to determine enriched motifs in the oPOSSUM paper (12). We were able to map 15 human genes listed in Ref. (28) to Refseq genes. As a control, we randomly selected the 1 kb upstream region of 1000 gene promoters from human. We applied TREMOR to the 15 foreground and 1000 background 1 kb promoters and detected TMs of sizes 1 through 5. The non-redundant set of significant TMs after each iteration is listed in the Supplementary Data.
Table 2 summarizes the results, especially highlighting the known key regulators of liver expression. In order to validate higher order TMs, we followed a similar approach as for the cell cycle TMs. For each TM-5, we scored all human gene promoters using the Mahalanobis vector distance and selected the genes with highest 25% of scores (set U) and the genes with lowest 25% of scores (set D). We then tested whether these genes in U have a greater expression in liver relative to the genes in D. We used the liver tissue expression from the Novartis dataset (22) and tested the expression difference using Mann–Whitney test. A histogram of the resulting 266 P-values from these Mann–Whitney tests is shown in Supplementary Figure S2. Over 32% of the TMs are significant at the 95% confidence level, which represents over a 6-fold enrichment. We contrasted this with the size-1 TMs, i.e. significant TFs. For the 17 significant TFs, we computed the P-value of differential expression of the target genes in an identical manner. The resulting P-values do not show an excess of low P-values (Supplementary Figure S2).
Table 2.
Summary of the results for human liver expression data
| TM-1 | TM-2 | TM-3,4,5 | |
|---|---|---|---|
| TREMOR | • 17 TM-1s detected—HNF-1, HNF-3alpha, STAT5A, GFI1B, IRF1, MEIS1A, AIRE, NF-AT, Pbx1b, HNF-4alpha1, POU3F2, NF-Y, MEF-2, AFP1, SRF, C/EBP, TCF-4. | • 31 TM-2s detected (however, not significant after multiple testing correction) | • 217, 224 and 266 TM-3s, TM-4s and TM-5s |
| • Well-known liver TFs HNF1-3,4 and C/EBP are included among these. | • 1 involved HNF-3 and 25 involved HNF-1. | • 185, 222 and 266 involved HNF. | |
| • 8 of the remaining 11 TFs have evidence of involvement in transcription in liver—STAT5 (44), GFI1b (45), IRF (46), Pbx1 (47), NF-Y (48), AFP1 (49), SRF (50) and Tcf-4 (51). | • Rank-1 TM-2 was (HNF-1 TATA). These TFs are known to interact (52). | ||
| • TM-2s at rank 2, (HNF-1 HNF-4), and at rank 4, (HNF-1 NF-Y) are supported (53). | |||
| OPOSSUM2 | TM-2 | TM-3 | |
| • 3 TM-2s detected | • 31 TM-3s detected TMs, but none of them include FORKHEAD TFs, while 188 of 234 TREMOR TM-3s include FORKHEAD factors. | ||
| • These combine zinc finger TF X2H2 with FoxA2, FoxD3 and FoxI1. | |||
| • TREMOR detects many more TMs but 81 of the 226 include FORKHEAD factors. | |||
| CREME | Even at the least stringent settings, namely, using the lowest matrix score threshold = 0.8 and the largest module length = 500 bp, as well as requiring only two TFs in the TM, CREME did not yield any TMs. | ||
For oPOSSUM2 and CREME, the results are compared to TREMOR. Unless otherwise specified, for TREMOR we only mention the TMs whose P-values were lower than the lowest P-value for the corresponding randomly permuted set (see text).
TMs in human muscle-specific gene promoters
Gene expression specific to muscle tissue is regulated by five primary classes of TFs—MyoD, SRF, MEF-2, TEF-1 and Sp-1 (29). We extracted a set of 44 well-established muscle-specific genes from the MTIR website (www.cbil.upenn.edu/MTIR/TOC.html). We then extracted the corresponding human Refseq IDs using the NIH David web service (david.abcc.ncifcrf.gov/conversion.jsp). Some of the genes have multiple isoforms and hence multiple Refseqs. We retained multiple Refseqs for a gene as long as the transcription start was more than 1 kb apart. This resulted in 57 unique Refseq Ids used as the foreground. As before, we used a set of 1000 randomly chosen human genes as control. For these foreground and control gene promoters, we applied TREMOR to compute TMs of sizes 1 through 5. The non-redundant set of significant TMs, after each iteration, is listed in Supplementary Data.
Table 3 summarizes the results, especially highlighting the known key regulators of muscle expression. There are two slightly different PWMs for SRF in TRANSFAC. The TM-2 at rank 8 includes the two SRF PWMs. Thus, multiple SRF sites provide a better indication of muscle-specific transcription than does a single SRF site. A pre-clustering of PWMs would have missed detecting this tendency. Notably, because oPOSSUM only searches for combinations from different structural classes, it did not detect the TM (SRF SRF). It was shown before that key cis elements regulating muscle-specific expression are conserved between human and mouse (30). Because oPOSSUM uses pre-computed conserved binding sites, relative to other datasets, in the muscle dataset oPOSSUM2 detects a large number of TMs. In fact, oPOSSUM detected 143 class-combinations and did not expand the class-combinations into TF-combinations, which are likely to be larger by an order of magnitude. In general, in other datasets oPOSSUM2 detected much fewer (44 in cell-cycle and 80 in liver data) significant TMs.
Table 3.
Summary of the results for human muscle expression data
| TM-1 | TM-2 | TM-3,4,5 | |
|---|---|---|---|
| TREMOR | • 19 TM-1s detected. | • 87 TM-2s detected | • 218 TM-3s detected. SRF, MEF-2 and MyoD are included in 119, 41 and 19 |
| • The top 2 TM-2s were SRF and MEF-2. | • 21 included SRF, 11 included MEF-2 and 7 included MyoD. | • Most core muscle TFs tend to group with non-core TFs in a TM. | |
| • MyoD was at rank 4. | • Rank-1 TM-2 is (SRF MEF-2). | • Rank 16 TM-3 is (SRF MEF-2 SMAD). | |
| • We did not detect SP1, probably because it is a ubiquitous signal. TEF-1 had a P-value of 0.06 and was thus not detected as significant. | • Rank-8 TM-2includes the two SRF PWMs (see text). | • Rank 28 TM-3 is (SRF MEF-2 MyoD). | |
| • Seven of the remaining 14 TFs have evidence of involvement in muscle gene regulation: SMAD (54), SREBP (55), p53 (56), PBX (57), Hox-1.3 (58) (this reference implicated Hox factors in general), COMP1 (59) (Myogenin interacts with COMP1), GATA-4. | • TEF-1 is part of a significant TM-2 SRF and with SMAD. | • 244 TM-4s detected. SRF, MEF-2 and MyoD are part of 177, 75 and 17 TM-3s. | |
| • Additional factor RREB was also detected previously by oPOSSUM2 in a slightly different dataset (13). | • 283 TM-5s detected. SRF is part of 232. | ||
| • TEF-1 yielded a P-value of 0.06 and missed detection | |||
| OPOSSUM2 | TM-2 | TM-3 | |
| • 293 TM-2s detected. SRF, MEF-2 and Myf (same as MyoD) were part of 37, 42 and 37. Compare with TREMOR above. | • In our dataset, 764 TM-3s were detected TMs. | ||
| • See text for additional comparative discussion | • In the original oPPOSSUM2 publication, using three different muscle datasets, the authors have reported top 5 TM-2 in each dataset. Greater than half of these were detected by TREMOR, notably (YY1 SRF), (YY1 Myf), (SRF E47) and (SRF MEF-2). | ||
| CREME | With the default setting, CREME did not yield any TMs. However, at the least stringent setting it detected 1 TM-2—(SRF SRF). TREMOR also detected a size-2 TM with two SRF motifs, in addition to several others. | ||
For oPOSSUM2 and CREME, the results are compared to TREMOR. Unless otherwise specified, for TREMOR we only mention the TMs whose P-values were lower than the lowest P-value for the corresponding randomly permuted set (see text).
In order to validate the higher order TMs detected by TREMOR, we again used the approach for the liver TMs. For each TM, we scored all human gene promoters using the Mahalanobis vector distance and selected genes with the highest 25% of the scores (set U) and genes with the lowest 25% of scores (set D). We then tested whether genes in U have a greater expression in muscle relative to genes in D. For this we used the muscle tissue expression from the Novartis dataset (22) and tested the expression difference using Mann–Whitney test. A histogram of the resulting 283 P-values from these Mann–Whitney tests is shown in Supplementary Figure S3. Almost 20% of the TMs are significant at the 95% confidence level. As a comparison, the figure also shows the P-value distribution for the target genes obtained by the 19 significant individual TFs.
Simulation-based comparison of Mahalanobis distance to Euclidian distance
Although, our comparative study with existing methods using real datasets provides some indication of the effectiveness of TREMOR, these analyses do not directly measure the relative advantage of using Mahalanobis distance (MD). The attractive feature of MD is that it down-weighs TMs with similar PWMs. The best way to directly assess the advantage of these two features is to compare the MD measure with the simpler Euclidian distance (ED) measure (see Methods section). We did this comparison based on simulated data as follows. We generated 1 kb long synthetic promoters (foreground and background) based on genome-wide nucleotide composition, and then planted randomly chosen TMs in the foreground. For instance, to insert a TM with two PWMs (X, Y), we generated the binding sites for X and Y according to base probabilities indicated in their PWMs and planted them at random, non-overlapping locations within the 1 kb random promoter.
Planted TMs of size 2
We conducted 150 random trials each involving 25 foreground and 100 background simulated promoter sequences. In each trial, we randomly selected a pair of PWMs (size-2 TM) and planted the randomly generated sequences corresponding to these two PWMs in 20 of the 25 foreground promoters. We ensured that the planted sequences were non-overlapping. For the remaining five foreground promoters, we planted a random number (between 1 and 8) of randomly selected PWMs in a non-overlapping fashion. Recall that our algorithm assumes the most parsimonious representation for a TM, and hence, a TM will only be expanded in size if the increase in size yields a decrease in corresponding P-value. In other words, unless the combination of two TFs to produce a TM-2 yields a decrease in P-value compared to the two P-values of the individual TFs, the two TFs will be treated as TM-1s by themselves. Therefore, when we did not include these five ‘noisy’ promoters then in a majority of cases one of two planted PWMs resulted in a very low P-value that could not be improved upon, thereby obscuring the actual planted PWM of a greater size, for both MD and ED. For each trial we then computed TMs of size 1, 2 and 3 using both the MD and ED measures. We noted the largest subset of the planted TM in the results for both MD and ED measures, in order to directly compare the ranks of the planted TM or a subset of it. In 121 (81%) of the 150 trials, both MD and ED detected a subset of the planted TM with equal cardinality. Of these 121, 89 were of size 2, i.e. the planted TM. We found that the ranks of the largest detected subset were substantially better for MD than those for ED (Wilcoxon signed rank test P-value = 0.001). Of the remaining 29 trials where the cardinality of the largest subset differed, in all but 3 trials MD detected one of the two PWMs in the planted TM at a rank better than that for the largest subset of the planted TM detected by ED (Wilcoxon signed rank test P-value = 0.031). A closer inspection of these 29 trials reveals that these planted TMs consisted of a pair of PWMs with high correlation relative to the pairs of PWMs in the other 121 trials (Mann–Whitney test P-value = 0.024). Given two similar PWMs, if one of the PWMs by itself discriminates between the positive and the control promoters better than the combination of the two TFs, then it is desirable to detect the individual TF (TM-1) as opposed to the TM-2. Indeed, for TMs with two similar PWMs, while ED may detect the planted TM, MD in fact detects one of the PWMs (the one with higher enrichment in the foreground set) as a significant TM of size 1. The rank analysis addresses both the relative sensitivity and the specificity of the methods. This analysis demonstrates the superiority of Mahalanobis distance over Euclidian in detecting TMs.
DISCUSSION
We have presented a novel method, TREMOR, for TM detection, and demonstrated its effectiveness using three human datasets. A large portion of TM-1s detected by TREMOR are supported by literature. For TFs of larger sizes where experimental data are lacking, besides presenting evidence for several individual cases, we have assessed the accuracy of TMs based on their ability to detect additional genes with similar expression patterns as the genes that were used to detect the TMs. In particular, in the cell cycle dataset, the genes detected by our algorithm using a genome-wide search reveal significant expression coherence in cell cycle.
Because of the obvious problems of redundancy and biases caused by groups of PWMs with similar DNA binding, previous approaches such as oPOSSUM2 replace groups of similar TFs with single representative PWMs. We have argued that doing so may result in loss of information because subtly different PWMs can have significantly different target gene sets, and this difference can be biologically relevant. Problems of redundancy caused by similar PWMs, however, need to be resolved in order to minimize any statistical bias caused by possible similarity among PWMs. We address these issues by using the Mahalanobis distance, which inherently incorporates the interdependence between the vector coordinates, i.e. PWMs. This allows us to avoid the arbitrariness of choosing representative PWMs. One evidence supporting the effectiveness of Mahalanobis distance is that very rarely do we see TMs with similar PWMs; yet unlike previous approaches, this scenario is permitted, and does happen: for instance, in the analysis of the liver dataset, we detected interactions between closely related PWMs for HNF-1,3 4. In muscle we detected a TM containing an SRF pair. CREME also detects this TM, and oPOSSUM2 does not. Thus, multiple SRF sites provide a better indication of muscle-specific transcription than does a single SRF site. An approach that pre-clusters PWMs will miss detecting this tendency.
Another practical challenge in detecting large TMs is the computational cost. Assessing all k-combinations for ∼600 known vertebrate PWMs in TRANSFAC is computationally prohibitive. oPOSSUM deals with this problem by only considering combinations of representatives. CREME avoids the combinatorial explosion by only considering the TF combinations that occur within a specified distance in a promoter. We have presented an iterative approach to build the TMs as a practical compromise. By only retaining 1000 TMs with lowest P-values in each iteration, the method can detect, in practice, arbitrarily large TMs. Although this heuristic is not exhaustive, we expect it to capture the TMs that are composed of smaller significant TMs. On a computer with two Opteron 275 dual-core CPUs and 8 GB of RAM, TREMOR finishes the analysis of the cell cycle dataset (largest of the three) within an hour. Thus, it is not the computational time but the biological interpretation of the results that presents an immediate challenge.
We have only considered the 1 kb promoter regions as in previous studies. Using a larger upstream region dilutes the TM enrichment and thus makes it harder to detect significantly enriched TMs. Note that we do not require the binding sites for the PWMs in a TM to be within certain distance from each other on a promoter. In other words, the binding sites can occur anywhere in the 1 kb region. Imposing a distance constraint between PWM sites can make the method more sensitive. However, the biological relevance of specific distance constraint is not always clear and also, imposing distance constraints adds significantly to the computational costs.
Most previous tools for TM detection rely on a pre-computed set of binding sites based on evolutionary conservation, or phylogenetic footprinting. Remarkably, TREMOR yields good results without using phylogenetic footprinting. Importance of evolutionary conservation in detecting functional elements is very well supported (30). However, evolutionary conservation is neither necessary (31) nor sufficient (32) for DNA elements to be functional. This implies that although oPOSSUM detects several significant TMs in muscle data where the conservation of essential cis elements is well established, it could miss important TMs in other datasets. In cases where the biological process under investigation is not well conserved across compared species, an over-reliance on conservation-based sites will miss the real signals. Application of TREMOR is preferable in those cases.
The recent ENCODE effort (33), based on chromatin immunoprecipitation and tiling array data for five transcription factors, shows that there is sharp peak of binding site density around the start site so that a large majority of the proximal sites are within 1 kb. However, the authors also show that this distribution is symmetric around the start site. Thus ideally we should include both upstream and downstream sequences. However, there are very few examples of experimentally validated binding sites in the downstream regions relative to the upstream regions. The performance of any TM detection method will deteriorate as we include larger sequences, simply because of decreased signal-to-noise ratio as we go farther from the gene start. Admittedly, our method is perhaps more vulnerable compared to other methods that pre-compute the binding sites based on evolutionary conservation. In principle, we can restrict our analysis to conserved regions and include a larger flanking region, however, at the risk of missing species-specific TMs. Our choice, although limited, still represents a reasonable compromise.
Because TREMOR uses the maximum score for each promoter, there is a possibility that similar PWMs within a detected TM achieve their maximum score on overlapping sites. We have assessed for the detected TM-2s composed of highly similar PWMs (covariance above 90th percentile), whether or not the max-scoring matches overlap. For liver data, there were seven size-2 TMs with high covariance. For each of the 15 gene promoters in the liver data, we identified whether or not the maximum-scoring hits for the two PWMs overlap. We computed for each TM the number of promoters for which the max-scoring matches overlap. The median, mean and SD of this number (of the total of 15) are 2.00, 2.00 and 2.24, respectively. Likewise, for smooth muscle tissue, there are 57 gene promoters and eight size-2 TMs identified with high covariance. The corresponding median, mean and SD of the number of promoters for which the max-scoring matches overlap are 12.5, 13.5 and 6.78. Thus, we conclude that we detect these TM not because of the overlapping matches.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
ACKNOWLEDGEMENTS
L.N.S. and S.H. are supported by NIH grant 1R21AI073422-01; L.-S.W. is supported by NIH training grant T32-HG000046-06. We thank the two referees for their suggestions. Funding to pay the Open Access publication charges for this article was provided by NIH grant 1R21AI073422-01.
Conflict of interest statement. None declared.
REFERENCES
- 1.Kadonaga JT. Regulation of RNA polymerase II transcription by sequence-specific DNA binding factors. Cell. 2004;116:247–257. doi: 10.1016/s0092-8674(03)01078-x. [DOI] [PubMed] [Google Scholar]
- 2.Ptashne M, Gann A. Transcriptional activation by recruitment. Nature. 1997;386:569–577. doi: 10.1038/386569a0. [DOI] [PubMed] [Google Scholar]
- 3.Segal E, Sharan R. Proceedings of the Eigth Annual International Conference on Computational Molecular Biology; San Diego, CA. New York, USA: ACM Press; pp. 141–149. [Google Scholar]
- 4.Blanchette M, Bataille AR, Chen X, Poitras C, Laganiere J, Lefebvre C, Deblois G, Giguere V, Ferretti V, et al. Genome-wide computational prediction of transcriptional regulatory modules reveals new insights into human gene expression. Genome Res. 2006;16:656–668. doi: 10.1101/gr.4866006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sinha S, Van Nimwegen E, Siggia ED. A probabilistic method to detect regulatory modules. Bioinformatics. 2003;19(Suppl. 1):I292–I301. doi: 10.1093/bioinformatics/btg1040. [DOI] [PubMed] [Google Scholar]
- 6.Zhao G, Schriefer LA, Stormo GD. Identification of muscle-specific regulatory modules in Caenorhabditis elegans. Genome Res. 2007;17:348–357. doi: 10.1101/gr.5989907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hannenhalli S, Levy S. Transcriptional regulation of protein complexes and biological pathways. Mamm. Genome. 2003;14:611–619. doi: 10.1007/s00335-002-2260-x. [DOI] [PubMed] [Google Scholar]
- 8.Matys V, Kel-Margoulis OV, Fricke E, Liebich I, Land S, Barre-Dirrie A, Reuter I, Chekmenev D, Krull M, et al. TRANSFAC and its module TRANSCompel: transcriptional gene regulation in eukaryotes. Nucleic Acids Res. 2006;34:D108–D110. doi: 10.1093/nar/gkj143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sandelin A, Alkema W, Engstrom P, Wasserman WW, Lenhard B. JASPAR: an open-access database for eukaryotic transcription factor binding profiles. Nucleic Acids Res. 2004;32:D91–D94. doi: 10.1093/nar/gkh012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Aerts S, Thijs G, Coessens B, Staes M, Moreau Y, De Moor B. Toucan: deciphering the cis-regulatory logic of coregulated genes. Nucleic Acids Res. 2003;31:1753–1764. doi: 10.1093/nar/gkg268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Karanam S, Moreno CS. CONFAC: automated application of comparative genomic promoter analysis to DNA microarray datasets. Nucleic Acids Res. 2004;32:W475–W484. doi: 10.1093/nar/gkh353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ho Sui SJ, Mortimer JR, Arenillas DJ, Brumm J, Walsh CJ, Kennedy BP, Wasserman WW. oPOSSUM: identification of over-represented transcription factor binding sites in co-expressed genes. Nucleic Acids Res. 2005;33:3154–3164. doi: 10.1093/nar/gki624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huang SS, Fulton DL, Arenillas DJ, Perco P, Ho Sui SJ, Mortimer JR, Wasserman WW. Identification of over-represented combinations of transcription factor binding sites in sets of co-expressed genes. Adv. Bioinform. Comput. Biol. 2006;3:3247. [Google Scholar]
- 14.Sharan R, Ben-Hur A, Loots GG, Ovcharenko I. CREME: cis-regulatory module explorer for the human genome. Nucleic Acids Res. 2004;32:W253–W256. doi: 10.1093/nar/gkh385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sandelin A, Wasserman WW. Constrained binding site diversity within families of transcription factors enhances pattern discovery bioinformatics. J. Mol. Biol. 2004;338:207–215. doi: 10.1016/j.jmb.2004.02.048. [DOI] [PubMed] [Google Scholar]
- 16.Hannenhalli S, Wang LS. Enhanced position weight matrices using mixture models. Bioinformatics. 2005;21(Suppl. 1):i204–i212. doi: 10.1093/bioinformatics/bti1001. [DOI] [PubMed] [Google Scholar]
- 17.Mahalanobis P. On the generalized distance in statistics. Proc. Natl Inst. Sci. India. 1936;2:49–55. [Google Scholar]
- 18.Mahony S, Auron PE, Benos PV. DNA familial binding profiles made easy: comparison of various motif alignment and clustering strategies. PLoS Comput. Biol. 2007;3:e61. doi: 10.1371/journal.pcbi.0030061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pilpel Y, Sudarsanam P, Church GM. Identifying regulatory networks by combinatorial analysis of promoter elements. Nat. Genet. 2001;29:153–159. doi: 10.1038/ng724. [DOI] [PubMed] [Google Scholar]
- 20.Banerjee N, Zhang MQ. Identifying cooperativity among transcription factors controlling the cell cycle in yeast. Nucleic Acids Res. 2003;31:7024–7031. doi: 10.1093/nar/gkg894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cho RJ, Huang M, Campbell MJ, Dong H, Steinmetz L, Sapinoso L, Hampton G, Elledge SJ, Davis RW, et al. Transcriptional regulation and function during the human cell cycle. Nat. Genet. 2001;27:48–54. doi: 10.1038/83751. [DOI] [PubMed] [Google Scholar]
- 22.Su AI, Wiltshire T, Batalov S, Lapp H, Ching KA, Block D, Zhang J, Soden R, Hayakawa M, et al. A gene atlas of the mouse and human protein-encoding transcriptomes. Proc. Natl Acad. Sci. USA. 2004;101:6062–6067. doi: 10.1073/pnas.0400782101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Storey JD, Tibshirani R. Statistical significance for genomewide studies. Proc. Natl Acad. Sci. USA. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sharan R, Ovcharenko I, Ben-Hur A, Karp RM. CREME: a framework for identifying cis-regulatory modules in human-mouse conserved segments. Bioinformatics. 2003;19(Suppl. 1):i283–i291. doi: 10.1093/bioinformatics/btg1039. [DOI] [PubMed] [Google Scholar]
- 25.Whitfield ML, Sherlock G, Saldanha AJ, Murray JI, Ball CA, Alexander KE, Matese JC, Perou CM, Hurt MM, et al. Identification of genes periodically expressed in the human cell cycle, & their expression in tumors. Mol. Biol. Cell. 2002;13:1977–2000. doi: 10.1091/mbc.02-02-0030.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Elkon R, Linhart C, Sharan R, Shamir R, Shiloh Y. Genome-wide in silico identification of transcriptional regulators controlling the cell cycle in human cells. Genome Res. 2003;13:773–780. doi: 10.1101/gr.947203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ktistaki E, Talianidis I. Modulation of hepatic gene expression by hepatocyte nuclear factor 1. Science. 1997;277:109–112. doi: 10.1126/science.277.5322.109. [DOI] [PubMed] [Google Scholar]
- 28.Krivan W, Wasserman WW. A predictive model for regulatory sequences directing liver-specific transcription. Genome Res. 2001;11:1559–1566. doi: 10.1101/gr.180601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wasserman WW, Fickett JW. Identification of regulatory regions which confer muscle-specific gene expression. J. Mol. Biol. 1998;278:167–181. doi: 10.1006/jmbi.1998.1700. [DOI] [PubMed] [Google Scholar]
- 30.Wasserman WW, Palumbo M, Thompson W, Fickett JW, Lawrence CE. Human-mouse genome comparisons to locate regulatory sites. Nat. Genet. 2000;26:225–228. doi: 10.1038/79965. [DOI] [PubMed] [Google Scholar]
- 31.Emberly E, Rajewsky N, Siggia ED. Conservation of regulatory elements between two species of Drosophila. BMC Bioinformatics. 2003;4:57. doi: 10.1186/1471-2105-4-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nobrega MA, Zhu Y, Plajzer-Frick I, Afzal V, Rubin EM. Megabase deletions of gene deserts result in viable mice. Nature. 2004;431:988–993. doi: 10.1038/nature03022. [DOI] [PubMed] [Google Scholar]
- 33.Birney E, Stamatoyannopoulos JA, Dutta A, Guigo R, Gingeras TR, Margulies EH, Weng Z, Snyder M, Dermitzakis ET, et al. Identification and analysis of functional elements in 1% of the human genome by the ENCODE pilot project. Nature. 2007;447:799–816. doi: 10.1038/nature05874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yao MW, Lim H, Schust DJ, Choe SE, Farago A, Ding Y, Michaud S, Church GM, Maas RL. Gene expression profiling reveals progesterone-mediated cell cycle and immunoregulatory roles of Hoxa-10 in the preimplantation uterus. Mol. Endocrinol. 2003;17:610–627. doi: 10.1210/me.2002-0290. [DOI] [PubMed] [Google Scholar]
- 35.Shukla S, Gupta S. Apigenin-induced cell cycle arrest is mediated by modulation of MAPK, PI3K-Akt, and loss of cyclin D1 associated retinoblastoma dephosphorylation in human prostate cancer cells. Cell Cycle. 2007;6:1102–1114. doi: 10.4161/cc.6.9.4146. [DOI] [PubMed] [Google Scholar]
- 36.Hale TK, Braithwaite AW. The adenovirus oncoprotein E1a stimulates binding of transcription factor ETF to transcriptionally activate the p53 gene. J. Biol. Chem. 1999;274:23777–23786. doi: 10.1074/jbc.274.34.23777. [DOI] [PubMed] [Google Scholar]
- 37.Yuan X, Li T, Wang H, Zhang T, Barua M, Borgesi RA, Bubley GJ, Lu ML, Balk SP. Androgen receptor remains critical for cell-cycle progression in androgen-independent CWR22 prostate cancer cells. Am. J. Pathol. 2006;169:682–696. doi: 10.2353/ajpath.2006.051047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McPherson LA, Loktev AV, Weigel RJ. Tumor suppressor activity of AP2alpha mediated through a direct interaction with p53. J. Biol. Chem. 2002;277:45028–45033. doi: 10.1074/jbc.M208924200. [DOI] [PubMed] [Google Scholar]
- 39.Gomez-del Arco P, Maki K, Georgopoulos K. Phosphorylation controls Ikaros's ability to negatively regulate the G(1)-S transition. Mol. Cell. Biol. 2004;24:2797–2807. doi: 10.1128/MCB.24.7.2797-2807.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tabach Y, Milyavsky M, Shats I, Brosh R, Zuk O, Yitzhaky A, Mantovani R, Domany E, Rotter V, et al. The promoters of human cell cycle genes integrate signals from two tumor suppressive pathways during cellular transformation. Mol. Syst. Biol. 2005;1:2005–2022. doi: 10.1038/msb4100030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Osterloh L, von Eyss B, Schmit F, Rein L, Hubner D, Samans B, Hauser S, Gaubatz S. The human synMuv-like protein LIN-9 is required for transcription of G2/M genes and for entry into mitosis. EMBO J. 2007;26:144–157. doi: 10.1038/sj.emboj.7601478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhu W, Giangrande PH, Nevins JR. E2Fs link the control of G1/S and G2/M transcription. EMBO J. 2004;23:4615–4626. doi: 10.1038/sj.emboj.7600459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wu F, Lee AS. CDP and AP-2 mediated repression mechanism of the replication-dependent hamster histone H3.2 promoter. J. Cell Biochem. 2002;84:699–707. doi: 10.1002/jcb.10094. [DOI] [PubMed] [Google Scholar]
- 44.Park SH, Wiwi CA, Waxman DJ. Signalling cross-talk between hepatocyte nuclear factor 4alpha and growth-hormone-activated STAT5b. Biochem. J. 2006;397:159–168. doi: 10.1042/BJ20060332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Schuh AH, Tipping AJ, Clark AJ, Hamlett I, Guyot B, Iborra FJ, Rodriguez P, Strouboulis J, Enver T, et al. ETO-2 associates with SCL in erythroid cells and megakaryocytes and provides repressor functions in erythropoiesis. Mol. Cell. Biol. 2005;25:10235–10250. doi: 10.1128/MCB.25.23.10235-10250.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lee HJ, Oh YK, Rhee M, Lim JY, Hwang JY, Park YS, Kwon Y, Choi KH, Jo I, et al. The role of STAT1/IRF-1 on synergistic ros production and loss of mitochondrial transmembrane potential during hepatic cell death induced by LPS/d-GalN. J. Mol. Biol. 2007;369:967–984. doi: 10.1016/j.jmb.2007.03.072. [DOI] [PubMed] [Google Scholar]
- 47.DiMartino JF, Selleri L, Traver D, Firpo MT, Rhee J, Warnke R, O’Gorman S, Weissman IL, Cleary ML. The Hox cofactor and proto-oncogene Pbx1 is required for maintenance of definitive hematopoiesis in the fetal liver. Blood. 2001;98:618–626. doi: 10.1182/blood.v98.3.618. [DOI] [PubMed] [Google Scholar]
- 48.Rodriguez L, Ochoa B, Martinez MJ. NF-Y and Sp1 are involved in transcriptional regulation of rat SND p102 gene. Biochem. Biophys. Res. Commun. 2007;356:226–232. doi: 10.1016/j.bbrc.2007.02.110. [DOI] [PubMed] [Google Scholar]
- 49.Nakao K, Miyao Y, Ohe Y, Tamaoki T. Involvement of an AFP1-binding site in cell-specific transcription of the pre-S1 region of the human hepatitis B virus surface antigen gene. Nucleic Acids Res. 1989;17:9833–9842. doi: 10.1093/nar/17.23.9833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Latasa MU, Couton D, Charvet C, Lafanechere A, Guidotti JE, Li Z, Tuil D, Daegelen D, Mitchell C, et al. Delayed liver regeneration in mice lacking liver serum response factor. Am. J. Physiol. Gastrointest. Liver Physiol. 2007;292:G996–G1001. doi: 10.1152/ajpgi.00493.2006. [DOI] [PubMed] [Google Scholar]
- 51.Sasaki T, Suzuki H, Yagi K, Furuhashi M, Yao R, Susa S, Noda T, Arai Y, Miyazono K, et al. Lymphoid enhancer factor 1 makes cells resistant to transforming growth factor beta-induced repression of c-myc. Cancer Res. 2003;63:801–806. [PubMed] [Google Scholar]
- 52.Marten NW, Hsiang CH, Yu L, Stollenwerk NS, Straus DS. Functional activity of hepatocyte nuclear factor-1 is specifically decreased in amino acid-limited hepatoma cells. Biochim. Biophys. Acta. 1999;1447:160–174. doi: 10.1016/s0167-4781(99)00165-7. [DOI] [PubMed] [Google Scholar]
- 53.Yabuki T, Ejiri S, Tsutsumi K. Ubiquitous factors that interact simultaneously with two distinct cis-elements on the rat aldolase B gene promoter. Biochim. Biophys. Acta. 1993;1216:15–19. doi: 10.1016/0167-4781(93)90032-9. [DOI] [PubMed] [Google Scholar]
- 54.Monzen K, Hiroi Y, Kudoh S, Akazawa H, Oka T, Takimoto E, Hayashi D, Hosoda T, Kawabata M, et al. Smads, TAK1, and their common target ATF-2 play a critical role in cardiomyocyte differentiation. J. Cell Biol. 2001;153:687–698. doi: 10.1083/jcb.153.4.687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Motoyama K, Fukumoto S, Koyama H, Emoto M, Shimano H, Maemura K, Nishizawa Y. SREBP inhibits VEGF expression in human smooth muscle cells. Biochem. Biophys. Res. Commun. 2006;342:354–360. doi: 10.1016/j.bbrc.2006.01.139. [DOI] [PubMed] [Google Scholar]
- 56.Schwarzkopf M, Coletti D, Sassoon D, Marazzi G. Muscle cachexia is regulated by a p53-PW1/Peg3-dependent pathway. Genes Dev. 2006;20:3440–3452. doi: 10.1101/gad.412606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Berkes CA, Bergstrom DA, Penn BH, Seaver KJ, Knoepfler PS, Tapscott SJ. Pbx marks genes for activation by MyoD indicating a role for a homeodomain protein in establishing myogenic potential. Mol. Cell. 2004;14:465–477. doi: 10.1016/s1097-2765(04)00260-6. [DOI] [PubMed] [Google Scholar]
- 58.Pownall ME, Gustafsson MK, Emerson CP., Jr Myogenic regulatory factors and the specification of muscle progenitors in vertebrate embryos. Annu. Rev. Cell Dev. Biol. 2002;18:747–783. doi: 10.1146/annurev.cellbio.18.012502.105758. [DOI] [PubMed] [Google Scholar]
- 59.Funk WD, Wright WE. Cyclic amplification and selection of targets for multicomponent complexes: myogenin interacts with factors recognizing binding sites for basic helix-loop-helix, nuclear factor 1, myocyte-specific enhancer-binding factor 2, and COMP1 factor. Proc. Natl Acad. Sci. USA. 1992;89:9484–9488. doi: 10.1073/pnas.89.20.9484. [DOI] [PMC free article] [PubMed] [Google Scholar]