Skip to main content
PMC home page
The Journal of Cell Biology logoLink to The Journal of Cell Biology
. 2001 May 14;153(4):881–888. doi: 10.1083/jcb.153.4.881

Nascent Focal Adhesions Are Responsible for the Generation of Strong Propulsive Forces in Migrating Fibroblasts

Karen A Beningo a, Micah Dembo b, Irina Kaverina c, J Victor Small c, Yu-li Wang a
PMCID: PMC2192381  PMID: 11352946

Abstract

Fibroblast migration involves complex mechanical interactions with the underlying substrate. Although tight substrate contact at focal adhesions has been studied for decades, the role of focal adhesions in force transduction remains unclear. To address this question, we have mapped traction stress generated by fibroblasts expressing green fluorescent protein (GFP)-zyxin. Surprisingly, the overall distribution of focal adhesions only partially resembles the distribution of traction stress. In addition, detailed analysis reveals that the faint, small adhesions near the leading edge transmit strong propulsive tractions, whereas large, bright, mature focal adhesions exert weaker forces. This inverse relationship is unique to the leading edge of motile cells, and is not observed in the trailing edge or in stationary cells. Furthermore, time-lapse analysis indicates that traction forces decrease soon after the appearance of focal adhesions, whereas the size and zyxin concentration increase. As focal adhesions mature, changes in structure, protein content, or phosphorylation may cause the focal adhesion to change its function from the transmission of strong propulsive forces, to a passive anchorage device for maintaining a spread cell morphology.

Keywords: focal adhesions, cell movement, cell adhesion molecules, actomyosin, fluorescence microscopy

Introduction

Cell migration plays an important role in many biological events, including embryonic development, wound healing, immunological responses, and cancer metastasis (Martin 1997; Bray 2001). Although it is generally recognized that the process involves complex mechanical interactions between cells and the underlying substrate (Lauffenberger and Horwitz 1996; Elson et al. 1997; Galbraith and Sheetz 1998; Sheetz et al. 1998), little is known about the source of these forces and how they are coordinated during directional migration. Studies with interference reflection microscopy (IRM) have long indicated that many cultured cells establish discrete contact sites—focal adhesions—where the cell membrane lies within 30 nm of the substrate (Abercrombie and Dunn 1975; Izzard and Lochner 1976). Through their association with the extracellular matrix via integrins and the actin-myosin cytoskeleton, focal adhesions constitute potential foci at which contractile forces are exerted on the substrate (Burridge and Chrzanowska-Wodnicka 1995; Miyamoto et al. 1995; Schoenwaelder and Burridge 1999).

Although it is clear that focal adhesions are involved in anchoring cells to the substrate, little is known about active contractile forces that might be transmitted through these structures to propel directional movements. A particularly intriguing issue is that, during the migration of a fibroblast, mechanical interactions at hundreds of focal adhesions must be coordinated in order to maintain both the direction of migration and the morphology of the cell in an efficient manner. To address this question, it is crucial to generate maps of both dynamic focal adhesions under a migrating fibroblast, and traction forces that a cell exerts on the substrate. We have now achieved this goal by combining recent developments in mapping traction forces and in green fluorescent protein (GFP) technology.

The output of the mechanical forces exerted by a migrating cell can be detected on elastic substrates. Early applications of wrinkling silicone sheets serve as a crude way to detect forces, but provide little or no quantitative information (Harris et al. 1980; Burton and Taylor 1997). Improvements in technology, mainly as a result of embedding beads into flexible substrates, have since allowed quantification of forces through large scale matrix computation that converts maps of substrate deformation (detected as local bead movements) into maps of traction stress (force per unit area; Oliver et al. 1998; Dembo and Wang 1999). The technique has further been refined into a form of microscopy, in order to provide images or movies of the magnitudes of traction stress at a temporal resolution within 1 min (Munevar et al. 2001). We have applied this approach to address several important questions. First, we asked if strong propulsive forces can be detected at focal adhesions, and if larger focal adhesions generate stronger traction forces. Second, we analyzed how forces exerted by focal adhesions in different regions are coordinated during cell migration: specifically, whether all focal adhesions exert forces in a similar manner, or whether a subset of adhesions is responsible for cell migration. Our results suggest that small, nascent focal adhesions at the leading edge exert transient forces to move the cell forward, whereas mature focal adhesions serve primarily as anchors to the substrate. This strategy allows the fibroblasts to migrate efficiently and responsively, without complex coordination of the mechanical output among the adhesion foci.

Materials and Methods

Cell Culture and Immunofluorescence

Goldfish fin fibroblast cells (CAR, CCL71; American Type Culture Collection) were stably transfected with enhanced GFP-zyxin and maintained as described previously (Kaverina et al. 1999). For paxillin and vinculin immunofluorescence, cells were plated on collagen-coated coverglass and were processed as described previously (Pelham and Wang 1997, Pelham and Wang 1999) using antibodies from Sigma-Aldrich.

Preparation of Polyacrylamide Substrates

Flexible polyacrylamide substrates were prepared and coated with type I collagen as described by Wang and Pelham 1998, with the following modifications: (a) a concentration of 5% acrylamide and 0.08% bisacrylamide was used; and (b) the concentration of fluorescent latex beads was increased by 6.25-fold in order to obtain a higher density of deformation vectors. The substrate had a Young's modulus of 2.4 × 104 newtons/m2, measured as in our previous studies (Lo et al. 2000). This flexibility was high enough to allow reliable determination of traction-induced deformation, but not to induce drastic changes in cell morphology or growth as reported previously with softer surfaces (Pelham and Wang 1997; Wang et al. 2000).

Microscopy

Cells plated on polyacrylamide substrates were observed with an Axiovert 100TV microscope (Carl Zeiss, Inc.). A Nikon 60× Plan-Apo water immersion objective lens was used to overcome the spherical aberration introduced by the polyacrylamide substrate. GFP-zyxin was detected with an optimized GFP filter set, and the red fluorescent beads were detected with a TRITC filter set (Chroma Technologies). A 100-W quartz halogen lamp was used for epiillumination in order to minimize radiation damage to the cell. Fluorescence images were collected using a cooled CCD camera with an EEV57 back-illuminated chip and an ST133 controller (Roper Scientific), at intervals of 1–2 min for 30–60 min. Each pixel on the camera images an area of 0.2 × 0.2 μm. At the end of recording, the cell was removed with a microneedle in order to record the distribution of beads without cellular traction forces. IRM of fixed cells on glass coverslips was performed by removing the emission filter from the fluorescence filter, and reducing the size of the epiillumination field diaphragm.

Calculation of Traction Stress and Monte Carlo Simulation

Traction stress was determined as described previously (Dembo and Wang 1999; Munevar et al. 2001). In brief, deformation of the substrate was determined as a matrix of vectors, by comparing the distribution of embedded beads in the presence and absence of the cell. The vectors were generated at a density of one per 2.25 μm2, where the deformation was at a density of at least two pixels along the x or y direction, and one per 9 μm2 elsewhere. The projected area of the cell was then divided into small quadrilaterals with a center-to-center distance of 1–2 μm. Traction stress at the center of each quadrilateral was assigned with a maximum likelihood algorithm using a supercomputer, such that the combination of traction stress across the cell yielded the observed pattern of substrate deformation (Dembo and Wang 1999). Traction stress between the centers of quadrilaterals was then generated by interpolation. After rendering the magnitude of traction stress as different intensities or colors, the distribution of traction stress was visualized as either a map of vectors or as an image. To analyze the relationship between traction stress and the intensity of zyxin, the pixel with the highest intensity of GFP-zyxin within a focal adhesion was determined and was plotted against the corresponding magnitude of traction stress.

Monte Carlo simulation was performed by assigning 16 force vectors of various magnitudes at random locations within a 35 × 35 μm square. The stiffness of the substrate was assumed to be identical to that used in the experiment. To simulate the situation in a real cell, a bias in direction was imposed such that these forces have a tendency to parallel one another in a local region and to point toward the center of the square. Exact displacement vectors of the substrate were calculated at a density of one per 2.8 μm2. Each vector was averaged with neighboring vectors within an area of 6.5 × 6.5 μm. This occurs during the actual detection of substrate deformation, based on the cross correlation of bead patterns in finite areas. Gaussian random noise equivalent to 0.3 pixel (0.065 μm) was then added to the x and y components of the displacement, and the magnitude was rounded to the nearest equivalent number of pixels. These modified displacements were then used as the basis for reconstructing the original traction field.

Results

Calculation of Traction Stress

Traction stress was determined by plating cells on collagen I–coated flexible polyacrylamide substrates, and analyzing the pattern of substrate deformation as a result of forces exerted by the cell. Although the exact cell behavior may differ from that seen on glass or plastic surfaces (Pelham and Wang 1997), it is likely to be closer to the behavior of cells migrating on flexible basement membranes or tissue surfaces. The calculation made no a priori assumption about the distribution or magnitude of traction stress, other than the confinement of traction stress within the cell boundary, and the global balance of forces and torques (Dembo and Wang 1999). This allowed us to determine the relationship between traction stress and focal adhesions in an unbiased manner.

The resolution of traction stress calculation was tested with Monte Carlo simulation. Hypothetical delta traction forces, similar in pattern and magnitude to what were observed with 3T3 fibroblasts (Dembo and Wang 1999), were applied to a defined area of a flexible surface. The deformation was calculated and degraded to mimic the loss of resolution during data collection (Materials and Methods). The modified deformation map was then treated as data for the calculation of a reconstructed traction stress distribution, which was compared with the original traction field. The results from 30 such simulations under various conditions indicated that our measurements were able to resolve pairs of delta function tractions, with a similar magnitude and orientation, separated by 5–6 μm (Fig. 1). The resolution of perpendicular forces was approximately two times better. As long as the deformation was higher than the noise, the resolution was not significantly affected by the stress magnitude.

Figure 1.

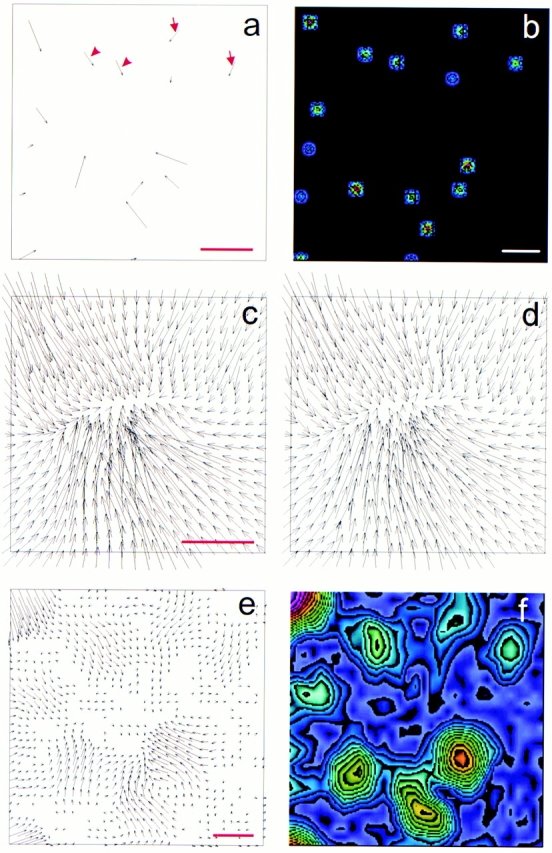
Figure 1

Open in a new tab

Monte Carlo simulation of traction stress analysis. Small patches of traction stress were first assigned at random locations within a square area (a and b). Exact deformation matrix was generated from this map at a finite resolution and density (c). After applying random noise and neighborhood averaging to mimic the resolution limit of the measurements (d), the modified deformation matrix was used to calculate the original traction stress (e and f). A pair of forces separated by ∼4.4 μm appears as a single large patch (arrowheads), whereas a pair separated by ∼8.0 μm is clearly resolved (arrows). Panels b and f show color rendering of the magnitude, with red corresponding to strong traction stress and blue corresponding to weak traction stress. Bars: (a) 4 × 106 dyn/cm2; (b) 20 μm (distance between traction forces); (c) 2 μm (substrate deformation); (e) 2 × 105 dyn/cm2 calculated traction stress.

Adhesion Plaques and Traction Stress Show Different Distributions

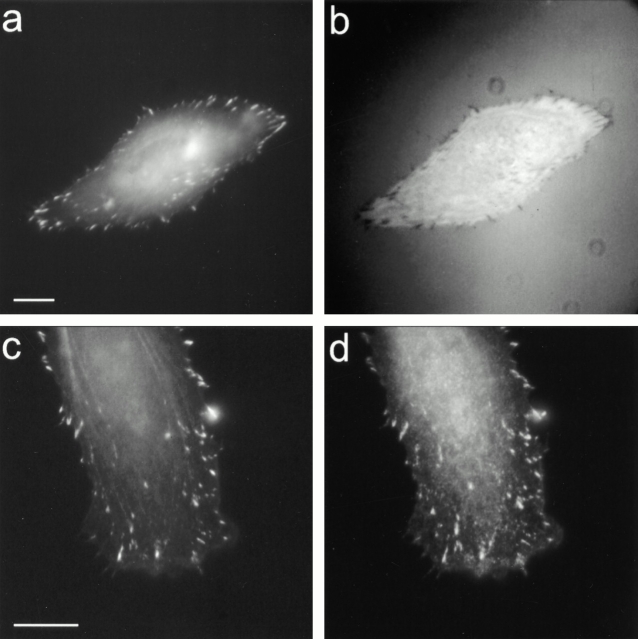
Since IRM does not work well at the interface of polyacrylamide and cell membrane, we used a transfected goldfish fibroblast line (CAR) that stably expresses GFP-zyxin (a known component of focal adhesions; Kaverina et al. 1999), for the detection of focal adhesions. When these cells were plated on glass, fluorescent plaques of GFP-zyxin correlated directly with dark plaques of focal adhesions revealed by IRM (Fig. 2, a and b). Moreover, immunostaining of these cells for paxillin (Fig. 2c and Fig. d) or vinculin (not shown), two other components of focal adhesions, showed a similar distribution as that for GFP-zyxin throughout the cell. These results are consistent with previous characterization of zyxin (Beckerle 1986, Beckerle 1997), and establish GFP-zyxin as a general marker for focal adhesions.

Figure 2.

Figure 2

Open in a new tab

GFP-zyxin as a marker for focal adhesions. Fish fin fibroblasts transfected with GFP-zyxin were plated on collagen-coated coverslips. IRM (b) shows the localization of GFP-zyxin at both large and small focal adhesions (a). Immunofluorescence staining of paxillin (d) shows a similar colocalization with GFP-zyxin (c) at the leading edge. Bars, 10 μm.

Fig. 3 shows focal adhesions of a typical migrating goldfish fibroblast, and the corresponding distribution of traction stress displayed as vectorial plots as well as pseudocolor images, with the magnitude of traction stress rendered as different colors. The general pattern of traction stress was similar to that observed with 3T3 cells (Dembo and Wang 1999). One unique feature of CAR cells is the lack of a sharp boundary between leading lamellipodia and lamella. Small, nascent focal adhesions form continuously and asynchronously in an area 10–20 μm from the leading edge, some of which develop into prominent focal adhesions that remain stationary as the cell migrates forward, whereas others disappear after a short period of time. Therefore, this region contains focal adhesions of different sizes and ages.

Figure 3.

Figure 3

Open in a new tab

Differences between the distribution of traction stress and focal adhesions. Distributions of traction stress at 0, 6, and 10 min are shown as either vector maps (a, d, and g), or color images after converting the magnitude into colors (b, e, and h). The corresponding distributions of GFP-zyxin show only a limited correlation with traction stress (c, f, and i). Some focal adhesions contain a low concentration of GFP-zyxin but generate strong forces (open arrow), whereas other focal adhesions show strong GFP-zyxin localization but generate relatively weak forces (filled arrows). Arrow in g, 105 dyn/cm2. Bar, 20 μm.

Strong traction stresses were detected near the leading edge and at the tip of the tail. Unlike forces at the tail of 3T3 cells which were sporadic and variable (Dembo and Wang 1999; Munevar et al. 2001), strong forces were consistently present at the tail of CAR cells. We suspect that this difference may be due to different density, stability, or distribution of focal adhesions in the tail region between the two cell lines. In some CAR cells, patches of strong traction also colocalized with focal adhesions along the lateral edge. However, as in 3T3 cells, the distribution of propulsive forces was limited only to the frontal region of the cell, whereas focal adhesions in the central and rear regions mediated predominantly resisting forces to cell migration. In addition, comparison between images of adhesions and traction stress indicated that there were numerous bright adhesion sites with little or no traction stress (Fig. 3, filled arrows), and that there were also patches of strong traction stress near the leading edge without a corresponding high intensity of GFP-zyxin (Fig. 3, open arrows). These differences cannot be explained by the limit in spatial resolution of traction analysis. They indicate that there is no simple relationship between the magnitude of traction stress and the size or zyxin concentration of the focal adhesion, when the whole cell is elevated.

Smaller, Fainter Plaques Exert Strong Traction Forces in the Leading Lamella

To further determine the relationship between traction stress and the intensity of GFP-zyxin, we focused on the frontal lamella region where propulsive forces for cell migration were located. Contrary to our initial speculation, scatter plots of traction stress versus zyxin intensity showed a reverse relationship. Despite the spread of the data points, due in part to the limited spatial resolution relative to the high density of focal adhesions in this region and the heterogeneity of plaques, it was clear that faint focal adhesions generally exerted stronger traction stress than did bright focal adhesions (Fig. 4 a). Analysis of the length of focal adhesions yielded a similar inverse relationship with traction stress (Fig. 4 b). From the high magnification view of the leading lamella (Fig. 4 d), it was also clear that traction stress was not simply a function of the distance from the leading edge. Furthermore, when similar analysis was applied to the tail region, the inverse relationship between GFP-zyxin intensity and traction stress was no longer detected (Fig. 4 c).

Figure 4.

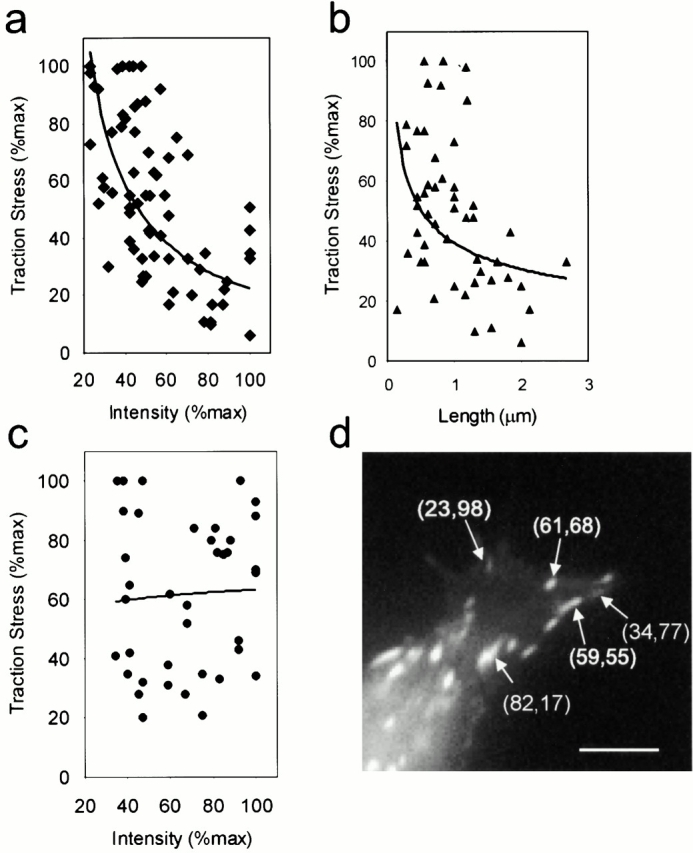
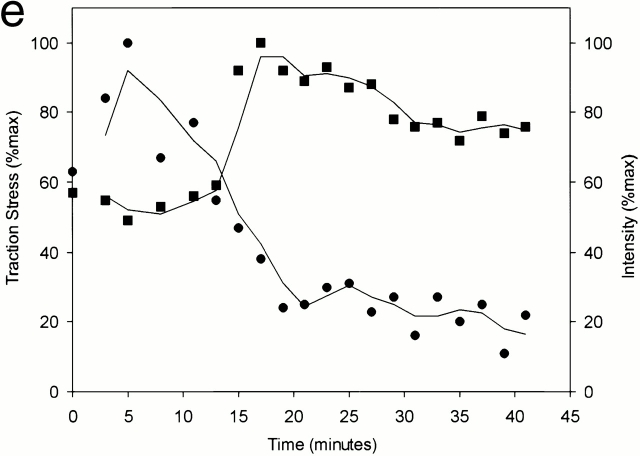
Figure 4

Figure 4

Figure 4

Open in a new tab

Relationship between the intensity of GFP-zyxin and traction stress. Relationship between the intensity of GFP-zyxin at focal adhesions and the corresponding traction stress is shown as scatter plots in the leading lamella (a) or tail region (c). Each point represents a single focal adhesion and is presented as percentage of the maximum within a given cell. The propulsive traction stress in the leading lamella shows an inverse relationship with the intensity of GFP-zyxin (a), whereas the resistive traction at the tail shows no such relationship (c). The plot was generated with measurements from five cells. The relationship between the long dimension of the focal adhesion plaque and traction stress shows a similar inverse relationship in the leading lamella (b). Panel d shows a high magnification image of GFP-zyxin in a leading lamella, with several focal adhesions labeled with their respective intensity (first number in parenthesis) and traction stress (second number in parenthesis), both represented as percentage of the maximum. The intensity of GFP-zyxin at a focal adhesion (▪) increases after its initial appearance to reach a plateau, whereas the corresponding traction stress (•) shows a brief increase followed by a steady decline (e). Both the fluorescence intensity and traction stress are indicated as percentage of the maximum for that cell. Panel f shows images of this process in a separate cell. Transient traction stress appears at a nascent focal adhesion, which continues to develop as the traction stress decreases to the background level (arrowheads). Some focal adhesions disappear concomitantly with the decrease of traction stress (arrows). The color bar shows the relationship between colors and the magnitude of traction stress in dyn/cm2. Time in minutes is indicated. Bar, 5 μm.

Traction Stress Diminishes during the Maturation of Focal Adhesion

The reverse relationship between traction stress and GFP-zyxin in the leading lamella suggests that traction forces may be coupled to the maturation of focal adhesions, during which the size and protein concentration increase. Therefore, we followed temporal changes of traction stress and the intensity of GFP-zyxin at specific nascent focal adhesions during their maturation. By studying isolated focal adhesions one at a time, we were also able to avoid the problem associated with the heterogeneity of focal adhesions. Fig. 4e and Fig. f, shows a typical result of such temporal analysis. The traction stress increased briefly after the initial appearance of a focal adhesion, reaching a peak 5 min after the initial detection, then decreased to a background, whereas the intensity of GFP-zyxin increased continuously to reach a plateau (Fig. 4 e). This behavior was observed with a total of 15 nascent plaques analyzed for a period of 30–45 min.

Discussion

Our results demonstrate that mechanical interactions between focal adhesions and the substrate undergo both quantitative and qualitative changes after their initial appearance near the leading edge. We observed that nascent focal adhesions, which have been referred to as focal complexes in some studies (Small et al. 1998), apply strong propulsive traction to drive cell migration. Subsequently, this force decreases, whereas the size of many focal adhesions continues to increase as they mature into large plaques. Eventually most of the stationary focal adhesions become centrally localized in a migrating cell and, despite their persistent substrate adhesion, exert only resistive forces against forward migration. Consistent with these results, observations of spontaneous and induced local release indicated that anterior propulsive forces are generated by active contractions, whereas forces at the tail reflect passive resistance to the frontal forces (Munevar, S., Y.-l. Wang, and M. Dembo, manuscript in preparation). The resistive loads are likely distributed among central/posterior adhesion sites and may show a positive correlation with the size of focal adhesions under certain conditions, although such a relationship was not detectable in the present study except for the strong forces at the tip of the tail.

Although several models have been proposed to explain the coordination of fibroblast migration, most of them are vague with respect to cell–substrate mechanical interactions. Although it is commonly assumed that such interactions are mediated by focal adhesions, our observations suggest a more complex relationship between adhesions and propulsive forces during the cyclic process of cell migration (Fig. 5). The process begins with the extension of the lamellipodia and the engagement of the integrins with the extracellular matrix. Subsequent recruitment of cytoskeletal components at nascent focal adhesions (Miyamoto et al. 1995) causes the generation of a pulse of propulsive traction force on the substrate. These focal adhesions may also be mobile under some conditions (Davies et al. 1994; Smilenov et al. 1999; Zamir et al. 2000). The plaques then either disassemble or mature into large focal adhesions, whose function changes from active propulsion into passive anchorage. This mechanism has several significant advantages. First, a division of labor between propulsive adhesions and anchorage adhesions at the leading edge, which was speculated previously (Rottner et al. 1999), would allow the cell to migrate while maintaining its spread morphology. Second, since cell migration is driven by transient pulses of propulsive forces in the leading lamella, minimal coordination is required among mechanical interactions at a multitude of focal adhesions. Finally, our mechanism facilitates rapid reorientation in response to environmental cues, simply by shifting the assembly of nascent focal adhesions to a new protrusive region. Because large, mature focal adhesions take a long time to assemble and are essentially fixed in orientation and position (Smilenov et al. 1999), it is very difficult to see how the traction forces and cell migration can change and adapt if such mature adhesions are responsible for propelling forward movement.

Figure 5.

Figure 5

Open in a new tab

Relationship between focal adhesions and mechanical forces during fibroblast migration. The formation of focal adhesions, accompanied by the generation of a pulse of propulsive forces, drives the forward movement. Cell migration is sustained by repeated formation of nascent focal adhesions, and thus repeated pulses of propulsive forces. Mature focal adhesions play only a passive role in anchoring cells to the substrate.

It will be important to understand the mechanism for the regulation of propulsive forces at nascent focal adhesions. Because actin filaments remain associated with mature focal adhesions, the contractile forces are either turned off or become disengaged from the extracellular matrix (Smilenov et al. 1999), e.g., through absorption of the forces by a rigid cortex or other cytoskeletal structures. More importantly, the transition in mechanical characteristics during the maturation of focal adhesion may not occur spontaneously, but in response to specific signals. The discovery of transient contacts between microtubules and newly assembled focal adhesions is particularly relevant in this regard (Bershadsky et al. 1996; Kaverina et al. 1998, Kaverina et al. 1999). Furthermore, it is becoming clear that focal adhesions are not invariable but heterogeneous structures, showing intriguing changes in their morphology, protein composition, and phosphorylation states in response to chemical or physical parameters (Zamir et al. 1999, Zamir et al. 2000; Katz et al. 2000). Although zyxin, vinculin, and paxillin appear to be present as fundamental building blocks, it is likely that other proteins may correlate positively with propulsive forces, and therefore play a role in the regulation of cell–substrate mechanical interactions. A detailed account of such changes in relation to traction forces would likely yield significant insights into the mechanism of fibroblast migration.

Acknowledgments

The authors wish to thank the Boston University Center for Scientific Computing for the use of their supercomputer facilities.

This study was supported by grants from the National Institutes of Health to Y.-l. Wang, K.A. Beningo, and M. Dembo.

Note added in proof: A recent paper (Balaban, N.Q., U.S. Schwartz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky, L. Addadi, and B. Geiger. 2001. Force and focal adhesion assembly: a close relationship studied using elastic micropatterened substrates. Nat. Cell Biol. 3:466–473) describes the measurements of traction forces in relatively stationary cells. See In Brief for a discussion of the relationship between the two studies.

Footnotes

This work was presented at the 43rd Annual Meeting of the American Society of Cell Biology in San Francisco, CA, December, 2000.

Abbreviations used in this paper: GFP, green fluorescent protein; IRM, interference reflection microscopy.

References

  1. Abercrombie M., Dunn G.A. Adhesions of fibroblasts to substratum during contact inhibition observed by interference reflection microscopy. Exp. Cell Res. 1975;92:57–62. doi: 10.1016/0014-4827(75)90636-9. [DOI] [PubMed] [Google Scholar]
  2. Beckerle M.C. Identification of a new protein localized at sites of cell–substrate adhesion. J. Cell Biol. 1986;103:1679–1687. doi: 10.1083/jcb.103.5.1679. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Beckerle M.C. Zyxin, zinc fingers at sites of cell adhesions. Bioessays. 1997;19:949–957. doi: 10.1002/bies.950191104. [DOI] [PubMed] [Google Scholar]
  4. Bershadsky A., Chavsovsky A., Becker E., Lyubimova A., Geiger B. Involvement of microtubules in the control of adhesion-dependent signal transduction. Curr. Biol. 1996;6:1279–1289. doi: 10.1016/s0960-9822(02)70714-8. [DOI] [PubMed] [Google Scholar]
  5. Bray, D. 2001. Cell Movement: From Molecules to Motility. M. Day, editor. 2nd ed. Garland Publishing, New York. 400 pp.
  6. Burridge K., Chrzanowska-Wodnicka M. Focal adhesions, contractility and signaling. Annu. Rev. Cell Biol. 1995;12:463–519. doi: 10.1146/annurev.cellbio.12.1.463. [DOI] [PubMed] [Google Scholar]
  7. Burton K., Taylor D.L. Traction forces of cytokinesis measured with optically modified elastic substrata. Nature. 1997;385:450–454. doi: 10.1038/385450a0. [DOI] [PubMed] [Google Scholar]
  8. Davies P.F., Robotewskyj A., Griem M.L. Quantitative studies of endothelial cell adhesiondirectional remodeling of focal adhesion sites in response to flow forces. J. Clin. Invest. 1994;93:2031–2038. doi: 10.1172/JCI117197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dembo M., Wang Y.-l. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 1999;76:2307–2316. doi: 10.1016/S0006-3495(99)77386-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Elson E.L., Felder S.F., Jay P.Y., Kolodney M.S., Pasternak C. Forces in cell locomotion. Biochem. Soc. Symp. 1997;65:299–314. [PubMed] [Google Scholar]
  11. Galbraith C.G., Sheetz M.P. Forces on adhesive contacts affect cell function. Curr. Opin. Cell Biol. 1998;10:566–571. doi: 10.1016/s0955-0674(98)80030-6. [DOI] [PubMed] [Google Scholar]
  12. Harris A.K., Wild P., Stopak D. Silicone rubber substrataa new wrinkle in the study of cell locomotion. Science. 1980;208:177–179. doi: 10.1126/science.6987736. [DOI] [PubMed] [Google Scholar]
  13. Izzard C.S., Lochner L.R. Cell-to-substrate contacts in living fibroblastsan interference reflection study with an evaluation of the technique. J. Cell Sci. 1976;21:129–159. doi: 10.1242/jcs.21.1.129. [DOI] [PubMed] [Google Scholar]
  14. Katz B.Z., Zamir E., Bershadsky A., Kam Z., Yamada K.M., Geiger B. Physical state of the extracellular matrix regulates the structure and molecular composition of cell-matrix adhesions. Mol. Biol. Cell. 2000;11:1047–1060. doi: 10.1091/mbc.11.3.1047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kaverina I., Rottner K., Small J.V. Targeting, capture, and stabilization of microtubules at early focal adhesions. J. Cell Biol. 1998;142:181–190. doi: 10.1083/jcb.142.1.181. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kaverina I., Krylyshkina O., Small J.V. Microtubule targeting of substrate contacts promotes their relaxation and dissociation. J. Cell Biol. 1999;146:1033–1043. doi: 10.1083/jcb.146.5.1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lauffenberger D.A., Horwitz A.F. Cell migrationa physically integrated molecular process. Cell. 1996;84:359–369. doi: 10.1016/s0092-8674(00)81280-5. [DOI] [PubMed] [Google Scholar]
  18. Lo C.-M., Wang H.-B., Dembo M., Wang Y.-l. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Martin P. Wound healingaiming for perfect skin regeneration. Science. 1997;276:75–81. doi: 10.1126/science.276.5309.75. [DOI] [PubMed] [Google Scholar]
  20. Miyamoto S., Akiyama S.K., Yamada K.M. Integrin functionmolecular hierarchies of cytoskeletal and signaling molecules. J. Cell Biol. 1995;131:791–805. doi: 10.1083/jcb.131.3.791. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Munevar S., Wang Y.-l., Dembo M. Traction force microscopy of migrating normal and H-ras transformed 3T3 fibroblasts. Biophys. J. 2001;80:1744–1757. doi: 10.1016/s0006-3495(01)76145-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Oliver T., Jacobson K., Dembo M. Design and use of substrata to measure traction forces exerted by cultured cells. Methods Enzymol. 1998;298:497–521. doi: 10.1016/s0076-6879(98)98042-9. [DOI] [PubMed] [Google Scholar]
  23. Pelham R.J., Wang Y.-l. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 1997;94:13661–13665. doi: 10.1073/pnas.94.25.13661. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Pelham R.J., Wang Y.-l. High resolution detection of mechanical forces exerted by locomoting fibroblasts on the substrate. Mol. Biol. Cell. 1999;10:935–945. doi: 10.1091/mbc.10.4.935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Rottner K., Hall A., Small J.V. Interplay between Rac and Rho in the control of substrate contact dynamics. Curr. Biol. 1999;9:640–648. doi: 10.1016/s0960-9822(99)80286-3. [DOI] [PubMed] [Google Scholar]
  26. Schoenwaelder S.M., Burridge K. Bidirectional signaling between the cytoskeleton and integrins. Curr. Opin. Cell Biol. 1999;11:274–286. doi: 10.1016/s0955-0674(99)80037-4. [DOI] [PubMed] [Google Scholar]
  27. Sheetz M.P., Felsenfeld D.P., Galbraith C.G. Cell migrationregulation of force on extracellular-matrix-integrin complexes. Trends Cell Biol. 1998;8:51–54. doi: 10.1016/s0962-8924(98)80005-6. [DOI] [PubMed] [Google Scholar]
  28. Small J.V., Rottner K., Kaverina I., Anderson K.I. Assembling an actin cytoskeleton for cell attachment and movement. Biochim. Biophys. Acta. 1998;1440:271–281. doi: 10.1016/s0167-4889(98)00080-9. [DOI] [PubMed] [Google Scholar]
  29. Smilenov L.B., Mikhailov A., Pelham R.J., Mercantonio E.E., Gundersen G.G. Focal adhesion motility revealed in stationary fibroblasts. Science. 1999;286:1172–1174. doi: 10.1126/science.286.5442.1172. [DOI] [PubMed] [Google Scholar]
  30. Wang H.-B., Dembo M., Wang Y.-l. Substrate flexibility regulates growth and apoptosis of normal but not transformed cells. Am. J. Physiol. 2000;279:C1345–C1350. doi: 10.1152/ajpcell.2000.279.5.C1345. [DOI] [PubMed] [Google Scholar]
  31. Wang Y.-l., Pelham R.J. Preparation of a flexible, porous polyacrylamide substrate for mechanical studies of cultured cells. Methods Enzymol. 1998;298:489–496. doi: 10.1016/s0076-6879(98)98041-7. [DOI] [PubMed] [Google Scholar]
  32. Zamir E., Katz B.Z., Aota S., Yamada K.M., Geiger B., Kam Z. Molecular diversity of cell-matrix adhesions. J. Cell Sci. 1999;112:1655–1669. doi: 10.1242/jcs.112.11.1655. [DOI] [PubMed] [Google Scholar]
  33. Zamir E., Katz M., Posen Y., Erez N., Yamada K.M., Katz B.Z., Lin S., Lin D.C., Bershadsky A., Kam Z., Geiger B. Dynamics and segregation of cell-matrix adhesions in cultured fibroblasts. Nat. Cell Biol. 2000;2:191–196. doi: 10.1038/35008607. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Cell Biology are provided here courtesy of The Rockefeller University Press

RESOURCES