Chromosome Pairing Does Not Contribute to Nuclear Architecture in Vegetative Yeast Cells

Abstract

There are several reports of a closer-than-random colocalization of homologous chromosomes in the vegetative nuclei of diploid budding yeast. Here, we studied by fluorescence in situ hybridization (FISH) the nuclear distribution of chromosomes and found a slight tendency toward closer proximity between homologous (allelic) loci than between any nonhomologous chromosomal regions. We show that most of this preferential association is not due to vegetative (also known as somatic) pairing but is caused by the polar orientation of interphase chromosomes (Rabl orientation). We quantified the occasional loss of detectable fluorescence signals that is inherent to the FISH method. Signal loss leads to the occurrence of a single signal that may be misinterpreted as the close association of two homologous chromosomal sites. The nuclear distribution of homologous loci, when corrected for the influence of nuclear architecture and methodological faults, was not different or was only marginally different from a random relative positioning as predicted by computer simulation. We discuss here several possibilities for the residual homologous proximity that do not invoke homology-dependent vegetative pairing, and we conclude that, in diploid budding yeast, constitutive vegetative pairing is a negligible factor for the organization of the interphase nucleus.

Somatic pairing, i.e., the pairing or association of homologous chromosomes in nonmeiotic cell types, was first described in Diptera (46) and has since then been well established in this order and most thoroughly studied in Drosophila melanogaster (13, 19, 24, 39). For many decades there has been a controversy among cytologists as to whether somatic or vegetative pairing is common, although less conspicuous than in Drosophila, in a wider range of organisms (for reviews, see references 1, 3, 8, 31, and 45).

Whereas the literature on cases of presumptive “somatic pairing” is abundant, contributions which deny its existence are rare. (The term “somatic pairing” is sometimes used to designate pairing or association of homologous chromosomes in vegetative [i.e., nonmeiotic] yeast cells, although, strictly speaking, yeast does not have somatic cells. It will be used here when reference to this literature is made.) This is because “observations on real or assumed chromosome pairing are much more apt to be published than observations showing a random chromosome arrangement which most cytologists have anyway taken for granted” (48). However, Vourc'h et al. (49) and Cremer et al. (9), who studied chromosome distribution in various cell types of humans and mouse lymphocytes, respectively, explicitly reported the absence of somatic pairing.

The search for somatic pairing was not least fueled by the expectation that it would confer certain advantages to organisms (see reference 30). One of these advantages would be an improved ability to carry out recombinational repair of DNA lesions. Whereas in replicated cells the DNA sister molecule can be used as a template for recombinational repair (27), in G₀/G₁ unreplicated diploid cells recombinational repair can occur by recruiting the homologous chromosome (for a review, see reference 14). In the case of damage it would be advantageous if the homologues were closely associated with the affected chromosome and thereby most easily available for repair.

Another possible advantage of somatic pairing could be the mutual influencing of transcriptional activity of allelic copies of genes. This regulation of transcription (probably by the physical contact with promoters or enhancer sequences in trans) which has come to be known as transvection or trans sensing, was discovered in Drosophila but has been proposed to exist also in other organisms (for reviews, see references 22 and 51). Finally, it has been hypothesized that a gradual increase of the juxtapositioning of homologous chromosomes over several generations preceding entry into meiosis might promote homologous pairing in meiosis (45).

Recently, the occurrence of nonmeiotic pairing has been reported in budding yeast. It was found to occur in a high proportion of premeiotic nuclei by Weiner and Kleckner (50). Also, Loidl et al. (37) observed the fusion of homologous chromosomal loci under premeiotic starvation conditions. Somatic or (to call it precisely) vegetative homologous pairing was subsequently claimed to occur also in interphase nuclei of vegetatively growing cultures (29; see also references 4, 5, and 6). On the other hand, a very low rate of fusion of homologous signals in interphase nuclei was reported by Guacci et al. (20) and was interpreted by these authors as being due to random contacts. Also, Lichten and Haber (33) questioned somatic/vegetative pairing since they found mitotic recombination of homologous sequences at allelic and ectopic chromosomal sites to be equally frequent. Moreover, vegetative pairing would seem to be in conflict with the dynamic behavior of chromosomes in interphase, as revealed by in vivo time-lapse microscopy (15).

Here, we wanted to test whether homologous chromosomal loci show vegetative pairing in interphase nuclei of diploid Saccharomyces cerevisiae. To do this, we used fluorescence in situ hybridization (FISH) to compare distances between signals at homologous loci to distances between signals at nonhomologous chromosome positions. Shorter average homologous than heterologous distances would indicate a preferential association of homologous chromosomal sites. We simulated the expected random distribution of chromosomal loci in spread yeast nuclei by a computer model and sought to determine whether the experimentally obtained relative chromosome distances deviate from distances obtained for randomly distributed chromosomes. We also discuss alternative explanations for the observed proximity between homologous chromosomal loci that do not invoke a homology recognition and pairing process but are based on the gathering of chromosomes or chromosome regions with similar properties, which may be dictated by spatial constraints within the nucleus.

MATERIALS AND METHODS

Stains, cell culture and preparation.

The yeast strains used in the present study are listed in Table 1. All strains except W303 are SK1 derivatives. To obtain cells for cytological investigation, liquid yeast extract-peptone-dextrose (YPD) was inoculated with 2 × 10⁶ to 5 × 10⁶ cells/ml from a fresh culture on a plate. Cells were grown at 30°C to a density of ca. 10⁷ cells/ml (late log phase) or to maximum density (stationary phase; usually at least 2 × 10⁸ cells/ml.).

TABLE 1.

Yeast strains used in this study

Strain	Relevant genotype	Source or reference
SK1 diploid	HO/HO	28
FKY74	Homozygous MATa; MATa/MATaho::LYS2/ho::LYS2 lys2/lys2 leu2::hisG/leu2::hisG his4/his4 ura3/ura3	34
W303 (FKY688)	MATa/MATα ura3-1/ura3-1 trp1-Δ2/trp1-Δ2 leu2-3,112/leu2-3,112 his3-11/his3-11 ade2-1/ade2-1 can1-100/can1-100	F. Klein
AMP115	MATa/α ho::LYS2/ho::LYS2 ura3/ura3 leu2::hisG/leu2::hisG trp1::hisG/trp1::hisG lys2/lys2 ime1-12::TRP1/ime1-12::TRP1	2
VG72-DM	MATa/MATα leu2 his3 ura3-MATa-URA3/ura3 TRP1/trp1 MET10/met10 (monosomic for I and III)	21

Meiotic cells were obtained by first growing cultures up to a density of 2 × 10⁷ cells/ml in glucose-free acetate medium (43). This presporulation growth took ca. 14 h. Cells were then transferred to 2% potassium acetate (sporulation medium) and incubated at 30°C for 4 h at a density of 4 × 10⁷ cells/ml.

In most of the experiments cells were fixed prior to spheroplasting and application of detergent (procedure C [25]). By this method good spatial resolution of the nuclei, as well as a reasonable maintenance of cell integrity, is obtained.

For the preparation of unspread (three-dimensionally preserved) nuclei, a modified protocol based on a previously described technique (17) was used. In short, cells from a 5-ml yeast culture were washed in YPD plus 1.1 M d-sorbitol (YPD-S) and then resuspended in 500 μl of YPD-S supplemented with 10 μl of 0.5 M dithiothreitol and 100 μg of Zymolyase 100T (Seikagaku Co., Tokyo, Japan). After digestion of the cell walls, cells were washed twice in YPD-S, fixed in 3.7% formaldehyde in YPD-S for 20 min at room temperature, washed two to three times in YPD-S, and finally resuspended in ∼100 μl of YPD-S. The cell suspension was dropped onto slides and left to dry at room temperature for 5 to 10 min. Slides were immersed in methanol at −20°C for 6 min and then in acetone at −20°C for 30 s, in phosphate-buffered saline (PBS) plus 3.7% formaldehyde for 20 min at room temperature, and finally in PBS supplemented with 0.1% Tween 20 for 5 min at room temperature. The slides were incubated overnight in 4× SSC (1× SSC is 0.15 M NaCl plus 0.015 M sodium citrate) supplemented with 0.1% Tween 20 at room temperature, dehydrated in an ascending ethanol series (70, 90, and 96%), and air dried. For the use with FISH (see below), the preparations were denatured in 70% formamide in 2× SSC at 72°C for 5 min, dehydrated again, and air dried.

Probes for FISH.

FISH probes for regions on chromosome arms VIIL, VIIR, and XVIL 200 and 400 kb away from the corresponding centromere, for a segment on chromosome arm IIIR distal to the HMR locus, and for a site adjacent to the ribosomal DNA tract on chromosome XII were produced by long-range PCR by using the Expand long template PCR system (Roche, Basel, Switzerland) according to the manufacturer′s instructions. Appropriate primers were selected by consulting the Saccharomyces Genome Database (7) and checked with the basic local alignment search tool (BLAST) at the National Center of Biotechnology Information (http://www.ncbi.nlm.nih.gov/BLAST/) for the absence of major repeated DNA elements. For template sizes of ca. 12 kb, we used the following PCR conditions: 2 min at 94°C; 10 cycles of 10 s at 94°C, 30 s at 58°C, and 10 min at 68°C; 20 cycles of 10 s at 94°C, 30 s at 58°C, and 10 min at 68°C; with a prolongation of 20 s per cycle and a final extension of an additional 10 min. The amplified PCR products were run on a 0.7% agarose gel, checked for appropriate length, and purified with the QUIAEX II gel extraction kit (Qiagen GmbH, Hilden, Germany) according to the manual provided by the manufacturer.

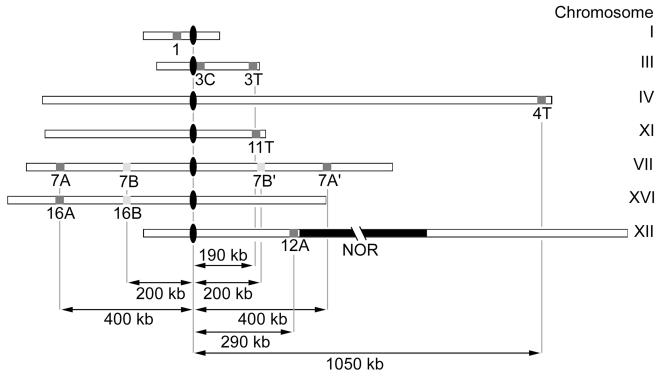
For loci on chromosome arms IVR and XIR, a cosmid clone (clone 70902) and a λ-clone (clone 70815) from the American Type Culture Collection (Manassas, Va.) were used as hybridization probes. The chromosomal locations of FISH probes are shown in Fig. 1. Specificity of probes was confirmed by FISH to condensed pachytene chromosomes (not shown).

FIG. 1.

Map of the FISH probes used (gray) and their genomic distances (in kilobases) from the respective centromeres (CEN). NOR indicates the ∼100 repeats of the RDN locus (not drawn to scale).

FISH.

The probes were labeled by nick translation with Cy3-dUTP (red) (Amersham Pharmacia Biotech UK, Ltd., Little Chalfont, England) or fluorescein-12-dUTP (green; Roche) as described earlier (36). Labeled probes were dissolved in hybridization solution (50% formamide, 10% dextran sulfate, 2× SSC) to a final concentration of ca. 10 ng/μl. After 5 min of denaturation at 95°C, the probes were dropped onto preparations, denatured for 10 min at 80°C, and hybridized for at least 36 h at 37°C. Posthybridization washes were carried out in 50% formamide in 2× SSC (37°C), 2× SSC (37°C), and 1× SSC (room temperature) for 5 min each. Finally, slides were mounted under a coverslip in Vectashield mounting medium for fluorescence (Vector Laboratories, Inc., Burlingame, Calif.) supplemented with 1 μg of DAPI (4′,6′-diamidino-2-phenylindole)/ml as a DNA-specific counterstain.

Microscopy and evaluation.

Preparations were evaluated by using a Zeiss Axioskop epifluorescence microscope equipped with single-band-pass filters for the excitation of red, green, and blue. Images were obtained by using a cooled black and white charge-coupled device camera controlled by IPLab Spectrum software (Scanalytics, Fairfax, Va.). Slides were encoded by one of the authors before being blindly evaluated by another. Intact nuclei were preselected in the DAPI-stained image. Grossly jagged or deformed nuclei were excluded from analysis. Three-dimensional distance measurements were performed on stacks of 0.2-μm optical sections.

Calculation and graphical representation of the relative positions of homologous versus nonhomologous chromosomal loci within nuclei.

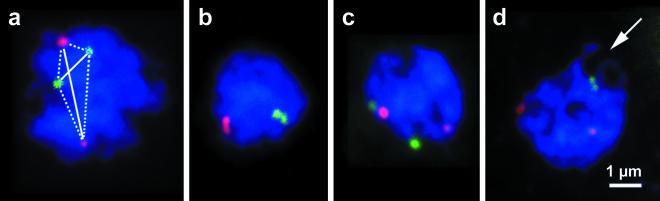
In diploid nuclei, two chromosomal loci were differentially labeled by FISH. This generally produced two homologous signal pairs of different colors (Fig. 2). The two distances between the respective homologous pairs were measured. Also, the four distances between all possible pairs of different (nonhomologous) FISH dots were measured (for the procedure, see reference 50), and the averages of both the homologous and the heterologous distances were calculated. The difference of the mean heterologous distances minus the mean homologous distances was calculated and expressed as a fraction of the nuclear diameter (calculated as the mean of the largest and the smallest diameters). The reason for this normalization is to account for different nuclear sizes. Throughout this study, we refer to this normalized difference of the average heterologous and average homologous distances as “d.” A positive d value indicates that in this nucleus the homologous chromosomal loci are in closer proximity than the heterologous loci. For each experiment, 100 nuclei (50 from two separate cultures each) were evaluated in this way and ranked according to increasing values of d. In the resulting graphs, the rank is given on the abscissa (x axis), and the ordinate represents the corresponding value d. Therefore, “many” datum points (i.e., nuclei) showing positive values of d indicated a tendency of homologous signals to be in closer proximity than heterologous ones. This will be quantified on the basis of the mathematical model.

FIG. 2.

Examples of FISH signals in semispread diploid yeast interphase nuclei which were used to determine the relative positions of chromosomal regions by measuring the two homologous (solid lines in panel a) and four homologous (broken lines in panel a) distances (see also reference 50). Equally colored dots (red-red and green-green) denote homologous chromosomal regions. (b) Both pairs of homologous signals associated. (c) One pair of nonhomologous signals associated. (d) Association of NOR-linked loci (green) is brought about by the fusion of nucleoli. The arrow denotes the single fused nucleolus. Blue, DAPI-stained chromatin.

Some of the data are presented in graphs according to Weiner and Kleckner (50). Here, the two homologous distances and the four nonhomologous distances are each plotted according to increasing values irrespective of their affiliation to a particular nucleus. Deviating from the presentation mode by Weiner and Kleckner (50), the distances are expressed as ratios to the nuclear diameter as described above. In these graphs, the distances between homologous signals (on the ordinate) show a slower increase for increasing rank (on the abscissa) than the distances between heterologous signals if vegetative associations prevail.

Computer simulations of the intranuclear distribution of chromosomal loci.

The positions of two pairs of chromosomes, randomly distributed in a spherical nucleus, after projection on a plane, were modeled by generating four random points on a circular disk of radius 1 as described below and partitioning them randomly into two homologous pairs. The two distances between the homologous points were then calculated and averaged, and the distances between all four possible pairs of nonhomologous points were calculated and averaged. This procedure was repeated many times, yielding a distribution of homologous and nonhomologous distances. Also, the distribution of the difference in the average distance among nonhomologous pairs and the average distance among homologous pairs within a nucleus was calculated. These distributions were ranked, and the quantities of interest (e.g., the mean) were calculated.

The orthogonal projection of a uniform distribution on a sphere of radius 1 to a circular disk of the same radius was constructed by using polar coordinates (r,φ) as follows. Projecting a sphere to a disk attaches a weight of (1 − r²)^1/2 to every point at distance r from the center. Since the circumference of a circle of radius r is proportional to r and a density must integrate to unity, the density function of r that produces our distribution is f(r) = 3r(1 − r²)^1/2. Therefore, the cumulative density function is F(r) = 1 − (1 − r²)^3/2 and, by inversion, the desired random values of r are generated as r = (1 − x^2/3)^1/2, where x is drawn from a uniform distribution on the interval (0, 1). The random values of φ are obtained from φ = 2πy, with y uniformly distributed between 0 and 1. Each such constructed random pair (r,φ) was then transformed to Euclidean coordinates (x₁, x₂). These points represent the projected positions of randomly distributed chromosome sites in the nucleus.

To compare the measured and simulated distributions of chromosome sites, we combined experimentally obtained and simulated curves in a single graph. The shaded area displays a two-sided numerically determined 90% confidence interval in the following sense: 1,000 numerical experiments, each with 100 nuclei, were simulated. For each experiment, the d values were calculated and ranked. For each given rank, the upper bound of the shaded area is the 95% quantile of the 1,000 d values having this rank, the lower bound is the 5% quantile. However, this does not necessarily imply that any of the 1,000 curves must lie completely within the shaded region. Clearly, experimental curves lying completely in the shaded area are in accordance with the null hypothesis of a random spatial distribution chromosomal loci within nuclei. We note that the determined upper and lower bounds are nearly unchanged if different sets of 1,000 numerical experiments of this kind are performed (results not shown).

RESULTS

Simulation of random distribution of homologous chromosomal loci by a computer model.

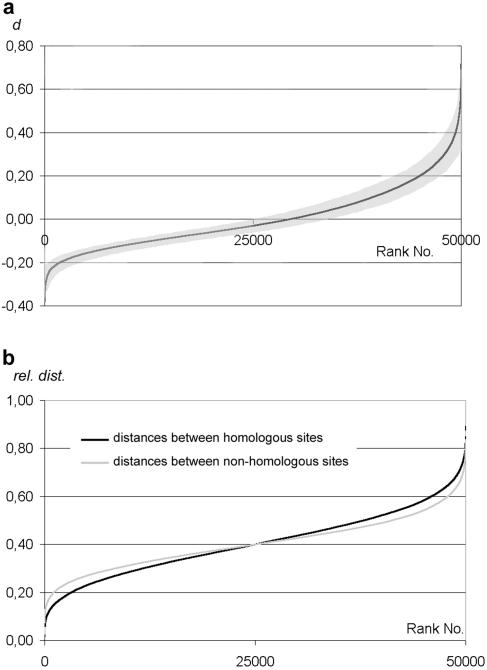
To test whether homologous sequences are on average closer together than nonhomologous sequences, distances between differently labeled homologous and nonhomologous FISH signals were measured and compared (Fig. 2). As a means to decide whether experimentally obtained data on the relative positioning of homologous chromosomal loci do indicate preferential association of homologues or reflect the random distribution of homologous chromosomes within nuclei, we simulated the random distribution of pairs of loci inside a sphere by using a computer model (see Materials and Methods). To do this, we calculated the distances of four randomly distributed points that were randomly divided in two homologous pairs, within the two-dimensional projection of a sphere (see Materials and Methods). Iterative runs of this model provide curves for random positioning of homologous FISH signals that can be directly compared to the curves for the observed distributions. Figure 3a shows a graph depicting an ideal random relative distribution of homologous points, plotted from 50,000 runs. Also shown is the area occupied by 90% of 1,000 iterations of the simulation with 100 datasets each. This area defines the 90% confidence interval which is shown for comparison in the graphs with experimental data throughout this study.

FIG. 3.

Graphs of a simulated ideal random relative distribution of homologous points plotted from 50,000 runs. (a) Distances between homologous and heterologous signals are represented as the difference d between the mean heterologous distances minus mean homologous distances within a nucleus (y axis) and ranked according to increasing d value. Nuclei where the mean homologous distance is smaller than the mean heterologous distance (i.e., where homologous loci are on average in closer vicinity than heterologous loci) are represented by a “d” (which is expressed as a percentage of the nuclear diameter) > 0. Also shown is the 90% confidence interval (shaded area) from 1,000 runs of 50 simulations each. All subsequent graphs depicting homologous versus heterologous distances follow this scheme. (b) Graphic representation of the same simulation according to Weiner and Kleckner (50). For each nucleus, the two homologous distances and the four nonhomologous distances were averaged and then ranked according to increasing values irrespective of their affiliation to a particular nucleus. Deviating from the graphs in (50), the distances are expressed as ratios to the nuclear diameter as described above.

An interesting feature of the simulation is that if the loci are randomly distributed within a sphere, there are more nuclei with a negative d value than with a positive d value (the abscissa is not crossed at 50%). This is due to the fact that there exist only two homologous distances but four heterologous distances, and the cases with all four heterologous distances being large are less frequent than those with two large homologous distances. The way in which distances between homologous versus nonhomologous loci are compared (see Materials and Methods) leads to an inherently larger difference in nuclei for which homologous distances are shorter than heterologous ones than in the reverse case. The consequence is that there are more than 50% datasets (i.e., “nuclei”) where the difference d of mean nonhomologous distances − homologous distances is a negative value (Fig. 3a). To see whether this bias is also reflected by the graphical format used for depiction of pairing in previous reports (see, for example, references 6, 32, 42, and 50) (see Materials and Methods), the same simulation is presented in this format in Fig. 3b. It was found that the curve representing the averaged homologous distances is slightly steeper than the curve representing the averaged nonhomologous distances (Fig. 3b). We note, however, that the average value of d in our simulation model is always very close to zero.

Assessment of the influence of the Rabl orientation on the preferential association of homologous loci.

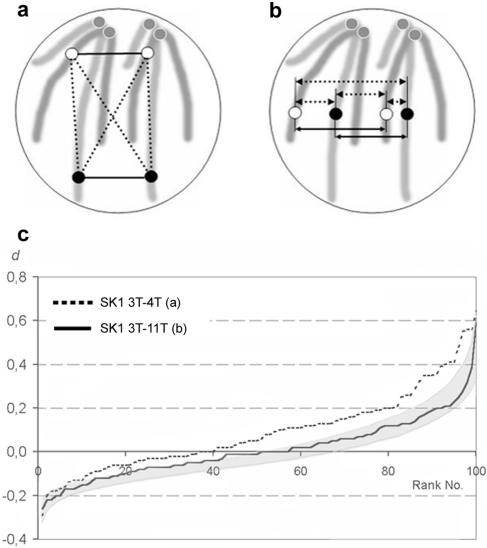
In budding yeast, as in many other organisms, centromeres are clustered near one pole of the interphase nucleus, and chromosome arms extend toward the opposite pole. This polarized organization of chromosomes is known as the Rabl orientation (see reference 26). As a consequence of the Rabl orientation, loci at different centromere distances would be assigned to positions at different nuclear latitudes. If nonhomologous loci had different genomic distances (in base pairs) from the centromeres, they would be separated within nuclei, resulting in a greater distance between heterologous than between homologous FISH signals (Fig. 4a). This might falsely suggest homologous pairing (see references 25 and 26 and Discussion).

FIG. 4.

Influence of the Rabl orientation on the association of chromosomal loci. (a) If Rabl orientation has an influence on the relative distances between homologous and nonhomologous loci, nonhomologous loci at different distances from the centromeres would on average be more distantly separated in interphase than homologous loci. (b) There should be no Rabl-induced bias toward longer nonhomologous distances if probes are at equal distances from the centromeres (homologous FISH signals are indicated by circles of the same color). Solid lines, homologous distances; dotted lines, nonhomologous distances. (c) Graphic representation of experiments (experiments 1 and 2 in Table 2) corresponding to the situations modeled in panels a and b. The dotted curve shows the d values for loci 3T and 4T (see Fig. 1). In 59% of the nuclei is d > 0 (i.e., the homologous loci are more closely positioned than heterologous loci). The solid curve shows the d values for 3T and 11T. In this case there is a much weaker preference for closer association between homologous than between heterologous loci, as in only 42% of the nuclei d > 0. The solid curve runs almost entirely within the interval defined by encompassing 90% of simulations of random positioning of homologous loci in Fig. 3a (shaded area).

To test the influence of the Rabl orientation, we compared homologous versus nonhomologous distances for pairs of loci at widely different and at equal distances from the respective centromeres. We used probes 3T and 4T, which are close to the right telomeres of chromosomes III and IV, respectively (Fig. 1). 4T has an 850-kb-larger genomic distance from its corresponding centromere than 3T. The mean nonhomologous 3T-4T distances were longer than the mean homologous 3T-3T and 4T-4T distances (i.e., d > 0; see Materials and Methods) in 59% of the nuclei (experiment 1 in Table 2 and Fig. 4c). If, on the other hand, homologous and nonhomologous distances involving loci 3T and 11T, which have similar genomic distances from their respective telomeres (∼190 kb, Fig. 1) are compared, d > 0 was obtained only in 42% of the nuclei (experiment 2 in Table 2 and Fig. 4c), a value which is only slightly different from the simulated random relative positioning of loci (41.2%, Fig. 3a).

TABLE 2.

Summary of experiments

Expt no.	Strain	Growth statusa	Probe pairsb	% Nuclei with d > 0	% Nuclei with single signals	d = 0 inside 90% confidence interval before and after correction for 10% signal loss		Corresponding figure(s)
						Before	After
1	FKY74	Stat	3T-4T	59	4.5	No	No	Fig. 4c
2	FKY74	Stat	3T-11T	42	5.5	Yes	Yes	Fig. 4c
3	SK1	Stat	7B-7B′	65	14.0	No	No
4	FKY74	Stat	7B-7B′	48	7.0	No	Yes
5	W303	Stat	7B-7B′	54	1.5	No	No
6	FKY74	Stat	7B′-16B	57	8.5	No	No
7	W303	Stat	7B′-16B	35	5.0	Yes	Noc
8	FKY74	Stat	7B′-16B	61	11.5	No	No
9	W303	Stat	7B-16B	50	4.5	No	Yes
10	SK1	Stat	7A-7A′	56	6.5	No	No
11	FKY74	Stat	7A-7A′	45	3.0	Yes	Yes
12	W303	Stat	7A-7A′	50	8.0	No	Yes	Fig. 5 and 8
13	FKY74	Stat	7A′-16A	53	6.5	No	Yes	Fig. 5 and 8
14	W303	Stat	7A′-16A	61	14.0	No	No
15	SK1	Exp	7A-16A	55	6.0	No	No
16	FKY74	Exp	7A-16A	42	5.5	Yes	Yes
17	W303	Exp	7A-16A	44	7.0	Yes	Yes
18	SK1	Stat	7A-16A	48	5.0	No	Yes
19	FKY74	Stat	7A-16A	48	10.5	No	Yes
20	W303	Stat	7A-16A	56	11.0	No	No
21	FKY74	Stat	7A-12Ad	87	10.5	No	No	Fig. 6
22	W303	Stat	7A-12Ad	70	6.5	No	No	Fig. 6
23	SK1	Spor 0 he	7A-16A	65	21.5	No	No	Fig. 7a
24	SK1	Spor 2 h	7A-16A	70	31.0	No	No	Fig. 7a
25	SK1	Spor 3 h	7A-16A	82	27.0	No	No	Fig. 7a
26	SK1	Spor 4 h	7A-16A	82	27.5	No	No	Fig. 7a
27	AMP115	Spor 0 he	7A-16A	44	4.5	Yes	Yes	Fig. 7b
28	AMP115	Spor 2 h	7A-16A	52	7.5	No	Yes	Fig. 7b
29	AMP115	Spor 3 h	7A-16A	51	5.5	No	Yes	Fig. 7b
30	AMP115	Spor 4 h	7A-16A	46	8.5	Yes	Yes	Fig. 7b
31	AMP115	Spor 24 h	7A-16A	43	6.0	Yes	Yes	Fig. 7b
32	FKY74	Stat	7A-16A	52	8.0	Yes	Yes	Fig. 9

^aGrowth status of the culture from which cells were measured. Stat, Stationary growing culture; Exp, exponentially growing culture; Spor, cells in sporulation for the period indicated.

^bTested pairs of loci as shown in Fig. 1.

^cAfter correction there is a smaller percentage of nuclei with d > 0 than in 90% of the runs of the simulation.

^dNOR-linked probe.

^eCells in presporulation medium.

Therefore, we conclude that Rabl orientation contributes to the preferential association of homologous chromosomal regions in interphase nuclei. This influence of the Rabl orientation was also observed by Burgess and Kleckner (5). To compensate for the Rabl effect when homologous and nonhomologous signal distances are compared, it is imperative to test loci of the same genomic distances from their respective centromeres (Fig. 1). For the following experiments combinations of FISH probes were used that meet this condition.

The search for homologous associations in vegetative cells.

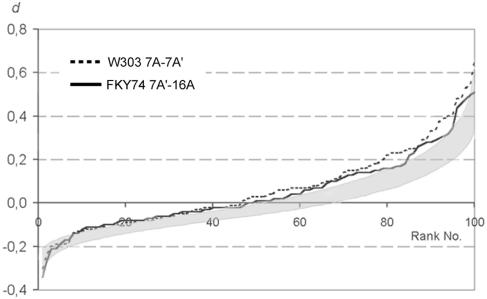
If vegetative pairing does exist at all in yeast, it is most likely to occur preferentially in G₀/G₁ (see the introduction and the Discussion for the rationale). Indeed, Burgess et al. (6) have claimed that vegetative pairing is particularly prominent during G₁ phase of the cell cycle. To establish whether vegetative pairing prevails under certain growth conditions, we compared the relative positioning of homologous and nonhomologous loci in nuclei of exponential and stationary cultures (experiments 2 to 20 and 32 in Table 2; Fig. 5). We did not observe a notable difference in the association of homologous loci between exponential and stationary cultures in parallel experiments with the same combinations of probes.

FIG. 5.

Examples of two experiments (experiments 12 and 13 in Table 2) in which the values for d (solid and broken lines, respectively) show a slight deviation from simulated d (shaded area depicting the 90% confidence interval), which suggests a preference for homologous loci to be adjacent.

To account for the possibility that a potential tendency toward vegetative association may be different for different chromosomal loci, we compared homologous versus heterologous distances for seven combinations of loci of similar centromere distances in three different strains under stationary growth conditions. Of a total of 19 experiments, 14 produced a curve that might be interpreted as a slight tendency toward the association of homologous loci compared to simulated random FISH signal distribution (Table 2 and Fig. 5).

Since yeast cells under stationary-growth conditions often tend to enter the sporulation pathway (see reference 11), it was important to determine whether unscheduled meiotic pairing contributed to the homologous associations observed. We estimated the frequency of meiotic cells in stationary cultures of the strains SK1 (which is known to be particularly prone to unscheduled meiosis) and W303. In cultures that had been stationary for 24 h, the frequency of spore tetrads was ∼2.5% in SK1 and 0% in W303 (n = 1,500 each). The frequency of tetrads is the accumulated frequency from meioses occurring throughout the entire period of culture. Therefore, the number of meiotic cells at a given time in the culture can be only a fraction of the number of spore tetrads. Moreover, we did not detect any cells with the meiosis marker Zip1p (47) by immunostaining in 1,000 cells scored (experiment not shown). Thus, the contribution of meiotic pairing to the generation of homologous associations in stationary cultures can be considered negligible.

Nuclear distribution of NOR-linked chromosomal sites.

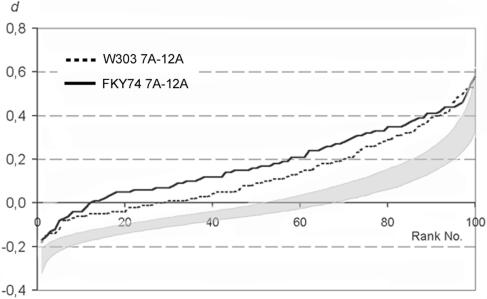
To get an impression as to how the observed nonrandom relative positioning of homologues compares to homologous pairing, we sought to determine how pairing would be portrayed by our graphs. An appropriate positive control for putative vegetative pairing is the association of nucleolus organizing regions (NORs). Therefore, we evaluated the intranuclear distribution of a pair of NOR-linked signals generated by a probe to near the proximal border of the RDN1 locus (12A, see Fig. 1) compared to a non-NOR-linked signal pair (7A, see Fig. 1). The NOR-linked loci are expected to exhibit a closer-than-random juxtaposition since the formation of a single joint nucleolus by the two NORs should confer a tendency to associate chromosomal regions adjacent to the ribosomal DNA tracts (Fig. 2d). (The fusion of nucleoli and nucleolar organizers is a well-known phenomenon in plants and animals [see, for example, reference 44 and references therein] and in diploid yeast [18].) Indeed, we found closer-than-random homologous distances in both strains tested (experiments 21 and 22 in Table 2). The plot of d for loci 7A and 12A reveals a significant difference from the simulated distances between randomly distributed signals (Fig. 6). Since loci 7A and 12A are not at exactly the same distances from their respective centromeres, Rabl orientation may have contributed to the prevalence of short homologous distances. However, since the Rabl effect is comparatively weak even for loci that are located at widely different genomic distances from their respective centromeres (Fig. 4), the prevalence of short homologous distances is likely to reflect the frequent association between NOR-linked homologous loci.

FIG. 6.

NOR promotes homologous associations. There is a large number of nuclei with d > 0 in two strain backgrounds (FKY74 and W303, experiments 21 and 22 in Table 2) if one of the two homologous probes is adjacent to the NOR. It is likely that the prevalence of short homologous distances reflects the association of NOR-linked loci, which is mediated by the fusion of nucleoli.

For no other loci tested did there exist a similarly strong prevalence of homologous proximity as for the NOR-linked sites. This suggests that in these other cases the observed bias toward positive d values is not sufficiently substantial to invoke vegetative pairing as an explanation. Hence, we searched for alternative explanations for the slight preference of homologous FISH signal pairs to be closer together than nonhomologous ones (see below).

Homologous associations under presporulation growth conditions and in meiosis.

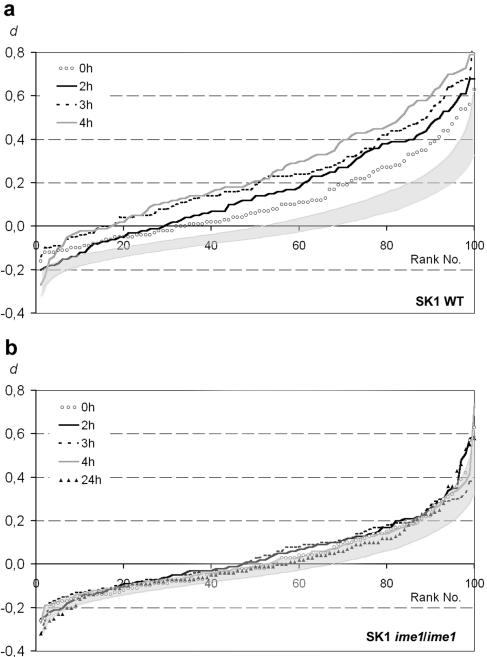
To study how homologous meiotic pairing changes the relative chromosome positioning as captured by our pairing assay, we subjected cells of the fast-sporulating stain SK1 to a protocol that is routinely used to ensure synchronous and efficient sporulation. This procedure includes presporulation growth in yeast extract and acetate and the subsequent transfer to sporulation medium (2% potassium acetate) (see Materials and Methods). Samples were taken after 14 h in presporulation medium (t = 0) and at t = 2, 3, and 4 h in sporulation medium, and homologous versus heterologous distances were measured between the loci 7A and 16A (Fig. 1; experiments 23 to 26 in Table 2). A d > 0 was found for 67, 71, 84, and 83% of the nuclei in the t = 0, 2, 3, and 4 h samples, respectively (Fig. 7a), reflecting the increase in pairing throughout meiosis. Nuclei at first meiotic division or later stages were identified by their shape and excluded from the evaluation. Immunostaining with Zip1p was performed on aliquots of the samples. Zip1p indicates the presence of the synaptonemal complex which mediates close chromosome pairing from zygotene through pachytene of meiosis (47). At the four time points 0, 66, 78, and 47% (n = 100 nuclei/time point) were positive for Zip1p. At the latest time point, Zip1p was reduced but pairing was probably maintained by chiasmata.

FIG. 7.

Tendency toward increasing d over a meiotic time course (times in sporulation medium indicated). (a) In the wild-type (SK1), the relative positioning of homologous and nonhomologous loci increasingly deviates from a simulated random positioning (shaded area), probably due to meiotic homologous pairing. Even under premeiotic growth conditions in medium containing acetate, chromosomal loci become redistributed. (b) In a meiosis-defective ime1 strain (AMP115), the d value is at no time grossly different from simulated random positioning (shaded area).

It is notable that even when the cells only had been grown in presporulation medium (t = 0) and zygotene has not yet commenced, as judged by the absence of Zip1p, there was significantly more homologous association than expected if association was random (Fig. 7a). To test whether associations under presporulation conditions were effected by meiotic genes that are induced in the presence of acetate, we used a meiosis-defective ime1Δ strain (experiments 27 to 31 in Table 2) (40). We observed no prevalence for homologous associations under premeiotic (presporulation) growth conditions in this strain (experiment 27 in Table 2; Fig. 7b). Therefore, we assume that previous findings of a tendency toward the proximity of homologous loci in presporulation cultures (37) are due to early meiotic events that lead to the primary meiotic alignment of homologous chromosomes.

Correction for FISH signal loss.

In the assay for homologous associations used here, the presence of a single FISH signal of one color in a diploid nucleus is interpreted as the fusion of homologous signals due to close pairing of the corresponding chromosomal loci. It is therefore important to identify and correct for nuclei where a single signal does occur due to method-inherent signal loss.

To determine the frequency of signal loss, we used a strain that is mostly diploid but possesses only one copy of both chromosomes I and III. Nuclei of this double-monosomic strain were labeled by FISH with a probe near the centromere of chromosome I in red and either probe 3C or 3T (depending on the experiment) on chromosome III (Fig. 1) in green. The frequency of the loss of either the red or the green signal was determined. Upon several repeats of the experiment with different color labels and loci on chromosome III, we found that signals were lost in 10 to over 30% of nuclei. We therefore can safely estimate that at least 10% of the cases where loci in the diploids appear as a single signal are due to signal loss.

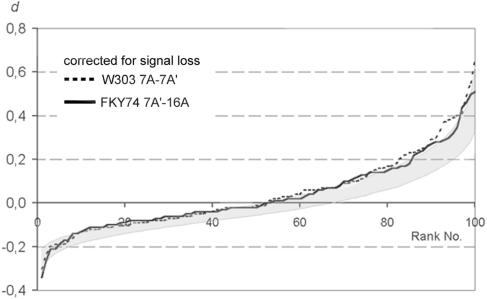
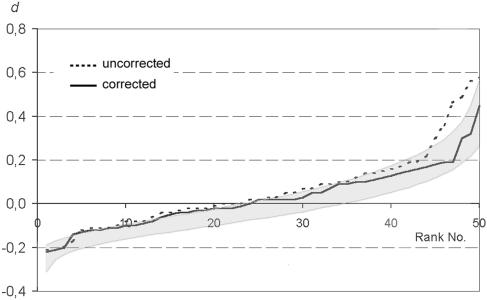
It is apparent that the experiments (i.e., experiments 3, 8, and 14) with a high frequency of single signals (see Table 2) were the ones in which the positions of homologues differed most clearly from a random distribution. We tested whether the prevalence for the proximity of homologous loci is retained after correction for 10% signal loss. To eliminate datasets generated by presumptive signal loss, nuclei (to a maximum of 10%) were excluded for which only a single spot of one color was present. In 14 experiments (i.e., experiments 3 to 6, 8 to 10, 12 to 15, and 18 to 20 in Table 2), the experimentally determined proportion of nuclei with d > 0 differed from the proportion of data sets with d > 0 in 90% of our simulations. After correction for 10% signal loss, in six of these experiments the proportion of nuclei with d > 0 did not differ any more from the proportion of data sets with d > 0 in 90% of our simulations (Fig. 8 and Table 2).

FIG. 8.

d values for the two experiments 12 and 13 (Table 2 and Fig. 5) after correction for 10% FISH signal loss. The corrected experimental data give a better fit with the simulated random distribution and show a better overlap with the area occupied by 90% of runs of the simulation (shaded area).

Distribution of chromosomal loci in three-dimensionally preserved nuclei.

Since it might be argued that our semispreading method, albeit very gentle, might disrupt homologous associations, we applied a preparation protocol for preserving the three-dimensional structure of nuclei and measured the homologous and heterologous distances of probe pair 7A-16A in three dimensions (experiment 32 in Table 2). A computer model, in which the three-dimensional distances of homologous and heterologous randomly distributed nuclei in a sphere were calculated directly, led to results in full accordance with the two-dimensional model described in Materials and Methods. The d values obtained from the three-dimensional measurements did not notably differ from the simulations considering 10% signal loss (Fig. 9), as did those of semispreads in which the same probes were used. This finding indicates that the relative positioning of homologues in two-dimensional preparations is not distorted.

FIG. 9.

Experimental data (dotted curve) from measurements of three-dimensional distances between loci 7A and 16A (experiment 32 in Table 2). If 10% signal loss is taken into account, the corrected experimental data give a better fit with the simulated random distribution and produce a curve (solid) that is almost entirely within the area occupied by 90% of runs of the simulation of random relative positioning in three dimensions (shaded area).

DISCUSSION

The search for vegetative pairing in S. cerevisiae.

Claims of the existence of vegetative pairing in budding yeast were based both on cytological observations of the association of homologous FISH-marked regions (6, 50) and genetic evidence for the preferential interaction of allelic chromosomal loci. Keeney and Kleckner (29) studied the behavior of a DNase I-hypersensitive site near the HIS4 locus on chromosome III, which had been created by insertion of ectopic sequences. There existed two alleles of this site, and it was found that DNase I sensitivity was increased on an assayed chromosome if the homologue carried the same allele. This trans effect can be explained by direct or indirect communication between the chromosomes, and Keeney and Kleckner (29) noted that direct, physical interaction would be in agreement with the proposed vegetative pairing. It is quite possible that these sites do frequently interact physically due to their neighborhood within the nucleus because they are close to the centromeres and the centromeres form a cluster in interphase cells (see, for example, references 25 and 26). However, it was not shown that nonhomologous regions at similar distances to the centromeres fail to interact with similar frequencies. Therefore, this trans effect is not necessarily a case for vegetative pairing. In fact, within centromere clusters, which are often ring-shaped, there is no notable preferential neighborhood between homologous centromeres (25).

Another noncytological assay for testing the frequencies of contacts between various chromosomal regions was undertaken by Burgess and Kleckner (5). These authors scored for restoration of prototrophy caused by the Cre-induced recombination between two loxP constructs: one downstream of a strong promoter and the other upstream of a promoterless ura3 gene. In one set of experiments, such a pair of constructs was inserted at opposite sides of the centromere of one and the same chromosome; in another set of experiments, the constructs were inserted at allelic sites of homologous chromosomes; and in a third, they were inserted on nonhomologous chromosomes. The rationale of the experiment was that relative levels of recombination between pairs of loxP sequences would reflect the relative probabilities of physical contact between the insertion sites. The authors found that recombination was most frequent between the loxP sequences on the two arms of one and the same chromosome. This can be readily explained by the juxtaposition of the arms of a chromosome that bends in the centromere as a consequence of the Rabl orientation (see Fig. 4a and below). Moreover, Burgess and Kleckner (5) observed a preference of interactions between allelic sites on homologous chromosomes over interactions between sites on nonhomologous chromosomes that prompted them to argue in favor of the existence of vegetative pairing in S. cerevisiae.

Here we attempted to verify previous reports on vegetative pairing in S. cerevisiae. We primarily searched for vegetative pairing in cells of stationary cultures, since it was reported by Burgess et al. (6) that somatic/vegetative pairing decreases in S-phase cells and, second, somatic/vegetative pairing would make most biological sense in G₀/G₁ cells, when there are no sister chromatids available for recombinational repair (see references 4 and 6).

Unlike the somatic pairing in Drosophila, vegetative pairing, as it was proposed to exist in budding yeast, is not characterized by the stable and intimate apposition of homologous chromosomes along their entire lengths. Rather, “pairing” is understood as sporadic and transient interactions between ever-changing pairs of homologous sites along chromosomes that may or may not be in contact at a given moment (29, 30). On the whole, these dynamic interactions would cause homologous chromosomes to be somewhat closer aligned than a random set of two chromosomes. Probing particular chromosomal loci is prone to underestimate the frequency and intimacy of these contacts. Weiner and Kleckner (50) estimated that about one interaction should on average occur per 65 kb. Thus, even if a given pair of homologous loci appeared separated in a particular nucleus at a given time, the presence of multiple associations should still be reflected by a loose side-by-side position of larger chromosome regions. Therefore, we did not define pairing via the frequency of closely associated loci, which produce a single FISH signal or two signals touching each other. Instead, we measured distances between homologous signals, expecting that if a particular locus is vegetatively paired at a given time, it would be reflected by a closer-than-random proximity of loci even when they are some distance away. Moreover, it was expected that this approach would minimize the danger of misinterpreting single signals created by signal loss as paired homologous loci (see below).

The Rabl orientation promotes a closer-than-random proximity of homologous chromosome loci.

The original reports on somatic/vegetative pairing in yeast were compromised by not taking into account the Rabl orientation. These reports were based on the comparison of the frequency or intimacy of associations between FISH signals at allelic and nonhomologous chromosomal sites. The predominance of associations of homologous over heterologous FISH signals was taken as evidence for nonmeiotic homologous pairing (37, 50). However, due to the centromere-telomere polarization, loci with the same distance from the centromere occupy the same latitude of the nucleus with respect to the centromeric pole. This causes allelic loci to be, on average, in closer proximity than two randomly selected loci (26). FISH with probes to regions at different chromosomal positions with respect to the centromere thus will result in homologous signals being closer together than nonhomologous signals (Fig. 4a); but this will be merely a function of centromere distances.

Burgess et al. (6) eliminated this sorting effect by intensely spreading nuclei to disrupt the Rabl orientation (see also reference 4). In the present study, we compensated for the influence of chromosome arm orientation by using only homologous and nonhomologous loci at identical centromere distances for the comparison of homologous and nonhomologous distances (Fig. 4b). Similarly, when Burgess and Kleckner (5) compared recombination at loxP sequences between allelic sites on homologous chromosomes and sites on nonhomologous chromosomes (see above), they corrected for the effect of the Rabl orientation by extrapolating recombination frequencies for nonhomologous sites at the same latitude. However, even after this correction a small preference for interactions between allelic sites remained (5). In the present study we also observed a small remaining preference for associations between homologous loci. We will evaluate below some observed and hypothetical factors that may confer a closer-than-random vicinity to homologues without vegetative pairing being involved.

Factors that may potentially contribute to the apparent proximity between homologous loci.

A serious problem in deriving the frequency of paired loci from the number of FISH signals is FISH signal loss since presence of a single signal due to a technical artifact could be misinterpreted as close pairing. At least 10% signal loss was estimated to occur in our standard FISH preparations (see Results). When we corrected for 10% signal loss, the relative positioning of homologous signals as experimentally determined was no longer significantly different from a simulated random distribution in 10 of 19 experiments (see Table 2).

For some of the experiments it may be assumed that the actual signal loss was higher than the conservatively estimated 10%, and correction for a higher loss might be sufficient to render all experiments not different from the simulation. However, in addition to the Rabl orientation and FISH signal loss, whose influences were experimentally confirmed, there are some other possibilities to explain a tendency by homologous loci to be in proximity. The first is different condensations of nonhomologous chromosomes which would cause regions of identical genomic distances (in base pairs) from the centromere to occupy different nuclear latitudes. Different condensations would compromise the compensation of the Rabl effect described above. Nonhomologous loci selected on the basis of their identical genomic distances from the centromeres would, in fact, have different nuclear distances from the centromeric pole and therefore be systematically separated by larger distances than sites on equally condensed (homologous) chromosome arms.

Also, the internal versus peripheral positioning of specific chromosomes or chromosome arms could potentially contribute to the closer proximity between homologous than between nonhomologous loci. Since, in yeast, telomeres are located at the nuclear periphery, loci on short arms would be located near the nuclear surface, whereas intercalary regions on long arms at a similar latitude would tend to occupy the interior of the nucleus. This would create a tendency of arms of similar lengths (and thus of homologues) to colocalize. Moreover, it was shown that certain (late-replicating) regions are located peripherally (23), which suggests that a different subset of chromosomal sites could have a preference for internal location. The same explanation was suggested by Cremer and Cremer (10) for the prevalence of homologous associations of chromosome territories of gene-dense human chromosomes, such as chromosome 19, which are preferentially located in the nuclear interior.

Finally, a mechanical sorting of the chromosomes within the mitotic spindle according to their sizes or strength of spindle attachment could influence the position of individual chromosomes within the nucleus (peripheral versus internal and also front versus rear half with respect to the position of the spindle pole at the preceding anaphase) (see references 38 and 41). In mammalian nuclei, chromosomes have a preference for a leading or lagging position on the anaphase spindle, which causes certain chromosomes to assemble at the bow or the rear compartment of the daughter nucleus. This positioning of chromosomes could be due to different “kinetochore strengths” (16). It could well create a certain tendency of homologous chromosomes to share a nuclear subregion (since they have similarly active kinetochores) and therefore to be in closer proximity than if they were distributed randomly within the nucleus.

Vegetative pairing contributes little if at all to nuclear organization.

Here we showed that there is only a weak preference for homologous chromosome regions to be closer together than nonhomologous chromosome sites in yeast interphase nuclei. We can offer no explanation for why Burgess et al. (6) observed a much higher incidence of homologous associations by a similar FISH approach. The disruption of associations by our preparation method is unlikely because we fixed the cells before applying a gentle detergent treatment for permeabilization. This method is even suitable to preserve the weak associations between chromosomally integrated tetracycline operator sequence repeats (12). Moreover, measurements of the same pairs of loci in three-dimensional preserved and semispread nuclei produced a very similar result (Fig. 9). In contrast, Burgess et al. (6) even applied a harsh spreading procedure, following the rationale that only “true” homologous associations would be sufficiently robust to resist.

We argue that the slight preference for spatial proximity of homologs described here and by other reports (5, 50) does not provide sufficient evidence to invoke vegetative pairing based on a homology recognition process. It may rather be imposed by nuclear topology. However, the possibility cannot be excluded that certain chromosomal loci may show a slight tendency toward homologous interactions and that vegetative pairing does occur only under certain physiological conditions and/or is induced as a response to stress conditions. In this respect, we have specifically tested whether irradiation can elicit vegetative pairing but have not yet obtained conclusive results (35). Finally, we want to note that there exists a machinery that could in principle establish and stabilize vegetative associations in mitotic yeast nuclei, since transgenic sequence repeats were found to associate in the presence of a sequence-specific binding protein (12).