Genome-Scale Analysis of the Uses of the Escherichia coli Genome: Model-Driven Analysis of Heterogeneous Data Sets

Abstract

The recent availability of heterogeneous high-throughput data types has increased the need for scalable in silico methods with which to integrate data related to the processes of regulation, protein synthesis, and metabolism. A sequence-based framework for modeling transcription and translation in prokaryotes has been established and has been extended to study the expression state of the entire Escherichia coli genome. The resulting in silico analysis of the expression state highlighted three facets of gene expression in E. coli: (i) the metabolic resources required for genome expression and protein synthesis were found to be relatively invariant under the conditions tested; (ii) effective promoter strengths were estimated at the genome scale by using global mRNA abundance and half-life data, revealing genes subject to regulation under the experimental conditions tested; and (iii) large-scale genome location-dependent expression patterns with approximately 600-kb periodicity were detected in the E. coli genome based on the 49 expression data sets analyzed. These results support the notion that a structured model-driven analysis of expression data yields additional information that can be subjected to commonly used statistical analyses. The integration of heterogeneous genome-scale data (i.e., sequence, expression data, and mRNA half-life data) is readily achieved in the context of an in silico model.

The increasing availability of complete genome sequences has ushered in an era of genome-enabled science that permits construction of in silico models at the genome scale (11, 17, 23, 25, 37). In addition to the number of genome sequences, the amounts of other high-throughput data types, including transcriptomic, proteomic, metabolomic, global mRNA decay, and interaction data, are growing at an ever-increasing rate (14). This wealth of genome-scale data highlights the need for scalable in silico methods with which to integrate and reconcile heterogeneous data sets (26).

Previously, a sequence-based framework for calculating the metabolic costs of expressing a gene and synthesizing its gene product was established (2). These costs are calculated directly from the DNA sequence, and estimates of ribosomal content can be used to scale the total protein-producing capacity of a cell and the requisite costs. The established framework, when scaled to account for all the genes in the Escherichia coli K-12 strain MG1655 genome (7), should allow explicit calculation of the material and energy costs required for expressing the entire genome, in addition to the costs for synthesizing the resulting proteome. Fundamental values for cellular biomass requirements have been experimentally measured for E. coli (22), but these values have never been calculated directly from the merging of sequence data with high-throughput gene expression data. Previous sequence-based cost estimates for protein synthesis have been calculated from expression estimates based on codon usage (1) but have not integrated actual expression or mRNA half-life data. A method for integrating such heterogeneous data sets would provide fundamental material and energy cost values, estimated effective promoter strengths on a genome scale, and the genome location distribution of gene expression in prokaryotes.

Expression profiling has been used to identify genes whose expression changes under shifting environmental conditions (4, 24, 31, 40, 46). A variety of methods have been developed with which to analyze these data, including coexpression pattern analysis for operon prediction (33), dimensionality reduction techniques (16, 18), and several types of clustering methods (3). A model-driven means by which to interpret and analyze expression data, however, has not been established. The availability of sequence data, expression data, and, most recently, global mRNA half-life data (6, 36) has created a need for such a structured analysis and integration of these disparate data sets. We developed a method that accomplishes this goal and used it to study the overall cost of maintaining a particular expression state, the distribution of individual effective promoter strengths, and the corresponding genome location-dependent characteristics of gene expression.

MATERIALS AND METHODS

In silico analysis framework.

The analysis framework established previously (2) describes a means of calculating the material and energy costs for maintaining a particular mRNA transcript and for synthesizing the resulting protein. For mRNA maintenance, the constituent nucleotide triphosphates are required to maintain the concentration of a transcript at a particular steady-state concentration (8). If the transcription rate, ν_mRNA (expressed in numbers of transcripts per cell per unit of time [typically per second]), is known for a gene, the requisite nucleotide demands can be calculated directly from the gene sequence.

Similarly, if the abundance of a particular transcript (m_i) relative to the total mRNA content (m_rel,i = m_i/m_tot, where 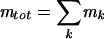) and the ribosomal content of the cell are known, upper boundaries on the amino acid requirements for synthesizing the encoded protein can be explicitly calculated. Thus, if the protein synthesis rate (i.e., the number of protein molecules translated per cell per unit of time) is known, the amino acid building blocks required to synthesize the encoded protein can be calculated directly from the sequence. In addition to the amino acid costs, one ATP and two GTP molecules are required for each peptide bond that is formed (2, 20).

Calculation of transcription state.

The transcription state is defined as the vector of all transcription rates in the genome, ν_mRNA,i (i = 1…N, where N represents the number of coding sequence open reading frames [ORFs] in the genome). The transcription state of the E. coli genome can be explicitly calculated by using sequence data if the following parameters are known: the effective promoter strengths (or ORF usages), the mRNA degradation rate of each transcript being synthesized, the mRNA amounts, and the free RNA polymerase (RNAP) concentration. At the genome scale, for each transcript:

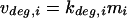(1)

where ν_deg,i, k_deg,i, and m_i are the degradation rate, the mRNA degradation rate constant, and the mRNA concentration, respectively, for the ith gene.

The transcription initiation rates (ν_mRNA,i) can be approximated if the effective promoter strength for each gene (q_i) (expressed in units of per molar per second), the RNAP concentration ([RNAP]), and promoter concentration ([P]_i) are known (28):

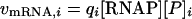(2)

It is assumed that transcription elongation is not limiting for protein synthesis, since once transcription initiation occurs, ribosomes may bind to the unfinished mRNA transcript and translation may commence at a rate comparable to the mRNA elongation rate (42).

In a steady state, the transcription rate must balance the mRNA degradation rate:

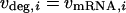(3)

It is therefore possible to reconcile data for mRNA concentrations, effective promoter strengths, and mRNA degradation rates in the following manner:

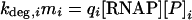(4)

The effective promoter strengths, which depend on both the intracellular conditions and the regulation present, can thus be calculated globally if large-scale mRNA concentration data (35, 44) and mRNA half-life data (6, 36) are available. If log-phase growth is assumed, the number of copies of each promoter per cell can be estimated from each gene's position on the chromosome and the growth rate of the cell (8). Since these effective promoter strengths are essentially normalized transcription rate constants, they are subject to regulation. Thus, the variance of each effective promoter strength across many data sets becomes a useful quantity. The vector of all effective promoter strengths, q = (q₁…q_N), constitutes the promoter activation state of the genome, where N is the number of coding sequences in the genome.

Metabolic cost of RNA synthesis.

The synthesis rate of each mRNA transcript, which determines the nucleotide triphosphates required, is set by the effective promoter strength for each (ith) gene. Neither the mRNA elongation rate nor the free RNAP concentration is assumed to be limiting for the synthesis rate of each transcript (8, 28). In the absence of large-scale promoter strength data, however, the transcription rate for each transcript may be estimated from the relative mRNA amounts (estimated from expression data) and from available mRNA decay rates (6, 36) (equation 1). It is possible to normalize the nucleotides required for mRNA maintenance when the total mRNA concentration ([mRNA]_tot) at a given growth rate is known (8).

Metabolic cost of protein synthesis.

The total protein synthesis rate (i.e., the overall capacity of the cell to synthesize protein) is limited by the number of ribosomes available to the cell (8, 19). Additionally, the relative abundance of each transcript (m_rel,i) determines the weighting of the synthesis rate for each protein since all mRNA transcripts compete for the pool of available ribosomes. This disregard for the potential effect of transcript length on ribosomal occupancy is probably valid since the messages are not necessarily saturating. In fact, the number of ribosomes in a typical E. coli cell is about 1 order of magnitude greater than the total number of messages (22). Thus, an upper boundary for each protein synthesis rate (ν_prot,i) can be set as follows:

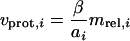(5)

where β is the maximal protein synthesis capacity of the cell (in number of peptide bonds formed per cell per unit of time; about 340,000 peptide bonds per cell per s [8]) as limited by the number of ribosomes present and a_i is the number of amino acids in each protein. The corresponding amino acid costs for supporting the upper boundaries for protein synthesis rates can be directly calculated from the known sequence. Additionally, the energy cost required for ribosomal binding, translocation along the ribosomes, and tRNA charging can be calculated for each protein synthesis rate.

Analyzing genome location-dependent patterns in gene expression.

Calculation of the transcription state of the genome requires a means of analyzing potential patterns in expression along the chromosome. Wavelet transform techniques (5) can be used to analyze and visualize the genome location-dependent variability of gene expression. While standard Fourier transforms allow identification of periodic patterns in stationary signals, wavelet transforms allow identification of both periodic and nonperiodic localized patterns and do not assume a stationary signal. In this work we used the continuous wavelet transform, which is better suited for visualizing patterns than its discrete counterpart (21). The continuous wavelet transform of signal x(t) [W(t,a)] (in our case, effective promoter strengths along the genome), is defined as

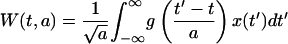(6)

where g([t′ − t]/a) is the wavelet transform filter centered at t and the width of the filter (a) is used to determine the scale at which patterns are analyzed. By choosing the filter function (g) we can extract different types of patterns from the data. Here we used the Morlet wavelet defined as g(t) = cos(5t)exp(−t²/2), which is particularly well suited for studying localized periodic patterns in data (5). The wavelet transform can be visualized by using a scalogram that displays the transform W(t,a) as a contour plot with location along the genome (t) on one axis and the scale (a) on the other axis. We evaluated the significance of the spatial patterns extracted through wavelet analysis by randomizing the gene order in the E. coli genome and recomputing the transform for each randomized genome. A P value for each individual W(t,a) was then calculated based on 1,000 randomized genomes by computing the number of times that a specific |W*(t,a)| for a randomized genome was larger than the true |W(t,a)|.

Experimental methods and normalization.

All mRNA expression data were generated from E. coli grown in batch culture as described in detail elsewhere (J. D. Glasner, T. Durfee, Y. Qiu, M. Liu, Y. Kang, C. Herring, C. R. Richmond, G. Plunkett 3rd, N. T. Perna, R. Mau, D. Frisch, S. Hinsa, S. Fendrick, G. Nodalski, P. Borelli, S. Phillips, N. Hermersan, and F. R. Blattner, unpublished data) and are available online (13; http://asap.ahabs.wisc.edu/annotation/php/logon.php). In most experiments we used the sequenced K-12 strain MG1655. Seventeen experiments involved strains derived from MG1655 with single ORF disruptions, and in 2 experiments (single spotted array hybridizations) we used strains DH5alpha and DH10B. In 39 of 49 experiments we used cells harvested at the early exponential phase growth, and in 10 experiments we used cells from late-exponential-phase or stationary-phase cultures. In 46 of the experiments we used cells grown in a MOPS (morpholinepropanesulfonic acid)-based minimal medium, while in 3 experiments we used Luria-Bertani media. Glucose was used as the carbon source in most minimal medium experiments (43 of 49 experiments), and in the other experiments we used acetate, glycerol, or proline as the carbon source. Data were collected by hybridization of fluorescently labeled cDNAs to either Affymetrix E. coli antisense oligonucleotide arrays (as described by Rosenow et al. [32]) or microarrays of spotted ORF-length PCR fragments (as described by Yang and Ames [44]). The oligonucleotide arrays contained probes for both ORFs and intergenic regions, but only the data corresponding to ORFs were considered in this study. For each ORF on the Affymetrix array we calculated the average difference value using the Microarray Suite software (Affymetrix, Inc., Santa Clara, Calif.). For spotted arrays the signal intensity for each ORF was taken to be the average intensity of duplicate spots on the array. Fluorescently labeled genomic DNA was used as a reference for the spotted arrays and thus provided an absolute measure of expression. To convert the signal values to estimates of transcript abundance, the simplifying assumption was made that for each experiment an average E. coli cell in the population contained 10,000 (gene-size) mRNA transcripts (22). The signal for each ORF on each array was scaled by the factor 10,000/sum of the signal intensities for each array. When replicate hybridizations were available, the scaled signal values were averaged across arrays. A small number of spots on each spotted microarray were disregarded when we averaged across replicates because of poor-quality PCR, spotting, or hybridization. For this reason the sums of the estimates for the numbers of copies per cell are slightly lower than 10,000 and vary across the spotted cDNA array experiments.

RESULTS

The in silico and experimental methods described above were used to address the following three questions. What are the metabolic resources required for expressing the entire E. coli genome under various conditions? What is the distribution of effective promoter strengths, and is this distribution gene function dependent? And do these estimated promoter strength distributions reveal genome location-dependent patterns in gene expression?

Metabolic cost of genome expression.

The cost of expressing the E. coli genome was calculated for a number of different steady-state mRNA concentration distributions. A number of random distributions were probed, as were mRNA concentrations derived directly from the 49 gene expression data sets generated in this study. All of these cost calculations were normalized by using parameters corresponding to a cell with a 40-min doubling time (Table 1). Thus, for the mRNA maintenance cost, the mRNA concentrations were normalized to a specified total mRNA concentration (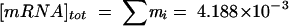M). Similarly, the protein synthesis rates (and the corresponding costs) were normalized by assuming that there were 21,040 active ribosomes per cell (8) or β =3.37 × 10⁵ peptide bonds/cell/s by assuming a peptide elongation rate of 16 amino acids/ribosome/s (42). Note that the amino acid costs given below are actually upper boundaries for the costs, since possible tRNA abundance constraints were not taken into account.

TABLE 1.

Calculated amino acid and nucleotide demands for expressing the E. coli genome^a

Amino acid(s) or nucleotide	Demands (mmol/g [dry wt]/h)		CV (%)
	Random	All data
Amino acids	316.93	276.10	6.4
Ala	0.66	0.66	1.7
Arg	0.38	0.39	1.6
Asn	0.27	0.28	1.4
Asp	0.36	0.37	2.2
Cys	0.08	0.07	8.6
Gln	0.31	0.30	3.0
Glu	0.40	0.43	4.7
Gly	0.51	0.53	1.8
His	0.16	0.15	4.8
Ile	0.42	0.42	1.3
Leu	0.74	0.69	3.4
Lys	0.31	0.35	7.3
Met	0.20	0.19	2.2
Phe	0.27	0.26	4.0
Pro	0.31	0.29	3.1
Ser	0.40	0.39	2.8
Thr	0.38	0.38	1.3
Trp	0.11	0.09	10.0
Tyr	0.20	0.19	3.1
Val	0.49	0.51	3.0
ATP	7.02	7.02	0.01
CTP	0.08	0.08	0.7
GTP	13.97	13.96	0.004
UTP	0.08	0.07	1.4
AMP	7.02	7.02	0.01
CMP	0.08	0.08	0.7
GMP	0.09	0.09	0.004
UMP	0.08	0.07	1.4
GDP	13.88	13.88	∼0
Pi	28.39	28.39	∼0

^aThe average protein length and the resulting by-product synthesis rate were included for each set of simulations. The random demands were derived from randomly generated data sets, while the demands for all data were derived directly from the 49 gene expression data sets used in this study. The CVs are the CVs for the data-based calculations across all 49 data sets. All results were normalized by using parameters corresponding to a doubling time of 40 min: total [mRNA], 4.188 × 10⁻³ M; total ribosomal content, 21,040 active ribosomes; mass, 4.33 × 10⁻¹³ g (dry weight)/cell; and density, 382.72 g (dry weight)/liter (8).

Simulated in silico expression profiles.

The costs of expressing a particular distribution of mRNA transcripts and of synthesizing the encoded proteins were calculated for three random mRNA concentration distributions: uniform, normal, and exponential. Since the calculations for any randomly generated expression profile, regardless of distribution, were nearly invariant, Table 1 shows the mean nucleotide and amino acid demands (as well as the resulting by-products) for a typical simulation. The coefficients of variation (CVs) were determined from calculating the costs given by 400 simulations, but they are not shown in Table 1 since they were all less than 1%.

Measured in vivo expression profiles.

The material and energy costs were then calculated for mRNA concentration distributions derived from available experimentally determined gene expression data, and the resulting costs and CVs are shown in Table 1. Gene expression data sets from 49 separate experiments (corresponding to 91 hybridizations, including 41 Affymetrix arrays and 50 spotted cDNA arrays) were generated as described above, and the numbers of transcript copies per cell were estimated for most of the 4,290 coding sequences in E. coli for each data set. For the spotted arrays, the numbers of transcript copies per cell were estimated from microarrays normalized by using genomic DNA as described above. The experimental conditions from which the data were derived varied widely and included exponential and stationary-phase growth in glucose minimal medium, exponential growth in acetate and glycerol minimal media, response to acid shock, response to cold shock, response to heat shock, growth in media containing an antibiotic, growth in Luria-Bertani broth, and various deletions grown on glucose minimal medium. In order to examine if the observed relative cost invariance was true for data sets available elsewhere, additional data sets were obtained from previous studies (41). The results for these data sets (data not shown) were comparable to those from our laboratory and did not alter the overall findings of this study.

Cost comparisons.

The averages and CVs from each computation of metabolic costs were compared. The variance in the results among the 400 random simulations was essentially negligible (all CVs were <1%). The 49 simulations resulting from expression data exhibited slightly higher variation (the average CV for the amino acid demands was 3.6%), but no CV was higher than 10% (for the tryptophan cost). There was not a statistically significant difference in the costs for any of the amino acids or nucleotides resulting from randomly distributed mRNA concentrations or data-based simulations. The mean protein length was about 40 amino acids shorter for the data-based simulations than would be expected if the mRNA distribution were random. The highest CVs for the data-based cost calculations were for tryptophan (10.0%), cysteine (8.6%), and lysine (7.3%), and the lowest were for isoleucine (1.3%), threonine (1.3%), and asparagine (1.4%). The amino acid composition of a related strain of E. coli (B/r) has been experimentally determined (22), and the calculated costs for E. coli K-12 correlate relatively well with the biomass data (results not shown).

Distribution of estimated effective promoter strengths.

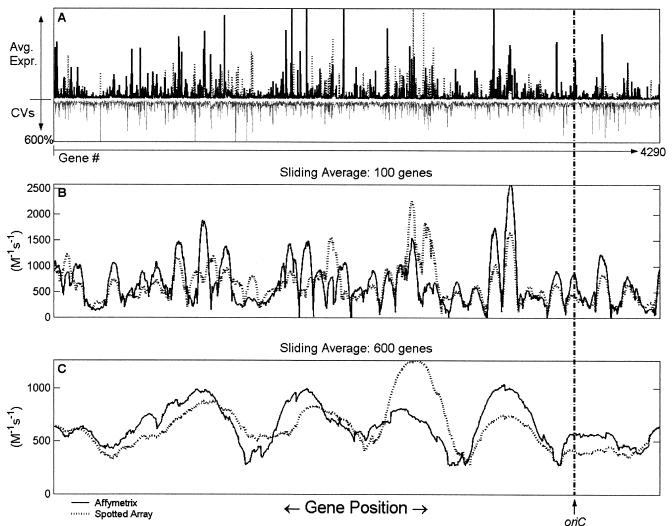
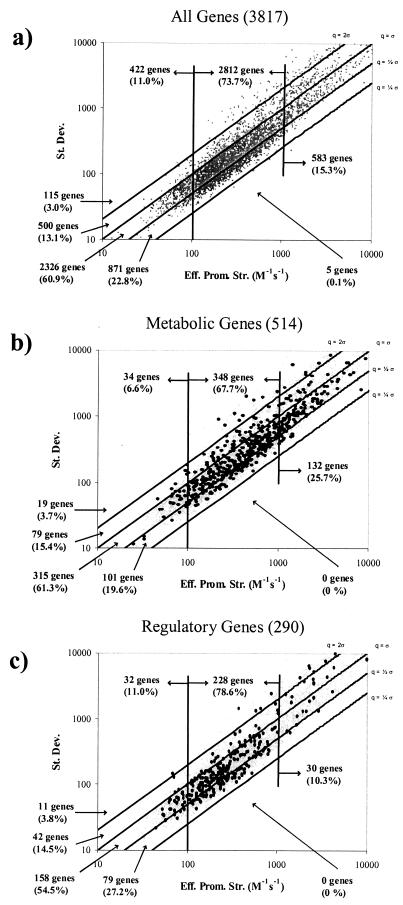
Using global mRNA half-life data (6), we calculated the effective promoter strength for each of the 49 sets of mRNA concentrations estimated from expression data (which included expression data from a variety of experimental conditions). The mean effective promoter strength and the corresponding CV were plotted for each of the 3,817 genes for which both expression data and half-life data were available (Fig. 1A). (Table 1 indicates the parameters used for calculation of promoter strengths.) In this analysis, the CV could be thought of as a measure of the extent to which a gene was subject to regulation under the experimental conditions tested. The highest expression levels generally corresponded to ribosomal protein components and associated protein synthesis enzymes, structural proteins, and membrane pore proteins (as classified by Serres and Riley [38]). Although the majority of CVs (the CVs for 60.9% of the 3,817 mean effective promoter strengths) fell between 50 and 100%, 115 genes had standard deviations that were equal to or greater than double their average expression levels. Over one-fifth of the genes (876 genes or 22.9%) had CVs of less than 50% (Fig. 2a).

FIG. 1.

Calculated average effective promoter strengths at different sliding average scales. The cellular parameters were chosen for a doubling time of 40 min (see Table 1), with an RNAP concentration of 1.456 × 10⁻⁶ M (8). The concentration of each promoter was chosen based on a C period of 45 min and a D period of 25 min (8), where the C period refers to the time between initiation and completion of one round of chromosomal replication, and the D period refers to the interval between the end of replication and cell division (22). The location of the origin of replication (oriC) is indicated for reference. (A) Plots of mean expression levels and CVs for the 20 Affymetrix data sets and the 29 spotted array data sets. The solid bars represent the mean effective promoter strengths calculated from experiments performed with Affymetrix arrays, the dotted bars represent the effective promoter strengths calculated from spotted array experiments; and the grey bars represent the CVs spanning all 49 data sets used in the calculations. (B) Plot of mean expression levels over a sliding average (with second-order Savitzky-Golay smoothing) of 100 genes for the Affymetrix array (solid line) and the spotted array (dotted line) data sets. (C) Same as panel B, but the sliding average was taken over a 600-gene window.

FIG.2.

Log-log plots of the standard deviations (St. Dev.) versus mean effective promoter strengths (Eff. Prom. Str.) for individual ORFs in 49 expression data sets. The gene information outside each plot indicates the numbers of genes between CV demarcations, and the gene information inside each plot indicates the numbers of genes whose promoter strengths were less than 100 M⁻¹ s⁻¹, between 100 and 1,000 M⁻¹ s⁻¹, and greater than 1,000 M⁻¹ s⁻¹. (a) Plot of all 3,817 genes for which effective promoter strengths were calculated. (b) Overlay of 514 metabolic genes (12). (c) Overlay of 290 regulatory genes (34).

If the genes known to take part in metabolism (12) were considered separately (Fig. 2b), their CVs (average, 81.9%) were comparable to the average CV for the 3,817 genes (78.2%). The average expression of the metabolic genes (891 M⁻¹ s⁻¹), however, was significantly higher than that of the average gene (632 M⁻¹ s⁻¹). The mean effective promoter strengths and CVs of genes implicated in regulation (34) were roughly equivalent to those of the overall genome (mean effective promoter strength, 559 M⁻¹ s⁻¹; mean CV, 79.5%) (Fig. 2c).

Genome location-dependent patterns in gene expression.

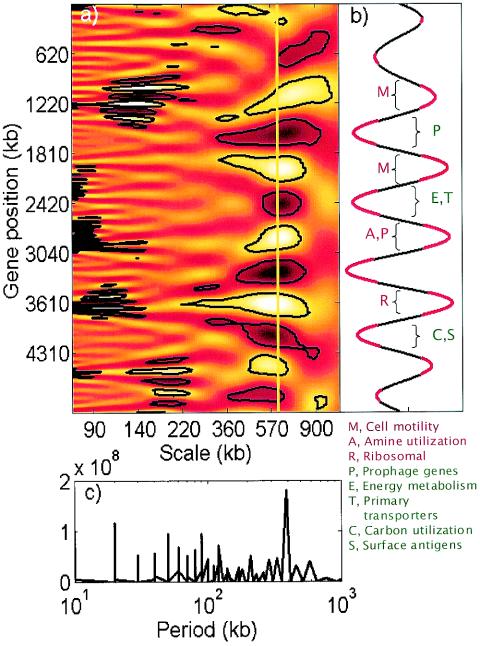
In order to elucidate potential genome location-dependent patterns in gene expression, wavelet transforms were applied to the effective promoter strength data as described above. Sliding averages of the calculated effective promoter strengths obtained by using Savitzky-Golay smoothing (Fig. 1B and C) indicated that there was nonrandom genome location-dependent variability along the E. coli chromosome. In particular, there appeared to be a periodic large-scale pattern of regions with high average expression. This pattern was present both in the data sets generated from Affymetrix experiments and in the data sets generated from spotted array experiments, implying that the observed pattern was not likely to be an artifact of the experimental platform (Fig. 1). In order to elucidate this pattern and other more subtle spatial patterns in the data, continuous wavelet and Fourier transforms were applied to the effective promoter strength data. The continuous wavelet transform of the average effective promoter strengths estimated from the 20 Affymetrix GeneChip experiments performed in this study (using the Morlet wavelet [5]) was represented in a scalogram (Fig. 3a). The major feature of the transform was the clear periodic pattern at a scale of approximately 600 kb. This pattern was observed in the spotted array data sets and was also detected by using other types of wavelet filters, such as the Marr wavelet used by Murray et al. (21), indicating that the observed pattern was not an artifact due to either the experimental platform or the particular transform used (results not shown).

FIG. 3.

Spatial variability of gene expression along the E. coli genome studied by using continuous wavelet and Fourier transforms of the effective promoter strength data. (a) Scalogram of the wavelet transform with the gene position on the y axis and the transform scale on the x axis. Lighter and darker regions correspond to higher and lower values of the coefficients, respectively. The regions enclosed by black contour lines were deemed to be statistically significant patterns compared to spatially randomized effective promoter strengths (P < 0.001). (b) Cross section of the wavelet scalogram in panel A at a scale of 610 kb. The regions with significantly nonrandom wavelet coefficients are indicated by red. Gene functional classes (classified according to GenProtEC 38) preferentially located in particular high-expression (red) or low-expression (green) regions (hypergeometric P < [0.001/number of functional classes]) are also indicated. (c) Fourier transform analysis of the effective promoter strength data. The only significant peak in the transform occurs at the approximately 600-kb period.

In the cross section of the scalogram at a scale of 610 kb (Fig. 3b), the regular periodic pattern extending over almost the entire length of the genome was readily observed. The same periodic component identified through wavelet analysis could also be identified as a peak in the Fourier spectrum (Fig. 3c) at a period of approximately 600 bp. However, the periodic pattern did not extend in a regular fashion throughout the whole genome, making standard Fourier analysis somewhat less suitable for this study than wavelet analysis.

The observed periodic pattern appeared in all the individual effective promoter strength data sets computed by using different expression profiles and hence did not seem to be specific to any particular experimental conditions. No such pattern was observed in the raw mRNA half-life data. A periodic pattern was, however, detected in the raw gene expression data (data not shown), but the pattern was somewhat less well defined than that in the effective promoter strength data. Since the effective promoter strengths were corrected for differential mRNA decay rates and distance from the replication origin, they seemed to be a more appropriate measure of the actual transcription rate than mRNA expression data alone.

Analysis of gene functional classes whose members are preferentially located in particular regions of high or low average expression within the periodic pattern (Fig. 3b) may elucidate the relationship between the observed periodicity and E. coli cellular function. Flagellar and other cell motility-related genes and genes encoding ribosomal and other translation-related proteins are preferentially located in one or more of the high-expression regions. On the other hand, genes involved in major metabolic functions, such as energy metabolism, carbon utilization, and transport, tend to be located in the low-expression regions. Furthermore, genes in certain functional classes are typically strongly enriched in only one or two of the high- or low-expression regions, indicating that there are potentially distinct roles for each of these regions. Note that the only data generated were data for protein-encoding ORFs. Thus, the rRNA and tRNA transcription rates were not considered in the analysis of genome location-dependent patterns.

DISCUSSION

We performed an integrated analysis of genome-scale gene expression in E. coli, based on simultaneous use of sequence data, gene expression data, and mRNA half-life data. The results from this integrative analysis are threefold: (i) the relative material and energy costs used to express the E. coli genome were essentially independent of the distribution of mRNA concentrations; (ii) an examination of the distribution of the effective promoter strengths of 49 gene expression data sets revealed that over 16% of the genes in E. coli vary in expression by more than 100% of the average promoter strengths under the conditions used; and (iii) a wavelet analysis of the distributions revealed a large-scale (∼600-kb) periodic pattern in the expression of genes in E. coli. The methods used were computationally simple and thus suitable for immediate integration into existing genome-scale metabolic models of E. coli (12, 29).

The apparent invariance of the costs for maintaining any expression state of the genome implies that the metabolic resources required to maintain a particular transcription and proteomic state are relatively constant and independent of external conditions. This invariance does not hold true, however, if a gene or small subset of genes with atypical amino acid composition is expressed at a level that is orders of magnitude higher than the level of expression of the rest of the genes (data not shown). Thus, microbes genetically engineered to express a particular protein at a high level may experience significant phenotypic effects associated with the cost imposed by such atypical expression. It is also possible that the dynamic range of microarrays and gene chips becomes limiting if a few transcripts are expressed at a very high level and therefore saturate the signal on the arrays (9, 30). To test the significance of this effect, cost simulations were performed in which the top 0.1% of genes with the highest expression levels were assigned values for number of copies per cell that were 10% higher than the level reported by the arrays. The highest CV was increased to just over 20% (for tryptophan), while the average CV of the amino acid costs increased from 3.6 to 8.1%, suggesting that a limited dynamic range in the experimental technology could have some effect on the calculated costs. Finally, it is possible that the observed invariance may have been due to a lack of probing the experimental conditions that would most alter the relative amino acid costs required for expression. However, the conditions chosen were quite varied, and hence we expected there to be differences in the overall metabolic costs between the conditions if such differences exist.

The variation in effective promoter strength was computed for the entire genome. In general, no clear patterns were found between gene category and variation in expression level. There was also no observed functional class bias either in the effective promoter strengths or in the variance across 49 different calculations. It is worth noting that these computations were biased by the experimental conditions under which each expression profile was measured. To better ascertain genes that are subject to regulation, it will be necessary to test more varied growth conditions (e.g., growth on other carbon sources, anaerobic growth, growth during diauxic shifts, etc.). If M9 medium (which contains a relatively large amount of phosphate) were used instead of MOPS medium, for example, one might expect the genes involved in the phosphate regulon to exhibit altered effective promoter strengths (and, consequently, increased CVs in the subsequent analysis), thus revealing the extent to which these genes were differentially regulated under the changing medium conditions (43). As more data sets are included in this type of integrated analysis, a better gauge of the variability in gene expression should be obtained, thus more completely revealing the extent to which each gene is subject to regulation.

An approximately 600-kb periodic genome location-dependent pattern in gene expression in the E. coli genome was detected by performing wavelet analysis of the effective promoter strength data generated in this study. The origin and significance of this pattern, however, are not clear. One possible explanation for the observed pattern is the existence of topological domains with potentially different levels of supercoiling in the E. coli chromosome (39). It has been estimated that there are 43 ± 10 such domains so that the average domain size is approximately 100 kb (39). No significant 100-kb periodicity was detected in the wavelet analysis except for particular localized patterns (Fig. 3a), although an irregular periodicity at a sliding average of 100 genes (∼100 kb) was observed (Fig. 1B). As the 600-kb periodicity corresponds to a multiple of the 100-kb topological domain scale, it is possible that the potential differences in gene expression in different topological domains indeed explain the observed pattern. However, the nature and locations of the topological domain boundaries in the E. coli genome are not known (10, 27, 45), making comparisons of the topological domain structure with the observed periodicity in expression challenging. Even if the origin of the periodic expression pattern is somewhat obscure, there is a clear tendency of genes in certain functional classes to cluster in either the high- or low-expression regions within this pattern (Fig. 3b). If the periodic pattern and the corresponding functional class clusters continue to be observed as more data sets are generated, this tendency may suggest how a genome location-dependent constraint on gene expression could act to shape gene order in genomes.

As genome-scale data, including mRNA expression data, mRNA half-lives, and proteomic data, are becoming more widely available, the need for integrating these heterogeneous data types is becoming stronger (26). As this study demonstrated, a higher-order biological analysis can be performed based upon the integration of multiple data types that cannot be done based on an analysis of individual data sets. Such integrated data analysis is enabled by genome-scale in silico models. Different data types demand a model to explicitly relate their values, thus revealing emergent properties that would otherwise be inaccessible (15).

The proposed model integrates three types of genome-scale data: sequence, gene expression data, and mRNA half-life data. This structured framework constitutes a novel means by which to analyze expression data and interpret the expression state of a cell. The scalability of the methods used to generate these data should greatly facilitate future integration of the genomic expression state with existing genome-scale metabolic models. This method therefore constitutes an important step in our progress towards achieving truly genome-scale integrated models of cellular function.