Trading force for speed: Why superfast crossbridge kinetics leads to superlow forces

Abstract

Superfast muscles power high-frequency motions such as sound production and visual tracking. As a class, these muscles also generate low forces. Using the toadfish swimbladder muscle, the fastest known vertebrate muscle, we examined the crossbridge kinetic rates responsible for high contraction rates and how these might affect force generation. Swimbladder fibers have evolved a 10-fold faster crossbridge detachment rate than fast-twitch locomotory fibers, but surprisingly the crossbridge attachment rate has remained unchanged. These kinetics result in very few crossbridges being attached during contraction of superfast fibers (only ≈1/6 of that in locomotory fibers) and thus low force. This imbalance between attachment and detachment rates is likely to be a general mechanism that imposes a tradeoff of force for speed in all superfast fibers.

The superfast fiber type is found where high-frequency contractions are required, such as in vertebrate eye muscles and in both vertebrate and invertebrate synchronous sound-producing muscles. These muscles have a series of modifications for speed, including a large volume of sarcoplasmic reticulum (SR) (1–7) to produce very rapid calcium transients (8) and low-affinity troponin to speed myofilament deactivation after [Ca²⁺] decline (8). It has been suggested that another required modification is extremely fast actomyosin crossbridge detachment, but this has not been directly measured (8). These muscles are also characterized by very low force generation (1, 4, 9). Even though large volumes of SR (and, additionally, large mitochondrial volumes in aerobic muscles) can reduce the space occupied by the force-generating myofibrils and thus total force (1, 4–7), in some cases the force per myofibrillar cross-section is substantially lower than in locomotory muscle (1, 4). This is puzzling particularly in vertebrate superfast muscle. The force per myofibrillar cross-sectional area generated by vertebrate locomotory muscle is nearly constant—about 200–300 kN/m² (10–14)—and this uniformity in force is consistent with the observation that myosin thick filaments in all vertebrate skeletal muscle fibers have the same length and number of myosin heads (15).

Here we examine the kinetics of the force generating crossbridges in the fastest vertebrate muscle known [the superfast toadfish swimbladder muscle used to make a 200 Hz “boatwhistle” mating call (8)] and compare them to the crossbridge kinetics of toadfish locomotory muscles. We assess the modifications made for high-frequency contractions and test whether these modifications are responsible for low force generation.

MATERIALS AND METHODS

Preparation of Intact and Skinned Muscle Fibers.

In toadfish, the anatomical segregation of different fiber types permitted us to dissect small bundles of fibers, which are pure in fiber type, from the slow-twitch red and fast-twitch white trunk musculature and the superfast-twitch swimbladder muscles. For intact fiber experiments, bundle size ranged from 6- ∼50 fibers (note that force/cross-sectional area of fibers was independent of bundle size). For skinned fiber experiments, the preparation size was further reduced and was adjusted for the size of the fibers: for red muscle, single fibers were used; for white muscle, the large single fibers were split longitudinally to ≈1/4 of their diameter, and for swimbladder muscle, bundles of 2–3 of these thin fibers were used. Preparations were skinned in 3% Triton X-100 for 20 min and then exposed to SR calcium pump blockers [10 μM thapsigargin or 20 μM 2, 5-di(tert-butyl)-1,4-benzohydroquinone)] throughout the experiments. Both treatments abolish SR Ca²⁺ pumping, thereby preventing the SR from interfering with the measurements. All experiments were conducted at a sarcomere length of 2.2–2.3 μm and a temperature of 15°C.

Intact Muscle Mechanics.

Muscle bundles were activated by direct supramaximal electrical stimulation from parallel plate electrodes while held isometrically between a fixed hook and a force transducer, as in ref. 8. Mean sarcomere length was measured by laser diffraction. The bundles were presented with either single stimuli (which produced twitches) or repetitive stimuli (which produced tetani). The rate of relaxation was measured in isometric twitches. The rate constant for the average decay in force was measured during the initial slow phase of relaxation (i.e., when force falls from 95% to 80%, as in ref. 16), when sarcomeres are generally isometric. It should be noted that during the fast relaxation phase (i.e., when force falls from 80% to 5%), the faster fall in force is likely because of large sarcomere rearrangements (17), which cause sarcomere shortening and an increase in the crossbridge detachment rate constant above the isometric value.

Skinned Fiber Stiffness Measurements and Calculation of the Proportion of Attached Crossbridges.

Active stiffness was measured in fully activated skinned muscle fibers by imposing a series of small stretch and release steps (2–4 nm/half-sarcomere) with a servo motor while recording force and sarcomere length. Striation spacing was detected by using white-light diffraction (18). In these experiments, activation was achieved by flash photolysis of caged Ca²⁺ (see below) because it improved sarcomere homogeneity, particularly in the white fibers. Each fiber was also subjected to the same sized steps after it had been put into rigor by immersion in ATP-free solutions (see Fig. 2), which are described in ref. 19. Stiffness was taken as the slope of a plot of the force change vs. sarcomere length change. Because the force–extension curve in rigor was nonlinear, stiffness was measured in rigor at approximately the same force measured in the active muscle.

Figure 2.

Active and rigor stiffness in skinned fibers of three muscle types from toadfish. Rapid length steps (complete in 200 μs) were applied by a servomotor while sarcomere length and force were monitored. Force is normalized to isometric tension in the active fiber. Note that because of the low active force in swimbladder, but normal Young’s modulus value in rigor, even a very small stretch applied to swimbladder fibers in rigor caused tension to rise to a level ≈3-fold higher than the active force. ΔSL is given in nm/half sarcomere. A sample motor trace (low noise) is shown (Bottom Left). For the red and white fibers, the force increase was slightly greater in the rigor than in the active fiber. In the case of the swimbladder, a 2-fold larger stretch was applied in the active fiber, but the force change was still just a small fraction of that in rigor. All experiments were conducted at 15°C.

The proportion of attached crossbridges during active contraction was compared with those attached in rigor and calculated based on the assumptions that (i) each myosin head contributes the same increment to stiffness in active contraction as in rigor, and (ii) 50% of compliance in a rigor fiber resides in the crossbridges and 50% in myofilaments (20). Then the proportion of crossbridges attached in active contraction is equal to (S_A/S_R)/(2 - S_A/S_R), where S_A is the fiber stiffness in active contraction and S_R is fiber stiffness in rigor. The proportion of attached crossbridges so calculated is a relative measure and does not explicitly depend on all the crossbridges being attached in rigor. If all the myosin heads do not attach or contribute equally to stiffness in rigor, however, this would lead to a corresponding overestimation of the number (an absolute measure) of attached crossbridges in active contraction. This possibility is considered later.

Crossbridge ATP Utilization (ATPase) Measurements.

The rate of ATP splitting by the crossbridges during isometric contraction was measured for the red, white, and swimbladder fibers with a fluorescent coupled-enzyme assay described in ref. 21. This assay uses a stoichiometric conversion of fluorescent NADH to nonfluorescent NAD for each molecule of ATP used by the crossbridges (22). The muscle chamber was mounted on a microscope, and we measured NADH fluorescence from a vigorously stirred 12-μl cuvette that held the isometrically contracting muscle fibers (21).

Rate of Force Development (k_develop) and Rate of Force Redevelopment (k_redevelop).

The rate of tension rise was measured under sarcomere length clamp after activation by flash photolysis of a caged Ca²⁺ compound [nitrophenyl (NP)-EGTA]. The force trace was fitted with a single exponential plus linear “creep” phase, and the rate constant of the exponential phase was taken as k_develop. NP-EGTA (23) is a Ca²⁺ chelator with high affinity (K_D = 80 nM) that photolyzes to iminodiacetic acids that have Ca²⁺ affinities several orders of magnitude lower (K_D ≅ 1 mM), thereby releasing bound Ca²⁺. Solutions were as described in ref. 23. Because the force–pCa relationship varies by approximately one log unit among the three fiber types, it was necessary to first titrate the NP-EGTA for each fiber type to set free [Ca²⁺] to just subthreshold. In this way, on photolysis, sufficient Ca²⁺ was released to saturate the troponin, as was confirmed by comparison to contractions at steady pCa of 4.4 (pCa = −log[Ca²⁺]).

Also, in swimbladder, the rate of force redevelopment was measured after a rapid slack shortening and a rapid stretch back to the starting length (24). In this muscle, holding the fixed ends isometric was sufficient to maintain constant sarcomere length during force redevelopment as monitored by white-light diffraction (18).

Calculations of Crossbridge Kinetics.

The rate constants of crossbridge attachment (f) and detachment (g) were calculated from the proportion of attached bridges (derived from stiffness measurements; see above and Table 1) and from crossbridge ATPase measurements by using the following equations:

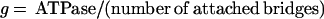1

and

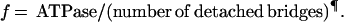2

These relationships assume (i) that f and g are effectively irreversible reactions; (ii) that the stiffness in the rigor state represents all the myosin heads in the fiber (i.e., the proportion of attached crossbridges during contraction estimated from stiffness represents the number of attached crossbridges); and (iii) that all myosin heads are cycling and participate in ATPase activity during active contraction. These assumptions have all been questioned (25–27), but their validity is not required for the main conclusions in the Discussion.

Table 1.

Stiffness, proportion of attached crossbridges, force, and force per attached crossbridge in three fiber types of toadfish

Fiber type	Young’s modulus in rigor MN/m2	Active/rigor stiffness	Proportion of attached crossbridges, %	Force per myofibrillar cross-section, kN/m2	Force per attached crossbridge, pN
Red	34.8	0.82	70	214	3.04
	(2.8)	(0.05)		(20)
White	25.6	0.76	61	228	3.71
	(3.9)	(0.03)		(19)
Swim	42.4	0.19	10.5	56	6.41
Bladder	(4.5)	(0.02)		(9)

Young’s modulus (Δstress/Δstrain) in rigor and the ratio of active to rigor stiffness was measured in experiments illustrated in Fig. 2. The proportion of attached crossbridges in active contraction (relative to that in rigor) was calculated as in Methods. Force per attached crossbridge is the quotient over the fiber’s cross-section of force and the number of attached crossbridges per half sarcomere. Note that if all myosin heads do not contribute to rigor stiffness, the number of attached crossbridges would be reduced and the force per attached crossbridge increased. All values are means of five to eight measurements with the SE shown in parentheses where appropriate. All experiments were conducted at 15°C. 

Determination of Myosin Head Concentration.

Several grams of intact muscle tissue were homogenized in a myosin extraction buffer (0.5 M KCl/0.1 M KH₂PO₄/0.05 M K₂HPO₄/10 mM EDTA/10 mM NaPP_i/4 mM 2-mercapthoethanol) containing proteolytic enzyme inhibitors and centrifuged at 10,000 × g for 30 min. The supernatant was retained and the pellet resuspended and recentrifuged. This procedure was repeated eight times. The remaining pellet was dissolved in 1 M NaOH by sonication for 1 hr at 50°C. All the supernatants were combined and run on SDS/PAGE gels by using our modification (28) of the technique of Talmadge and Roy (29). The gels were stained with Coomassie blue, and myosin concentration was estimated with laser densitometry by using a calibration curve obtained with myosin heavy chain standards (Sigma) with known protein concentration.

The concentrations of myosin heads in intact swimbladder and white muscle were measured to be 69 μM and 167 μM, respectively. The marked difference in concentration reflects the fact that in swimbladder, only about 50% of the fiber cross-section contains myofibrils (3). Myosin content could not be measured directly in red muscle because it makes up only a small proportion of the musculature of toadfish. A value of 117 μM was used for the red muscle, reflecting that in the species of fish in which it has been measured, the myofibrillar volume in red muscle is significantly reduced (compared with white) by its mitochondrial volume of 20%–30% (30).

RESULTS AND DISCUSSION

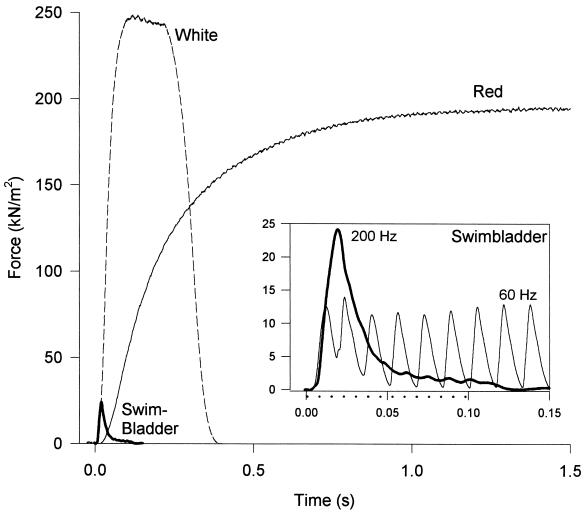
We found that intact swimbladder fibers contract and relax very rapidly but generate extremely low forces. Toadfish fast-twitch white and slow-twitch red fibers used for swimming generate normal forces of about 244 kN/m² and 192 kN/m² [note that when the red muscle value is corrected for 20%–30% mitochondrial volume (30), force per cross-sectional area of myofibrils is almost the same for the two fiber types]. By contrast, the swimbladder fibers generate only about 1/10 that value or 24 kN/m² (Fig. 1). Because of the high content of SR required for rapid reuptake of Ca²⁺ in the swimbladder fibers, myofibrils make up only about 50% of the fiber volume (3). Thus the force per cross-sectional area of myofibrils is 48 kN/m² or only about 1/5 that of the locomotory fibers.

Figure 1.

Force generation during repetitive stimulation in intact bundles of three fiber types of toadfish. Both the red muscle (stimulation frequency = 20 Hz) and the white muscle fibers (stimulation frequency = 50 Hz) produced classic tetanic responses, a smooth and steady force record. By contrast, at a stimulation frequency of 60 Hz, the swimbladder (Inset) produced nearly separate twitches, and at stimulation frequencies of 125 Hz and higher, the swimbladder fibers produced a smooth force record (same trace in main figure and Inset), but force fell rapidly after a peak despite continuous stimulation [the period of stimulation at 200 Hz is depicted by dotted line beneath the time axis (Inset)]. For purposes of illustration, amplitudes of individual traces were scaled to the mean isometric force for that fiber type. Maximum forces (mean ±SE, n = 4) are 192 ± 13 kN/m², 244 ± 19 kN/m² and 24 ± 1.4 kN/m² for the red, white, and swimbladder muscle, respectively. All experiments were conducted at 15°C.

One possible explanation for the low force production in this muscle (as well as other superfast muscles) is that activation might be very low even during a “tetanus” because of extremely rapid Ca²⁺ reuptake from the myoplasm (8). Although both the red muscle and the white muscle fibers produced classic tetanic responses, a smooth and steady force record when stimulated at 20 and 50 Hz, respectively, Fig. 1 Inset shows that swimbladder cannot be tetanized like normal locomotory muscles. If stimulated at 60 Hz, a high frequency for vertebrate muscle, it produces nearly separate twitches. If stimulated at 125–200 Hz, the fused force record rises somewhat higher for a brief time (still to a very low force), but then drops rapidly despite continuous stimulation. To test the possibility that low activation might be responsible for low force generation, we bypassed the normal Ca²⁺ release and reuptake mechanisms and activated permeabilized (“skinned”) muscle fibers with high and steady Ca²⁺concentrations. Under maximally activating conditions, we found that the steady force per cross-sectional area of myofibrils was still very low, 56 kN/m² or about 1/4 that of the other fiber types (Table 1). Force did not increase significantly compared with that of the intact muscle.

Given that activation is maximal, low force production could result from either few attached crossbridges or low force per attached crossbridge (31). To estimate the proportion of attached crossbridges, we compared the stiffness (change of force in response to a quick length change) in the active muscle fiber to that of the muscle fiber in rigor (32), where all the crossbridges are thought to be attached (33–35). In the red and white fibers, a quick stretch of a fiber in active contraction produced a force change only slightly lower than in rigor (Fig. 2), signifying that in active contraction, a considerable proportion of the crossbridges are attached (Table 1). A markedly different result was obtained in the swimbladder. In the experiment depicted in Fig. 2, even though a 2-fold larger stretch was applied in active contraction than in rigor, the force change was tiny in comparison to the response in rigor (Fig. 2). Thus, the ratio of active to rigor stiffness for red and white fibers had values of 0.75–0.82; however, the ratio for the swimbladder was only 0.19 (Table 1).

Because it has been recently determined that approximately half of the sarcomere compliance resides in the crossbridges and the other half in the myofilaments (20, 36–37), the stiffness measurements were corrected for this distribution of compliance as described in Methods (38). According to these calculations, about 60%–70% of the crossbridges were attached during isometric contractions in the red and white fibers compared with the number in rigor. However, under the same conditions, only about 10% of the crossbridges were attached in swimbladder fibers (Table 1). Importantly, the similarity of the Young’s modulus during rigor among the fiber types (Table 1) supports the assumption that in each fiber type a similar proportion of crossbridges are attached and contribute to rigor stiffness. Thus, the reduced force generated by swimbladder is unlikely to be caused by ultrastructural differences (e.g., large interfilament distances), which might prevent formation of force-generating crossbridges.

The above analysis suggests that there is a marked difference in the proportion of attached crossbridges in active swimbladder fibers—but what about the force per crossbridge? Dividing force by the calculated number of attached crossbridges suggests a higher (not lower) force per attached crossbridge for swimbladder fibers compared with the other two fiber types (Table 1). Thus swimbladder fibers generate low force in steady-state isometric contractions, not because of low force per attached crossbridge, but rather because there are few crossbridges attached.

Why are there so few crossbridges attached? To determine whether this feature is a consequence of rapid crossbridge kinetics, we estimated the crossbridge attachment rate constant (f) and the crossbridge detachment rate constant (g). The value g was taken as the quotient of the crossbridge ATPase rate and the proportion of attached crossbridges, and f was taken as the quotient of ATPase rate and the proportion of detached crossbridges (see Methods) (24, 31).

The ATPase rate per myosin head increased about 6-fold between the red and swimbladder fibers (Table 2). The value of g for the swimbladder (≈108 s⁻¹ at 15°C) is by far the fastest reported to date. By comparison, the most studied muscle, the rabbit fast-twitch psoas, has a g that is ≈50-fold lower (≈2- 3 s⁻¹ at 15°C) (24, 39, 40). The white and red muscles have detachment rate constants of about 10.3 and 2.8 s⁻¹, respectively.

Table 2.

Kinetic analysis of three fiber types in toadfish

Fiber type	ATPase head−1s−1	Proportion of attached crossbridges, %	f s−1	g s−1	f + g s−1	kdevelop s−1	kredevel s−1
Red	1.96	70	6.6	2.8	9.3	30
	(0.31)					(3.7)
White	6.30	61	16.2	10.3	26.5	81
	(0.44)					(6.5)
Swim-	11.4	10.5	12.7	108	121	440	435
bladder	(0.74)					(39)	(66)

ATPase values are calculated assuming myosin head concentrations of 117, 167, and 69 μM for the red, white, and swimbladder fibers, respectively, as described in Methods. f and g were calculated as described in Methods. k_develop was measured in experiments illustrated in Fig. 3. k_redevel was measured in release–restretch experiments described in Methods. All values are means of four to eight measurements with the SE shown in parentheses were appropriate. All experiments were conducted at 15°C. 

These crossbridge detachment rate constants are consistent with (i.e., they are equal to or greater than) the initial rates of relaxation from isometric twitches. The initial rates of relaxation (±SE, n = 6–7) are 104 ± 4 s⁻¹ for the swimbladder, 10.6 ± 1.6 s⁻¹ for the white, and 1.52 ± 0.26 s⁻¹ for the red muscles, respectively. The waveform of force decline during muscle relaxation reflects the occurrence of several sequential processes (i.e., Ca²⁺ reuptake, Ca²⁺ unbinding from troponin, and crossbridge detachment). In white and swimbladder muscle, the similarity between initial relaxation rates and the value of g, coupled with the fact that intracellular [Ca²⁺] falls below the threshold value for force generation before the decline in force (8), suggests that crossbridge detachment may be a rate-limiting step in relaxation. In the red muscle, by contrast, the value of g is somewhat faster than the initial relaxation rate, and myoplasmic [Ca²⁺], although falling, remains above threshold during much of the decline in force (8). This suggests that in the red muscle, Ca²⁺ reuptake may be the rate-limiting step in relaxation. Overall, this comparison demonstrates that modifications in actomyosin crossbridge detachment comprise another essential modification for high-frequency contractions. A muscle with the g of the red or white muscles could not relax as fast as swimbladder muscles do.

Although it is the modification of g that underlies the swimbladder’s fast relaxation, it is the relative value of f to g that underlies its low force. It is generally thought that in going from a slow fiber type to a fast one, f increases in proportion with g, maintaining a constant number of attached crossbridges [=f/(f + g)] and thus force (for example, see ref. 41). This is nearly the case for the red and white fibers. However, in the case of the swimbladder, this pattern is dramatically altered. In comparison with the fast-twitch white muscle, g increases approximately 10-fold in swimbladder although f does not increase at all. Thus, whereas in every other muscle studied g is less than or equal to f, in swimbladder g is 8.5-fold higher, resulting in few attached crossbridges.

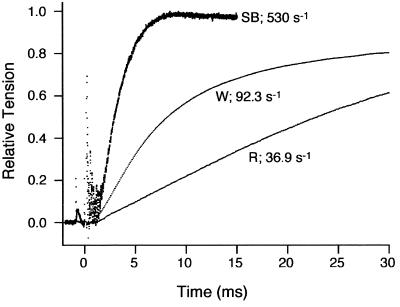
The rate constants for swimbladder fibers determined by the above procedure are extremely fast. We obtained additional evidence for the fast crossbridge kinetics by an independent technique. The rate of force development was measured by activating fibers with Ca²⁺ released by flash photolysis of NP-EGTA (23). Based on the assumption that the rate of Ca²⁺ binding to troponin and subsequent transitions in the regulatory system are rapid compared with the crossbridge attachment and detachment rates, in a two-state crossbridge model the rate of tension development (k_develop) during activation is equal to the sum of f and g (24). Fig. 3 shows that the k_develop changed dramatically with fiber type and was extraordinarily fast for the swimbladder [apparent rate constant = 440 s⁻¹ (Table 2)]. On swimbladder fibers, we also measured the rate of tension redevelopment (k_redevelop) (24, 39, 40) after a large release and restretch and obtained a similar value (435 s⁻¹). These results confirm the very rapid crossbridge kinetics calculated for swimbladder fibers from steady-state stiffness and ATPase measurements described above.

Figure 3.

Force records after photolysis of caged Ca²⁺ are shown for the red, white, and swimbladder fiber types. The rate constants for tension rise (k_develop) are derived from the traces as described in Methods. All experiments were conducted at 15°C.

The fact that for all three fiber types, the k_develop values are ≈3-fold faster than the respective sums of f and g obtained from steady-state measurements (Table 2) could be explained in several ways. First, the number of attached crossbridges may have been overestimated by comparing stiffness relative to rigor (e.g., as mentioned earlier, in the rigor fiber, all of the myosin heads may not be contributing to stiffness) (25, 26), and this would have led to an underestimation of the calculated value of g (see Eq. 1 in Methods). If fewer crossbridges were actually attached, then g would be increased, leading to an increased f + g, particularly in the swimbladder muscle. It should be noted that this overestimation would also affect the values of the force per attached crossbridge (Table 1). Second, not all myosin heads may participate in cyclical attachment, force generation, and ATP splitting during active contraction. For instance, if only one of the two heads of each myosin molecule cyclically attach during contraction, the attachment rate for its partner is effectively zero. In this case the cycling rate (i.e., ATPase rate) for the active head, and thus both f and g, would double. Third, crossbridge kinetics may be substantially faster during the first few crossbridge cycles after activation (i.e., during the k_develop measurement) than during steady contraction (42). Lastly, crossbridge attachment may be reversible with a rate constant of f₋ (24, 43). This would increase k_develop (= f + g + f₋) but not the ATPase rate. Irrespective of these additional factors, the swimbladder demonstrates a much higher g than other muscles.

In conclusion, the very fast relaxation rate of superfast swimbladder fibers has required the evolution of an extraordinarily fast crossbridge detachment rate constant. A high g by itself, however, does not result in low force. Rather, because the crossbridge attachment rate constant remains unchanged in the face of the large increase in detachment rate constant, the number of attached crossbridges during contraction of swimbladder muscle is low. Each attached crossbridge generates a normal force, so the total force production is low. Why f does not increase as much as g in these superfast fibers is unknown. Clearly with a higher f, the muscle would generate greater forces and thus fewer fibers would be necessary to produce sound. It is possible that molecular or physical constraints (e.g., diffusion of the myosin heads) limit the value of f below the ≈200 s⁻¹ required for a high proportion of the crossbridges to be attached. Further, even if a higher f were physically possible, there would likely be a large concomitant increase in the rate of ATP utilization [i.e., ATPase = f × g/(f + g)] (31) of each fiber above its already very high rate. This higher ATP utilization might not be supportable by the rate of intracellular ATP formation and diffusion.

Regardless of the underlying mechanism, a consequence of very low force output combined with very high ATP splitting is that the crossbridges of the swimbladder fibers require ≈18-fold and ≈6-fold more energy than those of the red and white muscles, respectively, to produce a given level of force. Thus toadfish strikingly illustrates that muscle designs can be mutually exclusive—the locomotory fibers are too slow to produce sound at 200 Hz (8), and at the low frequencies of steady swimming (2–5 Hz), the superfast swimbladder fibers are too costly to power locomotion because their high cost would likely require far more oxygen than the cardiovascular system could supply.

Finally, low force per cross-sectional area of myofibrils has been previously reported in other superfast muscles, although no mechanism was offered (1, 4). It is likely that an extremely high g combined with a normal f (i.e., g ≫ f) is responsible for low force in these muscles, too. Thus, this crossbridge mechanism [in addition to the previously identified reduction in myofibrillar volume (1–7)] makes a trade of force for speed a general design principle in superfast fibers.

ABBREVIATIONS

SR

sarcoplasmic reticulum

NP-EGTA

nitrophenyl-EGTA