Restoration of MRI Data for Field Nonuniformities using High Order Neighborhood Statistics

Abstract

MRI at high magnetic fields (> 3.0 T ) is complicated by strong inhomogeneous radio-frequency fields, sometimes termed the “bias field”. These lead to nonuniformity of image intensity, greatly complicating further analysis such as registration and segmentation. Existing methods for bias field correction are effective for 1.5 T or 3.0 T MRI, but are not completely satisfactory for higher field data. This paper develops an effective bias field correction for high field MRI based on the assumption that the nonuniformity is smoothly varying in space. Also, nonuniformity is quantified and unmixed using high order neighborhood statistics of intensity cooccurrences. They are computed within spherical windows of limited size over the entire image. The restoration is iterative and makes use of a novel stable stopping criterion that depends on the scaled entropy of the cooccurrence statistics, which is a non monotonic function of the iterations; the Shannon entropy of the cooccurrence statistics normalized to the effective dynamic range of the image. The algorithm restores whole head data, is robust to intense nonuniformities present in high field acquisitions, and is robust to variations in anatomy. This algorithm significantly improves bias field correction in comparison to N3 on phantom 1.5 T head data and high field 4 T human head data.

1. INTRODUCTION

The accurate acquisition of MRI data requires a homogeneous radio-frequency field, which is not possible to achieve. The inhomogeneity, sometimes termed the “bias field”, is more pronounced at MRI of high fields (> 3.0 T ), where the radio-frequency wavelength gets shorter, approaching the dimension of the human head or body. The local dielectric properties of these regions lead to nonuniformity of image intensity, greatly complicating further analysis such as registration and segmentation. Existing methods for bias field correction have been reasonably effective for 1.5 T or 3.0 T MRI, but are not completely satisfactory for higher field data. This paper develops an effective bias field correction for high field MRI especially for quantitative brain imaging at 4 T .

There have been several attempts to correct for nonuniformity during acquisition based on its physical properties. The nonuniformity of the transmission coil has been estimated from its frequency response to parameterized acquisition sequences.^1,2 In addition, the nonuniformity of transmission and receiver coil(s) combined has been approximated using phantoms.³ However, the physical correction methods are valid only for a particular MRI sequence, but do not account for the complicated interaction between the radio-frequency fields and the human body. It is not obvious how the combined nonuniformities can be accounted for during acquisition, especially for higher magnetic fields. Thus, existing methods for correction of the nonuniformities during acquisition are incomplete, time consuming, and clinically impractical.

As an alternative to physical corrections, several post-acquisition restoration methods have been proposed to account for the effect of nonuniformities that do not require additional acquisitions and are applicable to a range of MRI sequences. They make regularity assumptions about the field nonuniformity as well as anatomy and treat the nonuniformities in the same way irrespective of their sources. Typically, they operate on the logarithm of image intensities of the data^4–6 and assume that the bias field can be approximated by basis functions such as Gaussians, splines, polynomials, or sinusoids. The simplest approach to address this problem has been homomorphic filtering.^7,8 This is based on the assumption that the bias field corresponds to spatial frequencies lower than those of the anatomy. Thus, smoothing an image in the spatial or frequency domain gives the nonuniformity. Smoothing has also been applied to statistics of local histograms computed over image tiles.^7,9 The basic assumption of homomorphic filtering, that the spatial frequencies of the bias field are lower than those of the anatomy can be problematic for high field MR images. In such images the nonuniformity can extend from the low frequency part of their spectrum until the intermediate frequency range.

Another class of approaches derives bias field estimations by registering the data to a tissue template or atlas of expected intensity distribution and by computing either directly¹⁰ the difference between actual and expected values or using the templates as a prior for subsequent processing.^5,11 Bias field estimation has also been combined with tissue classification. Many of these approaches require initialization with manual presegmentation^12–15 while others are fully automatic. Some of these approaches estimate tissue classification based on expectation maximization¹⁶ over the histogram,^13–15,17 and fuzzy c-means classification.^18,19 Intensity tissue classification has also been combined with spatial Markov random fields.^{4–6,13–15} Estimating the bias field with registration and segmentation depends extensively on the prior assumptions. The accuracy of registration is affected when the image has an intense bias field such as that present in > 3 T images. This poses a problem when registration is used to extract the brain region from a head image. Also the priors of an algorithm may be unable to represent the intensity variations of anatomy or pathology in the data. Moreover, there may not be adequate contrast between the assumed tissue classes.

Several non-parametric approaches have been suggested that are more robust to inter and intra subject variability as well as pathology. One such class of non-parametric techniques is based on the retinex algorithm.^20–22 This algorithm uses the logarithm of the intensities and normalizes them to the geometric mean of the intensities within a neighborhood. Thus it enhances the components of the nonuniformity whose wavelength is close to the size of the neighborhood considered and hence introduces overshooting contours at the borders between different tissue regions.²¹ This problem can be alleviated but not resolved by using the multiresolution of an image in terms of a Gaussian or a more general wavelet representation.^22,23 Another class of non-parametric approaches assume that the image is a piecewise union of extensive regions of constant intensity. These methods compute image derivatives such as the gradient or Laplacian and threshold their low values assumed to be due to nonuniformities exclusively. The remaining derivatives are incorporated into a regularized cost functional whose minimization estimates the nonuniformity.^24,25 The assumption of extensive homogeneous regions may not hold as in the brain cortex in head imaging. Both retinex and variational methods operate locally and may not restore global image statistics. They also assume a distinction between a low frequency nonuniformity and a high frequency anatomy. More generally, corrections that use differential image properties may lead to different restorations for different image regions.²⁶

Another class of non-parametric techniques uses the global image intensity histogram.^27,28 These methods can capture global image properties. They assume that the bias field widens the intensity distributions of the various tissues. Thus, the inverse is assumed to provide a deconvolution for sharpening the histogram and restoring image uniformity. This is achieved by estimating a smooth estimate of the nonuniformity. A commonly used technique, N3,²⁸ was found to have a performance superior to those based on homomorphic filtering.²⁹ The ability of the intensity histogram to discriminate between different distributions affected by high fields is limited due to the corruption of the distributions caused by the spatial nonuniformity. A common sharpness optimality criterion for histogram based methods is minimum entropy, which corresponds to single peak histograms resulting from a flat image.^27,30,31 Thus, the entropy criterion can be problematic in terminating an iterative numerical algorithm.

To address the problem of uniformity restoration we use a nonparametric approach. In this study that is based on high order intensity coincidence or cooccurrence statistics. Since it is a nonparametric approach it is robust to subject anatomy, pathology, and intensity variations within a tissue. The cooccurrence statistics represent the intensities of different tissues as well as the joint intensities of adjacent tissues. The high order of coincidences favor dominant distributions and selectively decrease the contribution of noise to their variance. The unmixing of the bias field from these statistics is done by considering its physical effect on the original intensities, rather than their logarithm. The restoration is iterative with a robust stopping criterion based on the entropy of the distribution normalized with respect to the dynamic range, namely, the scaled entropy. Our algorithm was able to perform bias field restoration for human head data acquired under high field with an emphasis on the brain region that gives rise to the dominant distributions of the white matter and of the region around the interface between white matter and gray matter. It was found to have a better performance than N3 over the same data.²⁸

2. INTENSITY NONUNIFORMITY MODEL

We assume that the measured image I and intrinsic anatomic image I_A are related according to:

$$I=B{I}_A+N.$$ (1)

where matrix B contains the unknown nonuniform field and the noise N is additive. The statistics of I_A are assumed to consist of distributions that can be discriminated.

The Taylor series expansion of the bias field around a voxel x₀ gives:

$$B\left(\mathbf{x}\right)=B\left({\mathbf{x}}_0\right)+\nabla B\left(\mathbf{x}\right){\mid }_{{\mathbf{x}}_0}(\mathbf{x}-{\mathbf{x}}_0)+O\left({\mathbf{x}}^2\right).$$ (2)

Approximation up to the first order term leads to a bias field which is locally linear within a sphere of radius ρ = x − x₀ around x₀. Thus, quadratic and higher order terms are assumed to be negligible within distance ρ from x₀. The nonuniformity is recovered within a scale factor which does not affect the discriminability between tissues. We also assume that the noise N is stationary, Gaussian, and white.³² In addition to the spatially smooth variations the nonuniformity also has abrupt variations at the borders between different tissues. However, we assume that these can be absorbed into the tissue statistics.

3. METHODS

The objective of this work is to decompose the product in equation (1) to estimate I_A and a smooth B. We unmix the effect that nonuniformity B has on the statistics of I. This provides a rough estimate of the nonuniformity. We also assume that the nonuniformity B is spatially smooth, which is imposed directly by Gaussian smoothing. Thus, we do not consider noise in equation (1), which has high spatial frequencies. The restoration is iterative with a stable stopping criterion. An overview of the algorithm is sketched in figure 3.

Figure 3.

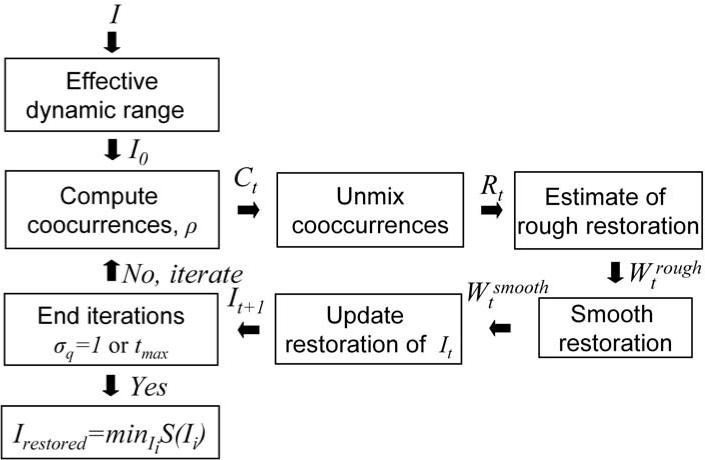
A block summary of the algorithm.

3.1. Determining the Valid Dynamic Range of the Image

The valid dynamic range of the MR contrast mechanism is detected and very bright artifacts due to instrumental imperfections or blood flow are removed. Such artifacts do not follow the nonuniformity assumption of equation (1). To this end we compute the histogram h of the original image I and the cumulative histogram ${\mathcal{H}}^{\prime }={\int }_{u}hdu$. The latter is normalized to unit L₁ norm $\mid \mathcal{H}\mid =1$. We compute the intensity value u^0.9 that corresponds to the upper 0.9 percentile of $\mathcal{H},\mathcal{H}\left(u^{0.9}\right)=0.9$. The intensity range up to 1.5 × u^0.9 is preserved, whereas the intensity range beyond that value is linearly compressed to the range (1.5 × u^0.9, 3.0 × u^0.9] with maximum intensity u_max = 3.0 × u^0.9 to provide an initial estimate of image I₀. The same intensity range [0, u_max] is maintained during the iterations t. The image is a map to this intensity range from its domain D, I_t : D → [0, u_max].

3.2. High Order Intensity Cooccurrence Statistics and their Properties

The statistics used in this work are the n^th-order cooccurrences of pairs of intensities within a spherical neighborhood in the image I_t with radius ρ, assuming that the field in windows of this size is linear. The count of intensities in range u ∈ [0, u_max] in a sphere of radius ρ around voxel x₀ is given by:

$$h_t({\mathbf{x}}_0,u)={\int }_{I_t^{-1}\left(u\right)\cap \mid \mathbf{x}-{\mathbf{x}}_0\mid \le \rho }d\mathbf{x}.$$ (3)

In an n^th-order cooccurrence of intensity range u₁ and intensity range u₂ the center of the spherical neighborhood has intensity within u₁ and the remaining window contains at least n − 1 voxels of the same intensity and at least n voxels of intensity u₂. Additional voxels of any of the two intensities within the spherical window ρ give the cooccurrence:

$$ct({\mathbf{x}}_0,u_1,u_2)=\{\begin{array}{cc}{h}_t({\mathbf{x}}_0,u_1)-(n-1)+h_t({\mathbf{x}}_0,u_2)-nif{I}_t\left({\mathbf{x}}_0\right)\in u_1\hfill & \cap h_t({\mathbf{x}}_0,u_1)\ge n\cap \hfill \\ \hfill & \cap h_t({\mathbf{x}}_0,u_2)\ge n\hfill \\ 0\hfill & otherwise.\hfill \end{array}\phantom{\}}$$ (4)

where c_t(x₀, u₁, u₂) is the cooccurrence at x₀ for iteration t. The image cooccurrences are given by integrating the voxel cooccurrences over the entire image domain. The cooccurrence statistics are computed with a two dimensional Gaussian Parzen window G(σ_c) to give a 2D matrix:

$$C_t(u_1,u_2)={\int }_D{c}_t(\mathbf{x},u_1,u_2)G\left({\sigma }_c\right)d\mathbf{x}.$$ (5)

This is the joint intensity distribution of n^th-order of an image with itself computed within spheres of radius ρ. The resulting matrix C_t is not necessarily symmetric. The cooccurrences of a region with a contiguous tissue lie close to the diagonal of matrix C_t. The joint cooccurrences of tissues around an interface of different tissues lie farther from the diagonal. To examine the properties of the cooccurrence matrix we assume that the distributions of I_A in the cooccurrence statistics C_A are Gaussian. The noise variance of the dominant distributions in the cooccurrence matrix is decreased with increasing cooccurrence order. Thus, the discriminability between the dominant distributions in C_A is increased.

The effect of the presence of additive zero mean Gaussian noise N in an image is an increase of the variance of the distributions in C_t. The effect of image intensity nonuniformity on an intensity cooccurrence between u₁ and u₂ where u₁ is the intensity of the central voxel at x₁ in a hypothetical anatomic image I_A is to scale and rotate it about the origin of C_t. The zero order term B_t(x₁) in equation (2) scales cooccurrences around the origin and the first order term ∇B_t(x₁) in equation (2) rotates them around the origin. Thus, the effect of the nonuniformity on C_t is easier to examine in polar coordinates (r, ϕ), where $r=\sqrt{u_1^2+u_2^2}$ and tan ϕ = u₂/u₁. We assume that the variation of the cooccurrence statistics of the nonuniformity B_t in the cooccurrence statistics C_Bt along the radial axis, r, is given by a Gaussian distribution for Δr, G(σ_r). It follows from³³ that the effect of the nonuniformity on σ_r is given by:

$$\Delta {\sigma }_r\left({\mathbf{x}}_1\right)\infty B\left({\mathbf{x}}_1\right)r.$$ (6)

The rotation angle Δϕ of the nonuniformity in its cooccurrence statistics C_Bt is given by:

$$\Delta \varphi (\varphi ,\alpha )=2{\sin }^{-1}\left[\frac{1}{\sqrt{2}}\sqrt{1-\frac{1+{\tan }^2\varphi (1+\alpha )}{\sqrt{(1+{\tan }^2\varphi )(1+{\tan }^2\varphi {(1+\alpha )}^2)}}}\right].$$ (7)

where α = ∇B. This relation can be derived from figure 1 (a) and is plotted in figure 1 (b). We also assume that the variation of a distribution in the azimuthal axis Δϕ gives rise to a unimodal Gaussian distribution G(σ_ϕ), where σ_ϕ corresponds to a certain value of α.

Figure 1.

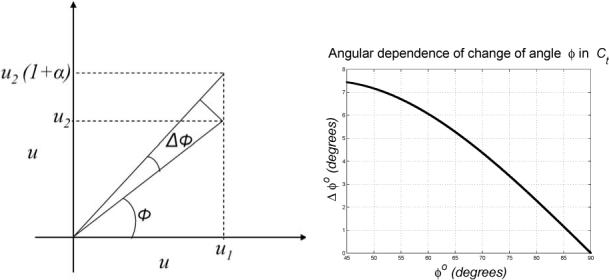
The effect of nonuniformity on the azimuthal size of the deconvolution filter. (a) An intensity pair (u₁, u₂) as a result of the nonuniformity becomes (u₁, u₂(1 + α)), α = ∇B. The angle ϕ of (u₁, u₂) with the horizontal axis becomes ϕ + Δϕ. (b) The effect of a constant nonuniformity α = 0.3 on the rotational angle Δϕ as a function of the angle ϕ. The effect on cooccurrences close to the diagonal is the highest.

3.3. Unmixing the effect of the Nonuniformity from the Cooccurrence Statistics

To decompose the product in equation (1) and estimate I_t and a smooth B_t we use the cooccurrence statistics to unmix the effect that the nonuniformity B_t has on C_t,where B_t is the estimate of B at iteration t. To unmix the effect of the nonuniformity we compute the inverse of the Gaussian nonuniformity distributions for Δr and Δϕ. The inverses of these distributions give the restoration filters of the cooccurrence matrix. The radial restoration filter is $f_r=\frac{G\left({\sigma }_r\right)}{{\Vert G\left({\sigma }_r\right)\Vert }_2^2+∊}$ and the angular restoration filter is $f_{\varphi }=\frac{G\left({\sigma }_{\varphi }\right)}{{\Vert G\left({\sigma }_{\varphi }\right)\Vert }_2^2+∊}$, where ∊ is very small nonzero constant. In equation (6) the radial distortion is proportional to r. Thus, the size of the radial deconvolution filter has the same linear dependence, σ_r ∝ r. The size of the radial restoration filter in the algorithm is its standard deviation normalized with respect to the dynamic range to give its normalized standard deviation:

$${\sigma }_r^n=\frac{{\sigma }_r}{u_{max}}.$$ (8)

The azimuthal restoration filter is represented in terms of angle in radians and hence it is inherently normalized to the radius r in C_t, which is the dynamic range. The standard deviation of the angular restoration filter, σ_ϕ, can be determined from equation (7). The 2D restoration filter f_q = f_r * f_ϕ is applied to the cooccurrence matrix C_t. This will map every cooccurrence (u₁, u₂) to the expected one $(u_1^q,u_2^q)$ to give the expected restored cooccurrence matrix $C_t^q$. The restoration of the cooccurrence matrix gives a restoration matrix R_t with a gain factor for each intensity cooccurrence. The gain is the ratio of the new position $u_1^q$ of the intensity of the central pixel over the initial position u₁ of the same intensity. Thus, the restoration factor or gain is $R_t(u_1,u_2)=u_1^q∕u_1$.

3.4. Estimation of the Spatial Nonuniformity

The restoration matrix R_t is backprojected to the image. We consider a sphere of radius ρ around a voxel x₁. The size of this neighborhood is the same as the size of the neighborhood that was used to compute the cooccurrence statistics C_t. This sphere gives $(\frac{4}{3}\pi {\rho }^3-1)$ intensity cooccurrences with the intensity of voxel x₁. These intensity cooccurrences index the restoration matrix R_t to get an equal number of gain factors. Their expected value gives a rough estimate of the restoration image $W_t^{rough}$ at x₁:

$$W_t^{rough}\left({\mathbf{x}}_1\right)=E_{{\mathbf{x}}_2}\left(R_t\left(I_t\left({\mathbf{x}}_1\right),I_t\left({\mathbf{x}}_2\right)\right)\right)=\frac{1}{(\frac{4}{3}\pi {\rho }^3-1)}\sum _{\mid {\mathbf{x}}_2-{\mathbf{x}}_1\mid \le \rho }{R}_t(I_t\left({\mathbf{x}}_1\right),I_t\left({\mathbf{x}}_2\right)).$$ (9)

This is the inverse of the rough estimate of the nonuniformity $W_t^{rough}\left({\mathbf{x}}_1\right)=1∕B_t^{rough}\left({\mathbf{x}}_1\right)$. The nonuniformity field is assumed to be smooth. Thus, the restoration image $W_t^{rough}$ is filtered with a spatial Gaussian filter G(σ_w) to give $W_t^{smooth{,}^{\prime }}=W_t^{rough}\ast G\left({\sigma }_w\right)$.

In practice the Gaussian distributions of the nonuniformity statistics can only be approximately inverted to give the deconvolution filters. As a result they contain a low frequency component that tends to contract the dynamic range of the image with iterations t. It is necessary to normalize the effective dynamic range since the standard deviation of the radial deconvolution filter is a function of u_max. The normalization is done with the cumulative histogram of the image I_t by rescaling the intensity range to ensure that the upper 0.9 percentile, u^0.9,t, of the cumulative histogram ${\mathcal{H}}_t,{\mathcal{H}}_t\left(u^{0.9,t}\right)=0.9$ remains constant with iterations t. That is:

$$W_t^{smooth}=W_t^{smooth{,}^{\prime }}\frac{u^{0.9,0}}{u^{0.9,t}}.$$ (10)

The restoration from equation (10) is applied to the restored image pixelwise $I_{t+1}=I_t\times W_t^{smooth}$ to improve its estimate.

3.5. Condition for End of Iterations

The Shannon entropy of the cooccurrence statistics of an image monotonically increases as it is corrupted with a smooth nonuniformity from which it follows that the Shannon entropy of the cooccurrence statistics of an image is larger than the one of the assumed intrinsic anatomic image, S(C₀) > S(C_A). However, the Shannon entropy of the cooccurrence statistics of an image with the normalized effective dynamic range, namely, the scaled entropy of the cooccurrence matrix is a non-monotonic function of the iterations t. The scaled entropy is used as a stopping condition of the iterations. When the scaled entropy increases S(C_t+1) > S(C_t) the size of the deconvolution filter is halved σ_q,t+1 = σ_q,t/2. The iterations end when the size of the deconvolution filter becomes unity, σ_q,tend = 1. The restored image is the one whose cooccurrence matrix has minimum scaled entropy t_q = min_t∈[0,tmax] S(C_t), where t_max is the maximum allowed number of iterations.

3.6. Implementation Issues of the Algorithm

The computational cost of the algorithm can be accelerated with minimal loss of accuracy. The deconvolution of C_t to get R_t can be accelerated by considering that the deconvolution filter f_q is separable. The size of the deconvolution filter is bounded in the implementation. This improves the robustness of the deconvolution with respect to noise and flow artifacts that can produce very high intensities. A bound on the size also avoids an unnecessary increase of the computational cost. Its maximum size ${\sigma }_{r,max}^n$ corresponds to radial distance in C_t equal to u^0.9,0 of the histogram of the original image I₀. That is, the maximum radial size of the filter is ${\sigma }_r=r{\sigma }_{r,max}^n∕u^{0.9,0}$. In effect ${\sigma }_{r,max}^n$ determines the radial size of the deconvolution filter. We also set a maximum value for the size of the angular deconvolution filter σ_ϕ,max for similar reasons. It is obtained for u^0.9,0 as well as ϕ = 45° in C_t and a certain value of α in equation (7). The small value of the spatial window of radius ρ for the computation of the cooccurrence statistics makes the significance of the radial standard deviation σ_r greater than that of the angular standard deviation σ_ϕ.

The computation of the cooccurrence matrix C_t with the discretized version of equation (5) can be accelerated by spatially subsampling the voxels in a sphere of radius ρ with a factor of Δρ. The same subsampling Δρ can be used to compute the rough nonuniformity correction $W_t^{smooth}$ in the discretized version of equation (9). The Gaussian filter applied to $W_t^{rough}$ is separable. The algorithm can be further accelerated by using a multiplicative factor for the smooth nonuniformity correction $W_t^{smooth}$ prior to applying it to the image. The computations can be limited by bounding the maximum allowed number of iterations t_max. The speed of the algorithm can also be increased without loss of accuracy by taking advantage of the fact that all the steps of the algorithm are fully parallelizable.

4. EVALUATION OF THE ALGORITHM

Our algorithm has been implemented in the C++ programming language. The algorithm was applied to whole head imaging data. A preprocessing step was used to remove the low signal regions with background or noise. To this end a Rayleigh distribution was fit to the diagonal self-cooccurrence statistics. The nonuniformity was computed over the foreground region and subsequently extrapolated over the low signal regions. The cooccurrence algorithm has been evaluated on phantom as well as real data. It was compared with N3,²⁸ a commonly used algorithm for bias field correction.²⁹ The parameters of N3 are the FWHM of the deconvolution kernel and the distance between the knots of the spline bases. The values used for these parameters are listed in table 1 and were combined with the least spatial decimation factor of two. The algorithm was evaluated for phantom images with the noise free and bias free MNI head phantom. The algorithm was also evaluated with human head images using the sharpness of the histograms of the restored images that was measured with the Shannon entropy. The nonuniformity was initialized to unity everywhere B₀(x) = 1, ∀x. The standard deviation of the Parzen window in equation (5) was σ_c = 1.5. The cooccurrence statistics in equation (4) were computed in a sphere of ρ = 9 mm with a subsampling factor of Δρ = 3 mm and the order of the statistics in the same equation was n = 3. The size of the deconvolution kernel was ${\sigma }_r^n$ and α = 0.3 in equation (7). The maximum number of iterations was set to t_max = 36.

Table 1.

Parameters used for N3 to correct phantom and human brain imaging data.

	Suggested phantom28	Tested for brain 4T	Used for brain 4T
FWHM of deconvolution	0.15	0.06,0.13,0,20	0.20
Distance of knots in space (mm)	200	20,110,200	20
Decimation in space	2−4	2	2

4.1. Phantom Data

We used the 1.5 T phantom brain and the phantom nonuniformities provided by MNI.^34,35 The spatial smoothing of the nonuniformity in the cooccurrence algorithm was σ_w = 77 mm. N3 was run with the parameters suggested for this dataset²⁸ given in the first column of table 1. We also computed the error maps for that data compared to the uncorrupted original phantom. The original as well as the restored images were normalized to zero mean and unit L₁ norm. They were subsequently subtracted to give the error image. The L₁ norm of the error image was used as a measure of the error.

The error value was lower in all cases with our algorithm compared to N3. This is summarized in table 2. The lower error demonstrates the improved performance of the algorithm as well as the improved stability of its stopping criterion. This is an indication that subsequent applications of the algorithm to an image will have a limited or no effect. Two example corrections with the highest level of simulated nonuniformity used, 40%, and noise levels of 3% and 5% are shown in figures 4(a) and (b), respectively. In each example the first row shows the original corrupted phantom with bias field and noise, the second row shows the restoration with N3, and the last row shows the restoration with the cooccurrence algorithm. The images are shown with the dynamic range windowed to that of the white matter. The N3 restoration contains a considerable residual of the bias. The white matter intensity in the image restored with the cooccurrence algorithm is more uniform. The average time duration of the cooccurrence algorithm is 37 min whereas that of N3 is 31 min.

Table 2.

The error is the absolute value of the difference between a corrupted phantom image and the noise free and bias free MNI phantom. A variety of synthetic bias fields B and noise levels N were used. In all cases the error of the cooccurrence algorithm is lower. The greater difference is that for the bias and noise free image.

	N = 0%	N = 3%	N = 5%	N = 5%	N = 5%
	B = 0%	B = 40%	B = 0%	B = 20%	B = 40%
N3 (10−2)	1.40	8.17	12.76	12.56	12.77
Cooccurrence (10−2)	0 (−100%)	7.50 (−8.21%)	12.43 (−2.54%)	12.20 (−2.92%)	12.27 (−3.92%)

Figure 4.

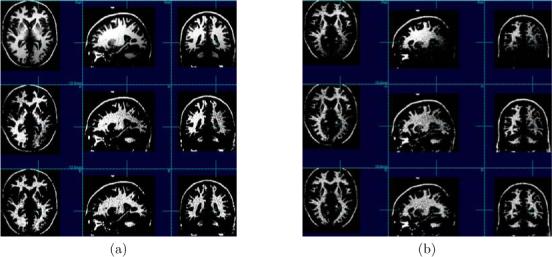
Restorations of two phantom images with nonuniformity of 40% and noise levels 3% and 5% in (a) and (b), respectively. In the first row is the original corrupted phantom, in the second row is the restoration with N3, and in the third row is the restoration with the cooccurrence algorithm. The N3 restoration contains a considerable residual of the nonuniformity. The improved performance of the cooccurrence algorithm is demonstrated by the higher uniformity of the white matter intensity in the image.

4.2. Human Head Data

Human brain MRI data were obtained at 4 T using a T 1-weighted magnetization prepared rapid gradient echo (MPRAGE) sequence and an 8-channel array head coil. The size of the images is 256 × 256 × 176 voxels with uniform voxel resolution of 1.0 mm × 1.0 mm × 1.0 mm. The parameters of the sequence are TR/TE = 2300/3.37 ms, TI = 950 ms, and a flip angle of 7°. The algorithm was applied to geriatric head data images, which were selected randomly from a large database. The 8-channel receiver coil had larger field nonuniformity than a conventional birdcage coil but provided better signal to noise, especially at the outer brain regions close to the coils. The spatial smoothing of the nonuniformity in the cooccurrence algorithm was σ_w = 25 mm. N3 was run for a variety of parameters in the ranges recommended by the authors and given in the third column of table 1. The objective of N3 is to sharpen the histogram distributions. We observed the histograms and selected the parameters that gave the image that had the histogram with the most compact distributions. We also verified our selection by measuring the sharpness with the decrease in the Shannon entropy of a histogram and selected the parameter set that minimized it. The best performing parameters were FWHM = 0.2 mm and distance of 20 mm between the knots, in the fourth column of table 1. The low distance between the knots is consistent with the fact that the 4 T magnetic field gives rise to nonuniformities with a small wavelength. The minimal entropy values are in table 3. In all test cases the entropy of the histogram of the image restored with our algorithm was lower than that of the image restored with N3 indicating that the new algorithm provides an improvement over N3.

Table 3.

In all cases the entropy of the image processed with the cooccurrence algorithm is lower than that of the entropy of the histogram of the image corrected with N3. This demonstrates the higher performance of our algorithm.

Image	N3	Cooccurrence
1	4.85	4.63
2	4.68	4.50
3	4.46	4.30
4	4.84	4.60
5	4.80	4.53
6	4.62	4.45
7	4.85	4.53
8	5.44	5.33
9	4.92	4.90
10	5.15	4.76

Representative corrections of four sets of data are shown in figure 5. In each example the first row shows the acquired image, the second row shows the restoration with N3, and in the last row is the restoration with the cooccurrence algorithm. The images are shown with the dynamic range windowed to that of the white matter. The N3 restoration contains a considerable residual of the nonuniformity and sometimes even accentuates it. Also N3 decreases image contrast by darkening the bright white matter and introducing overshooting contours at the borders between different regions such as between gray matter and white matter at the cortex. The white matter intensity in the image restored with the cooccurrence algorithm is more uniform. It took on average 1 : 23 hrs with the new algorithm to correct the volumetric MPRAGE datasets with 256 × 256 × 176 dimensions given in table 1. The duration of the restoration depends on the amount of the nonuniformity in an image. It took on average 2 : 21 hrs with N3. The cooccurrence algorithm is significantly more efficient.

Figure 5.

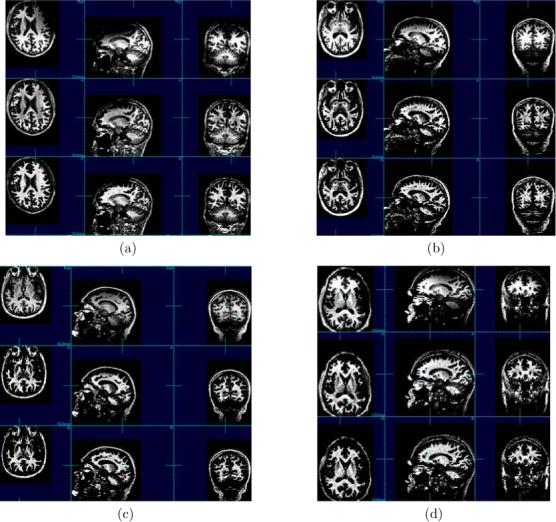
Examples of restorations of four human head images. In each example the first row shows the acquired image, the second row shows the restoration with N3, and in the third row is the restoration with the cooccurrence algorithm. The N3 restoration contains a considerable residual of the nonuniformity and sometimes even accentuates it. Also, it darkens the white matter and introduces overshooting contours at the borders between different regions such as between gray matter and white matter at the cortex. The improved performance of the cooccurrence algorithm is demonstrated by the higher uniformity of the white matter intensity in these images.

5. DISCUSSION AND CONCLUSION

Most intensity uniformity restoration algorithms operate on the logarithm of the image intensities. Even though this intensity transformation can make the problem additive it warps the dynamic range in a non physical way. As a result it can increase noise and decrease the contrast to noise ratio. In this work we operate on the original dynamic range with a physically motivated deconvolution. It is assumed that the corruption of the cooccurrence statistics is caused by a nonuniformity which has a unimodal Gaussian distribution in its cooccurrence statistics. This provides the deconvolution filter f_q. The assumption for the statistics of the nonuniformity corruption may not hold, particularly for high field data. However, the deconvolution is robust with respect to the shape of the deconvolution filter and is mainly dependent on its overall variance. The deconvolution based on cooccurrence statistics takes advantage of the fact that the nonuniformity B is smooth across the borders of different tissue regions.

One of the main assumptions of the deconvolution process is that in the intrinsic anatomic image I_A the variation of intensities within a tissue class is low compared to the distance between the means of the distributions of different tissue classes. The deconvolution is problematic if this discriminability assumption between the distributions in I_A is low or does not exist. In these cases the deconvolution introduces an error that tends to decrease the contrast to noise ratio. If the spatial frequencies of the error are higher than those of the anatomy, the smoothing step can remove them. Otherwise, the restoration will have a lower contrast. In effect the algorithm is unable to unmix nonuniformity between two regions with very similar statistics that are spatially close. The smoothing of $W_t^{rough}$ is done with a Gaussian which has a local effect. Smoothing with more global bases that are polynomials or splines may increase the nonuniformity in $W_t^{smooth}$. In conclusion, we developed a new non-parametric algorithm based on neighborhood intensity cooccurrences for image restoration from nonuniform field distortion. The new algorithm performed significantly better than the well-known N3 approach on high field, 4 T , phantom, and human brain MRI data.

Figure 2.

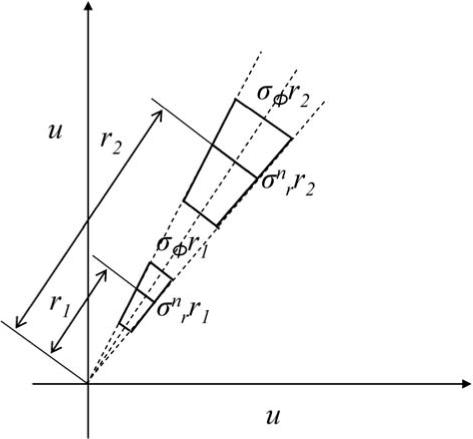
The radial and azimuthal size of the deconvolution filter change with its position on the cooccurrence matrix.