A molecular dynamics simulation study of oriented DNA with polyamine and sodium counterions: diffusion and averaged binding of water and cations

Abstract

Four different molecular dynamics (MD) simulations have been performed for ordered DNA decamers, d(5′-ATGCAGTCAG)·d(5′-TGACTGCATC). The counterions were the two natural polyamines spermidine³⁺ (Spd³⁺) and putrescine²⁺ (Put²⁺), the synthetic polyamine diaminopropane²⁺ (DAP²⁺) and Na⁺. The simulation set-up corresponds to an infinite array of parallel DNA mimicking the state in oriented DNA fibers or crystals. This work describes general properties of polyamine and Na⁺ binding to DNA. Simulated diffusion coefficients show satisfactory agreement with experimental NMR diffusion data of comparable systems. The interaction of the polyamines with DNA is dynamic in character and the cations mostly form short-lived contacts with the electronegative binding sites of DNA. Polyamines, Na⁺ and water interact most frequently with the charged phosphate atoms with preference for association from the minor groove side with O1P over O2P. There is a strong anti-correlation in the cation binding to the electronegative groups of DNA, i.e. the presence of a cation near one of the DNA sites repels other cations from binding to this and to the other sites separated by <7.5 Å from each other. In contrast to the other polyamines, DAP²⁺ is able to form ‘bridges’ connecting neighboring phosphate groups along the DNA strand. A small fraction of DAP²⁺ and Put²⁺ can be found in the major grooves, while Spd³⁺ is absent there. The results of the MD simulations reveal principal differences in the polyamine–DNA interactions between the natural (Spd³⁺, Put²⁺ and spermine⁴⁺) and synthetic (DAP²⁺) polyamines.

INTRODUCTION

Interaction of DNA with oppositely charged ions in solution has been an area of considerable interest during the last few decades. Most effort, from both the experimental and theoretical sides, has been concentrated on studies of the polyelectrolyte properties of DNA in the presence of simple metal ions. Attention has also been paid to interactions between DNA and complex multivalent molecular ions, such as the polyamines spermine⁴⁺ (Spm⁴⁺), spermidine³⁺ (Spd³⁺) and putrescine²⁺ (Put²⁺). Data on DNA interactions with multivalent cations have mainly been obtained in dilute solutions and described in terms of the influence of the charged ligands on DNA condensation (1–3) or DNA double helix–single coil transitions (4,5). Unfortunately, information obtained from these and many other experimental studies (see 6–14 and references cited therein) does not allow for the description of any structural aspects of polyamine binding to DNA.

Polyamines are present in millimolar concentrations in all eukaryotic cells, where they play a significant, but not yet clearly understood, role in biological reactions involving DNA or RNA (15,16). Recently, the interest in polyamine–DNA interactions was renewed in connection with observed condensation/decondensation in solutions of DNA and nucleosomes being influenced by polyamines (17). Another motivation for studying polyamine–DNA interactions is the use of polyamines as potential radioprotective agents (7,18) and anticancer drugs (19). Additionally, the polyamines (mostly Spm⁴⁺) are often used as a condensation agent to crystallize DNA from solution. Since the polyamines remain in the DNA crystals, their influence on the structure and other properties of DNA should be understood. However, the majority of X-ray studies do not report the presence of spermine, which was explained by the dynamic and delocalized character of polyamine binding to DNA (20). Other polyamines have only rarely been used for crystallization and to our knowledge there is only one such structure (21) relevant for the polyamines studied in the present molecular dynamics (MD) simulations. That work reports the presence of Spd³⁺ in the crystal of a DNA–RNA hybrid lying along one of the RNA strands, close to the phosphate groups (21).

Interactions of DNA with multivalent molecular ions have been relatively poorly studied theoretically. Even the smallest polyamines cannot be represented as simple point ions, an approximation inherent in ‘classical’ polyelectrolyte theories like the Manning condensation theory (22) and the Poisson–Boltzmann (PB) theory (23), or used in some Monte Carlo simulations (23,24). Only a few attempts have been made so far to go beyond the point ion approximation (24–26). Specific features of molecular ions, such as their charge distribution and internal degrees of freedom, can readily be taken into account in atomistic computer simulations. Previous MD simulations (27) from other groups on Spm⁴⁺ binding to DNA were limited by considerable simplifications in the models used (e.g. no explicit solvent molecules, lack of charge balance in the simulation cell, rigid structure of the DNA and limited simulation time).

MD simulations on the time scale of nanoseconds, performed with a full atomic resolution of DNA and water molecules with proper treatment of all electrostatic interactions using Ewald methods, have become feasible in the last few years (see 28–35 and references cited therein). Generally, these simulations were performed for a single oligonucleotide at high water content relevant to solution conditions and containing sodium as the counterion. One exception of relevance to the present work is the 15 ns long crystal simulation of the DNA decamer d(CCAACGTTGG)₂, comprising four duplexes in the simulation cell and including sodium as well as magnesium counterions, which was recently published by Bevan et al. (30). In a previous work, we have studied the behavior of water, Spm⁴⁺ and Na⁺ counterions around DNA (20,36) in an ordered system with three parallel DNA fragments in a hexagonal simulation cell, which is comparable to the state of oriented fibers or crystals. Here we account for results from MD simulations of DNA in the presence of the three polyamines diaminopropane²⁺ [NH₃⁺-(CH₂)₃-NH₃⁺] (DAP²⁺), Put²⁺ [NH₃⁺-(CH₂)₄-NH₃⁺] and Spd³⁺ [NH₃⁺-(CH₂)₃-NH₂⁺-(CH₂)₄-NH₃⁺]. For comparison we have performed a simulation of a ‘reference’ system containing only Na⁺ counterions. The simulations were carried out using similar conditions in terms of water content, simulation cell geometry, DNA sequence, etc. The only difference between the simulations is the nature of the counterions neutralizing the negative DNA charge. We also make comparisons with our previous simulations of spermine–DNA and Na⁺–DNA systems, obtained at somewhat higher water content (20,36). By keeping the main parameters in the MD simulations fixed, we are now able to observe the differences in the interactions between DNA and different counterions and to study the influence of different polyamines and Na⁺ on the DNA structure, dynamics and hydration. One additional advantage of the present MD simulation study is that we are able to mimic a realistic system corresponding to oriented fibers or crystals and we can compare our results with NMR and other experimental studies of oriented DNA fibers (37). Furthermore, the DNA state in vivo is commonly ordered and densely packed, therefore, from a biological point of view, there is a strong motivation to model a system under similar conditions.

In the present work the main focus is on general properties concerning the binding of counterions to DNA. Sequence-specific hydration and ion binding properties of DNA and the effect of different counterions on DNA structure will be discussed in subsequent work. We also compare simulated diffusion coefficients for water and polyamines with experimental data obtained on oriented DNA fibers (38). This is the first time that DNA simulations have been compared directly with such experimental data for a similar experimental system.

COMPUTATIONAL PROCEDURES

MD simulations have been carried out in a hexagonal cell with periodic boundary conditions imposed in the xy-plane and in the z-direction (20). In all simulations the cell contained three parallel ordered B-DNA decamers, 900 water molecules and counterions. The sequence of all three double helical DNA decamers in the simulation cell was the same, d(5′-ATGCAGTCAG)·d(5′-TGACTGCATC), with the 3′-end of the each strand connected to the periodic image along the z-axis. Such a simulation set-up corresponds to an infinite array of parallel ordered DNA, thus mimicking DNA in fibers or crystal-like structures. The periodic boundary conditions along the z-direction fix the average DNA twist and rise and help to hold the overall B-like DNA form, while leaving a lot of freedom for local DNA motions, as discussed in previous work (20,36,39,40; see also below).

Four 6 ns long simulations with 20 Spd³⁺, 30 Put²⁺, 30 DAP²⁺ and 60 Na⁺ as counterions for three DNA decamers were carried out. These systems are abbreviated below as Spd, Put, DAP and Na/15, where 15 stands for the number of water molecules per nucleotide. We will also use the abbreviation PA/15, referring to all polyamine–DNA simulations with 15 H₂O/nucleotide. The results from these four simulations will be compared with data from two previous simulations carried out under slightly different conditions (20,36). The first of these contained Na⁺ counterions (Na/20), while the second one contained a 1/1 (in charged groups) mixture of Na⁺ and Spm⁴⁺ (Spm/Na). The Na/20 and Spm/Na systems both contained 20 H₂O/nucleotide as well as 4 Cl^– co-ions. In the present simulations, the DAP, Put, Spd and Na/15 systems contained no co-ions. The set-up of the simulation cell mimics an infinite (or very long) ordered DNA system. Consequently, the present simulation system may be considered to model an array of infinitely long DNA molecules as oriented fibers prepared from high molecular weight DNA. This system is thus somewhat different from the DNA crystal simulations of oligonucleotides in the cell performed by Darden and co-workers (28,30).

The simulation software was the MDynaMix package (41) with the CHARMM 22 force field (42), to model both the DNA and polyamine molecules. For DNA we used the CHARMM parameter files directly as defined in the supplementary material of MacKerell et al. (42). For the polyamines (which are not explicitly described in the CHARMM force field) we used similar structural fragments found for amino acids in CHARMM 22. Thus, the force field parameters have not been independently optimized for the complete polyamine molecules and this may in principle affect the DNA binding properties. Detailed technical information and discussion about force field parameters for the polyamines, water [the simple point charge (SPC) model (43)] and Ewald summation parameters, as well as about procedures for generation of the initial configuration of the system and their equilibration, are collated in Supplementary Material (see also previous work; 39).

The DNA periodicity along the z-axis fixes the length and average helical twist and rise (10 bp/turn) and prevents any major bending of DNA. Although this effect may in principle affect the ion binding, we expect the influence to be small because the imposed periodicity leaves enough freedom for local atomic motions as well as variation of the local DNA structure. In support of the freedom of local groove dynamics within the restrictions of the model, we observed sequence-dependent variations of the minor groove width during the course of the simulation and in response to dynamic ion binding. In addition, we observed considerable time-dependent local (i.e. sequence-dependent) variation in helical twist and rise between consecutive base pairs. The combination of force field parameters and use of periodic boundary conditions has previously been used by us for simulation of the same DNA fragment with different monovalent counterions and was shown to reproduce stable, B-form-like DNA structures (39,40). In the present simulations, the DNA also maintained the B-form, which is confirmed by dominance of the sugar C2*-endo conformation, as well as by the values of inclination, groove width and other parameters clearly in the region of the structural features of the B-DNA double helix. We will analyze some of the structural features (including groove dynamics) of the DNA in subsequent work, focusing the analysis on the interplay between the DNA structure and polyamine binding (Korolev et al., in preparation).

An advantage of the present simulation set-up is that averaging over the three decamers effectively triples the statistical data set for averaging DNA structure and DNA–cation and DNA–water interactions collected over the 6 ns simulation time. Simulated diffusion coefficients were obtained from the slope of the time dependence of the mean square displacement. Radial distribution functions (RDF) and spatial distribution functions (SDF) and averaged structures of the DNA fragments were calculated from the MD data using the trajectory analysis procedures of the MDynaMix package (41).

The essential parameters for the simulated systems, together with some results, are gathered in Table 1. Each of the four simulated systems (DAP, Put, Spd and Na/15) has been previously studied experimentally in our group. The oriented DNA fibers of the corresponding DNA salts with similar water content have been prepared by the wet spinning technique and studied by diffusion and relaxation NMR techniques (38). The MD simulations of the current work with 15 water molecules/nucleotide (the PA/15 and Na/15 systems) correspond to ∼95% relative humidity (RH) for DNA fibers of the polyamine salts or 85% RH for the Na–DNA fibers, while the previous simulations with 20 water molecules/nucleotide correspond to 95% RH of Na–DNA (37) (also included in the tables). We will refer to this data while comparing simulation results obtained in the present study with experimental data. The experimental water diffusion data for Na–DNA at 85 and 95% RH have not been published before. The data were obtained as described in our previous experimental work (38).

Table 1. Properties of the simulated systems and experimental data on diffusion measured by the NMR method (38).

System	Cell dimension (Å)	Density (g/cm3)	Box volume (nm3)	Species concentration (M)	Diffusion parametersa: D × 1010 (m2/s), (R, Å)b	Experimental diffusion coefficienta,c, D × 1010 (m2/s)
DAP	40.3×34.9×33.1	1.318	46.6	32.07 (H2O)	4.6 (16.7) H2O	95% RH: 3.55/3.1 H2O
1.069 (DAP2+)	0.21 (3.57) DAP2+	0.65/0.50 DAP2+
Put	41.0×35.5×32.6	1.306	47.5	31.44 (H2O)	4.85 (17.1) H2O	95% RH: 3.3/3.4 H2O
1.048 (Put2+)	0.29 (4.17) Put2+	0.52/0.46 Put2+
Spd	40.95×35.5×33.1	1.300	48.0	31.15 (H2O)	3.5 (16.0) H2O	95% RH: 3.0/2.5 H2O
0.692 (Spd3+)	0.097 (2.38) Spd3+	0.18/0.17 Spd3+
Na/15	43.3×34.3×32.0	1.380	43.3	34.55 (H2O)	2.5 (13.1) H2O	85% RH: 2.1 H2O
2.303 (Na+)	0.55 (5.8) Na+	no data, Na+
Na/20	44.2×38.3×30.85	1.328	51.9	38.40 (H2O)	4.6 (17.1) H2O
2.045 (Na+)	1.3 (9.5) Na+	95% RH: 5.3 H2O
0.128 (Cl–)	2.5 (10.5) Cl–	no data, Na+

^aThe error in the calculation of the diffusion coefficient, D, is in the range 10–20% for the polyamines and 5–10% for water in the MD simulations (estimated from the variation of the component of D in the x and y directions) and about 5% in experimental NMR measurements (38).

^bR is the mean displacement calculated for 1 ns.

^cThe first figure is D_||, the component of diffusion parallel to the DNA helix axis, and the second is D_⊥, the perpendicular component.

RESULTS AND DISCUSSION

Diffusion

Diffusion is one of the few properties that is directly available from both simulations and experiment. In the case of ordered DNA systems, the diffusion coefficients of counterions and water are strongly affected by the molecular interactions with DNA and may serve as additional indicators of the degree of counterion binding. It is also well known that self-diffusion coefficients are difficult to reproduce in simulations because they depend strongly on the force field employed and a 2- to 3-fold difference is often considered as reasonable agreement (44). Satisfactory agreement between simulation and experimental results for the self-diffusion coefficients would suggest that other properties, not available from experiment, are also reasonably well described in the computer simulations. Calculated self-diffusion coefficients for ions and water from all simulations are gathered in the last two columns of Table 1 together with experimental NMR diffusion results obtained on oriented DNA fibers of the corresponding polyamine or Na⁺ systems (38).

For the polyamines, calculated diffusion coefficients are systematically lower than the experimental values (by a factor of 2–3). There are, however, differences between the simulated and experimental systems, which, particularly in the case of polyamine diffusion, are expected to give slower diffusion (smaller diffusion coefficients) in the simulations. Atomic absorption spectroscopy analysis detected 5 or less molar percent of Na⁺, relative to the DNA phosphate groups (38), as compared to the simulated systems that contain no counterions other than the polyamines. Furthermore, real DNA fibers contain defects and void space, making them somewhat different from the ideal packing of the simulation cell.

The simulated diffusion coefficients for water are higher than in the experiment, although the differences are not large. A lower content of water in the real fibers [13.8, 12.5, and 13.6 H₂O/nucleotide at 95% RH for DAP–, Put– and Spd–DNA, respectively (38)] may be an explanation. Additionally, ionic admixtures (like Na⁺) present in the real fibers reduce the mobility of water. However, the quantitative correspondence between simulation and experiment is actually rather good, given the problem of quantitative reproduction of experimental diffusion coefficients in simulations (44,45). An important result of our study is that, within statistical uncertainty, there is agreement in the trend of experimental and simulation data for water self-diffusion. Increases in the diffusion coefficients along the series: Na/15 < Spd < Put ≈ DAP (regarding the position of Na/20, see below). The order in the series can be explained by Na⁺ ions making water more structured and thereby more immobilized. The Spd position may be explained by the fact that the interaction (occupancies) of the Spd³⁺ amino groups with the phosphate group and with electronegative sites in the minor and the major grooves of DNA are weaker than in the case of of DAP²⁺ and Put²⁺ (see Table 2 and discussion below). The lower presence of Spd³⁺ near the DNA results in a more pronounced water–DNA interaction resulting in slower diffusion in the Spd system compared to the Put and DAP systems.

Table 2. Averaged occupancies of ions (N⁺ or Na⁺) near the phosphate oxygen atoms, in the minor and in the major grooves.

System	Ions					Water
	O1P	O2P	Minor groovea	Major groovea	Total	O1P	O2P	Minor groovea	Major groovea
DAP	0.42	0.10	0.20	0.27	0.97	2.14	2.15	0.82	0.94
Put	0.30	0.13	0.20	0.31	0.94	2.31	2.40	0.86	1.17
Spd	0.29	0.18	0.18	0.08	0.73	2.36	2.37	0.86	1.49
Na/15	0.34	0.10	0.075	0.23	0.74	2.47	2.53	1.07	n.d.
Na/20	0.15	0.056	0.023	0.22	0.45	2.97	2.79	1.22	n.d.
Spm/Nab	0.13/0.04	0.08/0.04	0.054/0.020	0.004/0.048	0.42	2.62	2.68	0.96	1.28

^aAveraged over all electronegative sites.

^bFirst value is for N⁺, second is for Na⁺.

Another result of the present simulations is that water diffusion is slowest in the Na/15 system, in both the experiment and in the MD simulations. Na⁺ ions organize water molecules making them less mobile, whereas the hydrocarbon groups of polyamines squeeze out solvent from the minor groove making water molecules generally more mobile. The presence of the DAP²⁺ and Put²⁺ polyamines has an influence on water mobility roughly similar to the addition of 5 water molecules to Na–DNA salt. The same conclusion was drawn previously in our study of spermine interactions with DNA (20,36). The values of the diffusion coefficients (both experimental and calculated) for the DAP and Put systems are fairly close and within the discrepancy expected between experiments and MD simulations. For the Na/20 system the positioning of water diffusion in the above series is different when comparing simulations and experiment, having the largest value of all in the experiments. This fast diffusion found experimentally for Na–DNA fibers at 95% RH may be explained by the higher (compared to simulations) water content [22 H₂O/nucleotide (38)] and imperfect structure of the real Na–DNA films, effects that are expected to increase for greater water content where crystallinity is poorer (46).

The observed differences in diffusion coefficients between the simulations and the experiment may also be due to deficiencies in the force field used and, in the case of the polyamines, to a limited simulation time. It is well known that diffusion coefficients are very sensitive to the details of the force field (44). From this point of view, the present result for the large organic polyamine and water (using the SPC model) molecules should be considered satisfactory, particularly since the simulated and experimental systems are not identical.

General features of polyamine and water binding to DNA

The observed diffusion of the polyamines corresponds to an averaged displacement of the molecule center of mass ranging from 6.0 (Spd³⁺) to 10 Å (Put²⁺) during the 6 ns simulation time. Such displacement is enough for the polyamine to find varying positions around DNA, given the facts that the distance between neighboring DNA surfaces is less than 6 Å and that the ends of these flexible molecules are more mobile than the centers of mass. Analysis of snapshots made during the simulations and of the observed statistics of contacts of DNA with the polyamine charged groups showed rapid wagging of the (CH₂)_nNH₃⁺ groups (n = 3 or 4), switching their binding positions, not only between the sites in the same DNA oligomer, but also between different oligomers. Several jumps of some polyamine molecules across the cell boundaries were observed in each of the PA/15 systems, demonstrating the dynamic character of the polyamine–DNA interactions. Due to the limited simulation time we did not observe equal results for the chemically equivalent amino groups of DAP²⁺ and Put²⁺. Nevertheless, we believe that our results still give realistic information pertaining to properties of real systems [see more discussion of this issue in our previous work on MD simulation of Spm⁴⁺ in ordered DNA (20,36)].

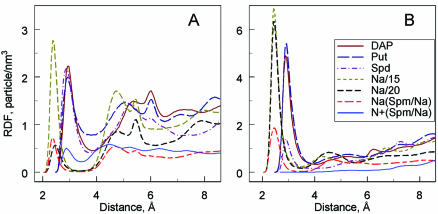
A practical way to display average structural properties of molecules in solution is to use SDF displaying the distribution of surrounding molecules or atoms in a local coordinate system fixed on the solvated molecule. To construct an SDF around the large flexible DNA molecule, the local coordinate system was fixed by the four phosphorous atoms of two neighboring nucleotide pairs (39). Additionally, we calculated RDF of the mobile species (polyamines, Na⁺, water) around electronegative groups of the DNA. To describe the general (non-sequence-specific) binding and dynamics we performed averaging of RDF and occupancies over all electronegative (hydrogen bond acceptor) sites of the DNA bases in the minor (sites T_O2, C_O2, A_N3 and G_N3 were taken into account) and in the major (sites A_N7, G_O6, G_N7 and T_O4) grooves. The corresponding sums of occupancies and intensities of the RDF were divided by four to evaluate the binding ‘per averaged site’ in the minor and in the major groove. The mean occupancies of the charged polyamine amino groups, Na⁺ ions and water near the charged O1P and O2P atoms of the DNA phosphate group and in the minor and the major grooves are collected in Table 2 (see also Fig. 5 displaying averaged RDF). Additional information can be obtained from tables and figures provided in the Supplementary Material. Tables 4S and 5S contain more detailed presentations of the simulation data, where the positions and intensities of the first maximum of RDF, averaged occupancies and residence times of water and cations near the electronegative sites on DNA are collected.

Figure 5.

RDF of ions near the electronegative sites in the minor (A) and in the major (B) grooves. Note that the scales in (A) and (B) are different.

In Figures 1 and 2, the SDFs of both ions and water are displayed around a 2 bp fragment of DNA, seen from the minor groove (Fig. 1) and from the top along the axis of the DNA double helix (Fig. 2). As an example, the average structure of an AC/TG fragment is displayed while the averaging of the SDF was made over all 2 bp fragments. One can see that the counterions, both polyamines and Na⁺ ions, prefer to be in the minor groove of DNA, where the ion SDF have a continuous band of maxima. In turn, water molecules interact extensively with the charged O1P and O2P atoms of the phosphate groups. This result is in agreement with the data of X-ray diffraction studies (47,48) and with other MD simulations (49) of DNA oligomers in the B-form.

Figure 1.

Spatial distribution functions of water, polyamine atoms and Na⁺ ions around a CA/GT fragment. View of the minor groove. Data are for the DAP (A), Put (B), Spd (C) and Na/15 (D) systems, averaging the MD trajectories over 6 ns, with three decamers with three repeated CA/GT fragments in each decamer (see text for details). Water (oxygen, red; hydrogen, gray) is shown for a particle density >40 p/nm³ (except for the Na/15 system, where this value is 50 p/nm³); SDF of the polyamine N⁺ atoms (blue) and Na⁺ (yellow) ions are drawn for a density >10 p/nm³; polyamine carbon and hydrogen atoms not shown. The small magenta balls show the position of the hydration sites of the DNA bases in the minor groove calculated according to Schneider and Berman (54) based on X-ray crystallography data.

Figure 2.

SDF of water, polyamine atoms and Na⁺ ions around a CA/GT fragment in the DAP (A), Put (B), Spd (C) and Na/15 (D) systems. View along the DNA helix axis. Color code and threshold densities of the SDF as in Figure 1. SDF of the carbon atoms of the polyamines (green) are added for a density >20 p/nm³.

A closer inspection of the SDF reveals some differences between the artificial (DAP²⁺) and the natural (Put²⁺ and Spd³⁺) polyamines. First, the site binding DAP²⁺ to the O1P atom inside the minor groove (seen also the SDF and RDF calculated around the PO₄^– group, as described below) does not have an analog in the Put and Spd systems. Instead, a compact area of high density of hydrogen atoms from H₂O is observed at precisely the same location where the amino group of DAP²⁺ can be observed. Secondly, in the DAP system, high presence of the DAP²⁺ amino group is seen in the second hydration layer in the middle of the minor groove. In the Put and Spd systems, no such SDF maximum can be observed. A possible explanation for this may be that the length of the DAP²⁺ molecule fits well in this location in the minor groove, with one amino group bound to O1P and the other in the middle of the minor groove. Another typical configuration of DAP²⁺ binding to DNA is the bridging of the O1P atoms from opposite DNA strands across the minor groove.

Sodium counterions, as well as polyamines, prefer to be in the minor groove. However, a substantial fraction of them is also associated with phosphate groups and in the major groove. In the major groove, Na⁺ ions bind mostly to the electronegative O6 and N7 atoms of guanine and adenine. This binding is strong enough to make the corresponding maxima visible even in the sequence averaged SDF (Fig. 2). The observed features of Na⁺ interactions with DNA agree well with previous MD simulations of DNA carried out at higher water content (31,36,50). Below we separately analyze the general (non-sequence-specific) data on interactions of water and ions with phosphate groups and in the DNA grooves.

Hydration and polyamine binding of the phosphate group

The most intense maxima of water SDF and RDF are found near the phosphate groups, as can be seen in Figures 1 and 2 (see also Supplementary Material, Tables 4S and 5S and Figs. 2S and 3S). A more detailed picture of the hydration of phosphate groups is shown in Figure 3, where the SDF of both water and ions are displayed in a coordinate system fixed on a phosphate group (Fig. 4S in Supplementary Material shows the same SDF at lower threshold values). The binding of water and ions to both O1P and O2P atoms is dynamic and delocalized in space. Sodium ions have longer residence times than polyamine amino groups and are more localized in the vicinity of the O1P atom than are the polyamine amino groups. The other oxygen atoms of the sugar–phosphate backbone serve as secondary binding sites with shorter residence times.

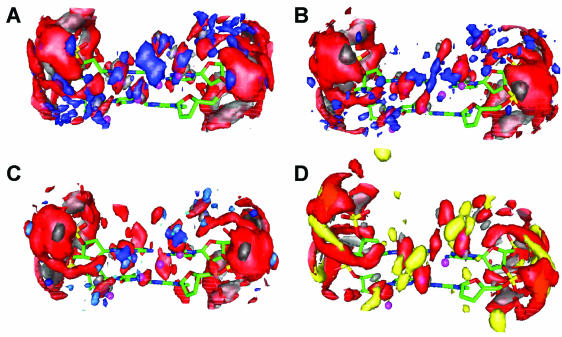
Figure 3.

Water (magenta) and ions (N⁺, blue; Na⁺, yellow) around the phosphate group of DNA in the DAP (A), Put (B), Spd (C) and Na/15 (D) systems. SDF are drawn for densities >100 p/nm³ for water oxygen and >20 p/nm³ for ions.

The negative electric field around the minor groove of B-DNA promotes accumulation of ions along the pass of the minor groove where the cations interact preferentially with O1P in comparison to the O2P atom (Figs 1 and 2). The asymmetry in O1P/O2P binding is especially strong for the synthetic polyamine DAP²⁺. This asymmetry is also large for Na⁺ counterions. Analysis of the MD trajectories shows that DAP²⁺ forms several bridges between neighboring phosphate groups along one of the sugar–phosphate backbones of the same DNA strand on the side of the minor groove. Indeed, the length of DAP²⁺ is very suitable for forming such bridges. For Put²⁺, which is longer, such conformations turned out to be less favorable because it needs to be bent in order to span the O1P–O1P distance along the DNA strand.

The occupancy of the ions in the first coordination sphere of the O1P atom decreases in the following order: DAP > Na/15 > Put ≈ Spd > Spm/Na ≈ Na/20. For the O2P atom this series is different: Spd > Put ≈ Spm/Na > DAP ≈ Na/15 > Na/20. In the sequence DAP, Put, Spd, there is a decreasing correlation in binding to O1P and O2P. The higher occupancy of the amino group near O1P (DAP > Put > Spd) at the same time decreases binding to the O2P atom (Spd > Put > DAP; see Table 2) (RDF are shown in Figs 2S and 3S of Supplementary Material). In contrast, the higher occupancy near O1P for Na⁺ ions (Na/15 > Na/20 > Spm/Na) leads to a more noticeable Na⁺ presence near the O2P atom (the same series is observed for Na–O1P and Na–O2P occupancy: Na/15 > Na/20 > Spm/Na).

It is clear that binding of the ions to the phosphate groups is also dependent on the properties of the hydration shell around the phosphates. Water molecules frequently bind to the O1P and O2P atoms, forming three characteristic SDF maxima around both oxygen atoms. This is also observed in X-ray studies (47,48). This hydration shell generally prevents ions from directly binding to the phosphate groups or at least reduces such binding. That is why most counterions are primarily concentrated in the minor groove. In the case of a lower water content, the hydration shell becomes weaker and the ions can more successfully compete for binding to the phosphate groups. For example, the Na⁺ occupancy calculated at different water content shows that the total (O1P + O2P) cation presence is roughly 2–3 times higher in the systems with 15 H₂O/nucleotide than that for the 20 H₂O/nucleotide systems. This observation shows the importance of a systematic analysis of water content in studying DNA crystals. The reason for the experimentally observed discrepancies in evaluation of the ion coordination at some positions near the DNA sites could originate from different water content in the crystals prepared in different laboratories. Our simulations show that even a small change in water content, such as from 20 to 15 H₂O/phosphate, which is in the range typical for DNA crystals, may substantially change the ion distribution around DNA.

Another feature is that Na⁺ ions do not dehydrate the phosphates as much as the polyamines. This has already been discussed in our previous work on the Spm/Na and Na/20 systems (20,36) and now it can also be seen from the comparison of water occupancies for the Na/15 and PA/15 systems.

SDF around the phosphate groups (Fig. 3) show that the polyamines display differences not only in the values of occupancies, but also in spatial positions of the amino group around O1P and O2P atoms. SDF of water at a high threshold value of 100 p/nm³ (Fig. 3) show a preferable location along three directions outside each of the O1P and O2P atoms with some replacement of H₂O with the cationic group at one of the positions. This feature was observed previously in both simulations (39) and X-ray experiments (47,48). Inspection of the SDF using a lower density threshold of 50 and 10 p/nm³ for water and cations, respectively, shows both the orientation and the intensities of the mobile components in the second coordination layer of the phosphate group (not shown; see Fig. 4S in Supplementary Material). Noticeable difference can be seen for Spd compared to Put and DAP.

Binding of water and polyamines to the DNA bases

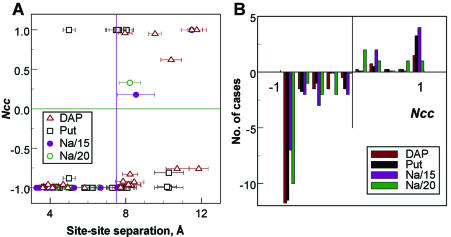
Correlations in ion binding. We have undertaken a special investigation of how the binding of a cation (Na⁺ or amino group of a polyamine) influences the presence of another cation at the neighboring site of the same groove. Figure 4A shows the normalized correlation coefficient (Ncc) for a number of pairs of electronegative sites in the DNA minor and major grooves, as a function of the separation between these sites. Figure 4B displays the distribution of the Ncc values calculated for 20 O1P/O2P pairs of the decamer. We define the value of Ncc by the expression: Ncc = (p₁₂ – p₁·p₂)/(p₁·p₂). Here p₁ and p₂ are the probabilities that sites 1 and 2, respectively, are occupied by cations and p₁₂ is the probability that sites 1 and 2 are simultaneously occupied by different cations. When the binding of a ligand to site 1 does not depend on the presence of another ligand at site 2, then the expected value of Ncc is 0. If presence of the ligand at site 1 precludes binding of the ligand to site 2, then p₁₂ = 0 and Ncc = –1. In the case of a positive cation–cation correlation, Ncc is expected to be positive. In Figure 4 positive Ncc values exceeding 1 were changed to Ncc = 1.

Figure 4.

Ion–ion correlation in binding of N⁺ and Na⁺ (A) to the electronegative sites in the minor and in the major grooves of DNA and (B) to O1P and O2P atoms of the phosphate group. (A) Normalized correlation coefficient (Ncc) is shown as a function of the distance between the DNA sites. Vertical and horizontal bars at 7.5 Å and Ncc = 0.0 are drawn as a visual aid. (B) Ncc values within a 0.2 range (e.g. between –1.0 and –0.8) counted for 20 O1P/O2P pairs of the DNA decamer. To highlight negative and positive ion–ion correlations, counts of negative Ncc were taken as negative numbers. For the DAP and Put systems, each O1P/O2P pair gives four Ncc values, since it is calculated over four possible combinations of the amino groups (e.g. N1–N1, N1–N5, N5–N5 and N5–N1 for DAP²⁺). To compare the counts determined in the Na/15 and Na/20 systems with the similar values of the DAP and Put systems, the latter two counts were divided by four. See text for details.

One can see from Figure 4A that for distances shorter than 8 Å a strong (close to –1) negative correlation in binding of the cations is observed. The single point of positive Ncc found in the Put system is relatively little populated (below 0.1 occupancy between the T15_O2 and A5_N3 sites and N6 of Put²⁺). The data presented in Figure 4A show that there exists a strong anti-cooperative effect in the penetration of ligands to the binding sites of the DNA bases. Typically, the presence of a cation at one site makes it unlikely that another cation will bind to sites of a neighboring base. It is only when the distance between the sites is 7–8 Å or more (second neighboring base or further) that simultaneous coordination of two neighboring cations becomes possible. The results calculated for the ion–ion correlation near the O1P and O2P atoms of the phosphate group (Fig. 4B) are not that convincing compared to the data calculated for the DNA bases (Fig. 4A). Still, most of the Ncc values are in the negative region with clear domination of a high (Ncc between –0.8 and –1.0) anti-correlation of the cation presence near O1P and O2P.

The present conclusion is valid for our sequence of double-helical DNA. It would be interesting to investigate if this effect of cation–cation repulsion has more general validity in biomolecules. Among other aspects it would be appealing to investigate the influence of DNA sequence. Our data show a strong Na⁺ coordination to the G_N7/O6 site in the major groove. However, there is only one single location where guanine bases are close to each other. It is of interest to investigate whether this cation–cation repulsion persists in DNA sequences where guanine bases are close to each other [as in a GG 2 bp step, known as a ‘radical trap’ (51)]. On the other hand, a recent MD study of ion binding and dynamics around bacterial and spinach chloroplast 5S rRNA loop E motifs reports significant occupancies of Na⁺ at several quite close positions near the RNA fragments (52), although the study does not provide information about the distances between ions coordinated to the neighboring sites. However, it demonstrates that the anti-correlation effect observed here should be considered separately for different systems before general conclusions can be made.

Our result may also have implications related to the mechanisms of biological reactions catalyzed by metal cations. Thus, the two-metal catalytic mechanism proposed for self-cleavage of the hammerhead ribozyme (53) (see also 34 for discussion) could be investigated in the light of the present findings.

Water and polyamines in the DNA grooves. Figure 4 shows that the presence of a cation at one site reduces the probability of another cation binding at the sites of the neighboring bases. Simultaneous coordination of the cation seems possible only at sites of the next nearest bases or even further away. This finding establishes an upper limit for the penetration of the cations into the grooves. Binding to the DNA bases depends primarily on such parameters as DNA sequence, local geometry of secondary sites near the principal hydrogen bond donor/acceptor, structure of the ligand, etc. However, for an ‘average’ DNA sequence, the presence of water and cations in the minor and the major grooves can be averaged due to the ion–ion correlation effect discussed above.

Figure 5 displays the RDF of ions averaged over all electronegative sites in the minor and major grooves (similar RDF for water are shown in Fig. 5S of Supplementary Material). From the data shown in Table 2 and in Figure 5, one can see that the presence of the polyamine amino groups is approximately the same for DAP²⁺, Put²⁺ and Spd³⁺ in the minor groove and similar for DAP²⁺ and Put²⁺ in the major groove. Interaction of the amino groups with the DNA bases brings the hydrophobic methylene groups into the grooves and decreases the presence of water (not shown; see Fig. 5S of Supplementary Material). Release of water from DNA due to the presence of the methylene groups of the polyamines makes water more mobile. This explains the faster diffusion of water in the polyamine systems compared to the polyamine-free system at the same water content observed in the experiment and in the MD simulations.

In the minor groove, the amino groups of the polyamines interact rather evenly with all four hydrogen bond acceptors. In the Na/15 system the major binding takes place at T_O2 sites, with lower occupancy at C_O2 and A_N3 sites and an absence of Na⁺ near the G_N3 group. The binding of cations to the minor groove is strongly dependent on the local DNA sequence and geometry. Residence times are also strongly dependent on the nature and the precise geometry of each binding site. These sequence-dependent aspects of counterion–DNA interactions will be discussed in a forthcoming work.

In the major groove, Na⁺ interacts strongly with G_O6/N7 and A_N7 sites and much less with the T_O4 group (Table 2). This binding is also site specific. The affinity for G_O6/N7 (and to some extent for A_N7) is high and the larger water content of the Na/20 system does not change the occupancy of this position. This type of binding is in contrast to other sites (phosphate groups and the sites in the minor groove), where water is capable of pushing Na⁺ away from the DNA in the Na/20 system. In the absence of competition with Na⁺, which is normally capable of strong coordination to G_O6/N7 sites, the polyamines DAP²⁺ and Put²⁺ show significant binding to hydrogen bond acceptors. G_N7/O6 is the major binding site, with some binding to A_N7 and a small affinity for T_O4 (Table 2).

Interestingly, Spd³⁺ [and Spm⁴⁺ in Spm/Na (20)] interacts considerably less with the bases in the major groove than does DAP²⁺ or Put²⁺. It is therefore worth mentioning that Spd³⁺ and Spm⁴⁺ are the most abundant polyamines in eukaryotic cells and are present at millimolar concentrations, whereas Put²⁺ is found in prokaryotes and DAP²⁺ is absent from living cells. Regulatory proteins use a ‘mosaic’ of hydrogen bond donors/acceptors in the major groove for recognition and binding to specific sites in DNA. The necessity to avoid competition between the densely charged polyamines DAP²⁺ and Put²⁺ and proteins for essential sites on DNA could be one of the reasons for the exclusion of these compounds from the composition of eukaryotic cells.

Analyzing the average residence times one can conclude that, apart from a few exceptions, the values for the polyamines are between 5 and 30 ps and show no regularity. On average, the residence times for amino groups are shorter than the corresponding ones for Na⁺ ions in the Na/15 system. As a comparison, the average time for a polyamine center of mass displacement of 3 Å is of the order of 1 ns. This means that the specific binding of polyamines to DNA is not important for their diffusion properties, which are determined by a combination of geometric (DNA as obstacles), electrostatic and hydrodynamic factors. Polyamines interact with DNA in a delocalized and dynamic manner, not forming any long-lived or structurally defined complexes. This is one of the reasons why polyamines are mostly not seen in X-ray studies of DNA crystals (20).

CONCLUSIONS

In this paper, the general properties of binding of different polyamines (DAP²⁺, Put²⁺ and Spd³⁺) and Na⁺ counterions to DNA are discussed on the basis of results calculated from all-atom MD simulations of a system of three parallel ordered DNA molecules in the presence of water and counterions, resembling real DNA in fibers or in crystals. Comparisons with previous results for Spm⁴⁺ counterions and for Na⁺ counterions with higher water content have been made. It should be mentioned that the imposed periodicity in the axial direction, which serves to mimic the infinite fibers, prevents any major bending and keeps the average helical twist and rise fixed, which may impose some restrictions that could affect the ion binding properties.

To visualize the average and sequence-independent distribution of molecular species around the DNA, SDF have been calculated around a dinucleotide base step and around the phosphate groups. This kind of averaging omits features of water/cation binding which are dependent on local details of each specific site and instead we obtain important sequence-independent ‘general’ characteristics of water and ion bind ing. Additional information is obtained in terms of RDF, occupancy numbers, residence times and self-diffusion coefficients.

The main conclusions from the present study are as follows. Polyamines, Na⁺ and water interact most frequently with the charged O1P and O2P atoms. Preferential binding to the O1P atom of the phosphate (from the minor groove side) can be observed. A rather special feature of DAP²⁺ is its ability to form ‘bridges’ connecting neighboring phosphate groups along the sugar–phosphate backbone of the DNA strands. A small fraction of divalent polyamines can be found in the major groove, while spermidine or spermine are nearly absent in the major groove. There is a strong anti-correlation of binding of counterions to the sites of the DNA bases in the minor and in the major grooves. Thus, binding of an NH₃⁺ group of a polyamine or Na⁺ to one site practically excludes binding of another cation to a neighboring site situated less than 8 Å away. Simulated diffusion coefficients show a reasonable agreement with experimental NMR results. Polyamines form only short-lived contacts with the electronegative binding sites of DNA and do not form any structurally defined complexes.

The present analysis intentionally avoids detailed description of structural and site-specific features of water/cation interactions with DNA. Also omitted is any interplay between ion binding, the role of the polyamine in nature and the local structure and dynamics of DNA. These results will be discussed in detail in subsequent work.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.