Vibro-acoustography: An imaging modality based on ultrasound-stimulated acoustic emission

Abstract

We describe theoretical principles of an imaging modality that uses the acoustic response of an object to a highly localized dynamic radiation force of an ultrasound field. In this method, named ultrasound-stimulated vibro-acoustography (USVA), ultrasound is used to exert a low-frequency (in kHz range) force on the object. In response, a portion of the object vibrates sinusoidally in a pattern determined by its viscoelastic properties. The acoustic emission field resulting from object vibration is detected and used to form an image that represents both the ultrasonic and low-frequency (kHz range) mechanical characteristics of the object. We report the relation between the emitted acoustic field and the incident ultrasonic pressure field in terms of object parameters. Also, we present the point-spread function of the imaging system. The experimental images in this report have a resolution of about 700 μm, high contrast, and high signal-to-noise ratio. USVA is sensitive enough to detect object motions on the order of nanometers. Possible applications include medical imaging and material evaluation.

The study of objects in terms of their mechanical response to external forces is of considerable interest in material science and medical diagnosis. Elastic constants are closely connected to the thermodynamic properties of materials and can be related to a wide range of physical parameters. Elastic constants can be determined by measuring deformation in response to an applied force. Although a static force can be used for this purpose, using a dynamic force is preferred if one is interested in measuring the dynamic characteristics of the material (1).

Changes in elasticity of soft tissues are often related to pathology. Palpation is a traditional example of estimating mechanical parameters for tissue characterization, where a static force is applied and a crude estimation of the tissue elasticity is obtained through the sense of touch. In palpation, force is exerted on the body surface, and the result is an accumulative response of all the tissues below. Physicians can sense abnormalities if the response to palpation of the suspicious tissue is sufficiently different from that of normal tissue. However, if the abnormality lies deep in the body, or if it is too small to be resolved by touch, then the palpation method fails.

Elasticity imaging, a subject extensively investigated in recent years, is a quantitative method that measures the mechanical properties of tissue. The general approach is to measure tissue motion caused by an external (or, in some methods, internal) force/displacement and use it to reconstruct the elastic parameters of the tissue. Some investigators have used static force to compress the tissue and measured the resulting strain by ultrasound (2, 3). Others have used external mechanical vibrators to vibrate the tissue and detected the resulting displacement in tissue by Doppler ultrasound (4–7). For a review of elasticity imaging methods, refer to ref. 8. A recently developed method uses an actuator to vibrate the body surface and then measures the strain waves with phase-sensitive MRI (9).

Most of the elasticity imaging methods are based on an external source of force resulting in a spatially wide stress-field distribution. This requires the stress field to pass through the superficial portion of an object before reaching the interior part. Analysis of the object response can be complicated because the stress-field pattern changes, often unpredictably, at different depths before it reaches the region of interest within the object. An alternative strategy is to apply a localized stress directly in the region of interest. One way to accomplish this is to use the radiation pressure of an ultrasound source(s). Based on this strategy, Sugimoto et al. (10) presented a method to measure tissue hardness by using the radiation force of a single focused ultrasound beam. In this method, impulsive radiation force was used to generate localized deformation of the tissue. Resulting transient deformation was measured as a function of time by an ultrasound Doppler method. Radiation force has also been used to generate shear elastic waves in tissues (11).

In this paper, we describe the principles of an imaging technique that produces a map of the mechanical response of an object to a force applied at each point. The method uses ultrasound radiation force to remotely exert a localized oscillating stress field at a desired frequency within (or on the surface of) an object. In response to this force, a part of the object vibrates. The size of this part and the motion pattern depend on object viscoelastic characteristics. The acoustic field resulting from object vibration, which we refer to as “acoustic emissions,”† is detected by a sensitive hydrophone and used to form the image of the object. This method benefits from the high spatial definition of ultrasound radiation force and high motion-detection sensitivity offered by the hydrophone. We call this technique ultrasound-stimulated vibro-acoustography (USVA). Some general aspects of this method, including some experimental results, have been outlined by the authors in ref. 12. Here we present the theoretical foundations of USVA.

METHODS

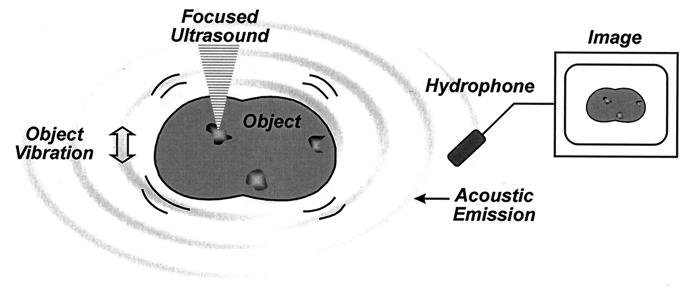
Our aim is to image an object based on its mechanical characteristics. This is achieved by vibrating the object by applying a highly localized oscillating force to each point of the object. The localized force is produced by modulating the intensity, and thereby the radiation force, of the ultrasound at low frequencies (normally in kHz range). The resulting sound emitted by the object is a function of object mechanical characteristics and the location of the excitation point. The image is produced by mapping the amplitude or phase of this sound, which is detected by a sensitive hydrophone, vs. position. Fig. 1 illustrates this method. In the following section, we describe the relationship between the USVA image and the properties of the object.

Figure 1.

Principle of ultrasound-stimulated vibro-acoustography.

THEORY

Generation of a Dynamic Radiation Force on a Target.

The acoustic radiation force is the time-average force exerted by an acoustic field on an object. This force is an example of a universal phenomenon in any wave motion that introduces some type of unidirectional force on absorbing or reflecting targets in the wave path. Radiation force is produced by a change in the energy density of an incident acoustic field. For a review of this phenomenon, refer to ref. 13. Consider a plane ultrasound beam interacting with a planar object of zero thickness and arbitrary shape and boundary impedance that scatters and absorbs. The radiation force vector, F, arising from this interaction has a component in the beam direction and another transverse to it. The magnitude of this force is proportional to the average energy density of the incident wave 〈E〉 at the object, where 〈 〉 represents the time average and S, the projected area of the object (14)

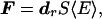1

where d_r is the vector drag coefficient with a component in the incident beam direction and another transverse to it. The coefficient d_r is defined per unit incident energy density and unit projected area. For a planar object, d_r is numerically equal to the force on the object. Physically, d_r represents the scattering and absorbing properties of the object and is given by (14)

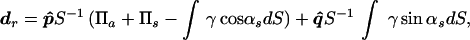2

where p̂ and q̂ are the unit vectors in the beam direction and normal to it, respectively. The quantities Π_a and Π_s are the total absorbed and scattered powers, respectively, and γ is the scattered intensity, all expressed per unit incident intensity. Also, α_s is the angle between the incident and the scattered intensity, and dS is the area element. The drag coefficient can also be interpreted as the ratio of the radiation force magnitude on a given object to the corresponding value if the object were replaced by a totally absorbing object of similar size. This is because |d_r| = 1 for a totally absorbing object. This coefficient can be determined for objects of different shapes and sizes. For simplicity, we assume a planar object normal to the beam axis. In this case, the transverse component vanishes, thus the drag coefficient (force) will have only a component normal to the target surface, which we denote by scalar d_r (F). Values of d_r for spheres, in terms of the diameter and the wavelength, are given in ref. 14.

To produce a dynamic radiation force, one can use an amplitude-modulated beam (15). Consider an amplitude-modulated incident (ultrasonic) pressure field, p(t), as

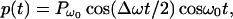3

where P_ω0, Δω/2, and ω₀ are the pressure amplitude, modulating frequency, and center frequency, respectively. In our analysis and experiments, we assume that the condition Δω ≪ ω₀ holds. In such a case, the energy density of the incident field has slow variations in time. To discriminate the slow time variations of a function, let us define the short-term time average of an arbitrary function ξ(t) over the interval of T seconds at time instance t, as 〈ξ(t)〉_T = 1/T ∫_t−T/2^t+T/2 ξ(τ)dτ, which is a function of t. The long-term time average (or simply the time average) is obtained by setting T → ∞. To compute the short-term time average of the acoustic-energy density relevant to field variations at Δω/2, we choose T longer than the ultrasound wave period but much shorter than the modulation period, that is 2π/ω₀ ≪ T ≪ 4π/Δω. Under this condition, the short-term time average of p²(t) is 〈p²(t)〉_T = (P_ω0²/4) (1 + cos Δωt). The energy density is given by p²(t)/ρc², where ρ and c are the density and propagation speed in the medium (16). We are interested in the time-varying component of the short-term time average of the energy density. Denoting this component by e_Δω(t), we can write: e_Δω(t) = (P_ω0²/4ρc²) cosΔωt. This component of the energy density produces a time-varying radiation force on the target (Eq. 1) at frequency Δω. The amplitude of this force, F_Δω, is

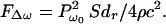4

This equation states that the time-varying force amplitude is proportional to the square of incident ultrasound pressure, or equivalently, to the incident power. If the object moves in response to this force, then the high-frequency ultrasound energy would convert to low-frequency mechanical energy.

Acoustic Emission from a Target Caused by a Dynamic Force.

The radiation force F_Δω vibrates the target object at frequency Δω. Object vibration results in an acoustic field in the medium (acoustic emission). This field is related to object shape, size, and viscoelastic properties. To present a conclusive analysis of this relationship, we have to assume an object with specific characteristics. Here we assume that the vibrating object has a circular cross-section of radius b and uniformly vibrates back and forth like a piston. This choice allows us to illustrate the concept in a simple form. We also consider an area S ≤ πb² of the piston surface to be projected normally by the beam. Similar solutions can be carried out for other objects.‡

The steady-state normal velocity amplitude of a piston, U_Δω, caused by a harmonic force F_Δω at frequency Δω, can be described in terms of the mechanical impedance Z_Δω,

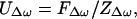5

where Z_Δω = Z′_m + Z_r is comprised of the mechanical impedance of the object in vacuum Z′_m, and the radiation impedance of the object Z_r, all defined at Δω. Modeling the object as a mass-spring system, Z′_m can be written in terms of Δω as (16, 17)

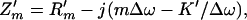6

where m, R′_m, and K′ are the mass, mechanical resistance, and spring constants of the object, respectively. The radiation impedance of the piston can be written (17) as Z_r = πb²(R_r − jX_r) [7], where R_r = ρc[1 − (c/Δωb)J₁(c/2Δωb)], [8], and X_r = (4ρc/π) ∫₀^π/2 sin [(2bΔω/c) cos α] sin² αdα [9], where J₁(⋅) is the first-order Bessel function of the first kind. In many applications of our interest, the wavelength is much greater than the object size, hence, (Δω/c)b → 0. In such cases Z_r assumes a simpler form as Z_r = πb³ρΔω(bΔω/2c − j8/3π) [10]. The mechanical impedance of the piston object can now be written as

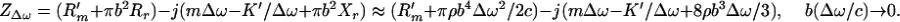11

Once we calculate U_Δω, we can calculate the pressure field it produces in the medium. We assume that the acoustic emission signal propagates in a free and homogenous medium. The farfield acoustic pressure caused by a piston source of radius b set in a planar boundary of infinite extent is given by (17),

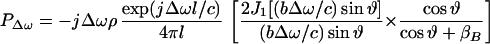12

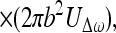where l is the distance from the observation point to the center of the piston, ϑ is the angle between this line and the piston axis, and β_B is the specific acoustic admittance of the boundary surface.§ The factor of two comes from the presence of the boundary wall, which would be replaced by unity if the boundary wall were not present (16). The acoustic emission field resulting from object vibration can be written in terms of the incident ultrasound pressure by combining Eqs. 4, 5, and 12, as

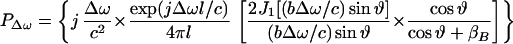13

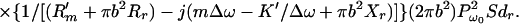For wavelengths long compared to the object size, i.e., when bΔω/c → 0, the term in the first brace approaches a constant, hence we may consider the contents of the first brace to be an object-independent function (the specific acoustic admittance β_B relates to the surrounding boundary surface). Under these conditions, the first brace in the above equation represents the effect of the medium on the acoustic emission field, which we may call the medium transfer function, and denote it by

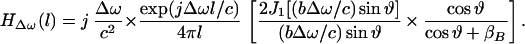14

The second brace in Eq. 13 is 1/Z_Δω, or the mechanical admittance of the object at the frequency of the acoustic emission (Δω), and we denote it by Y_Δω. It is convenient to combine this term with the next term (2πb²) in Eq. 13, as Q_Δω = 2πb²Y_Δω = 2πb²/Z_Δω, which is the total acoustic outflow by the object per unit force (acoustic outflow is the volume of the medium (e.g., the fluid) in front of the object surface that is displaced per unit time because of object vibration.). Function Q_Δω represents the object characteristics at the acoustic frequency. We may thus rewrite Eq. 13 in a more compact form as

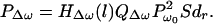15

Eq. 15 indicates that the acoustic emission pressure is proportional to: (i) the square of ultrasound pressure P_ω0; (ii) the ultrasound characteristics of the object, d_r, in the projected area S; (iii) the acoustic outflow by this object, Q_Δω, representing the object size b and its mechanical admittance at the acoustic frequency, Y_Δω; and (iv) the transfer function of the medium at the acoustic frequency, H_Δω(l). The above equation illustrates the basic nonlinear relationship between the ultrasound and acoustic emission pressure amplitudes. Note that neither the medium nor the object needs to be nonlinear for this relationship to hold. It is interesting to note that the projection area S and the vibrating area πb² play different roles. The projection area determines the extent of the force applied to the object (Eq. 4). The vibrating area, however, influences the total acoustic outflow in the medium caused by object vibration. The mechanism of object vibration is somewhat analogous to that of a loudspeaker, where the electromotive force is exerted at a small area of the membrane (usually at the center), causing the entire membrane surface to vibrate. In our method, the size of the vibrating area depends on the object structure. For a free suspended point object, smaller than the beam cross-section, the vibrating area would be the same as the projected area. For a large stiff plate, however, the vibrating area could be much larger than the projected area (similar to a loudspeaker). In some cases, it is more convenient to write the acoustic emission field in terms of the applied force F_Δω. Referring to Eq. 4, we can rewrite Eq. 15 as

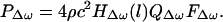16

Again in analogy to a loudspeaker, F_Δω, Q_Δω, and H_Δω(l) represent the electromotive force, dynamic characteristics of the membrane, and propagation medium transfer function.

Beam Forming.

To probe an object with the dynamic radiation force at high spatial resolution, it is ideal to confine the dynamic stress field to a very small region in three-dimensional space. We may define the resolution cell of the system as the volume within which the amplitude of the modulated field is high enough to produce a stress field on a target. The purpose of beam forming is to produce a resolution cell as small as possible. An amplitude modulated single-focused beam can provide a resolution cell that is small in diameter but long in depth direction. A superior strategy that can achieve a small resolution cell in all dimensions is to use two unmodulated focused beams at slightly different frequencies and allow them to cross each other at their focal regions. This is accomplished by projecting two coaxial confocal continuous-wave (CW) ultrasound beams on the object. An amplitude-modulated field is produced only at the interference region of the two unmodulated beams around their focal areas, resulting in a small resolution cell. For this purpose, elements of a two-element spherically focused annular array (consisting of a central disc with radius a₁ and an outer ring with the inner radius of a′₂ and outer radius of a₂) are excited by separate CW signals at frequencies ω₁ = ω₀ − Δω/2 and ω₂ = ω₀ + Δω/2. We assume that the beams are propagating in a lossless medium, in the +z direction of a Cartesian coordinate system (x, y, z), with the joint focal point at z = 0. The resultant pressure field on the z = 0 plane may be written as

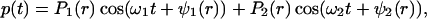17

where r = 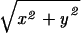is the radial distance. The amplitude functions are (16, 18)

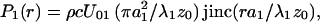18

and

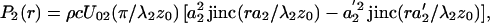19

where λ_i = 2π/ω_i, i = 1, 2, is the ultrasound wavelength, U_0i is the particle velocity amplitude at the i-th transducer element surface, and jinc (X) = J₁(2πX)/πX. The phase functions, ψ_i(r) = −πr²/λ_iz₀, for i = 1, 2, are conveniently set to be zero at the origin.

Now, we define a unit point target at position (x₀, y₀) on the focal plane with a drag coefficient distribution as

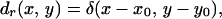20

such that d_r(x, y)dxdy is unity at (x₀, y₀) and zero elsewhere. This equation is merely used as a mathematical model because d_r is physically finite. In this case, the projected area can be considered to be S = dxdy. We replace d_rS in Eq. 1 with d_r(x, y)dxdy and follow the steps similar to those outlined in Eqs. 3 and 4 for the pressure field expressed by Eq. 17, then the complex amplitude of the normal component of the force on the unit point target can be found as

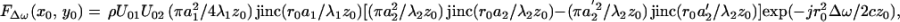21

where the arguments x₀ and y₀ are added to denote the position of the point target and r₀ = 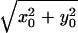. Eq. 21 describes the spatial distribution of the force (the stress field). This equation shows that the stress field is confined to the regions near the beam axis (r₀ = 0) and decays as the radial distance r₀ increases. The lateral extent of the stress field, and hence the resolution cell diameter, would be smaller at higher ultrasound frequencies (smaller λ₁ and λ₂). One can calculate the total force on an arbitrary object by integrating the force over the projected area. The axial extent of the resolution cell (depth resolution or the depth of field) can be determined by calculating the force F_Δω as a function of the depth variable, in a fashion as outlined in Eqs. 17 to 21. For conciseness, we will present only the measured values for the depth resolution in Results.

Loss in the propagation path would attenuate both ultrasound beams, thus less radiation force would be generated by the remaining ultrasound energy. In the case of soft tissues, the force attenuation factor is A(z₀) = exp[αz₀(ω₁ + ω₂)], where α is the attenuation coefficient of the tissue. Energy loss in the medium would also result in generation of a separate radiation stress on the medium along the ultrasound paths. However, because the two beams propagate along separate paths in the CW form, they exert mainly steady radiation stresses to the medium, which does not cause object or medium vibrations. Dynamic radiation force is produced only in the interference region around the focal area, which is another advantage of using two unmodulated beams over a modulated single beam.

Image Formation.

To produce an image, we scan the object in a plane and record the complex amplitude of the acoustic emission, P_Δω, at different positions. In this process, we keep Δω fixed. For transverse view images, the scan plane is the focal plane (x–y). Alternatively, for the parallel view the scan plane is the x–z plane. In the conventional ultrasound imaging context, these two views are called the C-scan and B-scan, respectively. Our main focus here is the transverse view imaging. In this case, the acoustic emission data obtained by vibrating the object at point (x, y) are assigned to the corresponding point (x, y) in the image.

Before defining the image, we need to define the function that represents the object. Referring to Eq. 15, the terms that are object dependent are the drag coefficient d_r and the function Q_Δω (assuming that H_Δω(l) is object independent). The object function g(x, y) is thus defined as the spatial distribution of these terms,

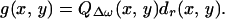22

Variables x and y are added to denote the dependency of d_r and Q_Δω on position. In particular, Q_Δω(x, y) implies the total acoustic outflow by the object when unit force is applied at point (x, y).

Commonly, an imaging system is studied through its point-spread function (PSF), which is defined as the image of a point object. To determine the PSF of our system, we consider a unit point target at the origin with unit mechanical response, Q_Δω(x, y) = 1. Hence, referring to Eqs. 20 and 22, we can write g(x, y) = δ(x, y). To obtain the PSF, we move this point object to every possible position (x₀, y₀) on the z = 0 plane and form the image using the resulting acoustic emission field, P_Δω(x₀, y₀). Because x₀ and y₀ are now being treated as variables, we may replace them by variables x and y, respectively. We define the normalized PSF of the coherent imaging system as the complex function

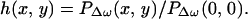23

Division by P_Δω(0, 0) cancels the constant multipliers. Referring to Eqs. 16 and 21, we can write

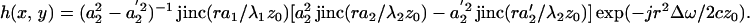24

This equation illustrates that the system PSF is a circularly symmetric function with the peak at the origin and decaying amplitude with increasing the radial distance r. Amplitude decays faster for higher ultrasound frequency. This function will be discussed further in the next section.

EXPERIMENTS

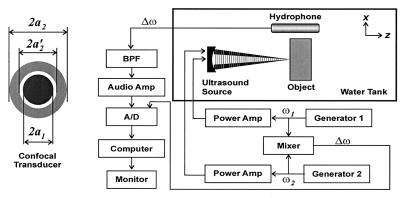
The experimental setup is shown in Fig. 2. The confocal transducer is constructed by using a spherical piezoelectric cap. The two elements are constructed by dividing the back electrode of the piezoelectric wafer into a central disc and the outer ring, such that the elements have identical beam axes and focal lengths. Radii of the elements are a₁ = 14.8 mm, a₂ = 22.5 mm, and a′₂ = 16.8 mm, and the focal distance is 70 mm. Transducer elements were driven by two stable radio frequency synthesizers [Hewlett–Packard 33120A and Analogic 2045 (Peabody, MA)] at frequencies of f₀ − Δf/2 and f₀ + Δf/2, where f₀ = 3 MHz, and the value of Δf = Δω/2π is stated separately for each experiment. The object was placed at the focal plane of the ultrasound beams in a water tank. Sound produced by the object vibration was detected by an audio hydrophone (International Transducer, Santa Barbara, CA, model 680, sensitivity −154 dB re 1V/μPa) placed within the water tank. The received signal was filtered and amplified by a programmable filter (Stanford Research Sunnyvale, CA, SR650) to reject noise, then digitized by a 12 bits/sample digitizer (Hewlett–Packard E1429A) at a rate sufficiently higher than the Nyquist rate for the particular Δf used. Data were recorded on a computer disc. For coherent imaging, which requires the phase information, the reference signal (i.e., cos Δωt) was obtained by electronic downmixing of the two driving signals and was recorded along with the hydrophone signal. The relative phase of the acoustic emission data was then calculated at each point by discrete Hilbert transform. We conducted two experiments. The first experiment is designed to verify the relationship between the acoustic emission pressure and the ultrasound pressure (Eq. 15), and the second is designed to experimentally measure the PSF stated in Eq. 24. These experiments are presented to prove the principles of the method. Further experiments, illustrating applications of the method for evaluation of object mechanical properties and tissue imaging, are presented in ref. 12.

Figure 2.

Ultrasound-stimulated vibro-acoustography system. The confocal ultrasound annular array transducer with two elements is shown on the left.

RESULTS

Acoustic Emission vs. Ultrasound Pressure.

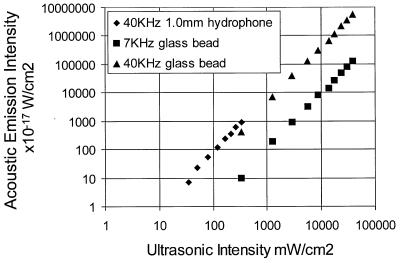
Eq. 15 states that the acoustic emission field amplitude is linearly proportional to the square of the incident ultrasound pressure, or equivalently, to the incident power. To test this hypothesis, a calibrated 1-mm-diameter ultrasound needle hydrophone, with its tip facing the ultrasound beam, was used to measure the ultrasound field at the focal point. The tip of the hydrophone also served as an object to generate the acoustic emission. Here, Δf was set at 40 kHz, and the radial distance from the tip of the needle hydrophone to the audio hydrophone was about 65 mm. The result is shown in Fig. 3. The slope of the acoustic emission intensity vs. ultrasonic intensity indicates that the intensity of the acoustic emission field is proportional to the square of the ultrasound intensity, or equivalently, the acoustic emission pressure amplitude is linearly proportional to the ultrasound power, as predicted by Eq. 15. In another experiment, a 450-μm-diameter glass bead was used as a point object. In this case, Δf was set at either 7 or 40 kHz. The radial distance from the glass bead to the audio hydrophone was about 50 mm. Again, the data indicate a quadratic relationship between the acoustic emission and ultrasonic intensities. These glass-bead data also show that increasing the frequency increases the acoustic intensity. This can be better understood by investigating the theoretical model presented in Eq. 13. If we assume that the mechanical admittance of the object is approximately constant at these frequencies, then the object behaves almost as a point source, and the acoustic pressure amplitude is proportional to Δω. Hence the acoustic emission intensities I_Δω1 and I_Δω2 at frequencies Δω₁ and Δω₂, respectively, are related by I_Δω2/I_Δω1 = (Δω₂/Δω₁)². Now, letting Δω₁ and Δω₂ correspond to 7 and 40 kHz, respectively, we can write the intensity ratio as: [I_Δω2/I_Δω1]_dB = 20 log (Δω₂/Δω₁) = 15 dB. The mean value of the intensity ratio calculated from the glass-bead data at 7 and 40 kHz is 16 dB, which is in close agreement with the theoretical result.

Figure 3.

Acoustic-emission field intensity vs. the combined ultrasound intensity.

PSF Measurement.

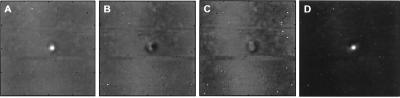
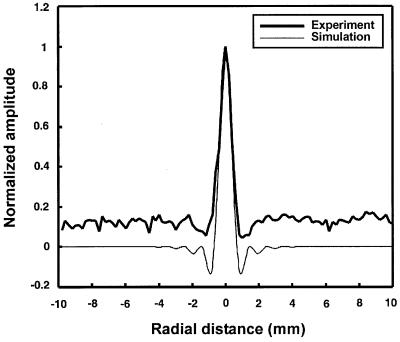
To demonstrate the image-formation process and support the theoretical derivation of the PSF (Eq. 24), we evaluated this function experimentally. For this purpose, we used a 380-μm diameter glass bead as a model for a point and placed it on a thin latex sheet. The latex sheet produces only a small change in the incident energy, and hence does not produce significant radiation force or acoustic emission. The entire object was placed in a water tank and the latex sheet surface was scanned in a raster format at 0.2-mm increments in either direction at Δf = 7.3 kHz. The amplitude and phase of the acoustic emission signal were calculated at each point relative to the reference signal data. The phase was normalized to the phase value at the center of the bead. The resulting in-phase, quadrature, phase, and magnitude images are shown in Fig. 4A–D. Transverse image resolution, defined as the −6-dB width of the bead image, is approximately 700 μm for the in-phase image in either dimension (refer to Fig. 5). To compare the experimental results with those of the theory, we calculated the profile of the PSF for the transducer parameters used in this experiment according to Eq. 24. Fig. 5 shows the theoretical PSF profile and the glass-bead profile obtained from the experiment (in-phase image profile, shifted to center at zero). This figure shows excellent agreement between theory and experiment for amplitudes above 20% of the peak. The experimental data show some background offset about 12% of the peak. We believe that this background offset is caused at least by the following sources: (i) acoustic emission by the latex sheet; (ii) the background acoustic noise in the experimental setup caused by equipment fans and some structural and building vibrations; (iii) nonlinearity of water that can produce a nonlinear mix of the two beams even in the absence of the object; and (iv) streaming as a result of energy absorption by water (14), which in turn can vibrate the latex sheet blocking the stream. To evaluate the depth resolution (or the slice thickness), we placed the glass bead on the beam axis and scanned it in the z-direction about the focal point. The depth resolution, defined as the distance between the points where the amplitude of the acoustic emission field drops to −6 dB of its peak, was 9 mm.

Figure 4.

USVA images of a 380-μm glass bead: (A) in-phase, (B) quadrature, (C) phase, and (D) magnitude. The phase in C ranges from −π radians (black regions) to +π radians (white regions), and was normalized to be zero at the center of the glass bead. (Modified with permission from ref. 12, copyright 1998, American Association for the Advancement of Science.)

Figure 5.

The theoretical PSF profile of the USVA system according to Eq. 24 and the glass-bead in-phase image profile (Fig. 4A) obtained from the experiment.

DISCUSSION

System Properties.

Spectral characteristics. In general, USVA images represent object characteristics at two ends of the spectrum: the drag coefficient at the ultrasound frequency and the mechanical admittance at the low acoustic frequency Δf. The ultrasound frequency is usually set at a value suitable to form the beam, whereas Δf can vary in a wide range depending on the application. If the two beams are produced by similar ultrasound transducer elements, then the practical upper limit for Δf is about equal to the transducer bandwidth. The lower limit of Δf is zero.

Sensitivity.

System sensitivity in detecting very small displacements is an important practical issue, especially when the allowable ultrasound power is limited (for example, in medical imaging). Motion measurement with ultrasound pulse echo has been used previously to study “stiffness” of tissues (10). However, the sensitivity of ultrasound pulse echo to motion, at common medical ultrasound frequencies, is limited to several micrometers. An advantage of USVA is its high displacement sensitivity. Cyclic displacement of 100 nm at 10 kHz produces an acoustic intensity of about 3.0 × 10⁻³ watts/cm². Hydrophones similar to the one used in these experiments are sensitive to as little as 10⁻¹⁵ watts/cm² and therefore are capable of detecting very small cyclic displacements. For instance, the hydrophone detected an acoustic pressure of about 15 × 10⁻³ Pa at a distance of 5 cm from the glass bead shown in Fig. 4. Under assumptions of isotropic vibration, this pressure would be produced by a similar-sized sphere vibrating with a displacement amplitude of about 6 nm. Sensitivity increases at higher frequencies because the acoustic emission pressure is proportional to frequency for constant mechanical admittance (Eq. 13).

Comparisons with pulse–echo systems.

Some contrasting features of USVA with respect to the conventional ultrasound pulse–echo imaging (B-mode and C-mode) are: (i) A pulse–echo image represents object microstructure by displaying its ultrasonic reflectivity distribution. The acoustic emission signal in a USVA system is proportional to the drag coefficient d_r(x, y), which is a local ultrasound parameter, and to the function Q_Δω(x, y), which represents the bulk response of the object at acoustic frequency Δω. Hence, a USVA image, in general, represents both the microstructure and macrostructure of the object. (ii) The echo signal in a pulse–echo system is a linear function of the incident ultrasound pressure amplitude and the amplitude reflection coefficient of the object. In USVA, however, the acoustic emission signal is proportional to the ultrasound power and the power reflection coefficient of the object. (iii) Pulse–echo systems are not directly sensitive to medium absorption. Absorption is indicated as relative changes in the amplitude of the echoes resulting from the scatterers within the medium. In a USVA system, the acoustic emission can be produced directly as a result of energy absorption by the medium, even if the medium is homogeneous (refer to Eq. 2). (iv) Pulse–echo systems are generally broadband. The USVA method presented here is basically a narrowband technique. (v) Pulse–echo systems achieve high depth resolution by transmitting short wideband pulses. A USVA system gains its depth resolution by tailoring beam geometry to limit the depth of the region where the two beams interfere. A USVA system does not require a wide bandwidth signal to achieve a high depth resolution. (vi) The data of USVA images are acquired one point at a time, which resembles the data acquisition in C-mode pulse–echo systems. B-mode pulse–echo systems, however, require much less acquisition time because the data are collected one line at a time.

Applications.

USVA promises applications in two general areas: medical imaging and material evaluation.

Medical applications.

USVA can be used to image tissues and evaluate their mechanical characteristics. To use USVA for in vivo applications, one must take into account limitations such as safe (ultrasound) power limit, tissue attenuation, body noise, and phase aberration. The ultrasound power required to generate a detectable acoustic emission depends on the object, acoustic noise, and receiver sensitivity. Experimental results shown in Fig. 3 demonstrate that ultrasound intensities as low as 30 mW/cm² are sufficient to detect the acoustic emission from a 1-mm-diameter object with our hydrophone in the water tank. This power value is much smaller than the FDA limit for safe diagnostic ultrasound applications. Tissue attenuation reduces the ultrasound intensity at the target, and hence the acoustic emission [by the factor A(z₀)]. Attenuation limits the usable ultrasound frequency, and hence, lowers the resolution. It also limits the signal-to-noise-ratio (SNR) because of the loss in the acoustic emission energy as a result of ultrasound attenuation by tissue. Direct effect of tissue attenuation on the acoustic emission signal is probably negligible because attenuation of the compressional waves at frequencies in the order of a few kHz in soft tissues is low. Sources of biological noise of the human body include cardiovascular and respiratory systems and muscle movements. Body noise is usually concentrated below 1 KHz and can be filtered out if Δf is above this value. The SNR can be improved by increasing the time duration of the signal recorded at each point (to increase the signal energy) and by using very narrowband filters (to reject the noise), while keeping the ultrasound power within the safe level. Phase aberration in tissue can reduce the sensitivity of the system by decreasing the effective ultrasound energy density at the beam interaction region. One may use known phase aberration correcting methods to reduce such an effect. The practical value of these methods for USVA remains to be studied.

Material evaluation.

Another field in which USVA can be potentially useful is material characterization, including mechanical parameter evaluation, imaging, and nondestructive testing of materials. USVA can be used for detection and imaging flaws in materials. Also, one may use USVA to evaluate the mechanical frequency response of an object at low frequencies. In such case, we are interested in determining Q_Δω(x, y) vs. frequency. We assume that the object is uniform within the projected area S. Then, the total radiation force on this object, 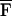_Δω, can be calculated by integrating F_Δω(x, y) over S. Referring to Eq. 21, one can show that for Δω ≪ ω₀, 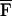_Δω is virtually independent of Δω. If H_Δω(l) is known and nonzero, then the function Q_Δω(x, y) can be estimated using Eq. 16 as Q_Δω(x, y) = P_Δω(x, y)/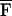_ΔωH_Δω(l). In practice, P_Δω(x, y) is obtained by sweeping Δω in the range of interest and recording the resulting acoustic emission (12).

ABBREVIATIONS

USVA

ultrasound-stimulated vibro-acoustography

PSF

point spread function

CW

continuous wave