Using models to identify routes of nosocomial infection: a large hospital outbreak of SARS in Hong Kong

Abstract

Two factors dominated the epidemiology of severe acute respiratory syndrome (SARS) during the 2002–2003 global outbreak, namely super-spreading events (SSE) and hospital infections. Although both factors were important during the first and the largest hospital outbreak in Hong Kong, the relative importance of different routes of infection has not yet been quantified. We estimated the parameters of a novel mathematical model of hospital infection using SARS episode data. These estimates described levels of transmission between the index super-spreader, staff and patients, and were used to compare three plausible hypotheses. The broadest of the supported hypotheses ascribes the initial surge in cases to a single super-spreading individual and suggests that the per capita risk of infection to patients increased approximately one month after the start of the outbreak. Our estimate for the number of cases caused by the SSE is substantially lower than the previously reported values, which were mostly based on self-reported exposure information. This discrepancy suggests that the early identification of the index case as a super-spreader might have led to biased contact tracing, resulting in too few cases being attributed to staff-to-staff transmission. We propose that in future outbreaks of SARS or other directly transmissible respiratory pathogens, simple mathematical models could be used to validate preliminary conclusions concerning the relative importance of different routes of transmission with important implications for infection control.

1. Introduction

When a pathogen first invades a new system of potential hosts, the relative contributions of different modes of transmission are not always clear. There are many factors that influence the ease with which the pathogen acquires new hosts. For example, the pathogen may be viable in a number of species, but fair better in some than in others, e.g. Japanese encephalitis virus is amplified very efficiently by pigs but probably less so by smaller wild birds. Alternatively, the host population may be highly structured so that small host subgroups are infected quickly, but jumps between subgroups are more difficult, e.g. foot-and-mouth transmission between distinct farms. Although it is common for mathematical models to be used qualitatively to investigate specific hypotheses regarding alternative modes of transmission in such pathogen–host systems, it is less common (although certainly not unknown) for them to be used as models in the inferential sense to compare multiple hypotheses. Here, we treat the outbreak of severe acute respiratory syndrome (SARS) in a single healthcare setting as an ecological event. We compare alternative explanations for the spread of the disease using incidence data, simple mathematical models of disease transmission and basic information theory.

The global outbreak of SARS during 2002–2003 infected 8096 people, killing 774 (WHO 2003). Two features of the epidemiology of SARS were used to describe the majority of the transmission that occurred. First, a very small number of individuals were able to infect large numbers of secondary cases during short episodes, while many infectious individuals infected few or no secondary cases. These episodes have been described as super-spreading events (SSE) and may have arisen from either unusual environmental transmission of the virus or true super-spreaders, i.e. individuals with extremely high levels of viral shedding (Riley et al. 2003). Second, many SARS cases were associated with healthcare settings. This implies that nosocomial transmission, where infection events occurred within a hospital, must also have played an important role. It has been difficult to tease apart these two competing effects because many SSE also took place in hospitals. Previous studies have focused mainly on characterizing either SSE (Fang et al. 2004; Lai et al. 2004; Li et al. 2004; Liao et al. 2005) or hospital transmission (Webb et al. 2004; Lu et al. 2005; Wong & Tam 2005; Yu et al. 2005).

The initial cluster of SARS cases in Hong Kong occurred in Hospital P and was first identified on 11 March 2003 (Lee et al. 2003). The apparent source of the outbreak was a 26-year-old man admitted on 4 March. A total of 143 cases were officially attributed to the cluster (SARS Expert Committee 2003). However, it seems likely that the identification of the index case influenced later epidemiological investigations. Lee et al. (2003) defined secondary cases as those who had had direct contact with the index case or visited his or her ward prior to isolation. Tertiary cases were defined to be household members of secondary cases. It was assumed that the use of nebulizer-based therapy for the index case might have contributed to the large number of secondary cases, which in turn motivated the broad definition of secondary cases. However, a subsequent retrospective study of a group of medical students in the hospital (Wong et al. 2004), some of whom were among the secondary cases, suggests that use of the nebulizer was not as important as first thought. Therefore, the relative importance of different modes of transmission remains unclear and has yet to be quantified. Below, we describe our use of a mathematical model and hospitalization episode data to quantify the relative importance of different routes of transmission in the Hospital P cluster. We tested three plausible hypotheses using variants of the mathematical model.

2. Material and methods

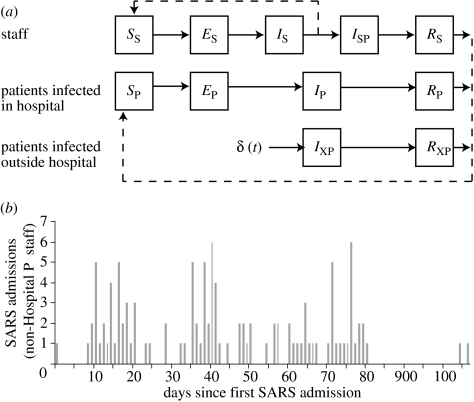
We developed a mathematical model of the transmission of SARS between the following four types of cases: the initial super-spreader admitted on 4 March; staff who worked at Hospital P (and who were later admitted there); patients infected during their stay at Hospital P; and individuals (later patients) infected outside Hospital P who were treated there. An overview of the dynamic model is presented in figure 1a and a description of key model assumptions is given below. Details of our assumptions about stage-specific waiting times and a definition of the model using differential equations are given in document ‘Supporting Methods and Sensitivity Analyses’ (available as electronic supplementary material). Some parameters and initial conditions of the transmission model are known or can be accurately estimated from other sources (table 1). The values for the other quantities, which were treated as parameters in the inferential sense, are presented in §3.

Figure 1.

Model structure and inputs. (a) The structure of the dynamic model. (b) The time-series of SARS admissions on days since the first admission. These cases are those which were known to have been community acquired and those for which no source can be reliably identified. See main text and electronic supplementary material.

Table 1.

Population sizes and waiting times.

parameter		value	notes
NS	total number of staff at risk of infection	2250	Total number of staff at the hospital used for the main runs. Sensitivity analyses were performed with smaller numbers (see electronic supplementary material).
NP	total number of patients at risk of infection	1315	Total number of hospital beds used for the main runs. Sensitivity analyses were performed with smaller numbers (see electronic supplementary material).
τE	average time from infection to onset of symptoms	4.6 days	Estimated from Hong Kong SARS integrated database.
nΓ	shape parameter for distribution of times from infection to onset of symptoms	2	Estimated from Hong Kong SARS integrated database.
τSW	average time that symptomatic staff continued to work after onset before admission	3.3 days	Calculated from Hong Kong SARS integrated database for Hospital P cases.
τG	generation time or serial interval; average time from the infection of an infector to the times of infection of all her infectees	8.4 days	Lipsitch et al. 2003
τDS	average duration from onset to discharge from the hospital	26.5 days	Calculated from Hong Kong SARS integrated database.
τOA	average time from onset of symptoms to admission for patients infected outside the hospital	3.98 days	Calculated from Hong Kong SARS integrated database for Hospital P cases.

A schematic of the transmission model is given in figure 1a. At any time t, S_P(t) was the number of susceptible patients; E_P(t) was the number of infected but not yet infectious patients; I_P(t) was the number of infectious patients; and R_P(t) was the number of recovered but still hospitalized patients. S_S(t) was the number of susceptible staff; E_S(t) was the number of exposed but not yet infectious staff; I_S(t) was the number of infectious staff still working; I_SP(t) was the number of infectious staff who had been admitted to the hospital at which they were infected; and R_S(t) was the number of hospitalized but recovered staff members. I_XP(t) was the number of infectious patients who were infected in the community and R_XP(t) was the number of those patients who were recovered but still hospitalized.

Patients infected in the community, or elsewhere outside Hospital P, were recruited at rate δ(t) into class I_XP(t). The function δ(t) was defined such that ${\int }_{t^{\prime }}^{t^{\prime }+\mathrm{\Delta }t}\delta (u)\text{d}u$ was equal to the number of cases imported on integer day t (for Δt→0) and equal to 0 for non-integer day t (figure 1b). In an ecological sense, these external infections were ‘imported’. They occurred throughout the period of the outbreak and were considered to be known exogenous events. For those infected inside the hospital, the onset of symptoms and the onset of infectiousness were assumed to occur simultaneously, which is reasonable for SARS (Fraser et al. 2004). The total number of staff included only those who had not yet been admitted, $N_{\text{S}}=S_{\text{S}}+E_{\text{S}}+I_{\text{S}}$. The total number of patients, N_p, included those staff who had been admitted as patients and both groups of non-staff patients (externally infected with SARS and others),

$$N_{\text{P}}=S_{\text{P}}+E_{\text{P}}+I_{\text{P}}+R_{\text{P}}+I_{\text{SP}}+R_{\text{S}}+I_{\text{XP}}+R_{\text{XP}}.$$

We assumed that the sizes of the staff and patient populations were large enough that saturation was never a significant driver of the reduction in disease incidence (see electronic supplementary material). We defined the baseline transmissibility to be β, the hazard at time t=0 that an infectious undiagnosed staff member from class I_S infected a susceptible staff member from class S_S. We assumed that the infectivity of patients relative to staff was α_P and that this was constant over time. The susceptibility of patients at time t relative to staff at time 0 was γ_P(t), and of staff at time t to staff at time 0 was γ_S(t). The impact of infection control measures was to alter susceptibility, i.e. γ_P(t) and γ_S(t) were not constant over time. The index case for the Hospital P cluster, admitted on 4 March, was represented as an initial constant infective force. This force was α_SSP times as infectious as staff at time 0 and lasted until time t_SSP. Using these elements, we defined a ‘basic’ force of infection at time t to be $\lambda (t)=\beta [I_{\text{S}}(t)/N_{\text{S}}+{\alpha }_{\text{P}}\{I_{\text{P}}(t)+I_{\text{SP}}(t)+I_{\text{XP}}(t)\}/N_{\text{P}}+{\alpha }_{\text{SSP}}]$ for t<t_SSP and $\lambda (t)=\beta [I_{\text{S}}(t)/N_{\text{S}}+{\alpha }_{\text{P}}\{I_{\text{P}}(t)+I_{\text{SP}}(t)+I_{\text{XP}}(t)\}/N_{\text{P}}]$ for later times. The force of infection experienced by staff was ${\lambda }_{\text{S}}(t)={\gamma }_{\text{S}}(t)\lambda (t)$ and by patients was ${\lambda }_{\text{P}}(t)={\gamma }_{\text{P}}(t)\lambda (t)$.

The differential equations description of the model given in the electronic supplementary material is for the special case where all waiting times were exponential. However, the distribution of times from infection to the onset of symptoms (and assumed start of infectivity) was not assumed to be exponential, because the variance for this waiting time was known to be much lower than that of the exponential (Leung et al. 2004b) and this is known to influence transmission dynamics (Wearing et al. 2005). These classes, E_S and E_P, were divided into n_Γ subclasses, each with exponentially distributed waiting times of average duration τ_E/n_Γ. The convolution of exponentials for infection subclasses was equivalent to assuming that individuals experienced gamma-distributed incubation times with mean τ_E and variance ${\tau }_E^2/n_{\Gamma }$. We calculated the average number of secondary cases caused by one typically infectious non-super-spreading index case in an otherwise susceptible population for this model, $R_0^{\text{XSS}}$(see electronic supplementary material), and used this, rather than β, as the underlying transmission parameter.

3. Results

We used the transmission model described above to investigate the relative plausibility of three different hypotheses (table 2). Parameters of the model were estimated using previously unpublished hospital episode data (see electronic supplementary material and figure 2). In staff, there were a large number of initial cases before a prolonged period of time when the average incidence appears to fall off gradually. In patients, overall, there were far fewer infections and the average incidence was approximately constant apart from apparent clusters at the start of the outbreak and between days 30 and 40. Those cases which were known to have acquired infection in the community, for which the location of infection could not be determined or which had previously been treated in another hospital, were treated as exogenous infections and their dates of admission to Hospital P were used to construct the ‘input’ time-series δ(t) (n=176). Model parameters were fitted to the ‘output’ time-series of dates of onset of symptoms of the staff working at Hospital P who were treated at Hospital P (n=164) and inpatients infected in Hospital P (n=65). Visitors (n=19) were excluded as it was impossible to estimate the duration of their exposure. Staff infected at Hospital P and treated elsewhere (n=11) were excluded as their numbers were small, their dates of onset were evenly distributed over the time of the outbreak, and we wished to keep the model structure as simple as possible. Our results are not sensitive to the exclusion of visitors and of staff treated elsewhere (see electronic supplementary material).

Table 2.

Estimated parameters. Values were obtained using approximate maximum-likelihood methods. We assumed that data arose from independent Poisson distributions for each type of infection for each day. The means of these distributions were the average daily model incidences, calculated using a deterministic version of the model. The use of this approximate likelihood function was validated by ensuring that unbiased estimates of model parameters could be recovered from data simulated with a (compartmental) stochastic version of the model. The number of parameters used to calculate the ΔAIC was the same as the number reported in this table, i.e. 6 for H₁, 5 for H₂ and 8 for H₃. As the ratio of parameters to data points was relatively high, we used the following formula: $\text{AIC}=-2l+2K+2K(K+1)/(n-K-1)$, where l was the log likelihood; K was the number of parameters; and n was the size of the dataset. The intervals given are based on the univariate likelihood profile. Note that, although the model was solved using a time-step of 0.1 days, we considered only integer-valued days for the duration of infectiousness of the super-spreader and for the times of intervention. In addition, due to the long time gap before the last two cases (see figure 1a), we estimated parameter values using data only for the first 82 days of the outbreak.

parameter		H1 interventions only	H2 super-spreader only	H3 super-spreader and interventions
$R_0^{\text{XSS}}$	basic reproductive number, excluding super-spreaders	174 (167, 181)	0.660 (0.624, 0.695)	0.595 (0.573, 0.617)
αSSP	infectivity of super-spreading patient, relative to that of staff	—	76.8 (65.5, 89.2)	48.6 (42.1, 55.8)
tSSP	duration of infectivity of super-spreading patient (days)	—	4.0 (3.6, 4.6)	4 (3.6, 4.5)
αP	infectivity of non-super-spreading patients relative to that of staff	0.0852 (0.0695, 0.106)	0.112 (0.058, 0.203)	0 (0, 0.00073)
γP(0)	susceptibility of non-super-spreading patients at time t=0, relative to that of staff at time t=0	0.302 (0.231, 0.388)	0.645 (0.482, 0.851)	0.382 (0.291, 0.492)
tI	time of intervention (days)	3.0 (2.9, 3.1)	—	25 (22.2, 27.8)
${\mathrm{\Delta }}_{\text{P}}^{\gamma }$	susceptibility of non-super-spreading patients after time t>tI, relative to that of staff at time t=0	0.010 (0.007, 0.013)	—	4.99 (3.42, 6.98)
${\mathrm{\Delta }}_{\text{S}}^{\gamma }$	susceptibility of staff after time t>tI, relative to that of staff at time t=0	0.0034 (0.0031, 0.0038)	—	1.29 (1.17, 1.41)
ΔAIC	0	14.3	2.21

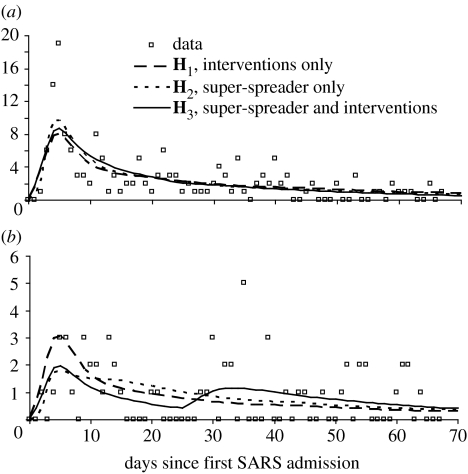
Figure 2.

Comparison of model output and data for three different hypotheses. Hypothesis H₁ is that the initial surge in cases was caused by poor infection control and that the outbreak was controlled by a reduction in the susceptibility of staff and patients at some time t_I. Hypothesis H₂ is that conditions for infection were constant over the duration of the outbreak and that the initial surge in cases was caused by a super-spreader. Hypothesis H₃ is that the surge in cases at the beginning was caused by a super-spreading individual and that conditions for infection also changed at some later time in the outbreak (i.e. combination of H₁ and H₂). (a) Staff infections (n=164) and (b) patient infections (n=59).

Without prior knowledge of an index case or super-spreaders, which would have been the case during an ongoing epidemic of a novel infectious agent as SARS was at the time, the time-series of patient admissions (figure 1b) and the incidence of hospital infection by date of onset (figure 2) could be consistent with a short initial period of poor infection control followed by a substantial drop in transmissibility as hygiene routines were tightened. These were the underlying assumptions for H₁ that the outbreak was controlled by a reduction in the susceptibility of staff and patients (i.e. through strict adherence to personal protective measures and precautions against respiratory droplets and fomites) at some time t_I. At that time, the susceptibility of patients dropped to ${\mathrm{\Delta }}_{\text{P}}^{\gamma }$ of its initial value and of staff to ${\mathrm{\Delta }}_{\text{S}}^{\gamma }$ of its initial value, i.e. before t_I, γ_P(t)=γ_P(0) and γ_S(t)=1; and after t_I, ${\gamma }_{\text{P}}(t)={\mathrm{\Delta }}_{\text{P}}^{\gamma }{\gamma }_{\text{P}}(0)$ and ${\gamma }_{\text{S}}(t)={\mathrm{\Delta }}_{\text{S}}^{\gamma }$. Transmissibility dropped from $R_0^{\text{XSS}}=174$ before day t_I to $R_t^{\text{XSS}}=0.640$ afterwards (note values for $R_t^{\text{XSS}}$ defined to be $R_0^{\text{XSS}}$ after t_I were calculated from the other estimated parameters in table 3 according to the definition of $R_0^{\text{XSS}}$ above). The most likely time of intervention was day 3, before which the index case was the only infectious patient in the hospital.

Table 3.

Estimated numbers of infections by different transmission sources for the three different hypotheses (see text and figure 2 for definitions of these hypotheses).

	infectee
	staff			patients
infector	H1	H2	H3	H1	H2	H3
super-spreader	—	56.0	59.4	—	21.2	13.4
‘other’ patients	58.2	54.8	0	23.7	19.0	0
staff	110.3	57.5	107.3	37.2	20.2	47.5
total	168.5	168.3	166.7	60.9	60.4	60.9
data		164			59

Both the very early estimated timing of intervention (as per H₁) and post hoc reports of a super-spreader motivated the definition of the second alternative hypothesis, H₂, that conditions for infection were constant over the duration of the outbreak and that the initial surge in cases was caused by the super-spreader. Given that the hospital was continuously challenged with new SARS patients (figure 1b), assuming that conditions for transmission were constant is reasonable. H₂ was tested by keeping the relative susceptibility of patients and staff constant, i.e. γ_P(t)=γ_P(0) and γ_S(t)=1. Under H₂, the basic reproductive number excluding super-spreaders $R_0^{\text{XSS}}=0.660$ (0.624, 0.695), which implies that, on average, conditions did not exist inside the hospital for the sustained transmission of SARS for non-super-spreading patients and staff. Although estimates for $R_0^{\text{XSS}}$ greater than 1 would have been surprising, given that the underlying rate of non-super-spreading transmission is constrained to be constant for the duration of the outbreak, an expected number of secondary cases of 0.660 should not be considered low. The duration of infectiousness for the super-spreader was 4 days, which is consistent with the reported severe cough from 4 March to 7 March (Wong et al. 2004). We estimated that this super-spreading index case was 76.8 times as infectious as a single infectious staff member, but that other patients were much less infectious than staff, α_P=0.112. Although H₂ appears to faithfully reproduce most of the dynamics of infections of staff and of patients (figure 2), according to our estimates of differences in the Akaike information criteria (AIC) between H₁ and H₂, these data do not support H₂ (ΔAIC, table 2).

The final hypothesis, H₃, is a combination of H₁ and H₂ (table 2). We assume that the initial case was fundamentally different from the other patients (as in H₂) and that the susceptibility of the staff and patients either increased or decreased at some later time point t_I (as in H₁). Since the ΔAIC for H₃ relative to H₁ is less than 4, both of these hypotheses are supported by the data (Burnham & Anderson 2002). Parameters concerning the super-spreader are broadly consistent with those obtained for H₂ (table 2). However, if a super-spreader is allowed, the most likely time for a step change in the susceptibility of staff and patients is significantly later in the course of the epidemic, at t_I=26 days: at the most likely parameter values, the model does not impose any change in transmission characteristics within the hospital before this time (note that this effect is conditional on their only being a single step change in transmission characteristics; see §4). The overall strength of the intervention is lower for H₃ than for H₁ with, for H₃, $R_0^{\text{XSS}}=0.595$ before day 25 and $R_t^{\text{XSS}}=0.768$ afterwards. Interestingly, the best fit under H₃ is achieved with no infectivity from non-super-spreading patients, α_P=0. The benefits of the additional model structure of H₃ can be seen graphically in figures 2b and 3c. The increase in relative susceptibility $({\mathrm{\Delta }}_{\text{P}}^{\gamma }=4.99)$ of patients at day 25 allows this model to reproduce the increase in cases in that group which occurred between days 30 and 40.

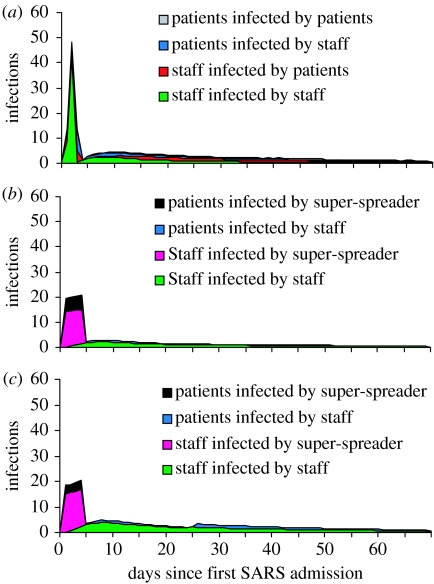
Figure 3.

Sources of infection for the three different hypotheses. (a) shows the breakdown of infections, by route of infection, for hypothesis H₁ that the initial surge in cases was caused by poor infection control and that the outbreak was controlled by a reduction in the susceptibility of staff and patients at some time t_I. (b) shows the same for H₂ that conditions for infection were constant over the duration of the outbreak and that the initial surge in cases was caused by the super-spreader. (c) shows the same for H₃ that the surge in cases at the beginning was caused by a super-spreading individual and that conditions for infection also changed at some later time in the outbreak (the combination of H₁ and H₂).

Figure 3 shows incident cases, by infective sources, predicted by the model over the first 70 days of the outbreak. Total numbers of infections by each source are presented explicitly in table 3. As should be the case, there is good consistency between the different models in table 3. All maximum-likelihood parameter estimates attribute more infections to staff than to the super-spreader. All the three models reproduce the total number of infections with reasonable accuracy.

4. Discussion

Our results suggest that hypothesis H₂ (super-spreading only) is an unlikely explanation for the patterns in these data, whereas there is no more support for H₁ (interventions alone) over H₃ (super-spreading and interventions). However, our estimated value of $R_0^{\text{XSS}}=174$ under H₁ requires that many staff members were extremely infectious for a very short time at the start of their infectious period, which is not consistent with other studies of SARS epidemiology. Therefore, in our discussion, we focus mainly on the implications of H₃. Our results are evidence that many of the SARS infections previously attributed to the single super-spreading index case at Hospital P (Lee et al. 2003) might actually have been a result of staff-to-staff transmission. For H₃, we estimated that 73 infections occurred between the super-spreader and healthcare workers (including medical students) and patients. This is substantially lower than the 97 reported at the end of the outbreak, based on case tracing data (SARS Expert Committee 2003). In addition, we estimated that all remaining 155 infections were from staff to other staff or patients.

In order to implement effective infection control policies, it is imperative that the most significant routes of transmission are identified as early as possible. With this in mind, extreme caution should be exercised when identifying and, in particular, publicizing early index cases in an outbreak. After such cases are identified, there will likely be a strong inclination to attribute cases to individuals already known to be infectious, i.e. field epidemiologists will be at risk of committing errors due to anchoring and availability heuristics. If this occurs, the relative importance of other routes of infection may well be underestimated.

One of the distinguishing characteristics of SARS is that very few infections occurred while the infector was asymptomatic (Fraser et al. 2004; Leung et al. 2004a). This low proportion of presymptomatic or asymptomatic transmission of SARS was not known at the time of the Hospital P outbreak. In future outbreaks of SARS or other novel respiratory diseases, the utmost priority should be placed on identifying early symptoms in healthcare workers. Although more rapid isolation of potentially infectious healthcare workers would have further exacerbated staffing problems, in retrospect, it would have been an efficient method of interrupting hospital transmission.

The transmission dynamics of the most likely hypothesis, H₃, which includes both super-spreading and varying status of infection control interventions, suggests that the vulnerability of patients to infection increased at some point later in the outbreak. It may have been that the increase in the number of SARS admissions between days 36 and 42 led to an overloading of the infection control policies that were in place. However, if this overloading were causal, we might have expected our estimated day of intervention to have occurred later than day 25. Alternatively, there might have been a significant change in the infection control procedures unrelated to SARS admissions. We note that our estimate for the day of increased patient susceptibility is the same day that the Hospital P accident and emergency department (Hospital Authority Review Panel on the SARS Outbreak 2003) reopened. However, we did not intend a priori to investigate the impact of this event. Therefore, the temporal coincidence between the estimated day of intervention and the reopening of accident and emergency should not be treated as evidence of causality.

The three hypotheses presented here, as defined by the variants of the mathematical model, are by no means exhaustive. However, using compartmental models, we were unable to reliably estimate parameters for model variants of greater complexity. For example, we would have preferred to investigate the use of multiple time points at which the impact of more than a single intervention could be assessed. When we tested the ability of this inferential framework to recover known parameter values from simulated datasets, the use of more than eight parameters led to unreliable results. Therefore, with this dataset, we were unable to refine the hypotheses using more complex model variants. Also, in using a compartmental model, we have had to aggregate information for whole groups of patients. For example, the onset dates of all staff members are known, but we were restricted here to using the average distribution of times from onset to admission in our model.

Some of these limitations could be addressed using an individual-based transmission model with data augmentation for the unseen events, e.g. McBryde et al. 2006. However, despite these potential limitations, we propose that the model structure and inferential methods used here are appropriate for identifying likely routes of transmission during the outbreak of an infectious disease in a healthcare setting. In particular, the system of inference used is generic and there is no need to construct a novel set of Markov chain updates for model variants. In addition, by using an absolute likelihood scale, it is more straightforward to compare models. Given the substantial resources employed for case and contact tracing during outbreaks, the additional use of models to choose between available hypotheses and therefore validate preliminary conclusions is warranted. The level of detail of data required for these analyses is no greater than would be gathered routinely in most instances.

More generally, the use of simple models and basic information theory to compare hypotheses during disease outbreaks is relatively straightforward to implement (and to test) and could be used more often. This approach allows for a useful systematic comparison between theories, as long as levels of support for different hypotheses are reported correctly. If incidence data are available for different host types and the natural history of the disease is well described, the time-series of infections can be used to estimate the relative importance of different routes of infection under a number of transmission assumptions. Further, if the time-scale for successful invasion is longer than in the example presented here, more time would be available for this type of analysis. For example, given the possible slow progression of influenza A H5N1 to endemicity in domestic poultry in parts of Southeast Asia (Chen et al. 2006), if suitable incidence and husbandry data were available, similar methods could be used to assess the relative importance of transmission among and between different host species and farm types.

Supplementary Material

Supporting methods and sensitivity analyses

We provide further details of the methods used to extract data from different sources and to construct the transmission model. Also, additional sensitivity analyses are described which demonstrate that our results are robust against a) alternative choices for effective population sizes and b) to the inclusion of an additional class in the model for staff infected at hospital P but treated elsewhere