Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2006 Dec 12;274(1610):727–733. doi: 10.1098/rspb.2006.0214

Male phenotypic quality influences offspring sex ratio in a polygynous ungulate

Knut H Røed 1, Øystein Holand 2, Atle Mysterud 3,*, Aage Tverdal 1, Jouko Kumpula 4, Mauri Nieminen 4
PMCID: PMC2197213  PMID: 17254998

Abstract

Evolutionary models of sex ratio adjustment applied to mammals have ignored that females may gain indirect genetic benefits from their mates. The differential allocation hypothesis (DAH) predicts that females bias the sex ratio of their offspring towards (more costly) males when breeding with an attractive male. We manipulated the number of available males during rut in a polygynous ungulate species, the reindeer (Rangifer tarandus), and found that a doubling of average male mass (and thus male attractiveness) in the breeding herd increased the proportion of male offspring from approximately 40 to 60%. Paternity analysis revealed indeed that males of high phenotypic quality sired more males, consistent with the DAH. This insight has consequences for proper management of large mammal populations. Our study suggests that harvesting, by generating a high proportion of young, small and unattractive mates, affects the secondary sex ratio due to differential allocation effects in females. Sustainable management needs to consider not only the direct demographic changes due to harvest mortality and selection, but also the components related to behavioural ecology and opportunities for female choice.

Keywords: differential allocation hypothesis, harvesting, male attractiveness, maternal investment, Trivers–Willard model

1. Introduction

Evolutionary theory of sex allocation predicts that mothers should adjust the sex of their offspring according to the fitness return (Trivers & Willard 1973; Maynard Smith 1980; Charnov 1981; Frank 1990; Leimar 1996; Hewison & Gaillard 1999). While empirical studies on many insect taxa have clearly supported sex allocation theory, for large mammals this is still a contentious issue (Sheldon & West 2004). The majority focus has been on the classical Trivers–Willard model (TWM, 1973), proposing that in species in which the variance in male reproductive success exceeds that of females, additional parental investment would benefit sons more than daughters, provided the offspring reproductive success is determined by phenotypic quality which in turn is at least partly determined by the level of maternal care during the juvenile stage (Maynard Smith 1980; Hewison & Gaillard 1999). Recent extensive meta-analyses of ungulate mammals showed that maternal condition around conception (rather than during gestation) was the best predictor of offspring sex ratio (Cameron 2004; Sheldon & West 2004), suggesting that TWM fits the ungulate model. However, there are a large number of studies failing to find any relationship between maternal condition and offspring sex ratio, including studies with very high quality data (e.g. Festa-Bianchet 1996; Lindström et al. 2002; Blanchard et al. 2004).

As TWM is merely one possible evolutionary mechanism (e.g. Charnov 1981; Frank 1990), the large discrepancy among studies suggests that other evolutionary mechanisms may also be important. So far, evolutionary models of sex ratio adjustment applied to mammals have ignored that females may gain indirect genetic benefits. The differential allocation hypothesis (DAH; Burley 1986; Sheldon 2000) predicts that females may increase fitness from producing sons when mating with attractive mates, because the sons may inherit the traits contributing to mating success. In polygynous mammals, the most favourable (and heritable; Kruuk et al. 2000) male trait is large body size, as size is decisive in intrasexual combat, which in turn determines fitness. If the DAH is applicable to polygynous mammals, we would predict offspring sex ratios biased towards males when the females are mating with large males.

Using a research herd of reindeer, we manipulated the male age and size structure during rut 10 times to test the predicted effects from the DAH of male phenotypic quality on the offspring sex ratio (table 1). Using two enclosures of approximately 15 km2, we manipulated the number, age and size of the males entering during the short rutting season, but the herd was joined the rest of the year to one of the enclosures experiencing similar conditions. Outside rutting period, females were together with both large and small males. The herd was supplementarily fed during the winters to level variation in maternal condition. As there was nevertheless some variation in autumn condition (table 1), we also tested for effects of maternal traits. As is typical for polygynous ungulates (Kruuk et al. 1999b), males of high body mass sired more calves in the study population (Røed et al. 2002), and mothers allocated more resources to male than to female calves (Holand et al. 2006a). Thus, two of the most important assumptions required for DAH to apply were fulfilled.

Table 1.

Reindeer breeding herd structure during the rut at the 10 manipulated treatments. (Mass (kg) gives the live body mass in mid-September, just prior to the rut and age is given in years.)

females males
treatment year number average age average mass number 1 year 2 years 3 years 4 years 5 years mass range average mass
1 1996 46 5.1 76.9 6 6 0 0 0 0 74–99 79.5
2 1996 43 5.1 79.5 6 3 0 0 3 0 75–140 103.8
3 1997 47 4.5 75.8 4 4 0 0 0 0 75–76 75.3
4 1997 47 4.5 73.6 18 9 6 0 0 3 59–139 84.6
5 1998 81 4.7 79.2 6 0 0 6 0 0 102–138 118.7
6 1999 75 4.6 74.5 3 0 0 0 3 0 120–140 131.0
7 2000 75 4.5 76.8 3 3 0 0 0 0 61–68 64.3
8 2001 80 5.2 83.6 11 11 0 0 0 0 68–89 79.2
9 2002 92 5.1 84.0 4 2 1 0 1 0 75–105 100.3
10 2003 53 5.5 80.7 4 1 1 2 0 0 95–120 108.5
Open in a new tab

2. Material and methods

(a) Study area and research herd of reindeer

The study was conducted at the Kutuharju Field Reindeer Research Station in Kaamanen, Finland (69° N, 27° E) in the period 1996–2003. The calf sex ratio has been analysed in 10 breeding herds, where the composition of males during the rut was manipulated (table 1), whereas the body condition and the age structure of the female segment were kept as stable as possible. Most males were replaced each season, although a few were repeatedly used up to three seasons, while approximately 10% of the oldest females were slaughtered each year and replaced by female yearlings. Two treatments were set up during each of the first two years with the herd separated in two adjacent areas (i.e. Lauluvaara, 13.8 km2; Sinioivi, 15 km2) during the rut (late September to early November), after which they were kept together in one area (Sinioivi). One treatment was set up in Sinioivi for each of the subsequent years. Mountain birches (Betula spp.) and pine (Pinus sylvestris) forests with numerous hills, lakes and bogs dominate the habitat in both these enclosures. The herds were supplementarily fed only during winter (Røed et al. 2002; Holand et al. 2003; Mysterud et al. 2003; Holand et al. 2006a).

During the calving season, all females were kept within a smaller enclosure where data on calf sex, birth date (daily observation) and mother–calf assignments were obtained and the calves were individually tagged. Blood samples were obtained from all individuals and analyses of paternity were based on scoring polymorphic DNA microsatellites (Røed et al. 2002). The mean (±s.d.) gestation period for these herds was previously estimated to be 222 (±2) days (Røed et al. 2002) and only calves born before 1st June were included in the analyses to avoid possible confounding effects of those conceived after the first main oestrous (Holand et al. 2006a).

(b) Statistical analyses

We used logistic regression to determine the relationship between sex ratio and candidate explanatory variables at a breeding herd scale. In total, the data included 527 calves that were sexed (for details see table 2). Out of these, 461 calves were conceived in the first rut and with known fathers. The offspring sex ratio did not differ between the full and the reduced datasets (table 2). At the individual level, we had a total of 418 offspring derived from 33 fathers and 148 mothers with data on all covariates. We therefore used generalized mixed-effects models (with a logit link and a binomial error term) at the individual level with two random factors: ‘father identity’ and ‘mother identity’ (using library lme4 in R v. 2.2.1; R Development Core Team 2006). The candidate terms for male phenotypic quality (mean at breeding herd level) were mass and age of males present, and mass and age of males that sired offspring. Individual sire mass was used at individual level analysis. The candidate terms for the TWM were female mass and age. Other candidate factors that may affect offspring sex ratio were adult sex ratio, date of birth and the proportion of females calving. At the breeding herd scale, we used the Akaike information criterion corrected for small sample size (AICc) to compare models (Burnham & Anderson 1998) and used goodness of fit to assess model fit to avoid overdispersion (table 3).

Table 2.

An overview of the number (n) of females in each treatment, the pregnancy rates (mainly determined by ultrasound), the calving rates, the total number of calves found with known sex (m, male; f, female), the number of calves conceived within first rut and with known father (used in analysis to table 3), and calves with all covariates known such as mother weight and birth date (used in individual analysis to table 4).

treatment females pregnancy rates calving rates known calves with known sex calves conceived within one ovulation, with known father (table 3) calves with all covariates known (table 4)
n n m f sex ratio n m f sex ratio n m f sex ratio
1 46 0.89 0.85 39 23 16 0.59 32 19 13 0.59 25 13 12 0.52
2 43 0.84 0.84 36 18 18 0.50 33 16 17 0.48 31 15 16 0.48
3 47 0.94 0.85 40 16 24 0.40 37 15 22 0.41 36 14 22 0.39
4 47 0.89 0.85 40 20 20 0.50 37 17 20 0.46 36 17 19 0.47
5 81 0.91 0.79 64 36 28 0.56 58 32 26 0.55 56 31 25 0.55
6 75 0.87 0.68 51 33 18 0.65 35 23 12 0.66 33 22 11 0.67
7 75 0.84 0.80 60 20 40 0.33 47 18 29 0.38 42 18 24 0.43
8 80 0.91 0.85 68 30 38 0.44 61 27 34 0.44 60 27 33 0.45
9 92 0.92 0.91 84 39 45 0.46 78 37 41 0.47 60 31 29 0.52
10 53 0.91 0.85 45 26 19 0.58 43 24 19 0.56 39 23 16 0.59
sum/mean 639 0.89 0.83 527 261 266 0.50 461 228 233 0.50 418 211 207 0.51
Open in a new tab

Table 3.

Predictive models of offspring sex ratio with a variable composition of the male segment in 10 experimental treatments in Kaamanen, Finland. (Models are logistic regression on the general form y=a+b(x). s.e., standard error; G, a test statistics for model fit that is ∼χ2 distributed; P model, test for overdispersion in the model; AICc, Akaike information criterion corrected for small sample size; ΔAICc, difference in AICc value relative to the best model (bolded); AICc−w, AICc weights. The AICc−w in line for the different hypotheses (in italics) are the summed values for parameters related to the specific hypothesis.)

parameter (x) a s.e.(a) b s.e.(b) Z P residual deviance d.f. G P (model) AICc ΔAICc AICc−w
differential allocation hypothesis 0.894
mean male age −0.6333 0.2703 0.2495 0.1036 2.409 0.016 5.118 8 0.640 1.000 51.855 0.999 0.236
mean male mass −1.2167 0.4680 0.0126 0.0048 2.606 0.009 4.120 8 0.515 1.000 50.856 0.000 0.389
mean sire age −0.5118 0.2587 0.1871 0.0921 2.032 0.042 6.854 8 0.857 0.999 53.590 2.734 0.099
mean sire mass −0.9972 0.4391 0.0094 0.0041 2.276 0.023 5.779 8 0.722 0.999 52.516 1.660 0.170
Trivers–Willard model 0.047
mean female age −0.9791 1.3713 0.1952 0.2789 0.700 0.484 10.523 8 1.315 0.995 57.260 6.404 0.016
mean female mass—September 1.0988 2.0726 −0.0141 0.0261 −0.541 0.588 10.720 8 1.340 0.995 57.457 6.601 0.014
mean female mass—October 2.0699 2.5901 −0.0267 0.0330 −0.808 0.419 10.359 8 1.295 0.996 57.096 6.240 0.017
various other factors 0.059
number of males 0.0680 0.1700 −0.0140 0.0222 −0.631 0.528 10.614 8 1.327 0.995 57.351 6.495 0.015
adult sex ratio (proportion of males) 0.0375 0.1623 −0.6548 1.4716 −0.445 0.656 10.815 8 1.352 0.995 57.552 6.696 0.014
mean birth date −2.0091 3.6150 0.0143 0.0260 0.550 0.582 10.711 8 1.339 0.995 57.448 6.592 0.014
proportion of females calving 1.0128 1.4483 −0.0113 0.0157 −0.716 0.474 10.501 8 1.313 0.995 57.237 6.381 0.016
Open in a new tab

3. Results

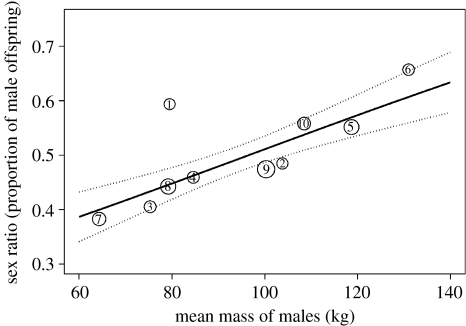
The manipulations of male phenotypic quality (and hence mate attractiveness) had a marked impact on the offspring sex ratio (figure 1; tables 3 and 4); a doubling of average male mass in the breeding herd led to an increase in the proportion of male offspring from approximately 40 to 60%. All models including a correlate of male phenotypic quality, supporting the DAH, vastly outperformed those expected from the TWM (table 3). Similar results were obtained when analysing this at the individual level, and fitting sire and mother identity as random terms in generalized mixed-effects models (table 4). The results were similar when running simpler models with each factor added in separate models (see electronic supplementary material). In some treatments, both large and small males were available during rut. Selective mating, if highly attractive males preferentially mated superior females, was nevertheless not a confounding factor because female phenotypic quality was controlled in the analysis and did not influence the calf sex ratio (tables 3 and 4). Moreover, offspring birth mass was not affected by the manipulation (table 4).

Figure 1.

Figure 1

Open in a new tab

The relationship between offspring sex ratio and average mate attractiveness (measured as mean mass of males greater than or equal to 1.5 years) in reindeer herds during the rut the year before calving. Dotted lines are 95% confidence intervals. The size of the circles is directly proportional to the sample size (i.e. the number of offspring born in each manipulation). The number within circles refers to the treatment number (see table 1).

Table 4.

Analysis of variation in (A) probability to give birth to a male calf and (B) birth mass as a function of female mass and age (predicted from Trivers–Willard model; TWM) and male body mass (predicted from differential allocation hypothesis; DAH). (Data derive from 10 manipulations of the male segment of reindeer herds in Finland. The models are (A) a generalized mixed-effects model (GLMM) with a logistic link and (B) a linear mixed-effects model (LME), both models with two random factors (both male and female identity). Factors for which the 95% confidence interval does not overlap 0 (and hence can be considered significant) are bolded.)

95% confidence interval
parameter estimate s.e. lower limit upper limit
(A) sex ratio
intercept −6.5900 3.2576 −13.1052 −0.0748
female age −3.5227 2.6560 −8.8348 1.7893
(female age)2 0.7943 2.2615 −3.7286 5.3173
female mass (September) 0.0225 0.0165 −0.0106 0.0555
male (sire) mass (Sep) 0.0097 0.0038 0.0021 0.0174
calf birth date (Julian date) 0.0273 0.0189 −0.0106 0.0652
(B) birth mass
intercept 4.4506 0.2349 3.9809 4.9204
calf sex (M versus F) −0.0031 0.1385 −0.2802 0.2740
female age 0.1108 0.1968 −0.2828 0.5043
(female age)2 −0.4861 0.1536 −0.7934 −0.1789
female mass (Sep) 0.0051 0.0015 0.0020 0.0081
male (sire) mass (Sep) 0.0002 0.0005 −0.0008 0.0011
calf birth date (Julian date) −0.0060 0.0014 −0.0087 −0.0032
female mass×calf sex −0.0005 0.0005 −0.0014 0.0005
male mass×calf sex 0.0015 0.0016 −0.0018 0.0047
Open in a new tab

4. Discussion

Our study provides support of the DAH (Burley 1986; Sheldon 2000); females produce more sons when mating with an attractive male. Studies on birds (Petrie 1994; Sheldon et al. 1999) and lizards (Calsbeek & Sinervo 2002; Olsson et al. 2005) show that the sex ratio is adjusted to mate attractiveness. For male birds providing care and for territorial lizards, mate choice may also provide some direct advantages in feeding. Reindeer are non-territorial and typical among ungulates with only females caring for the young. We are thus the first to report a skew in sex ratio related to mate attractiveness for mammals and, apart from peacock (Petrie 1994), for species with no paternal feeding or territoriality. Two earlier studies in the wildlife management literature report a similar effect of male age (and hence size) on offspring sex ratio (Ozoga & Verme 1985; Sæther et al. 2004), but with no link to any evolutionary model for optimal sex ratio adjustment. If differential allocation occurs, mothers can either produce more male offspring and/or invest more in offspring once they are conceived. Female birds laid larger eggs (Cunningham & Russell 2000) and deposited higher amounts of androgens in the eggs (Gil et al. 1999), and growth improved and survival of chicks increased (Petrie 1994), when mated to more attractive males. In the present study, female reindeer invested more when mating with an attractive male by producing more costly offspring (males), but apparently did not produce larger male offspring than usual (table 4).

The ‘sexy son’ hypothesis was developed during the late 1970s to early 1980s to understand why female birds accept mating with already mated males (Weatherhead & Robertson 1979). It was extended to the wider ‘good genes’ hypothesis (Gil et al. 1999), predicting that offspring fathered by preferred males should have increased viability resulting from superior genetic quality (Petrie 1994; Wedell & Tregenza 1999). Since size is decisive for lifetime reproductive success in many male mammals (Kruuk et al. 1999b), good genes should be linked to growth rate in males. In ungulates, the level of heritability of fitness related traits is often low due to environmental covariance (Kruuk et al. 2000, 2002). However, the highest heritability (h2=0.601) measured in red deer was found for male jaw size (a proxy for body size), heritability was quite high also for antler mass (h2=0.329), although the heritability of leg length was lower (Kruuk et al. 2000, 2002). An estimate of heritability of calf body mass in reindeer was 0.6 (Varo 1972). It is therefore likely that mating with large males has a selective advantage in terms of good genes. There may also be other indirect advantages of mating with preferred males promoting differential allocation, including other types of genetic benefits passed through the paternal line (through Fisherian, compatibility and male-manipulation mechanisms) and genetic benefits expressed only in daughters (good-mother genes; Cunningham & Russell 2001). In case of Fisher's hypothesis of runaway selection—similar to the sexy son hypothesis and the main alternative to the good genes hypothesis—the benefits to be gained by females would be in the form of genes for male attractiveness, but at equilibrium there is no net fitness gain to the female as would be expected from ‘good genes’ (Gil & Graves 2001).

There is a strong correlation between male size and reproductive success in ungulate mammals (Pemberton et al. 1992; Asa 1999; Coltman et al. 2002; for our population, see Røed et al. 2002). Intrasexual combats among male ungulates are the main determinants of access to females (Kruuk et al. 1999b). Thus, even passive female choice is enough to achieve mating with a large male. There may also be a small, direct benefit afforded by reduced harassment (Holand et al. 2006b). However, when only young males are present, mating is delayed by a few days (Mysterud et al. 2002), suggesting that females are reluctant to mate with young males and actively seek larger males. Females may also actively seek larger males (i.e. active female choice; Poole 1989). Thus, competition might be expected to have positive feedback for pre-copulatory female choice (Wong & Candolin 2005). Delayed breeding may have severe costs, as there is a considerable penalty on late breeding due to the strong seasonality at such high latitudes (Holand et al. 2006a).

Genetically, the quality of a male obviously does not change with age. Since it is rather unlikely that females can assess genetic quality directly, they have to use traits as cues, such as size or dominance. But why are females investing relative to male size, rather than age-specific size, which is probably more directly linked to genetic quality? Theoretically, it would be a beneficial tactic for females to use deviation from age-specific mean size as a guide in mate choice and investment pattern. However, it is unlikely that females can separate a large 1-year-old male (of high quality) from a small 2-year-old male (of low quality); at least, this is often not possible to a human observer. Age-specific size thus probably cannot be used as a reliable cue for female choice or DAH. A more reliable clue is for the biggest that are most likely to be of high quality, because poor genetic males will rarely be large. Therefore, investing less than average when mating with a small male and more when mating with a large one is probably the best strategy with the information available to a female. There was a very strong correlation between male size and dominance within each of the breeding groups/treatments in our study, but only when both small and large males were present (K. H. Røed et al. 2006, unpublished results). Therefore, it is not useful to directly link dominance rank to sex ratio in our specific case with manipulation of breeding herd composition. Within young males in a treatment (e.g. treatments 1, 3, 7 and 8 in table 1), even the most dominant one is a small male (and hierarchy seemed much less clear among the younger males). Our results suggest that females invest relative to male size and not rank (which is relative to other males present within each treatment). It is noteworthy that even in treatments with only small males, the females had, prior to the actual rut, been in herds with large males as well, so that they ‘know’ such males were present. This is important to note because investments are expected to be relative to what is available (West & Sheldon 2002). Owing to this design, our breeding herd level and individual level are not congruent with, respectively, between- and within-treatment scales, as the individual scale will also include the between-treatment effect. The individual analysis is important both to take into account that some of the individuals are used more than once and, since it directly assesses paternity, to enable us to link individual body mass of sires directly to offspring sex ratio.

Our study does not undermine the potential for the TWM to be operating as well. Indeed, the detailed data on red deer from the Isle of Rum, Scotland, have convincingly demonstrated that maternal dominance (within cohorts) affect offspring sex ratio and the subsequent fitness of those offspring as predicted by the TWM (Clutton-Brock et al. 1984, 1986; Kruuk et al. 1999a). In some cases, male mate choice is targeted towards the most fertile females (Berger 1989; Preston et al. 2005), which may confound observational studies of sex ratio trying to separate DAH and TWM, such as on Rum. However, there is currently no evidence that male mate choice is that important in red deer or reindeer. Even though we did not use maternal dominance directly (as on Rum), dominance is highly correlated with female age and mass in our population (Holand et al. 2004), suggesting that this is not due to traits measured. The lack of support for the TWM in our case may come from the fact that the herd is artificially fed during winter. However, there was nevertheless a quite large variation in female condition. Uncertainty remains regarding proximate mechanisms. Species with chromosomal sex determination have long been thought to be constrained in their sex allocation decisions by their means of sex determination. The cost of sex ratio adjustment to an individual female will depend heavily upon the mechanisms involved (West & Sheldon 2002). Substantial evidence has been found in several mammalian species that sex ratio adjustment occurs at or near implantation (Cameron 2004; Sheldon & West 2004). Evidence thus points to some aspects of sperm selectivity or production. Since females are uneasy at mating with small, young males, it has been argued that the adjustment of the secondary sex ratio could be related to females’ propensity to mate earlier or possibly within a narrower time window in their oestrous period with larger than smaller males (Mysterud et al. 2002). It remains to be determined with certainty how this affects the chemical environment in the females’ reproductive tract and subsequently the viability of y- and x-sperms.

Most populations of large herbivores are economically important and managed by humans. Often, more males than females are harvested, leading to female-biased population sex ratios (Milner et al. 2006). Our study provides a novel explanation for declining proportions of male offspring in heavily harvested populations (Mysterud et al. 2000; Sæther et al. 2004), because harvesting, by generating a high proportion of young, small and unattractive mates (Mysterud et al. 2002), affects the secondary sex ratio due to differential allocation effects in females. The secondary sex ratio can thus be affected by human-induced changes in the opportunities for female choice. Therefore, sustainable management needs to consider not only the direct demographic changes due to harvest mortality and selection (Coltman et al. 2003), but also the components related to behavioural ecology.

Acknowledgments

We wish to thank V. Tervonen and M. Tervonen and their crew at Kutuharju Experimental Reindeer Research Station in the Reindeer Herder's Association for their valuable assistance and logistic support. Thanks also to H. Gjøstein and M. Smith for their valuable field assistance and to H. Törmänen for keeping record of the production data and to L. Midthjell for her skilful assistance with genotyping. This study was partly supported by the Norwegian Reindeer Husbandry Research Council, the Research Council of Norway (Utmarksprogrammet to K.H.R. and Ø.H. and YFF to A.M.) and the Finnish Game and Fisheries Research Institute. We thank T. Slagsvold, an Editorial Board member and three anonymous referees for many insightful comments to a previous draft, N. G. Yoccoz for statistical advice and M. Festa-Bianchet and H. Kokko for discussions.

Supplementary Material

Electronic appendix

Analysis of variation in probability to give birth to a male calf as a function of female mass and age (predicted from TWM) and male body mass (predicted from DAH). (These are the same data as presented in table 4 of the main paper, but here models with fewer parameters are presented to show that results are robust to model specifications. The models are a generalized mixed-effects model (GLMM) with a logistic link and with two random factors (both male and female identity). Factors for which the 95% confidence interval does not overlap 0 (and hence can be considered significant) are bolded.)

rspb20060214s21.pdf (87.9KB, pdf)

References

  1. Asa C.S. Male reproductive success in free-ranging feral horses. Behav. Ecol. Sociobiol. 1999;47:89–93. doi:10.1007/s002650050653 [Google Scholar]
  2. Berger J. Female reproductive potential and its apparent evaluation by male mammals. J. Mammal. 1989;70:347–358. doi:10.2307/1381518 [Google Scholar]
  3. Blanchard P, Festa-Bianchet M, Gaillard J.-M, Jorgenson J.T. Maternal condition and offspring sex ratio in polygynous ungulates: a case study of bighorn sheep. Behav. Ecol. 2004;16:274–279. doi:10.1093/beheco/arh153 [Google Scholar]
  4. Burley N. Sexual selection for aesthetic traits in species with biparental care. Am. Nat. 1986;127:415–445. doi:10.1086/284493 [Google Scholar]
  5. Burnham K.P, Anderson D.R. Springer; New York, NY: 1998. Model selection and inference: a practical information-theoretic approach. [Google Scholar]
  6. Calsbeek R, Sinervo B. Uncoupling direct and indirect components of female choice in the wild. Proc. Natl Acad. Sci. USA. 2002;99:14 897–14 902. doi: 10.1073/pnas.242645199. doi:10.1073/pnas.242645199 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cameron E.Z. Facultative adjustment of mammalian sex ratios in support of the Trivers–Willard hypothesis: evidence for a mechanism. Proc. R. Soc. B. 2004;271:1723–1728. doi: 10.1098/rspb.2004.2773. doi:10.1098/rspb.2004.2773 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Charnov E.L. Princeton University Press; Princeton, NJ: 1981. The theory of sex allocation. [Google Scholar]
  9. Clutton-Brock T.H, Albon S.D, Guinness F.E. Maternal dominance, breeding success and birth sex ratios in red deer. Nature. 1984;308:358–360. doi:10.1038/308358a0 [Google Scholar]
  10. Clutton-Brock T.H, Albon S.D, Guinness F.E. Great expectations: dominance, breeding success and offspring sex ratios in red deer. Anim. Behav. 1986;34:460–471. doi:10.1016/S0003-3472(86)80115-4 [Google Scholar]
  11. Coltman D.W, Festa-Bianchet M, Jorgenson J.T, Strobeck C. Age-dependent sexual selection in bighorn rams. Proc. R. Soc. B. 2002;269:165–172. doi: 10.1098/rspb.2001.1851. doi:10.1098/rspb.2001.1851 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Coltman D.W, O'Donoghue P, Jorgenson J.T, Hogg J.T, Strobeck C, Festa-Bianchet M. Undesirable evolutionary consequences of trophy harvesting. Nature. 2003;426:655–658. doi: 10.1038/nature02177. doi:10.1038/nature02177 [DOI] [PubMed] [Google Scholar]
  13. Cunningham E.J.A, Russell A.F. Egg investment is influenced by male attractiveness in the mallard. Nature. 2000;404:74–76. doi: 10.1038/35003565. doi:10.1038/35003565 [DOI] [PubMed] [Google Scholar]
  14. Cunningham E.J.A, Russell A.F. Differential allocation and ‘good genes’. Trends Ecol. Evol. 2001;16:21. doi:10.1016/S0169-5347(00)02049-8 [Google Scholar]
  15. Festa-Bianchet M. Offspring sex ratio studies of mammals: does publication depend upon the quality of the research or the direction of the results? Ecoscience. 1996;3:42–44. [Google Scholar]
  16. Frank S.A. Sex allocation theory for birds and mammals. Annu. Rev. Ecol. Syst. 1990;21:13–55. doi:10.1146/annurev.es.21.110190.000305 [Google Scholar]
  17. Gil D, Graves J. Differential allocation and ‘good genes’. Trends Ecol. Evol. 2001;16:21–22. doi:10.1016/S0169-5347(00)02017-6 [Google Scholar]
  18. Gil D, Graves J, Hazon N, Wells A. Male attractiveness and differential testosterone investment in zebra finch eggs. Science. 1999;286:126–128. doi: 10.1126/science.286.5437.126. doi:10.1126/science.286.5437.126 [DOI] [PubMed] [Google Scholar]
  19. Hewison A.J.M, Gaillard J.-M. Successful sons or advantaged daughters? The Trivers–Willard model and sex-biased maternal investment in ungulates. Trends Ecol. Evol. 1999;14:229–234. doi: 10.1016/s0169-5347(99)01592-x. doi:10.1016/S0169-5347(99)01592-X [DOI] [PubMed] [Google Scholar]
  20. Holand Ø, Røed K.H, Mysterud A, Kumpula J.M, Nieminen M, Smith M.E. The effect of sex ratio and male age structure on reindeer calving. J. Wildl. Manage. 2003;67:25–33. [Google Scholar]
  21. Holand Ø, Gjøstein H, Losvar A, Kumpula J, Smith M.E, Røed K.H, Nieminen M, Weladji R.B. Social rank in female reindeer (Rangifer tarandus): effects of body mass, antler size and age. J. Zool. 2004;263:365–372. doi:10.1017/S0952836904005382 [Google Scholar]
  22. Holand Ø, Mysterud A, Røed K.H, Coulson T, Gjøstein H, Weladji R.B, Nieminen M. Adaptive adjustment of offspring sex ratio and maternal reproductive effort in an iteroparous mammal. Proc. R. Soc. B. 2006a;273:293–299. doi: 10.1098/rspb.2005.3330. doi:10.1098/rspb.2005.3330 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Holand Ø, Weladji R.B, Røed K.H, Gjøstein H, Kumpula J, Gaillard J.-M, Smith M.E, Nieminen M. Male age structure influences females' mass change during rut in a polygynous ungulate: the reindeer (Rangifer tarandus) Behav. Ecol. Sociobiol. 2006b;59:694–703. doi:10.1007/s00265-005-0097-5 [Google Scholar]
  24. Kruuk L.E.B, Clutton-Brock T.H, Albon S.D, Pemberton J.M, Guinness F.E. Population density affects sex ratio variation in red deer. Nature. 1999a;399:459–461. doi: 10.1038/20917. doi:10.1038/20917 [DOI] [PubMed] [Google Scholar]
  25. Kruuk L.E.B, Clutton-Brock T.H, Rose K.E, Guinness F.E. Early determinants of lifetime reproductive success differ between the sexes in red deer. Proc. R. Soc. B. 1999b;266:1655–1661. doi: 10.1098/rspb.1999.0828. doi:10.1098/rspb.1999.0828 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kruuk L.E.B, Clutton-Brock T.H, Slate J, Pemberton J.M, Brotherstone S, Guinness F.E. Heritability of fitness in a wild mammal population. Proc. Natl Acad. Sci. USA. 2000;97:698–703. doi: 10.1073/pnas.97.2.698. doi:10.1073/pnas.97.2.698 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kruuk L.E.B, Slate J, Pemberton J.M, Brotherstone S, Guinness F, Clutton-Brock T. Antler size in red deer: heritability and selection but no evolution. Evolution. 2002;56:1683–1695. doi: 10.1111/j.0014-3820.2002.tb01480.x. doi:10.1554/0014-3820(2002)056[1683:ASIRDH]2.0.CO;2 [DOI] [PubMed] [Google Scholar]
  28. Leimar O. Life-history analysis of the Trivers and Willard sex-ratio problem. Behav. Ecol. 1996;7:316–325. [Google Scholar]
  29. Lindström J, Coulson T, Kruuk L.E.B, Forchhammer M.C, Coltman D.W, Clutton-Brock T. Sex-ratio variation in Soay sheep. Behav. Ecol. Sociobiol. 2002;53:25–30. doi:10.1007/s00265-002-0545-4 [Google Scholar]
  30. Maynard Smith J. A new theory of sexual investment. Behav. Ecol. Sociobiol. 1980;7:247–251. doi:10.1007/BF00299371 [Google Scholar]
  31. Milner J.M, Bonenfant C, Mysterud A, Gaillard J.-M, Csányi S, Stenseth N.C. Temporal and spatial development of red deer harvesting in Europe—biological and cultural factors. J. Appl. Ecol. 2006;43:721–734. doi:10.1111/j.1365-2664.2006.01183.x [Google Scholar]
  32. Mysterud A, Yoccoz N.G, Stenseth N.C, Langvatn R. Relationships between sex ratio, climate and density in red deer: the importance of spatial scale. J. Anim. Ecol. 2000;69:959–974. doi:10.1046/j.1365-2656.2000.00454.x [Google Scholar]
  33. Mysterud A, Coulson T, Stenseth N.C. The role of males in the population dynamics of ungulates. J. Anim. Ecol. 2002;71:907–915. doi:10.1046/j.1365-2656.2002.00655.x [Google Scholar]
  34. Mysterud A, Holand Ø, Røed K.H, Gjøstein H, Kumpula J.M, Nieminen M. Effects of age, density and sex ratio on reproductive effort in male reindeer (Rangifer tarandus) J. Zool. 2003;261:341–344. doi:10.1017/S0952836903004114 [Google Scholar]
  35. Olsson M, Wapstra E, Uller T. Differential sex allocation in sand lizards: bright males induce daughter production in a species with heteromorphic sex chromosomes. Biol. Lett. 2005;1:378–380. doi: 10.1098/rsbl.2005.0327. doi:10.1098/rsbl.2005.0327 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ozoga J.J, Verme L.J. Comparative breeding behavior and performance of yearling vs. prime-age white-tailed bucks. J. Wildl. Manage. 1985;49:364–372. [Google Scholar]
  37. Pemberton J.M, Albon S, Guinness F.E, Clutton-Brock T.H, Dover G.A. Behavioral estimates of male mating success tested by DNA fingerprinting in a polygynous mammal. Behav. Ecol. 1992;3:66–75. [Google Scholar]
  38. Petrie M. Improved growth and survival of offspring of peacocks with more elaborate trains. Nature. 1994;371:598–599. doi:10.1038/371598a0 [Google Scholar]
  39. Poole J.H. Mate guarding, reproductive success and female choice in African elephants. Anim. Behav. 1989;37:842–849. doi:10.1016/0003-3472(89)90068-7 [Google Scholar]
  40. Preston B.T, Stevenson I.R, Pemberton J.M, Coltman D.W, Wilson K. Male mate choice influences female promiscuity in Soay sheep. Proc. R. Soc. B. 2005;272:365–373. doi: 10.1098/rspb.2004.2977. doi:10.1098/rspb.2004.2977 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. R Development Core Team. R Foundation for Statistical Computing; Vienna, Austria: 2006. R: a language and environment for statistical computing. [Google Scholar]
  42. Røed K.H, Holand Ø, Smith M.E, Gjøstein H, Kumpula J, Nieminen M. Reproductive success in reindeer males in a herd with varying sex ratio. Mol. Ecol. 2002;11:1239–1243. doi: 10.1046/j.1365-294x.2002.01509.x. doi:10.1046/j.1365-294X.2002.01509.x [DOI] [PubMed] [Google Scholar]
  43. Sæther B.-E, Solberg E.J, Heim M, Stacy J.E, Jakobsen K, Olstad R. Offspring sex ratio in moose Alces alces in relation to paternal age: an experiment. Wildl. Biol. 2004;10:51–57. [Google Scholar]
  44. Sheldon B.C. Differential allocation: tests, mechanisms and implications. Trends Ecol. Evol. 2000;15:397–402. doi: 10.1016/s0169-5347(00)01953-4. doi:10.1016/S0169-5347(00)01953-4 [DOI] [PubMed] [Google Scholar]
  45. Sheldon B.C, West S.A. Maternal dominance, maternal condition, and offspring sex ratio in ungulate mammals. Am. Nat. 2004;163:40–54. doi: 10.1086/381003. doi:10.1086/381003 [DOI] [PubMed] [Google Scholar]
  46. Sheldon B.C, Andersson S, Griffith S.C, Örnborg J, Sendecka J. Ultraviolet colour variation influences blue tit sex ratios. Nature. 1999;402:874–876. doi:10.1038/47239 [Google Scholar]
  47. Trivers R.L, Willard D.E. Natural selection of parental ability to vary the sex ratio of offspring. Science. 1973;179:90–92. doi: 10.1126/science.179.4068.90. doi:10.1126/science.179.4068.90 [DOI] [PubMed] [Google Scholar]
  48. Varo M. Investigations to the possibilities of reindeer breeding II. J. Sci. Agric. Soc. Finl. 1972;44:234–248. [Google Scholar]
  49. Weatherhead P.J, Robertson R.J. Offspring quality and the polygyny threshold: “The sexy son hypothesis”. Am. Nat. 1979;113:201–208. doi:10.1086/283379 [Google Scholar]
  50. Wedell N, Tregenza T. Successful fathers sire successful sons. Evolution. 1999;53:620–625. doi: 10.1111/j.1558-5646.1999.tb03797.x. doi:10.2307/2640798 [DOI] [PubMed] [Google Scholar]
  51. West S.A, Sheldon B.C. Constraints in the evolution of sex ratio adjustment. Science. 2002;295:1685–1688. doi: 10.1126/science.1069043. doi:10.1126/science.1069043 [DOI] [PubMed] [Google Scholar]
  52. Wong B.B.M, Candolin U. How is female mate choice affected by male competition? Biol. Rev. 2005;80:559–571. doi: 10.1017/S1464793105006809. doi:10.1017/S1464793105006809 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Electronic appendix

Analysis of variation in probability to give birth to a male calf as a function of female mass and age (predicted from TWM) and male body mass (predicted from DAH). (These are the same data as presented in table 4 of the main paper, but here models with fewer parameters are presented to show that results are robust to model specifications. The models are a generalized mixed-effects model (GLMM) with a logistic link and with two random factors (both male and female identity). Factors for which the 95% confidence interval does not overlap 0 (and hence can be considered significant) are bolded.)

rspb20060214s21.pdf (87.9KB, pdf)

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES