Abstract
Proper management of ecosystems requires an understanding of both the species interactions as well as the effect of climate variation. However, a common problem is that the available time-series are of different lengths. Here, we present a general approach for studying the dynamic structure of such interactions. Specifically, we analyse the recruitment of the world's largest cod stock, the Northeast Arctic cod. Studies based on data starting in the 1970–1980s indicate that this stock is affected by temperature through a variety of pathways. However, the value of such studies is somewhat limited by the fact that they are based on a quite specific ecological and climatic situation. Recently, this stock has consisted of fairly young fish and the spawning stock has consisted of relatively few age groups. In this study, we develop a model for the effect of capelin (the cod's main prey) and herring on cod recruitment since 1973. Based on this model, we analyse data on cod, herring and temperature going back to 1921 and find that food-web effects explain a significant part of the cod recruitment variation back to around 1950.
Keywords: multi-species, Barents Sea, cod, capelin, herring, climate
1. Introduction
There is an increasing appreciation of the fact that ecosystem management requires a solid understanding of interdependent effects (Stenseth et al. 2002): firstly, the impact of species interactions, which may result in unexpected population responses to for example harvesting (Yodzis 2001) and secondly, the impact of climate variations and trends, both the natural variation on decadal scales (Bengtsson et al. 2004) and the effects of global warming (IPCC 2001). The Code of Conduct for Responsible Fisheries of 1995 (FAO 1995) as well as the Reykjavik Declaration of 2001 on Responsible Fisheries (FAO 2002) call for an ecosystem-based approach to fisheries management. However, adopting such an approach has proven difficult due to limited data and a resulting lack of a proper understanding of the effects driving the dynamics of fish stocks. Such an understanding is crucial if one aims at predicting the ecological outcome of fisheries and environmental change. As a consequence, the vast majority of stocks are managed within a single-species perspective and without accounting for what might happen if climate should change. Our perspective within this contribution is to obtain an improved understanding of what has happened in the past and, by doing so, to provide an improved understanding of what might happen in the future should climate (and other features of the system) change—hence, a time-series approach.
Typically, the data available on fish abundance in marine ecosystems consist of survey-based abundance estimates only from a relatively short, recent period of time, as well as estimates and indices of a smaller number of species (those commercially important) derived from fisheries over a longer period of time. Multi-species models are typically ‘data-hungry’ and, as a result, the parameters of such models are necessarily based upon data from a fairly short (and recent) time period. Hence, our understanding of the dynamics of these systems is typically based upon observations corresponding to quite a narrow range of climatic and ecological conditions, which subsequently introduces an uncertainty about the ability of the model to predict future dynamics. Quite conceivably, the parameters describing the species interactions might change as the ecological and climatological state changes (Ciannelli et al. 2005). Here, we develop a simple statistical multi-species model, including climatic effects, based on the most recent and more detailed time-series data, to predict the recruitment of Northeast Arctic (NEA) cod (Gadus morhua). We then extend this model back in time, substituting abundance of species we have no information about with a function of the abundance of species for which we do have long time-series data. Using this approach, we can assess to what degree the long-term data are consistent with current knowledge and models based on a shorter term time-series. Our models are specific for the Barents Sea, but the methods are general and can be applied to analyse species interactions under climate variability in other systems, terrestrial as well as aquatic. Furthermore, our findings of the importance of trophic interactions should be of broad interest.
2. The cod–capelin–herring system of the Barents Sea
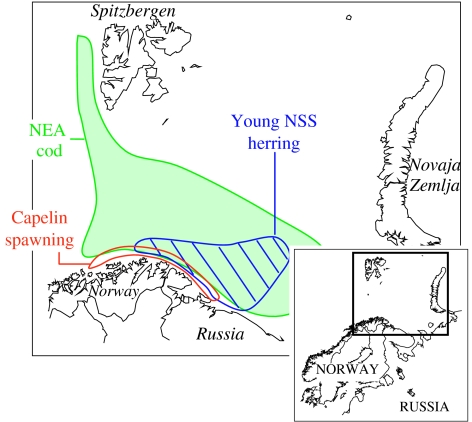
The NEA cod, co-managed between Norway and Russia (figure 1), is at present the largest stock of Atlantic cod accounting for half of all Atlantic cod fisheries. The rate of exploitation of the NEA cod increased steadily from the 1950s onwards (ICES 2004), and from 1969 onwards, the International Council for the Exploration of the Sea (ICES) expressed concern about the high exploitation rate. However, scientists expressed optimism in 1985 based on several successive years (1983–1985) of high survey indices of five-month-old cod (Nakken 1998). This expectation failed as a lack of capelin, the cod's main food, led to high cannibalism and low individual growth; as a result, the cod catches at the end of the 1980s were the lowest on record. The cod quotas were increased strongly in the 1990s but then reduced again; however, illegal fisheries on a huge scale are a major problem (ICES 2006).
Figure 1.
The Barents Sea with the distribution of the NEA cod (green), spawning stock of capelin (red) and young herring (blue). The young cod prey on age 1 and older capelin, their key food item. Young herring feed on capelin larvae. The capelin migrates to the northern coasts of Norway and Russia to spawn.
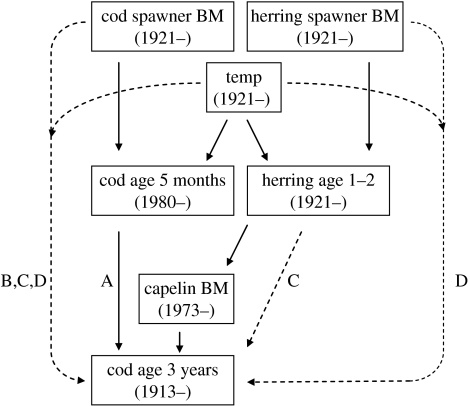
The recruitment of NEA cod—here, defined as the number of cod at age 3 in year t (Ncod age 3,t) was assumed to be affected by temperature in two ways. Firstly, larval abundance as measured at age five months (in year t−3) is positively correlated with the temperature in the year of spawning, probably because temperature is a proxy for several factors including the availability of the larvae's prey (copepod nauplii) and the advection of larvae to favourable areas. Secondly, combining several pieces of knowledge, one may expect cod to be influenced by a climate-induced food-web cascade (figure 2). Studies of cod stomachs show that the number of 1–2-year-old cod eaten by larger cod is influenced by the abundance of its key prey species, Barents Sea capelin Mallotus villosus (ICES 2004: fig. 3.14a); we therefore expect that cod recruitment is affected by capelin abundance in years t−1 and t−2. In turn, the recruitment of capelin is heavily affected by young (1–2-year-old) Norwegian Spring-spawning (NSS) herring (Clupea harengus), who eat capelin larvae (Gjøsæter & Bogstad 1998). Finally, the reproduction success (larval survival) of herring is strongly, positively correlated with sea temperature—as is the cod.
Figure 2.
Factors affecting the recruitment of NEA cod at age 3. Letters indicate pathways of models A–D (table 1). Solid and dotted lines indicate direct and indirect causation, respectively. Temperature affects cod recruitment of 3-year-old directly in the spawning year of cod, and possibly indirectly through the effect on herring. Higher temperatures at spawning time and more capelin have a positive effect on cod recruitment. However, high temperatures and resulting high herring recruitment will decrease capelin biomass, which will affect the cod recruitment negatively through cannibalism. Hence, indirect effects of temperature through herring and capelin might be negative. The capelin is also affected by a directed fishery.
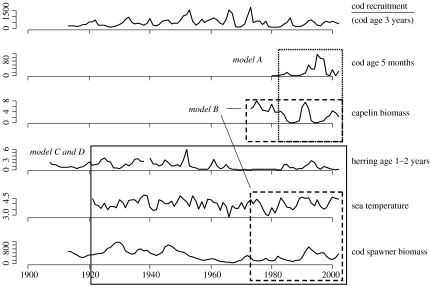
The fluctuations in the capelin, herring and cod stocks are shown in figure 3. The key link is capelin, which has collapsed three times since it started to be surveyed in 1973 (figure 3), each time following years of abundant herring cohorts. There were no collapses after the NSS herring collapsed (due to overfishing and unfavourable climate) in 1969 and before the herring started recovery in 1983, but anecdotes and landings indicate that collapses have occurred before 1969 (Gjøsæter 1998). Decadal trends in the general abundance of the NEA cod stock have been linked to long-term trends in temperature during the twentieth century (Godø 2003), but the relationship between cannibalism (or proxies of cannibalism) and recruitment has not been analysed.
Figure 3.
The most important time-series used in this paper. Cod recruitment (the time-series on the top) is the response variable of the models, and the main explanatory variables of models A–D are indicated by rectangles. For details and source of each variable, see text and table A1 in the electronic supplementary material.
3. Material and methods
(a) The data
The data (see figure 3 for data sources; see also table A1 in the electronic supplementary material) for cod and herring were age-specific abundance estimates, derived from virtual population analysis (VPA) based on commercial catch statistics. For cod, these estimates are available in two versions, one, since 1984, adjusted for added mortality of 3–5-year-old cod due to cannibalism, and one without such adjustment. We used the latter to avoid heterogeneity before and after 1984. For the same reason, we avoided using estimates that incorporate survey data for recent years, so we used only VPA estimates until 2002 (more recent estimates must incorporate survey data; Cotter et al. 2004). The capelin spawn only once before it dies and is not possible to estimate using VPA; its abundance is estimated based on acoustic surveys during September performed jointly since 1973 by the Institute of Marine Research (IMR; Bergen, Norway) and the Knipovich Polar Institute of Marine Fisheries and Oceanography (PINRO; Murmansk, Russia). In addition, we used joint IMR–PINRO survey estimates of cod of the ‘0-group stage’ (age approximately five months) and PINRO's temperature data from the Russian Kola meridian transect (33°30′ E and 70°30′ N to 72°30′ N).
(b) The modelling approach
The failure of single-species models in the 1980s (Nakken 1998) led to the development of multi-species models (Tjelmeland & Bogstad 1998; Hamre 2003). However, these models are based on the experience from a relatively recent time period from which reliable and (more or less) uniformly sampled survey data exist (for capelin, from 1973; for cod, from 1980). Using a series of models like we do here, we can take advantage of both the higher detail of the shorter time-series, as well as the large time coverage of the longer time-series (figures 2 and 3). Using the abundance of five-month-old cod (estimated from 1980), we are able to focus on the age range when we expect cannibalism to occur (from five months to 3 years), and to see whether a lack of capelin influences the survival of cod. When this relationship has been established, we construct a recruitment model, linking the abundance of spawners to recruitment 3 years after, taking into account the conditions for larval cod (i.e. sea temperature) and the abundance of capelin. To be able to analyse the period before the capelin surveys (i.e. 1921–1972; figure 3), we use past abundance of herring as a proxy for present capelin biomass, based on the herring–capelin relationship observed from 1973 onwards. Finally, we include a temperature-driven model for herring recruitment, resulting in a model for cod recruitment based on the cod spawning stock, the temperature and the herring spawning stock. If the longest time-series indicate an effect of food-web-mediated cannibalism, the interpretation is uncertain because we integrate so many processes (spawning, larval survival and cannibalism) by linking spawners to 3-year-old fish. However, our hypothesis of food-web-mediated cannibalism is strengthened if it is also supported by analysing the shorter series (i.e. the abundance of five-month-old cod). Moreover, this enables us to study the behaviour of the ecosystem in periods with less fishing pressure, as well as different climate regimes such as the warming of the North Atlantic between 1920 and 1940 and the subsequent cooling (1940–1960) (Bengtsson et al. 2004; Drinkwater 2006).
(c) The series of models
We investigated the effects of temperature and cannibalism on cod recruitment (Ncod age 3,t) using four models A–D (table 1). As a proxy for cannibalism on ages 1 and 2 cod, we used the ratio between the biomass of cannibalistic cod and the available biomass of capelin , both taken as means over years t−1 and t−2. For simplification, is estimated as the biomass of cod age 3–6, as these age groups have higher numbers and a larger degree of spatial and temporal overlap with ages 1 and 2 cod than cod above age 6. In the period 1984–2005, 3–6-year-old cod was responsible for 67% of the cannibalism on 1–2-year-old cod (unpublished results based on stomach samples). In models A and B, is taken as the availability of mature capelin in spring. The biomass of capelin was estimated during September. Capelin longer than 14.0 cm are expected to mature the following winter (Gjøsæter 1998), and we therefore let ABMcapelin be equal to the estimated biomass of capelin greater than 14 cm minus the biomass of capelin fished in this length group between the survey and the time of spawning (for details and the effects of changing this assumption, see the electronic supplementary material). The parameter e is included because variation in the capelin biomass may be less important when the biomass of capelin is large, as food becomes plentiful for cannibalistic cod. At this point, we only consider capelin as food for cannibalistic cod; later, we also investigate the effect of herring as a food source for cod.
Table 1.
Main causal models investigated in this paper. (The subscript t denotes time (years). Some terms (or combinations of terms, indicated by the underscore) were proxies for the real terms of interest (shown in parentheses). Data for the latter terms were not available for the time period considered (see figures 2 and 3; table A1 in the electronic supplementary material). In models C and D, we use proxies for proxies; each term is a proxy for the term below.)
| model | year-classes | ||
|---|---|---|---|
| A | equation (3.1) |
|
1980–1999 |
| B | equation (3.2) |
|
1972–1999 |
| C | equations (3.2)–(3.4a,b) |

|
1921–1999 |
| D | equations (3.2)–(3.6a–c) |

|
1926–1999 |
In all models, the response variable was log(Ncod age 3,t) from VPA estimates. Model fitting was in general done by minimizing least square errors using a Gauss–Newton algorithm (nls in the program R; www.r-project.org). We first tested whether the parameter e was significantly different from unity, and excluded it if it was not.
In model A (table 1; figure 2), we pinpoint the age range when the recruiting cod is most affected by cannibalism from age 5 months to 3 years. We assume a Gompertz relationship (Gompertz 1825; see also Stenseth et al. 1999) between the abundance at age five months and at 3 years, with the cod–capelin ratio as a proxy for cannibalism. We also included temperature (Temp) in the cod's spawning year as a proxy for the cod's spatial distribution; cod larvae are transported far east in warm years, which will affect the spatial distribution of this cohort for at least the first year of the cod's life (Helle et al. 2002).
| (3.1) |
for which parameters were estimated for cod year-classes 1980–1999 (3-year-old 1983–2002).
With model B, we combined cod spawning biomass and temperature in the cod's spawning year as a proxy for abundance at age five months, enabling us to parameterize the model using a somewhat longer time-series (i.e. back to 1973). We start by assuming that the cod's spawning stock biomass (SSB) and recruits are linked by the Beverton–Holt relationship f×SSB/(1+g×SSB) (Beverton & Holt 1957). We then modify this relationship by taking into account the positive effect of temperature in the year of spawning (year t−3) and the negative effect of the ratio between predatory cod and capelin in years t−2 and t−1. This modifies the log-transformed Beverton–Holt relationship to:
| (3.2) |
for which parameters were estimated for cod year-classes 1973–1999 (3-year-old 1975–2002).
In model C, we exploited the fact that predation from young (ages 1–2) herring on capelin larvae strongly affects capelin dynamics. Thus, the biomass of x-year-old capelin to a large extent depends on the abundance of young herring x years before. The age distribution of capelin fluctuates a lot, but on average, capelin of ages 1, 2, 3 and 4 constitutes, respectively, 27, 44, 25 and 4% of the total biomass of capelin. Although this age distribution varies strongly, we assume the biomass of capelin in year t to depend on a weighted average of the abundance of young herring 1–4 years before (WHt), defined as
| (3.3) |
where BMherr,t is the combined biomass of 1- and 2-year-old herring (in 106 t) in year t. Based on a plot of capelin biomass BMcapelin,t versus WHt, we fitted a nonlinear ‘hockey-stick’ regression with two log-linear segments:
| (3.4a) |
| (3.4b) |
The parameters (including the threshold WHthresh) were fitted by minimizing least square errors of log(BMcapelin,t) and this relationship, together with the observed capelin harvest from 1921, was used as a replacement for ABMcapelin in equation (3.2). The parameters were estimated both for the entire time-series (cod year-classes 1921–1999) and independently for the four time periods.
In model D, we completed the indirect causal chain temperature-herring–capelin–cod by including a recruitment model for herring, including the effect of temperature on herring recruitment success. We fitted a Beverton–Holt model adjusted for temperature to the spawning SSB and the number of age 0 herring from 1921 to 1998,
| (3.5) |
where SSB is given in 106 t and Nherr,age0 is given in numbers×10−9. To find the biomass of herring ages 1 and 2 (BMherr,t), we used the following equations
| (3.6a) |
| (3.6b) |
| (3.6c) |
where Fherr,age0 and Fherr,age1 are the observed fishing mortalities for ages 0 and 1, respectively, and Wherr,age1 and Wherr,age2 are the observed mean individual weights 1921–2003 for ages 1 and 2 (in kilogram). The fixed natural mortality at 0.9 is the same as the natural mortality for these age groups assumed in the VPA procedure (Toresen & Østvedt 2000). Using equations 3.3 and 3.4a,b and adding the effect of harvest, the predicted BMherr,t was used to predict ABMcapelin,t of equation (3.2). Then, the parameters of equation (3.2) were re-estimated both for the whole period (cod year-classes 1926–1999, constrained by the temperature data starting in 1921 and the time lags of equations (3.3) and (3.6a–c)) and for different sub-periods.
(d) Considering the effect of herring as food for cod
So far, we have assumed that capelin is the main food for cannibalistic cod, and that herring only affect cod in a negative way. However, cod also eat young herring and it has been suggested that in periods with much young herring, the cod can at least partly compensate for the decrease of capelin by switching to eat more herring. To test this, we modified models A, B and C by adding a term to equations 3.1 and 3.2 (i.e. testing whether including the ratio between young herring and cannibalistic cod when the recruiting cod is 1–2 years-old improves the models).
4. Results
The survival of cod from age five months to 3 years (model A; equation (3.1)), the period when we expect cod to be susceptible to cannibalism, showed a clear negative nonlinear effect of a high biomass ratio between cannibalistic cod and capelin (table 2), indicating a substantial increase in cannibalism when this ratio is high. There was also a trend for survival to increase with temperature in the spawning year. When investigating the spawner-recruitment relationship from 1972 onwards (model B; equation (3.2)), we found the same trends but with slightly stronger effect of temperature (table 2). This indicates an effect of cannibalism between age five months and 3 years. Since the cod–capelin ratio observed since 1973 has varied more than 100-fold, the estimate of parameter d in equation (3.2) (d=−0.16) indicates a twofold variation in cod recruitment due to variation in the cod–capelin ratio (exp(log(100)×0.16)=2.09). These conclusions were not changed if we changed the way we calculated the available capelin biomass after harvesting (see table A2 in the electronic supplementary material).
Table 2.
Estimated parameter values for equations (3.1) (model A) and (3.2) (models B and C). In both equations (3.1) and (3.2), the parameter c is the effect of the sea temperature in the cod's spawning year, and d is the effect of the biomass ratio between cannibalistic cod (i.e. potential cannibals) and capelin ratio. (The rightmost three columns show results of a likelihood ratio test when removing a term (Diff LL=difference in log likelihood). In the case of model B (equation (3.2)), the parameter e was found to not improve the fit of the models (Diff LL=0.96, d.f.=1, p=0.16) and was consequently removed; however, the cod–capelin ratio was also significant before e was removed (Diff LL=4.27, d.f.=2, p=0.014). In model C, e was not estimable.)
| parameter | estimate | s.e. | Diff LL | d.f. | p | |
|---|---|---|---|---|---|---|
| model A (equation (3.1))—fitted for cod year-classes 1980–1999 (R2=0.72) | ||||||
| intercept | a | 8.78 | 1.98 | |||
| cod at five months | b | 0.13 | 0.04 | |||
| temperature | c | 0.62 | 0.21 | 4.52 | 1 | 0.003 |
| cod–capelin | d | −0.97 | 0.32 | 10.54 | 2a | <0.001 |
| capelin nonlin. | e | 0.18 | 0.11 | 2.89 | 1 | 0.016 |
| model B (equation (3.2))—fitted for cod year-classes 1972–1999 (R2=0.54) | ||||||
| Beverton–Holt | log(f) | −1.12 | 0.74 | |||
| Beverton–Holt | log(g) | −4.68 | 0.77 | |||
| temperature | c | 0.70 | 0.18 | 7.00 | 1 | 0.000 |
| cod–capelin | d | −0.16 | 0.07 | 3.22 | 1 | 0.011 |
| model C (equation (3.2), utilizing equations (3.3) and (3.4a,b))—fitted for cod year-classes 1921–1999 (R2=0.22) | ||||||
| Beverton–Holt | log(f) | 0.06 | 0.73 | |||
| Beverton–Holt | log(g) | −4.32 | 0.76 | |||
| temperature | c | 0.49 | 0.16 | 4.34 | 1 | 0.003 |
| cod–capelin | d | −0.16 | 0.06 | 4.54 | 1 | 0.003 |
The cod–capelin term has two degrees of freedom (two parameters, d and e).
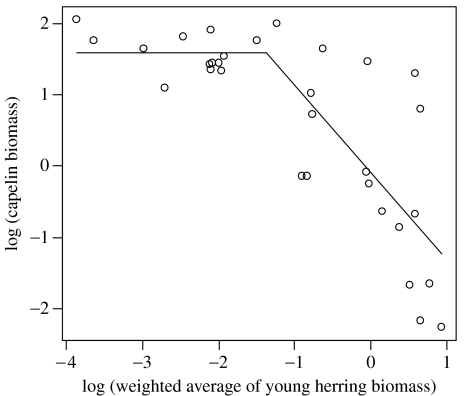
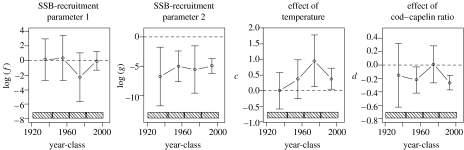
We were able to explain most of the variation in capelin biomass using equation (3.4a,b) (figure 4). The estimates indicated that the herring has no significant effect on capelin as long as the weighted average of herring biomass is below 0.25×106 t (WHthresh), but a strong negative effect if herring biomass exceeded this threshold. Replacing the observed capelin biomass in equation (3.2) with this relationship and re-estimating the parameters for cod year-classes 1921–1999 (model C), we found both the effect of temperature in the spawning year and the indirect effect of herring to be statistically significant (table 2) for the period as a whole. When estimating the parameters independently for four time periods (figure 5), we found the indirect effect of herring to be significant for cod year-classes 1943–1961 and 1981–1999, but not for cod year-classes 1962–1980 (which is not surprising, since there was extremely little young herring during most of this time period) or the earliest time period. There is no evidence for temperature in the spawning year to affect cod before 1962, while the parameters of the Beverton–Holt relationship indicate a constant effect of intra-specific competition (parameter g) for all periods (figure 5).
Figure 4.
Relationship between the ‘herring index’ WHt and the capelin biomass in year t. The parameters of equation 3.4a,b were k1=4.855, k3=1.580, k4=1.221 and WHthresh=0.225. R2=0.65. k2 was found not to differ significantly from zero.
Figure 5.
Parameter estimates of model C and their 95% confidence intervals. The parameters were estimated independently for four time periods of similar length (the earliest period is somewhat longer in order to avoid estimation problems): cod year-classes 1921–1942; 1943–1961; 1962–1980; and 1981–1999 (indicated by the shaded boxes).
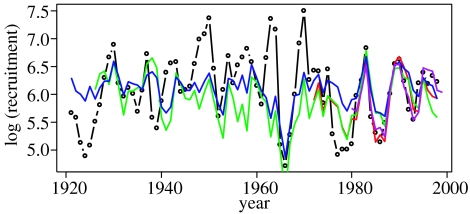
Finally, we predicted the biomass of young herring (equation (3.6a–c)) by fitting a temperature-dependent recruitment model for herring (equation (3.5)) to data from 1921 to 1998, obtaining m=0.32 (CI: 0.036–2.94), n=0.37 (CI: 0.16–0.86) and o=1.25 (CI: 0.68–1.82), which explained much of the variation in herring recruitment (R2=0.65). The predictions of the resulting model on cod recruitment (model D) were very similar to those of model C (figure 6).
Figure 6.
Observed and predicted abundance of cod year-classes 1921–1999 at age 3 (log transformed). Black line with dots: observed values; purple: model A; red: model B; blue: model C; and green: model D.
Calculating the explanation power (R2) of the different models for four different periods of time (table 3) shows that in the most recent period, we can explain most of the variance in cod recruitment (R2≧0.70) based on either capelin abundance (models A and B) or using the abundance of young herring as a proxy (model C). The explanation power is lower (R2=30–40%) for models C and D for the three earliest periods (1926–1982). In general, the models are good at explaining particularly small cohorts but not able to explain some exceptionally successful cohorts (such as year-classes 1963–1964 and 1969–1970; figure 6). For all periods, deleting the effect of the cod–capelin ratio reduces the explanation power of the models quite strongly, indicating a consistent and substantial effect of cannibalism. Deleting the effect of temperature in the cod's spawning year has a substantial effect in the period 1968–1982 but a smaller effect otherwise; in the most recent period, temperature is confounded with the cod–capelin ratio. Finally, we see that ignoring the effect of temperature on herring (by modifying and refitting equation (3.5)) has no effect, indicating no indirect effect of temperature on cod via herring and capelin.
Table 3.
Explanation power for the models A–D for different time periods covering year-classes 1926–1999 and the effect of deleting some model components of models B–D. The table shows R2 values (1−Σ(P−O)2/Σ (mean[O]−O)2, where P=predicted and O=observed values). In order to make the proportion explained comparable, we strived towards making time periods of equal length, but due to model estimation problems the periods are of somewhat unequal length (19, 23, 15 and 17 years). Bold and bold italic numbers indicate R2 values in the range 0.30–0.59 and 0.60–1.00, respectively.
| 1926–44 | 1945–67 | 1968–82 | 1983–99 | |
|---|---|---|---|---|
| model A | 0.77 | |||
| model B | 0.77 | |||
| model B: equation (3.2) without cod–capelin ratio | 0.31 | |||
| model B: equation (3.2) without temperature | 0.71 | |||
| model B: equation (3.2) without temperature and cod–capelin ratio | 0.16 | |||
| model C | a | 0.44 | 0.40 | 0.70 |
| model C: equation (3.2) without cod–capelin ratio | 0.04 | 0.24 | 0.30 | 0.31 |
| model C: equation (3.2) without temperature | b | 0.42 | 0.03 | 0.65 |
| model C: equation (3.2) without temperature and cod–capelin ratio | 0.01 | 0.20 | 0.02 | 0.16 |
| model D | 0.33 | 0.33 | 0.40 | 0.33 |
| model D: equation (3.2) without cod–capelin ratio | 0.04 | 0.24 | 0.30 | 0.31 |
| model D: equation (3.2) without temperature | 0.21 | 0.29 | 0.03 | 0.21 |
| model D: equation (3.2) without temperature and cod–capelin ratio | 0.01 | 0.20 | 0.02 | 0.16 |
| model D: equation (3.5) without effect of temperature on herring | 0.04 | 0.40 | 0.38 | 0.32 |
Impossible to fit model to the data from the first period.
The cod–capelin term has two degrees of freedom (two parameters, d and e).
Finally, we tested whether herring can also have a positive effect on cod recruitment as food for cod by adding a term for the ratio between cannibalistic cod and herring. However, this extra term did not at all improve the fit of the model to cod recruitment, neither in model A (likelihood ratio test: χ2=1.25; p=0.26), model B (χ2=0.17; p=0.68) or model C (χ2=0.34; p=0.56). Moreover, the estimates of the effect of the cod–herring ratio tended to be positive for most periods, not negative as expected (figure A2 in the electronic supplementary material).
5. Discussion
The series of models used here enable us to evaluate how cod recruitment is affected by both a positive effect of high temperatures in the cod's spawning year and cannibalism, which we demonstrate is effectively a delayed negative effect of good herring recruitment. Analysis of long time-series, such as cod VPA estimates and sea temperature, indicates that cannibalism has had a negative effect on cod recruitment at least back to the 1920s. Although one might think of other reasons for a correlation between cod–capelin ratio and cod recruitment, this indication of a cannibalism effect is considerably strengthened by combining the result from the long-term series with the analysis of shorter, more recent series such as cod abundance at five months age (1980-). These analyses pinpoint the negative effect of the cod–capelin ratio to survival through the period five months to 3 years. Testing a hypothesized causal chain with such a combination of analyses will increase the chance that we reject the hypothesis in the case where the hypothesis is really wrong; and conversely, if we are unable to reject the hypothesis, it strengthens our belief in it.
The benefit from doing this is that we are able to validate the current hypotheses on the effect of herring on capelin, capelin on cod cannibalism and climate on herring and cod recruitment (e.g. Tjelmeland & Bogstad 1998; Hamre 2003; Hjermann et al. 2004a,b). Moreover, such analyses can indicate previously unknown intra- or interspecific relationships, with their direction and magnitude. The modelling approach taken is obviously quite simplistic; for instance, the argument behind equation (3.3) can easily be criticized for being based on several implicit and unrealistic assumptions about capelin recruitment, growth and survival. Taking these simplifications and assumptions into account, the correspondence between the model and the observations is quite good. In fact, the relationship between observed and predicted values—using the model with a two-step trophical chain (herring–capelin–cod cannibalism)—is relatively strong from 1945 onwards. This indicates that the chain of processes we have assumed to be important—herring preying on capelin larvae, lack of capelin inducing cannibalism in cod—were important also before the recorded incidents of herring–capelin–cod chain reactions in the 1980s, 1990s and 2000s. It should be noted that the proportion of cod in the diet of cod was also high in the early 1960s and a sharp drop in the proportion of capelin in the diet of cod was observed in 1963 (Fig. 4 in Ponomarenko et al. 1978). This corresponds well with the capelin collapse observed in 1962–1964, following the occurrence of the very abundant 1959 year-class of herring in the Barents Sea (Gjøsæter 1998).
Hamre (2003) suggested that the collapses of capelin might have been less detrimental for cod in earlier times, when the herring stock was large, since the cod could eat herring when capelin was lacking. The proportion of herring in the diet of cod seems to have been markedly higher in the 1950s and 1960s than in the 1980s and 1990s (Gjøsæter & Bogstad 1998). We are now able to test Hamre's suggestion (2003), and the results of our overall analysis show no indication that periods with a high availability of herring as food for cod resulted in better survival for young cod. However, if the most recent period (since 1983) is analysed separately, herring seems to have had a positive effect. The conclusion is that if the herring stock should increase on the expense of the capelin, we cannot trust that herring can replace capelin as a source of fat in the cod's diet.
Our model results indicate that even in the years of heaviest exploitation, the capelin fisheries have not decreased the recruitment of age 3 cod more than around 10% (see figure A1 in the electronic supplementary material). Taking the large amounts of capelin harvested in some years, this may seem counter-intuitive. However, the massive herring-induced collapses of the capelin (more than 95% reduction of the biomass) dwarf the effects of fisheries. It should be noted, though, that here we take the short-term effect (less than a year) of fisheries into account, not over-fishing that results in lower reproduction of capelin.
Why does model C ‘break down’ when we go further back than 1945? Firstly, the data quality is expected to become poorer as we go further back, i.e. uncertainties in the catch statistics and age readings underlying the estimates of herring and cod become larger. This is supported by the fact that model D—which is based on the abundance of young herring predicted from a model—does better than model C, which is based on the estimated values. A second hypothesis is that the mechanisms affecting cod recruitment have changed. Indeed, the positive effect of high temperatures on cod recruitment was not important before 1967. We found that cod recruitment appears to have become more dependent on favourable climate in the year of spawning over the years. This is supported by figure 6 and figure A2 in the electronic supplementary material, showing no positive effect of temperature before 1967. The reason is believed to be that the cod constituting the spawning stock have become younger, smaller and more uniformly aged (Ottersen et al. 2006). In particular, the proportion of old (age greater than 10) cod decreased rapidly in the years following WWII, echoed by the sudden decrease in model performance when the analysis is extended back in time to periods before ca 1950 (figure 5b). For the last 20 years, it is hard to separate the effects of capelin–cod ratio from the effects of temperature, based on the data we have used in this study (table 3). The effects of climate on recruitment of several cod stocks with truncated age structures were studied by Brander (2005) and Stige et al. (2006). A third hypothesis is that our assumption that the amount of herring in the Barents Sea is proportional to the year-class strength of herring is incorrect. In some years, a major part of large year-classes grow up in other areas such as the fjords along the Norwegian coast or the Norwegian Sea (Holst & Slotte 1998).
Management of the fish stocks of the Barents Sea already include species interactions to some degree. The need for this was realized after the capelin collapse in the mid-1980s, and the subsequent dramatic effects on the cod (e.g. cannibalism) and other species, such as the mass migration of harp seals (Phoca groenlandica) to the coast of Norway where many of them drowned in fishermen's nets (Haug & Nilssen 1995). Following this, a large multi-species research program was initiated. Currently, predation by cod on mature capelin is included into the assessment of capelin, and predation by cod on cod (i.e. cannibalism) and haddock is included in the assessment of these species (ICES 2004). In addition, the effect of capelin on cod growth is taken into account in a qualitative way when cod growth is predicted. In addition, several authors have made long-term simulations with multi-species models for the Barents Sea and investigated the yield from the different species given different management strategies (e.g. Hamre 2003). The present analysis differs from these papers by being based on statistical time-series analysis, and by being heavily simplified, focusing on only a few key processes. As such, this represents a complementary approach to understand the ecosystem. For instance, the current work may help formulating some of the processes in more complex multi-species models for cod, capelin and herring. It may also help developing better medium-term predictions of the cod stock, for instance based on model A.
Interestingly, also the Baltic cod is negatively influenced by herring as well as by another clupeid fish, sprat Sprattus sprattus (Köster et al. 2001). However, the influence on Baltic cod is mainly direct, through predation of herring and sprat on cod eggs and larvae. While herring also eat substantial amounts of NEA cod eggs (Melle 1985), the time lag-structure of the Barents Sea system indicates that the indirect effect of herring on cod is more important than the direct effect (Hjermann et al. 2004b,c). The effect of herring on cod will therefore differ in important ways between the Baltic and the Barents Sea ecosystems. For instance, in the Barents Sea, a high biomass of herring will tend to increase the self-regulation of the cod stock. Thus, we expect the effect of herring on the cod to depend on the size of the cod stock in the Barents Sea, but less so in the Baltic Sea.
Our study highlights the importance of incorporating interspecific interactions in fishery management. While such interspecific interactions long have been recognized as an important issue in fishery management, their impact has been quantified for relatively few ecosystems. In this study, we have demonstrated that cod recruitment in a situation of food shortage (much 3–6-year-old cod and little capelin) can be expected to be only half of the recruitment in a situation with abundant high-quality food. Obviously, this has profound effects for both the dynamics of the cod and the entire ecosystem—and as a result, for the fisheries. However, in this case, even quite substantial harvesting of the preferred prey has a minor effect on recruitment. Finally, the results show that although temperature does affect the herring, and herring indirectly affects the NEA cod, the expected indirect negative effect of temperature on the cod is not detectable in the data.
Acknowledgments
This work was supported by grants from the University of Oslo, Hydro and Statoil, both directly and through Statoil's VISTA programme (D. Ø. H.) G.O. was supported by the Norwegian Research Council's ECOBE and CLIMAR projects and the Bjerknes Centre for Climate Research. We also thank Knipovich Polar Institute of Marine Fishery and Oceanography (PINRO, Murmansk) for kindly letting us use the temperature data from the Kola transect, and Kjell Nedreaas and Arvid Hylen (IMR, Bergen) for making the VPA estimates of cod for the years before 1946 available. We also thank the referees for their comments and advice on previous versions of this manuscript. This work was done within the framework of ICES and GLOBEC's (Global Ocean Ecosystem Dynamics) Cod and Climate Change programme.
Supplementary Material
Food web dynamics affect North-East Arctic cod recruitment
References
- Bengtsson L, Semenov V.A, Johannessen O.M. The early twentieth-century warming in the Arctic—a possible mechanism. J. Clim. 2004;17:4045–4057. doi: 10.1175/1520-0442(2004)017<4045:TETWIT>2.0.CO;2. [DOI] [Google Scholar]
- Beverton R.J.H, Holt S.J. On the dynamics of exploited fish populations. Chapman and Hall; London, UK: 1957. [Google Scholar]
- Brander K.M. Cod recruitment is strongly affected by climate when stock biomass is low. ICES J. Mar. Sci. 2005;62:339–343. doi: 10.1016/j.icesjms.2004.07.029. [DOI] [Google Scholar]
- Ciannelli L, Bailey K.M, Chan K.S, Belgrano A, Stenseth N.C. Climate change causing phase transitions of walleye pollock (Theragra chalcogramma) recruitment dynamics. Proc. R. Soc. B. 2005;272:1735–1743. doi: 10.1098/rspb.2005.3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotter A.J.R, Burt L, Paxton C.G.M, Fernandez C, Buckland S.T, Pax J.X. Are stock assessment methods too complicated? Fish Fish. 2004;5:235–254. [Google Scholar]
- Drinkwater K.F. The regime shift of the 1920s and 1930s in the North Atlantic. Prog. Oceanogr. 2006;68:134–151. [Google Scholar]
- FAO. Code of conduct for responsible fisheries. Food and Agriculture Organization; Rome, Italy: 1995. [Google Scholar]
- FAO. 2002 Report of the Reykjavik Conference on Responsible Fisheries in the Marine Ecosystem. Reykjavik, Iceland, 1–4 October 2001. FAO Fisheries Report 658.
- Gjøsæter H. The population biology and exploitation of capelin (Mallotus villosus) in the Barents Sea. Sarsia. 1998;83:453–496. [Google Scholar]
- Gjøsæter H, Bogstad B. Effects of the presence of herring (Clupea harengus) on the stock-recruitment relationship of Barents Sea capelin (Mallotus villosus) Fish. Res. 1998;38:57–71. doi: 10.1016/S0165-7836(98)00114-3. [DOI] [Google Scholar]
- Godø O.R. Fluctuation in stock properties of north–east Arctic cod related to long-term environmental changes. Fish Fish. 2003;4:121–137. [Google Scholar]
- Gompertz B. On the nature of the function expressive of the law of human mortality, and on the new mode of determining the value of life contingencies. Phil. Trans. R. Soc. B. 1825;115:513–585. [Google Scholar]
- Hamre J. Capelin and herring as key species for the yield of north–east Arctic cod. Results from multispecies model runs. Scientia Marina. 2003;67(Suppl. 1):315–323. [Google Scholar]
- Haug T, Nilssen K.T. Ecological implications of harp seal Phoca groenlandica invasions in Northern Norway. In: Blix A.S, Walløe L, Ulltang Ø, editors. Whales, seals, fish and man. Elsevier Science; Amsterdam, The Netherlands: 1995. pp. 545–556. [Google Scholar]
- Helle K, Pennington M, Bogstad B, Ottersen G. Early environmental influences on growth of Arcto-Norwegian cod, Gadus morhua, from the 0-group to adults. Environ. Biol. Fishes. 2002;65:341–348. doi: 10.1023/A:1020581415071. [DOI] [Google Scholar]
- Hjermann D, Stenseth N.C, Ottersen G. Competition by fishermen and fish cause collapses of Barents Sea capelin. Proc. Natl Acad. Sci. USA. 2004a;101:11 679–11 684. doi: 10.1073/pnas.0402904101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hjermann D.Ø, Stenseth N.C, Ottersen G. The population dynamics of northeast Arctic cod through two decades: an analysis based on survey data. Can. J. Fish. Aquat. Sci. 2004b;61:1747–1755. doi: 10.1139/f04-115. [DOI] [Google Scholar]
- Hjermann D.Ø, Stenseth N.C, Ottersen G. Indirect climatic forcing of the Barents Sea capelin: a cohort-effect. Mar. Ecol. Prog. Ser. 2004c;273:229–238. [Google Scholar]
- Holst J.C, Slotte A. Effects of juvenile nursery on geographic spawning distribution in Norwegian spring-spawning herring (Clupea harengus L.) ICES J. Mar. Sci. 1998;55:987–996. doi: 10.1006/jmsc.1998.0371. [DOI] [Google Scholar]
- ICES. 2004 Report of the Arctic Fisheries Working Group. ICES CM 2004/ACFM:28.
- ICES. 2006 Report of the Arctic Fisheries Working Group. ICES CM 2006/ACFM:25.
- IPCC. Cambridge University Press; Cambridge, UK: 2001. Climate change 2001: the scientific basis. Contribution of working group I to the third assessment report of the intergovernmental panel on climate change. [Google Scholar]
- Köster F, Hinrichsen H.H, St John M.A, Schnack D, MacKenzie B.R, Tomkiewicz J, Plikshs M. Developing Baltic cod recruitment models. II. Incorporation of environmental variability and species interaction. Can. J. Fish. Aquat. Sci. 2001;58:1534–1556. doi: 10.1139/cjfas-58-8-1534. [DOI] [Google Scholar]
- Melle, W. 1985 Predasjon på torskens egg og larver i Lofoten [predation on cod eggs and larvae in the Lofoten]. M.Sc. thesis. Bergen, Norway: University of Bergen.
- Nakken O. Past, present and future exploitation and management of marine resources in the Barents Sea and adjacent areas. Fish. Res. 1998;37:23–35. doi: 10.1016/S0165-7836(98)00124-6. [DOI] [Google Scholar]
- Ottersen G, Hjermann D, Stenseth N.C. Changes in spawning stock structure strengthens the link between climate and recruitment in a heavily fished cod stock. Fish. Oceanogr. 2006;15:230–243. doi: 10.1111/j.1365-2419.2006.00404.x. [DOI] [Google Scholar]
- Ponomarenko, V. P., Ponomarenko, I. Ya. & Yaragina, N. A. 1978 Consumption of the Barents Sea capelin by cod and haddock in 1974–1976. ICES C.M. 1978/G:23, p. 22.
- Stenseth N.C, Bjørnstad O.N, Falck W, Fromentin J.-M, Gjøsæter J, Gray J. Dynamics of coastal cod populations: intra- and inter-cohort density-dependence and stochastic processes. Proc. R. Soc. B. 1999;266:1645–1654. doi: 10.1098/rspb.1999.0827. [DOI] [Google Scholar]
- Stenseth N.C, Mysterud A, Ottersen G, Hurrell J.W, Chan K.S, Lima M. Ecological effects of climate fluctuations. Science. 2002;297:1292–1296. doi: 10.1126/science.1071281. [DOI] [PubMed] [Google Scholar]
- Stige L.C, Ottersen G, Brander K, Chan K.-S, Stenseth N.C. Cod and climate. Effect of the North Atlantic Oscillation on recruitment in the North Atlantic. Mar. Ecol. Prog. Ser. 2006;325:227–241. [Google Scholar]
- Tjelmeland S, Bogstad B. MULTSPEC—a review of a multispecies modelling project for the Barents Sea. Fish. Res. 1998;37:127–142. doi: 10.1016/S0165-7836(98)00132-5. [DOI] [Google Scholar]
- Toresen R, Østvedt O.J. Variation in the abundance of Norwegian spring-spawning herring (Clupea harengus, Clupeidae) throughout the 20th century and the influence of climatic fluctuations. Fish Fish. 2000;1:231–251. [Google Scholar]
- Yodzis P. Culling predators to protect fisheries: a case of accumulating uncertainties—response. Trends Ecol. Evol. 2001;16:282–283. doi: 10.1016/S0169-5347(01)02159-0. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Food web dynamics affect North-East Arctic cod recruitment