Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays

Abstract

Oligonucleotide arrays can provide a broad picture of the state of the cell, by monitoring the expression level of thousands of genes at the same time. It is of interest to develop techniques for extracting useful information from the resulting data sets. Here we report the application of a two-way clustering method for analyzing a data set consisting of the expression patterns of different cell types. Gene expression in 40 tumor and 22 normal colon tissue samples was analyzed with an Affymetrix oligonucleotide array complementary to more than 6,500 human genes. An efficient two-way clustering algorithm was applied to both the genes and the tissues, revealing broad coherent patterns that suggest a high degree of organization underlying gene expression in these tissues. Coregulated families of genes clustered together, as demonstrated for the ribosomal proteins. Clustering also separated cancerous from noncancerous tissue and cell lines from in vivo tissues on the basis of subtle distributed patterns of genes even when expression of individual genes varied only slightly between the tissues. Two-way clustering thus may be of use both in classifying genes into functional groups and in classifying tissues based on gene expression.

Recently introduced experimental techniques based on oligonucleotide or cDNA arrays now allow the expression level of thousands of genes to be monitored in parallel (1–9). To use the full potential of such experiments, it is important to develop the ability to process and extract useful information from large gene expression data sets. Elegant methods recently have been applied to analyze gene expression data sets that are comprised of a time course of expression levels. Examples of such time-course experiments include following a developmental process or changes as the cell undergoes a perturbation such as a shift in growth conditions. The analysis methods were based on clustering of genes according to similarity in their temporal expression (5, 6, 9–11). Such clustering has been demonstrated to identify functionally related families of genes, both in yeast and human cell lines (5, 6, 9, 11). Other methods have been proposed for analyzing time-course gene expression data, attempting to model underlying genetic circuits (12, 13).

Here we report the application of methods for analyzing data sets comprised of snapshots of the expression pattern of different cell types, rather than detailed time-course data. The data set used is composed of 40 colon tumor samples and 22 normal colon tissue samples, analyzed with an Affymetrix oligonucleotide array (8) complementary to more than 6,500 human genes and expressed sequence tags (ESTs) (14). We focus here on generally applicable analysis methods; a more detailed discussion of the cancer-specific biology associated with this study will be presented elsewhere (D.A.N. and A.J.L., unpublished work). The correlation in expression levels across different tissue samples is demonstrated to help identify genes that regulate each other or have similar cellular function. To detect large groups of related genes and tissues we applied two-way clustering, an effective technique for detecting patterns in data sets (see e.g., refs. 15 and 16). The main result is that an efficient clustering algorithm revealed broad, coherent patterns of genes whose expression is correlated, suggesting a high degree of organization underlying gene expression in these tissues. It is demonstrated, for the case of ribosomal proteins, that clustering can classify genes into coregulated families. It is further demonstrated that tissue types (e.g., cancerous and noncancerous samples) can be separated on the basis of subtle distributed patterns of genes, which individually vary only slightly between the tissues. Two-way clustering thus may be of use both in classifying genes into functional groups and in classifying tissues based on their gene expression similarity.

MATERIALS AND METHODS

Tissues and Hybridization to Affymetrix Oligonucleotide Arrays.

Colon adenocarcinoma specimens (snap-frozen in liquid nitrogen within 20 min of removal) were collected from patients (D.A.N. and A.J.L., unpublished work). From some of these patients, paired normal colon tissue also was obtained. Cell lines used (EB and EB-1) have been described (17). RNA was extracted and hybridized to the array as described (1, 8).

Treatment of Raw Data from Affymetrix Oligonucleotide Arrays.

The Affymetrix Hum6000 array contains about 65,000 features, each containing ≈10⁷ strands of a DNA 25-mer oligonucleotide (8). Sequences from about 3,200 full-length human cDNAs and 3,400 ESTs that have some similarity to other eukaryotic genes are represented on a set of four chips. In the following, we refer to either a full-length gene or an EST that is represented on the chip as EST. Each EST is represented on the array by about 20 feature pairs. Each feature contains a 25-bp sequence, which is either a perfect match (PM) to the EST, or a single central-base mismatch (MM). The hybridization signal fluctuates between different features that represent different 25-mer oligonucleotide segments of the same EST. This fluctuation presumably reflects the variation in hybridization kinetics of different sequences, as well as the presence of nonspecific hybridization by background RNAs. Some of the features display a hybridization signal that is many times stronger than their neighbors (≈4% of the intensities are >3 SD away from the mean for their EST). These outliers appear with roughly equal incidence in PM or MM features. If not filtered out, outliers contribute significantly to the reading of the average intensity of the gene. Because most features overlap in sequence with their neighbors we used a modified median filter to eliminate outliers from local neighborhoods of features, while preserving step-like changes in intensity. The features were arranged in the order they appear in the EST sequence, the PM-MM intensities in a moving window of five features were sorted, and the filtered intensity was given by the mean of the middle three sorted intensities. The total intensity of the EST was given by the mean filtered PM-MM intensity. To compensate for possible variations between arrays, the intensity of each EST on an array was divided by the mean intensity of all ESTs on that array and multiplied by a nominal average intensity of 50. The data set is available on the web at http://www.molbio.princeton.edu/colondata.

Correlations of Pairs of Genes.

To estimate the statistical significance of the correlation between genes, the distribution of correlation coefficients within 10⁴ randomized data sets was calculated. To control for the difference in mean expression in the two tissue types, the randomization preserved tissue identity (normal tissues were randomized with normal tissues, and tumors with tumors). This type of randomization also was used to obtain the dashed curve in Fig. 1C. The probability that the randomized data showed a higher correlation coefficient for the gene of interest than the nonrandomized data was used as an estimate of the statistical significance P.

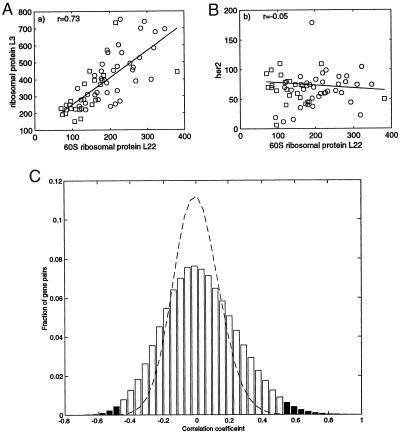
Figure 1.

Correlation between pairs of genes across the 62 tissue types. ○, tumor tissues; □, normal tissue; line, best fit (least-mean squares) with correlation coefficient r. (A) Correlation between 60S ribosomal protein L22 (EST number T47584) and ribosomal protein L3 (T57630). (B) 60S ribosomal protein L22 and her2 (M11730). Intensities are a measure of the mRNA concentration with 100 intensity units equal to roughly 10 messages/cell (8). (C) Probability histogram of correlation coefficients between pairs of genes. All pairs within the 2,000 genes with highest minimal intensity across the tissues were used. Dashed line, correlation coefficient for data where identity of tissues was randomized. Shaded regions, correlation with statistical significance P < 10⁻³. On average each gene scores such a significant correlation with about 30 other genes, and such an anticorrelation with about 10 other genes.

Data Clustering.

We used an algorithm, based on the deterministic-annealing algorithm (18, 19), to organize the data in a binary tree. To cluster the genes, each gene, k, was represented by a vector, V_k, whose components correspond to the intensity of the gene in each sample. Each vector was normalized so that the sum over its components is zero and the magnitude is one, |V_k| = 1. The genes were split into two clusters as follows: two cluster centroids C_j, j = 1, 2, were defined. A probability was assigned for belonging to cluster j: P_j(V_k) = exp(−β|V_k − C_j|²)/Σ_j exp(−β|V_k − C_j|²). This equation effectively fits the data with two Gaussians of variance (2β)⁻¹. The cluster centroids were determined by the self-consistent equation C_j = Σ_kV_k P_j(V_k)/Σ_kP_j(V_k), which was solved by iterations. For β = 0 there is only one cluster, C₁ = C_2. We increased β in small steps until two distinct, converged centroids emerged. Each gene k then was assigned to the cluster with the larger P_j(V_k). Each of the resulting two clusters then was separated into two by repeating the same procedure. The final result was an organization of the genes into a binary tree. To cluster the tissues the same algorithm was used, where each tissue, k, was represented as a vector, V_k, whose components correspond to the intensity of the genes for that tissue. Note that because of the normalization, the Euclidean distance between two vectors x and y is related to r, the correlation coefficient of x and y: |x − y|² = 2 (1 − r).

The binary trees obtained by the above procedure were used to reorganize the matrix of gene expression (Figs. 2 and 3). To this end, we included a routine that orders the tree branches in a deterministic way: Each pair of sibling branches was ordered according to the proximity of their centroids to the centroid of their parent’s sibling.

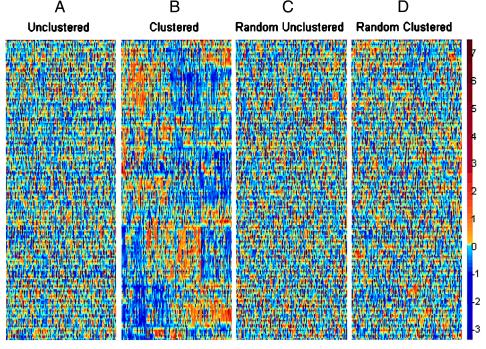
Figure 2.

Data set of intensities of 2,000 genes in 22 normal and 40 tumor colon tissues. The genes chosen are the 2,000 genes with highest minimal intensity across the samples. The vertical axis corresponds to genes, and the horizontal axis to tissues. Each gene was normalized so its average intensity across the tissues is 0, and its SD is 1. The color code used is indicated in the adjoining scale. (A) Unclustered data set. (B) Clustered data. The 62 tissues are arranged on the vertical axis according to the ordered tree of Fig. 3. The 2,000 genes are arranged on the horizontal axis according to their ordered tree. (C) Unclustered randomized data, where the original data set was randomized (the location of each number in the matrix was randomly shifted). (D) Clustered randomized data, subjected to the same clustering algorithm as in B. The data and the clustering program are available at http://www.molbio.princeton.edu/colondata.

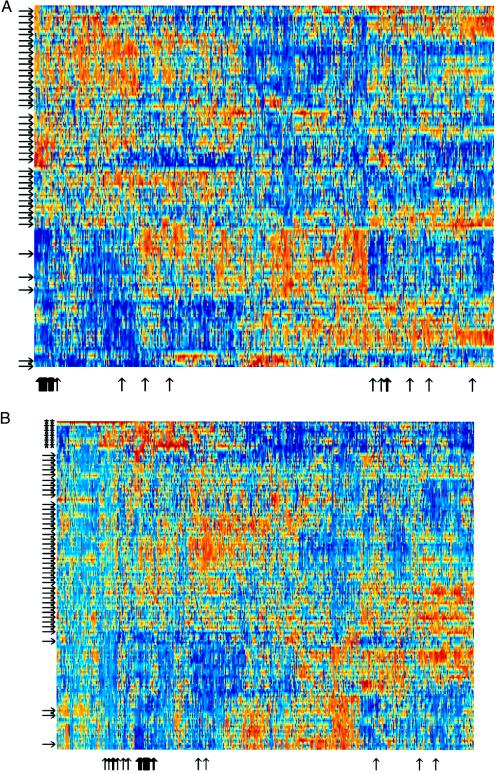
Figure 3.

(A) Expanded view of clustered data set of 2,000 genes in 22 normal and 40 tumor colon tissues. The genes chosen are the 2,000 genes with highest minimal intensity across the samples. Tumor tissues are marked with arrows on the left. Normal tissues are unmarked. Note the separation of normal and tumor tissues. Thin black vertical arrows on the bottom mark ESTs homologous to ribosomal proteins (see Table 1). Note that where these genes cluster the arrows group together and resemble a thick arrow. (B) Same as A but with EB and EB1 colon carcinoma cell lines (17) added to the data set (marked with ∗∗). Note the clustering of cell lines into a separate group with expression patterns markedly different from both tumor and normal in vivo tissues.

The present clustering algorithm is quite efficient. The computation time scales as the number of objects clustered times the number of layers in the tree, N log(N), rather than as N² to N⁴ in commonly used phylogenetic tree construction algorithms (15). In particular, the method does not require the computation of all distances between pairs of objects. The clustering programs are available on the web at http://www.molbio.princeton.edu/colondata.

RESULTS

Genes with Correlated Expression.

The intensity of each gene across the tissues can be thought of as a pattern that can be correlated with expression patterns of other genes. Graphically, correlation between genes can be seen by plotting the expression of one gene against the expression of another gene, as demonstrated for two ribosomal proteins in Fig. 1A. For this pair of genes, the correlation coefficient is relatively high (r = 0.73), and the correlation appears to be statistically significant (P < 10⁻³). Most genes show no significant correlation across tissues (Fig. 1 B and C). On average, each gene shows a strong correlation with on the order of 1% of the other genes on the array (Fig. 1C). A correlation between two genes could result either from a direct up-regulation of one by the other, or because they are similarly regulated by the physiological state of the cell. The correlation between pairs of genes, and an analogous correlation between pairs of tissues, is the basis for the two-way data clustering described below.

Two-Way Data Clustering.

To detect groups of correlated genes and tissues we used a clustering approach to the data set. Clustering can be thought of as forming a phylogenetic tree of genes or tissues. Genes are near each other on the “gene tree” if they show a strong correlation across experiments, and tissues are near each other on the “tissue tree” if they have similar gene expression patterns. Technically, we developed a fast algorithm, based on the deterministic annealing algorithm (18, 19), which separates a set of objects (genes or tissues) into two groups, then separates each group into two subgroups, and so on, until all the objects are arranged on a binary tree. Because this algorithm yields an unordered tree, we supplied a method for imposing an order on the tree branches so that a final, ordered list is obtained. This procedure was applied to both the genes and the tissues, using the same algorithm. We then used this two-way ordering of genes and tissues to rearrange the rows and columns of the data set, so that correlated genes and tissues are displayed near each other.

To help visualize the data, we plotted it by using a color code, with gene intensity varying from red (high intensity) to blue (low intensity) (Fig. 2A). The intensity of each gene is normalized so that the relative variation in intensity is emphasized, rather than the absolute intensity. The two-way clustering method applied to the gene expression data set yielded a matrix that appears to bear patterns (Figs. 2B and 3). The areas of high or low intensity correspond to groups of tens to hundreds of genes whose expression is coordinated to a substantial degree across groups of tissue samples. In contrast, the same algorithm applied to a randomized data set (Fig. 2 C and D) yielded a matrix with little apparent structure. This difference in patterning reflects the underlying organization of gene expression in the real data set.

Gene Clusters.

The clustering of the genes in the data set reveals groups of genes whose expression is correlated across tissue types. For example, 48 ESTs homologous to ribosomal proteins are represented within the set of 2,000 high-intensity genes used for the clustering. Most of these genes cluster together—as expected for genes that are regulated coordinately (Fig. 3A, arrows on the bottom). The intensity of the ribosomal protein genes is relatively low (blue) in the normal colon tissues and high (red) in the colon tumor tissues. This finding is in agreement with previous observations (20). Interspersed within the ribosomal protein cluster are ESTs homologous to genes that appear to be related to cellular metabolism such as an ATP-synthase component and an elongation factor (Table 1). A more detailed discussion of the gene clusters will be presented elsewhere (D.A.N. and A.J.L., unpublished work).

Table 1.

Part of the ribosomal protein cluster

Gene number	Sequence	Name
T63591	3′ UTR	60S acidic ribosomal protein P0 (human)
R50158	3′ UTR	Mus musculus L36 ribosomal protein178
T52642	3′ UTR	Guanylate kinase homolog (vaccinia virus)
R85464	3′ UTR	ATP synthase lipid-binding protein P2 precursor (human)
X55715	Gene	Human Hums3 mRNA for 40S ribosomal protein s3
T52185	3′ UTR	P17074 40S ribosomal protein
T56934	3′ UTR	Homo sapiens alpha NAC mRNA (transcriptional coactivator)
T47144	3′ UTR	JN0549 ribosomal protein YL30
T72879	3′ UTR	60S ribosomal protein L7A (human)
T57633	3′ UTR	40S ribosomal protein S8 (human)
T58861	3′ UTR	60S ribosomal protein L30E (Kluyveromyces lactis)
T52015	3′ UTR	Elongation factor 1-gamma (human)
T57619	3′ UTR	40S ribosomal protein S6 (Nicotiana tabacum)
T72938	3′ UTR	Ribosomal protein L10178
R02593	3′ UTR	60S acidic ribosomal protein P1 (Polyorchis penicillatus)
T48804	3′ UTR	40S ribosomal protein S24 (human)
R01182	3′ UTR	60S ribosomal protein L38 (human)
T61609	3′ UTR	H. sapiens gene for ribosomal protein Sa, partial cds178
H77302	3′ UTR	60S ribosomal protein (human)
U14971	Gene	Human ribosomal protein S9 mRNA, complete cds
H54676	3′ UTR	60S ribosomal protein L18A (human)
R86975	3′ UTR	40S ribosomal protein S28 (human)
T51560	3′ UTR	40S ribosomal protein S16 (human)
H09263	3′ UTR	Elongation factor 1-alpha 1 (H. sapiens)
T49423	3′ UTR	Breast basic conserved protein 1 (human)
T63484	3′ UTR	Human ornithine decarboxylase antizyme (Oaz) mRNA, complete cds
R02593	3′ UTR	60S acidic ribosomal protein P1 (P. penicillatus)
R22197	3′ UTR	60S ribosomal protein L32 (human)
T51496	3′ UTR	60S ribosomal protein L37A (human)

UTR, untranslated region. 

¹⁷⁸blast database homologue. 

Tissue Clusters.

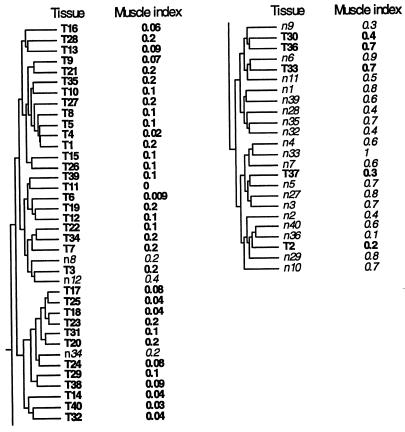
The clustering algorithm separated tumor and normal tissues into two distinct clusters (Figs. 3 and 4), probably primarily because of tissue composition. It is expected that the normal tissue samples include a mixture of tissue types, while the tumor samples are biased to epithelial tissue of the carcinoma. For example, among the 20 genes with the most statistically significant difference between tumors and normal tissues (by t test), were five muscle genes (not shown). To obtain a qualitative measure of the muscle content of each sample, we calculated a muscle index, an average over the intensity of 17 ESTs in the array that are homologous to smooth muscle genes (Fig. 4). Normal tissues had high muscle index, while tumors had low muscle index. The outlying tumors that clustered with the normal tissues proved to be the five tumors with the highest muscle index (Fig. 4), perhaps representing tumor samples with a high content of nonepithelial tissues. Similarly, the three outlying normal tissues in the tumor cluster appear to have relatively low smooth-muscle content. Thus the outliers in the tissue clustering might be accounted for by tissue composition.

Figure 4.

Clustering tree for the tissue samples. Tumors (T) and normal tissue (n) numbered such that tumor and normal tissues with the same serial number originate from the same patient. Tissue T18 is a tumor and tissue T19 is a metastasis from the same patient. The muscle index for each tissue is shown. The muscle index was defined as the average intensity of the ESTs on the array that are homologous to the following 17 smooth muscle genes: (D42054) human ORF (smooth muscle myosin-related), complete cds; (U37019) human smooth muscle cell calponin mRNA, complete cds; (T61597, R01216, T78485) caldesmon, smooth muscle (Gallus gallus); (T60155) actin, aortic smooth muscle (human); (M95787) smooth muscle protein 22-alpha (human); (J02854) myosin regulatory light chain 2, smooth muscle isoform (human); (T97948) calponin h2, smooth muscle (Sus scrofa); (R16199, R42761, R50839, H30638, T55741) myosin light chain kinase, smooth muscle (Gallus gallus); (T96548) actin, gamma-enteric smooth muscle (human); (X12369) tropomyosin alpha chain, smooth muscle (human); (H20709) myosin light chain alkali, smooth-muscle isoform (human). The index is normalized to vary between 0.0 and 1.0. The horizontal distance between tree nodes was determined by the relative value of β at which splitting occurred in the clustering algorithm (see Materials and Methods).

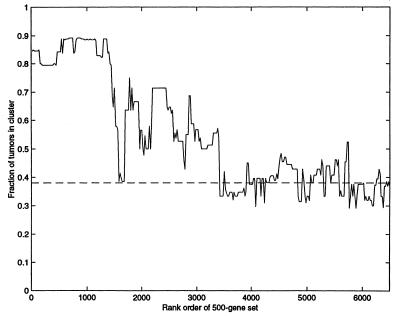
Does the separation between tumor and normal tissues depend on only a few genes (e.g., muscle-specific genes), or is it reflected in the majority of genes used to cluster? To test this, we performed clustering by using only a partial gene set, which lacks the genes that individually best separate tumor and normal tissues (using a 500-gene set that does not include genes with the most significant differences between tumors and normal tissue). Even if one removes the 1,500 genes with the most significant differences between tumor and normal tissues, the clustering algorithm still effectively separates tumor from normal tissues (Fig. 5). Thus, clustering distinguishes tumor and normal samples even when the genes used have a small average difference between tumor and normal samples. This finding suggests that for many genes there is a subtle, systematic difference between tumor and normal samples, forming a distributed pattern.

Figure 5.

Separation of tumor and normal tissues by clustering over a set of 500 genes. Genes were sorted by statistical significance (t test) of the difference in normal and tumors. Tissues were clustered by using a window of 500 genes selected from the sorted genes. The vertical axis denotes the fraction of tumors in the tumor rich cluster (|T − N|/(T + N) where N and T are the number of normal, tumor tissues). Dashed line indicates separation in a randomized data set. The horizontal axis denotes the starting point of the 500-gene window, so that at the left-hand side the most significant 500 genes are used, and at the right the least significant 500 genes.

Similarly, when cell lines derived from colon carcinoma (ref. 17 and M. Murphy, D.A.N., and A.J.L., unpublished work) were included in the data set, the clustering algorithm separated the cell lines into a cluster of their own, which is distinct from the colon tumor tissue samples (Fig. 3B, stars). The cell-line cluster was placed closer to the tumors than the normal tissue. Note that including the cell line tissues modifies the patterns obtained by clustering, because the expression patterns in the cell lines is so markedly different than either the tumor or normal in vivo tissues. the ribosomal proteins still cluster, with their relative intensity low in normal tissue, high in tumors, and very high in cell lines.

DISCUSSION

This work reports the application of techniques that proved useful in analyzing a large gene expression data set. A fast two-way clustering algorithm was developed to help identify families of genes and tissues based on expression patterns in the data set. Recent work demonstrated that genes of related function could be grouped together by clustering according to similar temporal evolution under various conditions (5, 6, 9–11). Here, it was demonstrated that gene grouping also could be achieved on the basis of variation between tissue samples from different individuals. Further, it was demonstrated that clustering of the tissues could detect differences between tumors of epithelial origin and muscle-rich normal tissue samples, even when the genes with significant bias (tumor-normal differences) were removed from the data set. Similarly, colon tumor cell lines were readily distinguished from in vivo colon tumors. Displaying the data with both samples and genes clustered revealed wide-scale patterns that hint at an extensive underlying organization of gene expression in these tissues.

It is worth noting that although the data-set was designed for studying colon tumors, the present analysis appears to allow access to additional information that may be relevant to the general regulation circuitry of the cell. Clustering can be thought of as a tool for reducing the dimensionality of the system. Instead of using thousands of gene intensities to describe the state of a tissue, one might, as a first approximation, use only the mean intensity of a few large clusters of genes (11). Clustering methods thus may help supply some of the basic elements for a compact, coarse-grained description of the state of the cell.

Finally, this study highlights the importance of improving tissue purity in the collection of in vivo samples. This method will allow a more reliable classification of tumors on the basis of gene expression patterns and will help characterize the differences between normal and tumor expression patterns. Because it appears likely that genomic instability in cancers can optimize gene expression for cell growth, the differences between normal and tumor expression patterns might help us understand what is being selected for as cancerous tissues evolve.

ABBREVIATION

EST

expressed sequence tag