Quantifier variables of the back surface deformity obtained with a noninvasive structured light method: evaluation of their usefulness in idiopathic scoliosis diagnosis

Abstract

New noninvasive techniques, amongst them structured light methods, have been applied to study rachis deformities, providing a way to evaluate external back deformities in the three planes of space. These methods are aimed at reducing the number of radiographic examinations necessary to diagnose and follow-up patients with scoliosis. By projecting a grid over the patient’s back, the corresponding software for image treatment provides a topography of the back in a color or gray scale. Visual inspection of back topographic images using this method immediately provides information about back deformity, but it is important to determine quantifier variables of the deformity to establish diagnostic criteria. In this paper, two topographic variables [deformity in the axial plane index (DAPI) and posterior trunk symmetry index (POTSI)] that quantify deformity in two different planes are analyzed. Although other authors have reported the POTSI variable, the DAPI variable proposed in this paper is innovative. The upper normality limit of these variables in a nonpathological group was determined. These two variables have different and complementary diagnostic characteristics, therefore we devised a combined diagnostic criterion: cases with normal DAPI and POTSI (DAPI ≤ 3.9% and POTSI ≤ 27.5%) were diagnosed as nonpathologic, but cases with high DAPI or POTSI were diagnosed as pathologic. When we used this criterion to analyze all the cases in the sample (56 nonpathologic and 30 with idiopathic scoliosis), we obtained 76.6% sensitivity, 91% specificity, and a positive predictive value of 82%. The interobserver, intraobserver, and interassay variability were studied by determining the variation coefficient. There was good correlation between topographic variables (DAPI and POTSI) and clinical variables (Cobb’s angle and vertebral rotation angle).

Introduction

The representation and evaluation of deformity of the surface of the back was, and indeed still is, a traditional objective in medical practice. In recent years, indirect noninvasive methods have been developed which are used for studying rachis deformities, particularly idiopathic scoliosis. These methods were developed to reduce the number of radiographic examinations necessary for the diagnosis and follow-up of rachis deformities [5, 16]; to quantify external deformity and its progress with treatment [7, 15]; and to characterize a deformity correctly that exists in the three planes of space and that has classically been defined by the Cobb angle measured in posteroanterior [8] radiographs. To meet these objectives, different systems for reconstructing the surface of the back have been devised [1, 14, 17]. Within this group of noninvasive methods there are those that are particularly advantageous, based on the projection of lines onto the back (structured light). Our method provides accurate topographies that are comparable with Moiré topography, but with the advantage of being more easily set up [3]. If these methods are to be applied to medical practice, deformity quantification systems must be devised. The main objective of this research work was to determine and evaluate two topographical variables that quantify deformity in two different planes in space, one taken from the bibliography (posterior trunk symmetry index, POTSI) [6] and the other, newly devised variable (deformity in the axial plane index, DAPI) [10] applied to topographies of the back obtained with the structured light method we designed [3], establishing normality criteria and evaluating its usefulness in the diagnosis of scoliotic deformity.

Materials and methods

Materials

We studied a total of 86 subjects. Fifty-six subjects without scoliosis, with a mean age of 17.16 years and standard deviation (SD) 5.15, 33 women and 23 men. Body mass index (BMI) was over 30 in three cases. Forty-two subjects of this group presented normal physical examination results (no rib hump asymmetry after bending forward and no clinical leg length discrepancy) and they formed the control group. The rest of the nonpathologic subjects (14 subjects) presented a Cobb angle of less than 10° in the posteroanterior radiograph with absence of vertebral rotation and they were classified as asymmetries.

The group with idiopathic scoliosis was made up of 30 patients. The mean age of these patients was 14.88 (SD 5.91); 22 were women and 8 were men. The BMI was over 30 in five cases. The type of curve, the lateral flexion value, and degree of vertebral rotation were analyzed from the posteroanterior rachis radiograph taken while the patient was standing.

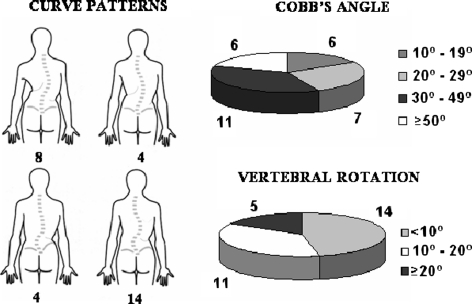
The type of curve was established following the Ponseti classification (Fig. 1). The angle value of the lateral flexion was determined by a Cobb angle and patients were classified into four groups (Cobb angle between 10° and 20°; between 20° and 30°; between 30° and 50°; or over 50°) taking as a basis the classification used by the Scoliosis Research Society (Fig. 1). The degree of vertebral rotation was quantified using the Pedriolle–Vidal method, and patients were classified into three groups depending on whether this angle value was less than 10°, between 10° and 20°, or over 20° (Fig. 1).

Fig. 1.

Scoliotic patients: radiographic parameters. The Ponseti classification was used to establish the type of curve. Cobb’s angle was categorized into four groups following the Scoliosis Research Society’s recommendations. The vertebral rotation angle was categorized into three groups following the Pedriolle–Vidal method

Method for obtaining topographic images

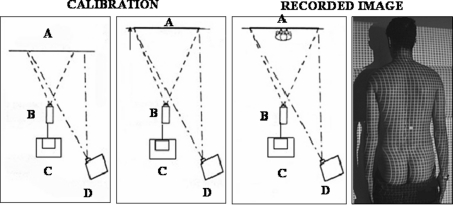
To determine the topographic map of the surface of the back we used an experimental device based on the projection of structured light [3]. To set up the technique coded light, i.e. structured light, is projected by means of a slide projector onto a white mobile screen. In our system the coded light consists of a grid with specific spacing. The images are captured by a digital camera and stored in a computer memory (Fig. 2).

Fig. 2.

Method for obtaining topographical images. A screen, B camera, C computer, D projector. In the calibration process the screen (A) is moved into two different positions and an image is taken of the projected grid in both positions. The patient is situated in front of the screen in the second position and an image of the grid projected over his/her back is taken

The procedure for obtaining topographies consists of an initial calibration of the system, which does not need to be repeated so long as the geometry of the set-up is not changed, the projection of the above-mentioned grid onto the patient’s back who is standing, and then recording this back image on a video camera connected to a personal computer (Fig. 2). By means of the imaging software we have designed, the topographic image of the back surface appears on the monitor and can thus be analyzed.

For the calibration process, two images are taken of the grid projected onto a flat screen at two positions separated by a specific distance (40 cm) perpendicularly to the screen. These two images are called the “front grid” and the “back grid”, and they need to be taken only once. Therefore, the routine for taking images of patients is simply to position the patient immediately in front of the screen situated in the position corresponding to the “back grid”, project the grid onto the patient and capture the image (“grid object”). The software identifies the correspondence between knots (points corresponding to the lines crossing in the grid) on the front grid, back grid, and object grid, which provides the three-dimensional coordinates of each of the points of the surface of the back [3]. The information obtained can be presented as curves of level. The system provides 40 shades of color, ranging from the most protruding point to the most sunken point. Therefore, the mean difference between one level and the next, or between one color and another, is a question of millimeters.

With regard to positioning the patient, the subject stands in front of the screen with the tips of his/her toes touching two stops situated on the floor, barefoot, with arms straight down and facing straight ahead, adopting a natural stance on both feet.

Variables studied to diagnose scoliosis

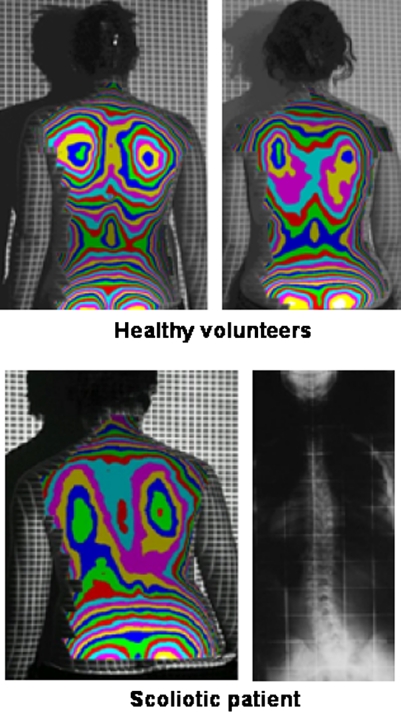
This graphic representation provides qualitative visual information about the symmetry of the back of the subject (Fig. 3). However, our group was interested in finding quantifying parameters of the possible deformity that would enable us to make a quantitative evaluation of the deformity.

Fig. 3.

Back surface topographies in color or gray scale. The points with the same color or gray scale correspond to points with same depth. Visual inspection shows the differences between normal and pathologic backs

In order to quantify asymmetry in the axial plane we devised a new variable called DAPI that basically consists of an addition of the difference of the depths of symmetrical points, at the level of the scapulae and waist. To quantify deformity in the coronal plane we used the POTSI variable that appears in the bibliography [6] where it was used to evaluate the response to surgical treatment. This variable is calculated by looking at the relative positions of landmarks such as the axillae, shoulders, and waist creases.

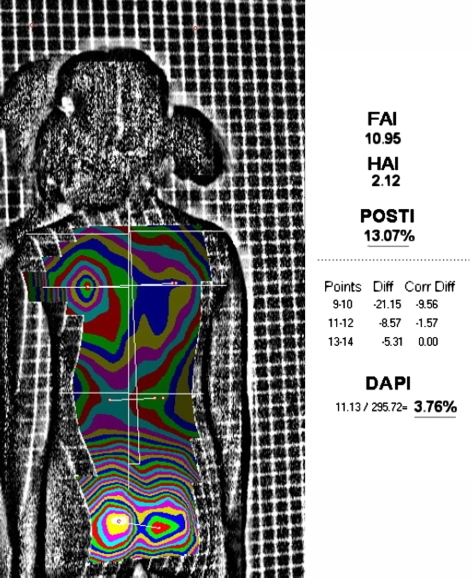
These variables can be automatically obtained from the topographic image on the computer monitor (Figs. 4, 5). By using the mouse as an interface, 14 anatomical points of interest are marked on the topographic reconstruction. From them the software calculates the variables value. The anatomical points referred to are as follows: 1. vertebral prominence of C7; 2. the top of the intergluteal furrow; 3. left shoulder (cross of the tangents to the shoulder and the arm); 4. right shoulder; 5. left axilla; 6. right axilla; 7. waist, left; 8. waist, right; 9. most prominent point of the left scapula; 10. most prominent point of the right scapula; 11. least prominent point of the waist line, left; 12. least prominent point of the waist line, right; 13. most prominent point of the left gluteus; 14. most prominent point of the right gluteus.

Fig. 4.

Calculation of the POTSI variable; addition of frontal asymmetry index (FAI) and height asymmetry index (HAI). Points 1–8 are anatomical points. I: Distance between points 1 and 2; A: y-component of I distance and reference line for the rest of measures; B–E are, respectively, the distance from points 5–8 to line A; F–H are, respectively, the y-component of the distance between points 3–4, 5–6, and 7–8

Fig. 5.

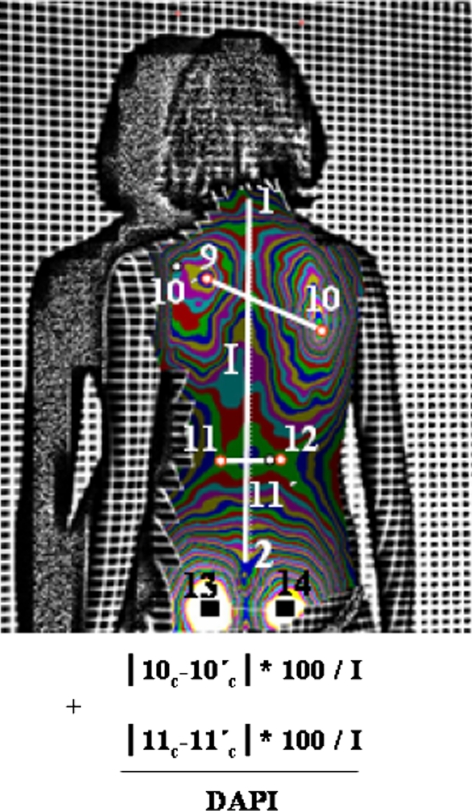
Calculation of the DAPI variable; addition of the difference of depths of the symmetrical points at the level of the scapulae and waist. Points 1, 2, and 9–14 are anatomical points. I: Distance between points 1 and 2, and reference line for the rest of measures; 10′ and 11′ symmetrical points of 10 and 11, following the line 9–10 and 11–12, respectively. The symmetrical point is found for the most prominent of each couple, 9 or 10 in one case and 11 or 12 in the other. Points 13 and 14 must have equal prominence if the patient is positioned correctly if not the prominence of points 9–12 is automatically recalculated (sub-index c)

Points 1–8 are used for determining the POTSI variable and points 1, 2, and 9–12 are used for determining the DAPI variable. Points 13 and 14 are used to correct, if it is necessary, the incorrect placement of the subject.

The POTSI variable has already been described by Inami et al. [6]. Figure 4 shows the procedure to determine this variable from the anatomical points 1–8.

The software also calculates the DAPI variable by the following internal procedure (Fig. 5):

• It draws the line that joins C7 (point 1) to the intergluteal furrow (point 2). The asymmetry, which is evaluated by means of this variable, is calculated from this line.

• Then it draws the lines on which the asymmetries are determined.

• The joining line between the two most prominent points of the scapulae (9–10).

• The joining line between the two least prominent points of the waist (11–12).

• Afterwards it locates the symmetrical point of the most prominent point situated on the two above-described lines (in the case of Fig. 4 these points are marked on the interscapula line as 10′ and on the waist line as 11′).

• The two points located in the most prominent area of both glutei (13 and 14) are used to correct, if it is necessary, the incorrect placement of the subject. For this, the hypothesis is that if a subject is correctly positioned the maximums of the glutei will be at the same depth. The correction is carried out by turning the figure around a vertical line until the glutei are at the same depth (the corrected data are expressed in the formula with the sub-index “c”). In the cases of paralytic scoliosis and scoliosis with very pronounced lumbar curves, the pelvis may be a deformed vertebra, so in these cases it would not be correct to use the criterion described above. Nevertheless, in these cases the DAPI and POTSI values would be so high that the slight error due to hypothetic incorrect placement would not be significant.

• Finally, the differences in depth between the symmetrical points, divided by the length of the vertical line drawn from C7 to the intergluteal furrow (I) are added up and the value is expressed as a percentage.

Consequently, after the anatomical points are marked on the topographic reconstruction the values of the POTSI and DAPI variables appear together with the topographic image (Fig. 6) and they are expressed as a percentage.

Fig. 6.

Back topographic reconstruction. The values of the POTSI and DAPI variables appear together with the topographic image

Statistical analysis

For the statistical analysis we used a SPSS v.10.0. We used the Kolmogorov–Smirnov test to check that the values of the topographic variables POTSI and DAPI of the control group followed a normal distribution. The representative group data were expressed as mean values ± standard deviations (SD). For each of the variables analyzed the intraobserver, interobserver, and interassay variation coefficients were determined. Correlation between POTSI and DAPI variables with Cobb’s angle and vertebral rotation angle were determined.

Results

Normality values in the diagnosis of scoliosis

The 42 controls presented DAPI values of 1.44±0.85 and POTSI values of 13.47±5.69. After verifying the normal distribution of the control values, we determined the upper normality limit of each variable according to the usual criterion of considering mean±2SD. Thus, DAPI values of 3 or under and POTSI values of 27.5 or under were considered normal.

Applying these limit values independently, the 86 subjects studied (42 controls, 14 with asymmetries, and 30 with scoliosis) were diagnosed as normal or pathologic as shown in Table 1. The results show that with the normality values obtained for DAPI and POTSI variables, the DAPI variable classifies scoliotic patients very well, although a high number of asymmetries are classified as scoliosis. On the other hand, the POTSI variable classifies asymmetries adequately although a great number of scoliotic patients are classified as normal.

Table 1.

Diagnosis of the cases with the following criterion: DAPI value ≤3 normal case, DAPI value >3 pathologic case, POTSI value ≤27.5 normal case, POTSI value >27.5 pathologic case

	Nonpathologic		Pathologic
	Control 42	Asymmetries 14	Scoliosis 30
Normal DAPI	40	8	7
Pathologic DAPI	2	6	23
Normal POTSI	41	14	17
Pathologic POTSI	1	0	13

With a view to improving the diagnosis capability of these variables we decided that as the asymmetries are considered as nonpathologic the upper normality limits of the DAPI and POTSI topographical variables could be re-calculated, in accordance with the criterion applied before, but with a group of nonpathologic subjects made up of controls and subjects with asymmetries. The POTSI value showed no appreciable change, while the limit value of the DAPI variable went to 3.9 and the corresponding distribution of the patients is shown in Table 2.

Table 2.

Diagnosis of the cases with the following criterion: DAPI value ≤3.9 normal case, DAPI value >3.9 pathologic case, POTSI value ≤27.5 normal case, POTSI value >27.5 pathologic case

	Nonpathologic		Pathologic
	Control 42	Asymmetries 14	Scoliosis 30
Normal DAPI	41	11	12
Pathologic DAPI	1	3	18
Normal POTSI	41	14	17
Pathologic POTSI	1	0	13

As is shown in Table 2, with these new normality values, the diagnosis capability of these two variables seems to be very similar because the number of pathologic and nonpathologic patients detected for each variable independently is almost the same. Nevertheless, we found that only seven scoliotic patients had high DAPI and POTSI values but 11 scoliotic cases had pathologic DAPI but normal POTSI, and six scoliotic cases had normal DAPI but pathologic POTSI. This was reasonable due to the different information provided by the two variables studied, which is why we devised a diagnostic criterion that combined both of them. Subjects were considered normal if the values of both variables were below the limit value (DAPI ≤ 3.9 and POTSI ≤ 27.5) but pathologic if either of them were over this value.

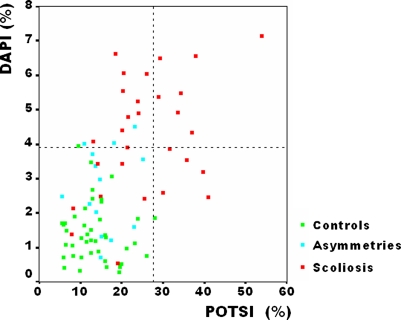
The distribution of cases following this criterion is shown in Table 3 and the graphic representation is shown in Fig. 7; the bottom left square shows the normality criterion and the other three show the pathology criterion.

Table 3.

Diagnosis of the cases with the combined criterion of both variables: DAPI value ≤3.9 and POTSI value ≤27.5 normal case; DAPI value >3.9 or POTSI value >27.5 pathologic case

	Nonpathologic		Pathologic
	Control 42	Asymmetries 14	Scoliosis 30
Normality diagnosis	40	11	7
Pathology diagnosis	2	3	23

Fig. 7.

Graph of the normal and pathologic cases according to their DAPI and POTSI values; value limits are marked by the dotted line. The bottom left square shows a normal diagnosis (normal DAPI and POTSI values) and the rest of the squares show a pathologic diagnosis (pathologic DAPI and/or POTSI values)

Using this criterion the method proposed presents 23 true positives, 7 false negatives, 51 true negatives, and 5 false positives. These data give the method 76.6% sensitivity and 91% specificity. The positive predictive value of the test is 82%, the negative predictive value is 87.9%, and the global value of the test is 86%.

Of the seven pathologic cases identified as normal using the combined diagnosis criteria (false negatives), six are patients with a main Cobb angle of less than 20°, two of them have 0° vertebral rotation, and four have ≤5° vertebral rotation; the seventh case presented a BMI >30.

Reproducibility of the values obtained using the DAPI and POTSI variables

We determined the DAPI and POTSI variables of 20 topographies, chosen at random, in order to analyze the reproducibility of the method. This was carried out twice, by the same observer (intraobserver) and once by a second, nonspecialized observer, but who was trained in using the analysis program (interobserver). Likewise, the consecutive topographies, with repositioning between them, were carried out on 20 subjects in order to evaluate the interassay variability.

For each of the variables analyzed, we studied the difference of the absolute value between the two determinations carried out on each of the topographic variables, thus obtaining the mean and the standard deviation, and we calculated the variation coefficient taking into account the standard deviation of the differences found and the normality limit value in each variable; these results are shown in Table 4.

Table 4.

Variability in POTSI and DAPI measurement

	Intraobserver		Interobserver		Interassay
	POTSI	DAPI	POTSI	DAPI	POTSI	DAPI
Mean	3.95	0.27	3.981	0.38	4.64	0.34
Standard deviation	4.15	0.2	4.17	0.3	4.08	0.31
Variation coefficient	4.15/27.5 (15.09%)	0.2/3.9 (5.13%)	4.17/27.5 (15.16%)	0.3/3.9 (7.69%)	4.08/27.5 (14.84%)	0.31/3.9 (7.95%)

Correlation between topographic variables (DAPI and POTSI) and clinical variables (Cobb’s angle and vertebral rotation angle)

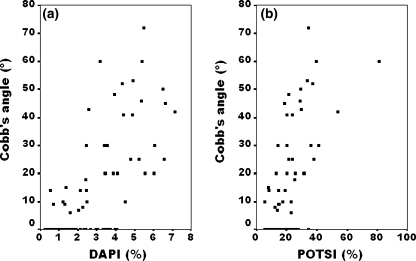
The topographic DAPI and POSTI variables describe the morphology of the back surface while Cobb’s angle and vertebral rotation angle (clinical variables) describe the morphology of the spine. There are consequently two different ways of viewing the study of scoliosis but of course there should be a dependence between these two kinds of variables. Table 5 shows the r-Pearson correlation coefficient between the two types of variables and as an example, Fig. 8 shows the dependence between Cobb’s angle versus DAPI and POTSI values.

Table 5.

r-Pearson correlation coefficient between clinical and topographic variables

	Cobb angle	Vertebral rotation
POTSI	0.668	0.518
DAPI	0.706	0.615

Fig. 8.

Cobb’s angle values versus DAPI and POTSI values. Good correlation is shown between variables (ar=0.668y, br=0.706)

Another interpretation of r-Pearson of clinical interest is the value of r², which is the variation percentage of a variable that is explained by the variation of the other variable. This interpretation means that 44.6% of POTSI variation is explained by a Cobb’s angle variation and 26.8% is explained by vertebral rotation variation. The percentages for the DAPI variable are slightly higher, 49.8% of DAPI variation is explained by the Cobb’s angle variation and 37.8% by vertebral rotation.

Discussion

To date, researchers have taken two factors separately as a basis for quantifying surface deformity. On the one hand there was the degree of right–left asymmetry, and on the other there was the size of rotational prominence. In order to quantify the rotational prominence the Suzuki Hump Sum (SHS) [13] was devised from the Moiré system. It is important to measure this rotational prominence because a significant rotational prominence may exist with only small degrees of lateral curvature [2]. However, this is a quantifying variable based on the addition of the difference in height of the gibbosity at three levels, from the shoulders to the waist line, relativizing it at the distance between the protrusions, without taking into account the size of the subject. It has been used to evaluate the progress of the deformity but, if used on its own, it has not proved useful for the follow-up of those patients in whom rotation is not the main deforming factor. That is why we wanted to find a new variable (DAPI) that would enable us to determine axial asymmetries improving on the disadvantages of the SHS variable. The POTSI was developed to quantify the degree of right–left asymmetry and it has been used to date to evaluate the correction of deformity after surgical treatment. However, normality values have not yet been established in either case, nor have they been used together to characterize the deformity in the two planes in space. The high correlation found between clinical variables (Cobb’s angle and vertebral rotation) and topographic variables (DAPI and POTSI) shows that even though they measure different deformities, variations in the vertebral column should appear as variations of topographic variables.

We have developed a computer program that automatically determines this new variable (DAPI) together with the POTSI variable, which simplifies obtaining these two values.

To establish diagnostic normality values, we only took healthy subjects into account. In other words, subjects with a Cobb angle of 0°, in the cases in which radiographs were available and/or a physical examination with normal results (no rib hump asymmetry and no leg length discrepancy) in those cases in which there was no radiographic study. We made this choice so as to have the best conditions for determining the limit value to be applied to the population. Considering these cases, the cut-off value for the POTSI variable was established at ≤27.5 and for the DAPI variable at ≤3. If we look at Table 1 in which the distribution of the cases in accordance with the above-mentioned criterion is shown, we can see that the DAPI variable has a greater capacity for discrimination between the groups of patients because it showed 6 of the 14 asymmetries as anomalous while the POTSI variable was incapable of differentiating between controls and asymmetries. The DAPI variable appears to be more sensitive as it showed 23 of the 30 scoliosis as pathologic, while the POTSI variable appears to be more specific as it diagnosed 41 of the 42 controls as normal and all of the asymmetries, but it was not sensitive as it only diagnosed 13 of the 30 scoliosis cases.

However, asymmetries cannot be considered pathologic as they do not meet the diagnostic criteria of scoliosis, nor do they require a specific diagnostic test nor any type of treatment. Consequently we recalculated the limit value, taking the normal group as the group made up of the control and asymmetric cases. While the limit value of the POTSI variable did not change, the DAPI variable went to 3.9. With this new criterion for the DAPI variable, 11 of the 14 asymmetries, and 41 of the 42 controls were diagnosed as nonpathologic, but it lost a certain degree of capacity for detecting scoliosis as it diagnosed 23 with the first limit value and this went to 18 with the new criterion.

As the diagnostic characteristics of the topographic variables are different and up to a certain point complementary, we decided to use a diagnostic criterion combining the two, so that if both the DAPI and POTSI variables are normal the case is considered as normal, but if one of them exceeds the limit value the case is considered pathologic. With this new diagnostic criterion, both the sensitivity and specificity of the method are improved with regard to the independent variables and its sensitivity (76.6%), specificity (91%), and positive predictive value (82%) are much greater than those of screening techniques which are usually used in medical practice [4, 11]. Specifically, the Adams test, which is the most widely used test in early detection programs, provides 73.9% sensitivity and 77.8% specificity for curves with a Cobb angle of over 10° [18].

Of the seven pathologic cases diagnosed as normal using the combined criterion, six of them are scoliosis cases with Cobb angles lower than 20° and the seventh case in which the Cobb angle is higher is that of a patient who is seriously overweight, this being one of the sources of error of the technique. As treatment is required when the Cobb angle is 20° or over, we re-calculated the sensitivity and specificity of the method in this case. The results obtained were 92 and 91.8%, respectively.

All the systems based on the reconstruction of the surface of the back have three problems in common, these being the placement of the patient, as this can lead to error in determinations [9, 12]; obesity, because it can hide the deformation; and the small size of children’s backs, because there are fewer lines involved.

With our system we have tried to avoid the placement problem by establishing a strict protocol for positioning the patient and for correcting the remaining malpositions automatically, when necessary, by means of software. By using this system, as can be seen in the variation coefficients in Table 4, the reproducibility of the method is good. The determination of DAPI variables—intraobserver, interobserver, and interassay—shows less variability than the POTSI variable. This is probably because it is more complicated to situate the points involved for calculating the POTSI variable, as some of them are located in the shaded areas the image projects on the left-hand side. On the other hand, the DAPI variable is carried out on anatomical points that are more easily identified on the topographic image, which is why it has less variability. In any case, both reproducibilities are comparable with those obtained for other measurement techniques used in clinical practice such as the Cobb angle [11] which gives an interobserver error of 7°–8° and an intraobserver error of 5°–6°, 10° being the highest normality value.

Regarding the possibilities of applying the method to overweight subjects, eight cases of BMI > 30 were included in our study, three of them were not pathologic and five were. They were all diagnosed correctly except for the subject mentioned above, who had a Cobb angle of 30° and a vertebral rotation ≤5°; this case was a false negative.

To assess the applicability of the method to young subjects, we considered the sample integrated only by subjects of under 14 years old. There were 28 cases in the sample (32.6% of the total sample) aged between 6 and 14 years old of whom 14 were not pathologic and 14 were. The positive predictive value for the test of this age group was 75%, a little lower than the general sample. However, there were only five false negatives for patients with Cobb angles of under 20°; two of them had a vertebral rotation of 0° and three of them had a vertebral rotation of ≤5°.

Conclusions

The visual inspection of back topographic images provides qualitative clinical information, as low depth variations are shown by strong color variations.

Values of DAPI and POSTI variables are strongly correlated with values of Cobb’s angle and vertebral rotation angle. To sum up, the topographic DAPI and POTSI variables developed from the topography of the back surface used in combination are useful for the early diagnosis of idiopathic scoliosis. The diagnostic criterion of normality (DAPI ≤ 3.9 and POTSI ≤ 27.9) and pathology (DAPI > 3.9 or POTSI > 27.9) allows a sensitivity, specificity, and positive predictive value of the method of 76.6, 91, and 82%, respectively. The method reproducibility of around 15% for the POTSI variable and 7% for the DAPI variable is similar to other medical techniques and adequate for carrying out scoliosis diagnosis.