Contribution of the active metabolite M1 to the pharmacological activity of tesofensine in vivo: a pharmacokinetic-pharmacodynamic modelling approach

Abstract

Background and purpose:

Tesofensine is a centrally acting drug under clinical development for Alzheimer's disease, Parkinson's disease and obesity. In vitro, the major metabolite of tesofensine (M1) displayed a slightly higher activity, which however has not been determined in vivo. The aims of this investigation were (i) to simultaneously accomplish a thorough characterization of the pharmacokinetic (PK) properties of tesofensine and M1 in mice and (ii) to evaluate the potency (pharmacodynamics, PD) and concentration-time course of the active metabolite M1 relative to tesofensine and their impact in vivo using the PK/PD modelling approach.

Experimental approach:

Parent compound, metabolite and vehicle were separately administered intravenously and orally over a wide dose range (0.3–20 mg kg⁻¹) to 228 mice. Concentrations of tesofensine and M1 were measured; inhibition of the dopamine transporter was determined by co-administration of [³H]WIN35,428 as the pharmacodynamic measure.

Key results:

Pharmacokinetics of tesofensine and M1 were best described by one-compartment models for both compounds. Nonlinear elimination and metabolism kinetics were observed with increasing dose. The PK/PD relationship was described by an extended E_max model. Effect compartments were used to resolve observed hysteresis. EC₅₀ values of M1, as an inhibitor of the dopamine transporter, were 4–5-fold higher than those for tesofensine in mice.

Conclusions and implications:

The lower potency of M1 together with ∼8-fold higher trough steady-state concentrations suggest that M1 did contribute to the overall activity of tesofensine in mice.

Introduction

Drug metabolites are critical determinants of the entire drug development process (FDA, 2005). Especially when metabolites show pharmacological activity, questions about their contribution to the overall pharmacological drug effect become crucial. Generally, their contribution depends on the relative potency, the relative concentrations and the mechanism of interaction between the parent drug and metabolite (Holford and Sheiner, 1982). For therapeutic use of these drugs, knowledge of the relative concentrations and relative potency of drug and metabolite(s) is of critical importance, as changes in the rate of metabolism or in the metabolic pathway could significantly alter the relationship between parent compound and metabolite, resulting in a higher probability of undesired, or the loss of favourable, pharmacological effects.

Tesofensine (NS2330) is a new central nervous system active drug under clinical development for Alzheimer's disease, Parkinson's disease (Thatte, 2001) and obesity. Tesofensine inhibits the presynaptic uptake of the monoamine neurotransmitters (noradrenaline, dopamine, 5-HT) and stimulates the cholinergic system indirectly. M1 is the only metabolite of tesofensine found in human plasma and shows the same qualitative pharmacological profile as the parent compound with higher in vitro potency (unpublished observations). M1 is formed by the de-alkylation of tesofensine by CYP3A4 and its trough concentrations (model-predicted) in humans after oral administration of tesofensine at steady-state were about one-third of the steady-state concentrations of tesofensine (Lehr et al., 2007). Tesofensine as well as the metabolite M1 revealed long half-lives of 234 and 374 h in humans, respectively (Lehr et al., 2007). Because of these observations, it is extremely important to elucidate the contribution of the metabolite M1 to the overall pharmacological activity of tesofensine in vivo.

Analysis of the in vivo effects of a single compound involves both pharmacokinetic (PK) and pharmacodynamic (PD) aspects. When there is an active metabolite to be considered as well, analyses become more complex as the time- and concentration-dependent dynamic processes for both active components need to be assessed. Added to this complexity, for in vivo studies, the number of samples (data points) is necessarily limited. Classical data analysis methods will not be successful in this situation. Recently, such analyses have been successfully performed using the PK/PD modelling approach (Johnson et al., 2002; Zuideveld et al., 2002; Moghadamnia et al., 2003; Kerbusch et al., 2004), with several advantages: first, the developed PK/PD model considers the formation of the metabolite from the parent compound allowing the characterization of the entire concentration–time profile of the parent compound and of the metabolite, as well as the PD characterization during the entire time course. Second, different ‘what if' scenarios can then be simulated, such as multiple dose prediction from single dose data (Holford et al., 2000). Finally, this modelling approach allows the PK and PD characterization of the parent compound and the metabolite from the limited data set—sparse data sampling—usually available from in vivo pharmacological trials (Van Bree et al., 1994).

In this paper, we have analysed, by PK/PD modelling, data from a study in mice where tesofensine, its active metabolite (M1) and vehicle were separately administered, intravenously and orally over a wide dose range. The pharmacological effect of the compounds were assessed from inhibition of the dopamine transporter using the tritium-labelled compound [³H]WIN35,428 for the in vivo labelling of the dopamine transporter (Stathis et al., 1995; Tatsumi et al., 1999; Bergstrom et al., 2001). This radioligand binds with high affinity to the dopamine transporter in vitro (dissociation constant (K_d)∼10 nM) and in vivo, shows high specific to nonspecific binding ratios (Carroll et al., 1995) and occupies the same binding site of the dopamine transporter as tesofensine and M1. Tesofensine and M1 inhibit the binding of [³H]WIN35,428 in a competitive manner by 100%.

The main objectives of the study were (i) to simultaneously accomplish a thorough characterization of the PK properties of tesofensine and M1 in mice, and (ii) to evaluate the potency and concentration–time course of the active metabolite M1, relative to tesofensine and their impact in vivo using the PK/PD modelling approach.

Methods

Animals

The animal procedures and experiments were performed in accordance with the guidelines of the Danish Committee for Experiments on Animals. Female Naval Medical Research Institute (NMRI) mice (Taconic M&B, Ry, Denmark) with an average weight of 25 g were used in this study. The animals were housed in standard plastic cages under normal 12-h light/dark cycles and a temperature of 19–21 °C. Tap water and food (Brogaarden, Hørsholm, Denmark) were provided ad libitum.

Experimental protocol

Dosage regimen and sampling schedule

Mice received the citrate salt of tesofensine (NeuroSearch, Ballerup, Denmark) or the fumarate salt of M1 (NeuroSearch, Ballerup, Denmark) as solution orally (gavage) or intravenously (tail vein; bolus). Doses administered were calculated based on the salt form. Bioanalytical measurements and modelling, however, used the doses of the free base. Oral doses of tesofensine and M1 were 1, 3, 10 and 20 mg kg⁻¹, and intravenous (i.v.) doses were 0.3, 1, 3, 5 and 10 mg kg⁻¹. The vehicle was an aqueous solution containing 5% Tween 80 (Merck, Darmstadt, Germany). Vehicle or test substances dissolved in the vehicle were administered to the NMRI mice (i.v.: 0.25 ml; p.o.: 0.75 ml). Each mouse was weighed and dosed according to body weight. Forty-five minutes before the respective sampling time point 2.0 μCi of [³H]WIN35,428 (Perkin-Elmer, Boston, MA, USA) in 0.2 ml saline (Københavns Amts Sygehuse, Glostrup, Denmark) were injected intravenously via the tail vein. Additional animals were used for the determination of nonspecific binding where WIN35,428 (2.5 mg kg⁻¹, i.p.) (NeuroSearch, Ballerup, Denmark) was injected at the time of [³H]WIN35,428 injection. At the sampling time points, the mice were killed by cervical dislocation.

At the times listed in Table 1, plasma samples for the determination of tesofensine and M1 concentrations (PK) were taken. In addition, samples for the determination of % inhibition of the binding in the brain (PD) were taken at the same time points as for the PK samples. Consequently, for every mouse, two to three measurements, that is one data point for % inhibition (PD), one for M1 (PK) and (if applicable) one for tesofensine (PK), were available for PK/PD modelling.

Table 1.

Sampling scheme for PK and PD samples

Treatment	Dose (mg kg−1)a	PKb and PDc sample time points (h)
Tesofensine i.v.	0.3	0.75, 1.5, 3
	1	0.75, 1.5, 3
	3	0.75, 1.5, 3
	5	17.5
	10	17.5
M1 i.v.	0.3	0.75, 1.5, 3
	1	0.75, 1.5, 3
	3	0.75, 1.5, 3
	5	17.5
	10	17.5
Tesofensine p.o.	1	0.75, 1.5, 3
	3	0.75, 1.5, 3
	10	0.75, 1.5, 3, 16
	20	16
M1 p.o.	1	0.75, 1.5, 3
	3	0.75, 1.5, 3
	10	0.75, 1.5, 3, 16
	20	16

^aBased on salt form.

^bPK, tesofensine and/or M1 plasma measurements.

^cPD, inhibition of in vivo [³H]WIN35,428 binding.

Overall, 228 mice were investigated in this study. In detail, three mice per sample point were treated with the parent compound (n=66) or the metabolite (n=66), respectively, four mice per time point were treated with vehicle (n=64) and two mice per time point (n=32) were investigated to determine the nonspecific binding.

Blood sampling

Approximately 400 μl blood was collected from each mouse at the time of death in glass vials containing potassium EDTA (340 mM, 25 μl) (BD Vacutainer Systems, Plymouth, UK). The blood was immediately mixed with the anticoagulant by gentle inversion about 10 times. Vigorous shaking was avoided to prevent haemolysis. Whole blood was centrifuged at 4 °C at ∼2100 g for 10 min. Samples were centrifuged within 30 min after collection, with intermittent ice bath storage of the samples prior to centrifugation. The plasma samples were transferred and stored in a freezer (−20 °C) within 1 h. The frozen plasma samples were shipped on dry ice at the end of the study to the analytical laboratory (Boehringer Ingelheim, Biberach an der Riss, Germany).

Sampling for determination of dopamine transporter inhibition

The samples for the determination of the inhibition of the dopamine transporter by tesofensine and/or M1 were obtained as follows: mice were decapitated at the planned sampling time points and the brains were quickly removed and dissected on ice. Striatum, which contains the highest concentration of dopamine transporters, was isolated and tissue was weighed and dissolved in 1 ml 2% sodium laurylsulphate (Sigma-Aldrich, Vallensbæk Strand, Denmark) for 24–48 h.

Data acquisition

High-performance liquid chromatography analysis of tesofensine and M1

Tesofensine and M1 concentrations in plasma were determined by a fully validated high-performance liquid chromatography coupled to tandem mass spectrometry method using deuterated tesofensine (Boehringer Ingelheim, Biberach an der Riss, Germany) and deuterated M1 (Boehringer Ingelheim, Biberach an der Riss, Germany) as internal standards. Details of the analytical method can be found elsewhere (Lehr et al., 2007). In brief, the assay comprised sample clean-up by automated solid phase extraction in the 96-well plate format. Chromatography was achieved on a reversed-phase HLPC column with gradient elution. The analytes were detected and quantified by high-performance liquid chromatography coupled to tandem mass spectrometry using electrospray ionization in the positive ion mode. Linearity ranged between 0.1 and 50 ng ml⁻¹ using a plasma volume of 200 ml. Inaccuracy and imprecision were below ±6% relative error and <11% coefficient of variation, respectively (n=at least 11). Concentrations determined in ng per ml were used for PK modelling.

Measurement of dopamine transporter inhibition

To the solubilized tissue, 2 ml of scintillation cocktail (Perkin-Elmer) were added, and the amount of radioactivity per mg of tissue was determined by conventional liquid scintillation counting using a Tri-CarbTM counter (Perkin-Elmer Life and Analytical Sciences, Downers Grove, USA). Groups of mice treated with vehicle served as controls for estimation of total binding. The percentage of inhibition of the dopamine transporter was used as the measure of pharmacological activity (=PD) and was calculated as follows:

 

Data analysis

Parameter estimation and model selection

The PK and PD analyses were performed using the software NONMEM, version V (Beal and Sheiner, 1998). The chosen estimation method was the first-order method. The ADVAN6 subroutine was used to express the models in differential equations. Parameter estimates and s.e. of the parameter estimates expressed in % were determined.

PK/PD modelling was performed in a sequential manner. First, the PK models for tesofensine and M1 were developed. Modelling started with the i.v. data of M1, then the i.v. data of tesofensine and subsequently the oral data of M1, and finally the oral data of tesofensine were added. Thus, four key PK models were available. Based on the final PK models, parameter estimates were fixed and the PD data were fitted sequentially as described for PK. Ultimately, PK/PD models were estimated again without fixing the PK parameters, allowing a simultaneous estimation of PK and PD parameters. Considering this model building strategy, four different PK/PD models describing a different raw data situation were developed, optimized and finalized. The model with all data included was the final model; the other three were named intermediate key models.

Each mouse was considered as an individual. The individual PK and PD parameters θ_j were modelled assuming a log-normal distribution:

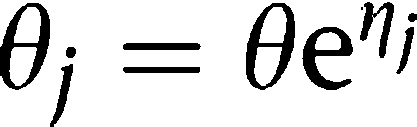where θ is the population mean and η_j are independent symmetrically distributed random effects parameters with a zero mean and a variance of ω². For the PK models, variability was implemented on the volume of distribution (V_d) and for the PD models on the EC₅₀ parameters. As only one PK and PD data point per mouse was available, the estimated variability represented both interindividual and residual variability.

Goodness-of-fit was analysed using the objective function value (Akaike, 1974) and various diagnostic methods (Jonsson and Karlsson, 1999). If models were classified as nested, one model was declared superior over the other model if the objective function value was reduced by 3.84 (P<0.05 with 1 d.f.).

Pharmacokinetic analysis

One- and two-compartment models were examined to describe the data available. Linear and saturable Michaelis–Menten (MM) kinetics were examined to describe the absorption, metabolism and elimination of tesofensine and M1, respectively. Within the linear range (plasma concentration≪K_m/V_d) of tesofensine and M1 the PK parameters clearance (CL) and terminal half-life (t_1/2) could be derived from the MM parameters estimated according to the following equations:

Calculation of CL

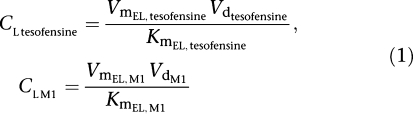  Calculation of half-life

where

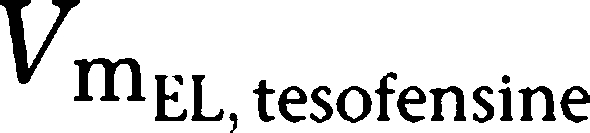
  and 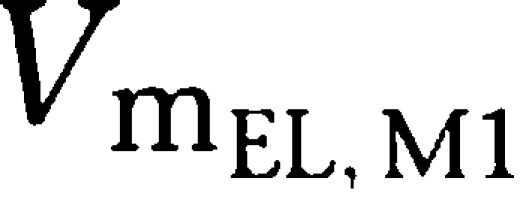  were the maximum elimination rates of tesofensine and M1, respectively, from the central compartments and

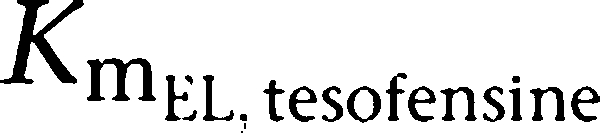
  and 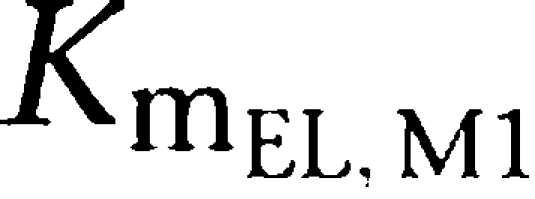  the amounts yielding 50% of the respective maximum MM rate (V_m).

  and 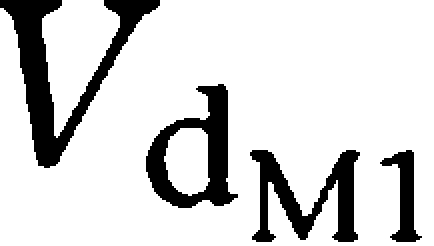  were the respective volumes of distribution.

Pharmacodynamic analysis

Different types of PD models were investigated to assess the effect of tesofensine and M1 on the inhibition of the dopamine transporter. The effect of M1 given alone was described by a maximum effect (E_max) model (Equation (3)).

E_max model

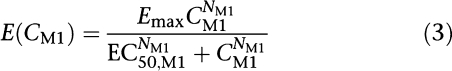where E_max was the maximum effect attributable to M1 and EC_50,M1 was the concentration producing 50% of the E_max, N_M1 was the Hill factor affecting the shape of the curve and C_M1 reflected the concentration of M1 in the central or hypothetical effect compartment, depending on the link chosen between PK and PD.

If parent compound and metabolite were present, a competitive interaction between tesofensine and M1 at the binding site of the dopamine transporter occurred. Considering this pharmacological situation, a model reflecting this interaction situation (Holford and Sheiner, 1982) was applied (Equation (4)).

Competitive interaction model

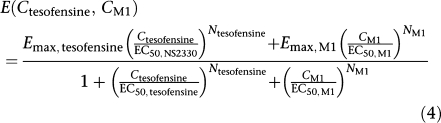where two different E_max values and Hill factors were present for each compound. Under the assumption that these two PD parameters were equal for both compounds Equation (4) could be simplified to Equation (5).

Simplified competitive interaction model

If only one compound was present, Equation (5) was reduced to a simple E_max model (Equation (3)) for the remaining compound.

The link between PK and PD for all available data was investigated using hypothetical effect compartments. Mathematically the concentration–time profiles in the hypothetical effect compartments were described by the following differential equations:

Differential equations of effect compartments

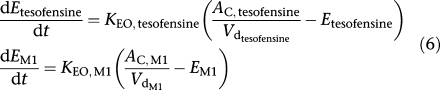where K_{EO, tesofensine} and 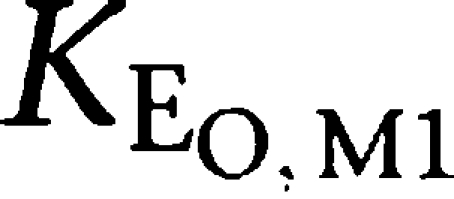reflected the rate constants of tesofensine and M1,

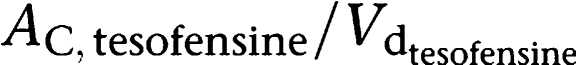
  and 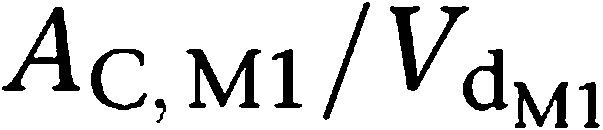  were the plasma concentrations in the central compartments, and E_tesofensine and E_M1 the concentrations in the hypothetical effect compartments of tesofensine and M1, respectively.

Simulations

The final PK/PD model was used to simulate mean concentration–effect–time profiles using different scenarios. In the first simulation, 1 mg kg⁻¹ tesofensine was (a) intravenously and (b) orally administered using a single dose regimen. In addition, 1 mg kg⁻¹ tesofensine was orally administered using a multiple dose regimen every 6 h. In a second simulation, the mean effect–time profiles were predicted where tesofensine was administered orally in doses of 1–10 mg kg⁻¹ as (a) single dose or (b) multiple dose every 6 h. For both simulations, the predicted plasma concentrations and the % occupancy of the dopamine transporter were calculated every 0.1 h using Berkeley Madonna (Berkeley Madonna, Version 8.0.1, 2000). Figures were generated using SigmaPlot (SPSS, Version 8.0, 2002).

Results

Pharmacokinetics

The data set for PK modelling consisted of 197 plasma concentrations from 132 mice with 65 plasma concentration measurements of tesofensine and 132 plasma concentration measurements of M1 at five different time points. One plasma concentration value of tesofensine was below the lower limit of quantification and was removed from the data set. Plasma concentrations measured showed a wide range from 1.26 to 296 ng ml⁻¹ for tesofensine and from 2.67 to 483 ng ml⁻¹ for M1. The variability of the plasma concentrations within a dose group at a particular time point was generally low.

Plasma concentrations versus time of tesofensine and M1 were best described by one-compartment models for both compounds. Absorption of tesofensine or M1 after oral administration was best described by a first-order process (absorption rate constant (K_a)). Implementation of nonlinear elimination pathways (MM) into the model as well as a nonlinear first-pass metabolism of tesofensine to M1 improved the predictability of the model, with estimation of the maximum elimination rates of tesofensine and M1 from the central compartments (

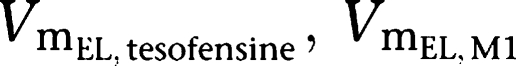
) and the amounts (

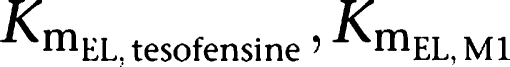
) yielding 50% of the respective V_m. Metabolic formation of M1 from tesofensine was accounted for by an MM metabolism step with estimation of the maximum rates

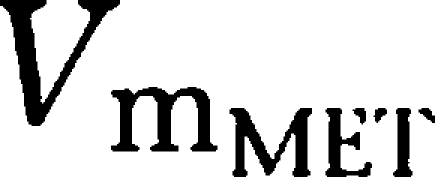
  and 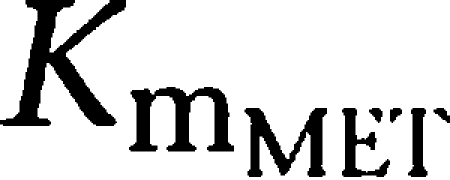  as the amount yielding 50%

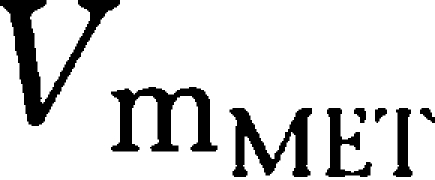
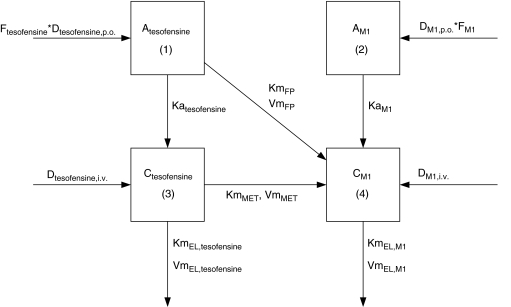
. The fraction of dose available to gut enterocytes was described by the factor F. A schematic representation of the model can be found in Figure 1.

Figure 1.

Schematic illustration of the PK model for tesofensine and M1 after i.v. and oral administration. The subscripts tesofensine and M1 denote the respective parameter of the parent compound and the metabolite. D represents the doses administered orally or intravenously; F, the fraction of dose available to gut enterocytes; K_a, the first-order absorption rate constants and C, the concentrations in the central compartments. V_m are the maximum rates and K_m, the amounts yielding 50% V_m, where the subscripts FP, MET and EL denote the first-pass, the metabolism and elimination processes.

Parameter estimates of the final PK model using all data available are shown in Table 2. Volumes of distribution were found to be large with 17.7 l kg⁻¹ (tesofensine) and 13.6 l kg⁻¹ (M1), respectively. Due to the limited data in the absorption phase, K_a was fixed to constant values of 10 and 5 h⁻¹ for tesofensine and M1, respectively. Sensitivity analysis showed that fixing of K_a had no significant impact on the parameter estimates. The sparse data did not allow estimating significantly different MM constants (K_m) for the four nonlinear MM processes of the model. Thus, all K_m values were assumed to be equal and estimated to be 3.59 mg kg⁻¹. To obtain K_m values on a concentration basis for better interpretability, the kg-based K_m value was set in relation to the corresponding volumes in the central compartments (that is K_m/V_d) and led to 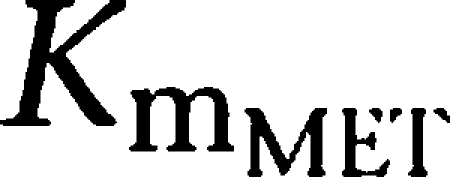a and a 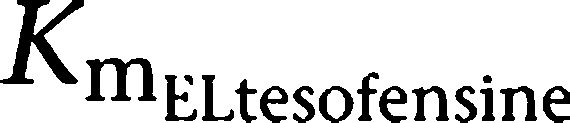value of 203 ng ml⁻¹ and a 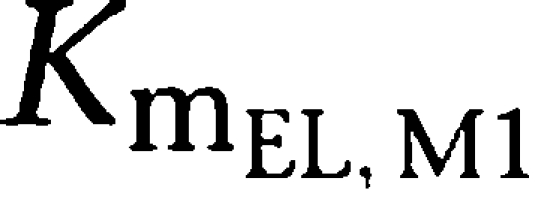value of 264 ng ml⁻¹. For the linear PK range of tesofensine and M1, the PK parameters CL and half-life were derived according to Equations (1 and 2). CL of tesofensine was found to be high with 5.3 l h⁻¹ kg⁻¹ and moderate for M1 with 1.9 l h⁻¹ kg⁻¹. The resulting half-lives in mice were 2.3 and 4.9 h for tesofensine and M1, respectively.

Table 2.

Parameter estimates of final PK model

PK model parameter	Population estimate	Relative s.e.%
Katesofensine (h−1)	10 FIX	/
KaM1 (h−1)	5 FIX	/
Vdcentral tesofensine (l kg−1)	17.7	6.1
Vdcentral M1 (l kg−1)	13.6	9.1
VmFP (mg h−1 kg−1)	11.9	19.9
VmMET (mg h−1 kg−1)	0.823	21.5
VmEL, tesofensine (mg h−1 kg−1)	0.250	39.7
VmEL, M1 (mg h−1 kg−1)	0.506	14.4
KmFP (mg kg−1)	3.59	21.0
KmMET (mg kg−1)	3.59	21.0
KmEL, tesofensine (mg kg−1)	3.59	21.0
KmEL, M1 (mg kg−1)	3.59	21.0
Ftesofensine (%)	87.2	5.1
FM1 (%)	109	9.3
Variability
Tesofensine (%)	35.7	17.1a
M1 (%)	36.3	11.4a

^aGiven on the variance scale.

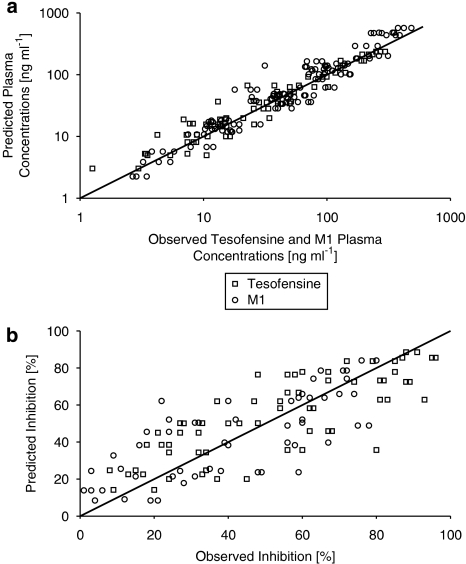
All parameters were estimated with high precision (relative s.e. ⩽39.7%, Table 2), variability (comprising interindividual and residual variability) was moderate with about 36% for the PK of tesofensine and M1, respectively. The goodness-of-fit plot showing the observed versus the predicted concentrations of both compounds is presented in Figure 2a. In general, all concentrations were randomly and closely spread around the line of identity, indicating that the data were very well described by the model.

Figure 2.

Goodness-of-fit plot of the final PK model (a) with observed plasma concentrations of tesofensine and M1 versus predicted concentrations (tesofensine, n=65; M1, n=132) and of the final PD model (b) with predicted inhibitions (as %) of the dopamine transporter versus observed inhibitions (tesofensine, n=66; M1, n=66).

Pharmacodynamics

The data set for PD modelling included 132 measurements from 132 mice at five different time points. Seven PD values were lower than zero and were set to zero for modelling purpose. Observed inhibition of the dopamine transporter showed a wide range of values from 0 to 94% inhibition.

The PD effect of all data available was best described by an extended E_max model (Equation (5)), which accounted for the competitive interaction between tesofensine and M1 on the binding site of the dopamine transporter. It was assumed that both compounds could achieve a complete inhibition of the dopamine transporter and so the efficacy parameter E_max for both compounds was set to 1. This assumption was further substantiated as E_max was 0.95 when estimated. Additionally, this model did not show a statistically significant drop in the objective function value and other parameter estimates were very similar. Implementation of a Hill factor was not necessary, as the Hill factor was 0.98 when estimated, which also did not have any significant influence on the objective function value.

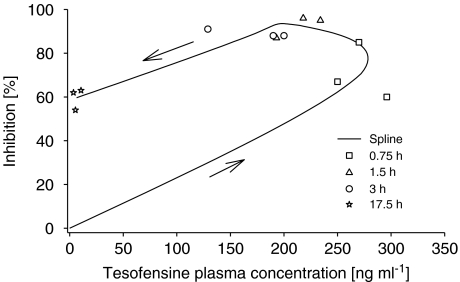
The data analyses revealed the necessity to use effect compartments (Equation (6)) in the final model (Δ objective function value: −44, 2 d.f.) to resolve the hysteresis in the concentration–effect relation of tesofensine and M1. Figure 3 shows, as an example, the concentration–effect relation after administration of 10 mg tesofensine.

Figure 3.

Concentration–effect plot of tesofensine after 10 mg p.o. administration. Arrows indicate the direction of the hysteresis.

PD parameter estimates of the final PK/PD model including all data available are shown in Table 3. EC₅₀ values were 72.3 nM (23.7 ng ml⁻¹) for tesofensine and 363.1 nM (114 ng ml⁻¹) for the metabolite M1. PD parameter estimates obtained by intermediate key models are listed in Table 4. Comparison of parameter estimates for EC₅₀ showed a four- to fivefold higher EC₅₀ value of M1 in comparison to those of tesofensine. Comparing EC₅₀ values regarding different administration routes, no significant changes in EC₅₀ parameter estimates were found between i.v. administration and a combination of i.v. and p.o. administration.

Table 3.

Parameter estimates final PK/PD model

PD model parameter	Population estimate	Relative standard error %
EMAX (%)	100 FIX	/
EC50,tesofensine (nM)	72.3	15.1
EC50,M1 (nM)	363.1	11.9
KEO,tesofensine (h−1)	0.555	29.0
KEO,M1 (h−1)	0.878	24.3
Variability
Tesofensine (%)	77.5	14.9a
M1 (%)	89.3	15.3a

^aGiven on the variance scale.

Table 4.

EC₅₀ values of key and final models

Raw data	EC50 tesofensine (nM)	EC50 M1 (nM)	EC50 M1/EC50 tesofensine
M1 i.v.a	NA	318.4	NA
M1 i.v.+tesofensine i.v.a	76.2	309.2	4.1
M1 i.v.+tesofensine i.v. and p.o.	81.4	340.8	4.2
M1 i.v. and p.o.+tesofensine i.v. and p.o.	72.3	363.1	5.0

NA, not applicable.

^aBased on central compartment concentrations.

In the final PK/PD model (Table 2 and 3), all reported PK and PD parameter were estimated simultaneously, all PD parameters were estimated with high precision (relative s.e. ⩽29%, Table 3). Variability (comprising interindividual and residual variability) was found to be high with 77.5% and 89.3% for the PD of tesofensine and M1, respectively. The goodness-of-fit plot showing the observed versus the predicted inhibition measurements of both compounds is presented in Figure 2b. All measurements were randomly distributed around the line of identity, indicating that the data were well described by the model.

Simulations

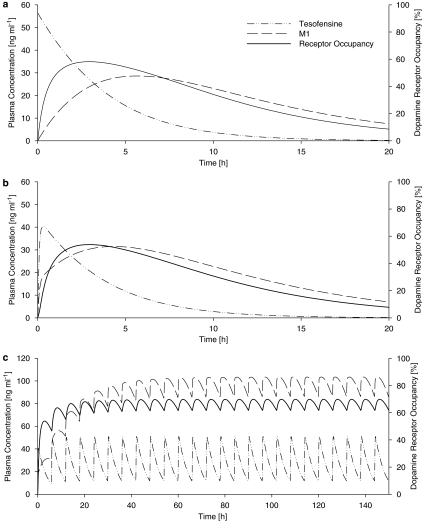
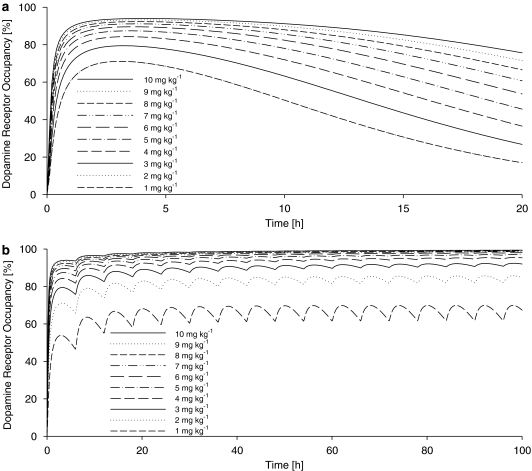
Based on the final population, PK/PD model simulations were performed with the results depicted in Figure 4 and 5 to demonstrate the concentration–effect–time profile at different scenarios. Figures 4a and b reveal that the maximum dopamine receptor occupancy was estimated to be ∼60 and ∼55% after a 1 mg kg⁻¹ i.v. and p.o. tesofensine administration, respectively. At steady state (Figure 4c), the maximum dopamine receptor occupancy was estimated to range between ∼60% (trough) and ∼70% (peak value). The trough steady-state plasma concentrations of M1 were ∼8-fold higher than the tesofensine concentrations. Figure 5a shows that even at the highest simulated dose of 10 mg kg⁻¹, complete inhibition was not achieved after a single dose. However, with a multiple dose regimen of 4 mg kg⁻¹ administered every 6 h, an ∼95% receptor occupancy could be achieved (Figure 5b).

Figure 4.

Simulated plasma concentration– (left y axis) and effect– (right y axis) time profiles after (a) single i.v. administration of tesofensine (1 mg kg⁻¹), (b) single oral administration of tesofensine (1 mg kg⁻¹) and (c) multiple oral administration of tesofensine (1 mg kg⁻¹ every 6 h).

Figure 5.

Simulated effect–time profiles after a broad range (1–10 mg kg⁻¹) of oral tesofensine after (a) single dose administration and (b) multiple dose administration of tesofensine every 6 h.

Discussion and conclusions

The investigation and data analysis presented here demonstrate the successful application of the PK/PD modelling approach to sparse data obtained in an experimental pharmacological study. The analysis provided crucial knowledge about the PK and pharmacological activity in vivo of the major metabolite M1 in relation to tesofensine.

The modelling approach allowed, for the first time, the PK characterization of tesofensine in mice and the PK characterization of M1 after oral and i.v. administration of M1. The structural PK model revealed a simple one-compartment model for both compounds. Presumably, with more frequent sampling, a more complex model might evolve. Nevertheless, the data available were very well described and according to the principle of parsimony, the simple one-compartment model was assessed as sufficient. Distribution volumes were found to be large for both compounds, exceeding the total volume of body water, suggesting extensive distribution into tissues. These findings were consistent with results from other in vivo investigations with tesofensine, for example, the distribution volumes of tesofensine in rats were 18 and ∼8.6 l kg⁻¹ in humans (Lehr et al., 2007). Compared to tesofensine, the V_d of M1 in mice was 23% lower, which might be caused by the increased hydrophilicity of the metabolite.

Nonlinearity observed in the PK of both compounds was presumably caused by the high doses administered. The highest tesofensine dose administered within this experimental pharmacology trial (20 mg kg⁻¹) exceeded the highest non-lethal dose in mice threefold (∼7 mg kg⁻¹). In humans, much lower doses ⩽∼0.017 mg kg⁻¹ (1 mg absolute dose) were administered as multiple doses (Lehr et al., 2007). Nonlinearity in human PK has not been observed so far and might not be expected to occur within the therapeutic plasma concentration range. Within the linear PK range of tesofensine and M1, CL of tesofensine in mice was found to be high at 5.3 l h⁻¹ kg⁻¹ and comparable with the CL of 6 l h⁻¹ kg⁻¹ in rats (unpublished observations). In Cynomolgus monkeys and minipigs, a lower CL of tesofensine of 1.8 and 1.5–2.6 l h⁻¹ kg⁻¹ was observed, respectively, and in humans a much lower tesofensine CL of ∼0.03 l h⁻¹ kg⁻¹ was observed, presumably caused by a reduced affinity of the drug to the human CYP3A4 system, responsible for the major metabolism pathway (Lehr et al., 2007). CL of M1 in mice was found to be moderate with 1.9 l h⁻¹ kg⁻¹ and ∼64% lower than the CL of tesofensine.

In particular, the focus of the present analysis was to determine the contribution of the metabolite M1 to the overall pharmacological activity. Generally, both tesofensine and M1 were able to achieve maximum inhibition of almost 100%. Comparison of EC₅₀ values of key models revealed a four- to fivefold higher in vivo potency of tesofensine in mice compared to M1, as shown by the inhibition of the dopamine re-uptake transporter in mice. Previously, studies had been performed to assess the in vitro activity of tesofensine and M1 (unpublished observations) where the effect of both compounds on the uptake of [³H]dopamine, [³H]5-HT and [³H]noradrenaline in synaptosomes prepared from rat brain were explored. Investigations of the [³H]dopamine uptake resulted in IC₅₀ values of 6.5 and 3.0 nM for tesofensine and M1, respectively. These results are different from the results of the present analysis. Generally, discrepancies between in vivo and in vitro investigations are well known (Heykants et al., 1988; Lin et al., 1994; Barnard and Gurevich, 2005). One explanation might be a poorer distribution to the striatum of the more hydrophilic M1 and/or slower transporter binding (different transport mechanisms, different efflux transporters) compared to tesofensine, although in vivo investigations in mice showed a very good and comparable blood–brain barrier permeability of both compounds (unpublished observations). However, distribution specifically to the striatum has not been explored so far and might not correlate with blood–brain barrier permeability. The difference might also have resulted from a significant discrepancy in the in vivo plasma protein binding between tesofensine and M1, but this was similar for tesofensine (94.7%) and M1 (94.9%) in mice. Another explanation might be the differences in the assays used to determine in vitro and in vivo activity. It should be noted that the assessment of the in vitro activity of tesofensine and the metabolites were performed on different occasions, using different groups of animals and using different species (rats in vitro, mice in vivo); all these variations in experimental procedures might also contribute to the differences reported above. Finally, it should be realized that, in general, in vitro models provide static systems, whereas in vivo models reflect a more complex time- and concentration-dependent dynamic system. Thus, as in vivo investigations are closer to the biological reality, results from such investigations are favoured when evaluating the contribution of metabolites to the overall pharmacological effect (FDA, 1997). However, further experimental investigations might be necessary for this new compound, assessing the possibilities mentioned above.

In this study, the in vivo activity of both compounds with respect to the dopamine transporter was successfully investigated. Tesofensine and M1 showed multiple modes of action inhibiting additionally the noradrenaline and 5-HT transporters. The in vivo activity of both compounds with regard to these transporters is still unknown. In vitro investigations resulted in IC₅₀ values for tesofensine of 11 and 1.7 nM for the [³H]5-HT and [³H]noradrenaline uptake, respectively. Corresponding IC₅₀ values for M1 were 2.0 and 0.6 nM, respectively (unpublished observations). Thus, both compounds showed at the 5-HT and noradrenaline transporters, in vitro potency ratios in the same range as they did at the dopamine transporter. It might be speculated that results from the dopamine transporter studies might roughly be transferable to the other monoamine transporters. However, further in vivo investigations are mandatory to confirm this.

As the metabolite (M1) has not yet been given to humans, this investigation was performed in mice and raises questions about the prediction of results in humans from animal data. Wu and Gu (1999) investigated the drug inhibition profiles of four different dopamine transporter inhibitors using mouse and human dopamine transporters in vitro. Bupropione and amphetamine showed similar affinity for mouse and human dopamine transporters (K_d: ∼0.75 μM), whereas differences were seen for cocaine and ritalin (

0.14 and 0.038 μM,

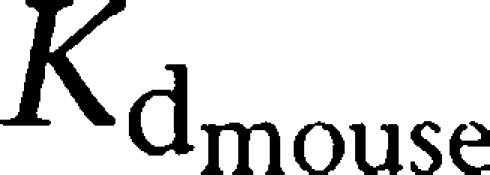
0.29 and 0.12 μM, respectively). They also investigated the amino-acid sequence of the dopamine transporter from both species and found 93.5% homology. Overall, high structural amino-acid homology and comparable affinity of human and mouse dopamine transporter support the validity of translating the animal results to the human situation, in this system.

Data analysis showed that the PD effect lagged behind the plasma concentration–time profile that was accounted for by introducing an effect compartment model to link the PK with the PD. The use of effect compartments for central nervous system active compounds is not uncommon in literature (Gupta et al., 1990; Lee et al., 1999; Bouw et al., 2001). The equilibrium half-life between the central and the effect compartments (t_1/2) were comparable for both compounds with 1.25 h (tesofensine) and 0.8 h (M1), respectively. In theory, hysteresis in the effect might have been caused by distribution processes of the molecules between the plasma and the central nervous system where several permeation barriers, such as the blood–brain barrier, had to be overcome (Pardridge, 1998). However, in the context of the proposed clinical indications for this drug, where chronic treatment of the patients is intended and required, this time delay might prove to be unimportant.

The results from these investigations allowed the assessment of the contribution of the metabolite M1 in terms of potency and presence to the overall pharmacological activity. In mice, the ∼8-fold higher trough steady-state concentrations together with the ∼5-fold lower potency of M1 suggest that the active metabolite M1 contributes to the overall activity despite the lower relative potency. In humans, the steady-state plasma concentrations of M1 are approximately 60% lower, compared to those of tesofensine (Lehr et al., 2007), suggesting that the contribution of M1 to the overall activity might be lower. Nevertheless, the findings from these analyses will allow the incorporation of this knowledge in further PK/PD analyses to provide a complete and reliable picture of the parent compound and the active metabolite.

In summary, our analysis has used the PK/PD modelling approach for the thorough characterization of the PK properties of tesofensine and its metabolite. Moreover and very importantly, this approach also allowed the assessment of the potency of the promising new compound tesofensine and its metabolite. In addition, several ‘what if' scenarios elucidating the relative presence and impact of the metabolite after single and multiple dose administration of the parent compound were simulated. Hence, this investigation also showed the successful application of the PK/PD approach. We hope our success will encourage the application of similar approaches to other drug candidates to facilitate assessment of the effects of the presence and the potency of metabolites. With the urgent need of a better understanding of the overall characteristics of a drug (FDA, 2004), the application of modelling and simulation techniques may become one of the basic tools of future research and development.

Abbreviations

A

amount

C

concentration

CL

clearance

E_max

maximum effect

K_a

absorption rate constant

K_d

dissociation constant

K_EO

rate constants effect compartment

K_m

MM constant

MM

Michaelis-Menten

N

Hill factor

PD

pharmacodynamic/s

PK

pharmacokinetic/s

t_1/2

terminal half-life

V_d

volume of distribution

V_m

maximum MM rates

Conflict of interest

Charlotte Kloft has received fees for consulting by Boehringer Ingelheim.