Abstract
Vancomycin-resistant enterococci (VRE) recently have emerged as a nosocomial pathogen especially in intensive-care units (ICUs) worldwide. Transmission via the hands of health-care workers is an important determinant of spread and persistence in a VRE-endemic ICU. We describe the transmission of nosocomial pathogens by using a micro-epidemiological framework based on the transmission dynamics of vector-borne diseases. By using the concept of a basic reproductive number, R0, defined as the average number of secondary cases generated by one primary case, we show quantitatively how infection control measures such as hand washing, cohorting, and antibiotic restriction affect nosocomial cross-transmission. By using detailed molecular epidemiological surveillance and compliance monitoring, we found that the estimated basic reproductive number for VRE during a study at the Cook County Hospital, Chicago, was approximately 3–4 without infection control and 0.7 when infection control measures were included. The impact of infection control was to reduce the prevalence from a predicted 79% to an observed 36%. Hand washing and staff cohorting are the most powerful control measures although their efficacy depends on the magnitude of R0. Under the circumstances tested, endemicity of VRE was stabilized despite infection control measures, by the constant introduction of colonized patients. Multiple stochastic simulations of the model revealed excellent agreement with observed pattern. In conjunction with detailed microbiological surveillance, a mathematical framework provides a precise template to describe the colonization dynamics of VRE in ICUs and impact of infection control measures. Our analyses suggest that compliance for hand washing significantly in excess of reported levels, or the cohorting of nursing staff, are needed to prevent nosocomial transmission of VRE in endemic settings.
Keywords: nosocomial infections, mathematical models
Increasing antibiotic resistance in common bacterial pathogens, in both hospitals and communities, presents a growing threat to human health worldwide. Certain groups of pathogens, in which the frequency of resistance has risen rapidly in recent years, pose a particular threat to severely ill patients in settings such as intensive-care units (ICUs), oncology wards, and transplantation units. The recent emergence of vancomycin-resistant enterococci (VRE) as a nosocomial pathogen is a striking example of this new danger to vulnerable patients. During the past 7 years, the prevalence of VRE in hospitals has risen dramatically in both the United States and the United Kingdom, with for example, a 34-fold increase in VRE in ICUs in the United States from 1989 to 1993 (0.4% to 13.6%) (1, 2). Treatment options often are limited to combining antibiotics or experimental compounds (3, 4), with resistance already being reported to the most recent antibiotic, Quinupristin/Dalfopristin.
Although the initial rise in the incidence of VRE was observed in ICUs, recent years have seen a spread to non-ICU wards and inter-hospital transmission (1, 2, 5, 6). Reported incidence of VRE infections is believed to grossly underestimate the true prevalence because many patients act as carriers of enterococci (7–9). Molecular epidemiological studies of early endemic infections suggested clonal outbreaks (8). More recent ICU studies have appeared to involve more than one clone, perhaps demonstrating frequent introductions from other parts of the hospital (9–11). The rapid spread of VRE in Europe and North America may, in part, be explained by the organism’s ability to colonize the gastrointestinal tract and skin and persist in the environment of the human host (9). The commensal nature of enterococci had generated the belief that new outbreaks in hospital settings were a consequence of endogenous sources. Recent studies, however, have demonstrated that transmission via the susceptible patient contact with the hands of contaminated health care workers (HCWs) is a very important determinant of the spread and persistence of VRE (8, 9, 12).
Once VRE is detected in a hospital, well-designed surveillance and infection control programs are needed. To date, however, little quantitative work has been published on how best to achieve the desired outcome of control and eradication (13). In this paper we present a theoretical framework that describes the transmission dynamics and persistence of VRE in the ICU. Our analyses facilitate quantitative definition of the relative impact of different infection control practices and generate precise criteria for control and eradication in different ICU settings. The theory is validated by using available transmission surveillance data and shows excellent agreement with observed patterns.
Surveillance Methods
A previous study conducted at the Cook County Hospital, Chicago, measured the relative efficacy of various barrier precautions in preventing nosocomial spread of VRE (11). During this study rectal surveillance cultures were taken daily and environmental cultures monthly. By using pulsed field gel electrophoresis, 19 VRE strain types were identified during a 19-week period. Many important epidemiological determinants were measured, including staff-patient contact rates, length of stay (LOS), and compliance with infection control measures. In this and a subsequent study (9), environmental contamination was low level and transient, suggesting that patients were the major source reservoir of VRE.
The Basic Reproductive Number R0
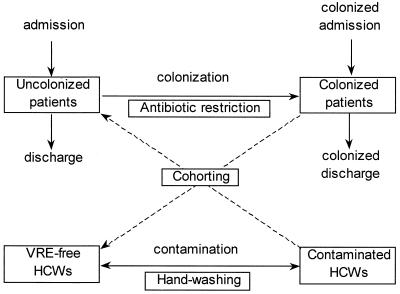
The transmission dynamics of nosocomial spread (or cross acquisition) of VRE in an ICU can be captured by using a set of differential equations (see Appendix), which describe the changes over time in the number of HCWs and patients with and without colonization (which precedes infection) (14). If HCWs are viewed as vectors and patients as definitive hosts, the resulting model is similar in structure to those used in the study of vector-borne infections such as malaria (i.e., Ross-Macdonald equations, 14) (Fig. 1). A central concept in infectious disease dynamics is the basic reproductive number, R0, which defines the average number of secondary colonized patients generated by a primary case in a VRE-free ICU. If the basic reproductive number is greater than unity, each colonized patient can generate at least one subsequent case and an epidemic can occur (with probability 1 − 1/R0), and colonization can persist in the absence of infection control. If R0 is less than unity the outbreak cannot be maintained and will stutter to extinction in due course.
Figure 1.
Ross-Macdonald model of indirect patient-HCW-patient VRE transmission in an ICU showing the possible effect of infection control measures. Once patients become colonized they are assumed to remain colonized for the duration of their stay in the ICU.
For vector-borne transmission the basic reproductive number, R0 comprises two components; Rp from patient to HCW and Rh from HCW to patient (i.e., R0 = RpRh, see Appendix). In both instances Rp = patient-HCW contact rate × probability of colonization × length of stay; and Rh = HCW-patient contact rate × probability of contamination × duration of contamination. The contact rates from HCW-patient and patient-HCW will depend on staffing levels and are equal only when one-to-one staffing is possible.** Contamination of HCWs is relatively transient (typically hours), whereas patients remain colonized for their LOS (typically days). Therefore, each colonized patient will contaminate many HCWs (Rp ≫ 1), whereas a contaminated HCW will colonize patients only infrequently (Rh ≪ 1).
Assuming that the number of patients and HCWs remains constant, analysis of the model (see Appendix) shows that the endemic prevalence of VRE colonization in patients, yp, and contamination of HCWs, yh, are, respectively,
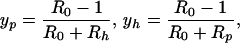 |
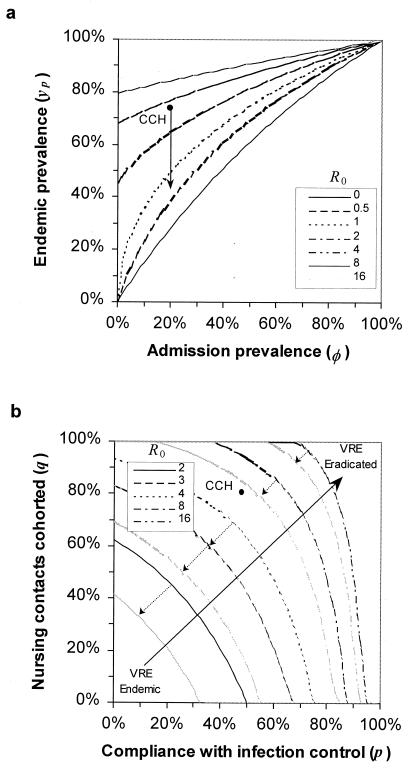
when there are no colonized admissions. Because Rp is much greater than Rh the prevalence of contamination in HCWs will be very low (although the incidence may be high), which provides an explanation of the observational finding that even in endemic settings, culturing the hands of HCWs yields few VRE isolates. Where patients are already colonized on admission to the ICU, the admission prevalence provides a lower bound on the endemic prevalence (because colonization is assumed to be irreversible for the patient LOS). Endemic prevalences above this bound show the impact of nosocomial transmission (Fig. 2a) and can approach 100% when R0 is high.
Figure 2.
(a) Endemic prevalence of VRE colonization as a function of admission prevalence (parameters used: δ = 55%, Rh = 0.1R0). Transmission of VRE always increases the endemic prevalence above the admission prevalence. Arrow indicates the effect of infection control measures on the endemic prevalence of VRE colonization at Cook County Hospital (CCH) ICU. (b) Combined infection control and nurse cohorting measures necessary to eradicate endemic VRE colonization assuming no further VRE-colonized patient admissions. Contours show R(p, q) = 1. Gray lines indicate the effect of a 50% reduction in third-generation cephalosporin usage (parameters used: α = 50% of LOS, α′ = 25%, relative risk ξ = 3). Increased cohorting of nursing staff frequently can be more effective than other precautions, although when R0 is large cohorting only nursing contacts will not be sufficient. Antibiotic restriction facilitates VRE control when transmission is low, but has little effect when VRE is highly endemic.
The Impact of Infection Control
Changing staffing patterns will affect transmission and hence R0. If patients receive a constant number of contacts per day, then increasing the number of HCWs will reduce the per-capita HCW-patient contact rate, and nosocomial transmission will fall (15). Conversely, if staffing resources are limited the HCW-patient contact rate will remain constant, whereby increasing the number of HCWs will increase the number of HCW-patient contacts, leading to an increase in transmission.
Barrier precautions, such as the use of gowns and gloves, and hand washing serve to reduce the likelihood that HCWs will become contaminated with VRE (16–18). If the probability of compliance is P per patient contact, and precautions are 100% effective in removing VRE contamination, then HCWs have a reduced probability of transmitting VRE to their next patient. Where efficacy is less than 100%, compliance should include the measured efficacy accordingly. With control measures in operation the effective reproductive number is defined as R(P) = (1 − P)R0. Nosocomial transmission of VRE can be eradicated provided the effective reproductive number is less than unity. This condition provides a threshold compliance rate for control of transmission; Pc = 1 − 1/R0. For example, if the basic reproductive number is 2 then control is possible with 50% compliance (in the absence of further colonized admissions). If precautions reduce both acquisition and transmission of VRE by HCWs (as might be expected for hand washing before and after patient contact) the overall effect is squared and the threshold for eradication is reduced to Pc = 1 − 1/√R0. When the nosocomial transmission is very intense (high R0) eradication by hand washing measures alone will be much more difficult given reported compliance rates (Fig. 2b).
Because the contact rate appears as a squared quantity (because two contacts are required for patient-patient transmission), changes in mixing patterns can prove highly effective in reducing transmission. When HCW-patient contacts are cohorted (via e.g., patient isolation or one-to-one nursing) reducing HCW-patient mixing reduces the effective number of HCWs who contribute to transmission. If a total of Nh HCWs are subdivided into medical staff (who are not cohorted), and Nn nursing staff (who have a probability q of having cohorted contacts), then the effective number of HCWs contributing to transmission is Nh − qNn, and the effective reproductive number R(q) = R0(1 − qn), where n is the proportion of nursing staff. There is an equivalent cohorting threshold for control of transmission; qc = (1 − 1/R0)/n. Cohorting can provide a highly effective mechanism for reducing transmission. For example, if half of nursing contacts are cohorted (i.e., 50% of nurses return to the same patient for the next contact), then transmission will be reduced by up to half (depending on the nursing ratio). If the HCW-patient ratio is very high (e.g., one-to-one nursing), then the majority of nursing contacts can be cohorted (perhaps as much as 80%) and transmission reduced accordingly. Contact reduction of this nature has been used successfully to control several endemic ICU infections (15, 19–22).
Antibiotic treatment with agents providing VRE with a selective growth/transmission advantage, such as vancomycin or third-generation cephalosporins, has been shown to increase the risk of VRE colonization (9, 22). Antibiotic restriction policies therefore may provide the potential for reducing the selection pressure (and hence probability of patient acquisition). If antibiotic selection pressure gives an increased relative risk, ξ, of acquisition whist the patient is receiving treatment, and patients receive antibiotics for a fraction, α, of their LOS, then the probability per contact of VRE colonization is increased by a factor of 1 + α(ξ − 1). Restricting antibiotics will reduce α and hence R0 accordingly. For example, suppose patients receive third-generation cephalosporins for 50% of their stay and that the relative risk of VRE acquisition is 3 during antibiotic therapy. If third-generation cephalosporin consumption is halved (perhaps by substitution to other compounds without the same selective advantage), then the basic reproductive number (and hence transmission) will fall by 25%.‡‡
Combining two control measures, such as hand washing and cohorting HCWs, is a very effective approach to combating VRE transmission. The effective reproductive number takes the form R(p, q) = (1 − p)(1 − qn)R0, and control of transmission requires that this be less than unity (Fig. 2b). When the endemic prevalence of VRE is low, eradication is possible with modest compliance levels. However as transmission increases, the cohorting of staff into patient-specific groups (contact control) can be very effective even for moderate levels of staff compliance. Reducing the proportion of days patients receive antibiotics makes infection control programs even more effective, although the effect is less noticeable when R0 is large (Fig. 2b).
Observed Patterns and Parameter Estimation
Parameter estimation is based on a detailed study of a 16-bed ICU in Cook County Hospital, Chicago. During the course of a 133-day period of observation in 1995, 189 patients were admitted to the ICU (Table 1) (11). Of the newly admitted patients, 28 already were colonized with VRE (φ = 14.8%, 95% CI 9.7–19.9), and 45 patients acquired VRE after admission. VRE-positive patients had a mean stay in the ICU of 10.9 days (95% CI 0.1–21.7), compared with 7.0 days (95% CI 2.4–11.6) for VRE-negative patients and received antibiotics for 67.7% (95% CI 29.3–100) of their stay (c.f. 47.7%, 95% CI 3.3–92.7). Averaging the time series data gives a mean bed occupancy 87.2% (95% CI 72.9–100) and a mean endemic prevalence of 36.1% (95% CI 2.5–67.7). Infection control measures were implemented, in the form of hand washing and the use of gloves and gowns, with a mean staff compliance of 50.5% (95% CI 31.1–69.7) (for hand washing) and an estimated 80% of all nursing staff-patient contacts were cohorted.
Table 1.
Parameter estimates for VRE transmission in the Cook County Hospital ICU
| Symbol | Interpretation | Value | Units and notes |
|---|---|---|---|
| Study duration | 133 | Days | |
| Np | Number of beds | 16 | |
| Xp | Uncolonized patients | 116 | |
| Yp | Colonized patients | 73 | |
| Λ | Admission rate | 1.36 | Patients/day |
| Dp | LOS (uncolonized) | 9.8 | Days |
| δ | Increase in LOS | 55.1% | |
| Nh | Number of HCWs | 10 | Average for 24 hr |
| n | Nursing HCWs | 79.4% | Average for 24 hr |
| Dh | Duration of contamination* | 1/24 | Days |
| a | Per-capita contact rate | 1.38 | /HCW/patient/day |
| aNh | Patient-HCW contact rate | 13.8 | Contacts/patient/day |
| aNp | HCW-patient contact rate | 22.1 | Contacts/HCW/day |
| bp | Colonization probability* | 6% | /Contact |
| bp | Contamination probability* | 40% | /Contact |
| R(p, q) | Effective reproductive number | 0.69 | |
| p | Compliance with hand washing/barrier precautions | 50.1% | |
| q | Nursing contact cohort probability* | 80% | |
| R0 | Basic reproductive number | 3.81 | |
| φ | Admission colonization prevalence | 14.9% | |
| yp | Endemic colonization prevalence | 36.1% | Model = 36.1% |
Estimated value.
Although patients are assumed to remain colonized for the duration of their stay, HCWs become only transiently contaminated. Colonized patients therefore may transmit VRE to many HCWs, but contaminated HCWs will transmit VRE to patients infrequently. This finding implies that Rh is much greater than Rp, and the effective reproductive number (which will be measured in practice) is approximately (see Appendix)
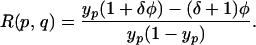 |
δ is the percentage increase in LOS for colonized patients and yp the observed prevalence (which depend on hand washing and cohorting). This expression provides a quantitative measure of the transmission levels within an endemic setting. For example, at Cook County Hospital where yp = 36.1%, φ = 14.9%, and δ = 55.1%, this relationship gives an effective reproductive number R(p, q) = 0.69. Because the effective reproductive number is below unity, transmission alone is unable to sustain VRE in the ICU, implying that colonized patient admissions from other parts of the hospital are stabilizing VRE persistence in the ICU.
To estimate the basic reproductive number, and hence evaluate the impact of infection control we calculate R0 = R(p, q)/(1 − p)(1 − qn). For the study at Cook County Hospital, with p = 50.5% and qn = 63.4%, the estimated basic reproductive number is R0 ≈ 3.81. This finding implies that, in the absence of infection control measures, a single patient admitted with VRE would have given rise to 3–4 additional cases during their stay in the ICU. The resulting endemic prevalence would have been 79.3% (including colonized admissions) or 73.7% (excluding colonized admissions). Therefore, in the Cook County Hospital setting, the implementation of infection control measures over the duration of the study have reduced the prevalence of VRE from a potential 79.3% to an observed 36.1%. The reduction in transmission is considerable, with an 81.8% reduction in the reproductive number R0. Even with these considerable reductions, new VRE-positive admissions continue to stabilize VRE transmission in the ICU in spite of infection control measures and staff cohorting.
Because the numbers of patients and staff are small (typically less than 30), stochastic effects will dominate. Monte Carlo simulations of the model are used to solve the full model (rather than numerical solutions of the simplified continuous model with constant patient number) (23). Stochastic simulation assume that the seven rates described by the continuous model are the means of Poisson distributions, and each numerical simulation generates the times of any of the seven events described (Fig. 1). Comparison of model predictions with observation requires multiple simulations, with estimation of mean and 95% confidence interval at each time point. All programs are written in fortran and are available on request.
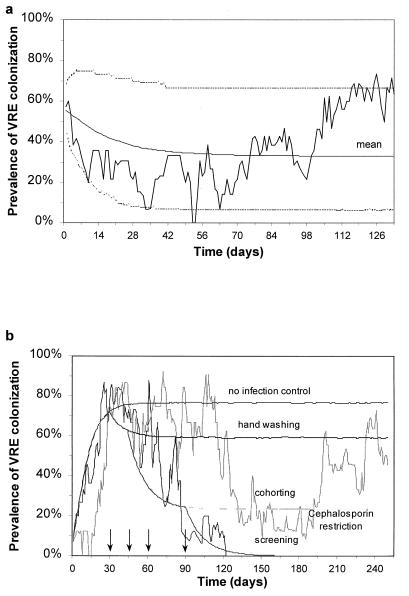
Fig. 3 shows a comparison between the predictions of the model and the observed pattern and reveals good agreement in both qualitative and quantitative terms. The model correctly estimates the number of patients admitted (186.1, 95% CI 166.1–206.1), bed occupancy (81.1%, 95% CI 54.9–100) and endemic VRE prevalence (yp = 36.1%, 95% CI 7.1–65.1). Furthermore, the model correctly reproduces the short-term temporal correlations observed by time series analysis of the auto-correlation function (data not shown).
Figure 3.
(a) Time series data showing prevalence of VRE colonization in a 16-bed ICU in Cook County General Hospital, Chicago, showing observed prevalence, with mean and 95% confidence intervals generated by 105 stochastic realizations of the model using parameters shown in Table 1 (dashed lines). LOSs are highly variable, and a mean value is calculated by using the relationship 1/μ = occupancy × beds × study duration/number of patients in study. (b) Two simulated VRE outbreaks in an ICU showing both eradication and endemic stability using the same infection control measures (all parameters are as before). A single VRE-positive patient is admitted on the first day of the outbreak. After 30 days strict infection control measures are implemented (P = 50%). After 45 days a program of cohorting nursing staff with individual patients begins (qn = 64%). After 60 days antibiotic restriction is used to reduce consumption by 50% (α′ = 25%, ξ = 3). However, this intervention proves ineffectual because nosocomial transmission already has been contained. Finally, after 90 days all further VRE-positive admissions are isolated. Other curves indicate the mean cumulative effects of each successive policy for 105 stochastic simulations.
Discussion
In many hospital settings in Europe and North America the emergence of VRE as a nosocomial pathogen presents a major threat to patients receiving intensive care. The recognition that transmission in ICU settings is largely determined by patient-HCW-patient contacts provides the template for quantitative analysis of transmission dynamics and the impact of various control interventions. By the measurement of a few basic epidemiological parameters via intensive microbiological surveillance in a defined setting, and applying a simple mathematical framework, it is possible to calculate with precision the level of a specified infection control procedure, and the associated compliance rate, required to eliminate VRE.
Compliance rates for basic infection control measures, such as hand washing, have been reported to vary from 20% to 40%, but may be higher for well-motivated nursing and other medical staff (16–18). By using transmission data for VRE in an endemic setting, we estimate that the basic or case reproductive number R0, which provides a quantitative measure of transmission, lies in the range 3–4. Implementing infection control measures with reported compliance levels could result in an effective reproductive number of less than unity. Because the threshold compliance necessary for control is in excess of 50%, these observations suggest that in most hospitals much more rigorous training and more effective monitoring of compliance is required. Cohorting nursing staff with individual patients is also an effective method of reducing R0. We introduce a cohorting measure, the proportion of nursing staff cohorted to one patient (or equivalently the probability that a patient receives a repeat contact from the same nurse). Cohorting reduces the effective numbers of HCWs acting as vectors, although if R0 is large cohorting of nurses alone would be insufficient to control transmission. To date there have been few measures of this important epidemiological parameter, although our preliminary studies suggest that cohorting may be as high as 80% in some settings and is likely to frequently exceed hand-washing compliance.
The intensive use of antibiotics provides VRE with a selective growth advantage and has been associated with a high prevalence of VRE (9). Antibiotic reduction policies may reduce this selective advantage and in doing so, the probability that a patient will become colonized during contact with a contaminated HCW. Because reductions in antibiotic consumption (as measured by patient days of treatment) give linear reductions in R0, the endemic colonization prevalence will have greatest impact when R0 is low. The beneficial effects of infection control measures may be canceled out by inappropriate antibiotic use, particularly during a unit’s first experience of VRE. Optimizing antibiotic use policies must be based on a careful assessment of prevailing resistance levels to other drugs and emerging resistance concerns (e.g., vancomycin-resistant staphylococci).
Our numerical results show that the rapid turnover of patients, coupled with the very short transient HCW contamination, contribute to the inherent stability of the transmission process within ICUs. The model correctly reproduces observed transmission dynamics of VRE within an ICU. However heterogeneities in severity of illness, LOS, and treatment may influence fluctuations in both prevalence and occupancy to a greater extent than our model suggests. The model framework can be modified in a straightforward manner to take account of other complications, such as heterogeneity in compliance (either over time, or between staff) and the contamination of the ICU environment (9). For simplicity we have not included the environment in our analysis because our data support the view that the environment plays a minimal role in some settings. Where contamination is extensive, or “common sources” are contaminated, environmental sources could provide a background colonization rate over and above that produced by patient-HCW-patient transmission.
Finally, we return to the key message arising from the analyses. Given the threat posed by VRE in hospitals worldwide, much is to be gained by a quantitative understanding of the transmission dynamics of the pathogen. If sensibly used in conjunction with quantitative microbiological surveillance, a robust mathematical framework provides a precise template for assessing the degree of control required for the eradication of VRE, and indeed other pathogens, in intensive care settings.
Acknowledgments
D.J.A. and R.M.A. thank the Wellcome Trust for grant support, Richard Bax for helpful discussions, and SmithKline Beecham for travel assistance. M.J.M.B. thanks Merck Sharpe & Dohme and the Infectious Diseases Society of the Netherlands and Flanders for grant support.
ABBREVIATIONS
- VRE
vancomycin-resistant enterococci
- ICU
intensive-care unit
- HCW
health care worker
- LOS
length of stay
- CI
confidence interval
Methods
The model of patient-HCW-patient VRE acquisition (i.e., cross-acquisition) describes the temporal dynamics of Np patients and Nh HCWs, consisting of four ordinary differential equations for the four groups of interest (Fig. 1); Uncolonized patients (Xp), colonized patients (Yp), VRE-free HCWs (Xh) and contaminated HCWs (Yh);
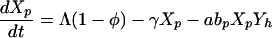 |
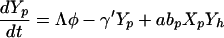 |
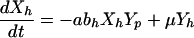 |
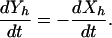 |
Patients are admitted to the ICU at a rate Λ per day and some fraction, φ are already colonized with VRE. They have an average LOS of 1/γ days (γ is the uncolonized discharge rate) if they remain uncolonized or Dp = 1/γ′ otherwise. HCWs are assumed to mix homogeneously with patients at a per-capita rate a/patient per HCW per day, with HCWs becoming contaminated with probability bh per contact if the patient is colonized with VRE (aNp is analogous to the vector biting rate in the Ross-Macdonald model). Contaminated HCWs can transmit VRE for an average duration Dh = 1/μ (typically hours), and patients have a probability bp of becoming colonized during contact with a contaminated HCW. Once a patient becomes colonized, they are assumed to remain so for the remainder of their stay.
If the number of beds remains fixed (reflecting the considerable resources needed to maintain them), then the admission rate equals the discharge rate (i.e., Λ = γXp + γ′Yp). Therefore, Xp + Yp = Np and the model simplifies such that the prevalence of patient colonization (yp = Yp/Np) and HCW contamination (yh = Yh/Nh) are determined by
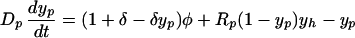 |
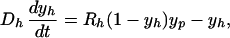 |
where δ = (γ − γ′)/γ′, is the percentage increase in LOS for colonized patients, Rp = bpaNhDp is the HCW-patient reproductive number, and Rh = bhaNpDh is the patient-HCW reproductive number (see text). The basic reproductive number, R0, is the product RhRp, reflecting the patient-HCW-patient nature of nosocomial transmission, i.e.,
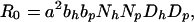 |
(notice that a appears as a squared quantity). A heuristic derivation is as follows. A colonized patient will have aNh contacts with HCWs per day, and a total of aNhDp contacts during their stay. If the probability of contaminating a HCW is bh per contact, there will be an average of bhaNhDp HCW contaminations. Each contaminated HCW subsequently will come into contact with aNpDh patients whilst contaminated, and transmit VRE with a probability of bp per contact. Therefore a contaminated HCW will on average colonize bpaNpDh patients giving a2bhbpNhNpDhDp secondary cases. The endemic prevalences can be determined when dyp/dt = dyh/dt = 0, which after substitution gives the following quadratic equation
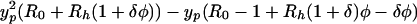 |
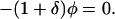 |
VRE is always endemic provided φ > 0, because there is one positive solution (and continual reintroduction of colonized patients). If Rh is negligible in comparison with R0 we obtain
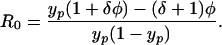 |
Footnotes
e.g., if 100 contacts/day are observed in a 10-bed ICU with five HCWs, the per-capita contact rate is 100/(10 × 5) = 2 contacts/patient per HCW per day. The patient-HCW contact rate is 5 × 2 = 10 contacts/patient per day, while the HCW-patient contact rate is 10 × 2 = 20 contacts/HCW per day.
Factor = (α − α′)(ξ − 1)/(1 + α(ξ − 1)) = (0.5 − 0.25)(2)/(1 + 0.5(2)) = 0.25. Note that the maximum possible reduction in transmission will be α(ξ − 1)/(1 + α(ξ − 1)) or 50% when antibiotic selection pressure ceases completely.
References
- 1.Centre for Disease Control. Morbid Mortal Wkly Rep. 1995;44:1–13. [Google Scholar]
- 2.Public Health Laboratory Service. CDR Weekly. 1996;6:1. [Google Scholar]
- 3.Palmer S M, Rybak M J. Pharmacotherapy. 1996;16:819–829. [PubMed] [Google Scholar]
- 4.Husani R, Raad I. Curr Opin Intensive Care. 1997;10:431–434. [Google Scholar]
- 5.Chow J W, Kuritza A, Shlaes D M, Green M, Sahm D F, Servos M J. J Clin Microbiol. 1993;31:1609–1611. doi: 10.1128/jcm.31.6.1609-1611.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Strausbaugh L J, Crossley K B, Nurse B A, Thrupp L D. Infect Control Hosp Epidemiol. 1996;17:129–140. doi: 10.1086/647257. [DOI] [PubMed] [Google Scholar]
- 7.Jordens J Z, Bates J, Griffiths D T. J Antimicrob Chemother. 1994;34:515–528. doi: 10.1093/jac/34.4.515. [DOI] [PubMed] [Google Scholar]
- 8.Boyce J M, Mermel L A, Zervos M J, Rice L B, Potter-Bynoe G, Giorgio C, Medeiros A A. Infect Control Hosp Epidemiol. 1995;16:634–637. doi: 10.1086/647028. [DOI] [PubMed] [Google Scholar]
- 9.Bonten M J, Hayden M K, Nathan C, Van Voorhis J, Matushek M, Slaughter S, Rice T, Weinstein R A. Lancet. 1996;348:1615–1619. doi: 10.1016/S0140-6736(96)02331-8. [DOI] [PubMed] [Google Scholar]
- 10.Morris J G, Jr, Shay D K, Hebden J N, McCarter R J, Jr, Perdue B E, Jarvis W, Johnson J A, Dowling T C, Polioh L B, Schwalbe R S. Ann Internal Med. 1995;123:250–259. doi: 10.7326/0003-4819-123-4-199508150-00002. [DOI] [PubMed] [Google Scholar]
- 11.Slaughter S, Hayden M K, Nathan C, Hu T C, Rice T, Van-Voortis J, Matushek M, Franklin C, Weinstein R A. Ann Internal Med. 1996;125:448–456. doi: 10.7326/0003-4819-125-6-199609150-00004. [DOI] [PubMed] [Google Scholar]
- 12.Noskin G A, Stosor V, Cooper I, Peterson L R. Infect Control Hosp Epidemiol. 1995;16:577–581. doi: 10.1086/647011. [DOI] [PubMed] [Google Scholar]
- 13.Sebille V, Chevret S, Valleron A J. Infect Control Hosp Epidemiol. 1997;18:84–92. doi: 10.1086/647560. [DOI] [PubMed] [Google Scholar]
- 14.Anderson R M, May R M. Infectious Diseases of Humans: Dynamics and Control. Oxford Univ. Press Oxford; 1991. [Google Scholar]
- 15.Haley R W, Cushion N B, Tenover F C, Bannerman T L, Dryer D, Ross J, Sanchez P J, Siegel J D. J Infect Dis. 1995;171:614–624. doi: 10.1093/infdis/171.3.614. [DOI] [PubMed] [Google Scholar]
- 16.Albert R K, Condie F. N Engl J Med. 1981;304:1465–1468. doi: 10.1056/NEJM198106113042404. [DOI] [PubMed] [Google Scholar]
- 17.Simmons B, Bryant J, Neiman K, Spencer L, Arheart K. Infect Control Hosp Epidemiol. 1990;11:589–594. doi: 10.1086/646100. [DOI] [PubMed] [Google Scholar]
- 18.Doebbelling B N, Stanley G L, Sheetz C T, Pfaller M A, Houston A K, Annis L, Li N, Wenzel R P. N Engl J Med. 1992;327:88–93. doi: 10.1056/NEJM199207093270205. [DOI] [PubMed] [Google Scholar]
- 19.Knight P, Cassady G. J Perinatol. 1990;10:357–360. [PubMed] [Google Scholar]
- 20.Reish O, Ashkenazi S, Naor N, Samra Z, Merlob P. J Hosp Infect. 1993;25:287–291. doi: 10.1016/0195-6701(93)90115-g. [DOI] [PubMed] [Google Scholar]
- 21.Ruuskanen, O. (1995) J. Hosp. Infect. 30, Suppl., 494–497. [DOI] [PubMed]
- 22.Karanfil L V, Murphy M, Josephson A, Gaynes R, Mandel L, Hill B C, Swenson J M. Infect Control Hosp Epidemiol. 1992;13:196–200. doi: 10.1086/646509. [DOI] [PubMed] [Google Scholar]
- 23.Renshaw E. Modeling Biological Populations in Space and Time. Cambridge, U.K.: Cambridge Univ. Press; 1991. [Google Scholar]