A D-Optimal designed population pharmacokinetic study of oral itraconazole in adult cystic fibrosis patients

Abstract

What is already known about this subject

• Itraconazole is a triazole antifungal used in the treatment of allergic bronchopulmonary aspergillosis in patients with cystic fibrosis (CF).

• The pharmacokinetic (PK) properties of this drug and its active metabolite have been described before, mostly in healthy volunteers.

• However, only sparse information from case reports were available of the PK properties of this drug in CF patients at the start of our study.

What this study adds

• This study reports for the first time the population pharmacokinetic properties of itraconazole and a known active metabolite, hydroxy-itraconazole in adult patients with CF.

• As a result, this study offers new dosing approaches and their pharmacoeconomic impact as well as a PK model for therapeutic drug monitoring of this drug in this patient group.

• Furthermore, it is an example of a successful d-optimal design application in a clinical setting.

Aim

The primary objective of the study was to estimate the population pharmacokinetic parameters for itraconazole and hydroxy-itraconazole, in particular, the relative oral bioavailability of the capsule compared with solution in adult cystic fibrosis patients, in order to develop new dosing guidelines. A secondary objective was to evaluate the performance of a population optimal design.

Methods

The blood sampling times for the population study were optimized previously using POPT v.2.0. The design was based on the administration of solution and capsules to 30 patients in a cross-over study. Prior information suggested that itraconazole is generally well described by a two-compartment disposition model with either linear or saturable elimination. The pharmacokinetics of itraconazole and the metabolite were modelled simultaneously using NONMEM. Dosing schedules were simulated to assess their ability to achieve a trough target concentration of 0.5 mg ml⁻¹.

Results

Out of 241 blood samples, 94% were taken within the defined optimal sampling windows. A two-compartment model with first order absorption and elimination best described itraconazole kinetics, with first order metabolism to the hydroxy-metabolite. For itraconazole the absorption rate constants (between-subject variability) for capsule and solution were 0.0315 h⁻¹ (91.9%) and 0.125 h⁻¹ (106.3%), respectively, and the relative bioavailability of the capsule was 0.82 (62.3%) (confidence interval 0.36, 1.97), compared with the solution. There was no evidence of nonlinearity. Simulations from the final model showed that a dosing schedule of 500 mg twice daily for both formulations provided the highest chance of target success.

Conclusion

The optimal design performed well and the pharmacokinetics of itraconazole and hydroxy-itraconazole were described adequately by the model. The relative bioavailability for itraconazole capsules was 82% compared with the solution.

Introduction

Cystic fibrosis (CF) is the most common lethal autosomal recessive disorder in White subjects caused by a defect which leads to a variety of abnormalities in the CF transmembrane conductance regulator gene. Morbidity and mortality in CF patients are most commonly caused by progressive respiratory diseases (>90% of deaths) [1]. These are also the primary factors leading to frequent hospitalization for patients with CF and a primary cause of mortality [1, 2].

Allergic bronchopulmonary aspergillosis (ABPA) is a complication of CF, occurring in approximately 10% of patients mostly after the age of 6 years, but is probably still underdiagnosed [3, 4]. It presents as a hypersensitive reaction to Aspergillus fumigatus (AF) [5]. ABPA has been reported to have a worsening effect on lung function and causes a more rapid decline in respiratory function [6].

Oral corticosteroids are the main anti-inflammatory therapy for ABPA in patients with asthma and those with CF. Itraconazole (Sporonax®, Janssen-Cilag, Sydney, NSW, Australia) is a broad-spectrum, oral antifungal agent with activity against many fungal pathogens, including Aspergillus species, and has been used to reduce steroid requirements by decreasing AF cultures in the sputum [5, 7, 8]. At present, little is known about the absorption and disposition of itraconazole in CF patients, although it is known that plasma drug concentrations are highly variable in patients with CF [9] and this may affect their response to the drug.

Therapeutic drug monitoring recommendations have not been established in CF patients with ABPA. However, in neutropenic patients it has been shown in several studies that the antifungal effect can be enhanced by ensuring that itraconazole plasma trough concentrations at steady state (C_min,ss) exceed 0.5 mg l⁻¹ [10–13]. Although there is no defined upper limit to the therapeutic range, some studies have suggested a decrease in dose when trough concentrations exceed 2 mg l⁻¹ [13]. This target range has been carried over for the plasma monitoring of itraconazole in CF patients.

Itraconazole is a highly lipophilic, poorly water soluble drug [14], and widely distributed in the body with a reported volume of distribution of 11 l kg⁻¹ [14]. It is metabolized to a number of compounds, of which at least one (hydroxy-itraconazole) has antifungal activity against a similar variety of species compared with the parent drug [15].

Several studies have shown that the absorption from capsules requires low gastric pH. Administration of capsules with food or with an acidic beverage (e.g. cola) is reported to be an effective way to improve absorption [14, 16, 17]. In contrast, absorption from the oral solution is less influenced by gastric acidity because it is solubilized in a cyclodextrin complex [18]. For the solution, the best condition for absorption is reported to be in the fasting state, which leads to more rapid absorption and to higher peak concentrations [19–21]. The oral bioavailability of itraconazole solution taken under these conditions by healthy volunteers can be up to 60% higher than that of the capsules taken with food [18, 20, 22]. The elimination of itraconazole has been described by some studies as being saturable [17, 23] and by others as linear [24].

The use of d-optimal designs has been suggested for population approach studies to provide more precise population parameter estimates [25], but also to allow a more economical use of resources (e.g. fewer patients, fewer samples) to provide these results. To facilitate this, samples are taken at times which provide as much information as possible. The advantage of optimal population designs also lies in the ability to account for borrowing strength between individuals and to provide designs that allow good estimation of the population parameters, while for any individual the design might be too sparse to allow the full profile to be characterized. d-optimal designs have been developed previously and have made use of optimal sampling time windows to provide more flexibility in clinical settings [26–29].

The overall aim of this study was to estimate in CF patients the population pharmacokinetic properties of itraconazole and its active metabolite hydroxy-itraconazole after administration of both capsule and solution, primarily to estimate the relative bioavailability comparing capsule and solution. The pharmacokinetic information obtained from the study was intended to improve dosing regimens in these patients. In addition, we sought to assess the performance of the d-optimal design developed for this study.

Methods

Optimal design

The principles of optimal design has been described previously [29] and are only briefly recounted here for clarity. The design was performed using the POPT software (version 2, http://www.uq.edu.au/pharmacy/sduffull/POPT.htm), written in high performance language for MATLAB software, specifically for optimizing designs for nonlinear mixed effects models, such as those which arise in population pharmacokinetic and/or pharmacodynamic settings.

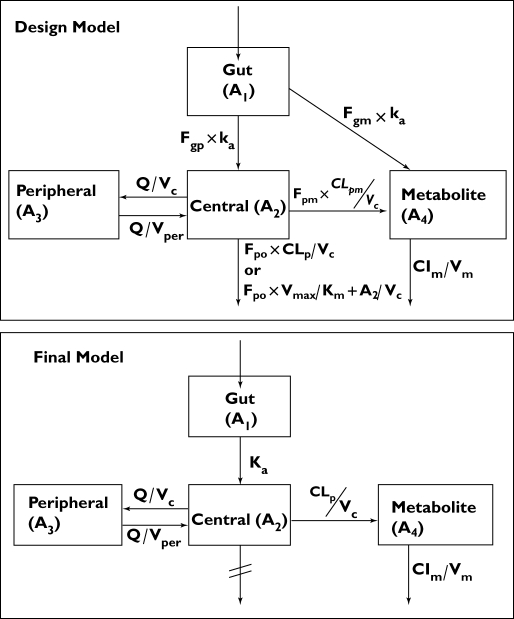
Prior information regarding itraconazole and its active metabolite hydroxy-itraconazole were obtained from several sources [17, 24, 30, 31] and provided the basis of the structural model for the design: a two-compartment (2-cpt) model for the parent with a first-order formation rate to a one-compartment (1-cpt) model for the metabolite (Figure 1). The kinetics of absorption for the two oral forms of itraconazole were assumed to be linear, but different for each formulation as described in the literature [30, 32]. Because saturable elimination of itraconazole has been described in some studies [17, 23], but not in others [24], we developed two competing models with either linear or nonlinear elimination from the central compartment for each of the solution and capsule formulations, providing a total of four models.

Figure 1.

Compartmental model for the design development and the final model describing the pharmacokinetics of itraconazole and hydroxy-itraconazole. g, Gut; p, parent; m, metabolite; o, out; c, central; per, peripheral

The d-optimality product criterion used in this study design is provided by:

(1)

where M_F is the Fisher Information Matrix (FIM), ψ^k represents the vector of all population parameters, p_k is the number of parameters in the kth model and Ξ is the population design. The product d-optimal design provides a design that optimizes over both competing models simultaneously. The design therefore allows for two absorption models and uncertainty in the disposition model. Optimization of this criterion would yield the best sampling times for estimation of the parameters over all models simultaneously. Finally, sampling windows were estimated around each of the sampling times in order to ensure that the design was clinically feasible. A sampling window represents a region of planned suboptimality where sampling times taken from any point within the window ensure that the loss of efficiency of the design is minimal. The estimations of these windows was done posthoc by a simulation of 1000 random designs with sets of sampling times, which were distributed uniformly as windows around the optimal times. Afterwards, the designs using optimal sampling windows were assesed in terms of efficiency and all times within these chosen windows had an efficiency >85% compared with the optimal design times. Further details of this joint method can be found in a recent paper [29]. Patients were divided randomly into the three groups of sampling times. The optimal sampling times and windows for three groups of 10 patients with different sampling times are summarized in Table 1.

Table 1.

Optimal sampling time and windows after administration of itraconazole capsules and solution for three groups with 10 patients per group

	Capsule		Solution
Group	Optimal sampling time postdose (h.min)	Window (h.min)	Optimal sampling time postdose (h.min)	Window (h.min)
1	1.14	0.06–3.00	0.17	0.06–1.00
	8.56	7.00–10.00	3.55	3.00–3.30
	25.49	24.00–27.00	3.56	3.30–4.00
	51.45	50.00–53.00	3.56	4.00–4.30
2	6.13	5.00–8.00	0.18	0.06–1.00
	9.50	8.00–11.00	4.06	3.00–4.00
	29.29	28.00–29.30	4.06	4.00–5.00
	29.29	29.30–31.00	72.00	69.00–72.00
3	8.08	7.00–10.00	0.17	0.06–1.00
	28.00	26.30–29.30	4.22	3.00–6.00
	72.00	69.00–70.30	27.08	26.00–29.00
	72.00	70.30–72.00	72.00	69.00–72.00

Patients and sampling

The study was designed to recruit 30 adult patients with CF, who were given two single doses of 200 mg itraconazole on two separate occasions (72 h apart), once as two 100-mg Sporanox® capsules and then 20 ml of a 10 mg ml⁻¹ Sporanox® oral solution. These patients were not taking itraconazole for clinical indications and were in hospital for management of a chest exacerbation. Patients were not eligible for the study if they had impaired hepatic function or were pregnant at the time of recruitment. Other medications and treatment were not changed for study reasons. A diagnosis of ABPA was not part of the inclusion or exclusion criteria. Patients with pancreatic insufficiency were instructed to take pancreatic enzymes with their meals as supplementation, in particular, with the meals taken on the study days. Patients with gastroesophageal reflux disease, who were treated with antireflux medications (such as proton pump inhibitors, which can alter gastric pH), were asked to take these medications 2 h after the itraconazole dose on the study days (as per Sporonax® product information [30, 32]) to ensure best absorption of itraconazole.

Eight blood samples (0.5 ml each) per patient were taken at a time within each optimal sampling window by fingerprick. Four of these samples were drawn after a single dose of 200 mg itraconazole capsules, and then four samples were drawn after a single dose of 200 mg itraconazole oral solution. Additional blood samples were approved by the ethics committee if patients volunteered and they were taken at random times. Each participating patient was given a timetable with blood sampling times of their randomized group after their consent. The ‘quality of life’ for patients with CF is very important and often these patients continue normal life (e.g. work, social activities) during their frequent hospital visits. Therefore, it was necessary to confirm sampling times with the patient and times were individualized appropriately to ensure compliance with the optimal design. The exact times of blood sampling were recorded for the data analysis.

Ethics

The study was performed in accordance with the Declaration of Helsinki and its amendments. Before the study began, the protocols were approved by the Ethics Committees of The Prince Charles Hospital and The University of Queensland, Brisbane, Australia. Written informed consent was obtained from all patients before their participation.

Drug analysis

Plasma concentrations of itraconazole and hydroxy-itraconazole were assayed by the study investigators using a simple, selective and validated high-performance liquid chromatography (HPLC) method previously developed by two of us [33]. Briefly, 100 µl of plasma samples was prepared for analysis with a protein-precipitation method. Itraconazole and hydroxy-itraconazole were detected fluorometrically after reverse-phase separation. The limit of quantification (LOQ) of the assay was 0.075 mg l⁻¹ and the limit of detection (LOD) was 0.04 mg l⁻¹. Intraday and interday imprecision (CV%) were 4.8–17.3% and 6.3–16.6% for itraconazole and 4.6–17.9% and 7.02–18.4% for hydroxy-itraconazole, respectively. Inaccuracy was −7.1 to −14.7% for itraconazole and −0.1 to −9.7% for hydroxy-itraconazole.

Data analysis

Modelling

Modelling was performed using the first order conditional estimation (FOCE) method with interaction in NONMEM, version 5.1 level 1 (GloboMax LLC, Hanover, MD, USA) in conjunction with a G77 FORTRAN compiler and Wings for NONMEM (http://wfn.sourceforge.net). Compartmental models with first-order or zero-order input and linear and/or nonlinear disposition were evaluated. The model was parameterized so that the apparent clearance (CL/F) and the apparent volume of distribution (V/F) for both parent drug and metabolite were estimated simultaneously. The fraction (f_m) of itraconazole metabolized to hydroxy-itraconazole has not been reported in the literature and was therefore fixed to 1. The apparent clearance and volume for hydroxy-itraconazole were estimated as CL_m/(F × f_m) and V_m/(F × f_m), respectively. The relative bioavailability (F_rel) was determined by fixing F_rel to 1 for administration of the oral solution and then estimating F_rel for the capsule. The between-subject variability (BSV) was modelled assuming a log normal distribution. Between-occasion variability was not considered. The residual unexplained variability (RUV) for itraconazole and hydroxy-itraconazole was evaluated as either an exponential, additive or combined exponential and additive model, with and without an interaction between parent and metabolite RUV values. For the model-building process all plasma samples with a concentration below the LOD were assigned to values which were half the value of LOD (0.5 × LOD = 0.02 mg l⁻¹).

To explain between-subject variability, possible relationships between pharmacokinetic parameters and patient characteristics such as total body weight, lean body weight [34], age and effect of coadministration of proton pump inhibitors and/or H2-blockers were investigated. After a visual assessment of the covariate parameter relationship, each covariate was introduced into the structural model one at a time and the pattern of residuals and changes in the BSV, RUV and the objective function value (OFV) were examined. Nested models were compared using the likelihood ratio test in which the change in OFV approximates the χ² distribution (χ²_1,0.01 > 6.6).

Model evaluation

The modelling diagnostics included an assessment of the ‘goodness-of-fit’ plots, precision of the parameter estimates, change in the OFV and a degenerate visual predictive check (VPC) on the final model using an ActivePerl (Version 5.8.4) script. The VPC involved 1500 Monte Carlo simulations for parent drug and metabolite from the final population model parameters. The simulated concentrations were generated for a 200-mg dose either from capsule or oral solution over 72 h. The 5th, 50th (population median response) and 95th percentiles were plotted against time postdose and the patients' data were superimposed. The stability and robustness of the final model were assessed via an internal evaluation method which involved bootstrapping with replacement to assess how accurately the value of the population parameters of a sampled distribution can be estimated in the wider population and to assess stability and predictive performance of the pharmacokinetic model [35, 36].

Missing data

The final model was evaluated with respect to the handling of missing data in which concentrations were below the LOD. Four methods were assessed, corresponding to methods M1, M5, M6 and M4 from Beal's paper in 2001 [37]. The methods were: M1, where all values below the LOD (BLOD) were discarded from the dataset; M5, where all BLOD values were assigned to half of the LOD; M6, where the closest missing BLOD value was assigned to half of the LOD and all previous (if during absorption) or subsequent (if during elimination) missing samples were deleted; and M4, where the contribution of the expectation of each missing concentration to the likelihood is estimated. The last method was modelled in NONMEM using numerical integration with FOCE and the −2 Log-Likelihood function. The parameter estimates of these four models were compared as well as the standard errors of the estimates and the residual error.

Simulation

Itraconazole and hydroxy-itraconazole plasma concentrations arising from several alternative dosage regimens were obtained by Monte Carlo simulation (n = 2000) and compared with the reported C_min,ss target range for antifungal therapy of 0.5–2 mg l⁻¹ [13] once daily, and twice daily dosing of 200 mg (representing the current standard dosing strategy), 400 mg once per day and 300–1000 mg twice daily over 7 days (day 1 being the day of the first dose, and day 7 representing steady state). A success under this range is described as an itraconazole concentration that falls within the described range of 0.5–2 mg l⁻¹. For all scenarios, simulations were also performed for the metabolite simultaneously with the parent drug. The target recommendation for a combined ‘active’ concentration of itraconazole and the active metabolite hydroxy-itraconazole currently provides only a lower limit of a minimum steady-state concentration of 1–1.5 mg l⁻¹ [38] (which is three times the itraconazole lower limit). Because there is no recommendation on a maximum steady-state ‘active’ concentration, the recommended C_min,ss range of 0.5–2 mg l⁻¹ for itraconazole was then extrapolated to a range of 1.5–6 mg l⁻¹ (6 is three times the itraconazole upper boundary) for the combined ‘active’ level range. The target success was then also assessed for this range.

Results

Study population and concentration data

Thirty patients (18 male) were recruited for the study over a period of 18 months and provided 241 plasma samples. Patient characteristics are provided in Table 2.

Table 2.

Characteristics of study patients [median (range)] and plasma samples.

Demographic data
Number of patients	30
Sex	18 male, 12 female
Age (years)	25 (16–61)
Weight (kg)	57 (46–86)
Height (cm)	169 (149–186)
Lean body weight (kg)*	46 (36–64)
Number of comedications per patient	13 (7–21)
Pharmacokinetic data
Number of total blood samples	241
Number of blood samples per patient	8
Itraconazole concentrations (mg l−1), range	0.04–0.77
Number of itraconazole concentrations	111 (46.0%)
below LOD (LOD = 0.040 mg l−1)
Capsules	81 (33.6%)
Solution	30 (12.4%)
Hydroxy-itraconazole concentrations (mg l−1), range	0.04–0.86
Number of hydroxy-itraconazole concentrations below LOD (LOD = 0.040 mg l−1)	67 (27.8%)
Capsules	50 (20.8%)
Solution	17 (7.0%)

^*Calculated as per Cheymol [34]. LOD, Limit of detection.

The prospective application of an optimal design was found to be successful. Due to the sampling windows, most of the samples could be collected within the daily hospital routine, but still at times that were near optimal for estimating the population pharmacokinetic parameters. Thirty-one percent of blood samples were taken at the optimal time (±5 min) and 94% of all samples were taken within the defined sampling windows. Six percent of blood samples were taken outside the sampling window.

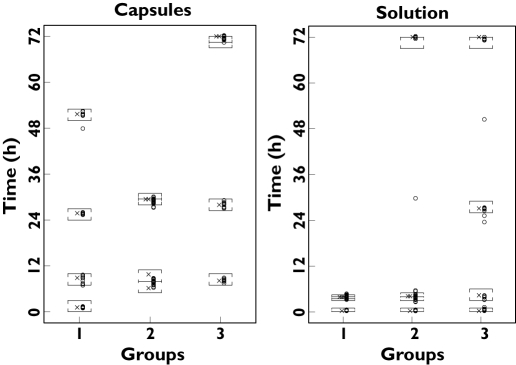
Only one additional sample was obtained from one patient who had the blood sample taken during the study period, which had been requested by the doctor for another test and who agreed to use it as an extra sample for this study. In less than 10% of cases the blood sampling times requested by the physicians matched exactly the blood sampling windows for this study. In these cases the blood samples for the study were obtained together with those requested by the physicians, to minimize the discomfort of the patient from extra venipuncture. As shown in Figure 2, most samples were taken close to the optimal times and within the optimal windows.

Figure 2.

The two panels show the sampling time windows ([]) and the exact optimal sampling times (✗) as per design for each group and the times of the samples taken from the patients (○) over 72 h after capsule or solution administration of itraconazole

None of the patients withdrew from the study. One patient noticed slight nausea for a short period after administration of the oral solution, but continued in the study without further problems. All necessary clinical data from each patient (e.g. weight, current medication, etc.) were collected from the medical records and during interviews. Three patients had previously been prescribed itraconazole for the treatment of ABPA; however, the elapsed time between the last prescribed dose of itraconazole and recruitment to this study in all three cases was >6 months.

From the measured plasma samples, 46% of the itraconazole and 28% of the hydroxy-itraconazole concentrations were below the LOD (0.04 mg l⁻¹). Three-quarters of these samples below the LOD were observed after the administration of the capsules and one-quarter after the solution.

Population pharmacokinetics

Several structural models were considered for describing the time course of itraconazole and hydroxy-metabolite concentrations simultaneously. The final model selected used general linear processes to describe the distribution of the drug between compartments. A 2-cpt model for itraconazole with first-order absorption from the gut described the itraconazole population data best (ΔOFV −152, compared with a 1-cpt model). The conversion to hydroxy-itraconazole was best described by a first-order process and first-order elimination. The final model was therefore comparable to only one of the potential competing models considered in the original design (Figure 1). Incorporating saturable elimination processes did not improve the model fit. A proportional error model was shown to be sufficient to characterize the residual unexplained variability for both the parent drug and the metabolite.

Inclusion of relative bioavailability (F_rel) of capsule to oral solution improved the fit of the data to the model further (ΔOFV −114.5). The typical population value of F_rel (BSV) in the final model was estimated to be 0.817 (62.3%). The model could also discriminate between the absorption rate (BSV) for capsules [k_a cap = 0.0315 h⁻¹ (91.9%)] and solution [k_a sol = 0.125 h⁻¹ (106.3)], indicating more rapid absorption from the latter. The addition of a lag time of 19.5 min for the oral absorption of itraconazole from either capsule or solution also improved the fit (ΔOFV −24.2). The estimates of apparent CL_m and V_m of the metabolite were 18.3 l h⁻¹ and 2.6 l, respectively. The final model supported random effects on the following parameters: Cl_p (clearance of parent drug (itraconazole)), V_c (volume of distribution of the central compartment for itraconazole), k_a cap, k_a sol and F_rel.

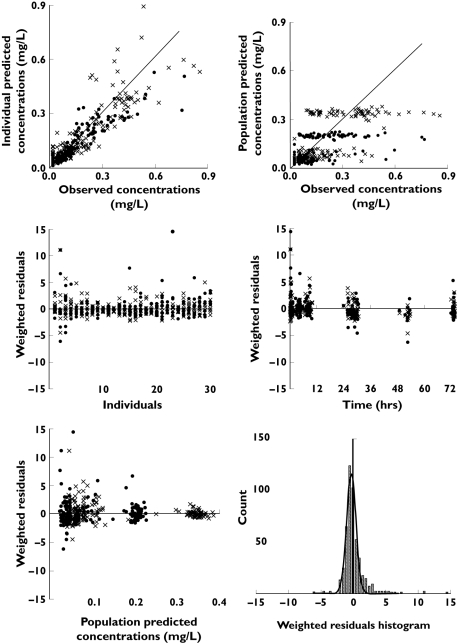
Diagnostic plots did not show any obvious correlation between individual parameter estimates and screened covariates. Inclusion of these covariates into the final model did not show a significant reduction of the OFV or a reduction of the BSV and therefore confirmed the graphical observations. Consequently, none of the BSV within this population could be explained by the influence of any observed covariates. The final estimated population pharmacokinetic parameters of all fixed and random effects of the final model are summarized in Table 3 and diagnostic plots are given in Figure 3. The weighted residuals vs. time plots showed the points to be symmetrically distributed with most of them within −5 and +5 units as shown in Figure 3, therefore no evidence of bias was noticeable. The few samples with weighted residuals outside ±5 were examined and were from three different patients. There was no trend observed and none of the data points could be justifiably omitted from the dataset. As shown in Table 3, the estimated parameters had acceptable relative standard errors.

Table 3.

Final parameter estimates from the final model and the parameter estimates from 200 bootstrap replicates with their relative standard error (RSE %) and the expected RSE from the design

Parameter	Final model, mean (RSE %)	200 bootstrap replicates, mean (RSE %)	Design expected RSE (%)
Pharmacokinetic parameters
Clp (l h−1)	31.5 (14.0)	29.3 (15.7)	8.6
Vc (l)	56.7 (33.9)	50.8 (37.2)	16.4
ka cap (h−1)	0.032 (46.7)	0.026 (34.8)	8.4
ka sol (h−1)	0.125 (44.2)	0.111 (29.4)
Frel	0.817 (23.5)	0.88 (19.2)
Q	71.3 (35.3)	68.0 (16.6)
Vper	2090 (35.0)	2245 (38.0)
CLm (l h−1)	18.3 (12.9)	17.2 (14.4)	10.7
Vm (l)	2.67 (49.8)	2.3 (51.9)	10.7
tlag (min)	19.3 (1.68)	19.3 (2.2)
Between-subject variability (%)
BSV Clp	22.1 (75.2)	21.9 (73.3)	40.0
BSV Vc	77.3 (48.5)	85.8 (53.2)	82.2
BSV ka cap	91.9 (33.5)	87.3 (30.5)	41.2
BSV ka sol	106.3 (31.4)	101.7 (26.3)
BSV Frel	62.3 (24.7)	60.7 (22.6)
Residual variability (CV %)
Proportional error
Itraconazole (%)	40.8 (16.6)	40.3 (15.5)
Hydroxy-itraconazole (%)	47.9 (12.7)	46.7 (14.2)

Cl_p, clearance of parent drug (itraconazole); V_c, volume of distribution of the central compartment for itraconazole; k_a cap, absorption rate for capsules; k_a sol, absorption rate for solution; F_rel, relative bioavailability; Q, intercompartment clearance; V_per, volume of distribution of peripheral compartment for itraconazole; CL_m, clearance for hydroxy-itraconazole; V_m, volume for hydroxy-itraconazole; t_lag, lag-time; BSV, between-subject variability.

Figure 3.

Diagnostic plots of the final model showing the individual and population predicted vs. observed plasma concentrations of itraconazole (•) and hydroxy-itraconazole (✗) (mg l⁻¹) as well as the weighted residuals

Model evaluation

The mean parameter estimates resulting from the bootstrap procedure were very similar to the population estimates of the final model, providing confidence in the estimates for the parameters of the final model, and demonstrated that the model was stable and robust when different combinations of subjects from the original dataset were used. The results of 200 bootstrap replications are summarized in Table 3. The asymptotic standard errors provided by NONMEM for the final model and empirical values from bootstrap were also similar in magnitude to those predicted from the FIM associated with the d-optimal design as shown in Table 3. An explanation for the differences between the RSEs predicted by the FIM and the RSEs from the final model could be that the inverse of the FIM is only an approximation to the lower bound of the covariance matrix. First, the FIM itself relies on a linearization of the model, which may introduce bias; second, the relationship of the FIM to the standard errors (through the covariance matrix) is an asymptotic result; and third, the expected standard errors from the FIM are based on the nominal optimal design rather than the executed design. All of these factors will lead to discrepancies between predicted and actual standard errors.

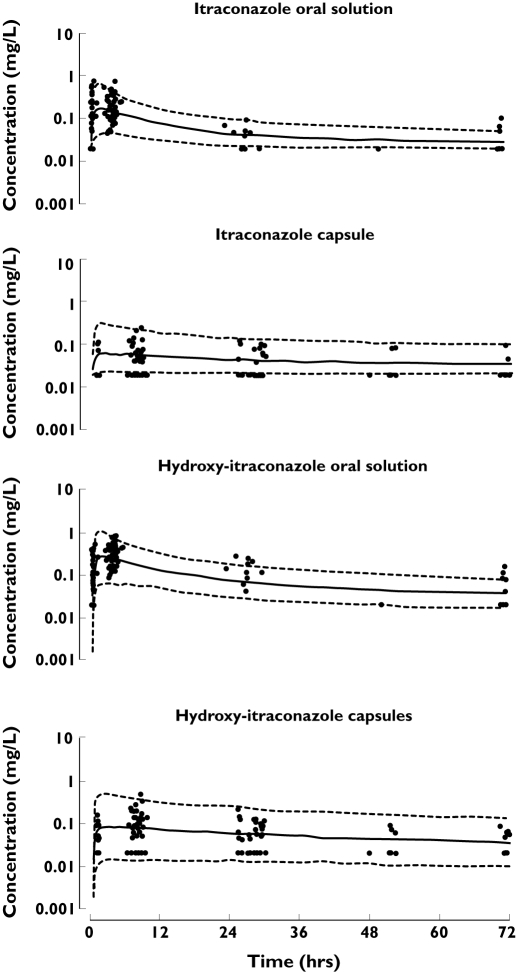
The VPC was performed for itraconazole as well as for the hydroxy-itraconazole concentration data in which the dataset was split into capsules and oral solution categories. The 5th, 50th and 95th percentiles of these simulations and the patients' data over a 72-h interval are shown in Figure 4 for the scenarios described above. These figures represent an internal visual evaluation of the model and show that about 90% of the data of itraconazole and metabolite concentrations fit well within the 5th to 95th percentiles band and the data were symmetrically distributed around the median. For itraconazole capsules, a slight overprediction by the model was seen; however, the data lying below the 5th percentile are BLOD samples (fixed to a value of half the LOD).

Figure 4.

Observed itraconazole and hydroxy-itraconazole plasma concentrations [•, not below the limit of detection (BLOD), ✗, BLOD] (mg l⁻¹), 5% and 95% prediction intervals (---) of simulated data as well as the median value () of the simulated data for both capsules and oral solution after a single dose

To assess further the rigor of the final model (analysed using the M5 method described by Beal) [37] with respect to the options for handling BLOD samples, the model was analysed with modified datasets in which the data for the BLOD samples were either discarded (M1), entered as measured (M4), or the first value BLOD was assigned to half the LOD and all previous (if during absorption) or subsequent (if during elimination) BLOD samples were discarded from the dataset (M6) as described by Beal [37]. All these models resulted in successful convergence under FOCE. However, for the M4 model the parameters for volume of the peripheral compartment (V_per) and the intercompartment clearance (Q) were fixed and the residual error model was changed to a combined proportional and additive error model to account for the more complicated error model. For this model the covariance step was aborted and no values for the relative standard error of estimation could be reported. The results of the parameter estimates from the final model were comparable to the different methods accounting for missing data (M1, M4, M5, M6) and provided similar parameter estimates, as seen in Table 4.

Table 4.

Summary of estimated parameters and relative standard error (RSE %) from four different methods evaluating datasets with data below the limit of detection (BLOD)

Method description	Method 1 BLOD = discard	Method 5 = final modelBLOD = 1/2LOD	Method 6 1st BLOD = 1/2LOD, others discarded	Method 4 BLOD = censored, −2LL function
Parameter	Mean (RSE %)	Mean (RSE %)	Mean (RSE %)	Mean
Pharmacokinetic parameters
Clp (l h−1)	23.2 (20.3)	31.5 (14.0)	30.7 (11.5)	29.8
Vc (l)	74.3 (42.7)	56.7 (33.9)	72.4 (28.7)	132
ka cap (h−1)	0.021 (21.9)	0.032 (46.7)	0.041 (38.0)	0.029
ka sol (h−1)	0.132 (30.5)	0.125 (44.2)	0.138 (31.3)	0.168
Frel	1.61 (19.1)	0.817 (23.5)	0.722 (21.3)	0.751
Q	83.3 (20.9)	71.3 (35.3)	79.9 (20.7)	71.3c
Vper	2660 (25.3)	2090 (35.0)	1610 (25.3)	2090c
CLm (l h−1)	14.9 (20.1)	18.3 (12.9)	18.0 (10.6)	15.4
Vm (l)	3.98 (45.5)	2.67 (49.8)	2.83 (42.4)	4.75
tlag (min)	18.3 (2.66)	19.3 (1.68)	17.7 (1.93)	17.4
Between-subject variability (CV %)
BSV Clp	49.6 (83.3)	22.1 (75.2)	15.6 (94.3)	26.6
BSV Vc	96.0 (64.1)	77.3 (48.5)	67.9 (51.1)	183.0
BSV ka cap	62.4 (54.1)	91.9 (33.5)	102.0 (28.3)	66.6
BSV ka sol	126.9 (25.3)	106.3 (31.4)	110.5 (47.7)	90.6
BSV Frel	37.9 (53.3)	62.3 (24.7)	63.2 (28.3)	40.1
Residual variability (CV %)
Proportional error
Itraconazole	30.2 (27.5)	40.8 (16.6)	45.0 (12.7)	83.2
Hydroxy-itraconazole	34.0 (11.9)	47.9 (12.7)	46.8 (12.9)	33.7
Additive error
Itraconazole				0.0084
Hydroxy-itraconazole				0.0511

c, Fixed; −2LL, −2 Loglikelihood; Cl_p, clearance of parent drug (itraconazole); V_c, volume of distribution of the central compartment for itraconazole; k_a cap, absorption rate for capsules; k_a sol, absorption rate for solution; F_rel, relative bioavailability; Q, intercompartment clearance; V_per, volume of distribution of peripheral compartment for itraconazole; CL_m, clearance for hydroxy-itraconazole; V_m, volume for hydroxy-itraconazole; t_lag, lag-time; BSV, between-subject variability.

Simulation

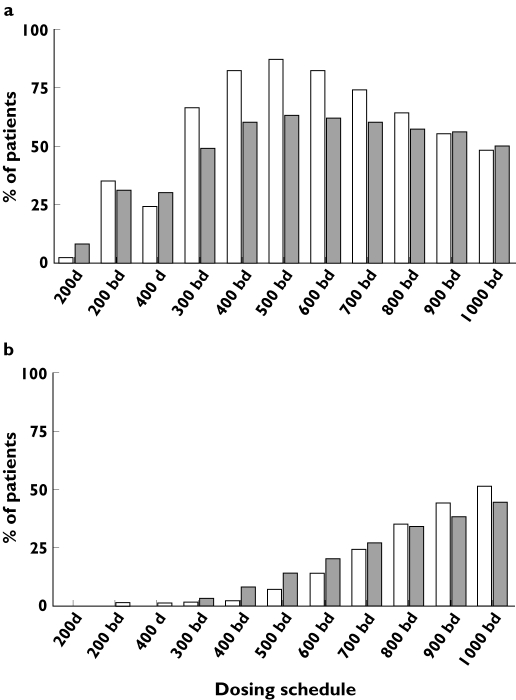
Simulations using the final model showed that the current dosing regimen of 200 mg twice daily would provide a target C_min,ss for only 35% of patients when administered as the solution, and 31% for the capsules. We estimated that for a 500-mg twice daily regimen target success would be achieved for 87% of the patients taking the solution and 63% for the capsules. For the ‘active’ target range from the sum of itraconazole and hydroxy-itraconazole concentrations the 500-mg twice daily dosing regimen would achieve target success for 84% of patients on the solution and 60% of the patients on the capsules.

Discussion

This study investigated the population pharmacokinetics of itraconazole and hydroxy-itraconazole in adult patients with CF, in particular, the relative bioavailability of the two commercially available oral products of itraconazole. The study was performed according to a d-optimal design [29], to support a sparse sampling population approach. As shown, applications of the optimal design resulted in precise parameter estimates for the final model which was similar in structure to one of the plausible models considered in the design (see Figure 1). This model described the data well. The sampling windows were sufficient to provide flexible sampling (see Figure 2) and still efficient enough to support a standard model building strategy. One of the reasons for the high percentage (94%) of samples taken within the optimal windows was the individualized information provided to the patients and that the main study investigator coordinated the sampling. However, during the design development the large proportion of BLOD concentrations observed after a standard single dose of itraconazole was not expected and therefore the design was not adjusted to avoid them. From prior information collected for the design development, peak concentrations (C_max) of 0.24 mg l⁻¹ after a single dose of itraconazole capsules (taken with food) and a C_max of 0.55 mg l⁻¹ after the oral solution (taken while fasting) were expected [17, 21]. However the median C_max in these CF patients after a single dose of capsules was found to be 0.064 mg l⁻¹ and 0.235 mg l⁻¹ for the solution. These values were estimated from the predicted individual posthoc parameter estimates and are summarized in Table 5. The t_max values from this study and those of Barone et al. in 1993 and 1998 were similar (04.15 h vs. 4.5 h for the capsules and 1.94 vs. 2.2 for the solution) [17, 21]. The low itraconazole plasma concentrations were probably due to reduced absolute bioavailability of the drug in these patients compared with healthy volunteers. Low itraconazole plasma concentrations and a high variability of the pharmacokinetics for itraconazole have been described for children [9, 39] as well as for adult CF patients [9]. Other studies have suggested that disease-influenced changes in the gastrointestinal tract can alter drug absorption [40, 41]. Most CF patients have pancreatic insufficiency and, despite regular pancreatic enzyme supplementation with meals and snacks, fat malabsorption is still possible which could affect the absorption of lipophilic drugs (such as itraconazole). Furthermore, the lack of interaction between proton pump inhibitors and/or H2-blockers on F_rel of itraconazole in this study may be due to the 2-h gap between these drugs and the itraconazole dose and that this study was not powered to observe this interaction. However, these findings should not necessarily be extrapolated to other clinical scenarios.

Table 5.

Peak concentrations in plasma (C_max) and time to C_max (t_max), AUC_0–∞ determined from the posterior Bayes estimates parameter estimates from NONMEM. Reported as median (range) and 90% confidence intervals (CI)

	Cmax (mg l−1)	tmax (h)	AUC0–∞ (mg h−1 l−1)	Frel (AUCcap/AUCsol)
Capsules	0.064 (0.018–0.23)	4.15 (1.78–105.31)	4.42 (2.15–23.81)	0.76 (range 0.30–3.40) (CI 0.36, 1.97)
Solution	0.23 (0.038–1.094)	1.94 (0.85–20.86)	6.32 (3.76–8.47)

The handling of data below the LOD and LOQ continues to be a challenge in pharmacokinetic analyses. Nevertheless, the consensus is that these samples cannot be ignored or assigned to a value of zero [37]. To evaluate this model with regard to its validity with this amount of BLOD data and also to assess how and if it influenced the results of the final model, we evaluated the final model with methods suggested by Beal in 2001 [37]. One widespread practice is to assign half the LOD value to all BLOD samples. Either the value of the LOD or the LOQ should be known, depending on the cooperation between the analytical and the pharmacokinetic chemist. In our case, both values as well as the measured value below the LOD were available (the assay and the pharmacokinetic modelling were performed by the first author). We have used M5 for the model-building process and have tested the other commonly used methods also (M1, M6). Furthermore, we have also used one of the more sophisticated methods (M4) suggested by Beal. Using the simple M5 method provided comparable results to the more complex but theoretically better M4 (integration method). From the results, the expected bias underprediction in M1 for Cl_p can also be seen in Table 4. In Figure 4 (showing the VPC), there is also clear evidence of bias if all BLOD samples were to be ignored which provides support that method M5 is working. If all BLOD data were to be ignored then the median prediction by the model would be expected to pass through the middle of the remaining data, which would then be associated with bias in the parameter estimates and in the model predictions.

Surprisingly, no major differences between M4, M5 and M6 were described. Beal described the same tendencies and preferred M6 over M5 only in the case of a large amount of BLOD data [37]. In the present study, there was little difference between the parameters estimated with M5 and M6. Method 4 required a more complex set-up and run times were significantly longer.

Hitherto there have been no population pharmacokinetic data from itraconazole and hydroxy-itraconazole in adult patients with CF. A recent ‘traditional’ pharmacokinetic study reported that CF patients had low peak concentrations [9]. However, in the present study a combined model for the concentration–time relationship for itraconazole and its main metabolite has been established. In addition, the target success after several dosing schedules was assessed after simulations in which the model developed from this single-dose study was extrapolated to steady-state concentration–time profiles. It was clearly demonstrated that twice-daily dosing is preferred over once-daily dosing for the same total daily dose. Furthermore, it can be seen that the dosing regimen providing most patients with a target success would be 500 mg twice daily of either solution or capsules. At this dosing regimen about 24% more patients would achieve this target using the oral solution formulation, but at the same time only half as many patients would be at risk of concentrations >2 mg l⁻¹ compared with the capsules (7% vs. 14%). The number needed to treat (NNT) at this dosing regimen was 4 for the solution compared with capsules. This means, for every four patients treated with the solution one additional patient will achieve a target success compared with the capsule but at an additional current cost of AUD $220 per day for an Australian public hospital. Figure 5 also shows that doses above 600 mg twice daily do not provide any additional benefit but present a higher risk of adverse effects (e.g. hepatotoxicity). This risk should be considered, particularly in this group of patients due to their multiorgan disease. At this stage the high between-subject variability (ranging between 22.1 and 106.3%) should be highlighted, which shows that dose individualization and therapeutic monitoring for this drug are required in these patients.

Figure 5.

(a) The percentage of patients achieving the therapeutic target range (C_min,ss = 0.5–2 mg l⁻¹) with different dosing schedules. (b) The percentage of patients at risk of toxicity at these doses. bd, Twice daily; d, once daily; white bars, solution; grey bars, capsules

In conclusion, the d-optimal designed population pharmacokinetic model was developed and evaluated for itraconazole and its active metabolite in adult CF patients. None of the between-subject variability could be explained by a screened covariate. The simulation of the final pharmacokinetic model provided suggestions for a new dosing strategy in these patients to achieve a prespecified target concentration. Since the therapeutic target is still doubtful in ABPA, the potential risks of these dosing schedules need to be assessed on an individual basis and further investigation could be valuable in an attempt to improve antifungal management in patients with CF.