Redesigning protein pK_a values

Abstract

The ability to re-engineer enzymatic pH-activity profiles is of importance for industrial applications of enzymes. We theoretically explore the feasibility of re-engineering enzymatic pH-activity profiles by changing active site pK_a values using point mutations. We calculate the maximum achievable ΔpK_a values for 141 target titratable groups in seven enzymes by introducing conservative net-charge altering point mutations. We examine the importance of the number of mutations introduced, their distance from the target titratable group, and the characteristics of the target group itself. The results show that multiple mutations at 10Å can change pK_a values up to two units, but that the introduction of a requirement to keep other pK_a values constant reduces the magnitude of the achievable ΔpK_a. The algorithm presented shows a good correlation with existing experimental data and is available for download and via a web server at http://enzyme.ucd.ie/pKD.

The application of enzymes in industrial processes often requires that the enzyme must function under very specific and sometimes quite unphysiological conditions. Several industrial processes will benefit from the application of enzymes with re-engineered pH-dependent characteristics (e.g., starch liquefaction for the production of ethanol and high-fructose syrup [Shaw et al. 1999], detergent applications [Ito et al. 1998], and dye bleaching [Cherry et al. 1999]), and consequently, there is a strong interest in developing experimental and theoretical methods for changing the pH-dependent characteristics of enzymes. Advances have been made in the fields of protein engineering and directed evolution, and it is presently possible to routinely optimize the performance of enzymes for a range of conditions using either rational engineering or screening/selection-based approaches (Cherry et al. 1999; Farinas et al. 2001). Unfortunately, not all characteristics of enzymes are equally easy to optimize and successes in rational re-engineering of enzymatic pH-activity profiles remain few despite decades of studies on enzyme structure-function relationships.

The pH-dependence of enzymatic activity is often determined by the pK_a values of active site groups but can also be limited by protein stability at extreme pH values. In the present work we concern ourselves only with re-engineering enzymatic pH-activity profiles by changing active site pK_a values, and we therefore ignore the cases where protein stability is the limiting factor.

There are a few experimental examples of active site pK_a values that have been changed (and thus the pH-activity profile re-engineered) to yield an efficient mutant enzyme (Thomas et al. 1985; Russell et al. 1987; Meiering et al. 1992; Loewenthal et al. 1993; Cha and Batt 1998; Joshi et al. 2000; Le Nours et al. 2003; Hirata et al. 2004; Kim et al. 2006), but the pK_a shifts have been modest and often the essential mutations have been found using comparative protein engineering strategies (i.e., mutations are introduced based on comparisons with a homologous enzyme that possesses the desired pH-activity profile).

Therefore, the conclusion from two decade's work is that very specific point mutations in the active sites can change the pH dependence of enzymatic activity, but unless such specific active site point mutations are known (e.g., from comparative studies), there is not much hope of achieving a dramatic pH-activity profile shift with rational engineering methods. This somewhat disheartening conclusion is reached because mutations that give large pH-activity profile shifts normally are close to the active site and therefore likely to give mutant enzymes that are inactive or have dramatically reduced activity. Distant point mutations, on the other hand, mostly give mutant enzymes with wild-type activity but also produce very small pH-activity profile shifts.

We further explore the strategy of changing enzymatic pH-activity profiles using charged mutations. Specifically, we investigate the possibility of introducing multiple point mutations far from the active site that will change active site pK_a values through charge–charge interactions (charge-only mutations) without perturbing the active site structure through other effects. This strategy has been advocated before and was explored by Fersht and coworkers in a series of articles (Thomas et al. 1985; Russell and Fersht 1987; Russell et al. 1987; Sternberg et al. 1987; Loewenthal et al. 1993) and yielded promising results for Subtilisin and Barnase, although no systematic experimental or theoretical study was performed to assess the general feasibility of the approach.

We report the development of a novel, fast algorithm (pKD) for the redesign of protein pK_a values using charge-only mutations. We validate the performance of pKD using experimental data and theoretical tests (see Materials and Methods), and we apply the algorithm to assess the feasibility of changing enzymatic pH-activity profiles and protein pK_a values in general using charge-only mutations.

We apply pKD for the redesign of 141 titratable groups in seven enzymes to determine the feasibility of re-engineering protein pK_a values in general. We examine the connection between the number of point mutations, their distance from the target group, and the ΔpK_a values achievable. In light of our findings, we comment on the general feasibility of re-engineering enzymatic pH-activity profiles using charge-only mutations.

Changing protein pK_a values

The degree of protonation of a protein titratable group, at a given pH, is determined by the free-energy difference (ΔG_a) between the accessible protonation states for the titratable group. The pH dependence of ΔG_a is typically described by a single equilibrium constant (the pK_a value), although this description breaks down for strongly coupled groups. ΔG_a is determined by the relative strength of the interactions between the protonation states of the titratable group and the rest of the atoms in the protein. To change the degree of protonation of a particular residue at a certain pH (hereafter referred to as “redesigning the pKa value”), we therefore must change the way one or more of the protonation states interact with the rest of the protein.

Since at least one protonation state carries a net charge, we can change the energy of that state by inserting or removing charged residues around the titratable group. The problem of redesigning a pK_a value therefore consists of identifying the point mutations that change ΔG_a in the way that we desire. In the present work we combine a standard modeling algorithm (Chinea et al. 1995) with a new fast ΔpK_a calculation routine based on energy calculations from the WHAT IF PBE-based pKa calculation package (WIpKa) (Nielsen and Vriend 2001). WIpKa is comparable in accuracy to other pKa calculation packages (Bashford and Karplus 1990; Yang et al. 1993; Antosiewicz et al. 1994; Karshikoff 1995; Demchuk and Wade 1996; Alexov and Gunner 1997; Sham et al. 1997; Mehler and Guarnieri 1999; Mongan et al. 2004; Warwicker 2004; Li et al. 2005; Khandogin and Brooks 2006; Krieger et al. 2006), and has been benchmarked extensively to assess its sensitivity to structural errors (Nielsen and McCammon 2003b) and performance on mutant proteins (Lambeir et al. 2000; Joshi et al. 2001). In the Materials and Methods section we show that pKD is much faster than WIpKa and is as accurate, thus making it ideally suited for the present purpose.

The pKD algorithm carries out three tasks:

• (1) Identification of all point mutations that change the net charge of the enzyme but maintains its fold and activity.

• (2) Calculation of ΔpK_a values for all single-point mutations.

• (3) Identification of the sets of mutations that fulfill the design criteria.

All three steps are described in detail in the Materials and Methods section, but to appreciate the special design problem that pK_a values present, it is advantageous to acquire a basic understanding of the effects that titratable groups have on each other. The insertion of a titratable group with a negatively charged state (in the following, called an acid) generally increases the pK_a of the residue it interacts with, whereas the insertion of a positively charged residue (a base) generally lowers the pK_a value of its interaction partner. In both cases, the magnitude of the pK_a shift is directly proportional to the interaction energy between the two titratable groups, and this has resulted in ΔpK_a values being calculated with the relation

where ΔΦ is the change in electrostatic potential at the target group due to the inserted group.

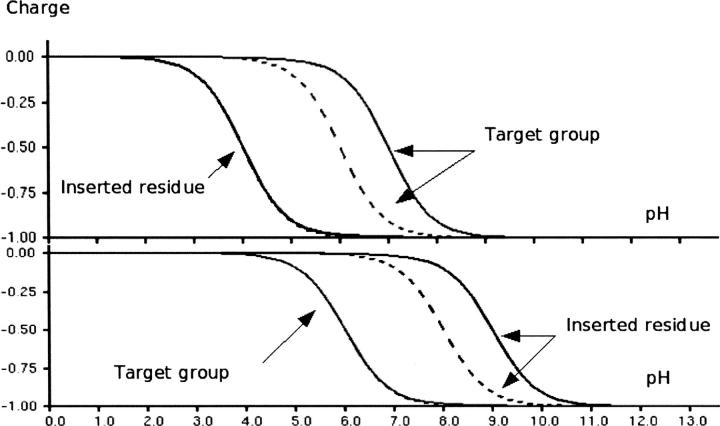
An interaction behaving in such a way is illustrated in Figure 1 (top), where the insertion of an acid with an interaction energy of 2.3 kT changes the pK_a value of the target group by one unit. However, in Figure 1 (bottom), the insertion of the acid has no effect on the target group, because the inserted group titrates at much higher pH values than the target group. We therefore define the “intrinsic pK_a value” (Bashford and Karplus 1990) as the pK_a value of a titratable group when it does not interact with the charged states of other titratable groups. In Figure 1 (top) the intrinsic pK_a value of the inserted group is two units lower than that of the target group. In Figure 1 (bottom) the situation is reversed with the inserted group having the higher intrinsic pK_a. Thus, for a titratable group to induce a pK_a shift in another titratable group it must have an appropriate intrinsic pK_a value to behave according to Equation 1. Figure 1 presents a simple, clear-cut case for two groups, with a relatively weak interaction energy (2.3 kT) and a large difference in the intrinsic pK_a values. In situations where there are multiple groups, strong interaction energies, and similar intrinsic pK_a values, the effects become more difficult to rationalize and Equation 1 inevitably also fails to describe these situations. When calculating ΔpK_a values in target groups originating from single- or multiple-point mutations, it is thus essential to use a full description of the energetics of the system to accurately calculate the resulting ΔpKa values.

Figure 1.

The importance of the intrinsic pK_a when redesigning protein pK_a values. In the top panel an acid with an intrinsic pK_a of 4.0 is inserted so that it interacts with the target group (intrinsic pK_a 6.0) with an interaction energy of 2.3 kT/e. This results in the pK_a of the target residue being elevated 1.0 unit. Similarly, in the bottom panel we insert an acid with an intrinsic pK_a value of 8.0 that interacts with the target acid with an interaction energy of 2.3 kT/e. However, since the intrinsic pK_a value of the inserted group is larger than that of the target residue, the pK_a value of the target group remains 6.0, whereas the pK_a value of the inserted group is elevated by 1.0 units.

The effect of point mutations on catalytic activity

A large fraction of the residues in any given enzyme can be mutated to yield a mutant form whose activity is similar to the wild type. This has been illustrated convincingly for small enzymes such as T4 lysozyme (Karpusas et al. 1989; Kuroki et al. 1998), and for bigger enzymes it is likely that even larger fractions of the residues can be mutated with little effect on the catalytic properties of the molecule.

The effect of a mutation on the pK_a value decreases with increasing distance between the site of mutation and the target pK_a value. Similarly, the effect of a point mutation on the catalytic activity of an enzyme is generally inversely related to the distance to the active site, but whereas electrostatic effects generally are expected to decrease by 1/r, effects arising from nonelectrostatic forces are expected to decrease at least by 1/r ⁶.

In most cases, we are unable to predict the quantitative effect of a point mutation on the catalytic activity, and therefore it is not desirable to mutate residues too close to the active site. Similarly, we cannot mutate residues too far from the active site since they will have practically no effect on the active site pK_a values. We are therefore left with residues in an intermediate distance range, where 1/r ⁶ terms are small and electrostatics are significant, and it is here that we can construct charge-only mutations. In the following, we identify the maximum range for charge-only mutations by calculating the maximum inducible ΔpK_a value for 141 target groups as a function of the number of mutations and their distance from the target group.

Results

We investigate the solution space of the pKD algorithm when applied for the redesign of target group pK_a values in seven enzymes (Table 1). We calculate the magnitude of ΔpK_a values obtainable for single targets and observe the dependence of the target ΔpK_a values on the number of mutations we use and on their proximity to the target group. Finally, we use our results to re-evaluate the prospects of redesigning enzymatic pH-activity profiles using mutations outside the active site and illustrate that evolution has favored changing active site pK_a values with local effects rather than long-range effects.

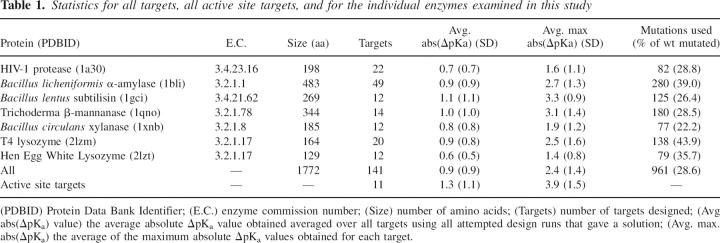
Table 1.

Statistics for all targets, all active site targets, and for the individual enzymes examined in this study

The data set

The data set consists of seven enzymes (Table 1). The total number of titratable groups in the data set is 451, and of these, 141 (31%) have calculated pK_a values in the 2.0 → 12.0 range, and these were used in the pK_a redesign calculations. The seven enzymes vary considerably in size and geometry, and we therefore anticipate the environments of the titratable groups to be broadly representative of the environments of titratable groups in water-soluble globular proteins. Furthermore, the calculated pK_a values for the active site residues in the seven enzymes are in qualitative agreement with experimental findings with regard to the identity of the proton donor.

The effect of single mutations

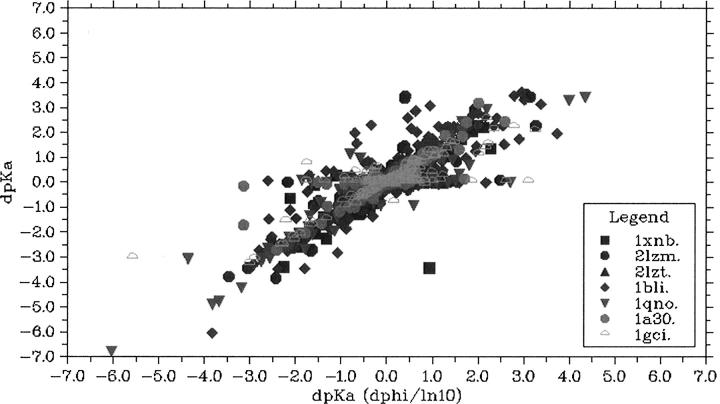
Using quite restrictive mutation selection criteria, we found 1016 mutations to fulfill the criteria for solvent accessibility (minimum 30%) and rotamer library population and we proceeded to calculate the 37,284 ΔpK_a values that these mutations induce. Figure 2 shows the ΔpK_a values calculated with pKD as a function of the ΔpK_a values calculated using Equation 1. The majority of ΔpK_a values are calculated equally well with both methods, but for a significant fraction there is a marked difference in the results. These cases fall into two general categories: (1) mutations where the intrinsic pK_a value of the mutant is inappropriate for inducing a pK_a shift in the target, and (2) mutations that interact strongly with the target residue and thus cause either a breakdown of typical Henderson-Hasselbalch titrational behavior or create a nonadditive titratable system (Nielsen 2006).

Figure 2.

The correlation between the ΔpK_a value calculated with ΔΦ/ln(10) compared with the ΔpK_a value calculated with the Monte Carlo method for all single mutations in the test set. ΔΦ/ln(10) (Equation 1) gives highly inaccurate results for a number of mutations due to the lack of description of effects related to the intrinsic pK_a differences for both the inserted residue and the target residue.

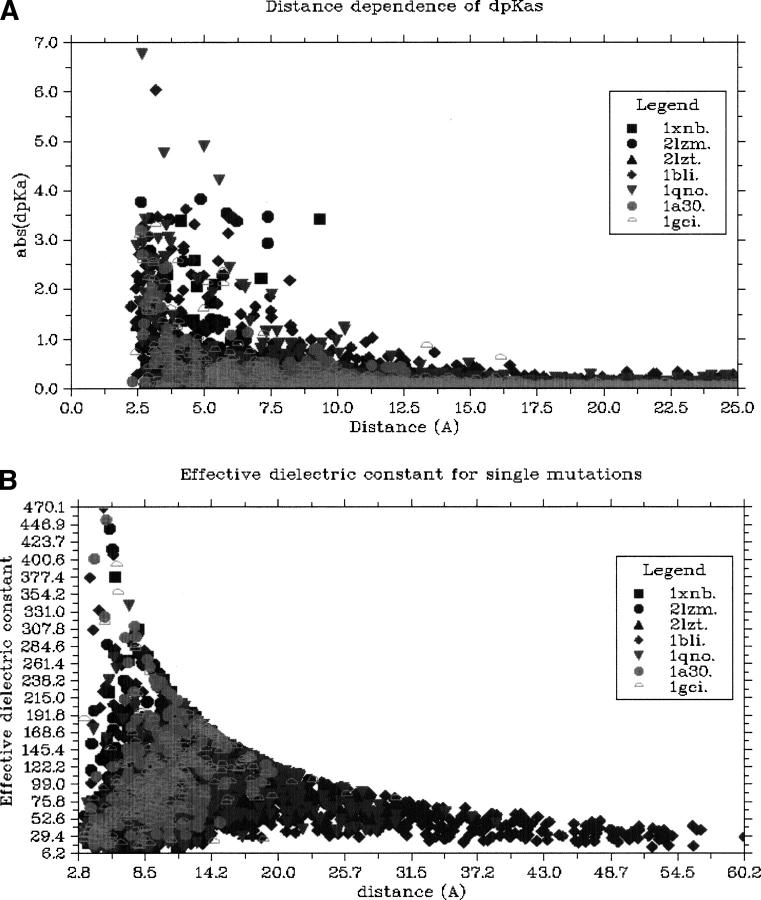
Figure 3A shows the distance dependence of ΔpK_a values for single mutations, and it is seen that a single mutation must be quite close (<13Å) to a target residue to achieve a significant effect on the target pK_a value. Our aim is to alter active site pK_a values exclusively through electrostatic forces, but we do not know the exact distance at which mutations no longer affect active sites through nonelectrostatic forces. Studies have shown point mutations more than 15Å from the active site to affect catalytic activity (Rajagopalan et al. 2002), and we are therefore left with an uncomfortably narrow (or indeed nonexisting) distance range where charge-only mutations can be engineered “safely.” Drops in catalytic activity for mutations in this range have been observed for BLI (Nielsen et al. 1999, 2001), D-xylose isomerase (Cha and Batt 1998), and BCX (Joshi et al. 2001), but for Subtilisin, significant pK_a shifts have been achieved with little change in catalytic activity (Russell and Fersht 1987).

Figure 3.

(A) The distance dependence of the effect of single mutations. Above 12.5 Å the effect of a point is rarely above 0.5 units. (B) ɛ_apparent as a function of distance between the formally charged atoms of mutated residue and the target group. The large variation in ɛ_apparent for small distances is an effect of the dielectric properties of the protein molecule and the appropriateness of the pKa values for inducing a ΔpKa. At larger distances ɛ_apparent becomes representative of the “average” dielectric properties of the protein and its surrounding solvent.

A crucial factor in determining how close mutations can be made is the apparent dielectric constant (ɛ_apparent), which describes the efficiency with which the electrostatic field is transmitted from the site of mutation to induce a ΔpK_a for the target group. Figure 3B shows the ɛ_apparent calculated from the predicted ΔpKa values as a function of the distance between charged atoms of the target and the mutated residue. Two effects determine the magnitude of ɛ_apparent as reported in Figure 3B: the appropriateness of the intrinsic pK_a values of the system for achieving a ΔpK_a (see Fig. 2), and the dielectric constant of the volume between the mutated residue and the target group. In the calculations, the dielectric properties of the protein are modeled both by using a dielectric constant in the PBE runs, and also by optimizing the hydrogen-bond network before every PBE calculation, thus allowing many protein dipoles to respond to the electric field. The combination of these effects produces very high and very low values of ɛ_apparent for mutations very close to the target groups, since the response of the target group is strongly influenced by the detailed dielectric properties of the target group surroundings. As the distance between the mutated residue and the target group grows, the maximum values of ɛ_apparent decrease due to calculation-specific restrictions (due to reasons of accuracy we consider only ΔpKa values ≥0.1), but it is evident that the minimum values of ɛ_apparent also increase. This is to be expected since the effect of mutations at larger distances to a larger extent will be modulated by the average dielectric properties of the protein and the solvent surrounding it than will mutations very close to the target group.

Multiple mutations

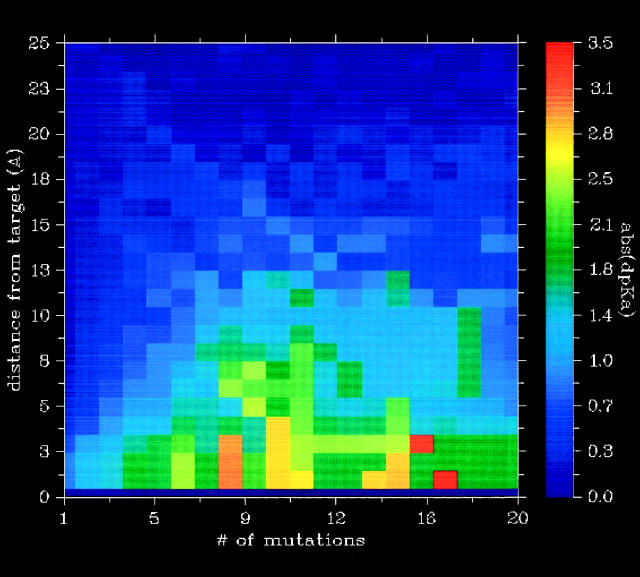
The use of multiple charge-only mutations might extend the distance range that is useful for redesigning active site pK_a values since the collective effect of multiple distant point mutations might be as powerful as a few mutations close the active site. Figure 4 shows the average maximum ΔpK_a value obtainable for all targets as a function of the number of mutations used and the minimum distance between the mutated residue and the target group. Clearly, there is an added effect of using multiple mutations as compared with using single mutations, but for distances larger than 13Å, the ΔpK_a values obtainable are quite modest even when using a large number of mutations. This result is heavily dependent on how many point mutations one is willing to squeeze in at a certain distance around the active site and also where in the enzyme the active site is located. Shallow enzyme active sites on the surface of proteins severely restrict the number of point mutations that can be constructed, whereas many more mutations can be constructed around deeply buried active sites.

Figure 4.

The average maximum abs(ΔpK_a value) obtainable for all targets as a function of a number of mutations and minimum distance allowed between any atom of the mutated residue and any atom of the target residue. Above 13Å, pK_a shifts are generally quite small even when using multiple mutations.

Are active sites special?

So far we have examined the redesign of any protein pK_a value, but in order to re-engineer pH-activity profiles one needs to redesign active site pK_a values. Active sites constitute very special environments in proteins and it is therefore possible that the conclusions reached on the feasibility of redesigning a general protein pK_a value are not valid for active sites. Specifically, we examine the effect of the strong electrostatic interactions found in active sites.

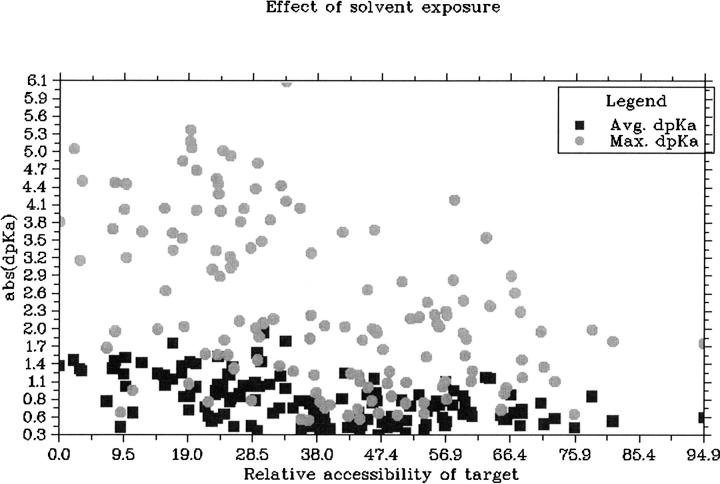
Active sites are known to harbor very strong electrostatic interactions, and it is therefore possible that changes in active site pK_a values somehow could be ‘buffered’ by a network of titratable groups that maintain the catalytic residues in their catalytically competent protonation state. Such buffering effects can exist in artificially constructed systems (Nielsen 2006), but it is uncertain whether enzyme active sites display such effects. Table 1 compares the average ΔpK_a values obtained for active site targets with those obtained for all targets, and it is clear that active site ΔpK_a values are not buffered by their environment. In contrast, the results show that it is slightly easier to change the pK_a values of active site targets than it is to change the pK_a value for the average target. Active site targets tend to be more buried than the average target and Figure 5 shows that buried targets are easier to redesign simply because it is possible to perturb the electrostatic field in active sites more because the remoteness from solvent diminishes dielectric screening effects. It should be noted that the pK_a values of catalytic residues are often predicted to be highly perturbed compared with their model pK_a values, especially for larger enzymes, and that in those cases one would need to engineer much larger ΔpK_a values in order to achieve a measurable effect.

Figure 5.

The correlation between the ΔpK_a value obtainable for a target and its solvent accessibility. Circles show the maximum abs(ΔpK_a value) obtained for targets, whereas the squares show the average abs(ΔpK_a value) for the targets.

Discussion

We have shown that the re-engineering of protein pK_a values using site-directed mutagenesis depends critically on the number of mutations and their distance from the target residue. We have furthermore performed a number of in silico design experiments where we have introduced the additional constraint that the pKa value of a neighboring residue should remain constant. In all cases, this extra constraint limits the maximum ΔpK_a that can be achieved with a fixed number of mutations. Nevertheless, we show that it is theoretically possible to achieve significant pK_a shifts for target groups using a high number of point mutations, all being a minimum of 10 Å from the target group. However, we have no data to prove that mutations at 10 Å are at a “safe” distance from an enzyme active site. Indeed, experimental studies (de Kreij et al. 2002; Rajagopalan et al. 2002) have shown that even mutations at very large distances can have an effect on the catalytic activity of an enzyme, thus making re-engineering of pH-activity profiles using multiple charge-only mutations a risky operation.

When examining the determinants of the pK_a values of catalytic groups in naturally occurring enzymes, it is obvious that the use of charge-only mutations has not been favored during evolution. Indeed, the removal of all nonactive site titratable groups in Hen Egg White Lysozyme and Bacillus circulans xylanse favors a further elevation of the proton donor pK_a value (calculations not shown), and the enzyme electrostatic field as a whole seems to “work against” the active site.

Thus, enzyme active sites have been carefully optimized to perturb the pK_a values of the catalytic residues as required. This perturbation is typically achieved by a combination of desolvation effects and strong electrostatic interactions with neighboring residues, and we are currently unable to re-engineer enzyme active site pK_a values in this way since it is near impossible to maintain a high catalytic efficiency when introducing multiple-point mutations in an active site.

Seen in this light, the re-engineering of pH-activity profiles using charge-only mutations, however unappealing, remains our sole option for rational engineering. Therefore, this option deserves proper attention in coming years to improve our theoretical and experimental understanding of the importance of electrostatic fields in enzyme active sites.

The question remains as to why naturally occurring enzymes have chosen to perturb active site pK_a values using short-range desolvation effects and strong electrostatic interactions in the active site. We speculate that the reason for this is a division of labor between the enzyme surface and the active site itself. The surface surrounding the active site has been proven to play an important role in attracting substrates (Antosiewicz et al. 1995; Livesay et al. 2003), and the protein surface in general is subject to multiple evolutionary pressures such as the requirement for the protein to be soluble, to adapt to its subcellular location (Andrade et al. 1998), and to form interdomain and interprotein interactions. It is tempting to conclude that given these multiple restraints, it proved evolutionarily less costly and more flexible to let the protein surface adapt to the solvent conditions and interaction partners, while the active site was left to evolve its pH-dependent characteristics autonomously. It has indeed been found that active site pK_a values often can be predicted from the electrostatic properties of the enzyme active site itself and its immediate surroundings (Nielsen and McCammon 2003a).

In summary, we have shown that it is theoretically possible to achieve pK_a shifts for protein titratable groups using multiple charge-only mutations quite removed from the target titratable group. However, when attempting to re-engineer enzymatic pH-activity profiles it remains to be investigated whether significant pK_a value shifts can be obtained for catalytic residues while maintaining the wild-type catalytic efficiency. Work on confirming the practical feasibility of re-engineering pH-activity profiles is currently ongoing.

Materials and methods

Preparing PDB structures

PDB structures were regularized using WHAT IF (Vriend 1990). All missing side-chain atoms were rebuilt using the CORALL function. All ligands, cofactors, and crystal water molecules were deleted prior to pK_a calculations.

Calculating pK_a values for wild-type proteins

pK_a values for wild-type protein structures were calculated using the WHAT IF pK_a calculation suite (Nielsen and Vriend 2001). All parameters were set as stated previously, except that the dielectric constant for the protein was set to 8 at all times. The WHAT IF pK_a calculation algorithm uses a standard PBE-based pK_a calculation scheme (Yang et al. 1993) coupled with a hydrogen-bond optimization algorithm (Hooft et al. 1996). Briefly, the effect of the nontitratable protein environment is modeled by calculating the intrinsic pK_a value for each titratable group. The intrinsic pK_a values are used as the starting point for calculating the effects on the pK_a values of the charge–charge interactions between all pairs of titratable groups. These effects are quantified by calculating the fractional degree of protonation of each titratable group at a predetermined pH range using either explicit evaluation of the Boltzmann sum (for small systems) or Monte Carlo sampling (Beroza et al. 1991). pK_a values are determined as the pH value where a given group is half-protonated.

Calculating electrostatic interaction energies

The electrostatic interaction energy is calculated by solving the PBE for each possible mutation, and subsequently by measuring the electrostatic interaction potential at the sites of both all wild-type and all mutant titratable groups. We used Delphi II (Nicholls and Honig 1991) for solving the PBE. Values for the PBE solver were set as follows: (ɛ_protein, 8; ɛ_solvent, 80; ion exclusion radius, 2 Å; solvent probe, 1.4 Å; T, 298.15 K; final grid resolution, 0.25 Å/grid point; ionic strength, 0.144 M). In cases where two titratable groups were further apart than 15 Å, a lower final grid resolution was used to calculate the interaction energy.

Overview of the pKD algorithm

The work of the algorithm can be divided into three phases: (1) selecting mutations that could contribute to a design solution, (2) calculating ΔpK_a values for each of those mutations, and (3) combining these mutations to arrive at the solution closest to the design goals.

Selecting mutations

In this study we consider only mutations that alter the net charge on the protein and furthermore we use a restrictive set of selection criteria to ensure that the mutations perturb the protein structure, and hence catalytic activity, as little as possible.

We alter the net charge of the protein by removing or inserting a charged residue or by substituting a charged residue for another charged residue of the opposite sign.

We allow all titratable groups to be mutated to a neutral residue of approximately the same size (Asp →Asn, Glu → Gln, His → Phe, Lys → Leu, Arg → Leu), and we also allow the insertion and the reversal of charges at a number of positions. The insertion of a charged residue and the swapping of one charged residue for an oppositely charged one requires a more sophisticated approach, since not all charged residues can be accommodated at any given position in the protein. Mutations are selected so that they are compatible with the local environment, and we mutate only residues that are at least 30% solvent exposed in order to minimize the effect on the protein structure. Each of the five charged residues (Asp, Glu, His, Arg, Lys) are then modeled at the position, and we select only those who are contained in a standard backbone-specific rotamer library (Chinea et al. 1995). Specifically, we require the modeled residue to achieve a WHAT IF rotamer score of at least 0.0.

Calculating ΔpK_a values for all single mutations

A typical full-fledged protein pK_a calculation with full hydrogen-bond optimization and determination of protonation states using a Monte Carlo algorithm takes anywhere between minutes to days, depending on the size of the protein and the pK_a calculation package used. The straightforward way of calculating ΔpK_a values for a point mutation is to perform two full pK_a calculations (one for the mutant and one for the wild type) and then subtract the corresponding pK_a values. When evaluating ΔpK_a values for tens (or hundreds) of point mutations and combinations of these (see later), this becomes intractable. In the case of a charged residue inserted into the protein, we calculated the charge–charge energies between the inserted group and all other titratable groups using a standard PBE calculation, and we calculate the intrinsic pK_a value by explicitly modeling the residue and then performing the standard desolvation energy and background energy calculations (Yang et al. 1993). The intrinsic pK_a values and charge–charge interaction energies for all other titratable groups are known from the wild-type pK_a calculation, and we can now simply insert the new group in the charge–charge interaction matrix and recalculate the titration curves for all groups. In order to achieve high accuracy in the single-mutation ΔpK_a values, we calculate the fractional degree of protonation from pH 0 to pH 14.0 in steps of 0.05 pH units using 200,000 Monte Carlo steps for each pH value.

We ignore the fact that the intrinsic pK_a values of wild-type titratable groups will change when mutations are inserted in their vicinity. However, given that we are interested in ΔpK_a values at larger distances, this approximation becomes reasonable.

The method presented here provides a significant speed-up as compared with calculating ΔpK_a values by explicitly modeling point mutations and calculating pK_a values from scratch using a modeled structure. The speed-up factor scales nonlinearly with the number of titratable groups in the protein, the strength of group interaction energies, and calculation parameters. With the setup presented here, the speedup factor ranges from 10 for HEWL to ~1000 for BLI.

Finding combinations of single mutations that constitute a design solution

Design solutions are found by minimizing the score

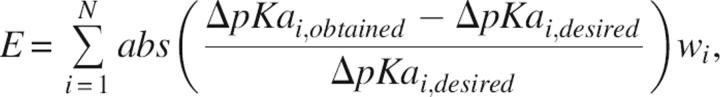where the sum is over all residues specified in the design criteria, and w _i is a user-specified weight associated with the prioritization of individual parts of the design criteria. Only point mutations that change a pK_a value at least 0.1 unit for any target group are allowed in a design solution.

Initially, we find the 20 solutions that give the lowest score by using a simple Monte Carlo search (250,000 steps) using simple addition of the ΔpK_a values from single mutations to calculate the ΔpK_a values of sets of mutations.

This simple addition of ΔpK_a values introduces inaccuracies due to the accumulated error inherent in determining pK_a values from titration curves, and we therefore recalculate the ΔpK_a values for the 20 best combinations of mutations using the same methodology as described above for calculating ΔpK_a values for single mutations. In the case of multiple mutations, we calculate titration curves at every 0.1 pH unit, and initially only in a 4 pH unit range centered on the wild-type pK_a value of the target group. This is feasible since we determine pK_a values simply by finding the pH value at which the group is half-charged. In cases where a 4 pH unit range is inadequate, we expand this range to the full 0 → 14 range.

The functionality of the pKD algorithm is available at http://enzyme.ucd.ie/pKD (Tynan-Connolly and Nielsen 2006).

Validating the accuracy of the algorithm

When designing protein pK_a values we must make sure that we can obtain solutions that are accurate, that we explore the solution space sufficiently, and that we find an optimal set of mutations.

The performance of the pK_a design algorithm depends on the accuracy with which we can calculate ΔpK_a values resulting from sets of point mutations. These ΔpK_a values are dependent not only on the accuracy of the calculated pairwise interactions between the mutated group(s) and all other titratable groups, but since ΔpK_a responses to interaction energies in some cases are nonlinear, the ΔpK_a also depends on the accuracy of the calculated pK_a values for the wild-type structure. To obtain a reliable design solution, we therefore need to address the issues of (1) errors in the calculated pK_a values of the wild-type structure, and (2) inaccuracies in calculating ΔpK_a values.

Errors in calculated pK_a values for the wild-type protein

To understand why errors in the calculated pK_a values for the wild-type enzyme are important, consider the case presented in Figure 1, where the intrinsic pK_a value plays a large role in determining the effect of an inserted group. In proteins, most groups have pK_a values that are perturbed from their solution values, and if an inserted residue is to affect the pK_a value of a target group, then the intrinsic pK_a value of the target group must be on the “correct side” of the pK_a value of the target group. If the pK_a values of the wild-type protein are calculated incorrectly (i.e., the calculated values are different from the experimental values), then the pKD algorithm might give incorrect solutions due to the effects mentioned above.

Inaccuracies in the calculation of protein pK_a values arise mainly from an inaccurate representation of the protein structures. These might be due to inaccuracies in the experimentally determined X-ray structure or from an insufficient representation of the protein dynamics. The most common source of inaccuracies in X-ray structures are due to crystal contacts, which can have a profound impact on the accuracy of calculated pK_a values (Nielsen and McCammon 2003b), but also factors such as resolution, cofactors, etc. can influence the result of the pK_a calculation. Here we use proteins that are relatively well behaved with protein pK_a calculations.

Inaccuracies in calculating ΔpK_a values

In standard pK_a calculation packages, pK_a values are determined from calculated titration curves. These titration curves are calculated by combining the effects of the local environment (captured in the intrinsic pK_a) with information on the pairwise interaction energies of titratable groups.

In a typical pK_a design calculation for Glu 35 in HEWL there are 45 positions that can be mutated to one or more residues, yielding a total of 1.2 × 10⁸ possible ways of introducing six point mutations. Clearly, it is not feasible to model each of these mutant proteins and submit them to a full pK_a calculation, and therefore, we make a number of approximations as described in the above section to speed up the process. Most significantly, we assume that the extra charge–charge interaction energies originating from a single mutation is not influenced by the presence of other mutations, and secondly, we assume that the intrinsic pK_a value of an inserted residue is independent of all other inserted residues. These assumptions hold for single mutants, but break down when the density of mutations increases so that the dielectric boundary is changed significantly (assumption no. 1) and when mutations are made close to each other (assumption no. 2).

To examine the accuracy of the ΔpK_a values calculated by the pKD algorithm, we explicitly modeled 22 sets of mutations in 2lzt and 1gci and calculated the resulting ΔpK_a by subtracting mutant from wild-type pKa values, which both were determined using a full-fledged pK_a calculation with the WHAT IF pK_a calculation package (Nielsen and Vriend 2001). We found the average difference between the ΔpK_a values from pKD and the ΔpK_a values calculated from the full pK_a calculation program to be 0.13 units (data not shown).

Validation on experimental data

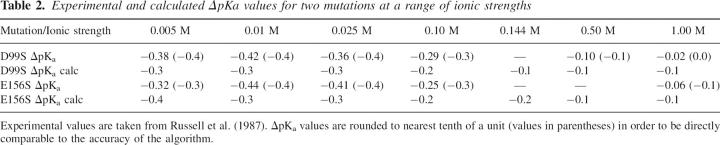
The ultimate test of the accuracy of the pKD algorithm is to compare calculated ΔpK_a values with experimentally measured ΔpK_a values. Unfortunately, little very experimental data exists on the effect of point mutations on pK_a values. We tested the performance of the pKD algorithm using the data on the point mutation D99S and E156Q in Subtilisin (Russell et al. 1987) using the PDB entry 1GNS. The results are presented in Table 2 and show a good correlation between calculated and experimentally measured ΔpK_a values for the two mutations over a range of ionic strengths. Note that the ΔpK_a calculations are accurate only to within 0.1 pH unit due to the iterative method used when calculating titration curves.

Table 2.

Experimental and calculated ΔpKa values for two mutations at a range of ionic strengths

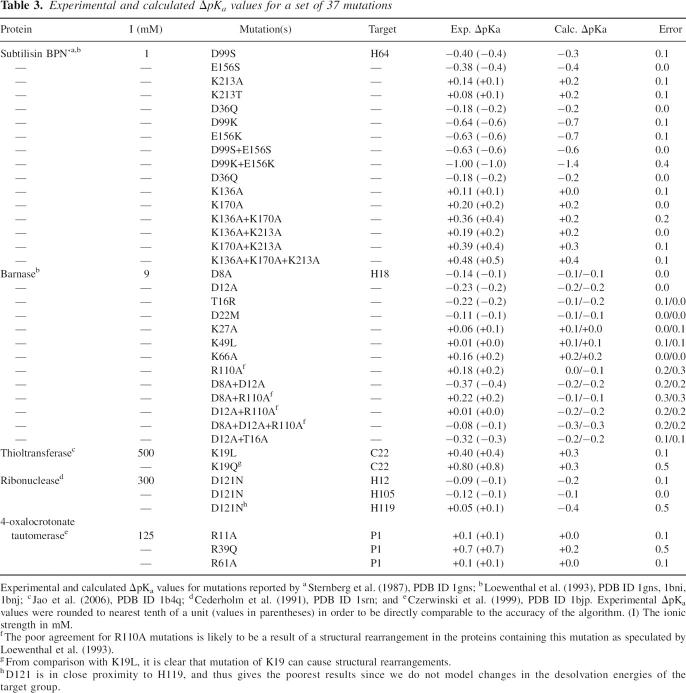
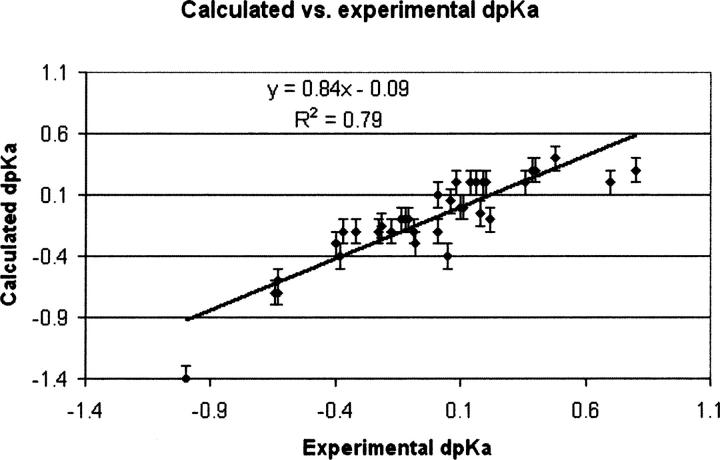
Furthermore, we validated the performance of the pKD algorithm using a set of 37 point mutations (Table 3), which clearly shows that pKD is able to reproduce experimental data with good accuracy. Figure 6 displays experimental ΔpK_a values plotted versus theoretical ΔpK_a values, and the corresponding fit showing a correlation coefficient (R²) of 0.79.

Table 3.

Experimental and calculated ΔpK_a values for a set of 37 mutations

Figure 6.

Plot of calculated ΔpK_a values vs. experimentally determined ΔpK_a values for the values shown in Table 3. The calculations are able to reproduce the experimental values reasonably well, with a R ² of 0.79.

The WHAT IF pK_a calculation package, on which the pKD algorithm depends for calculating electrostatic energies, has furthermore been validated using experimental data from site-directed mutations in separate studies (Lambeir et al. 2000; Joshi et al. 2001), and the collective data from these validation studies and the comparisons above allows us to assume that the pKD algorithm is sufficiently accurate for the purposes of this work given the limitations of current pK_a calculation methodology.

Definition of active sites

The residues constituting the active site were defined as residues that have at least one heavy atom within 5 Å of one of the catalytic residues. The catalytic residues for the individual structures were defined as: 1GCI (Subtilisin): Asp 32, His 64, Ser 221; 2LZM (T4 lysozyme): Asp 20, Glu 11; 2LZT (HEWL): Glu 35, Asp 52; 1XNB (Xylanase): Glu 78, Glu 172; 1BLI (α-amylase): Asp 231, Glu 261, Asp 328; 1QNO (β-Mannanase): Glu 169, Glu 276; 1A30 (HIV-1 protease): Asp 25(A), Asp 25(B).

Calculating the apparent dielectric of interactions

The effective dielectric constant at the ionic strength used in the calculations (0.144 M) was calculated according to the equation:

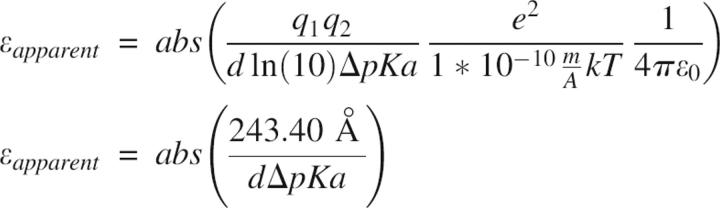where d is the distance (in Å) between charged atoms, q ₁ and q ₂ are the formal charges present on the titratable groups (−1 for acids, +1 for bases), ΔpK_a is the observed pK_a change, e is the elementary charge, k Boltzmann's constant, T the temperature (298.15K), and ɛ ₀ is the vacuum permittivity.